摘要:采用分子动力学方法研究了纳米尺度下硅(Si)基锗(Ge)结构的Si/Ge界面应力分布特征, 以及点缺陷层在应力释放过程中的作用机制. 结果表明: 在纳米尺度下, Si/Ge界面应力分布曲线与Ge尺寸密切相关, 界面应力下降速度与Ge尺寸存在近似的线性递减关系; 同时, 在Si/Ge界面处增加一个富含空位缺陷的缓冲层, 可显著改变Si/Ge界面应力分布, 在此基础上对比分析了点缺陷在纯Ge结构内部引起应力变化与缺陷密度的关系, 缺陷层的引入和缺陷密度的增加可加速界面应力的释放. 参考对Si/Ge界面结构的研究结果, 可在Si基纯Ge薄膜生长过程中引入缺陷层, 并对其结构进行设计, 降低界面应力水平, 进而降低界面处产生位错缺陷的概率, 提高Si基Ge薄膜质量, 这一思想在研究报道的Si基Ge膜低温缓冲层生长方法中初步得到了证实.
关键词: Si/Ge界面/
分子动力学/
界面应力/
缺陷层

English Abstract

全文HTML

--> --> -->

硅(Si)基异质集成技术是目前半导体发展的方向之一, 受到广泛的关注. 锗(Ge)具有优异的半导体、光学特性, 且与Si半导体工艺完全兼容, 是理想的Si基异质集成材料之一, Si基Ge材料广泛应用于Si基异质集成技术研究, 在新型电子器件、光电集成等领域得到了广泛关注^[1?15]. 与Si材料相比, Ge具有高载流子迁移率、窄禁带宽度等众多优势. 高载流子迁移率可使Ge应用于提升场效应晶体管(FET)性能, 而窄禁带宽度使Ge具有良好的光电子特性, 可应用于1.30—1.55 μm波长激光的探测器制备. 此外, 在常温下, Ge与砷化镓的晶格失配只有0.07%, 因此可作为Si基上生长砷化镓薄膜材料的衬底, 从而实现Si基砷化镓光电器件的集成^[16].
然而, Ge与Si具有很大的晶格失配(达到4.2%)和热失配, 导致Si基Ge薄膜材料一般具有很高的穿透位错密度和表面粗糙度, 不利于器件制备, 且会严重降低器件性能. 为了在Si基上生长高质量的Ge薄膜, 研究人员开发了多种工艺方法来降低位错密度和表面粗糙度, 比如: 渐变缓冲层方法^[17,18]、选区外延方法^[19,20]、低温缓冲层方法以及高低温两步生长方法^[21?29]. 到目前为止, 高低温两步生长方法结合循环退火工艺是最常用的Si基Ge薄膜生长方法. 该方法中低温层一般采用Ge或者Ge-Si材料, 通过这种方法可以制备出位错密度低至1×10⁶ cm^?2, 表面粗糙度小于1 nm的Si基Ge薄膜^[28,29].
在微观层面, 科研人员在高低温两步生长方法制备的Si基Ge薄膜材料的低温层中观察到了大量的点缺陷^[25,30?32], 由此推断低温层中存在的大量点缺陷可以与位错进行作用, 吸收Ge与Si之间的失配应力能量, 降低Si和Ge之间的应力, 从而减小穿透位错密度. 但少有研究低温层对位错密度影响的理论证据, 以及失配应力受低温层的影响机制. 本文从应力角度入手, 针对低温缺陷层对Si/Ge界面失配应力影响机制开展研究, 希望能从应力层面揭示低温缓冲方法的作用本质. 基于这种思想, 采用分子动力学模拟方法, 从原子尺度上研究Si/Ge界面结构特征及应力特性, 从而揭示Si/Ge界面应力在缺陷层存在时的应力释放机制, 在此基础上建立异质材料界面应力释放模型, 为Si基异质材料生长工艺优化提供参考. 本文采用分子动力学方法模拟了不同尺度、不同缺陷密度条件下的Si和Ge界面体系应力分布, 研究了在微观下体系尺寸和缺陷密度对Si/Ge界面应力的影响规律.

采用由Tersoff^[33]提出的Si, Ge体系经验势函数(简称Tersoff势函数)进行模拟. 该势函数广泛应用于模拟研究Si, Ge材料的分子结构及热力学特性, 模拟结果与实际相符^[34?37].
Tersoff势函数重写为如下形式:

$\left\{\!\!\begin{aligned}& \varPhi = \sum\limits_i {{\varPhi _i} = \frac{1}{2}\sum\limits_{i \ne j} {{V_{ij}}} } ,\\& {V_{ij}} = {f_C}({r_{ij}})[{f_R}({r_{ij}}) + {b_{ij}}{f_A}({r_{ij}})],\\& {f_R}({r_{ij}}) = {A_{ij}}\exp ( - {\lambda _{ij}}{r_{ij}}),\\& {f_A}({r_{ij}}) = - {B_{ij}}\exp ( - {\mu _{ij}}{r_{ij}}),\\& {f_C}({r_{ij}}) = \left\{ \begin{aligned}& 1,{r_{ij}} < {R_{ij}},\\& \frac{1}{2} + \frac{1}{2}\cos [{\rm{\pi }}\frac{{{r_{ij}} - {R_{ij}}}}{{{S_{ij}} - {R_{ij}}}}],{R_{ij}} < {r_{ij}} < {S_{ij}},\\& 0,{r_{ij}} > {S_{ij}},\end{aligned} \right.\\& {b_{ij}} = {\chi _{ij}}{(1 + {\beta _i}^{{n_i}}{\zeta _{ij}}^{{n_i}})^{ - \frac{1}{2}{n_i}}},\\& {\zeta _{ij}} = \sum\limits_{k = i,j} {{f_C}({r_{ik}}){\omega _{ik}}g({\theta _{ijk}})} ,\\& g({\theta _{ijk}}) = 1 + \frac{{{c_i}^2}}{{{d_i}^2}} - \frac{{{c_i}^2}}{{{d_i}^2 + {{({h_i} - \cos {\theta _{ijk}})}^2}}},\\& {\lambda _{ij}} = \frac{{{\lambda _i} + {\lambda _j}}}{2},{\mu _{ij}} = \frac{{{\mu _i} + {\mu _j}}}{2},{A_{ij}} = \sqrt {{A_i}{A_j}},\\& {{B_{ij}} = \sqrt {{B_i}{B_j}} ,{R_{ij}} = \sqrt {{R_i}{R_j}} ,{S_{ij}} = \sqrt {{S_i}{S_j}} },\end{aligned}\right.$

式中Φ为原子势能; 下标i, j和k为原子序号; ${r_{ij}}$为原子间距; θ_ijk为原子键角; 其他参数如表1所列, 1 ? = 0.1 nm.
本文所涉及的所有分子动力学模拟过程均采用Lammps软件包^[38]进行. 模拟过程如下.

参数	Si	Ge
A/eV	1.8308×103	1.769×103
B/eV	4.7118×102	4.1923×102
λ/??1	2.4799	2.4451
μ/??1	1.7322	1.7047
β	1.1000×10?6	9.0166×10?7
n	7.8734×10?1	7.5627×10?1
c	1.0039×105	1.0643×105
d	1.6217×101	1.5652×101
h	?5.9825×10?1	?4.3884×10?1
R/?	2.7	2.8
S/?	3.0	3.1
注: ${\chi _{{\rm Si} -{\rm Ge}}} = 1.00061$.

表1Tersoff势函数参数^[33]
Table1.Parameters of Tersoff potential function^[33].

1) 建立包含Si/Ge界面结构的无缺陷一维简化界面模型, 如图1所示. 体系x-y方向采用周期性边界条件, z方向采用自然边界条件. 模拟过程中: 体系Si层x-y平面尺寸d_Si = 217 ?, 满足周期性边界条件; 为了克服Si和Ge之间的晶格失配对模型的影响, Ge层在x-y方向采用自然边界条件, 同时增加一个真空层, 达到与Si层相同的尺寸, 真空层的厚度要大于20 ?, 从而可以采用相同的周期性边界条件. Ge层x-y方向尺寸分别为60, 100, 140和190 ?, 其他区域为真空层; z方向尺寸为200 ?, 其中衬底Si厚度L_Si = 80 ?, Ge厚度L_Ge = 120 ?.
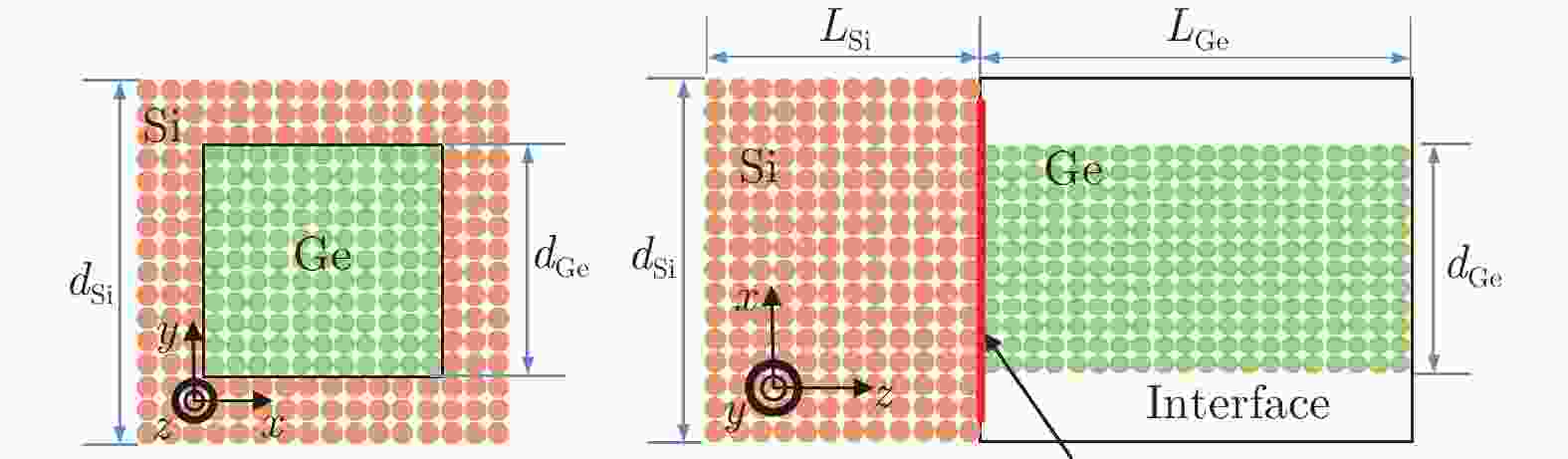图 1 Si/Ge界面模拟示意图
Figure1. Schematic diagram of simulation of Si/Ge interface.

2) 对体系进行充分弛豫, 弛豫过程为: 先升温到1100 K, 在1100 K下弛豫800 ps (1 ps = 10^?12 s); 再降温到300 K, 并在300 K下弛豫500 ps; 获得接近平衡态的体系, 计算Si/Ge界面两边的应力分布. 应力计算方法^[39]为: 以Si/Ge界面为零点, 10 ?为间隔, 将整个体系z方向分成若干方块, 如图2所示, 计算每一个方块内的平均应力, 以此作为该方块中心处的应力值, 分析体系在z方向的应力分布.
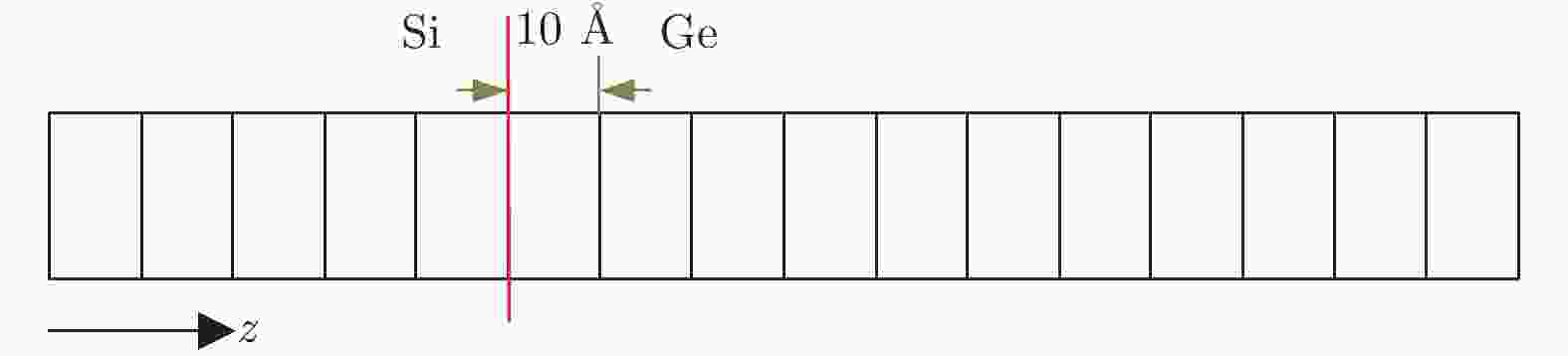图 2 Si和Ge体系应力计算示意图
Figure2. Diagram of stress calculation of Si and Ge system.

3) 改变Ge在x-y方向的尺寸, 重复以上步骤, 对比Ge尺寸对Si/Ge界面应力的影响.
4) 在Si和Ge材料之间引入缺陷层(Ge), 充分弛豫后计算界面应力变化, 分析缺陷层对Si/Ge界面应力释放过程的影响机制.
在模拟过程中, Ge在x-y方向的尺寸(d_Ge)分别为60, 100, 140和190 ?, 引入的点缺陷密度分别为0.5×10²¹, 1.0×10²¹, 2.0×10²¹和3.0×10²¹ cm^?3. 模拟过程中体系温度由Berendsen热浴法控制, 模拟时间步长取为1.0 fs (1 fs = 10^?15 s).

2

-->

3.1.Ge尺寸对Si/Ge界面应力分布的影响

首先对不同Ge尺寸下的Si/Ge界面应力分布进行分析, 结果如图3所示. 从图3可以看出, 应力随着远离界面而迅速降低, 表明Si/Ge界面应力主要集中在界面附近.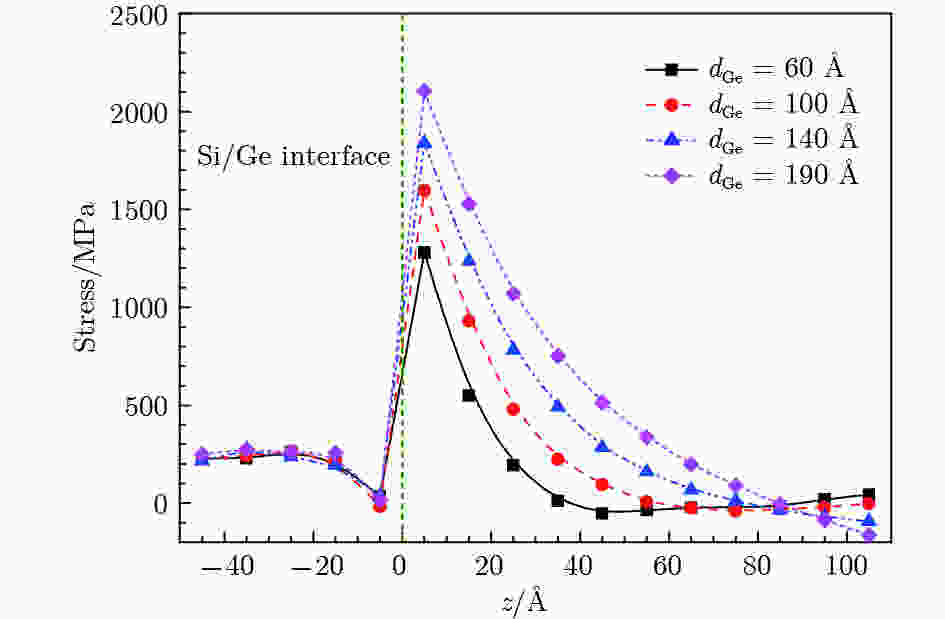
图 3 不同Ge尺寸下Si/Ge界面应力的变化
Figure3. Variation of stress at Si/Ge interface under different sizes of Ge.

为获取Ge尺寸对Si/Ge界面应力下降速度的影响规律, 计算了不同Ge尺寸下, 应力下降到200 MPa (与模型中衬底Si的应力相当)的位置与界面的间距(L_Gstress), 结果如图4所示. 从图4结果可以看出, 应力下降到200 MPa的位置与界面的间距与Ge尺寸具有近似线性递增的关系, Ge尺寸越小, 越有利于界面应力的快速释放. 随着Ge尺寸的增加, Si/Ge界面应力释放速度迅速降低.
产生这一现象的内在原因是Ge在小尺寸下界面应力的释放机制. 在一维界面模型中, Ge利用边界扩展的机制来释放失配应力, 应力释放速度与边界总长度呈正比. 而界面的总应力与界面原子失配程度以及界面的面积有关, 在原子类别一定时, 界面面积越大, 界面总应力越大. 界面应力从峰值下降到200 MPa的距离与界面总应力以及应力释放速度密切相关, 总应力越大, 应力释放需要的距离越大, 而应力释放速度越大, 应力释放需要的距离越小, 如(2)式所示:

${L_{{\rm{Gstress}}}}{\rm{ = }}A\frac{{{F_{{\rm{total}}}}}}{{{V_{{\rm{Stress}}}}}}, $

式中L_Gstress为应力下降到200 MPa需要的距离; 在一维界面模型中A近似为一个常数; F_total为Si/Ge界面总应力; V_Stress为应力释放速度. F_total与Si/Ge界面面积成正比, V_Stress与Si/Ge界面周长成正比, 而在一维界面模型下界面面积与周长的比值与Ge尺寸成正比, 由此推导L_Gstress与Ge尺寸成正相关, 这与图4所示的计算结果一致.
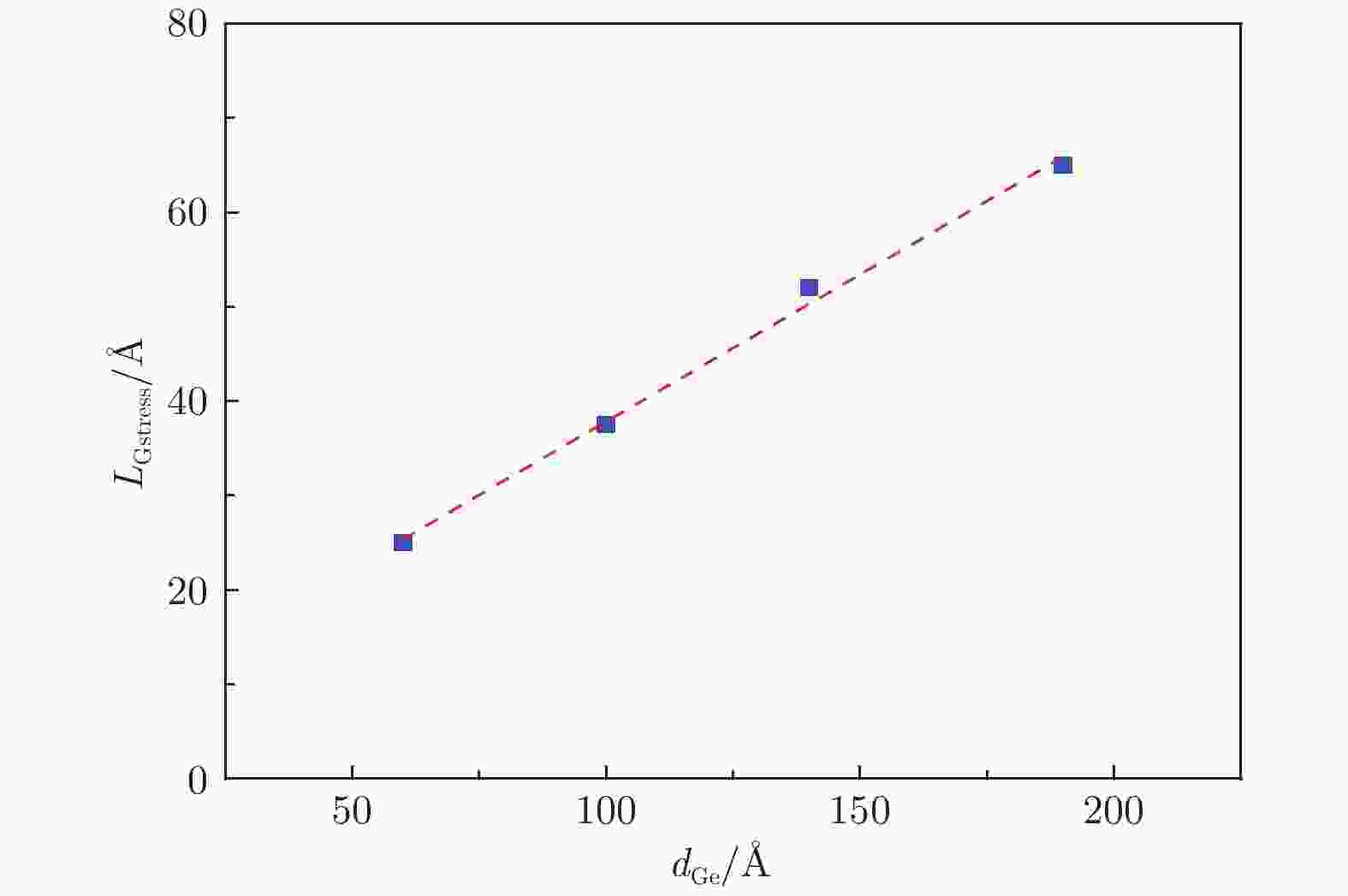图 4 应力下降到200 MPa的位置与界面间距L_Gstress与Ge尺寸的关系
Figure4. Relationship between distance L_Gstress and Ge when stress is relaxed to 200 MPa.

2 -->

3.2.缺陷缓冲层存在下的Si/Ge界面应力释放机制

为了研究缺陷缓冲层在Si/Ge界面应力释放过程中的作用机制, 在上述模型基础上, 固定Ge尺寸为100 ?, 在Si/Ge界面引入不同缺陷密度的缓冲层, 研究缺陷密度对界面应力的影响.
引入缺陷层后的界面应力分布如图5所示. 从图5可以看出, 缺陷层中的应力水平显著降低, 缺陷的存在可以有效释放Si/Ge界面应力; 随着缓冲层缺陷密度的增加, 应力降低程度越明显. 同时观察到Ge中没有缺陷的区域, 应力有一定程度的增加, 这与缺陷层在Ge内部形成的新的缺陷界面有关.
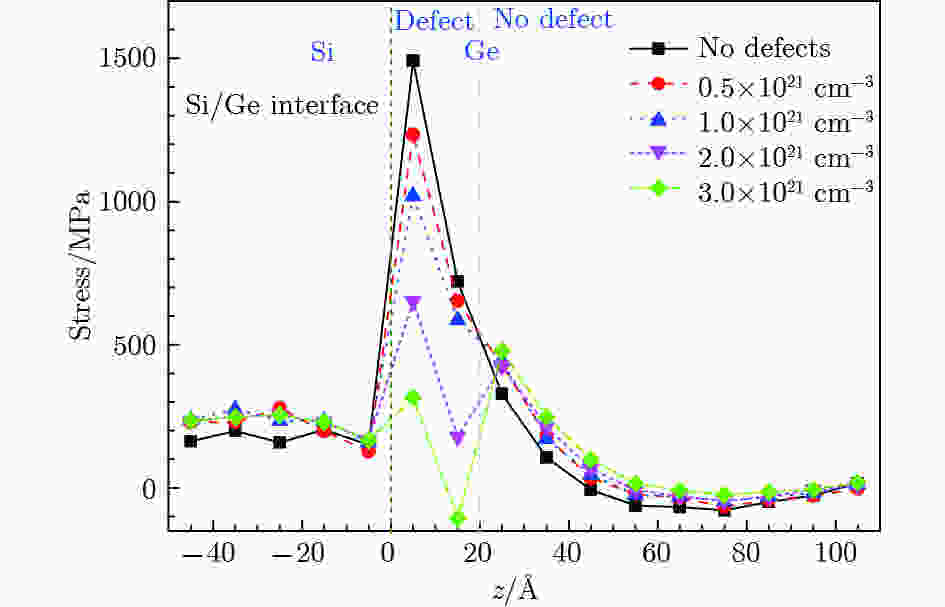图 5 缓冲层缺陷密度对Si/Ge界面应力的影响
Figure5. Effect of different point defect density on stress at Si/Ge interface in buffer layer.

为了进一步分析缺陷在Si/Ge界面应力释放过程中的作用机制, 采用x-y方向尺寸为100 ?的周期性Ge材料模型, 并在内部引入厚度为20 ?的缺陷层, 缺陷密度分别为0.5 × 10²¹, 1.0×10²¹, 2.0 × 10²¹和3.0×10²¹ cm^?3. 采用与第2节相同的弛豫过程, 对Ge体系进行充分弛豫, 计算其z方向应力分布, 结果如图6所示. 缺陷在Ge体系内部引入了压应力, 并且随着缺陷密度越高, 引入的压应力越大, 这也证实在Si基Ge结构中, 缺陷层是降低界面应力的主要机制.
图 6 不同密度的空位缺陷对应力的影响规律
Figure6. Effect of different point defect density on the stress.

从图5和图6的结果均可以看出, 缺陷的引入使得界面应力发生变化, 且缺陷密度对界面应力有较大的影响. 为了更深入分析Ge缺陷密度对Si/Ge界面应力的影响, 计算在不同缺陷密度条件下界面应力差, 同时计算了单独缺陷存在时Ge内部产生的应力差, 结果如图7所示. 当缺陷密度小于1.0 × 10²¹ cm^?3时, Si/Ge界面应力差与缺陷密度存在比较好的线性递减关系, 随着缺陷密度的继续增加, 应力下降速度降低. 同时可以看到, 在只有缺陷存在时, Ge内部应力差与缺陷密度呈近似线性递减, 且当下降的速度与缺陷密度小于1.0 ×10²¹ cm^?3时, 下降速度相当. 由此可以推断, 当缺陷密度小于1.0 × 10²¹ cm^?3时, 缺陷密度产生的应力变化起主要作用, 当缺陷密度进一步增大时, 存在其他的机制抵消了一部分缺陷产生的应力变化, 使得随缺陷密度增加, 应力下降速度降低.
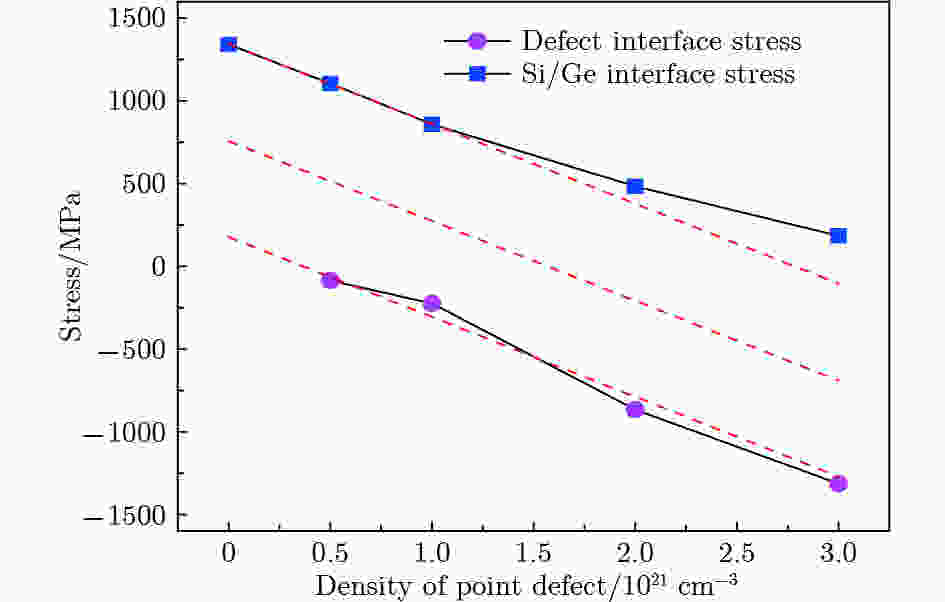图 7 Si/Ge界面应力差及单缺陷产生的应力差与缺陷密度的关系
Figure7. Relationship of the Si/Ge interface stress difference and the single defect interface stress difference with the defect density.

综上所述, 在Si/Ge界面处增加缺陷缓冲层可以有效降低界面应力, 且在高缺陷密度下存在额外的机制延缓了界面应力的释放, 缺陷层的引入是Si/Ge界面应力释放的一种有效途径. 参考这一结果, 可以通过对缺陷缓冲层的缺陷密度进行优化设计, 整体降低界面应力, 减小位错缺陷产生的概率, 从而达到提升Si基Ge薄膜质量, 这对Si基Ge薄膜生长工艺的设计与优化具有重要参考意义.

采用分子动力学方法研究并初步揭示了Si基Ge结构Si/Ge界面应力分布特征, 以及在缺陷缓冲层存在下的应力释放机制. 结果表明: 在纳米尺度下, Si/Ge界面应力分布曲线与Ge尺寸密切相关, 界面应力下降速度与Ge尺寸存在近似的线性递减关系; 同时, 在Si和Ge界面处增加一个富含空位缺陷的缓冲层, 可显著改变Si/Ge界面应力分布. 在此基础上对比分析了点缺陷在纯Ge结构内部引起应力变化与缺陷密度的关系, 缺陷层的引入和缺陷密度的增加可加速界面应力的释放, 其内在机理为: 缺陷引入压应力, 可在一定程度上抵消Si/Ge界面因晶格失配产生的张应力, 从而达到降低界面应力的效果; 且随着缺陷密度的增加, 引入的压应力越大, 界面应力降低值越大. 根据缺陷缓冲层缺陷密度对界面应力的影响, 初步解释了在缺陷缓冲层存在下Si/Ge界面应力的释放机制. 基于以上研究结果, 可通过在Si基Ge薄膜生长过程中引入缺陷层, 并对缺陷缓冲层的缺陷密度等参数进行设计优化, 降低界面应力水平, 减小Si/Ge界面处因大应力产生位错缺陷的概率, 从而提高Si基Ge薄膜质量, 这一思想在Si基Ge膜的低温缓冲层生长方法中得到了验证. 本文的研究结果对于Si基Ge材料生长工艺的开发具有指导意义, 同时对于异质材料生长技术的研究也具有一定参考价值.