摘要: 基于运动学理论、感应电流定理和电荷守恒定律, 分析了分布作用谐振腔的渡越时间效应, 推导了各个谐振腔工作于
${\text{π}}$ 模的电子注与微波之间的能量转换系数、电子负载电导和电子负载电纳, 计算结果显示采用分布作用谐振腔有利于提高速调管的工作效率. 利用三维电磁仿真软件, 设计了一款工作于W波段的分布作用速调管. 完成了速调管的加工和封接, 搭建了测试平台, 开展了相关实验研究. 实验结果显示, 当电子注电压20.8 kV, 电流0.3 A, 输入功率30 mW时, 在中心频率95.37 GHz处, 得到了175 W峰值脉冲输出功率, 电子效率2.8%, 增益34.6 dB, 3 dB带宽大于90 MHz.
关键词: W波段 /
分布作用速调管 /
渡越时间效应 /
电子负载 English Abstract Design and experimental analysis of W-band extended interaction klystron amplifier Zeng Zao-Jin Hu Lin-Lin Ma Qiao-Sheng Jiang Yi Chen Hong-Bin Institute of Applied Electronics, Chinese Academy of Engineering Physics, Mianyang 621900, China Received Date: 13 December 2018Accepted Date: 09 January 2019Available Online: 01 April 2019Published Online: 20 April 2019Abstract: Beam loading is an important parameter in extended interaction klystron, which can be used to analyze the influence of beam on resonant frequency and ohm loss Q , and study the match condition between input cavity and external power source, etc. Based on the kinematical theory, law of induce current, principle of charge conservation under the small signal condition, and one-dimensional (1D) mode, the transit time effect of electron in ${\text{π}}$ mode standing wave electric treld in a multiple-gap resonator is analyzed, and the expressions of electron load conductance and electron load susceptance in the multiple-gap resonator are presented. The results show that the electron load conductance of extended interaction cavity can change in a bigger extension than that of traditional single gap cavity, which means that the loaded Q of extended interaction cavity can be adjusted in a bigger extension to realize a desired Q . And the results also show that the electron load susceptance of extended interaction cavity can change in a bigger extension than that of traditional single gap cavity, which means that the loaded frequency of extended interaction cavity can also be easily adjusted to a desired value. The influence of gap number on the power exchange between beam and microwave is also investigated, which shows that the maximum power exchange between beam and microwave electric field increases with the number of resonator gaps increasing, and so does the efficiency of klystron. A W band extended interaction klystron amplifoer is designed by the above theory analysis and three-dimensional (3D) PIC code. The simulation results show that when beam voltage is 20.8 kV, current is 0.28 A, input power is 30 mW at a frequency of 94.77 GHz, the extended interaction klystron can produce 443 W output power. The responding electron efficiency is 7.6%, the gain is 41.7 dB, and the 3 dB bandwidth exceeds 150 MHz. The extended interaction klystron is machined and tested, and the experimental results show that the maximum output power of 175 W is obtained with a beam of 300 mA, a voltage of 20.8 kV, and an input microwave power of 30 mW at a frequency of 95.37 GHz in a magnetic field of 0.62 T. The responding electron efficiency is 2.8%, the gain is 34.6 dB, the 3-dB bandwidth exceeds 90 MHz. This study is meaningful for designing and developing greater power extended interaction klystrons.Keywords: W-band /extended interaction klystron /transit-time effect /beam loading 全文HTML --> --> --> 1.引 言 在云雨测量雷达、地球物理探测、空间碎片探测等领域的应用需求引导下, 微波源的频率正渐渐往毫米波段发展[1 ] . 其中W波段属于毫米波段的一个大气窗口, 目前已在通信、雷达等领域得到了广泛应用[2 -4 ] . 在W波段, 固态器件在输出功率方面受到限制, 在系统要求大功率微波源时, 主要采用电真空器件. 因此, 小型化、轻量化的大功率毫米波电真空器件是重点研究的方向[5 , 6 ] .[7 ] . 分布作用速调管单位长度的高增益使得高频结构比传统速调管短, 因此分布作用速调管比传统速调管更加小型化、轻量化, 具有广阔的应用前景, 特别适合在毫米波、亚毫米波段工作[2 ] . 分布作用速调管高频结构是由数个多间隙谐振腔组成的[2 ] . 多间隙谐振腔是一个比单间隙复杂得多的振荡系统, 直观上看, 多间隙谐振腔等效于将一小段行波管慢波结构截断而成的谐振腔. 它兼具速调管和行波管的优点, 是两者性能妥协的产物.[8 ] . 在脉冲峰值功率方面, CPI研制了中心频率95 GHz、脉冲峰值功率3000 W的分布作用速调管[9 ] . 在平均功率方面, CPI研制了在94.94 GHz处平均功率大于400 W的分布作用速调管, 其工作电压16.6 kV, 电流617 mA, 工作占空比27%, 脉宽$12\;{\text{μ}}{\rm{s}}$ , 输入功率4 mW[10 ] . 国内研究W波段分布作用速调管的主要有中国工程物理研究院、中国科学院电子学研究所、北京真空电子技术研究所和电子科技大学等单位. 其中, 北京真空电子技术研究所在2018年报道了其研制的W波段分布作用速调管, 脉冲峰值功率为1.5 kW, 3 dB带宽为800 MHz, 是目前国内最高水平[11 ] .[6 , 12 -15 ] , 但是这些结果只能表征电子注的引入对谐振腔损耗的影响. 无法分析电子的引入对谐振腔谐振频率的影响. 本文基于运动学理论、感应电流定理和电荷守恒定律, 研究电子注在多间隙谐振腔${\text{π}}$ 模场中的渡越时间效应, 推导多间隙谐振腔的电子负载电导和电子负载电纳的表达式, 分析间隙数对电子注渡越时间效应和电子注与微波之间能量交换的影响, 然后分析电子注的引入对谐振腔损耗的影响, 最后分析电子注的引入对谐振腔谐振频率的影响. 根据理论分析结果, 设计工作于W波段的分布作用速调管, 并完成速调管的加工和封接, 最后搭建测试平台, 开展相关实验研究. 实验结果显示, 当电子注电压20.8 kV, 电流0.3 A, 输入功率30 mW, 轴向引导磁感应强度0.62 T时, 在中心频率95.37 GHz处, 得到了175 W峰值脉冲输出功率, 电子效率2.8%, 增益34.6 dB, 3 dB带宽大于90 MHz.2.多间隙谐振腔电子负载的理论分析 电子负载是表征电子注对谐振腔中微波场的影响的参量. 电子负载的计算对于速调管的设计极为重要[16 ] , 根据电子负载可以分析电子注对谐振腔中微波损耗的影响、电子注对谐振腔中微波谐振频率的影响、工作模式和非工作模式振荡发生的条件, 确定输入腔与标准波导之间的耦合孔大小等. 电子负载主要由两部分组成: 一部分是电子注和高频场之间实际交换的功率, 这部分功率属于有功功率, 用电子负载电导G b 表征; 另一部分是电子注在微波场正半周吸收能量, 在微波场负半周释放能量, 即吸收无功功率, 这部分能量影响谐振腔的谐振频率, 用电子负载电纳B b 表征[17 ] . 电子导纳中存在的有功分量证明, 谐振腔的一部分高频能量, 消耗在飞越间隙的电子的动能的改变上. 由于这个导纳, 使谐振腔的等效衰减增加. 电子导纳的无功分量使谐振频率改变, 这种改变是相较于没有电子注时的谐振频率. 如果将谐振腔等效为一个并联谐振腔, 如图1 所示. 那么引入电子注后谐振腔可以等效为如图2 所示的电路模型.图 1 谐振腔等效电路Figure1. Equivalent circuit mode of cavity.图 2 引入电子注后谐振腔等效电路Figure2. Equivalent circuit mode of cavity with beam.${\text{π}}$ 模的N 间隙谐振腔中的电场分布可近似用图3 表示. 设定第一个间隙的入口处坐标为0, 那么电子在N 间隙谐振腔中第n (n =$1,2,\cdots,N $ )间隙感受到的电场可表示为图 3 多间隙谐振腔${\text{π}}$ 模场示意图Figure3. E -field of ${\text{π}}$ mode in multiple-gap cavity.E m 为间隙电场幅值; $\omega = 2{\text{π}}f$ , f 为谐振腔的谐振频率; ν 0 为电子的初始速度; d 为间隙宽度; L 为相邻间隙的距离. 由于漂移管中没有电场, 电子在漂移管中做自由运动速度不会发生改变. 由感应电流定理可知, 感应电流与电场有关, 所以电子在漂移管中运动不会产生感应电流, 而电子负载由感应电流确定, 因此计算电子负载只需要计算间隙中产生的感应电流即可. 为了简化分析, 可以忽略电子在漂移管中的运动过程, 这对电子负载的计算是没有影响的. 对于工作于${\text{π}}$ 模的N 间隙谐振腔, 当电子进入某一个间隙时, 相邻间隙电场与此间隙电场相位相差${\text{π}}$ , 如果选择周期L 使电子在两个间隙之间的渡越角为${\text{π}}$ , 那么电子在每一个间隙中感受到的电场相同. 忽略电子在漂移管中的运动状态, 电子在N 间隙谐振腔中第n (n =$1,2,\cdots, N $ )间隙感受到的电场可表示为(如图4 所示)图 4 多间隙谐振腔${\text{π}}$ 模场简化图Figure4. Simplified E-field of ${\text{π}}$ mode in multiple-gap cavity.2.1.单间隙谐振腔电子负载的理论分析 2.1.单间隙谐振腔电子负载的理论分析 在大信号条件下, 由文献[18 ]可知, 电子在间隙中的速度和电流都是由超越方程确定的, 不能同小信号条件下一样得到近似的解析表达式, 而电子负载与电子在间隙中的速度和电流有关, 因此电子负载很难得到解析表达式. 本文主要基于小信号假设对电子负载进行理论分析. 假设电子电压为U 0 , 电流为I 0 , 间隙电压幅值为U m = E m d , 电子进入间隙入口处的时间为t 0 . 电子在间隙中的运动方程为m 和e 分别为电子的质量和电荷量.t = t 0 时, z (t 0 ) = 0, ν (t 0 )=ν 0 , 同时$\dfrac{1}{2}m\nu _0^2 = e{U_0}$ , 可得α = U m /U 0 为间隙电压与直流电压的比值, θ 0 = ωd/ν 0 为电子通过间隙的直流渡越角.t 到达间隙某一处时, 电子的实际渡越角与直流渡越角之间相差一个微小量δ , 即φ 0 为电子进入单间隙谐振腔时电场的相位, φ 为t 时刻电场的相位, θ 1 = ωz/ν 0 .4 )式两边乘以ω/ν 0 , 并采用近似式cosδ ≈ 1, sinδ ≈ δ , 同时因为α , δ 均是极小量, 忽略它们的二次及以上多次项, 可得τ 1 为电子注离开单间隙谐振腔的时间, 结合(5 )式和(6 )式可得电子通过单间隙谐振腔的实际渡越角与直流渡越角之间的差值δ 1 为[11 ] , 可得6 )式代入(9 )式, 可得10 )式可以确定每一处的对流电流, 根据感应电流定理, 当间隙中电场是均匀场时, 总的感应电流是间隙内对流电流交变分量对间隙宽度的平均值[11 ] :${\\tilde i_1}\left( {{\theta _1},t} \right)$ 为${i_1}\left( {{\theta _1},t} \right)$ 的交变分量.${\text{π}}/2$ 的部分分别对应电子负载电导G b 和电子负载电纳B b , 可得2.2.双间隙谐振腔电子负载的理论分析 -->2.2.双间隙谐振腔电子负载的理论分析 下面分析电子在双间隙谐振腔中电子负载表达式. 对于两间隙谐振腔, 电子注在第一个间隙中的运动情况与单间隙谐振腔中相同. 在第二个间隙中, 电子的运动方程为t = τ 1 时, z (τ 1 ) = d , 结合(8 )式, 可得t 到达双间隙谐振腔第二间隙中某一处时, 电子在第二个间隙中实际渡越角与直流渡越角之间相差一个微小量ξ 2,2 , 即φ 1 为电子进入双间隙谐振腔第二个间隙时的电场相位, θ 2 = ω (z – d )/ν 0 .16 )式两边乘以ω/ν 0 , 采用近似式cosξ 2,2 ≈ 1, sinξ 2,2 ≈ ξ 2,2 , 同时因为α , ξ 2,2 均是极小量, 忽略它们的二次及以上多次项, 可得τ 2 为电子离开双间隙谐振腔的时间, 由(17 )式和(18 )式可得电子通过双间隙谐振腔第二个间隙的实际渡越角与直流渡越角之间的差值ξ 2 为δ 2 为$\omega(\tau_2 - t_0) =2\theta +\delta_2 $ 代入(15 )式, 可得电子离开双间隙谐振腔的归一化电子速度为10 )式和(18 )式代入(22 )式, 可得${\tilde i_2}\left( {{\theta _2},t} \right)$ 为${i_2}\left( {{\theta _2},t} \right)$ 的交变分量.2.3.N 间隙谐振腔电子负载的理论分析 -->2.3.N 间隙谐振腔电子负载的理论分析 根据单间隙谐振腔和双间隙谐振腔中电子负载电导和电子负载电纳的表达式, 猜想它们可能具有通用表达式. 根据数学归纳法, 假设对于间隙数1 ≤ n ≤ N – 1的谐振腔, 相关参数具有如 (29 )—(35 )式的表达式.t 到达n 间隙谐振腔第n 个间隙中某一处时, 电子在第n 个间隙中的实际渡越角与直流渡越角之间相差一个微小量ξ n , n τ n –1n – 1间隙谐振腔的时间.n 间隙谐振腔的实际渡越角与直流渡越角之间的差值δn 为n 间隙谐振腔的归一化电子速度为τn 为电子离开n 间隙谐振腔的时间.n 间隙谐振腔的感应电流为n 隙谐振腔的归一化电子负载电导和归一化电子负载电纳为n = 1, 2)的推导结果, 各种参数满足上述表达式.N 间隙谐振腔, 电子在N 间隙谐振腔的前N – 1个间隙中的运动状态与N – 1间隙谐振腔相同. 在第N 个间隙中, 电子的运动方程为t 到达N 间隙谐振腔的第N 个间隙中某一处时, 电子在第N 个间隙中的实际渡越角与直流渡越角之间相差一个微小量ξ N , N φN –1 为电子进入N 间隙谐振腔第N 个间隙时的电场相位, θN = ω [ z – (N – 1)d ]/ν 0 .N 间隙谐振腔的第N 个间隙的实际渡越角与直流渡越角之间的差值ξN 为N 间隙谐振腔的实际渡越角与直流渡越角之间的差值δN 为N 间隙谐振腔的归一化电子速度为τN 为电子离开N 间隙谐振腔的时间.N 个间隙中的对流电流为6 )式、(30 )式和(38 )式代入(42 )式, 同时由于α , δ , $\xi_{2,2},\;\xi_{3,3},\; \cdots, \xi_{N,N}$ 均是极小量, 忽略它们的二次及以上多次项, 可得N 间隙谐振腔的第N 个间隙的感应电流为${\\tilde i_N}\left( {{\theta _N},t} \right)$ 为${i_N}\left( {{\theta _N},t} \right)$ 的交变分量.N 间隙谐振腔的总感应电流为N 间隙谐振腔的归一化电子负载电导和归一化电子负载电纳为46 )式和(47 )式为N 间隙谐振腔电子负载电导和电子负载电纳的通用表达式.N 间隙谐振腔高频场之间交换的能量为G bN /G 0 和归一化电子负载电纳B bN /G 0 与间隙渡越角θ 0 之间的关系如图5 和图6 所示. 由图5 可知, 间隙数越多, 电子注能从微波场吸收的功率极值越大, 这表示间隙数的增加有利于电子注与微波之间的能量交换.图 5 归一化电子负载电导与渡越角的关系Figure5. G bN /G 0 versus θ 0 of multiple-gap cavity.图 6 归一化电子负载电纳与渡越角的关系Figure6. B bN /G 0 versus θ 0 of multiple-gap cavity.[19 ] Q 0 表征谐振腔的固有损耗, Q b 表征电子注引起的损耗, Q ext 表征由耦合孔等引起的损耗. 电子注引起的损耗Q b 为[18 ] R /Q 表征谐振腔的特征阻抗.Q total > 0时, 表示谐振腔内总的能量随着时间减小, 谐振腔不会发生振荡. 当Q total < 0时, 表示谐振腔内总的能量随着时间增加, 谐振腔发生振荡.图5 可以看出, 电子负载电导G bN 为正值时, 表示电子注从微波场中吸收能量, 此时微波场中能量不但被电子注吸收能量, 同时还被腔壁损耗掉, Q total > 0, 不会发生自激振荡. 当电子负载电导G b n Q total < 0, 则会发生自激振荡, 反之不会产生自激振荡. 在设计速调管振荡器时, 需要使谐振腔工作于负电导区, 以形成自激振荡.B bN 为正值时, 电子注对于谐振腔而言呈电容性, 图2 的电路模型可以等效为图7 所示电路模型. 此时谐振腔的谐振频率f 为51 )式可知, 当电子电纳B bN 为正值时, 电子注的引入使得谐振腔频率降低.B bN 为负值时, 电子注对于谐振腔而言呈电感性, 图2 的电路模型可以等效为图8 所示电路模型. 此时谐振腔的谐振频率f 为52 )式可知, 当电子电纳B bN 为负值时, 电子注的引入使得谐振腔频率降低.图 7 B bN 为正值谐振腔等效电路Figure7. Equivalent circuit mode of cavity when B bN > 0.图 8 B bN 为负值时谐振腔等效电路Figure8. Equivalent circuit mode of cavity when B bN < 0.图6 和上述分析可知, 谐振腔间隙数越多, 谐振腔加载电子注后的谐振频率能够在更大范围内变化. 上述公式推导是一维模型的前提下进行的, 然而在实际谐振腔中电场不仅沿纵向变化, 而且沿横向也在变化, 因此理论推导只能得到有限制条件的近似结果. 推导过程中基于小信号条件假设才得到了上述简明的解析表达式, 所以对于谐振腔是否会发生工作模式的自激振荡和非工作模式的振荡的计算只有在注波互作用开始的阶段比较准确. 但是, 小信号理论和一维模型表征的基本规律是正确的, 可以作为分布作用速调管初始设计的指导依据.3.分布作用速调管高频结构仿真设计 高频结构是扩展互作用速调管中束波能量交换的场所, 它设计的好坏决定了管子的带宽和功率水平. 高频结构尺寸多, 影响参数复杂, 各个参数间又相互联系, 不能单独追求某一项性能, 必须综合考虑, 合理设计[17 ] . 设定电子注电压20.8 kV, 电流300 mA, 输入微波功率30 mW, 中心频率为94.8 GHz. 多间隙谐振腔最核心的尺寸, 即间隙渡越角θ 0 初值由(48 )式确定, 其他相对次要的尺寸根据分布作用速调管的工作频率和微波场在电子注通道中的分布情况确定. 通过三维电磁仿真软件CHIPIC建立了分布作用速调管高频结构模型, 如图9 所示. 高频结构由四个多间隙谐振腔组成, 包括输入腔、输出腔和两个中间腔, 其中输入腔和输出腔由5间隙谐振腔组成, 中间腔由3间隙腔组成, 输入腔与输出腔采用相同结构, 中间两个谐振腔采用相同结构. 仿真过程中, 先用本征模计算程序计算各个谐振腔的工作模式, 改变谐振腔尺寸使各个谐振腔谐振于目标中心频率94.8 GHz, 然后在输入端口馈入微波, 在群聚电流基频分量最大处放置第一个中间腔, 接着在群聚电流基频分量最大处放置第二个谐振腔, 按相同方法增加中间腔数, 直到群聚电流基频分量达到饱和, 在基频分量饱和处放置输出腔. 在实际计算时, 为了给调频结构让位, 微调了各个谐振腔的位置.图 9 分布作用速调管高频结构模型Figure9. Model of the extended interaction cavity.V gap 与输入功率P in 之间的关系式为[20 , 21 ] f in 表征输入信号的频率, R /Q 表征谐振腔的特性阻抗, Q ext 表征由于输入腔开耦合孔导致的损耗.Q a 表征谐振腔的全部损耗, 包括谐振腔的固有损耗Q 0 和引入电子注的损耗Q b . 即53 )式可以看出, 在输入功率一定的条件下, 当Q ext = Q a 时, 输入腔间隙上建立的电压最大, 此时信号在输入端口反射最小. 因此在设计输入腔的耦合孔时需要根据计算出来的Q a 确定. 根据计算得到Q 0 = 736, Q b = –864, 可得Q ext = 804时反射最小.[22 ] . 多间隙耦合腔存在多个谐振模式多间隙腔的模式竞争, 包括非工作高次模式竞争和多间隙腔结构所引起的模式竞争. 由于高次模式离工作模式的频率间隔一般比较大, 高次模式引起的模式竞争比较容易避免. 所以需要重点研究的是多间隙腔结构引起的模式竞争[17 , 23 ] . 各个模式的纵向场分量Ez 沿轴向的分布如图10 和图11 所示, 相应的各个模式的Q total 与工作电压U 的关系如图12 和图13 所示, 由图可以看出, 在工作电压附近, 输入腔和中间腔均不会发生振荡.图 10 输入腔各模式Ez 沿轴向的分布Figure10. Ez versus axial distance of each mode in input cavity图 11 中间腔各模式Ez 沿轴向的分布Figure11. Ez versus axial distance of each mode in middle cavity.图 12 输入腔各模式Q total 与电压U 的关系Figure12. Q total versus U of each mode in input cavity.图 13 中间腔各模式Q total 与电压U 的关系Figure13. Q total versus U of each mode in middle cavity.图14 —图17 所示. 图14 为输入腔端口监测的功率, 由图可知微波源馈入输入腔的功率基本被输入腔和电子注吸收, 实现了良好的匹配. 电子注通过输入腔时, 受到输入腔中微波场的影响, 产生速度调制, 在随后的漂移管中产生密度调制, 通过加入中间腔, 电子注产生了更强烈的调制, 最终在输出腔入口处达到最佳调制, 电子注在输出腔入口处达到了122%的调制深度, 如图15 所示. 图16 为输出腔端口处监测的瞬时输出功率波形, 输出功率为443 W, 中心频率为94.77 GHz. 设计的分布作用速调管效率较低, 主要原因是阴极发射密度较低, 为了增加电子流通率, 增加了电子注孔的尺寸, 而电子注孔对效率影响极大. 引入电子注后使谐振腔的谐振频率发生了偏移, 因此最佳工作点不是谐振腔的谐振频率94.8 GHz. 图17 为输出功率与输入信号频率之间的关系曲线, 由图可以看出, 3 dB带宽大于150 MHz.图 14 瞬时输入功率波形Figure14. Waveform of input microwave.图 15 调制电流基频分量沿轴向的分布Figure15. fundamental modulated current amplitude versus axial distance.图 16 瞬时输出功率波形Figure16. Waveform of output microwave.图 17 输出功率与输入信号频率的关系Figure17. Output power versus input frequency.4.分布作用速调管实验研究及分析 24.1.实验研究 4.1.实验研究 通过理论分析和数值计算, 完成了分布作用速调管的设计. 根据设计结果加工了零件并焊接装配成整管, 完成了分布作用速调管的实验研究. 图18 为分布作用速调管样管实物, 图19 为分步作用速调管测试系统. 测试原理为: W波段固态信号源产生的微波信号经可调衰减器后通过输入窗馈入扩展互作用速调管, 在高频腔体中与电子束相互作用产生放大信号; 从输出窗传输出来的放大信号一路经定向耦合器被负载吸收, 另一路由定向耦合器耦合出来并连接衰减器后作为测试信号; 测试系统采集到的信号通过示波器监测. 图20 为电压20.8 kV, 电流300 mA时的测试结果, 当输入信号频率95.37 GHz, 输入信号功率30 mW时, 得到175 W脉冲输出功率. 图21 为输出功率与微波源信号频率的关系曲线. 由图21 可以看出, 当输入信号频率为95.37 GHz时, 输出功率最大, 3 dB带宽大于90 MHz.图 18 分布作用速调管实物Figure18. Picture of extended interaction klystron.图 19 分布作用速调管测试系统Figure19. Test system of extended interaction klystron.图 20 高频样管测试结果Figure20. Test result of extended interaction klystron.图 21 高频样管输出功率与输入信号频率的关系Figure21. Measured output power vs input frequency.4.2.测试结果分析 -->4.2.测试结果分析 工作频率方面, 测试得到最大输出功率点在输入信号频率95.37 GHz处, 而仿真得到的最大输出功率点在输入信号频率94.77 GHz处, 经分析, 导致这种差别的原因主要是加工引起的误差. 输出功率方面, 在相同的输入条件下, 仿真得到输出功率443 W, 测试得到的输出功率175 W, 产生这种差别的原因初步分析主要有两点, 一是在实验中仅得到83%的电子流通率, 与电子光学系统仿真得到100%电子流通率差别较大, 这导致实验中群聚电流分布与仿真群聚电流分布差别较大, 所以由群聚电流基频分量决定的谐振腔的位置尤其是输出腔的位置与在仿真中的最佳位置差别较大, 最终导致输出功率有较大差别. 二是设计的调频结构未能实现频率的连续调节, 这导致分布作用速调管很难工作在最佳工作点. 带宽方面, 在相同的输入条件下, 仿真得到3 dB带宽大于150 MHz, 测试得到3 dB带宽约90 MHz, 初步分析原因与输出功率产生差别的原因一样, 也是由于电子流通率较差和调频结构未能实现连续调节导致的.5.结 论 本文基于运动学理论、感应电流定理和电荷守恒定律, 研究了电子注在多间隙谐振腔${\text{π}}$ 模场中的渡越时间效应, 推导了多间隙谐振腔的电子负载的表达式, 分析了间隙数对电子注渡越时间效应的影响. 结果表明, 采用多间隙谐振腔有利于提高速调管效率, 并且可以使谐振腔的有载Q 值在更大范围内变化, 可以使速调管不通过引入介质增加损耗而增加工作带宽. 此外, 根据电子负载电纳的计算结果还可以得知, 与单间隙谐振腔相比, 电子注在与多间隙谐振腔中微波场作用时会使谐振腔的谐振频率发生更大的偏移. 最终基于理论分析和数值模拟, 设计了一款工作于W波段的分布作用速调管放大器, 并完成了分布作用速调管放大器的加工和实验研究, 实验测试在中心频率95.37 GHz处得到峰值脉冲输出功率175 W, 3 dB带宽大于90 MHz, 为进一步研制更高功率和更高效率的速调管奠定了基础. 下一阶段的研究工作主要从以下五个方面着手: 一是减小电子注孔尺寸, 提高分布作用速调管的电子效率和输出功率; 二是适当增加发射电流, 调高分布作用速调管的输出功率; 三是改进电子光学系统的设计, 改进电子枪的装配工序, 并增加磁场的调节夹具, 提高电子注在分布作用速调管中的流通率; 四是改进谐振腔的调频结构, 使谐振腔的频率调节尽可能接近连续调节; 五是在设计时采用各个谐振腔频率参差分布的方法, 增加分布作用速调管的带宽. 

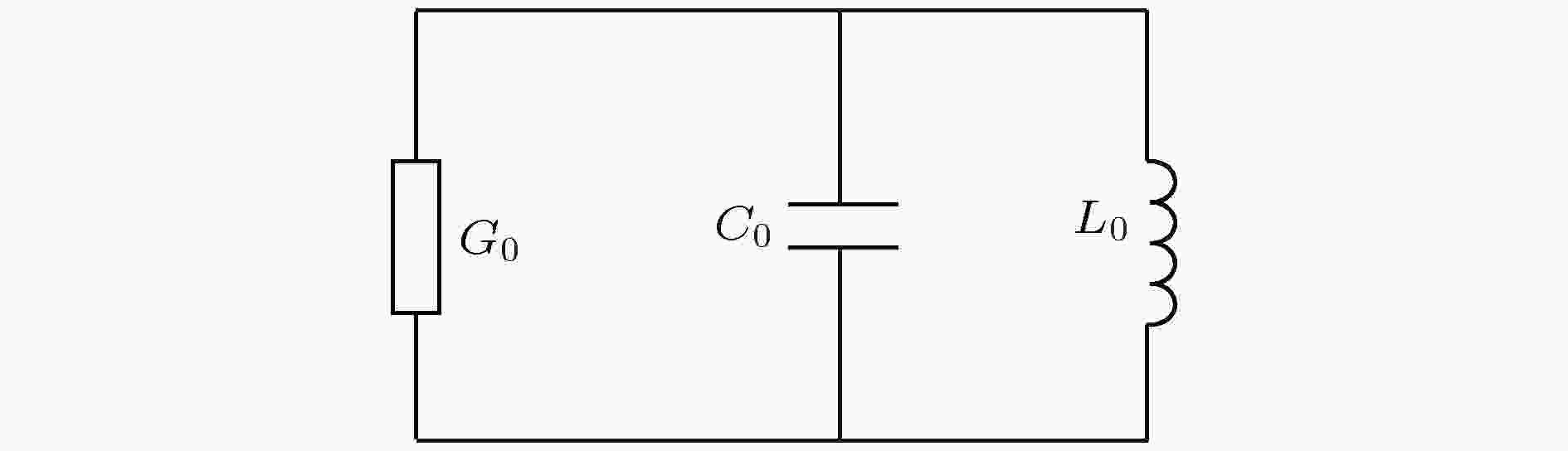 图 1 谐振腔等效电路
图 1 谐振腔等效电路 图 2 引入电子注后谐振腔等效电路
图 2 引入电子注后谐振腔等效电路

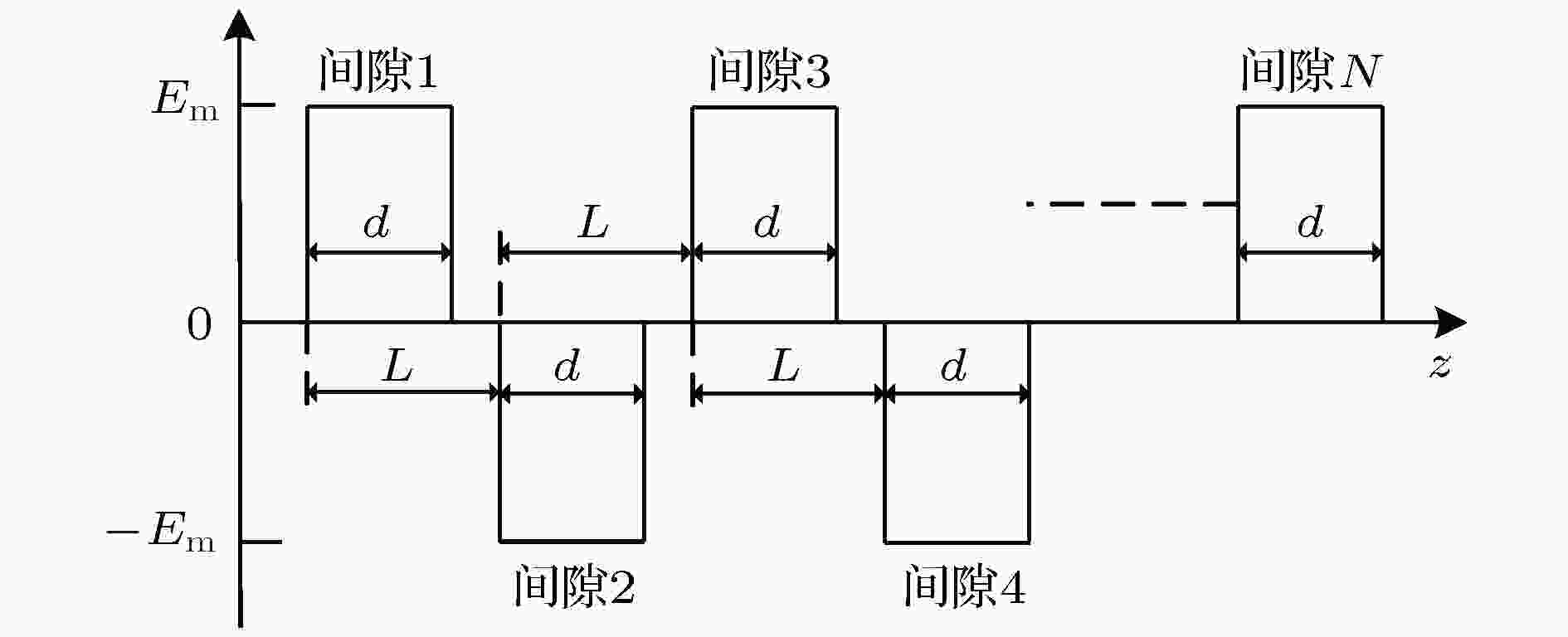 图 3 多间隙谐振腔
图 3 多间隙谐振腔












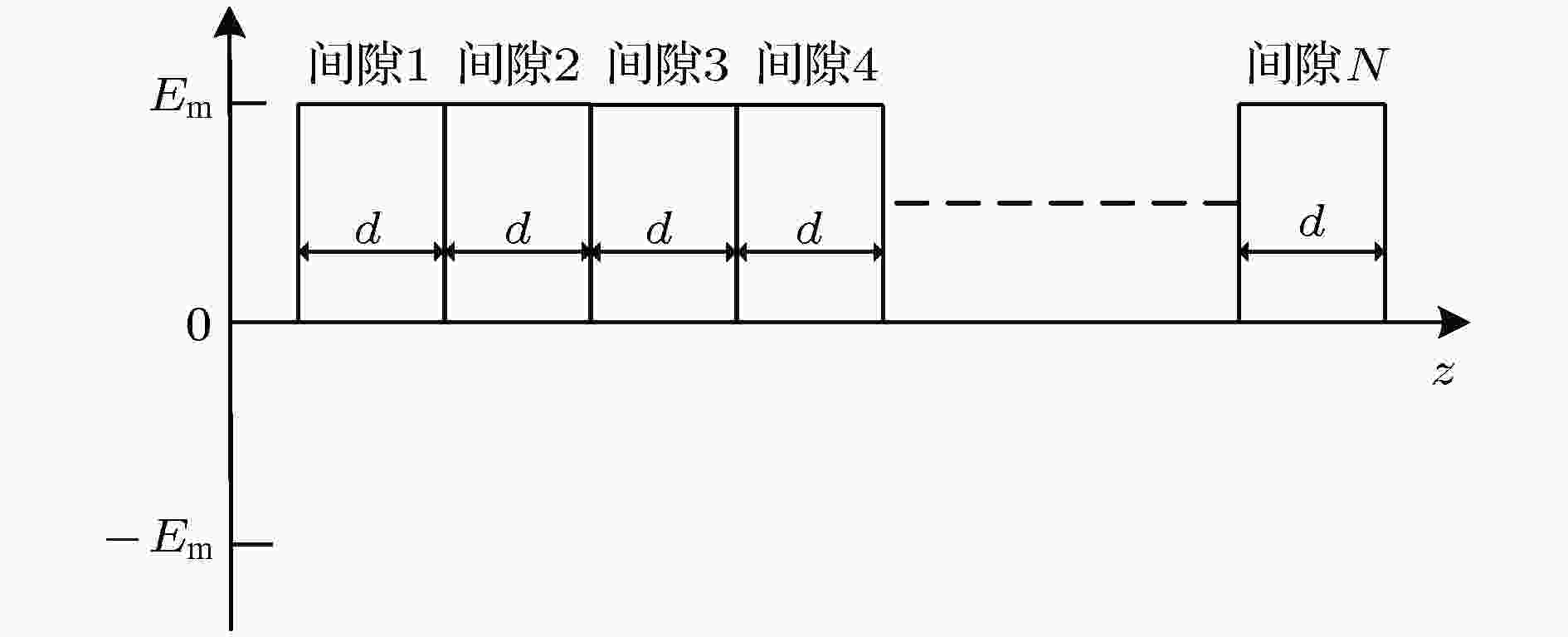 图 4 多间隙谐振腔
图 4 多间隙谐振腔











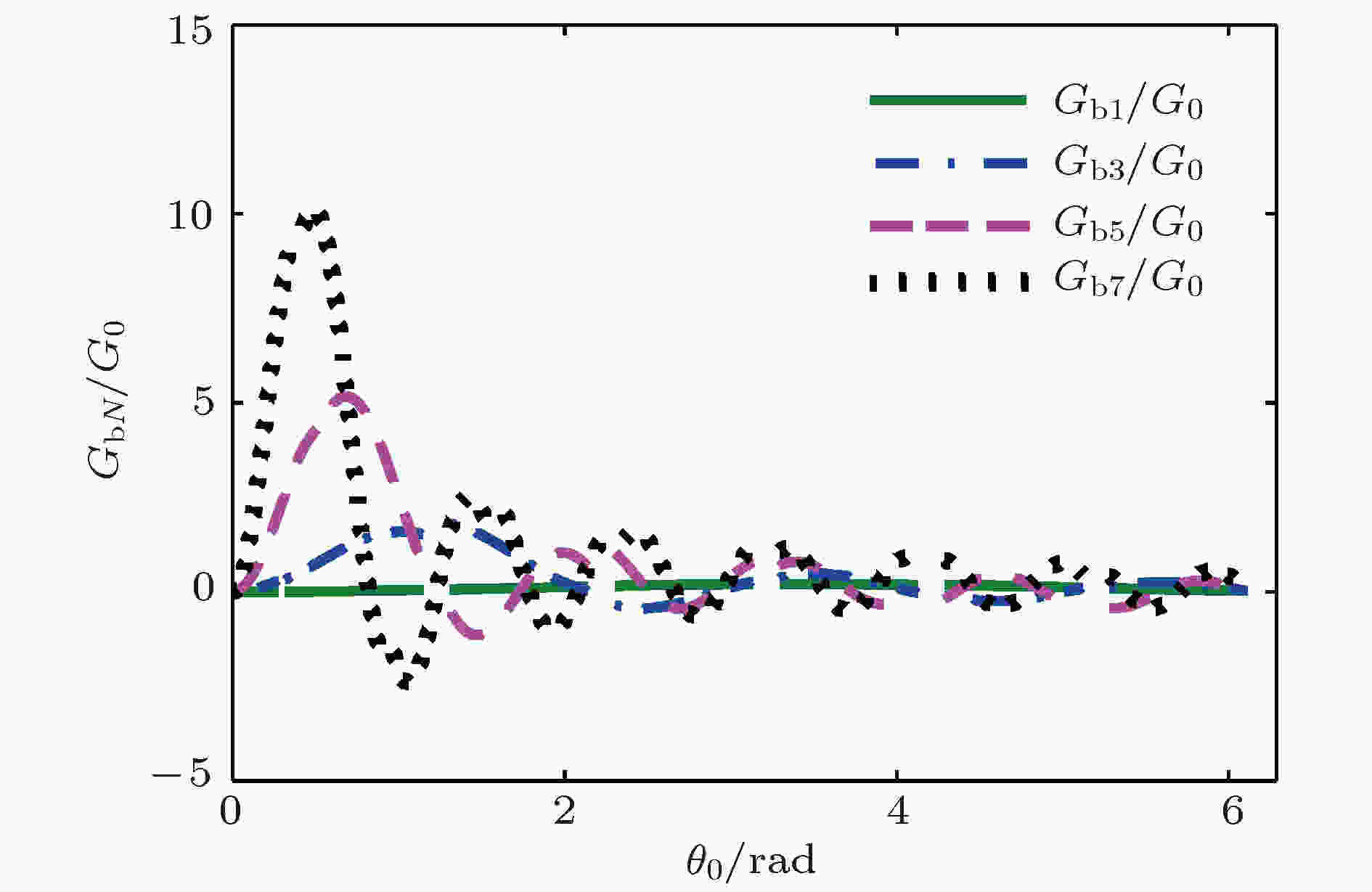 图 5 归一化电子负载电导与渡越角的关系
图 5 归一化电子负载电导与渡越角的关系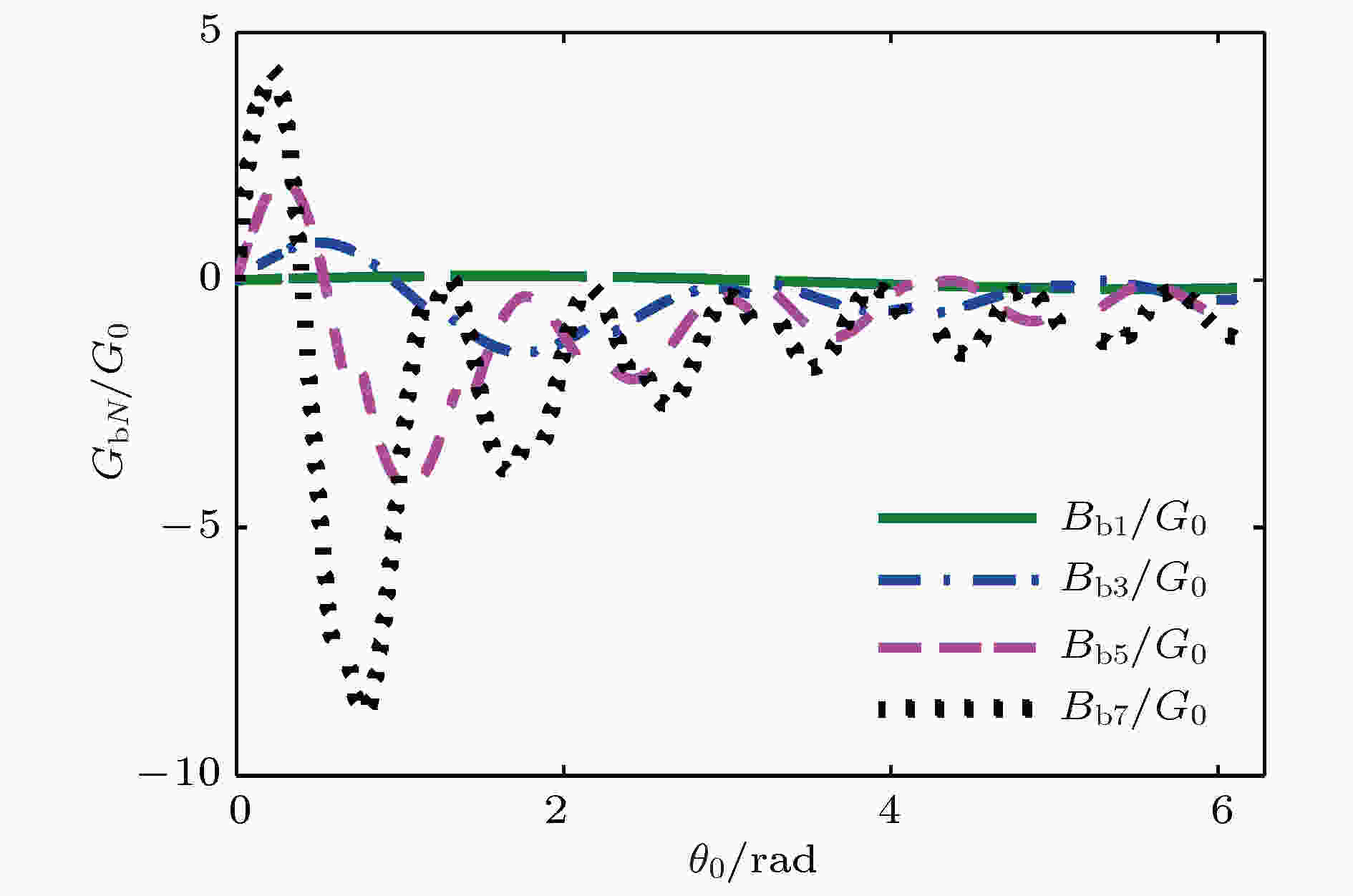 图 6 归一化电子负载电纳与渡越角的关系
图 6 归一化电子负载电纳与渡越角的关系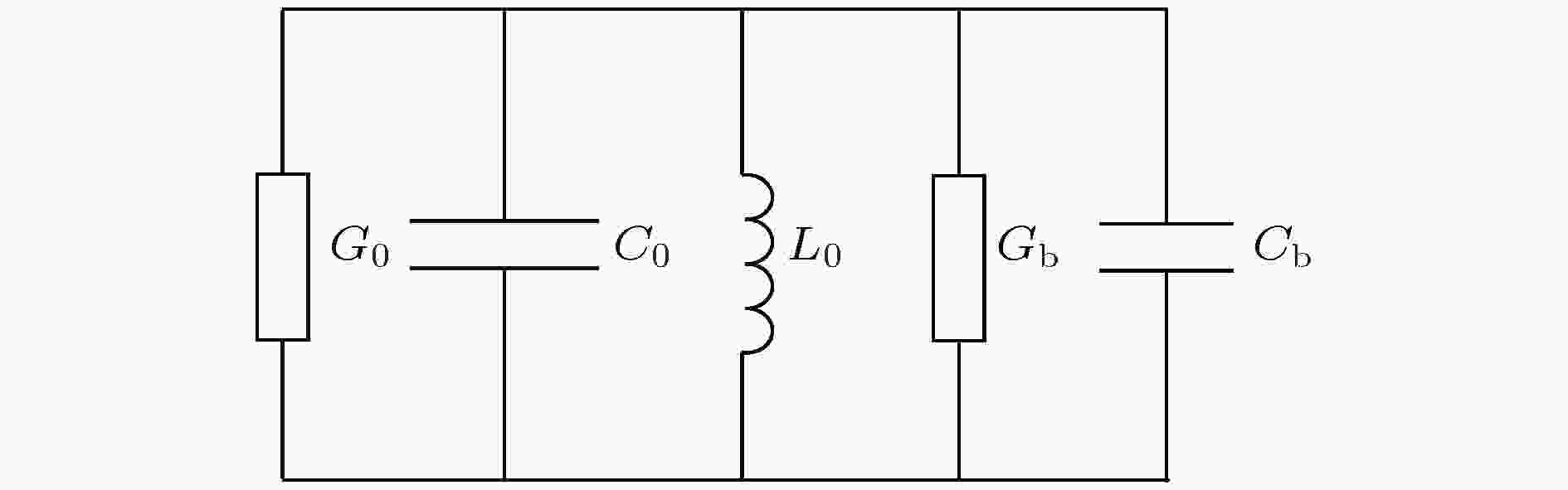 图 7 BbN为正值谐振腔等效电路
图 7 BbN为正值谐振腔等效电路 图 8 BbN为负值时谐振腔等效电路
图 8 BbN为负值时谐振腔等效电路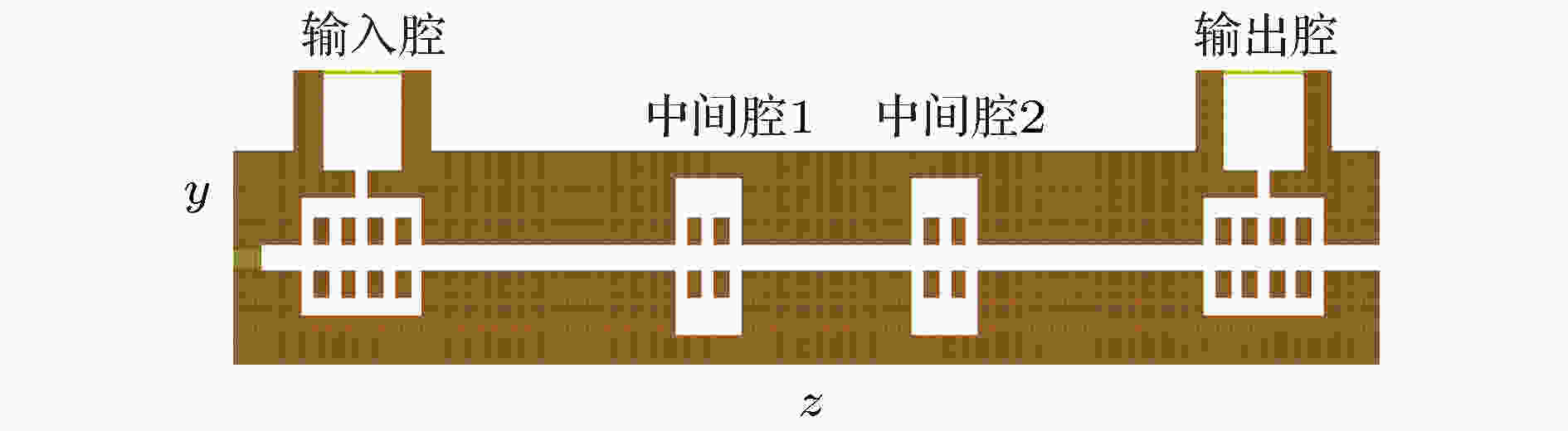 图 9 分布作用速调管高频结构模型
图 9 分布作用速调管高频结构模型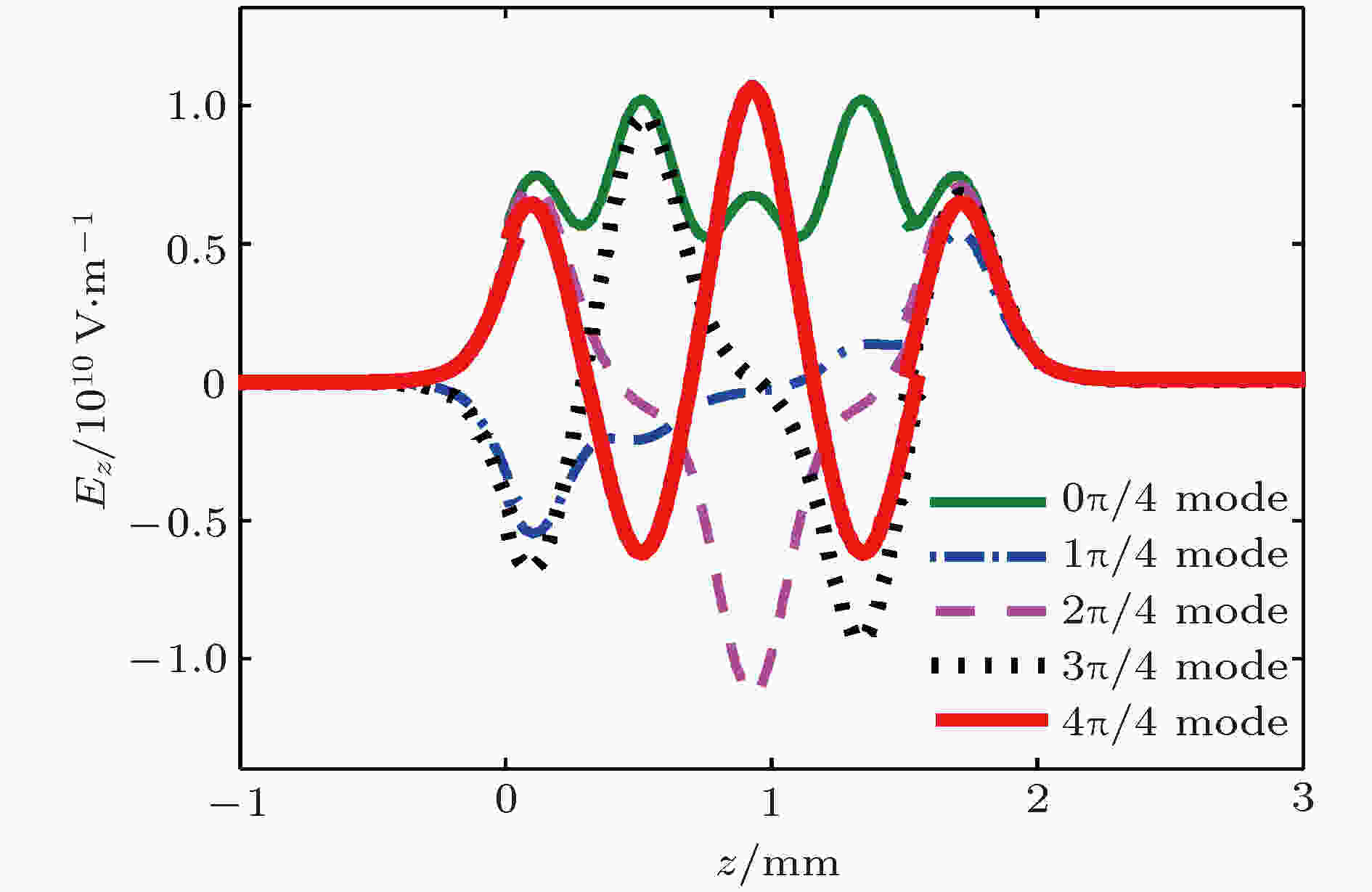 图 10 输入腔各模式Ez沿轴向的分布
图 10 输入腔各模式Ez沿轴向的分布 图 11 中间腔各模式Ez沿轴向的分布
图 11 中间腔各模式Ez沿轴向的分布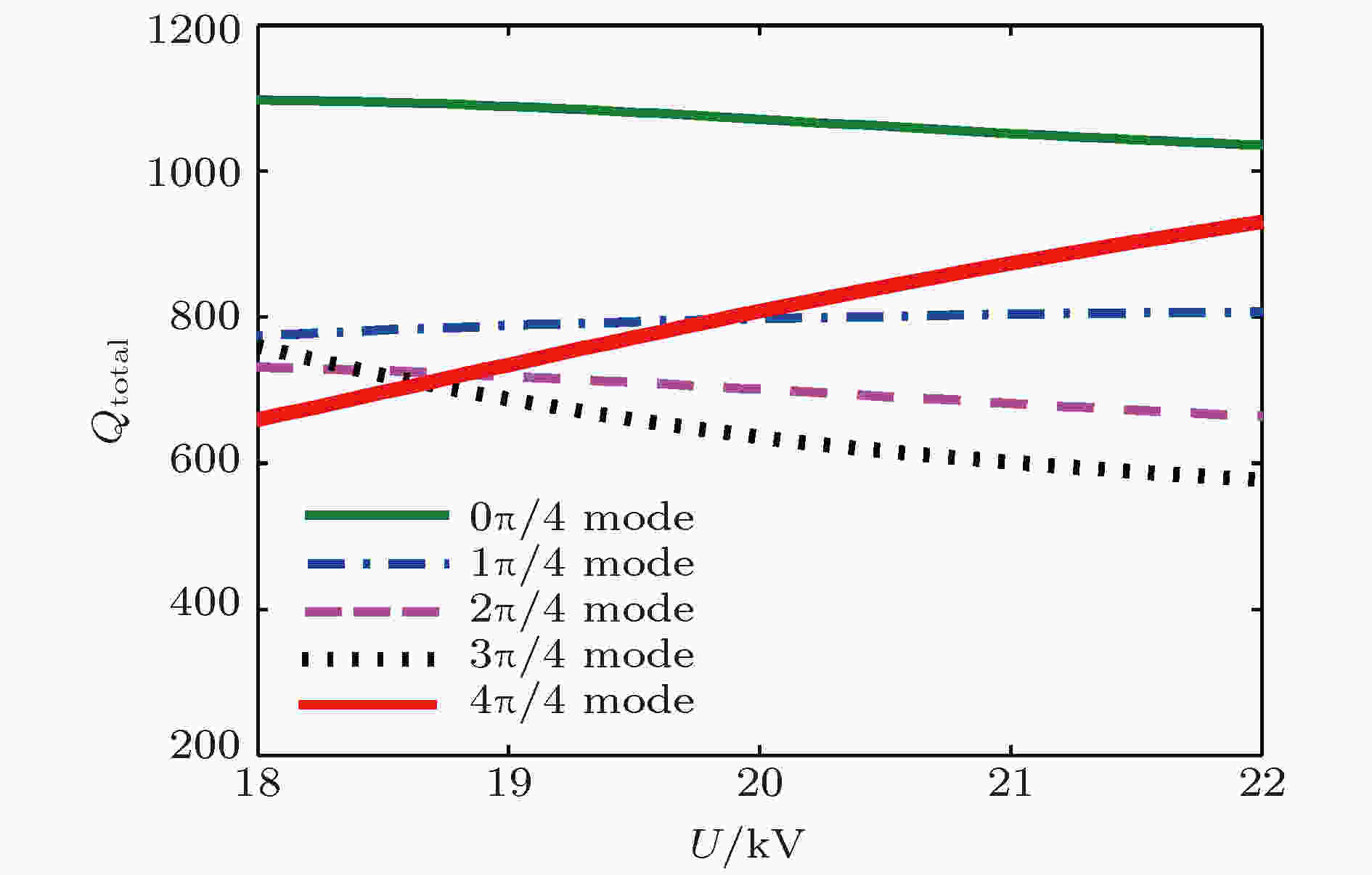 图 12 输入腔各模式Qtotal与电压U的关系
图 12 输入腔各模式Qtotal与电压U的关系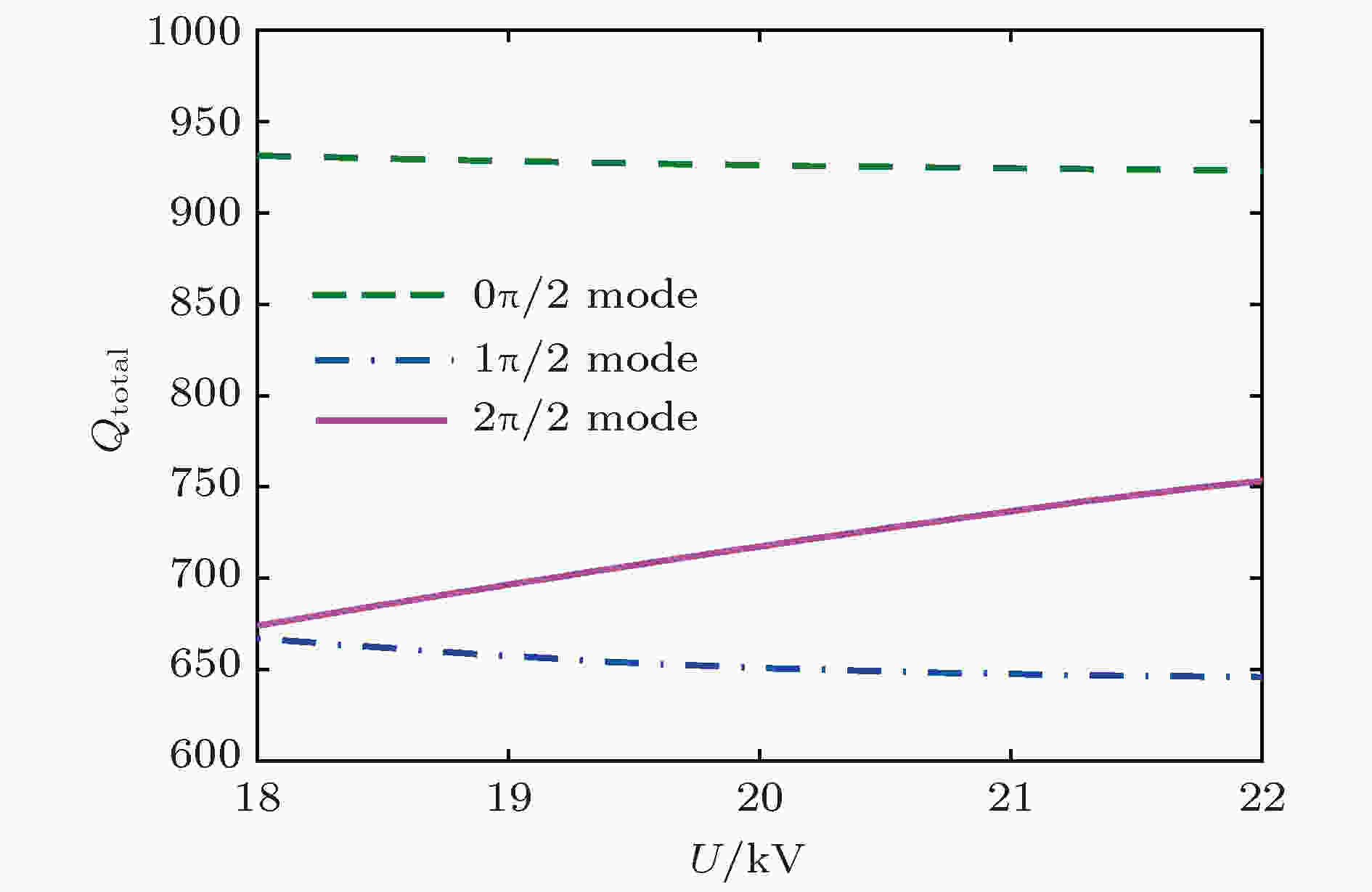 图 13 中间腔各模式Qtotal与电压U的关系
图 13 中间腔各模式Qtotal与电压U的关系 图 14 瞬时输入功率波形
图 14 瞬时输入功率波形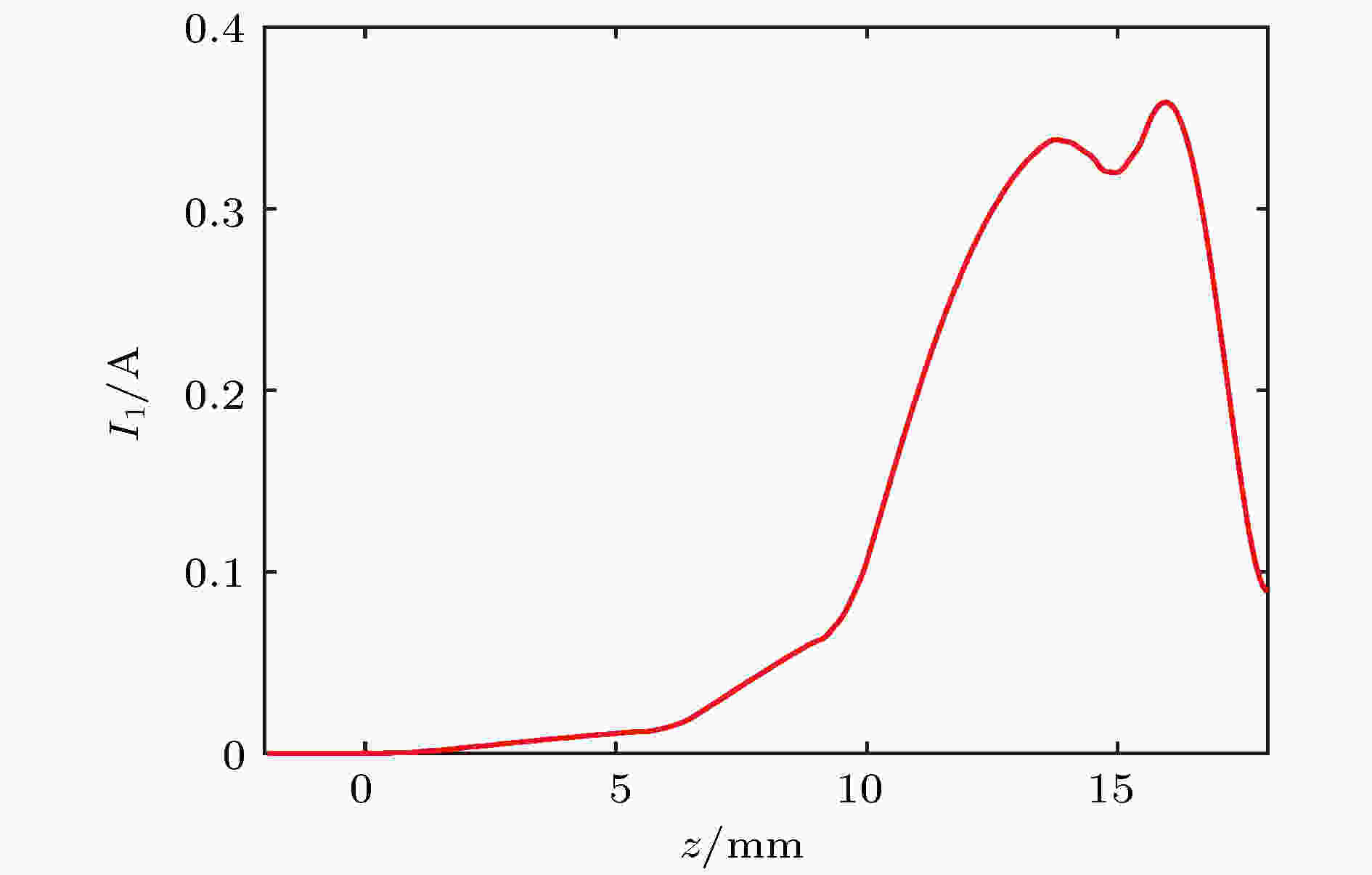 图 15 调制电流基频分量沿轴向的分布
图 15 调制电流基频分量沿轴向的分布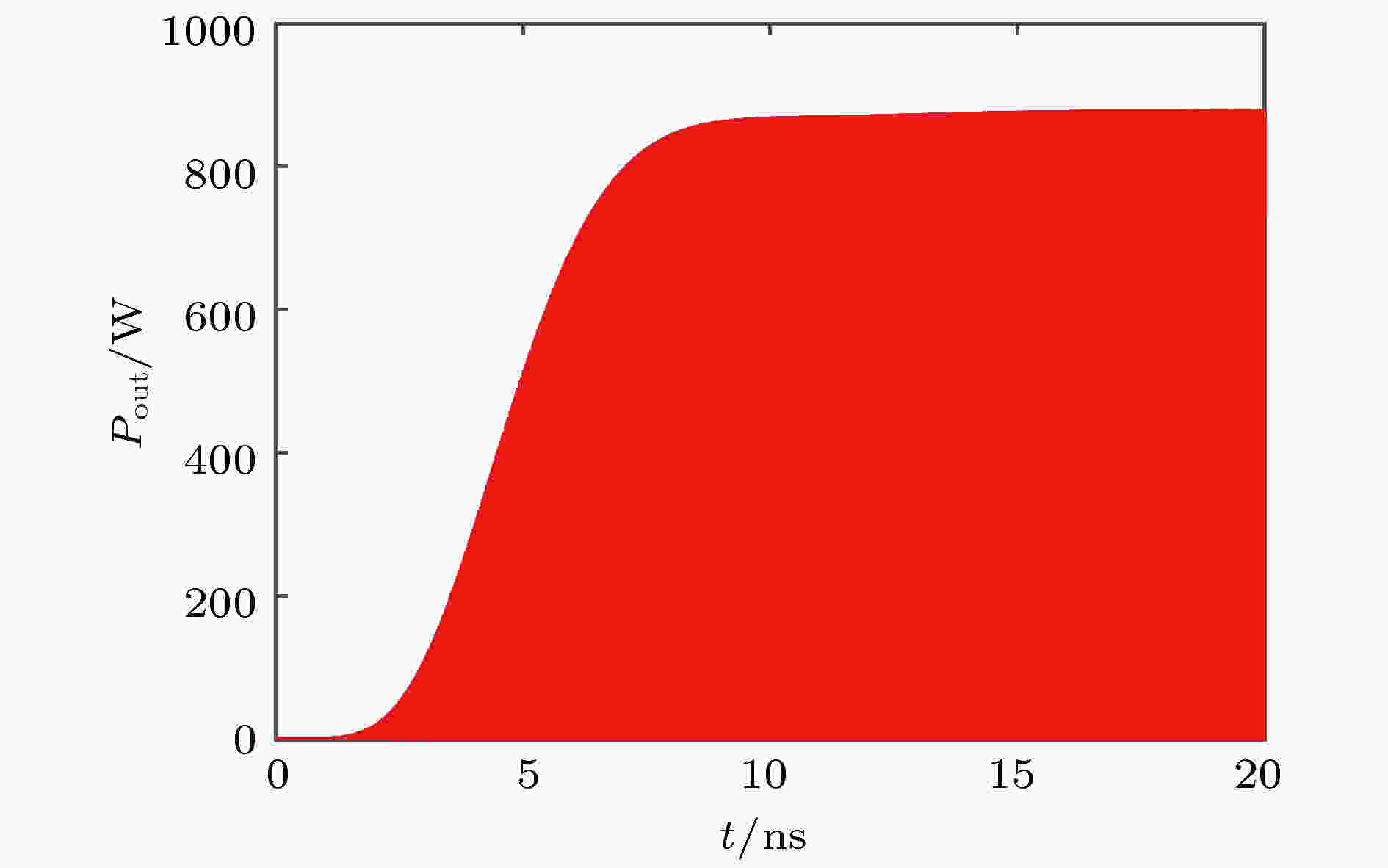 图 16 瞬时输出功率波形
图 16 瞬时输出功率波形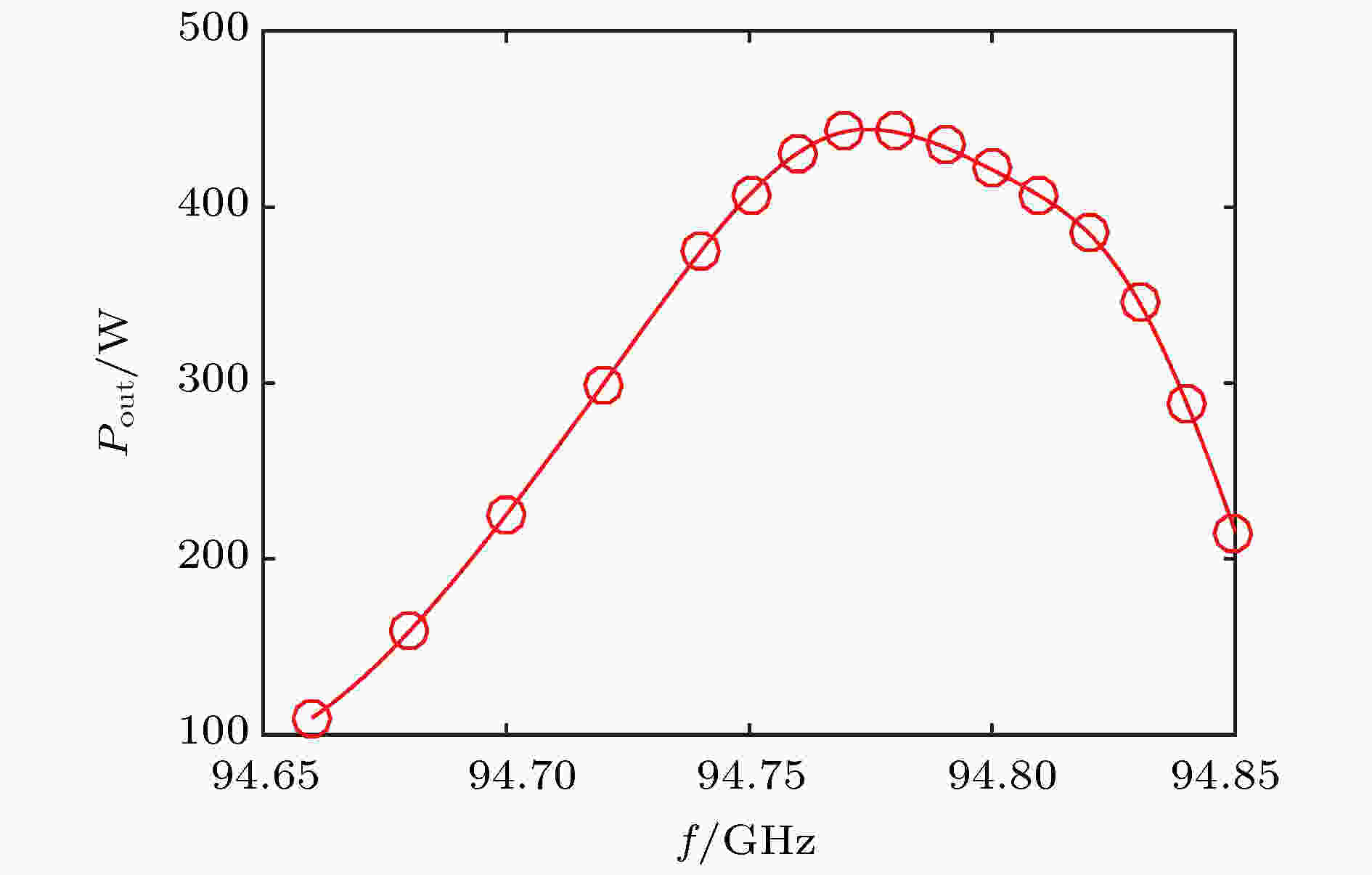 图 17 输出功率与输入信号频率的关系
图 17 输出功率与输入信号频率的关系 图 18 分布作用速调管实物
图 18 分布作用速调管实物 图 19 分布作用速调管测试系统
图 19 分布作用速调管测试系统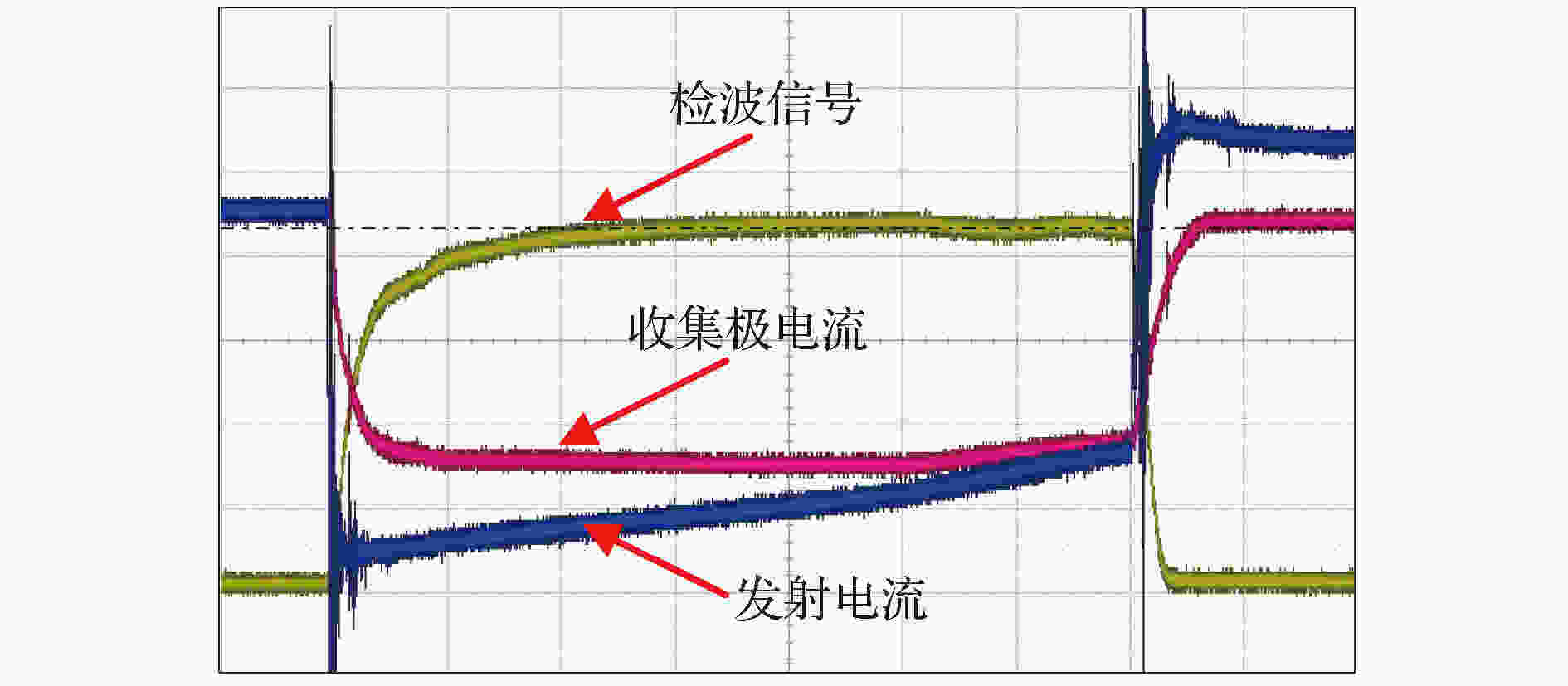 图 20 高频样管测试结果
图 20 高频样管测试结果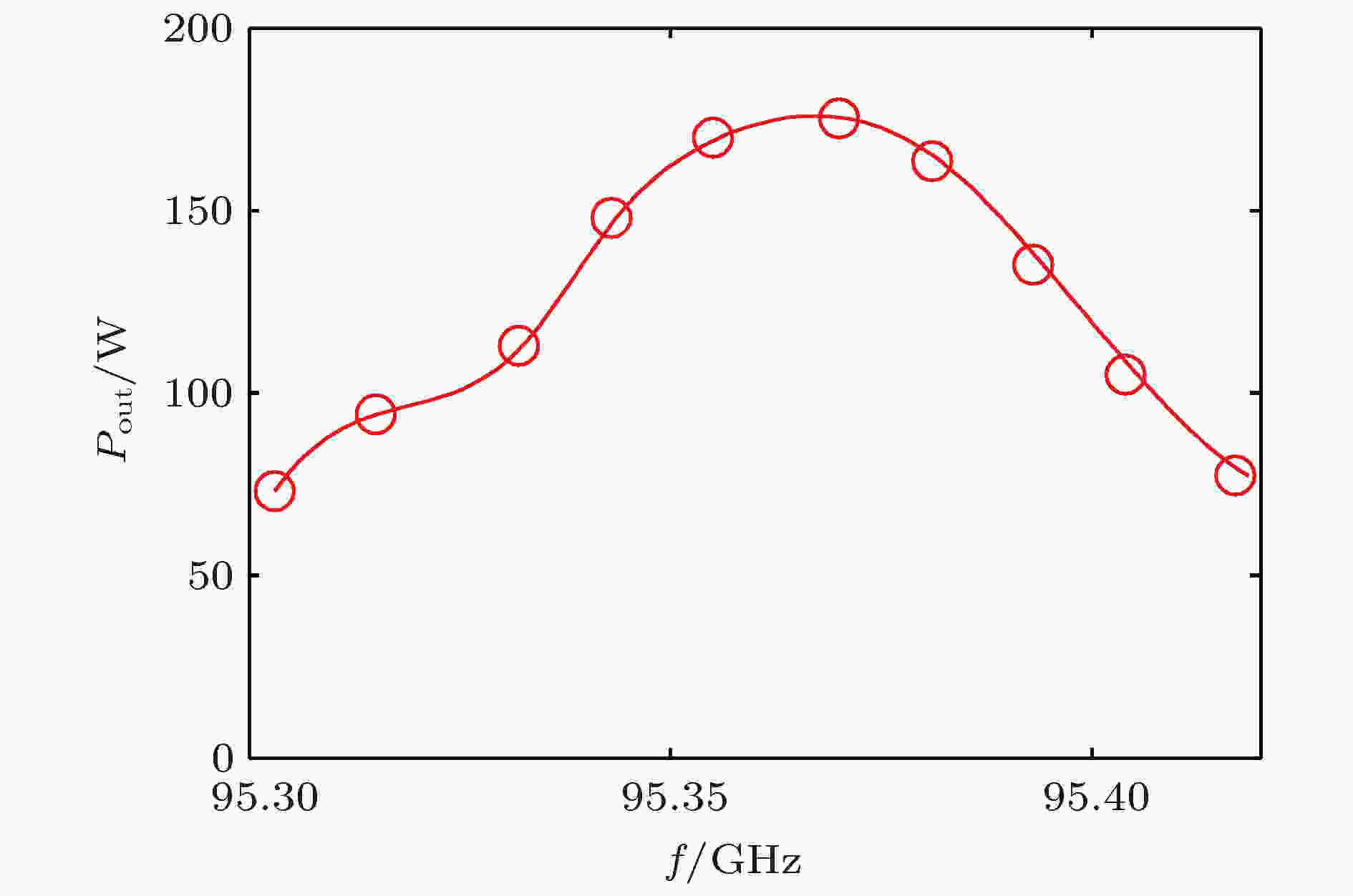 图 21 高频样管输出功率与输入信号频率的关系
图 21 高频样管输出功率与输入信号频率的关系


