摘要:采用第一性原理计算对Ce_0.8La_0.1Th_0.1在高压下fcc-bct的结构相变、弹性性质及热力学性质进行了研究讨论. 通过对计算结果的分析, 发现了合金在压力下的相变规律, 压强升高到31.6 GPa附近时fcc相开始向bct相转变, 到34.9 GPa时bct相趋于稳定. 对弹性模量的计算结果从另一角度反映了结构相变的信息. 最后, 利用准谐德拜模型对两种结构的高温高压热力学性质进行了理论预测.
关键词: Ce基合金/
第一性原理计算/
相变/
高压

English Abstract

全文HTML

--> --> -->

稀土元素指镧(La)、铈(Ce)、镨(Pr)等17种元素, 能实现光、电、磁范畴内的特殊能量转换、传导输送及储存等功能. 随着科技的不断发展, 稀土资源已广泛应用于电子信息、污染治理、清洁能源、航空航天、生命技术、医疗卫生等各个方面, 与稀土元素相关的研究成为了现代世界前沿科学的重要组成部分. 储量丰富的稀土元素Ce目前在钢铁、有色金属及合金和发火合金等产业中已有广泛应用, 在电子工业、原子能工业、精密仪器工业的应用也有了新的突破, 为军事、科技、生产助力. Ce作为多形相变材料的一种, 电子态极容易出现跃迁, 具有丰富的相变信息. 常温常压下的Ce存在稳定的γ相, 该相具有fcc面心立方晶体结构. Bridgman^[1-3]在测量Ce电导率和等温压缩线时首先发现了Ce在0.8 GPa左右的γ—α相变, 这一现象引发了大量****的关注. 1949年, Lanson和Tang^[4]在X射线衍射实验中证实了Ce的γ—α相变其实是一种同构相变, 相变过程伴随着17%左右的体积塌缩. 2012年, 潘昊等^[5]低压冲击金属Ce的γ—α相变, 进行了数值模拟研究. 我们前期运用第一性原理计算结合晶格动力学的方法证明, 随着压强的升高, Ce的相变顺序为α-Ce→α''-Ce→bct-Ce, 相变压强分别为5.36 GPa和14.37 GPa^[6].
Ce基合金由于其良好的固溶性, 是核武器关键材料钚(Pu)潜在的替代品, 由于目前的国际规则, 并不能对Pu进行直接的实验研究, 因此Ce基合金作为其潜在的替代品成为了研究的热点. 目前已有****对Ce-Th, Ce-La, Ce-La-Th合金的物理性质进行了一系列的理论预测与实验测量, 主要关注同构相变的信息. Lawson等^[7]用实验测得了Ce_0.9Th_0.1存在γ—α同构相变. Lawrence等^[8]测量了温度在4.2—300 K区间、压强在0—12 kPa区间时不同组分Ce_0.9－xLa_xTh_0.1体系(x = 0.10, 0.11, 0.14, 0.17)的电阻率变化情况, 以此确定了Ce-La-Th合金的γ—α同构相变的压强温度边界. Drymiotis等^[9]实验测量了Ce_0.8La_0.1Th_0.1中γ—α相变中伴随的外加磁场变化, Ruff等^[10]通过X射线衍射实验证实了Ce_0.8La_0.1Th_0.1也存在体积塌缩的同构相变. 目前对于Ce基合金高压相变的研究较为匮乏. 我们前期用第一性原理计算了Ce_xTh_1–x合金体系的结构相变随组分的变化规律^[11], 发现fcc-bct相变压强随Ce组分的增加而减小, 也即随着Th的加入, 提高了合金的相变压强. 我们采用密度泛函理论结合准谐近似对两种不同组分的Ce-La合金的相变及状态方程(EOS)进行了研究^[12], 发现在压力的作用下, Ce-La合金从fcc结构转变到bct结构, 而在fcc结构中, 又有γ—α同构相变发生. 本文分别计算了两种不同组分的Ce-La合金(Ce_0.875La_0.125和Ce_0.963La_0.037)的相变压强, 结果表明随着La含量的增加, 相变压强升高. 高压环境下对Ce-La-Th体系的科学研究还较为匮乏, 本文对Ce_0.8La_0.1Th_0.1在压力下fcc-bct的相变情况和热力学性质进行了研究讨论.

采用基于密度泛函理论的虚晶近似(VCA)对无序合金Ce_0.8La_0.1Th_0.1进行计算模拟. VCA是通过将元素的赝势进行混合来产生一种新的势函数. 我们前期也采用这种方法成功预测了Ce-Th合金随组分变化的相图^[11]. Ce存在f电子, 在计算中, 需要慎重处理. 我们前期采用密度泛函理论(DFT)+U的方法对纯Ce做了较为深入的探讨^[12]. 发现f电子在较低的压强区间, 对Ce的同构相变起决定性的作用. 但是在较高压强区间(同构相变之后), 对fcc-bct的相变影响并不明显. 在前期计算纯Ce和Ce-La合金时, 高压对f电子的关联效应有较强的抑制作用, DFT+U方法计算的体系能量与直接的DFT方法没有明显的差异. 因此, 本文采用DFT直接计算较高压强下的fcc和bct结构的物理性质. 在电子结构计算时, 使用了CASTEP程序包的平面波赝势方法, 交换关联相互函数采用的是广义梯度近似(GGA)框架下的Perdew-Burke-Ernzerhof (PBE)形式, 为获得准确的计算结果, 我们的平面波截断能均取为500 eV, Ce, La和Th的价电子分别取5s²5p⁶4f¹5d¹6s², 5s²5p⁶5d¹6s²和6s²6p⁶6d²7s². 计算中对fcc和bct两种结构分别采用了15 × 15 × 15 和13 × 13 × 17 Monkhorst pack网格, 为了保证计算的精度使得总能的收敛精度达到10^–6 eV/atm. 本文利用准谐德拜模型计算热力学性质, 非平衡的Gibbs自由能(G^*)包含了静态能量、晶格振动能以及体积变化带来的能量改变, 可以写成如下形式:

${G^*}{\rm{(}}x;P,T{\rm{)}} = E{\rm{(}}x{\rm{)}} + PV{\rm{(}}x{\rm{)}} + {A_{{\rm{Vib}}}}{\rm{(}}x;T{\rm{)}}, $

其中E(x)为静态能量, 可以直接从电子结构计算中得到; PV项代表压强作用下焓值的改变; A_Vib是Helmholtz自由能, 包含了晶格振动对内能的贡献和熵的改变. Blanco等^[13]发展了考虑热效应的准谐Debye模型. 根据这个模型, A_Vib可以用如下近似求得^[14-17]:

${A_{{\rm{Vib}}}}{\rm{(}}\varTheta ;T{\rm{)}} = nkT\left[\frac{9}{8}\frac{\varTheta }{T} + 3{\rm{ln(}}1 - {{\rm{e}}^{ - \varTheta /T}}{\rm{)}} - D{\rm{(}}\varTheta /T)\right], $

其中Θ是Debye温度, n是每个单位分子式中原子的数目, D(Θ/T)是德拜函数, 定义如下:

$D{\rm{(}}y{\rm{)}} = \frac{3}{{{y^3}}}\int\limits_0^y {\frac{{{x^3}}}{{{{\rm{e}}^x} - 1}}} {\rm{d}}x.$

当获得了高温高压的自由能之后, 通过适当的热力学表达式就能求其他热力学性质. 采用这种方法, 邓世杰等^[18]对Ti₂AlX (X = C, N)的热力学性质做了成功的预测.

2

-->

3.1.结构相变

我们计算了Ce_0.8La_0.1Th_0.1合金fcc相及bct相的能量-体积关系, 获得了其各自的状态方程. 得到的fcc相及bct相在0 GPa, 0 K下的平衡体积V₀, 体积模量B₀的数据如表1所列, 同时表中也列出了Ce_0.875La_0.125及纯Ce的理论值和实验值作为参照. Ce_0.8La_0.1Th_0.1合金bct相的平衡体积V₀ = 28.91 ?³, 体积模量B₀ = 35.96 GPa. 随着La, Th的加入, 相对于纯Ce而言, 平衡体积V₀增加, 而体模量B₀减小. 随着Th的加入和La成分的减少, Ce_0.8La_0.1Th_0.1合金的体模量略大于Ce_0.875La_0.125合金.

		V0/?3	B0 / GPa
Present	Ce0.8La0.1Th0.1	28.91	35.96
Calc.[12]	Ce0.875La0.125	28.00	32.50
Calc.	Pure Ce	27.07[6], 24.7[22]	41.72[6], 48.4[22], 37[23]
Expt.	Pure Ce	29.0[20], 28.06[24]	20[20], 35.0[25]

表1零温零压下fcc相Ce-La-Th合金的平衡体积(V₀)及体积模量(B₀)
Table1.Equilibrium volume (V₀) and bulk modulus (B₀) of Ce-La-Th of fcc phase at 0 GPa and 0 K.

对Ce_0.8La_0.1Th_0.1合金的fcc—bct相变进行计算和分析, 将得到的fcc相和bct相的体积-压强关系, 与纯Th^[19]、纯Ce^[20]、Ce_0.76Th_0.24^[21]及Ce_0.875La_0.125^[12]的数据进行比对, 如图1. 本文的数据与已有的Ce基合金及纯Ce的体积-压强变化的规律相吻合.
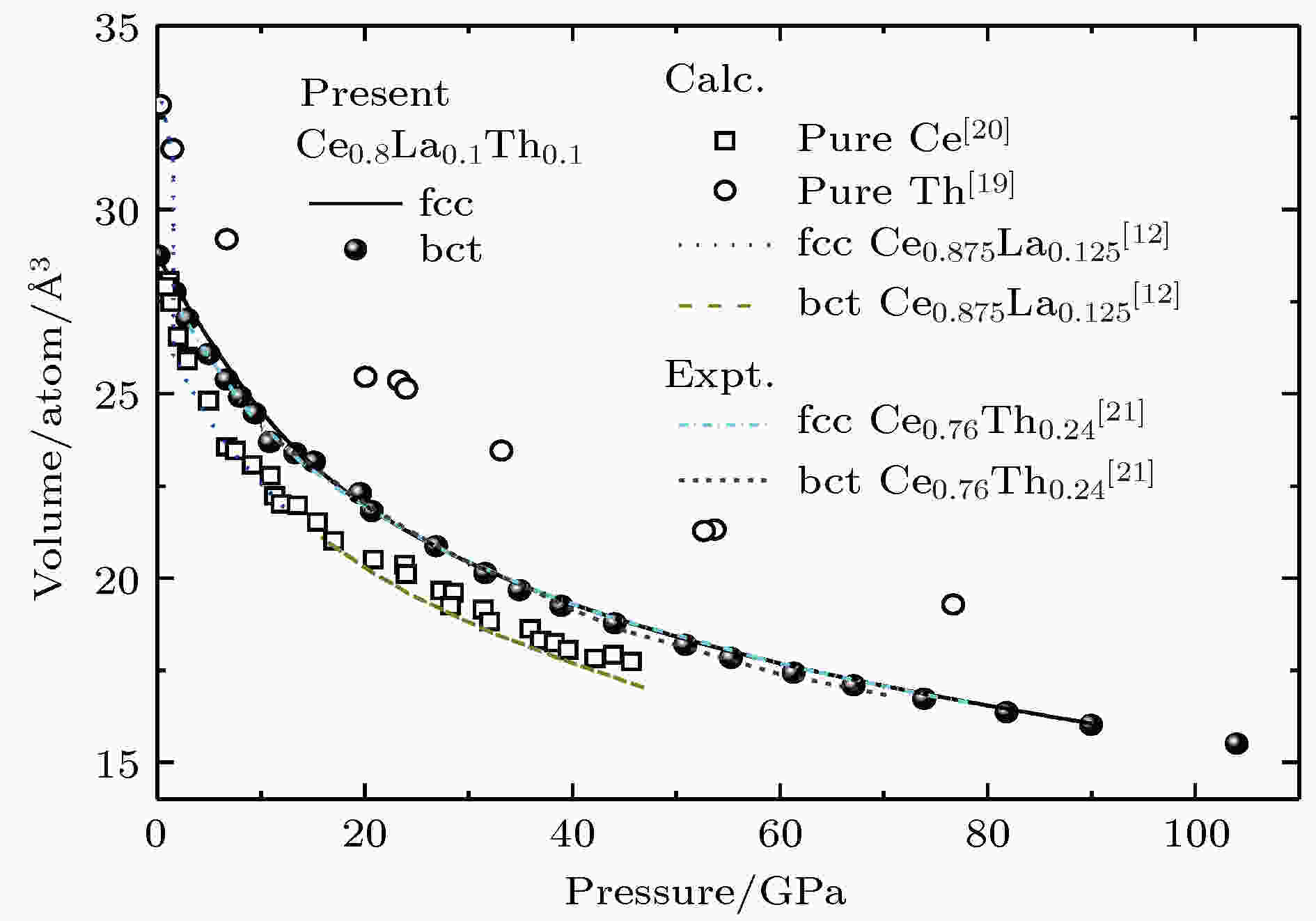图 1 体积随压强变化的规律(黑色实点为直接加压结构优化后的结果, 黑色实线为状态方程拟合结果), 并与已有的Ce^[20], Th^[19], Ce_0.875La_0.125^[12]的计算值及Ce_0.76Th_0.24^[21]实验值进行比较
Figure1. The EOS of fcc and bct Ce-La-Th together with the experimental data (the black solid point is the result of the structure optimization, the black solid line is the fitting result of the EOS), together with the experimental data for Ce_0.76Th_0.24^[21] and the calculated results for Ce^[20], Th^[19], Ce_0.875La_0.125^[12].

通过对总能的计算结果表明, fcc和bct两种相结构之间焓的差异非常小, 几乎接近计算误差值, 这意味着不能再通过比较焓变的差异来判断相变压强.
对bct相固定体积进行结构优化, 晶格常数的计算结果如图2所示. 随着体积的减小, 当体积减小至20.14 ?³时, 晶格常数a, c的线性规律发生变化, 这意味着晶体结构出现了变化, 相变开始发生. 计算得到的轴向比c/a与已有的Ce_0.76Th_0.24^[21], Ce^[6], Th^[11], Ce_0.875La_0.125^[12]数据进行了对比. 当压强小于31.6 GPa时, c/a的值约等于, 随着压强的增加, fcc相变得不稳定, 开始向bct相转变. 在34.9 GPa附近时, bct相趋于稳定 c/a的值约等于1.65, 与我们前期计算得到的CeTh, CeLa合金的fcc相, bct相的c/a的值在误差范围内吻合^{[11, 12]}.
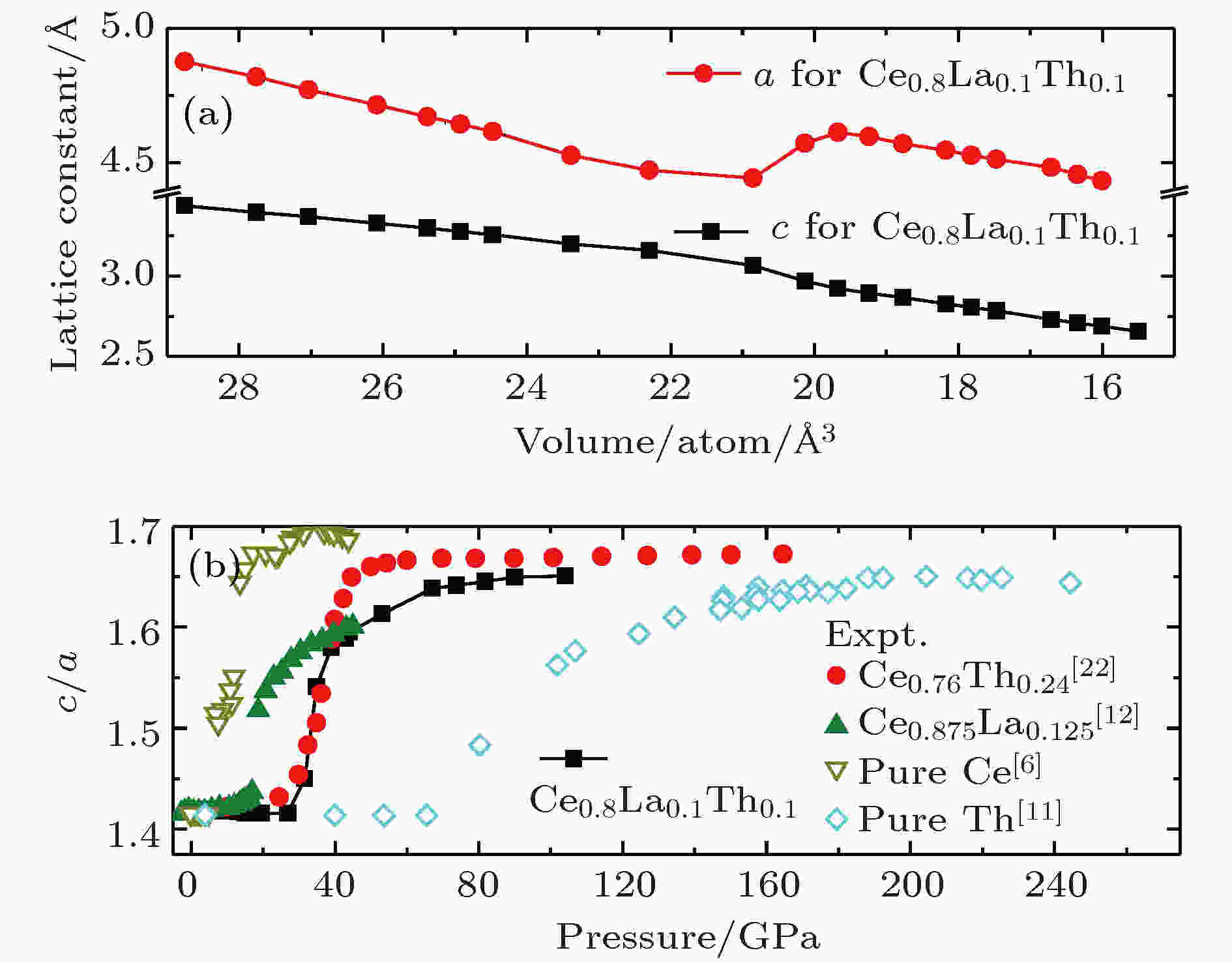图 2 (a) 晶格参数随体积的变化关系; (b) 轴向比c/a随压强的变化关系, 并与已有的Ce_0.76Th_0.24^[21]实验结果和Ce_0.875La_0.125^[12]、纯Ce^[6]、纯Th^[11]计算结果进行比较
Figure2. (a) Lattice constants a and c of Ce_0.8La_0.1Th_0.1 as functions of volume; (b) the calculated axial ratio (c/a) of bct phase as functions of pressure.

2 -->

3.2.弹性性质

本文计算了Ce_0.8La_0.1Th_0.1合金fcc相及bct相结构的弹性性质, 在不同压强下的弹性常数如图3所示. 对于fcc相而言, 随压强增加, 所有的弹性常数都是线性增加的. 弹性常数C₁₁, C₄₄在相变压强附近开始出现非线性的变化. 对bct相而言, 在压强增加的变化趋势下, 越过相变压强后弹性常数线性增加的趋势变得更加明显. 根据弹性常数, 能够计算出多晶的弹性模量, 对于Ce_0.8La_0.1Th_0.1合金, 多晶的弹性模量(剪切模量G、体模量B和杨氏模量E )能够根据Voigt-Reuss-Hill近似得出.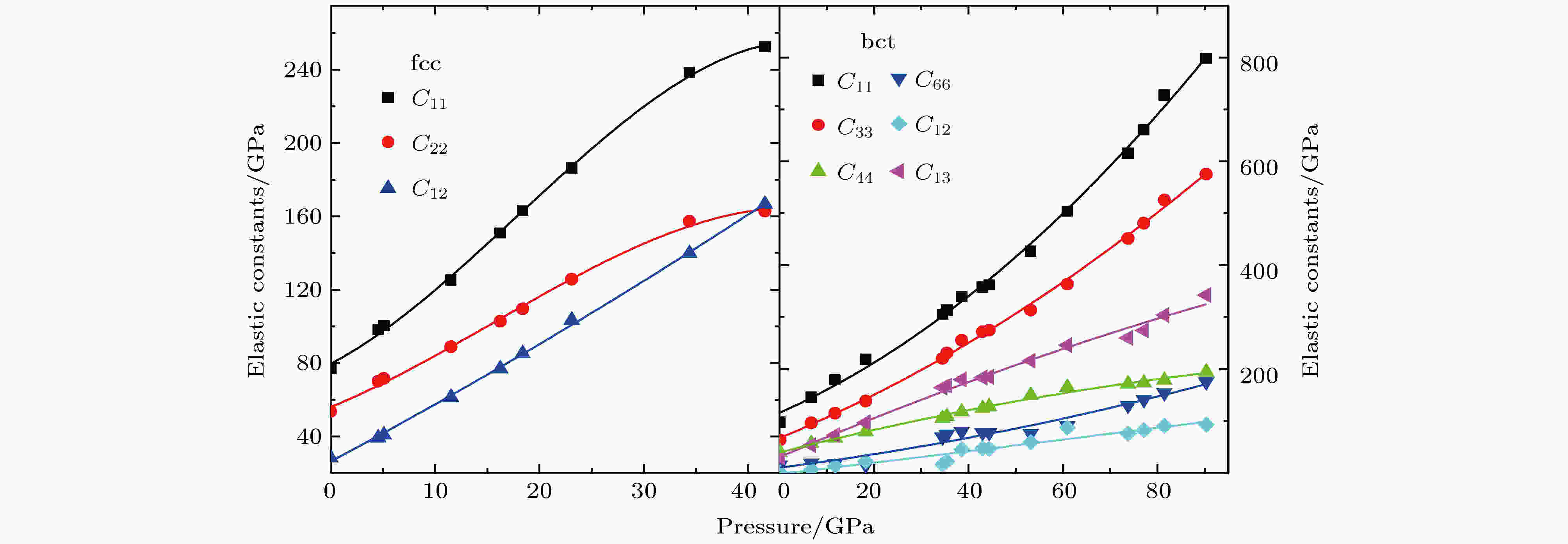
图 3 Ce-La-Th合金fcc相及bct相弹性常量随压强的变化
Figure3. Elastic constants as functions of pressure.

如图4所示, 随着压强的增加, 弹性模量呈线性增加的趋势, 而杨氏模量E和剪切模量G则在相变压强附近出现“变软”的趋势; 随着相变的完成, 新相趋于稳定, 杨氏模量E和剪切模量G随压强增加的关系再次趋于线性. 通过弹性模量,能够计算德拜温度. 如图5所示, 在0 GPa压强下, Ce_0.8La_0.1Th_0.1合金的德拜温度为228.85 K, 高于纯Ce已有的德拜温度研究值^{[26, 27]}. 根据已有的研究^[12], 德拜温度随着La组分的增加而增加, Ce_0.875La_0.125在零温零压下德拜温度为140.9 K, 遂认为在Ce_0.8La_0.1Th_0.1合金中, La和Th元素的掺杂导致了德拜温度的升高, 原子间作用力也会因此升高, 本文的计算结果是合理的. 在大约34.4 GPa时, fcc相德拜温度随压强增加呈减小的趋势, 而bct结构与fcc结构的德拜温度十分接近, 并随压强增加呈线性增加的趋势. 意味着结构相变开始发生, 在41.6 GPa附近, fcc结构转变为bct结构, 此时德拜温度为330 K.
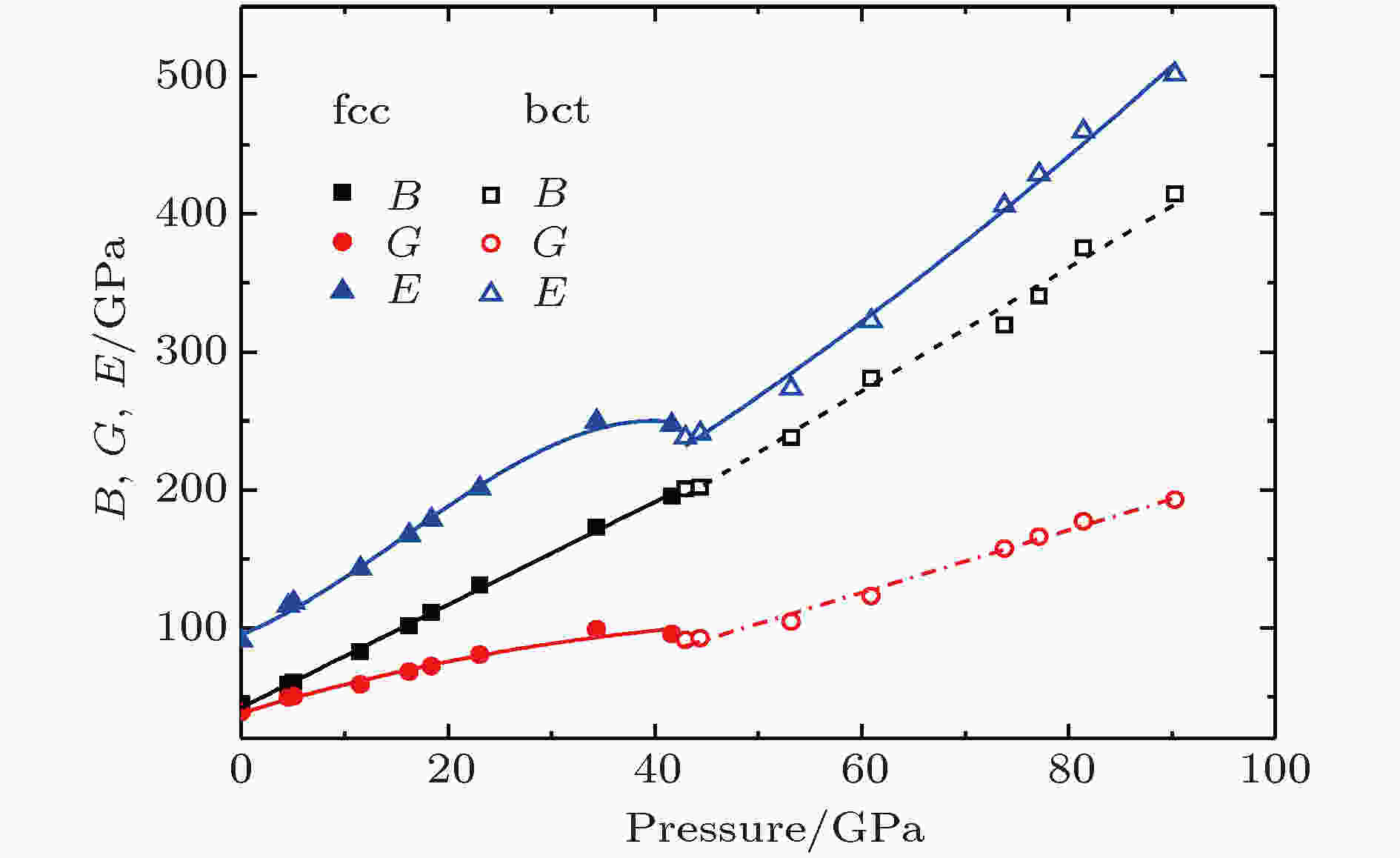图 4 剪切模量G、体模量B和杨氏模量E随压强的变化
Figure4. Shear modulus G, bulk modulus B and Young′s modulus E as functions of pressure.

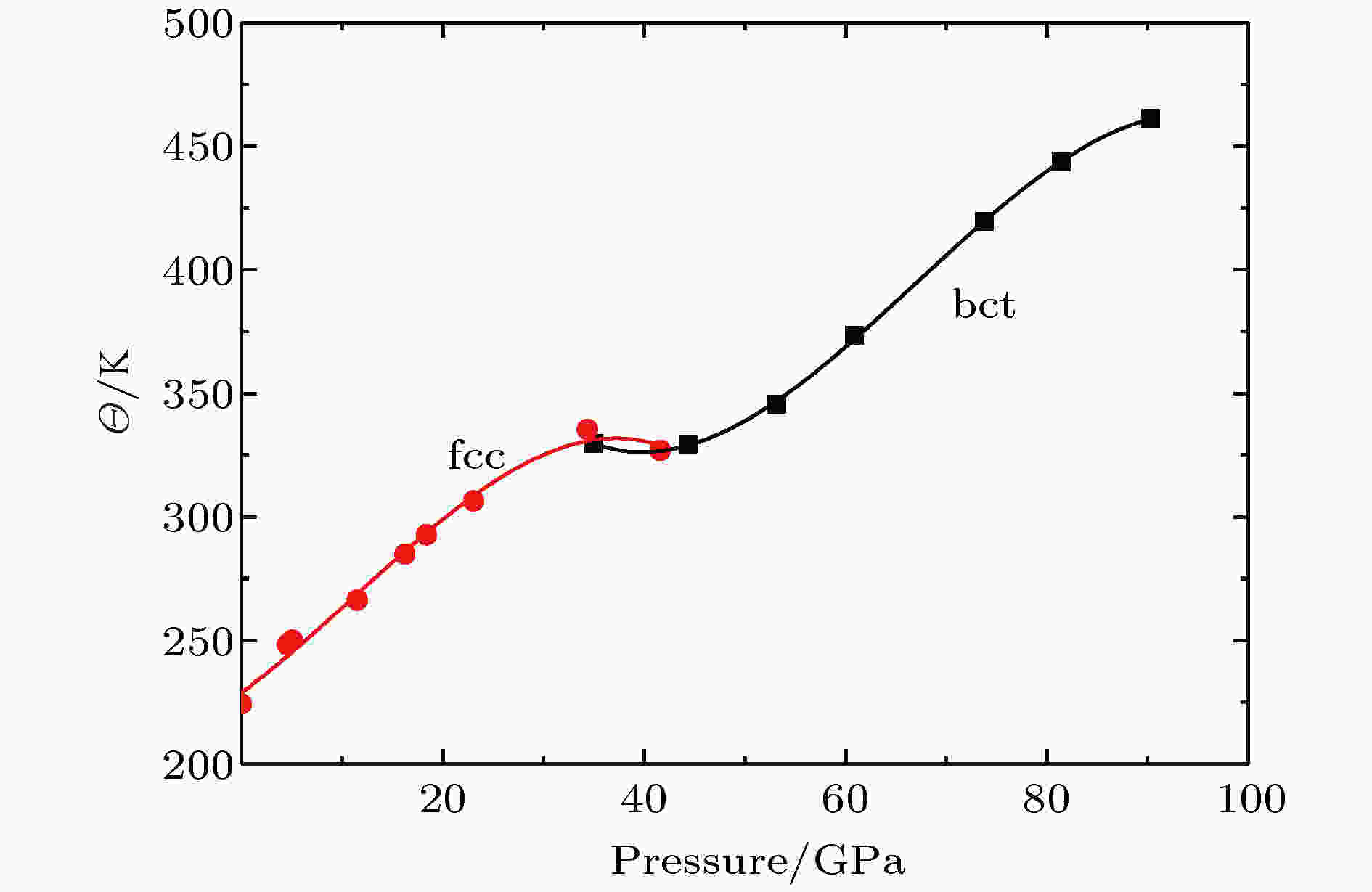图 5 德拜温度随压强的变化
Figure5. The Debye temperature as a function of pressure.

2 -->

3.3.热力学性质

利用准谐德拜模型获得了Ce_0.8La_0.1Th_0.1的热力学性质和不同温度下的等温压缩曲线. 如图6所示, 当温度为300 K, 压强从0 GPa上升到40 GPa时, fcc相体积缩小了约34.6%. 而在零压下, 当温度从300 K上升到1000 K时, fcc的体积膨胀了约11.1%. 高压状态下温度对体积的影响逐渐减小, 高温的非谐效应在压力的作用下被抑制. 当压强大于40 GPa时bct相稳定存在, 当温度为300 K, 压强从40 GPa上升到80 GPa时, bct 相体积缩小了约13.9%, 而在零压下, 当温度从300 K上升到1000 K时, bct相体积膨胀了约8.2%.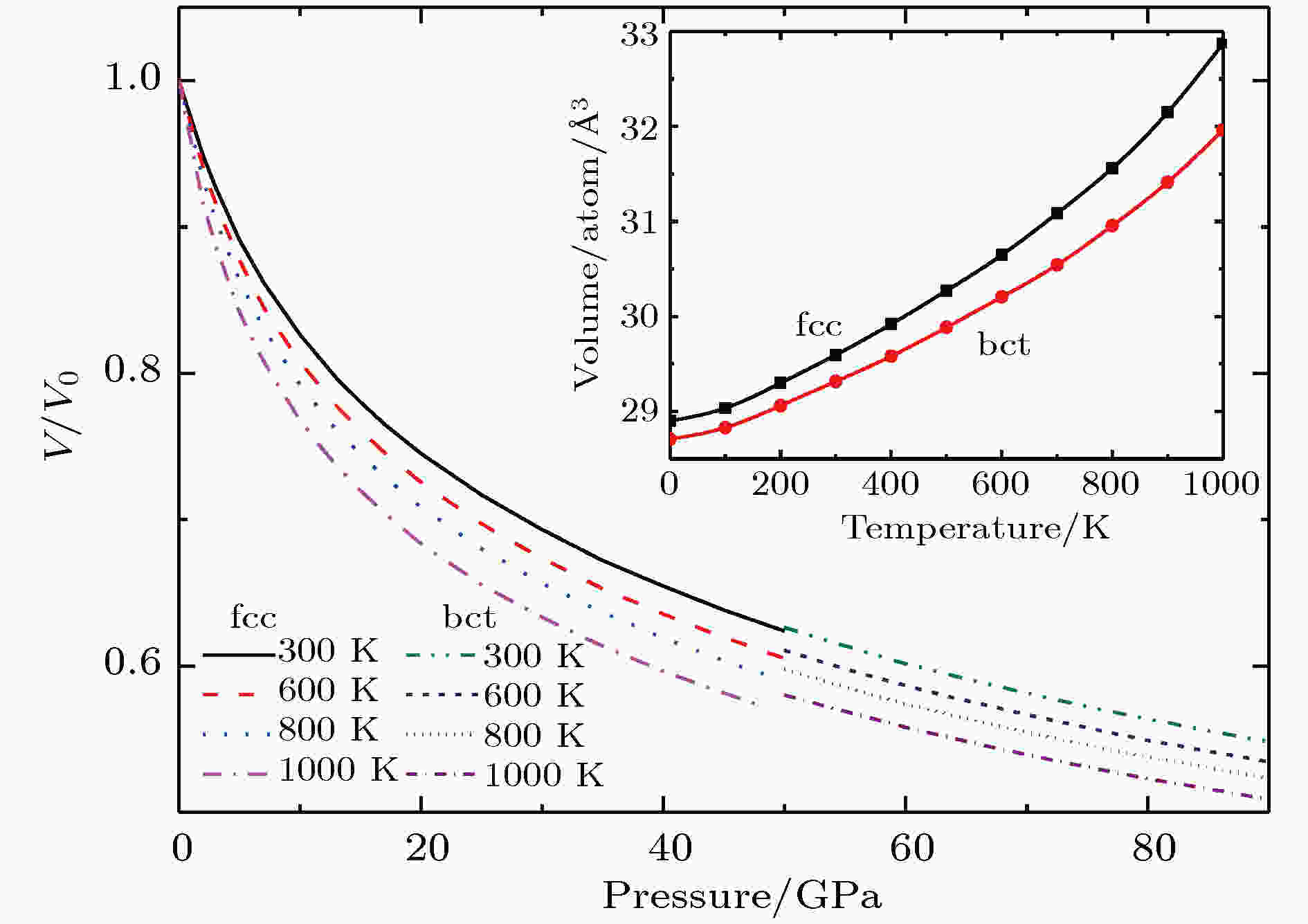
图 6 不同温度下的等温线, 其中V₀为零温零压下的体积, 小图为零压下体积随温度的变化
Figure6. Isotherms at different temperatures, where V₀ is the volume at zero temperature and zero pressure; the volumes at zero pressure as functions of temperature (the insert) .

分别计算了fcc相和bct相定容热容C_V随温度和压强变化的关系, 以及熵S随温度和压强的变化关系. 如图7所示, C_V随着温度升高迅速增加, 在高温下接近25 J/(mol·K)的极限, 热容在不同温度下随压强的变化情况几乎是单调递减的. 当温度超过600 K后, 不同等温线之间的差距变小. 计算得到在常温常压下的熵值约为49.44 J/(mol·K), 随温度的升高, 熵值几乎迅速单增, 在不同的温度下, 熵值随压强的增加而减小.
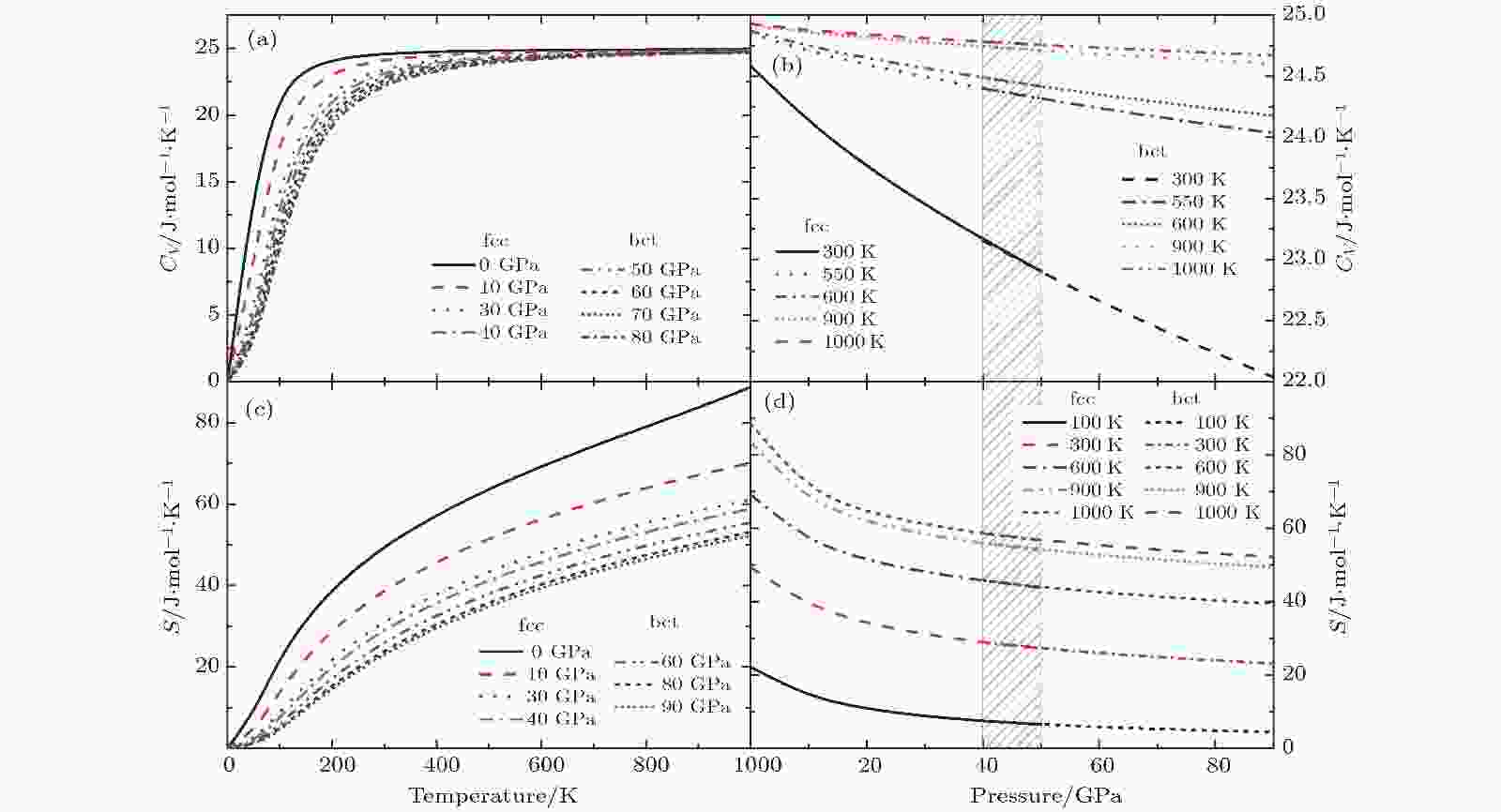图 7 定容热容C_V随温度(a)和压强(b)的变化, 以及熵S随温度(c)和压强(d)的变化; 图中阴影区域包含fcc和bct两相的数据
Figure7. The constant volume heat capacity C_V versus temperature (a) and pressure (b), and the entropy S versus temperature (c) and pressure (d).

本文采用第一性原理计算对Ce-La-Th合金在高压下fcc—bct的相变及热力学性质进行了研究讨论. 获得了Ce-La-Th合金体积随压强变化的规律, 随着压强的增加, 体积减小至20.1 ?³时, 晶格常数a, c的线性变化规律发生突变, 这意味着晶体结构出现了改变, fcc相开始变得不稳定. 通过分析轴向比c/a的值随压强变化的关系发现, 压强在大约31.6 GPa时fcc相开始向bct相转变, 在大约34.9 GPa时, bct相趋于稳定. 弹性性质的计算结果表明, 随着压强的增加, 在相变压强附近, 某些弹性常量出现非线性增加的情况, 当新相结构变得稳定再次趋于线性. 根据弹性常量计算得出的体模量随压强呈线性增加的趋势, 而杨氏模量E和剪切模量G则在相变压强附近出现“变软”的趋势, 当新相bct相趋于稳定时弹性模量再次趋于线性. 弹性德拜温度的计算结果与结构变化的规律类似, 从另一角度说明了相变的信息. 热力学性质的研究结果表明定容热容C_V随着温度升高而迅速增加, 在不同温度下随压强的变化呈单调递减. 随温度升高, 熵值迅速单增, 而在不同的温度下, 熵值随压强的增加而减小. 高压对温度带来的非谐效应有明显的抑制作用.