全文HTML
--> --> -->围绕纳米晶合金体系热稳定性较弱的关键问题, 研究人员进行了大量的实验研究和理论计算. Liu和Kirchheim[10-13]在多类合金体系中采用基于平衡态溶质偏聚理论的热力学计算和实验, 证实部分溶质元素通过晶界偏聚作用可有效增强纳米晶合金体系的热稳定性, 抑制中高温时纳米晶粒快速长大现象. Darling等[14]在Fe-Zr体系中的热力学计算和分子动力学模拟表明溶质元素的晶界偏聚效应可有效降低晶界形成能, 从而稳定纳米晶结构. Schuh等[15]基于偏聚热力学和蒙特卡罗模拟, 获得了不同温度下钨基纳米晶体系的稳定化元素优选图. 以W-Ti体系为例进行了实验验证, 结果表明在1100℃高温下退火1周仍能保持纳米晶平均晶粒尺寸约22 nm, 显示出W-Ti纳米晶体系优异的热稳定性. 综上, 选择合适的溶质元素, 使其产生强的偏聚作用, 能有效降低晶界形成能, 从而显著提高体系的热稳定性, 稳定纳米晶组织.
第一性原理计算作为微观尺度计算中的重要研究方法, 在合金材料的研究中得到了广泛的应用[16]. 根据第一性原理的预测结果, 优选不同合金体系中适合的掺杂元素, 可有效减少实验的盲目性, 提高研发效率, 同时揭示元素作用的微观机理, 为新材料设计提供理论支撑[17]. 进一步地, 对于纳米合金偏聚体系, 第一性原理可以从体系电子结构和能量的角度对体系的偏聚行为进行量化分析, 且所需经验参数极少, 因此非常适合用于界面特征分析和强偏聚元素筛选[18,19]. 例如, Reza等[20]在铝合金中采用第一性原理, 研究了界面的电子结构和溶质原子与界面原子的键合方式, 通过电荷密度和轨道相互作用分析揭示了不同族溶质元素在界面处成键的键强和键性的变化规律. Wu等[21]通过第一性原理对多类钨晶界类型和多种钨基合金掺杂元素体系进行了偏聚能、断裂能和强化能的计算, 研究了多种溶质元素对界面结合强度的影响机理. 孟凡顺等[22]通过第一性原理界面拉伸模拟, 分析了Zn掺杂对铜基材料特征晶界的成键能力和力学性能的影响机制. 综上, 基于第一性原理可有效探索不同溶质元素对钨基合金晶界性质的影响作用. 进一步地, 研究表明强偏聚元素通常有助于增强钨基纳米晶合金的热稳定性, 抑制高温下发生晶粒快速长大, 钨基合金体系中的强偏聚掺杂元素包括In, Ru, Sc和Th等[15] .
目前, 第一性原理较多的集中于溶质元素的优选, 缺乏溶质浓度对合金体系中溶质原子在界面扩散、偏聚、析出等行为的影响机制研究, 致使其预测结果与实际材料体系的实验结果仍存在较大偏差. 基于以上原因, 本文以目前鲜见报道的W-In体系强偏聚体系为例, 基于第一性原理晶界偏聚模型, 引入溶质浓度效应, 系统研究了W-In体系在不同溶质浓度和界面偏聚位点下的溶质偏聚行为和键合特征, 从电子结构层面揭示了W-In体系的键合方式和界面稳定化机制, 预测高热稳定性W-In体系的最佳溶质浓度添加范围.
2.1.模型构建
由于具有较高的晶界占据比例和较低的晶界能量,







































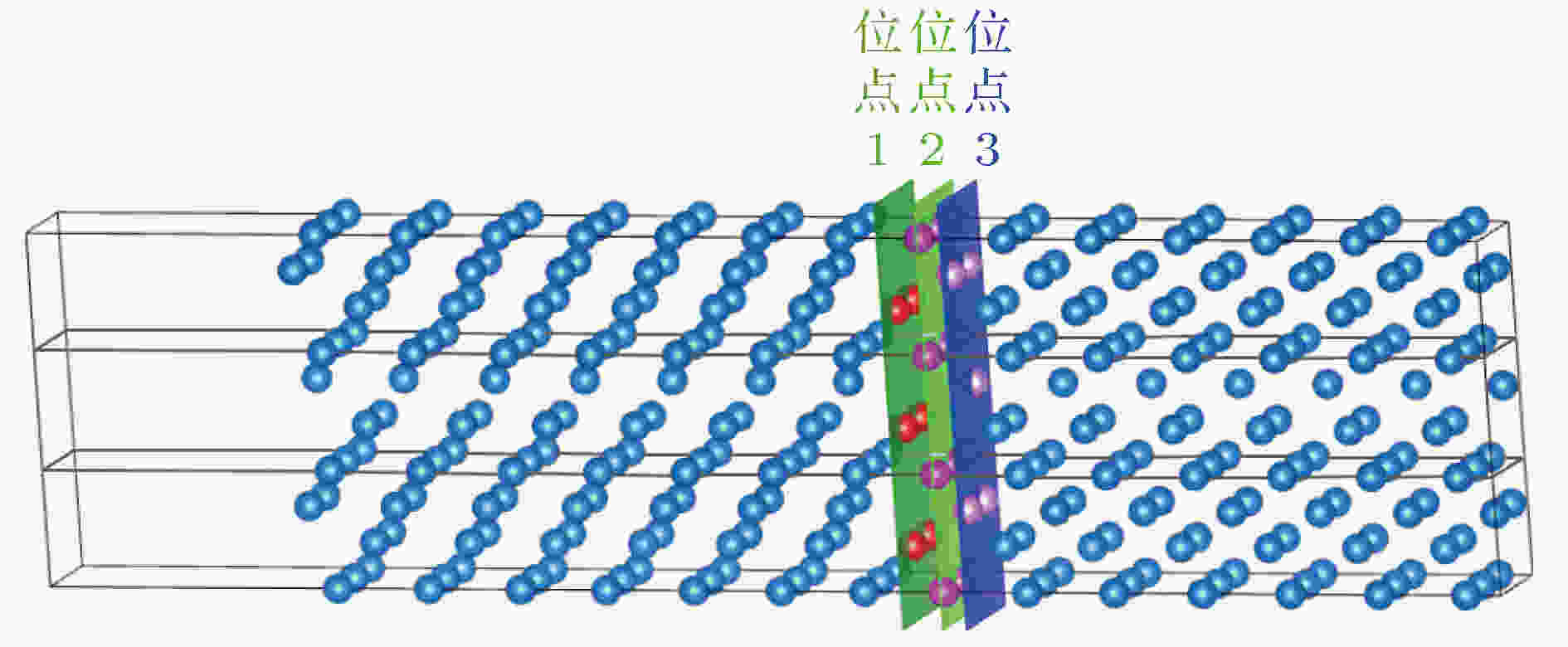 图 1
图 1 

Figure1. Diagram of


2
2.2.计算方法
本文所有的计算工作, 均采用Materials Studio软件中的CASTEP[25]软件包完成. 本文采用了超软赝势(ultrasoft pseudopotential, Usp)[26]进行模型计算, W和In的价电子结构分别为5s25p65d46s2和4d105s25p1, 泛函形式采取GGA-PBE (Perdew-Burke-Ernzerhof generalized gradient approximation)方法[27,28]. 对晶体结构和界面结构的优化计算采用BFGS方法[29]搜索最优结构, 平面波截断能为400 eV, k点设置为为5 × 5 × 1, 各项收敛参数为能量小于2 × 10–6 eV/atom, 原子间的相互作用力小于0.05 eV/?, 最大应力偏差小于0.1 GPa, 原子的最大位移变化小于0.002 ?.对溶质晶界偏聚行为的定量描述, 可以直接计算从晶界较远处偏聚到晶界区域的能量变化, 从而获得偏聚能. W-In体系中偏聚能计算公式[30]可表示为


此外, 对于不同溶质浓度下W-In体系的弹性常数计算, 采用W晶胞的2 × 2 × 2超胞进行模型构建, 总计包含16个原子, 计算中最大应变振幅设置为0.003, 每步应变步数为6.
3.1.键合作用分析
布居分析可得到电子在晶体内的分布情况, 量化键合作用的类型和强度, 同时能够为体系基态性质提供更多细节信息. 通常认为键布居数越接近0, 键的离子性越强; 反之越偏离0, 共价性越强. W-In体系晶粒内部和晶界区域的部分Mulliken键布居计算结果如图2所示. 图 2 不同溶质浓度下晶内和晶界区域的W—In键Mulliken布居分析 (a) xA = 0.0488; (b) xA = 0.0732; (c) xA = 0.122
图 2 不同溶质浓度下晶内和晶界区域的W—In键Mulliken布居分析 (a) xA = 0.0488; (b) xA = 0.0732; (c) xA = 0.122Figure2. Mulliken population analysis of W—In bond at grain interior and grain boundary at different solute concentrations: (a) xA = 0.0488; (b) xA = 0.0732; (c) xA = 0.122.
通过图2对比晶内区域和晶界区域的W— In键布居值可以发现, 在不同溶质浓度下, In原子由晶粒内部偏聚到晶界区域的过程中, 均发生了明显的键性变化: W—In键由离子键转变为共价键. 为了进一步探究W-In体系的键性转变现象, 接下来通过电荷密度图、差分电荷密度图和态密度图对键性转变现象进行系统的分析.
图3展示了不同溶质浓度下W-In体系的电荷密度和差分电荷密度. 如图3左图所示, 不同溶质浓度下界面处W—In键之间的电荷密度均小于晶内区域W—In键之间的电荷密度, 体现出与键布居结果相悖的电荷密度分布特征. 上述分析表明, 电荷密度没有反映出晶界W—In键的共价键特征. 其主要原因是: 在晶内区域, 原子排布有序, In原子掺杂之后, 与周围W原子的平均成键距离略短于界面区域W—In键的平均成键距离, 不同区域W—In键键长差异, 使得界面区域W—In键之间的电荷密度分布相比晶内区域W—In键的电荷密度分布可能略低, 二者对比分析导致界面W—In键的共价特征不明显. 为了排除电荷密度分析中晶内和晶界区域W—In键键长对键性分析的干扰, 进一步采用差分电荷密度对键性进行了分析, 以避免单纯通过电荷密度分析体系键性所导致的结果误判.
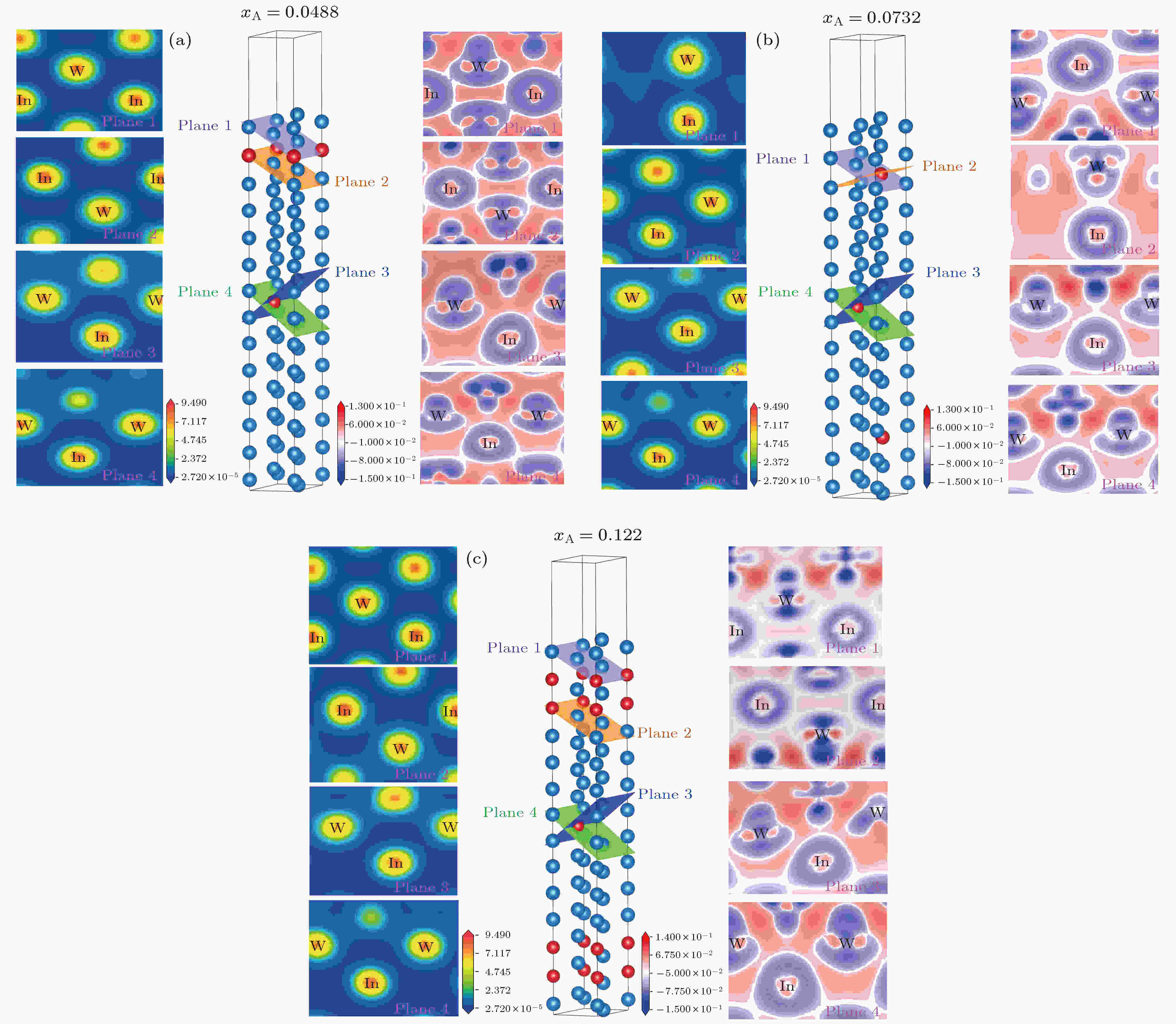 图 3 不同溶质浓度下W-In界面特性的电荷密度和差分电荷密度 (a) xA = 0.0488; (b) xA = 0.0732; (c) xA = 0.122
图 3 不同溶质浓度下W-In界面特性的电荷密度和差分电荷密度 (a) xA = 0.0488; (b) xA = 0.0732; (c) xA = 0.122Figure3. Charge density and charge density difference of W-In interface characteristics at different solute concentrations: (a) xA = 0.0488; (b) xA = 0.0732; (c) xA = 0.122
不同溶质浓度下的差分电荷密度图如图3右侧图所示. 差分电荷密度相比电荷密度, 反映的不是电荷聚集的程度, 而是电荷转移情况, 因此即便键长变化导致电荷密度变化, 但共价键(电子共用)和离子键(电子转移)的本质差异仍可以体现. 对应于电荷密度, 对不同的界面模型进行了差分电荷密度进行了计算, 结果如图3右侧图所示, 其中蓝色代表缺失电子, 红色代表富集电子, 白色代表不变.
通过观察晶内区域和晶界区域的差分电荷密度图可以发现, 在不同溶质浓度下, 晶内区域W—In键对应的W和In原子之间为白色, 表明二者之间不存在电子共用情况, 即不体现共价键的特性; 而在晶界区域, 构成W—In键的W原子和In原子之间呈现红色, 表明二者之间之间存在共用电子现象, 体现共价键特性. 通过上述分析, 采用差分电荷密度图可以明显区分晶内区域和晶界区域的W—In键的键性差异.
为了进一步研究键性变化, 对成键原子的态密度进行分析, 结果如图4所示. 我们可以发现晶界区域W原子和In原子偏态密度(PDOS)的共振强度明显高于晶粒内部, 表明在晶界区域形成共价键. 共价键的形成使得更容易产生强的偏聚效果, 使晶界能大大降低, 提高稳定性.
 图 4 不同溶质浓度晶内和晶界区域W和In原子的PDOS (a) xA = 0.0488; (b) xA = 0.122
图 4 不同溶质浓度晶内和晶界区域W和In原子的PDOS (a) xA = 0.0488; (b) xA = 0.122Figure4. PDOS of W and In atoms at grain interior and grain boundary at different solute concentrations: (a) xA = 0.0488; (b) xA = 0.122
溶质元素偏聚前后和基体的键合方式发生突变, 这在合金界面分析中较为少见, 结合W-In体系的电子结构特点, 现对体系偏聚过程中的键性转变现象作如下分析: W的价电子结构为 5s25p65d46s2, In的价电子结构为 4d105s25p1. 晶内区域W和In原子排布规则, 其中W原子提供4—6个价电子, In原子则提供3个价电子, 此时对应的W—In键中, 原子之间电荷分布的中心向W+4~+6离子实偏移, 具有离子键的成分[32]. 而在晶界区域, 由于结构较为松散, 空间较大, W周围存在大量悬链键, 未成键电子较多的聚集在W原子附近, 导致W原子的价态降低, 氧化性减弱, In原子周围的电子不再发生明显的转移, 而更多地出现在W和In之间, 导致键性从离子性转变为共价性.
2
3.2.溶质浓度效应
基于不同溶质浓度下的偏聚模型, 得到了多类界面偏聚位点下偏聚能随溶质浓度的变化关系, 如图5所示.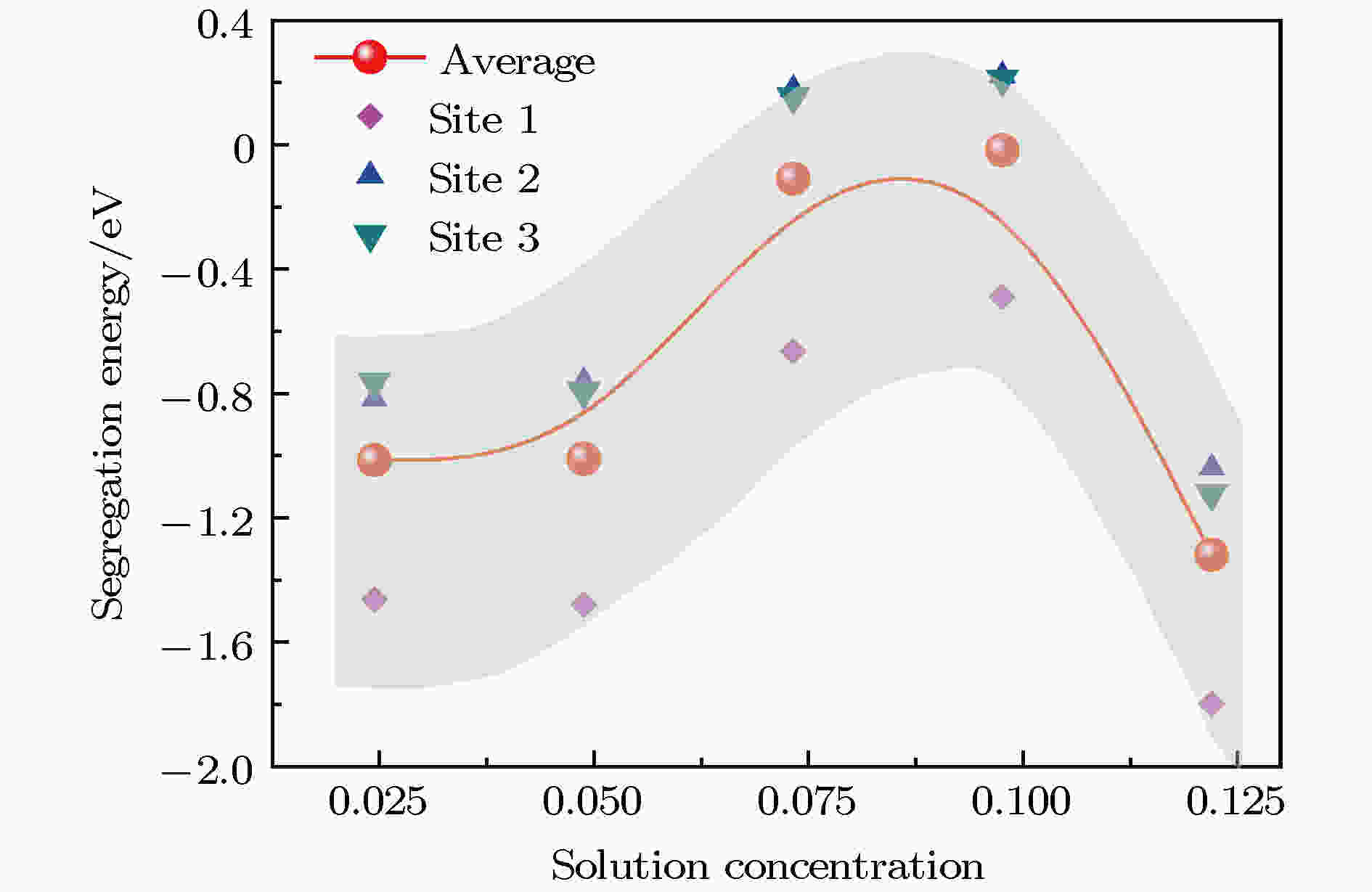 图 5 不同位点下偏聚能随溶质浓度的变化关系
图 5 不同位点下偏聚能随溶质浓度的变化关系Figure5. Segregation energy as a function of solute concentration corresponding to different sites.
由图5可以发现, 随着溶质浓度的增加, 偏聚能呈非单调变化的规律, 表明溶质偏聚能力随溶质浓度的增加先减弱再增强, 存在极值规律. 在极值点之前, 随溶质浓度的增加, 偏聚能趋于零, 表明其偏聚能力快速衰减; 但是随着溶质浓度的进一步增加, 超过极值点对应的浓度时, 体系偏聚能力显著提升. 根据经典理论, 通常认为偏聚能低于–0.5 eV的体系为强偏聚体系[33], 由图5可知, 当溶质浓度大于0.0976时, W-In体系再次成为典型的强偏聚体系.
为了分析偏聚能随溶质浓度变化的极值规律, 进一步对偏聚前后W-In体系的电子结构进行了分析. 如图6所示, 极值点所对应的溶质浓度为0.0976时, 偏聚前后体系中W和In原子的PDOS存在类似的共振关系, 说明此时In原子在晶内和晶界处与W原子的成键差异较小, In原子并不具有较强的晶界偏聚趋势. 进一步地, PDOS同时反映了W-In体系偏聚前后体系的形成能. 较小的PDOS差异说明W-In体系在该浓度点下偏聚前后的形成能差异较小. 形成能[34]可描述为
 图 6 溶质浓度为0.0976时溶质偏聚前后体系晶内和晶界区域W和In原子PDOS
图 6 溶质浓度为0.0976时溶质偏聚前后体系晶内和晶界区域W和In原子PDOSFigure6. PDOS of W and In atoms at grain interior and grain boundary before and after segregation at solute concentration of 0.0976.


不同溶质浓度下偏聚前后体系在晶内和晶界区域的键强和电子结构差异, 导致了不同溶质浓度下体系整体稳定性的差异, 并反映在偏聚前后的形成能差异中, 最终导致偏聚能随溶质浓度变化的非单调变化规律.
2
3.3.最佳浓度范围
为了确定W-In体系达到强偏聚所需的最佳溶质浓度范围, 进一步对其力学稳定性进行了分析. W-In属于立方晶系, 具有3个独立的弹性矩阵元(C11, C12, C44), 通过基于第一性原理的弹性常数计算, 得出结果见表1. 根据体心立方力学稳定性判据:| 溶质浓度 | C11 | C12 | C44 | C11 – C12 | C11 + 2C12 |
| 0 | 501.5 | 203.4 | 127.2 | 298.1 | 908.3 |
| 0.0625 | 488.0 | 201.7 | 140.0 | 246.3 | 2128.5 |
| 0.125 | 364.5 | 222.3 | 143.9 | 220.6 | 809.1 |
| 0.25 | 208.0 | 245.9 | 138.6 | –37.9 | 699.8 |
表1不同溶质浓度下的W-In体系弹性常数计算结果
Table1.Calculation results of elastic constants of W-In system at different solute concentrations. GPa
 图 7 W-In体系溶质浓度选取范围示意图
图 7 W-In体系溶质浓度选取范围示意图Figure7. Diagram of solute concentration selection range in W-In system.
综上, 结合W-In体系的电子结构和能量计算, 系统地揭示了W-In体系晶界偏聚过程中的溶质元素键性转变机制, 定量描述了体系的溶质偏聚行为, 预测了W-In体系热稳定性随溶质浓度的变化规律. 以上计算为钨基体系溶质元素优选提供了理论支撑, 同时为钨基纳米晶合金材料设计研发提供了新的思路.
1) 基于第一性原理, 首次建立了考虑溶质浓度效应的W-In体系晶界偏聚模型, 预测了该体系溶质原子偏聚过程中W—In键从离子性向共价性的转变规律. 结合几何结构和差分电荷密度分析, 揭示了键性变化的内在机理: 晶界结构和晶内结构的差异, 导致晶界区域内W原子价态降低, 氧化性减弱, 最终导致W—In键性转变.
2) 通过不同溶质浓度偏聚前后体系稳定性和电子结构, 揭示了偏聚能随溶质浓度非单调变化规律的内在机理, 进一步结合W—In键的PDOS分析, 获得了W-In体系偏聚能随溶质浓度变化规律的电子结构机理: 溶质浓度较大地影响了W-In键偏聚前后的键强度, 导致溶质浓度趋于0.0976时偏聚能力明显下降, 最终形成偏聚能随溶质浓度的极值规律.
3) 结合物相力学稳定性和溶质晶界偏聚分析, 在不考虑空位浓度的情况下, 模型预测其纳米晶体系中具有高热稳定性的最佳溶质浓度添加范围: 0.106—0.125; 同时也得到了需要规避的溶质浓度范围: 0.0632—0.106. 该模型对于W-In纳米晶合金材料的设计研发尤其是浓度调控起到了理论指导作用.
