摘要:纳米流体中悬浮的纳米颗粒可以增强其导热性能已经得到广泛认可, 然而纳米流体颗粒增强传热的机理目前尚不清楚. 研究表明, 纳米颗粒的聚集是纳米流体导热系数增大的重要机制, 而且纳米颗粒聚集的形态对纳米流体的导热系数有重要影响, 但是目前的导热系数模型大多是建立在Maxwell有效介质理论的“静态”和“均匀分散”假设基础上. 本文用平衡分子动力学模拟Cu-Ar纳米流体, 采用Green-Kubo公式计算导热系数, 采用Schmidt-Ott关系式计算不同聚集形态下的分形维数. 对比导热系数与分形维数可以发现: 在相同体积分数下, 较低的分形维数会有更高的导热系数, 分析了分形维数与导热系数的定量关系. 此外, 通过径向分布函数可以看出纳米颗粒紧密聚集与松散聚集的差异, 基液分子在纳米颗粒附近的纳米薄层中处于动态平衡状态. 研究结果有助于理解纳米颗粒聚集形态对导热系数的影响机理.
关键词: 纳米流体/
聚集形态/
分形维数/
导热系数

English Abstract

全文HTML

--> --> -->

近20年来, 纳米流体作为传热介质能极大地提高传热性能, 引起了众多****的兴趣. 1995年, Choi^[1,2]发现在液体中加入纳米颗粒大大提高了液体的导热性能, 尤其是在低纳米颗粒体积分数的情况下(一般小于0.01%)尤为明显. 所谓纳米流体就是纳米颗粒稳定悬浮在液体中形成的胶体. 通常使用有效导热系数来评估纳米流体的导热性能, 有效导热系数模型最初是根据Maxwell有效介质理论建立的^[3], 模型假设纳米颗粒在液体中是静态和均匀分散的. 此后, Hamilton和Crosser^[4], Xuan等^[5], 王补宣等^[6]以及Prasher等^[7]分别考虑了非球形纳米颗粒、纳米颗粒的布朗运动、纳米颗粒外的纳米薄层以及纳米颗粒的聚集, 建立了新的有效导热系数模型. 但是, 以上这些模型都是在Maxwell模型的框架基础上得到的, 并不能摆脱纳米颗粒在液体中是静态和均匀分散的假设. 目前的实验结果、理论结果和数值模拟结果之间尙有不少矛盾之处, 原因是迄今为止纳米流体强化传热的微观机理尚不清楚. Lin等^[8]研究了球形颗粒和柱状颗粒纳米流体的导热, 发现柱状颗粒的纳米流体导热强于球形颗粒的纳米流体. 李屹同等^[9]针对ZnO-水纳米流体, 研究了纳米颗粒周围液体分子的密度分布, 解释了纳米层提高纳米流体导热系数的机理; 但是Xue等^[10]的结论是纳米颗粒周围的纳米层对热传递没有影响, 如果考虑界面热阻, 纳米层甚至会降低热导率. Keblinsk等^[11]对一系列实验结果的综合分析表明, 布朗运动、纳米层和近场辐射都不是提高纳米流体热导率的关键原因, 最根本的是纳米颗粒的聚集.
在实验中很容易观察到纳米颗粒的聚集^[12,13], 颗粒聚集对于导热系数的影响方面已经有不少成果^[14-25]. Sedighi和Mohebbi^[14]通过分子动力学研究得出, 在一定的纳米颗粒浓度下, 纳米颗粒的聚集可以提高纳米流体的导热系数. Hong和Kim^[15]的研究也表明纳米颗粒的凝胶状聚合可以大大增加导热系数. 最令人惊讶的是含有Fe₃O₄纳米颗粒的磁流体在外磁场的作用下形成直链状聚集, 该方向上的导热系数是基液的三倍^[16], 比其他聚集状态下的导热系数大得多. 尽管如此, 一些研究工作表明, 由于聚集形态各异, 纳米粒子的聚集并不一定能提高纳米流体的导热系数^[17]. Thaseem和Christopher^[18]也表示, 在不同聚集形态下, 5%体积分数下的纳米流体的导热系数可以增加51%或减少32%. 为了探索颗粒聚集对有效导热系数的影响规律, 研究者已经建立了一些导热系数模型, 如Xuan等^[19]较早在Maxwell有效介质理论^[3]基础上建立了考虑颗粒聚集的有效导热系数模型; Feng等^[20]建立了一个考虑纳米颗粒聚集的新模型, 研究表明纳米粒子越小, 聚集越多, 有效热导系数越大; Wang等^[21]在Hamilton^[4]模型的基础上, 用聚集体等效半径和分形维数建立了有效导热系数模型; Evans等^[22]在Bruggeman模型和Maxwell-Garnett理论的基础上, 建立了一个考虑纳米颗粒聚集的新模型, 并用蒙特卡罗直接模拟得到了验证; Prasher等^[23]将聚集的颗粒分成在骨架和在死端两类, 分别考虑对导热的影响后进行叠加, 得到了与聚集体惯性半径、分形维数和化学维数相关的导热系数模型, 最后与模拟结果比较时也只考虑了分形维数d_f = 1.8一种情况; Xiao 研究组^[24,25]以分形理论为基础建立了有效导热系数的分形模型, 模型包含静态部分和动态部分, 静态部分根据Maxwell-Garnett模型得到, 动态部分考虑了旋转椭球的Brownian运动引起的对流传热, 其中旋转引起的对流传热和尺寸分布都与分形维数相关. 总之, 目前已经建立的考虑颗粒聚集的导热系数模型, 依然以Maxwell有效介质理论为基础, 再考虑聚集对尺寸分布、纳米层和布朗运动等的影响, 没有涉及纳米流体中聚集体的分形维数对导热系数的影响的定量分析, 也没有验证静态部分和动态部分简单叠加的正确性.
聚集类型有两种^[26], 分别为克服第一势能壁垒的紧密聚集(reaction limited aggregation, RLA)和克服第二势能壁垒的松散聚集(diffusion limited aggregation, DLA). Gaganpreet ^[27]从介观角度分析了纳米流体的传热, 结果表明: 松散聚集情况下纳米颗粒聚集体分形维数较低、规模较大、导热系数较高, 且松散聚集体生长迅速, 但容易被剪切稀化. Kang等^[28]和Duan等^[29]的研究也表明, 聚集形态对导热系数和黏度的影响很大, 更大规模的聚集会导致更大的导热系数和更大的黏度, 产生非牛流特征, 而超声处理后, 聚集结构被打破, 导热系数减小, 黏度也会减小, 非牛顿流现象就会消失. Lin等^[30]研究了Al₂O₃纳米颗粒在湍流作用下聚集和破碎对导热的影响, 得到了努赛尔数与聚集体平均尺寸的关系表达式.
分子动力学模拟是研究纳米流体传热强化的有效方法, 但由于计算量庞大, 只适合于模拟小系统. 最近几年有使用分子动力学模拟来探究纳米粒子聚集行为对纳米流体导热系数影响的报道^[14], 在分子动力学模拟中, 计算纳米流体导热系数的方法有: 平衡态分子动力学模拟和非平衡态分子动力学模拟. 平衡态分子动力学模拟基于Green-Kubo公式, 非平衡态分子动力学模拟基于导热系数的定义. 此外, 不同分子之间的势函数难以确定和评估, Cu-Ar纳米流体的势函数有经验值, Kang等^[31]利用Lennard-Jones (L-J)势描述了氩原子之间的相互作用, 并采用嵌入原子势(embedded atom method, EAM)描述了铜原子之间的相互作用. Lee等^[32]对纳米流体中颗粒聚集和非聚集状态下的热导系数进行了分子动力学模拟, 结果表明纳米颗粒聚集时的热导系数比非聚集的情况下提高了35%. 李凌等^[33]研究了Cu-Ar纳米流体时也得到了类似结论.
综上可知, 直链状聚集时导热系数比其他聚集状态大得多, 说明聚集形态会对导热系数产生重要影响. 然而, 迄今为止还没有纳米颗粒聚集形态对导热系数的影响的定量研究, 也未见导热系数模型采用静态部分和动态部分简单叠加的正确性验证. 本文针对Cu-Ar纳米流体, 用分子动力学模拟的方法, 定量分析分形维数对纳米流体导热系数的影响, 揭示添加纳米颗粒增强纳米流体传热系数的内在机制.

与文献[14, 34]一样, 本文选用Cu-Ar纳米流体来研究导热系数, 这是采用分子动力学手段研究不同聚集形态下纳米流体导热系数的理想选择, 因为在Cu-Ar纳米流体中仅需考虑两体势, 而不用像以水为基液时还需要考虑点电荷等因素, 大大减小了计算量. 本文模拟中采用L-J势函数, 其与液氩的实验数据非常吻合. 分子动力学是基于牛顿第二定律来计算模型中每个原子的运动状态的一种数值模拟方法, 即

${m_i}\frac{{{{\rm{d}}^2}{{ x}_i}}}{{{\rm{d}}{t^2}}} = \sum\limits_j {{{F}_{{ij}}}} ,$

式中${m_i}$为第$i$颗原子的质量, ${{{x}}_i}$为第$i$颗原子的位置矢量, ${{F}_{{ij}}}$为截断半径内第$j$颗原子对第$i$颗原子的作用力. 分子动力学中, 采用(1)式对颗粒的坐标及速度进行更新, 其他宏观的物理量可以用统计物理的方法计算得到.
2

-->

2.1.势函数的选择

在模拟中选取Ar作为基液, Cu纳米颗粒为面心立方结构, 其晶格常数为3.165 ?^[34]. 为了简便起见, 假设Cu纳米颗粒中的所有Cu原子具有相同的速度和加速度^[32]. Ar-Ar之间采用L-J势函数:

${\varphi _{ij}} = 4{\varepsilon _{ij}}\left[ {{{\left(\frac{{{\sigma _{ij}}}}{r}\right)}^{12}} - {{\left(\frac{{{\sigma _{ij}}}}{r}\right)}^6}} \right],(r < {r_{\rm{c}}}),$

式中${\varepsilon _{ij}}$为势阱深度; ${\sigma _{ij}}$为两颗颗粒相互作用为0时的距离; $r$为第$i$颗颗粒与第$j$颗颗粒之间的距离; ${r_{\rm{c}}}$为截断半径, ${r_{\rm{c}}}$一般大于2.5${\sigma _{ij}}$.
对于Cu原子之间的相互作用, 可以采用更加精准的EAM势函数^[35]. 经过试算比较, 发现Cu原子之间用EAM势和用L-J势时结果相差无几, 但用L-J势时计算量明显减小, 故采用用L-J势. Ar原子与Cu原子之间的作用可以用Berthlot混合法则求得^[36]:

$\left\{ \begin{aligned}&{\varepsilon _{{\rm{Ar {\text{-}} Cu}}}} = \sqrt {{\varepsilon _{{\rm{Ar {\text{-}} Ar}}}} \cdot {\varepsilon _{{\rm{Cu {\text{-}} Cu}}}}}, \\&{\sigma _{{\rm{Ar {\text{-}} Cu}}}} = \left( {{\sigma _{{\rm{Ar{\text{-}} Ar}}}} + {\sigma _{{\rm{Cu{\text{-}}Cu}}}}} \right)/2.\end{aligned} \right.$

此外, 三种原子之间的作用关系如图1所示, 所有颗粒的截断半径统一设置为10 ?, 具体结果列于表1.
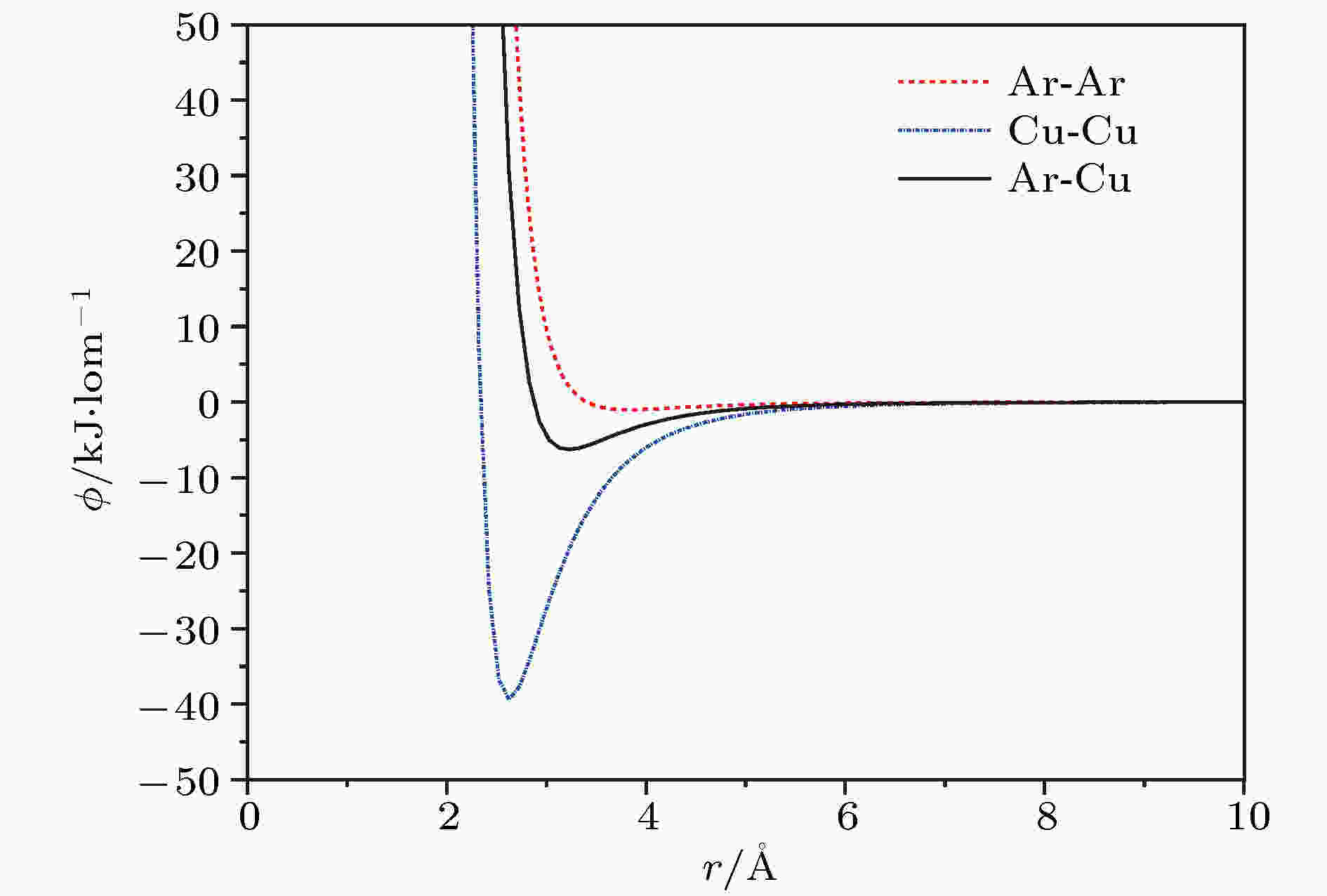图 1 不同原子间的相互作用势
Figure1. Potential functions between various particles interaction.

原子	$\varepsilon $/10–2 eV	$\sigma $/nm
Ar-Ar	1.0437	0.3405
Cu-Cu	41.0156	0.2338
Ar-Cu	6.5429	0.2871

表1势函数参数
Table1.Parameters of potential functions.

2 -->

2.2.导热系数的计算

平衡分子动力学与非平衡分子动力学都可以计算纳米流体的导热系数, 本文选择平衡分子动力学, 原因有: 1)在平衡分子动力学中, 可以用单次模拟来计算纳米流体的导热系数, 而在非平衡分子动力学中, 需要模拟多个体系求得多个温度梯度; 2) 当系统处于非平衡状态时, 非平衡分子动力学的计算稳定性不如平衡分子动力学, 而且当热通量过大时可能会引起模拟体系的崩溃; 3)与非平衡分子动力学方法相比, 平衡分子动力学方法计算纳米流体所需要的模拟体系的体积更小, 可大大减少计算量^[37].
本文中的模拟采用正则系综(NVT), 即原子的数量$N$, 系统的体积$V$, 系统的温度$T$均保持不变. 在该系综下, 可以采用Green-Kubo公式计算纳米流体的导热系数, 因为不存在外加的驱动力, 故系统一直处于线性响应状态. 纳米流体的导热系数可由以下公式求出:

$k = \frac{1}{{3{K_{\rm{B}}}TV}}\int\limits_0^t {\left\langle {{{{J}}_0}} \right.\left. {{{{J}}_t}} \right\rangle } {\rm{d}}t,$

式中$k$为导热系数; ${K_{\rm{B}}}$为Boltzman数; $\left\langle {{{{J}}_0}} \right.\left. {{{{J}}_t}} \right\rangle $为热流自相关函数, ${{{J}}_0}$,${{{J}}_t}$分别为时刻0与时刻$t$的热流矢量, 尖括号为系综平均或时间平均.
2 -->

2.3.分形维数的计算

颗粒聚集体通常是由一定数量的基础颗粒聚集成随机的微结构. 由于聚集过程复杂, 纳米流体中的大多数聚集体具有较广的尺寸分布^[38]. 尽管它们的大小、形状、回转半径和颗粒密度各不相同, 但这些具有复杂几何形状的聚集体可以用分形维数去衡量^[39]. $N$颗直径为${d_{\rm{p}}}$的颗粒组成的聚集体, 其回转半径为${R_{\rm{g}}}$, 则Schmidt-Ott公式可表示为

$N = {\left( {\frac{{{R_{\rm{g}}}}}{{{d_{\rm{p}}}}}} \right)^{{D_{\rm{f}}}}},$

式中${D_{\rm{f}}}$为分形维数, 是评估聚集形态的主要指标, 表示纳米颗粒的填充程度. 理论上分形维数的大小在1.0—3.0范围内, 在纳米流体中, 分形维数大多在1.4—2.7范围内. 本文中每个纳米颗粒在聚集体中的位置可以通过分子动力学模拟得到, 随后可以根据如下公式计算回转半径, 即聚集体中两个死端^[40]的最大距离

${R_{\rm{g}}} = \max \{ r_{ij}^{{\rm{de}}}\} ,$

式中${\rm{de}}$表示死端(dead end), $r_{ij}^{{\rm{de}}}$为第$i$个死端到第$j$个死端的距离.
2 -->

2.4.其他参数设置

在模拟中先使用NVT进行弛豫, 再在微正则系综(NVE)下收集数据, 并在三个方向上均使用周期边界条件^[41]. 每个时间步各原子的位置与速度采用Verlet算法, 这一算法在Ar和Cu体系中具有良好的稳定性^[42]. 在分子动力学模拟中, 时间步长是影响计算量、准确性和稳定性的关键, 太小的时间步长会导致计算量巨大, 而太大的时间步长会导致系统崩溃, 对Cu-Ar纳米流体在85 K的恒温条件下进行经过一系列试验计算后, 确定时间步长设置为10 fs.

2

-->

3.1.模型验证

在计算Cu-Ar纳米流体的导热系数之前, 先计算液氩的导热系数, 以验证计算方法和程序. Sarkar和Selvam^[43] 研究表明, 当颗粒数目大于500时, 系统的导热系数与系统中的颗粒数无关. 本文中, 4000颗Ar原子以面心立方结构(FCC)分布在5.72 nm × 5.72 nm × 5.72 nm的模拟盒子中. 在弛豫阶段, 采用Nose-Hoover热浴使得系统的温度保持在85 K. 在收集数据计算导热系数阶段, 撤去热浴, 以免影响热流的计算^[39]. 热流计算公式如下:

${{J}} = \frac{1}{V}\left(\sum\limits_i {{e_i}{{{v}}_i}} - \sum\limits_i {{{{S}}_i}{{{v}}_i}} \right),$

式中${{J}}$为热流矢量; ${e_i}$为第$i$颗原子的能量, 即动能与势能之和; ${{{v}}_i}$为第$i$颗原子的速度矢量; ${{{S}}_i}$为第$i$颗原子的应力张量.
由于模拟是针对的离散时间的, 故(3)式可以离散为

$k({t_M}) \!= \!\frac{{\Delta t}}{{3{K_{\rm{B}}}V{T^2}}}\!\sum\limits_{m = 1}^M {\frac{1}{{N - m}}}\!\sum\limits_{n = 1}^{N - m} {\left\langle {{J}} \right.(m + n){{J}}(n\left. ) \right\rangle } ,$

式中${t_M}{\rm{ = }}M\Delta t$; ${{J}}(m + n)$为模拟中第$(m + n)$时间步时的热流矢量, 平均热流矢量随时间变化被称为热流自相关函数; $N$为模拟总时间步数; $M$为计算导热系数所需要的步数. 为了避免收集的数据之间存在关联性, 每隔10个时间步进行一次数据采样, 采用1000个数据计算导热系数. 如此进行100次, 将计算得到的100个导热系数做算术平均得到最终的导热系数. 由于聚集体时在不断运动中, 隔了10个计算步, 聚集体的位置也发生了变化, 这种做法相当于空间中对100维进行平均.
如图2所示, 归一化的热流自关联函数很快收敛到0, 这样就可以进行数据采样了. 图3所示为每次计算得出的导热系数, 图中每根细线代表一次计算, 粗线代表最终的平均结果. 由于氩的熔点和沸点非常接近, 分别为84和87.5 K, 为此本文模拟85 K下的液氩的导热系数, 数值为0.131 W/(m·K), 与文献[30]中液氩在85 K下实验得到的0.129 W/(m·K)相比, 误差仅为1.55%.
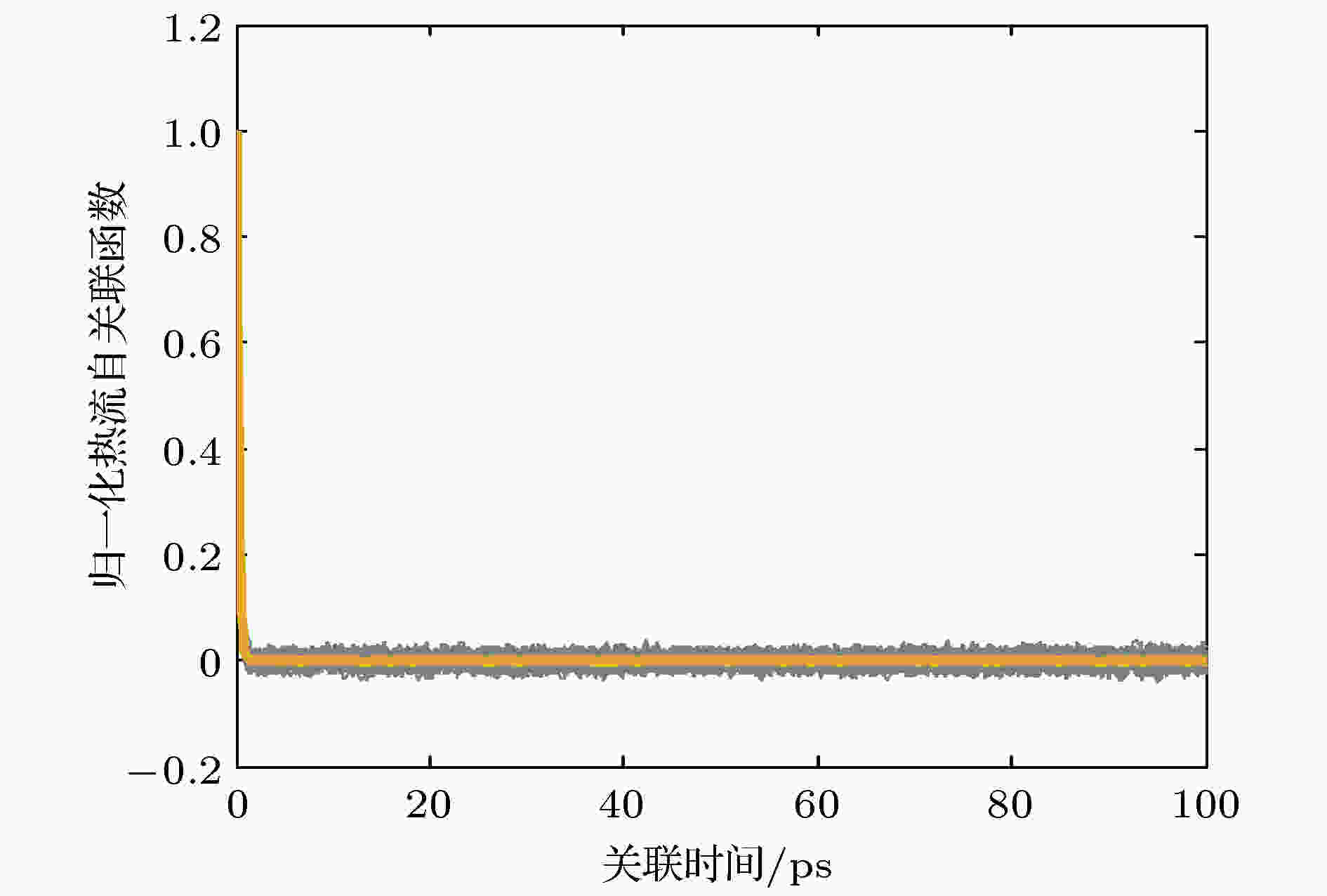图 2 归一化的热流自关联函数
Figure2. Normalized heat current autocorrelation function.

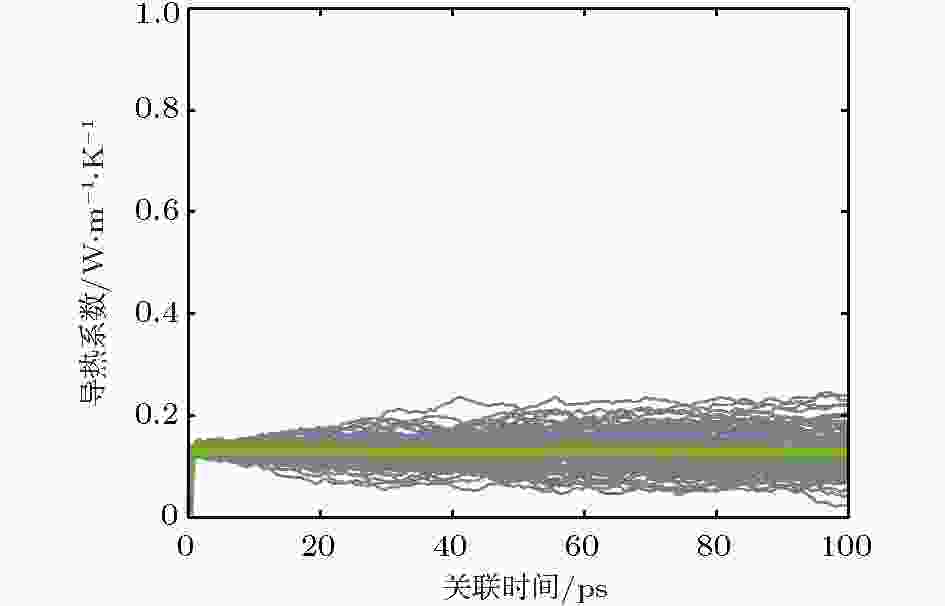图 3 液氩在85 K时的导热系数
Figure3. Thermal conductivity of Ar at 85 K.

由于Cu-Ar纳米流体没有实验得到的导热系数, 故通过与已发表的数值模拟结果对比来判断模型的有效性. 如图4所示, 在模拟盒子的中心位置, 用一颗由327颗铜原子组成的粒径为1.926 nm的铜纳米颗粒代替原本位置上共计79颗的Ar原子, 则纳米颗粒的体积分数为2%. 铜原子堆积方式为面心立方堆积. 图5为Cu-Ar纳米流体的模型. 采用与计算液氩导热系数相同的方式计算前文所描述的2%体积分数的Cu-Ar纳米流体, 其结果为0.165 W/(m·K), 与文献[30]中得到的结果相吻合, 验证了计算模型和程序的有效性.
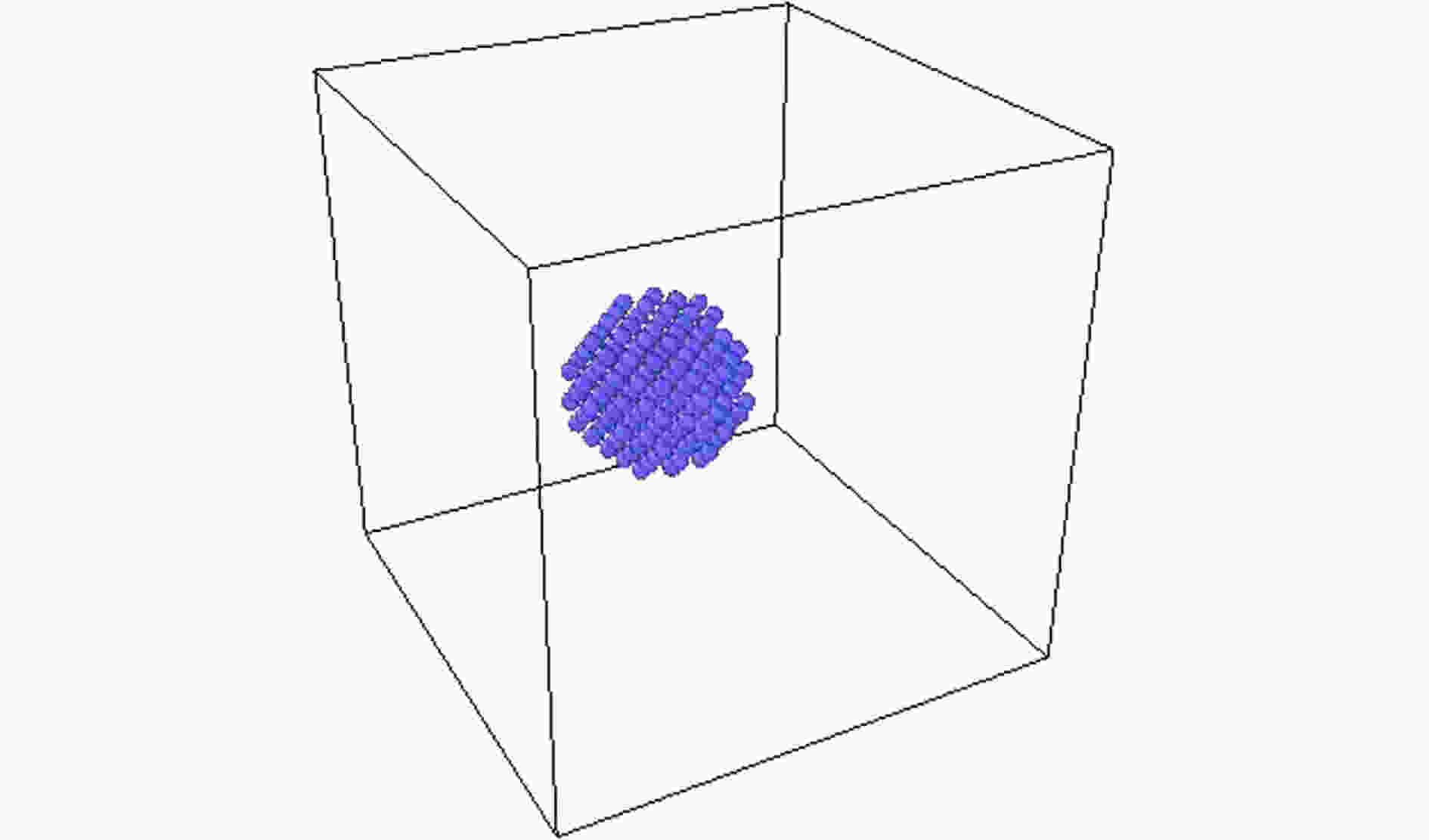图 4 铜纳米颗粒模型
Figure4. Model of Cu nanoparticle.

图 5 Cu-Ar纳米流体模型
Figure5. Cu-Ar nanofluid model.

2 -->

3.2.纳米颗粒周围的纳米薄层

纳米颗粒周围的纳米薄层被认为是纳米流体导热系数的重要影响因素之一, 但仍有不少研究人员提出相反的观点^[9,10,14,34]. 为了揭示纳米颗粒周围纳米薄层增强导热的内在机理, 采用分子动力学模拟来获取在能量最小化后运行10个时间步的Cu纳米颗粒周围Ar原子的分布, 如图6所示. 由于Cu原子与Ar原子之间更强的相互作用, 部分Ar原子被吸引聚集在铜纳米颗粒周围. 纳米颗粒周围0.5 nm的Ar原子分布如图7(a)所示, 在该时间点2000时间步后, 这些原子的位置如图7(b)所示. 由图可见部分Ar原子会离开原来的纳米薄层, 但是会有大约相同数量的Ar原子被吸附, 纳米薄层达到一种动态平衡. 这可能是纳米薄层增强传热的关键机理, 因为这种动态平衡下纳米颗粒与Ar原子间可以不断产生能量交换, 也因此用界面热阻的观点解释显得不合理^[10].
图 6 能量最小化后的纳米薄层结构
Figure6. Nanolayer at minimizational system energy.

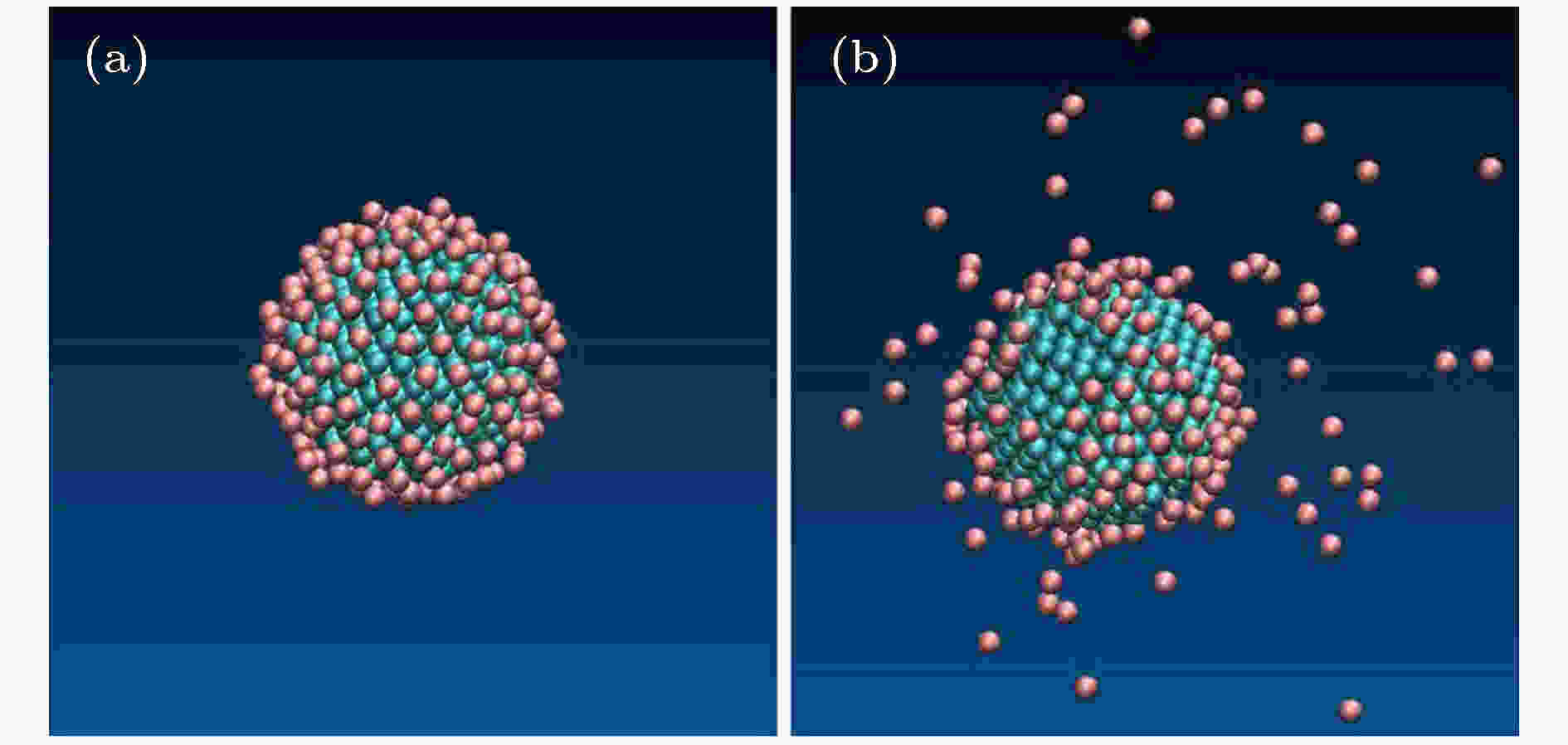图 7 铜纳米颗粒周围的Ar原子初始分布(a)和2000步时的分布(b)
Figure7. Initial distribution (a) and at 2000th time-step (b) of Ar-atoms around Cu-nanoparticle.

2 -->

3.3.纳米颗粒聚集

当纳米颗粒间的斥力较小而引力较大时, 颗粒会产生聚集. 如引言中所述, 聚集方式有紧密聚集RLA和松散聚集DLA两种^[26]. 当电子浓度足够高时, 静电引力克服颗粒之间的斥力时会产生紧密聚集, 而当电子浓度中等情况下, 不能完全克服颗粒之间的斥力则会产生松散聚集. 在本文的模拟体系中, 采用两颗相同大小的纳米铜颗粒进行模拟. 图8(a)和图8(b)分别显示了紧密聚集和松散聚集两种聚集, 从图8可以清楚地看出: 松散结构中的两个铜纳米颗粒之间存在一层Ar原子, 而在紧密聚集中的两个纳米颗粒之间有直接接触.
图 8 纳米颗粒聚集　(a)紧密聚集; (b)松散聚集
Figure8. Aggregation of nanoparticles: (a) Compact aggregation; (b) loose aggregation.

径向分布函数可以解释为局部密度(local density)与总体密度(bulk density)之比, 写作:

$g(r) = \frac{{n(r)}}{{{\rho _0}V}} \approx \frac{{n(r)}}{{4{\text{π}}{r^2}{\rho _0}\delta r}}, $

$G(r) = 4{\text{π}}{r^2}\rho g(r), $

式中$r$为距中心原子的距离, ${\text{δ}}r$为球壳厚度, $n(r)$为球壳内的粒子数, ${\rho _0}$为理想晶体中数密度; $g(r)$为对分布函数, $G(r)$为径向分布函数. 对于液体体系, 参考原子的附近($r$值较小)区域密度不同于系统的平均密度, 但与参考原子距离较远时区域密度应与平均密度相同, 即$r$值较大时, 径向分布函数的值接近1. 图9(a)所示为液氩体系的对分布函数, 体现了液体分子短程有序、长程无序的特点. 而含有一颗纳米颗粒的对分布函数与液氩不同, 如图9(b)所示, 其最左侧出现的峰是由于Cu-Ar之间的作用大于Ar-Ar之间的作用造成的, 由此可以推断, 在纳米颗粒周围形成了一层由Ar原子组成的致密的纳米薄层.
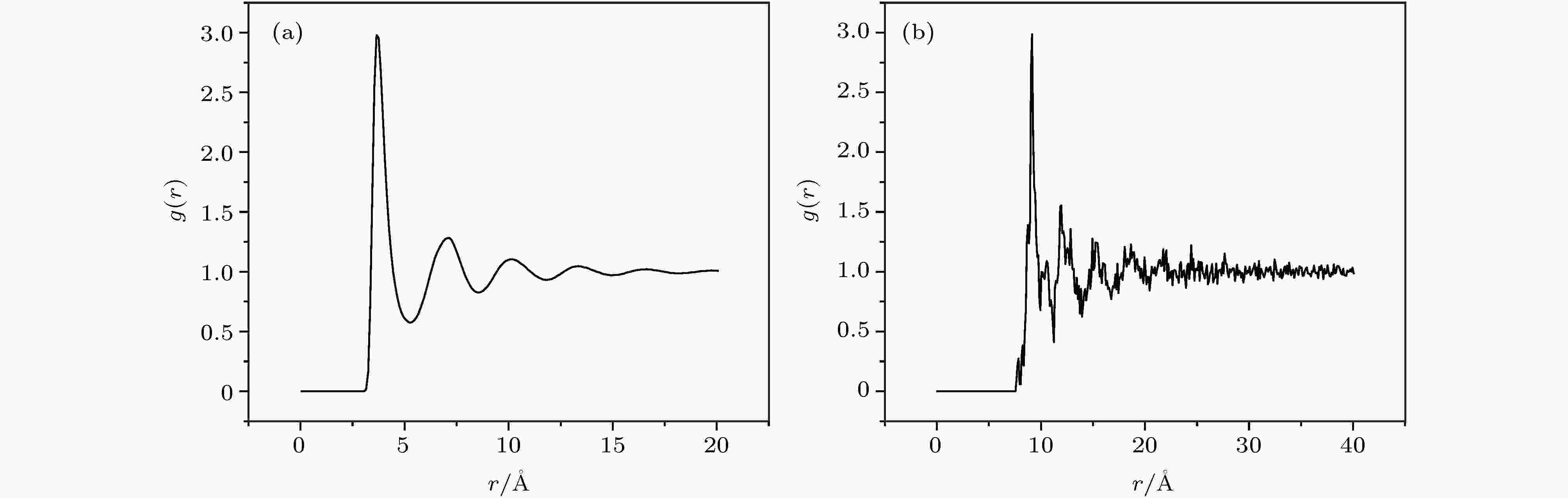图 9 对分布函数　(a)液氩体系; (b) Cu-Ar纳米流体
Figure9. Pair correlation function of fluid Ar (a) and nanofluid Cu/Ar (b).

当模拟体系中存在两颗纳米颗粒时, 情况发生了变化. 图10(a)所示为两颗纳米颗粒未发生聚集时的对分布函数, 图10(b)所示为两颗纳米颗粒发生松散聚集时的对分布函数, 观察可见两者几乎相同, 而且与图10(b)中存在单颗纳米颗粒的情形十分类似. 在图10(b)中, 两颗纳米颗粒中心的距离经计算为22.358 ?, 而图中第一个峰出现的位置距纳米颗粒的中心为11.142 ?. 前者略大于后者的2倍. 这一现象表明, 松散聚集可以理解为纳米颗粒及其周围的纳米薄层作为一个整体产生聚集, 其中纳米薄层占6.358 ?, 纳米颗粒的粒径为16 ?. 而在如图10(c)所示的紧密聚集中, 两颗纳米颗粒质心的距离为15.237 ?, 略小于纳米颗粒的粒径, 这与图8(a)和图8(b)所示的情形一致.
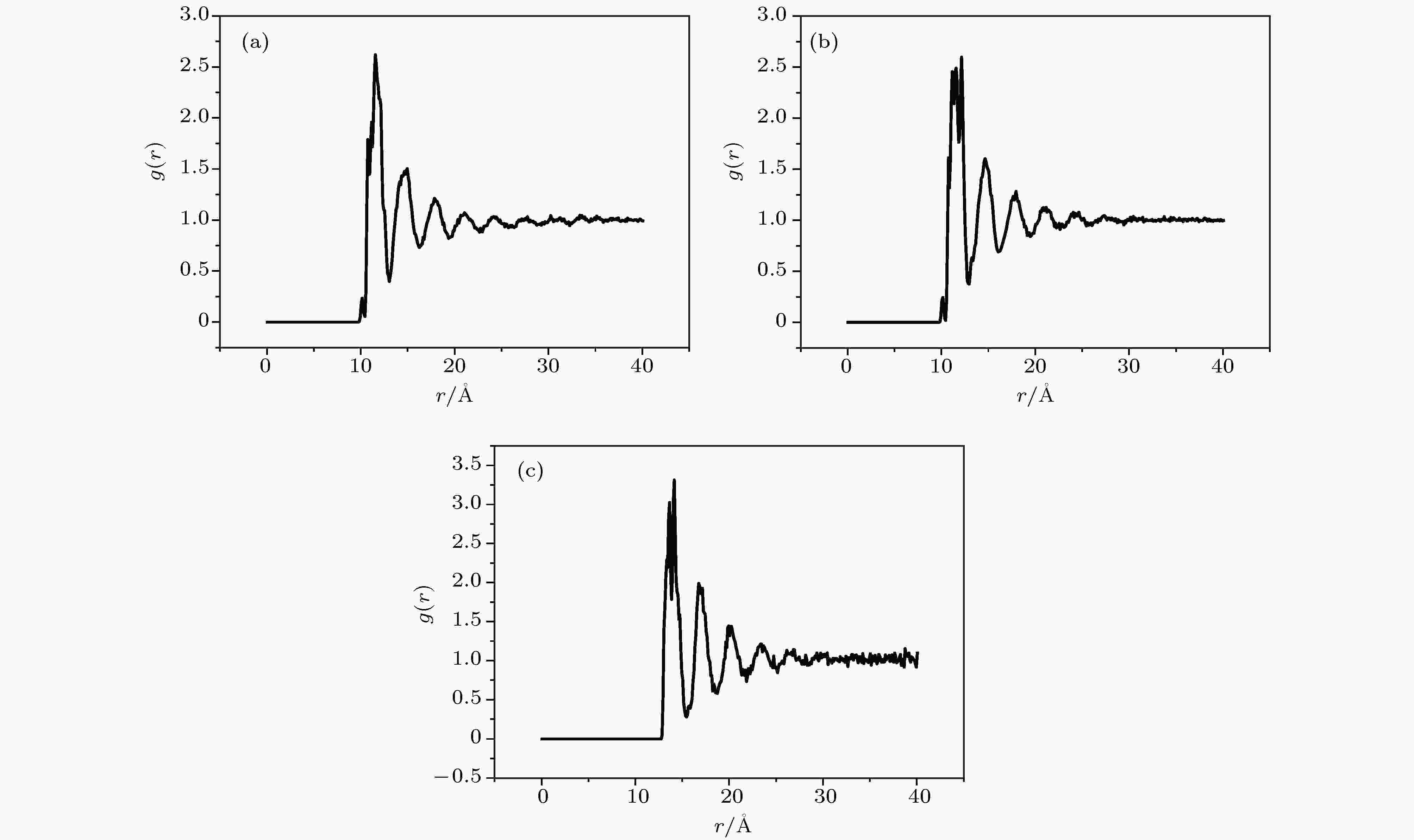图 10 两颗纳米颗粒下纳米流体的对分布函数　(a)分散; (b)松聚集; (c)紧聚集
Figure10. Pair correlation function of nanofluid with two nanoparticles: (a) Dispersed nanoparticle; (b) loose aggregation; (c) compact aggregation.

2 -->

3.4.聚集形态和热导系数

一些研究表明, 在分散状态下纳米颗粒的形状会对于强化传热产生影响^[7,44-46]. 然而, 在聚集状态下纳米颗粒形态对传热的影响尚无定量的研究. 通过分子动力学模拟计算了Cu-Ar纳米流体的导热系数, 并根据模拟得到的纳米颗粒的质心位置计算分形维数. 为了减少计算量, 本文选用包含3—6颗纳米颗粒的小系统. 在模拟中, 纳米颗粒的大小根据其体积分数计算确定, 以便在只改变体积分数的情况下, 模拟盒中存在相同数量的纳米粒子. 计算结果列于表2和表3中.

体积分数	2%							3%							4%
颗粒数目	3			4				3			4				3			4
聚集形态
分形维数	1.07	1.72		1.36	1.55	1.70		1.06	1.75		1.48	1.69	1.90		1.06	1.72		1.34	1.59	2.01
导热系数/W·m–1·K–1)	0.168	0.172		0.194	0.189	0.171		0.235	0.216		0.241	0.221	0.217		0.268	0.253		0.254	0.246	0.242

表23—4颗纳米颗粒下的导热系数与分形维数
Table2.Thermal conductivity for various aggregation morphologies with 3?4 particles.

聚集方式
分形维数	1.31	1.33	1.39	1.45	1.60	1.67	1.98
导热系数/W·m–1·K–1)	0.321	0.335	0.315	0.294	0.278	0.271	0.252

表36颗粒4%体积分数时导热系数与分形维数
Table3.Thermal conductivity for various aggregation morphologies with 6 particles.

从表2中可以看出, 分形维数在1—2之间, 这与大多数实验结果不符(大部分为1.4—2.7范围), 其主要原因是本文模拟体系中的纳米颗粒数少(最多6颗), 而实验测量中是有成百上千的纳米颗粒聚集在一起. 另外从表2还可以看出, 体积分数越大, 导热系数越大, 但其增量随体积分数的增大而减小, 这与已发表的研究成果相一致^[47]. 另外, 分形维数越小, 对应的导热系数越大, 但由于纳米颗粒大小的不同, 会存在一些例外, 如对比表2与表3中4%体积分数下的结果, 可以发现分形维数为1.60的6个颗粒的导热系数为0.278 W/(m·K), 而分形维数为1.59的4个颗粒的导热系数为0.246 W/(m·K), 其原因是同体积分数下, 6个纳米颗粒的粒径更小. 从具有相同体积分数的3个颗粒和4个颗粒的比较中也可以得出同样的结论. 从图11中可更清楚地看出, 在体积分数和纳米颗粒尺寸一定的情况下, 随着分形维数的增加, 热导系数几乎线性减小, 而且这种关系随着体系中颗粒数的增大更加明显.
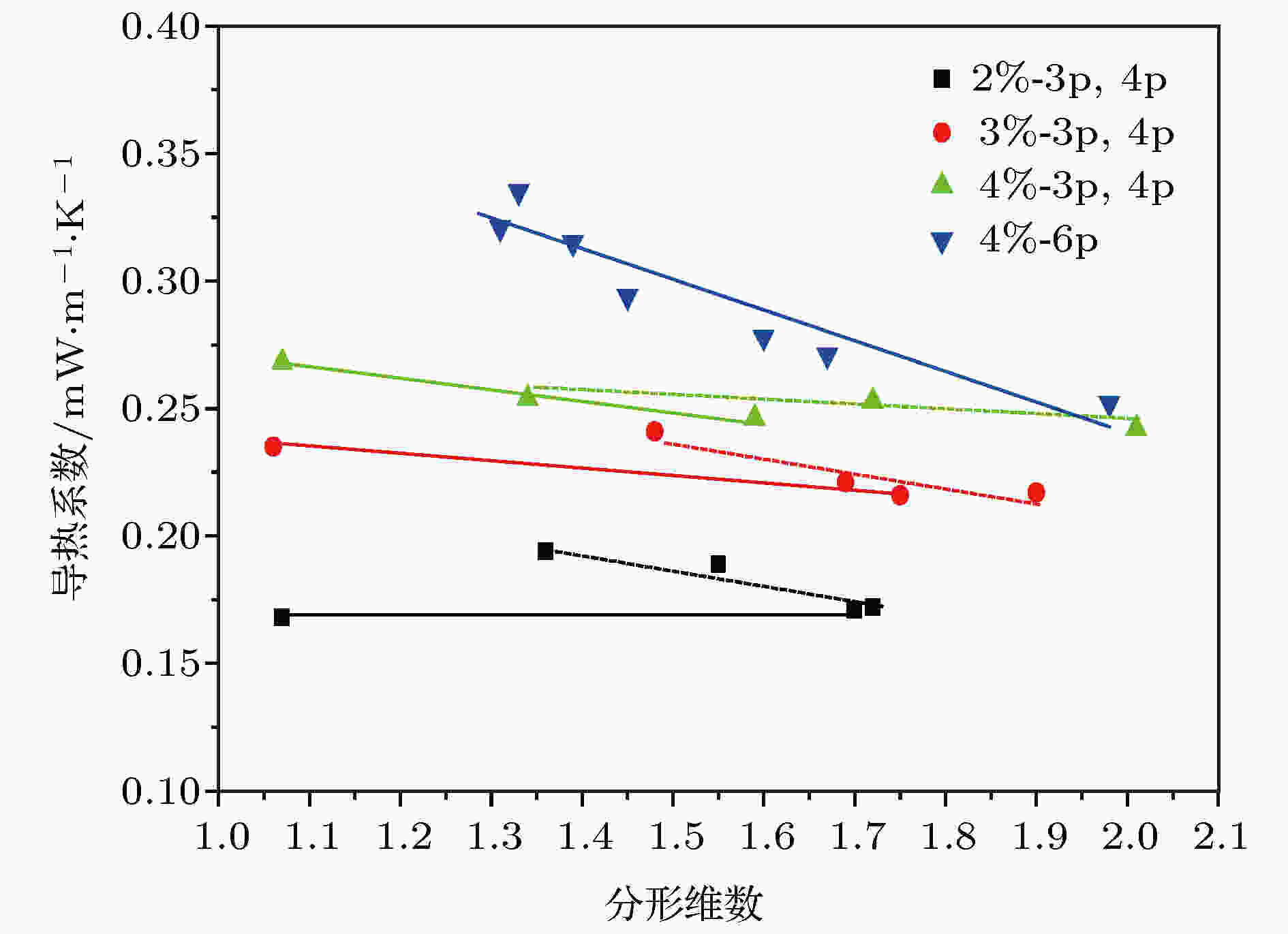图 11 分形维数与导热系数对比(3颗为实线, 4颗为虚线)
Figure11. Thermal conductivity at various fractal dimensions (3-p solid line, 4-p dash line).

现有的研究成果表明, 纳米颗粒的聚集对纳米流体的导热性有着很大的影响. 采用平衡态分子动力学模拟并通过Green-Kubo公式计算热导系数; 随后, 从模拟中获取纳米颗粒的质心位置并通过Schmidt-Ott公式计算出聚集体的分形维数; 此外, 还分析了单颗纳米颗粒和两颗纳米颗粒情况下的对分布函数. 本文得出以下结论:
1)纳米颗粒的聚集方式可分为紧凑聚集(RLA)和松散聚集(DLA)两种, 松散聚集情况下, 两颗纳米颗粒之间存在着纳米薄层, 而紧密聚集情况下两颗纳米颗粒直接接触;
2)纳米颗粒周围纳米薄层的厚度可以从径向分布函数中读出, 此外, 纳米薄层中的基液分子达到动态平衡, 这应该是纳米层增强传热的内在机理之一, 也说明界面热阻来解释边界层传热是不合理的;
3)纳米颗粒体积分数越大, 纳米流体的导热系数就越大, 但其增量会随体积分数的增大而减小,如果纳米颗粒的体积分数和粒径均固定, 导热系数随聚集体分形维数的减小而几乎线性增大, 且较小尺寸的纳米颗粒聚集更有利于提高纳米流体的导热系数.