摘要:本文采用基于密度泛函理论的第一性原理平面波赝势和局域密度近似方法, 优化了立方和六方氮化硼的几何结构, 系统地研究了零温高压下立方和六方氮化硼的几何结构、力学、电学以及光学性质. 结构与力学性质研究表明: 立方氮化硼的结构更加稳定, 两种结构的氮化硼均表现出一定的脆性, 而六方氮化硼的热稳定性则相对较差; 电学性质研究表明: 立方氮化硼和六方氮化硼均为间接带隙半导体, 且立方氮化硼比六方氮化硼局域性更强; 光学性质结果显示: 立方氮化硼和六方氮化硼对入射光的通过性都很好, 在高能区立方氮化硼对入射光的表现更加敏感. 此外, 还研究了高温高压下立方氮化硼的热力学性质, 并得到其热膨胀系数、热容、德拜温度和格林艾森系数随温度和压力的变化关系. 本文的理论研究阐述了高压下立方氮化硼和六方氮化硼的相关性质, 为今后的实验研究提供了比较可靠的理论依据.
关键词: 氮化硼/
电子结构/
弹性性质/
光学性质

English Abstract

全文HTML

--> --> -->

Ⅲ-Ⅴ族材料的氮化硼(Boron Nitride, BN), 有着优良的性能. 立方氮化硼(cubic Boron Nitride, c-BN)的硬度、弹性模量仅次于金刚石, 石墨化温度、对铁族元素的化学稳定性远远优于金刚石^[1-4], 这使它在机械加工、高温深井、地热等钻探方面有着无可比拟的优势. 从紫外光到红外光的波长范围内, c-BN的透过率都很好^[3,5], 可用作光学窗口的保护涂层材料. c-BN通过掺入不同的杂质元素^[2,3,6,7], 可以制作成不同类型的半导体, 在高温、高功率和高频电子设备方面具有很大的应用潜力^[8,9]; c-BN 也可以制成在紫外范围内工作的紫外(ultraviolet, UV)探测器和UV发光二极管^[3,4]. c-BN的热导率比较高, 与GaAs, Si等半导体材料的热膨胀系数相近, 可用作散热封装材料^[10]. 六方氮化硼(hexagonal Boron Nitride, h-BN)是最轻、离子型最强的Ⅲ-Ⅴ族材料. h-BN的熔点高^[11]、耐腐蚀^[12], 是优良的高温耐火材料. 二维的h-BN纳米片有很好的导热率, 在热封装材料方面有着潜在的应用价值^[13,14]. h-BN在室温下是宽带隙半导体^[15,16], 经过掺杂的h-BN在微电子和光电子^[17-21]等方面有着广泛的应用. 另外, h-BN的纳米结构可用作高导热和电绝缘的聚合复合材料的填料^[22]. 因此, c-BN和h-BN的研究引起了人们的极大兴趣和广泛关注.
目前, 理论计算的准确性和可靠性都得到了极大提高, 计算结果在研究领域也得到了广泛的认可和接受, 很多研究者对BN也进行了一系列的理论研究. 如: 2012年, 李宇波等^[23]采用密度泛函理论(density functional theory, DFT)下的平面波赝势方法, 详细分析了c-BN不同空位的能带结构、电子态密度. 2016年, 王帅^[24]采用第一性原理平面波超软赝势的方法, 计算了c-BN及其掺杂体系的电子结构、形成能和磁学性质. 2017年, Lu等^[25]采用包含色散力校正的DFT方法, 研究了气体分子在Co掺杂单层BN表面的吸附情况. 2018年, 张宁超和任娟^[26]采用第一性原理方法, 研究了稀土金属La吸附掺杂对BN纳米管储氢性能的影响. 2006年, 贾建峰和武海顺^[27]采用第一性原理计算创造性地研究了h-BN纳米管内含有C纳米管的结构与电学性质. 2007年, Azevedo等^[28]采用数值原子轨道展开价电子波函数, 研究了h-BN不同缺陷的稳定性和形成能. 2009年, Azevedo等^[29]给出了h-BN电子结构和磁性性质等. 2016年, 颜平兰和李金^[30]采用DFT方法, 研究了不同应变状态单原子层h-BN的光学性质. 2017年, 卢浩^[31]利用第一原理计算, 得到h-BN/Sb在应力作用下, 其间接带隙可转变成直接带隙.
综上所述, 现有的研究主要涉及BN的结构、力学、电学等方面, 很少有文献报道其热学和光学方面的内容. 为此, 本文采用基于DFT的第一性原理方法系统地计算c-BN和h-BN的结构、力学、光学、热力学和电子结构方面的性质, 并与已有的计算结果和实验数据进行比较.

本文计算是在Material Studio软件中的CASTEP模块中完成的. 计算时分别选用局域密度近似(local density approximation, LDA)近似下的CA-PZ方法描述电子间的交互关联能, 超软赝势(ultrasoft pseudopotential, USPP)描述原子核与价电子之间的相互作用, 用平面波基组的方法展开电子波函数. 赝势计算考虑的原子核外层电子组态为: B: 2s² 2p¹和N: 2s² 2p³. 经收敛性测试, 最终确定c-BN和h-BN的平面波截断能 E_cutoff = 600 eV, K点分别取11 × 11 × 11(c-BN)和11 × 11 × 4(h-BN), 使用自洽循环求解Kohn-Sham方程的能量收敛值设为5 × 10^–6 eV/atom, 最大应力控制在2 × 10^–3 eV·?^–1以内. 计算时, 采用Broyden-Fletcher-Goldfarb-Shenno(BFGS)最小算法先对BN单胞中原子位置进行结构优化, 使结构达到最稳定的状态, 并在此基础上分别计算c-BN和h-BN的力学性质、光学性质、电子结构以及c-BN的热力学性质. 最后, 值得说明的是, 本文选用模守恒赝势(norm-conserving pseudopotentials, NCPP)和较大截断能(E_cutoff = 900 eV)计算声子谱.

2

-->

3.1.结构性质

计算时, 首先对c-BN和h-BN的晶胞进行结构优化, 以寻找最稳定的结构状态, 经过优化的晶格常数如表1所列.

结构	晶格常数/?	a	c
c-BN	实验值	3.615
	本文计算值	3.576
	其他计算值	3.583[6], 3.627[32], 3.589[33], 3.581[34], 3.576[35], 3.583[36]
h-BN	实验值	2.504[37]	6.661[37]
	本文计算值	2.485	6.610
	其他计算值	2.485[32], 2.489[33], 2.489[36]2.496[38], 2.489[39]	6.491[32], 6.561[33], 6.501[36], 6.490[38], 6.501[39]

表1c-BN和h-BN 晶胞晶格常数的计算值和实验值^[6,32?39]
Table1.Calculated and experimental value of lattice constants for c-BN and h-BN cells^[6,32?39]

由表1可以看出, 计算结果与实验值符合较好, 说明本研究可靠性比较高. 为了获得表1中列出的理论平衡体积V₀, 首先计算得到0 K时的E-V数据, 然后用三阶Birch-Murnaghan状态方程拟合得到V₀, 相应的图形如图1所示.
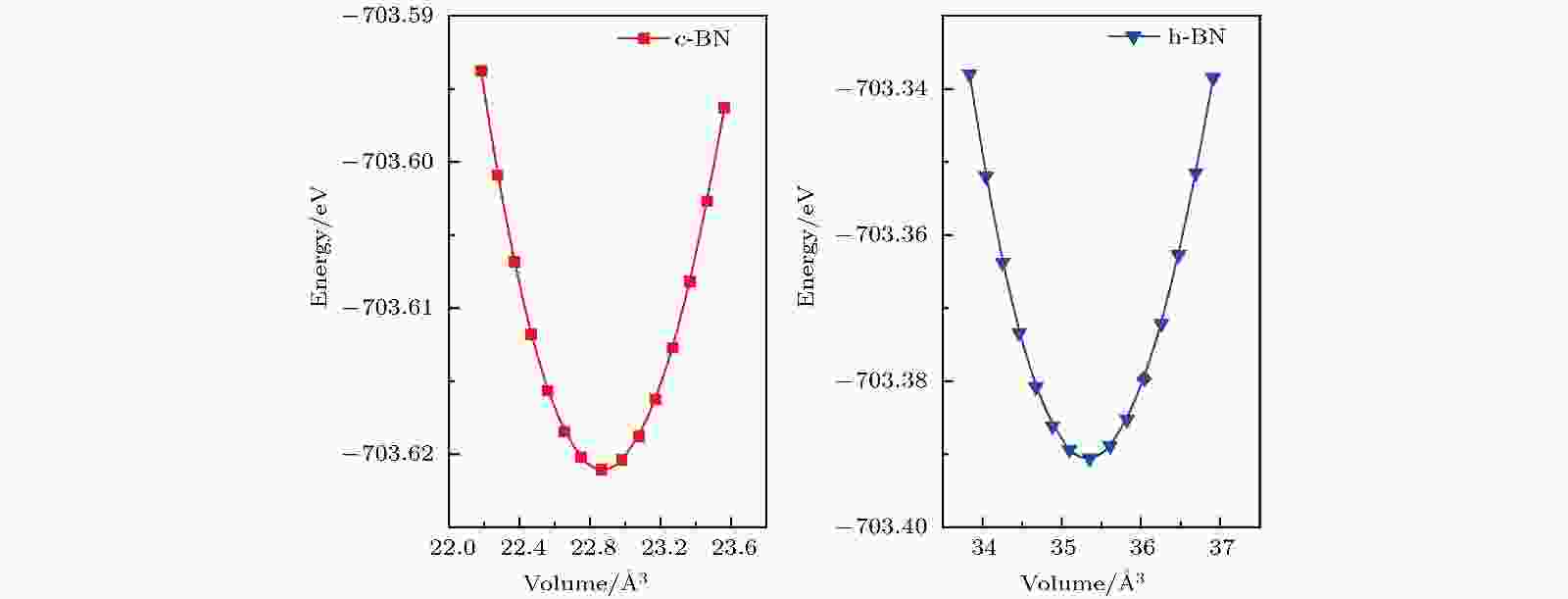图 1 0 GPa和0 K下c-BN和h-BN的总能量与晶胞体积关系
Figure1. Relationship between total energy and cell volume of c-BN and h-BN at 0 GPa and 0 K

从图1中可以清楚地看出, c-BN和h-BN的总能量E都随着其体积V的增加, 呈现出先减小后增加的趋势. 在E-V图中, 当c-BN的体积V = 22.865 ?³时, 其能量达到最小值E = –703.621 eV; h-BN的体积V = 35.352 ?³时, 其能量达到最小E = –703.391 eV.
2 -->

3.2.力学性质

3 -->

3.2.1.弹性常数

本文采用VRH平均算法计算晶体的弹性常数, 立方晶系和六方晶系中的体积模量B和剪切模量G分别表示为${B_{}} = ({B_{\rm{V}}} + {B_{\rm{R}}})/2$和$G = ({G_{\rm{V}}} +$$ {C_{\rm{R}}})/2$, 其中的${B_{\rm{V}}}$, ${B_{\rm{R}}}$, ${G_{\rm{V}}}$, ${G_{\rm{R}}}$分别为:
立方晶系

${B_{\rm{V}}} = {B_{\rm{R}}} = \frac{{{C_{11}} + 2{C_{12}}}}{3},$

$\mathop G\nolimits_V \; = \;\frac{{\mathop C\nolimits_{11} \; - \;\mathop C\nolimits_{12} \; + \;\mathop {3C}\nolimits_{44} }}{{\mathop 5\nolimits_{} }},$

$\mathop G\nolimits_R \; = \;\frac{{\mathop 5\nolimits_{} \left( {\mathop C\nolimits_{11} \; - \;\mathop C\nolimits_{12} } \right)\;\mathop C\nolimits_{44} }}{{\mathop {4C}\nolimits_{44} \; + \;3\left( {\mathop C\nolimits_{11} \; - \;\mathop C\nolimits_{12} } \right)}},$

六方晶系

$\mathop B\nolimits_V \; = \;\frac{{\mathop 2\nolimits_{} \left( {\mathop C\nolimits_{11} \; + \;\mathop C\nolimits_{12} } \right)\; + \;\mathop C\nolimits_{33} \; + \;\mathop {4C}\nolimits_{13} }}{{\mathop 9\nolimits_{} }},$

$\mathop B\nolimits_R \; = \;\frac{{\left( {\mathop C\nolimits_{11} \; + \;\mathop C\nolimits_{12} } \right)\;\mathop C\nolimits_{33} \; + \mathop {2C}\nolimits_{13}^{\,2} }}{{\mathop C\nolimits_{11} \; + \;\mathop C\nolimits_{12} \; + \;\mathop {2C}\nolimits_{33} \; - \;\mathop {4C}\nolimits_{13} }},$

$\mathop G\nolimits_V \; = \;\frac{{\mathop {7C}\nolimits_{11} \; + \;\mathop {5C}\nolimits_{12} \; + \;\mathop {12C}\nolimits_{44} \; + \;\mathop {2C}\nolimits_{33} \; - \;\mathop {4C}\nolimits_{13} }}{{\mathop {30}\nolimits_{} }},$

$\mathop G\nolimits_R \;\mathop = \nolimits_{} \;\frac{{\mathop 5\nolimits_{} \mathop {\left[ {\,\left( {\mathop C\nolimits_{11} \; + \;\mathop C\nolimits_{12} } \right)\,\mathop C\nolimits_{33} \; - \;\mathop {2C}\nolimits_{13}^{\,2} } \right]}\nolimits^{\,2} \mathop C\nolimits_{44} \mathop C\nolimits_{66} }}{{\mathop {6B}\nolimits_V \mathop C\nolimits_{44} \mathop C\nolimits_{66} \; + \;\mathop 2\nolimits_{} \mathop {\left[ {\,\left( {\mathop C\nolimits_{11} \; + \;\mathop C\nolimits_{12} } \right)\;\mathop C\nolimits_{33} \; - \;\mathop {2C}\nolimits_{13}^{\,2} } \right]}\nolimits^{\,2} \left( {\mathop C\nolimits_{44} \; + \;\mathop C\nolimits_{66} } \right)}}.$

杨氏模量E和泊松比υ由下式计算:

$E\; = \;\frac{{9BG}}{{3B\; + \;G}},$

$\upsilon \; = \;\frac{1}{2}\left(1\, - \;\frac{E}{{3B}}\,\right).$

德拜温度${{\varTheta }_D}$与平均声速${V_m}$的关系表达式为

${{{\varTheta }}_D}\; = \;\frac{h}{K}\left[ {\frac{{3n}}{{4{\text{π}} }}\left( {\frac{{{N_A}\,\upsilon }}{M}} \right)} \right]{\;^{1/3}}\,{V_m}$

其中$h$表示普朗克常数($h\; = \;6.626\;068\;96\; \times \; {10^{ - 34}}\rm{J \cdot}$s), $K$表示玻尔兹曼常数($K\!=\!$1.380 650 5 × 10^–23 J/K), ${N_A}$表示阿伏伽德罗常数(${N_A}\!=\!$ 6.022 140 82 × 10²³ mol^–1), $n$表示每单位的原子数, $M$表示每单位的质量, $\rho $表示物质密度. 平均声速${V_m}$的表达式为

${V_m}\; = \;{\left[ {\frac{1}{3}\left( {\frac{2}{{V_{\rm{s}}^{\rm{3}}}}\; + \;\frac{1}{{V_{\rm{l}}^{\rm{3}}}}} \right)} \right]^{\; - \;\frac{1}{3}}},$

其中${V_s}$ 表示横波声速, ${V_l}$ 表示纵波声速, 二者又可从Navier方程中计算得到, 表达式为:

${V_{\rm{s}}}\; = \;\sqrt {\;\;\frac{G}{\rho }\;\;}, $

${V_{\rm{l}}}\; = \;\sqrt {\frac{{B\; + \;4G/3}}{\rho }} .$

通过以上公式, 得到了表2所列的c-BN和h-BN的弹性常数C_ij、德拜温度Θ_D、平均声速V_m、体积模量B、剪切模量G、杨氏模量E和泊松比υ等相关参数, 并与实验数据和现有理论值进行了比较. 结果显示: 两种结构的计算结果均与现有实验值和理论值符合得较好.

	方法	C11/GPa	C12/GPa	C13/GPa	C33/GPa	C44/GPa	ΘD/K	Vm/m·s–1	B	G	E	B/G	υ
c-BN	实验值	820[40]	190[40]			480[40]			389—407[40]
	本文计值	824.43	186.37			479.76	1929.94	11590.90	399.06	407.38	911.85	0.98	0.12
	其他计算	823[35]	185[35]			479[35]	1765[35]	10783[35]		407[35]	910[35]	0.975[35]	0.12[35]
		824[36]	193[36]			476[36]			403[36]	404[36]		0.998[36]	0.12[36]
		820[41]	194[41]			477[41]			375.923[41]	409[41]	854.81[41]	0.97[41]	0.12[41]
		815[42]	194[42]			494[42]	1790[42]		381[42]	398[42]		0.957[42]
		820[43]	194[43]			477[43]
h-BN	实验值	811[40]	169[40]	0[40]	32[40]	7[40]			26—335
		811[44]	169[44]	0[44]	27[44]	8[44]
	本文计值	925.98	212.04	2.26	29.83	5.95	424.94	2928.86	142.88	98.85	240.98	1.45	0.22
	其他计算	927[36]	223[36]	1[36]	32[36]	7[36]			145[36]	100[36]		1.45[36]	0.22[36]
		930[42]	218[42]	1[42]	29[42]	7[42]			158[42]	104[42]		1.519[42]
									141[45]	98[45]	239[45]	1.44[45]	0.22[45]
		923.48[46]	212.23[46]	2.56[46]	28.08[46]	4.06[46]

表20 K和0 GPa时, c-BN和h-BN的弹性常数C_ij、德拜温度Θ_D和平均声速V_m^{[35,36,40?46]}
Table2.Elastic constants, Debye temperature and average sound velocity of c-BN and h-BN at 0 K and 0 GPa^{[35,36,40?46]}

利用弹性常数, 可以判断具有一定空间结构的晶体的力学稳定性, 根据玻恩稳定性判据, 对于立方晶系有:

$\mathop C\nolimits_{11} + \mathop {2C}\nolimits_{12} > 0,\quad \mathop C\nolimits_{44} > 0,\quad \mathop C\nolimits_{11} - \mathop C\nolimits_{12} > 0;$

对于六方晶系有:

$\begin{split}&\mathop C\nolimits_{11} > 0,\quad \mathop C\nolimits_{11} - \mathop C\nolimits_{12} > 0,\quad \mathop C\nolimits_{44} > 0\;\\&\left( {\mathop C\nolimits_{11} + \mathop C\nolimits_{12} } \right)\mathop C\nolimits_{33} - \mathop {2C}\nolimits_{13}^{2} > 0.\end{split}$

通过表2的数据可知, c-BN和h-BN都符合玻恩稳定性判据, 说明二者都具有一定的力学稳定性. 维氏硬度(H_V)与B, G之间的关系为

$\mathop H\nolimits_{\mathop V\nolimits_{} } \;\mathop {\rm{ = }}\nolimits_{} \;\mathop 2\nolimits_{} \mathop {\left( {\frac{{\mathop G\nolimits^{\;3} }}{{\mathop B\nolimits^{\;2} }}} \right)}\nolimits^{\;\mathop {0.585}\nolimits_{} } .$

计算得h-BN的维氏硬度仅为19.094 GPa, c-BN的维氏硬度为68.923 GPa, 与现有实验值65 GPa相差不大. 材料的脆性可以用B/G的大小粗略估算, 比值大于1.75^[47]时认为是韧性材料, 否则认为是脆性材料, 由表2可知c-BN和h-BN均为脆性材料. 同时, 泊松比υ的值也可以估算材料的脆性, 当υ < 1/3时可认为是脆性材料, 由表2可知c-BN和h-BN都是脆性材料, 这与B/G的判断结果一致.
压力P在影响材料的物理性质方面起着重要的作用^[48,49], 另外还计算了零温下c-BN和h-BN的弹性常数随P的变化关系, 并将其展示在表3中. 从表3可以看出, 0—50 GPa的范围内, c-BN和h-BN都符合玻恩稳定性判据, 说明二者都具有一定的力学稳定性. 对于可粗略判断材料脆性的B/G, 我们发现c-BN和h-BN的B/G都在一直增加, 即二者的韧性越来越好. c-BN的B/G由0.980(0 GPa)增加到1.181(50 GPa), 而h-BN则由1.445(0 GPa)增加到1.729(50 GPa). 另外, c-BN和h-BN的泊松比υ一直递增的变化也证明了这一点.

	P/GPa	C11/GPa	C12/GPa	C13/GPa	C33/GPa	C44/GPa	B/GPa	G/GPa	υ
c-BN	0	824.43	186.374			479.76	399.06	407.38	0.119
	5	830.11	185.83			493.23	400.59	415.80	0.124
	10	889.09	226.27			527.81	447.21	437.96	0.130
	15	911.61	241.91			540.63	465.15	446.14	0.137
	20	932.97	257.00			552.40	482.33	453.61	0.142
	25	954.49	272.25			563.79	499.66	460.89	0.147
	30	975.51	287.24			574.81	516.66	467.91	0.152
	35	996.42	302.42			585.82	533.75	474.82	0.157
	40	1017.22	596.23			317.36	550.65	481.48	0.161
	45	1037.37	332.13			606.51	567.21	487.92	0.166
	50	1057.25	346.87			616.50	583.66	494.15	0.170
h-BN	0	925.98	212.04	2.26	29.8	5.95	142.88	98.85	0.219
	5	1031.35	249.81	5.35	63.99	8.14	176.61	112.09	0.228
	10	1148.41	283.48	26.06	132.72	26.16	231.48	145.44	0.240
	15	1200.62	306.01	39.36	160.84	34.24	256.67	158.80	0.244
	20	1246.22	327.55	53.25	187.08	42.77	280.31	171.49	0.246
	25	1287.16	348.45	67.73	211.76	51.53	302.83	183.49	0.248
	30	1320.57	372.62	82.18	236.37	60.42	324.77	194.15	0.251
	35	1353.78	393.22	96.91	259.96	69.28	345.92	204.72	0.253
	40	1385.71	412.37	111.71	283.31	78.45	366.65	215.30	0.254
	45	1414.63	431.89	126.68	306.37	87.53	386.99	225.13	0.256
	50	1445.81	447.45	141.74	328.44	96.53	406.75	235.27	0.258

表30 K时, 压力P对c-BN和h-BN的弹性常数C_ij, B, G的影响
Table3.Effect of pressure on the elastic constants of c-BN and h-BN at 0 K

如图2所示, 随着P的增加, c-BN和h-BN的弹性常数C_ij都随着P的增加而单调增大, 这表明c-BN和h-BN的可压缩性随P的升高而变得越来越差. 无论是c-BN还是h-BN, 随着P的变化C₁₁的变化都是最明显的, 这说明C₁₁对P最为敏感.
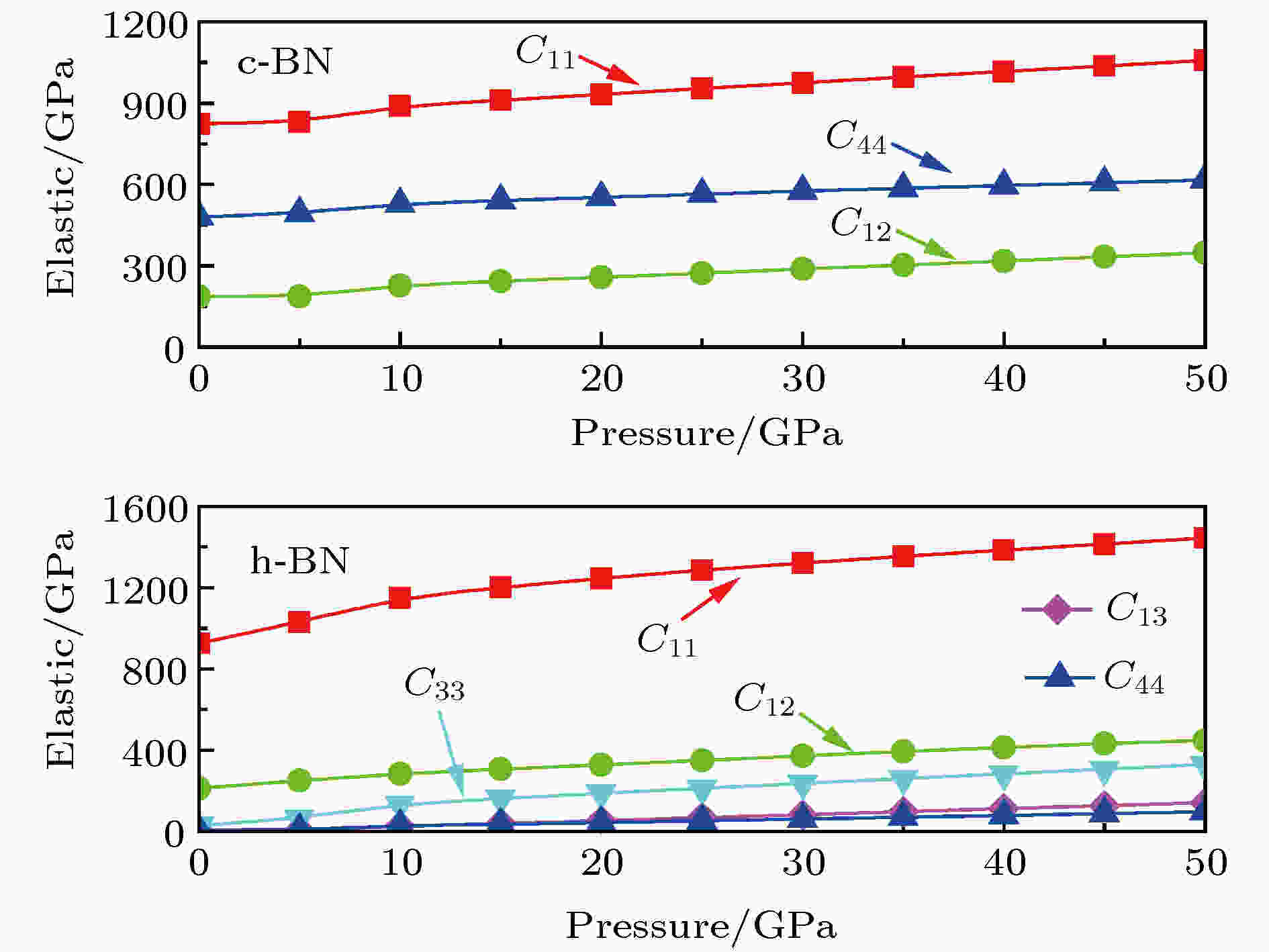图 2 0 K时, 压力对c-BN和h-BN的弹性常数的影响
Figure2. Effect of pressure on the elastic constants of c-BN and h-BN at 0 K

3 -->

3.2.2.声子谱

晶格动力学规定, 若结构给定, 那么所有该结构的简正振动模的频率都为有限实值^[50], 也就是说不应该出现虚频. 对于Brillouin区的任一波矢, 若声子频率出现虚数, 则说明该结构在此条件下属于亚稳态, 将最终被能量更低的稳定结构取代. 计算得到c-BN和h-BN结构的声子谱如图3所示, 在c-BN结构的Brillouin区中任一波矢的声子频率都没有出现虚数, 这说明其具有声子稳定性. 反观h-BN结构, 在Brillouin区的K点到M点区域内, 有虚频声子出现, 这说明h-BN声子不稳定, 可知h-BN在零温零压时处于亚稳态.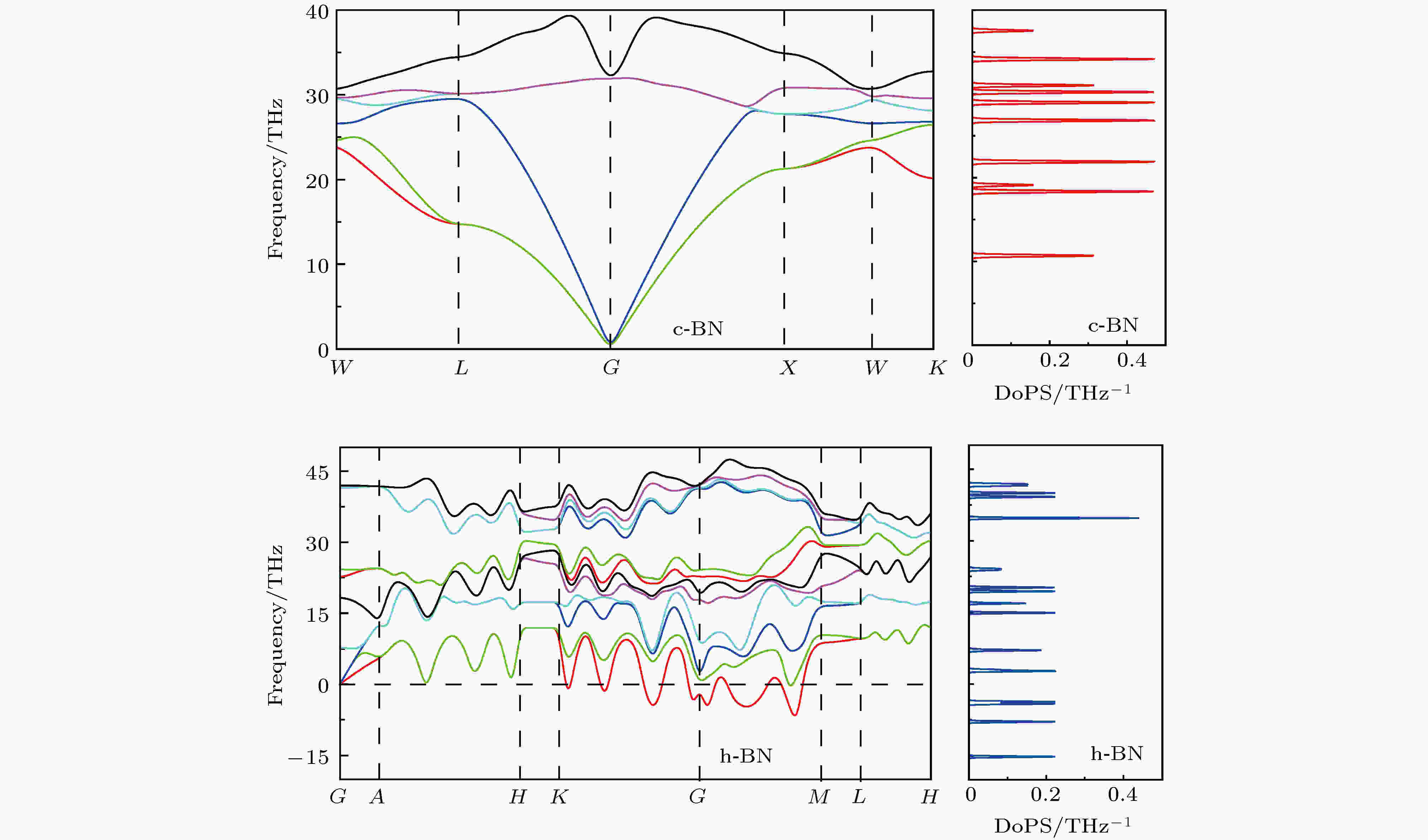
图 3 0K和0GPa时c-BN和h-BN的声子谱和声子色散
Figure3. Phonon spectrum and density of phonon states of c-BN and h-BN at 0 K and 0 GPa

2 -->

3.3.热力学

热力学性质在材料研究方面具有潜在的意义, 晶体的热力学性质受外界温度T和压力P的影响很大^[51]. 利用德拜模型^[52]计算c-BN的热膨胀系数α、晶格体积的变化V/V₀、比热容C_V, 德拜温度Θ_D、格林艾森系数γ等参数. 当考虑声子效应时, 非平衡条件下的吉布斯函数G^*(V, P, T)可以表示为

${G^*}\left( {V,\;P,\;T} \right)\; = \;E\left( V \right)\; + \;pV\; + \;A\left[ {{\Theta _D}\left( V \right),\,T} \right],$

其中$E\left( V \right)$ 表示每个单胞的总能量, $pV$表示恒静压条件, Θ_D表示德拜温度, ${A}$表示亥姆霍兹自由能, 由下式给出:

$\begin{split}&A\left( {{\varTheta }_{D}},T \right)=nKT\Bigg[ \frac{9{{\Theta }_{D}}}{8T}+3\ln \Bigg.\\&\quad \Bigg. \left( 1-{{\bf{e}}^{-{{\varTheta }_{D}}/T}} \right)-D\left( {{\varTheta }_{D}}/T \right) \Bigg],\end{split}$

其中$D\left( {{\varTheta }_{D}}/T \right)$ 表示徳拜积分, ${n}$表示每单位中的原子数, ${K}$表示玻尔兹曼常数. 若B_S表示静态压缩绝热近似的体积模量, 则有

$\mathop B\nolimits_{\rm{S}} \;\mathop \approx \nolimits_{} \;\mathop B\nolimits_{} \left( {\mathop {\,V}\nolimits_{} } \right)\;\mathop = \nolimits_{} \;\mathop V\limits_{} \left[ {\frac{{\mathop {\rm{d}}\nolimits^{\;2} \;E\left( V \right)}}{{\mathop {\operatorname{d} V}\nolimits^2 }}} \right].$

而关于体积V的非平衡吉布斯函数G^*(V, P, T)可以表示为

$\mathop {\left[ {\frac{{\mathop {\partial G}\nolimits^{\;*} \left( {V,\;p,\;T} \right)}}{{\mathop {\partial V}\nolimits_{} }}} \right]}\nolimits_{\mathop {{p},\;T}\nolimits_{} } \;\mathop {\rm{ = }}\nolimits_{} \mathop {\;0}\nolimits_{} .$

通过求解方程(20), 可以得到热力学状态方程. 等温体积弹性模量$\mathop B\nolimits_{\mathop T\nolimits^{} } $、热容$\mathop C\nolimits_{\mathop V\nolimits^{} } $和热膨胀系数α的计算方程式为:

${{B}_{T}}\left( p,T \right)=V{{\left[ \frac{{{\partial }^{2}}{{G}^{*}}\left( V,p,T \right)}{\partial {{V}^{2}}} \right]}_{p,T}},$

${{C}_{V}}=3nk\left[ 4D\left( {{\Theta }_{D}}/T \right)+\frac{3\left( {{\varTheta }_{D}}/T \right)}{1-{{\rm{e}}^{{{\varTheta }_{D}}/T}}} \right],$

$\mathop \alpha \nolimits_{} \; = \;\frac{{\gamma \;\mathop C\nolimits_{\rm{V}} }}{{\mathop B\nolimits_T \;V}}, $

其中γ为

$\gamma \; = \;\frac{{\;\rm{d}\,\ln \;{{\varTheta }_D}\left( V \right)}}{{\rm{d}\,\ln \;V}}.$

c-BN标准元胞体积V/V₀随温度和压力的变化如图4所示. 由图4(a)可以看出, 压力P一定时, 0 GPa时V/V₀的值不随温度T发生改变; 大于0 GPa时, V/V₀的值随T的升高而减小. 从图4(b)中可以看出, V/V₀对P的变化更敏感, 并且P越大、T越高(0 GPa除外), V/V₀的变化越明显, 也就是说c-BN正变得越来越难以被压缩, 这与弹性常数分析得到的结果是一致的.
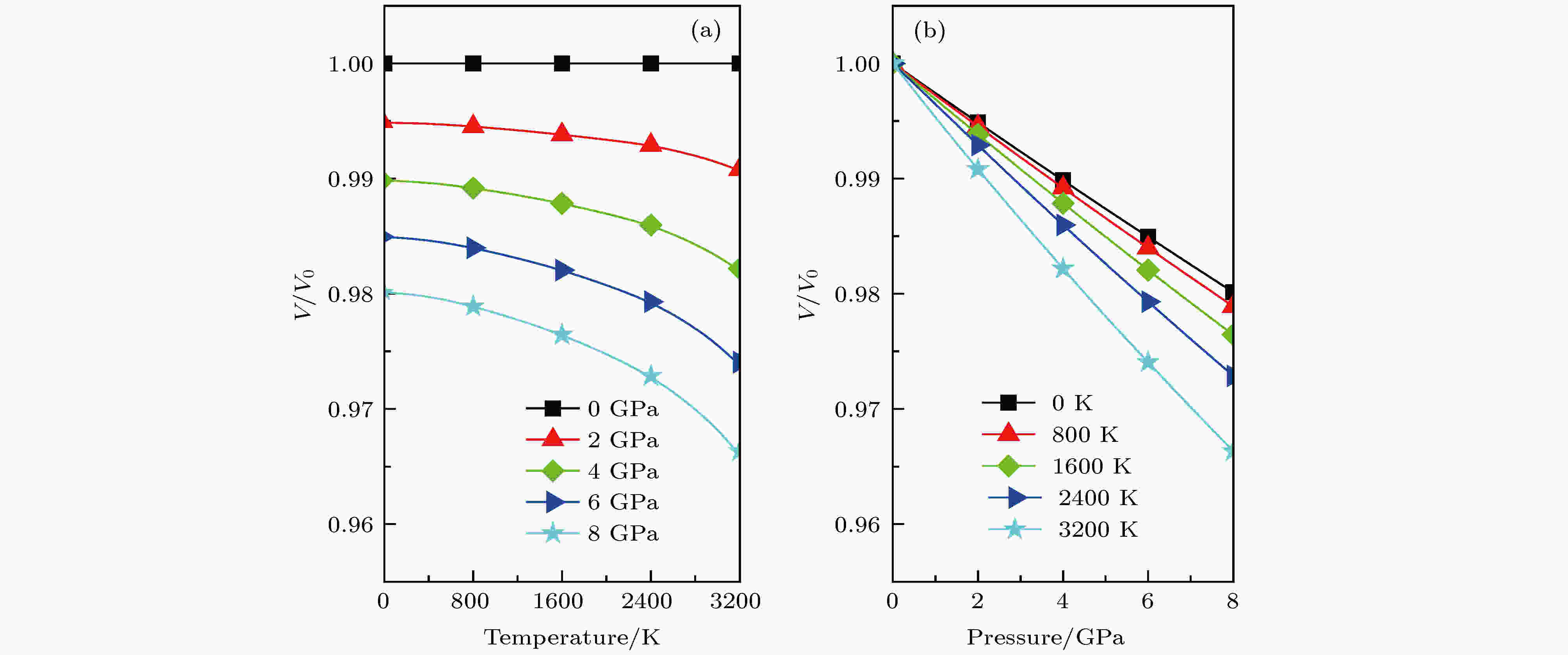图 4 温度(a)和压力(b)对c-BN标准元胞体积V/V₀的影响
Figure4. The normalized primitive cell volume V/V₀ versus temperature (a) and pressure for the c-BN

热容C_V是晶体的关键物理参数, 它提供晶体振动和传热过程的一些重要信息. 如图5(a)所示, 在温度不变时, 除0 K不发生变化外, C_V随着P的增大而减小, 但减小量很小. 从图5(b)可以清楚地看出, 随着温度的增加, C_V的增加量逐渐变小, 这可以从C_V关于T的斜率逐渐减小看出. 这是由于在较高温度区域, C_V的非谐波效应受到抑制. 具体来说, 当T小于800 K时, C_V很大程度上取决于T, 这是使用德拜模型的结果, 在较高温度区域, C_V的非谐波效应受到抑制, C_V的增加量逐渐减小, 并最终趋于零. 也就是说, 随着T的持续增长, C_V遵循德拜定律, 并接近Dulong-Petit极限.
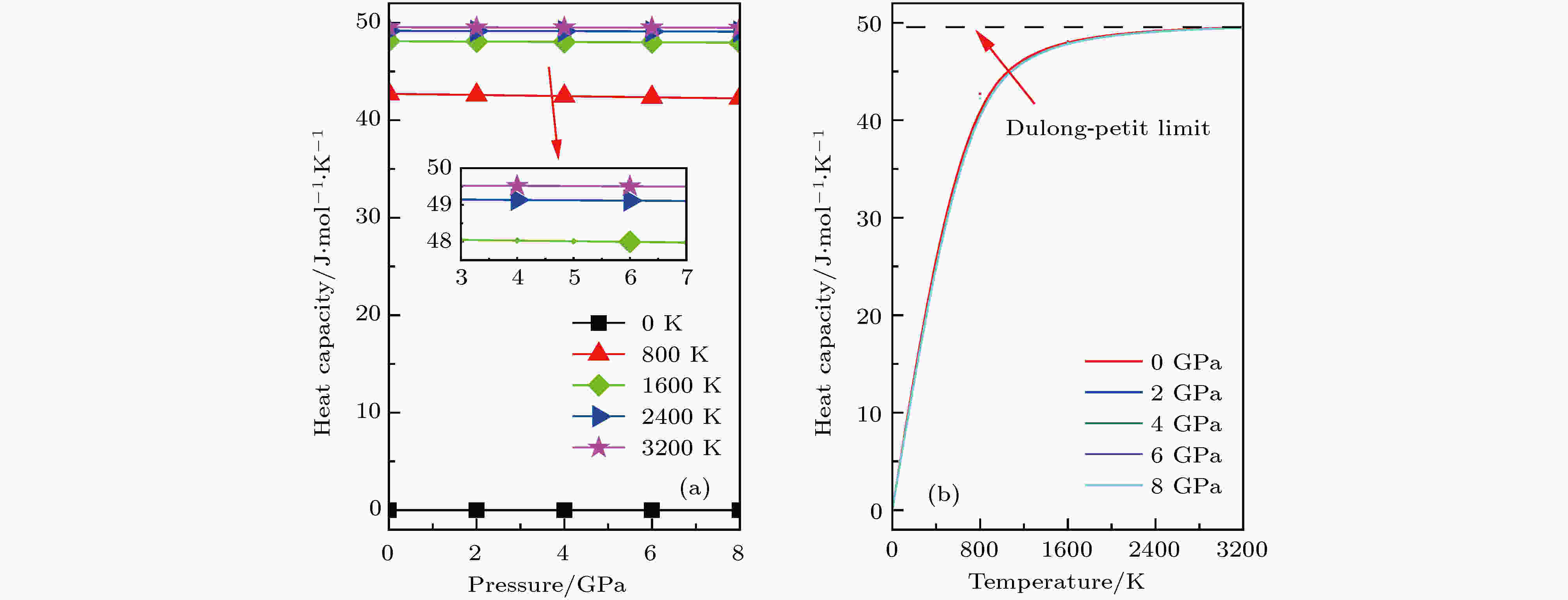图 5 c-BN比热容C_V与压力(a)和温度(b)之间的关系
Figure5. The heat capacity C_V versus temperature and pressure for the c-BN

固体的热膨胀反映了晶体结合的非谐波效应, 对于非立方对称性晶体, 其热膨胀通常是各向异性的^[53]. 由图6(a)可以看出, T恒定时, c-BN的热膨胀系数α随着P的增加, 除了0 GPa一直为0外, 其他都逐渐减小, 且变化越来越缓和; 这是由于非谐波效应随压力升高而变弱导致的. 如图6(b)所示, 低温区的α随温度T几乎呈指数的上升趋势, 而随着T的升高, 这种上升趋势逐渐缓和, 直到趋近于线性关系, 这也是非谐波效应随温度升高而变弱导致的. 图6也揭示了T对α的影响远大于P, 这表明T对晶格非谐波效应影响较大.
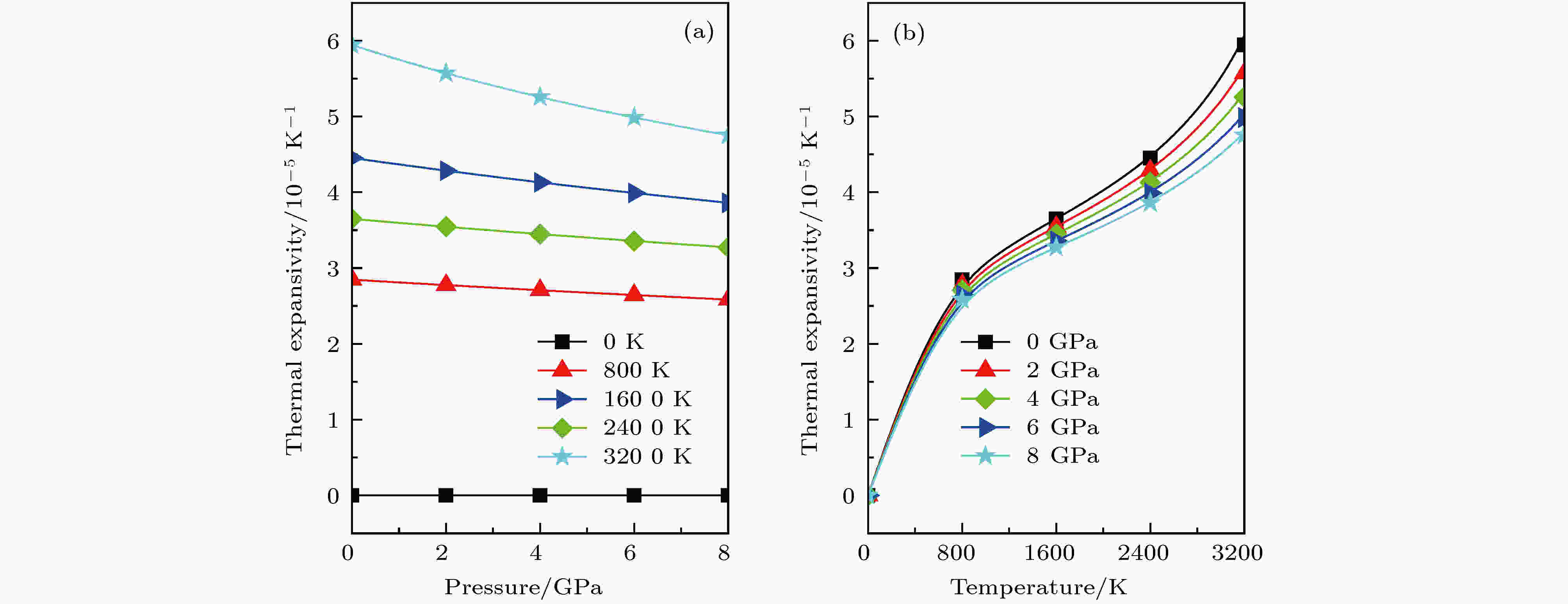图 6 c-BN的热力学膨胀系数α与压力(a)和温度(b)的关系
Figure6. The thermodynamic expansivity α versus pressure (a) and temperature (b) for the c-BN

徳拜温度Θ_D是材料的基本参数, 与许多物理性质密切相关, 当温度低于Θ_D时, 晶格的振动激发主要来自于声子振动. 本文计算的Θ_D在0 K和0 GPa时为1464.2 K, 从图7(a)可以看出, 在T一定时, c-BN的德拜温度Θ_D随着P的增加几乎呈线性增大, 这意味着声子振动激发的频率随P的增加而增大. 如图7(b)所示, 在P一定的情况下, Θ_D随着T的增加而减小, 且在相同的压力间隔下减小速度加快, 且二次函数能够很好地拟合Θ_D与T的关系.
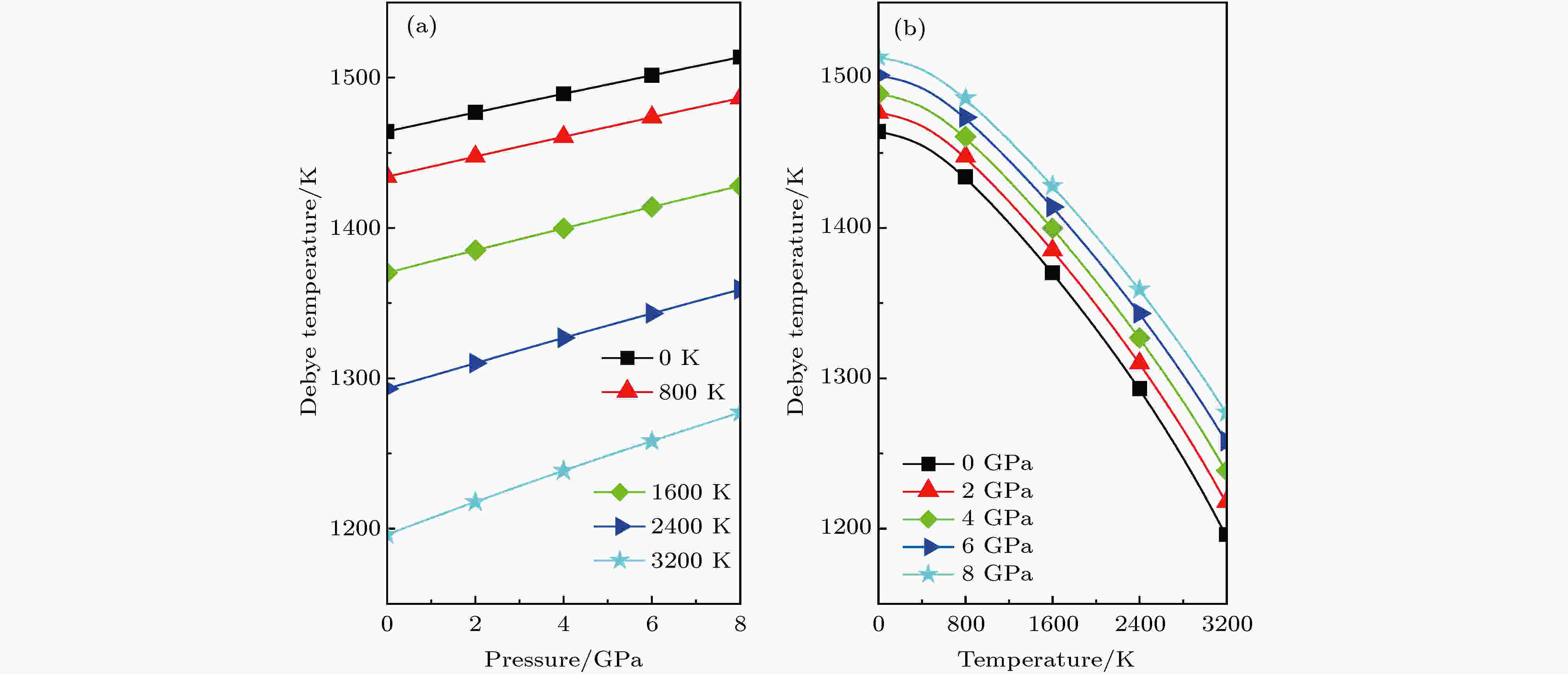图 7 c-BN的徳拜温度Θ_D与压力(a)和温度(b)的关系
Figure7. The Debye temperature Θ_D versus pressure (a) and temperature (b) for the c-BN

格林艾森系数γ反映晶格的非谐波效应程度, 从图8(a)可以看出, 在T一定的情况下, c-BN的γ随P的增加逐渐减小, 即非谐波效应降低, 且在高温区域比低温区域减小得更快. 从图8(b)可以看出, 在P一定的情况下, c-BN的γ随T的增加而增大, 即非谐波效应升高. 图8也说明P对非谐波效应的影响程度大于T. γ越高, 原子间作用力越大, 换而言之, 晶胞的体积也就越小, 这可以从V/V₀(图4)关于T的变化以及弹性常数的计算分析中得知.
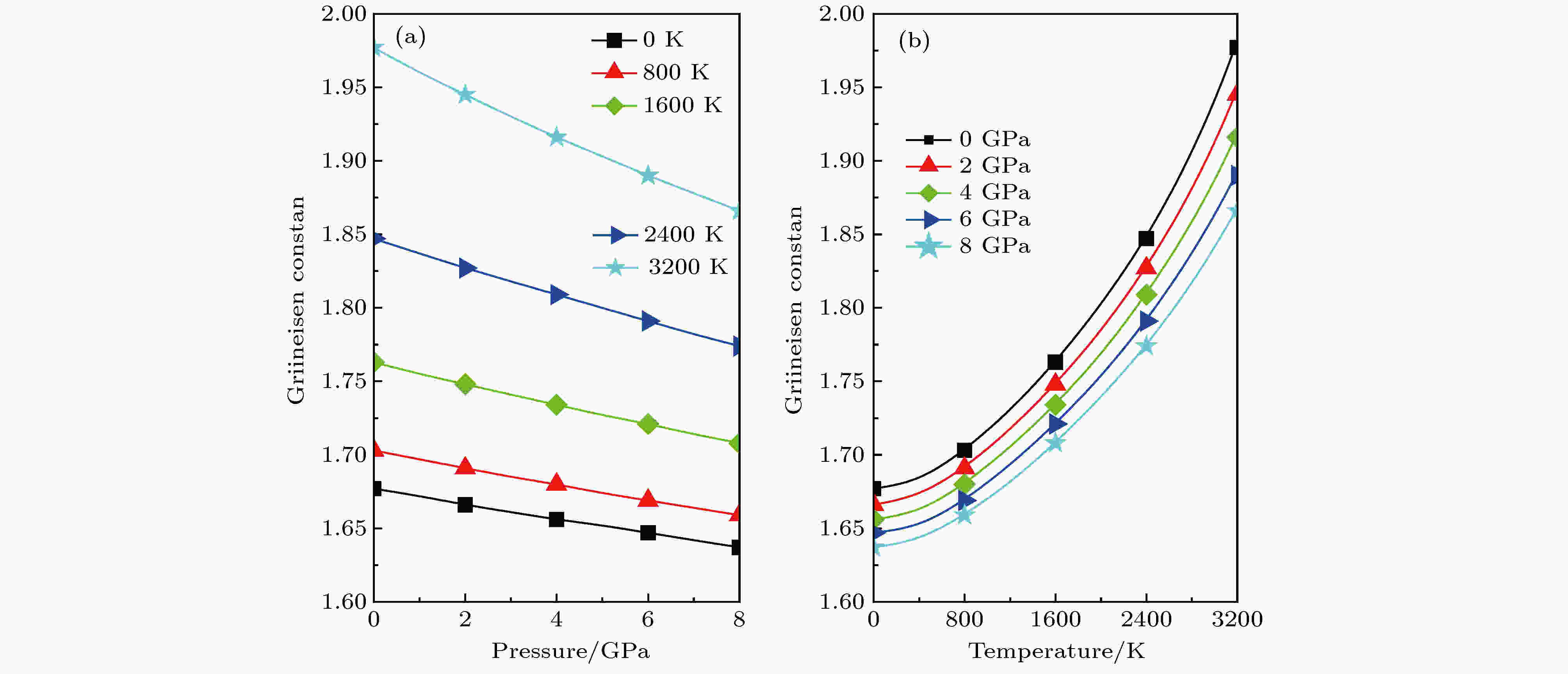图 8 c-BN的格林艾森系数γ与压力(a)和温度(b)的关系
Figure8. The Grüneisen parameter γ versus pressure (a) temperature and (b) for the c-BN

2 -->

3.4.电子结构

能带结构和态密度(density of states, DOS)对于分析材料的物理性质至关重要^[54,55]. 如图9所示, 本文计算了零温零压时c-BN和h-BN沿Brillouin区高对称点方向的能带结构. 在c-BN和h-BN能带结构的计算中, 选取了费米能级E_F附近–25—25 eV的能带结构(E_F为0 eV, 在图9中用黑色实线标出), 计算的带隙宽度如表4所列.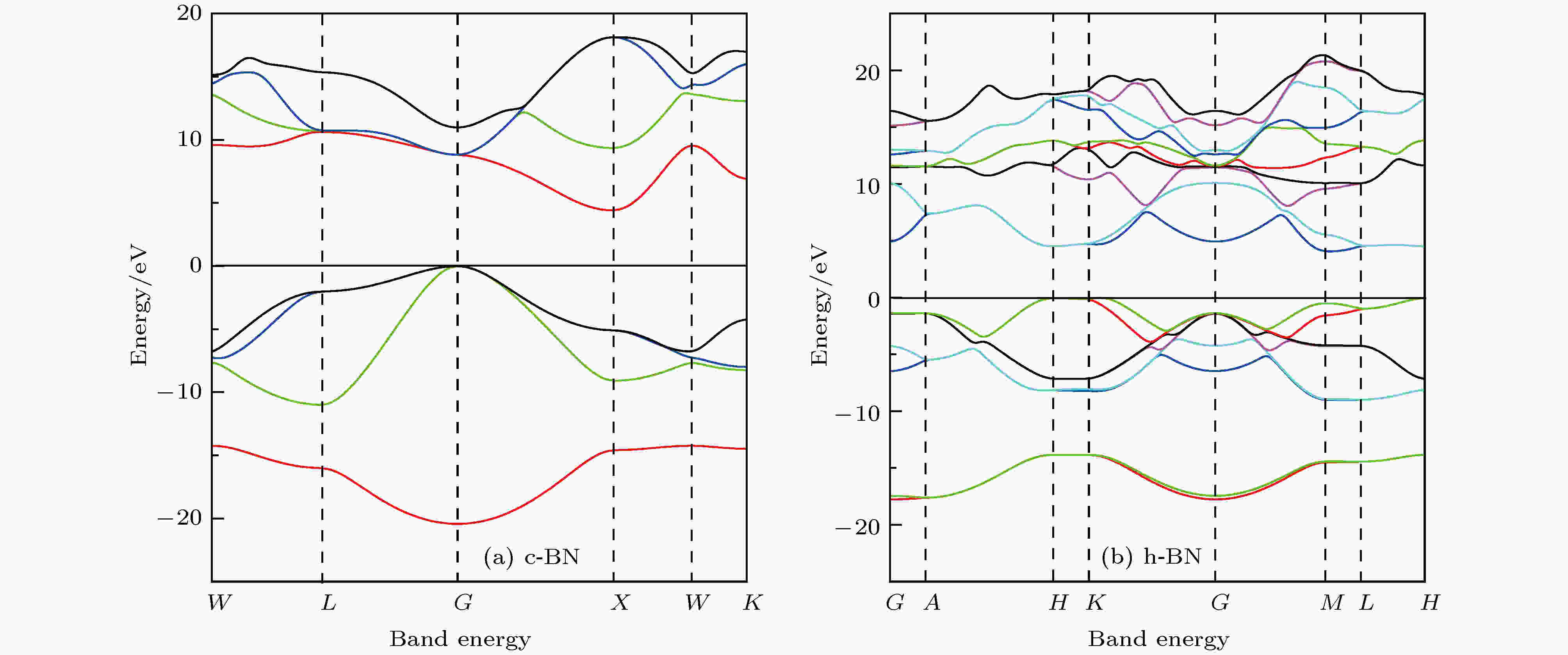
图 9 0 GPa和0 K下c-BN (a)和h-BN (b)的能带结构
Figure9. Band structures for c-BN (a) and h-BN (b) at 0 GPa and 0 K

	c-BN			h-BN
Eg/eV	实验	本文计算	其他计算	实验	本文计算	其他计算
	5.38 [56]	4.391	4.11 [57]	5.955 [58]	4.071	3.378—4.194 [59]
			4.81 [33]			4.01 [33]
			4.24 [60]			4.07 [62]
			4.67 [61]			4.95[63]

表4c-BN和h-BN的带隙宽度^[33,50—57]
Table4.Bandgap of c-BN and h-BN^[33,50—57]

如图9所示, c-BN价带的顶点在G点, 而导带的底点在X点, 即价带的最高点与导带最低点不在同一点, 故c-BN属于间接带隙; 同样, h-BN价带的最高点在K点附近, 而导带的最低点在M点附近, h-BN也属于间接带隙. 在c-BN能带结构中, 有价带在G点附近穿过E_F进入导带, 这说明E_F附近存在自由电子, 使得c-BN表现出一定的金属性质; 同样, h-BN的能带结构中, 在H, K两点附近也有价带穿过E_F进入导带, h-BN也表现出一定的金属性质. 结合表4中的计算结果可知: c-BN和h-BN的带隙宽度分别为4.391和4.071 eV, 均大于2.2 eV, 故c-BN和h-BN都可归为宽带隙半导体. 同时, 由表4可以看出, 本文的计算结果与现有理论值和实验值之间的差异均在30%左右, 这是由于DFT计算的是基态近似的结果, 而在真实体系中的能隙属于激发态, 这在计算材料界是普遍存在的现象, 并不影响人们对c-BN和h-BN电子结构的分析和研究.
态密度是用来描述固体中电子能级的物理量, DOS峰值的尖锐程度反映了该区域相互作用的强弱 ^[51,54,64]. 为了进一步了解c-BN和h-BN的电子结构特性, 计算了零温零压时的总DOS和分波态密度(partial density of states, PDOS).
如图10(a)所示, c-BN由B的2s2p和N的2s2p轨道杂化而成, B和N对c-BN的总DOS几乎同时开始贡献. c-BN的DOS中, B的2s轨道和N的2p轨道在相同能量处存在多个能量重合, 可以明显看出B和最近的N之间形成的是sp³杂化的共价键. c-BN有3个连续区域, 分别对应着能带图9(a)中的3个带隙. c-BN的3个连续区域分别是: 价带底的–20.781— –13.912 eV, 对应于能带图中价带的最下面一条, 主要来源于B的2s和N的2p轨道; 价带上部的–11.161—0.215 eV, 对应于能带图中价带的其他三条, 主要来源于B的2p和N的2p轨道, 可以看出B的2p轨道贡献最大, 其局域性也最强; 导带的4.809—18.273 eV, 对应于能带图中的导带, 主要来源于B的2p和N的2s2p轨道. 同样地, 从图10(b)中可以看出, h-BN的总DOS也由B的2s2p和N的2s2p轨道杂化而成, 且几乎同时开始贡献, B和最近的N之间形成的则是sp²杂化的共价键. h-BN也同样存在与图9(b)相对应的3个连续区域, 分别是: 价带底的–18.118— –13.377 eV, 对应于能带图中价带的最下面两条, 主要来源于N的2s和B的2p轨道; 价带上部的–9.451—0.451 eV, 主要来源于B的2p和N的2p轨道, 对应于能带图中价带的其他能带, 可以看出N的2p贡献最大, 其局域性也最强; 导带的3.726—21.302 eV, 对应于能带图中的导带, 主要来源于B的2s2p轨道. E_F位于峰和谷之间的位置, 可以定性地表明材料的稳定性和导电性. 在E_F处, c-BN和h-BN的总DOS均不为零, 因此, 两者的成键类型主要为共价键, 但其中还有一些离子成分参与, 说明均有一定的金属性质.
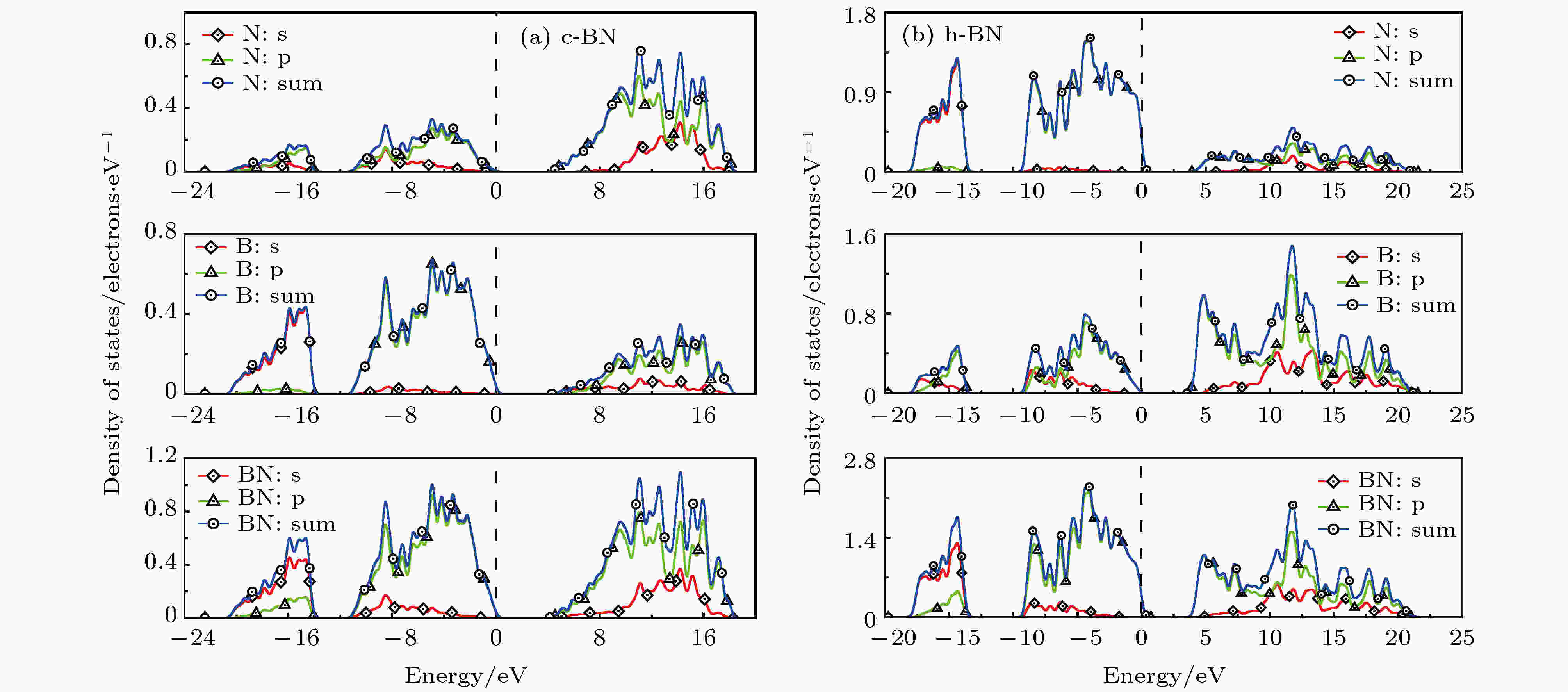图 10 0 GPa和0 K下c-BN和h-BN的态密度
Figure10. Density of states for c-BN and h-BN at 0 GPa and 0 K

比较c-BN和h-BN的总DOS可以发现: c-BN的价带较宽而导带较窄, h-BN的导带较宽而价带较窄. c-BN的每个连续区域的DOS的峰值都比较尖锐, 说明局域性较强, B, N之间的相互作用较强; sp³轨道杂化的空间结构和较强的共价键, 使得c-BN在硬度、化学惰性和热稳定性等方面有着优良的性能. h-BN在价带的局域性较强, 而在导带的DOS峰带隙较宽, 趋势相对比较平滑, B, N之间的相互作用较弱; 相对于c-BN稳定性较差, 在外部环境发生变化时, 其结构会发生相应的改变; sp²轨道杂化的空间平面结构使得其沿c轴方向强度较差, 这和前面所述一致.
2 -->

3.5.光学性质

当光照到物体表面时, 随着入射光频率ω的变化, 其光学性质会发生一定的变化, 主要表现在对光的折射率n、反射率R、干涉、衍射以及对光的吸收I、色散等. 光具有波粒二象性, 当光在介质中传播时, 光子的电场扰动使介质中的电子发生跃迁, 这需要用复介电函数进行描述:

$\mathop \varepsilon \nolimits_{} \left( \omega \right)\;{\rm{ = }}\;\mathop \varepsilon \nolimits_1 \left( \omega \right)\; + \;\mathop {{\rm{i}}\,\varepsilon }\nolimits_2 \left( \omega \right),$

其中$\omega $表示入射光的频率, $\mathop {\rm i\,\varepsilon }\nolimits_2 \left( \omega \right)$表示复介电函数的虚部, $\rm i\,$表示虚数单位, $\mathop \varepsilon \nolimits_1 \left( \omega \right)$表示复介电函数的实部, 可以利用Kramers-Kronig方程求解:

$\begin{split}&\mathop {\mathop \varepsilon \nolimits_2 \left( \omega \right)}\nolimits_{} \;\mathop {\rm{ = }}\nolimits^{} \;\frac{{\mathop {4\,{\text{π}}}\nolimits^2 }}{{\mathop m\nolimits^2 \mathop \omega \nolimits^2 }}\,\sum\limits_{{\rm{V}},\;{\rm{C}}} {\int\limits_{{\rm{BZ}}} {\mathop {\rm{d}}\nolimits^3 } } K\frac{{\mathop {\left| {e\; \cdot \;\mathop M\nolimits_{{\rm{CV}}} \left( K \right)} \right|}\nolimits^2 }}{{\mathop {\text{π}}\nolimits_{} }}\;\mathop \times \\&\quad \mathop \delta \left[ \mathop E\nolimits_{\rm{C}} \left( K \right)\; - \;\mathop E\nolimits_{\rm{V}} \left( K \right)\; - \;\mathop {h\,\omega }\nolimits_{} \right],\end{split}$

$\begin{split}&\mathop {\mathop \varepsilon \nolimits_1 \left( \omega \right)}\nolimits_{} \;\mathop {\rm{ = }}\nolimits_{} \;\mathop 1\nolimits_{} \; + \;\frac{{\mathop {4\,{\text{π}}\,e}\nolimits^{\mathop 2\nolimits_{} } }}{{\mathop m\nolimits^2 }}\\&\quad \sum\limits_{{\rm{V,}}\;{\rm{C}}} {\int\limits_{{\rm{BZ}}} {\mathop {\rm{d}}\nolimits^3 } } K\frac{{\mathop {\left| {e\; \cdot \;\mathop M\nolimits_{{\rm{CV}}} \left( K \right)} \right|}\nolimits^{\mathop 2\nolimits_{} } }}{{\mathop {\text{π}}\nolimits_{} \left[ {\mathop E\nolimits_{\rm{C}} \left( K \right)\; - \;\mathop E\nolimits_{\rm{V}} \left( K \right)\;} \right]}}\;\mathop \times \nolimits^{} \\&\quad \mathop {\frac{{{h^3}}}{{\mathop {\left[ {\mathop E\nolimits_{\rm{C}} \left( K \right)\; - \;\mathop E\nolimits_{\rm{V}} \left( K \right)} \right]}\nolimits^2 \; - \;\mathop h\nolimits^2 \mathop \omega \nolimits^2 }}}\nolimits_{} , \end{split}$

其中$m$表示自由电子的质量, $e$表示自由电子的电荷量($e$ = 1.602 177 33 × 10^–19 C), ${\rm{C}}$表示物质组成的导带, ${\rm{V}}$表示物质组成的价带, ${E_{\rm{C}}}\left( K \right)$表示导带上的本征能级, ${E_{\rm{V}}}\left( K \right)$表示价带上的本征能级, ${\rm{BZ}}$代表第一布里渊区, $K$表示倒格子, $h$表示普朗克常数, $\mathop {\left| {e\; \cdot \;\mathop M\nolimits_{\rm CV} \left( K \right)} \right|}\nolimits^{} $表示动量跃迁矩阵元, 有了复介电函数便可以计算出其他光学性质.
光从一种介质进入另一种介质时, 会在介质的表面发生反射和折射, 光的折射率与复介电函数之间存在以下关系:

$\mathop \varepsilon \nolimits_1 \; = \;\mathop n\nolimits^2 \left( \omega \right)\; - \;\mathop k\nolimits^2 \left( \omega \right), $

$\mathop \varepsilon \nolimits_2 \; = \;2\;n\left( \omega \right)\;k\left( \omega \right), $

其中$n\left( \omega \right)$表示折射率, $k\left( \omega \right)$表示消光系数. 在光的反射过程中, 介质表面反射光的能量与接受光能量的比值, 可以用光的反射率R描述:

$\mathop {R\left( \omega \right)}\nolimits_{} \;\mathop = \nolimits_{} \mathop {\left| {\;\frac{{\sqrt {\mathop \varepsilon \nolimits_1^{} \left( \omega \right)\; + \;\mathop {i\,\varepsilon }\nolimits_2^{} \left( \omega \right)} \; - \;1}}{{\sqrt {\mathop \varepsilon \nolimits_1^{} \left( \omega \right)\; + \;\mathop {i\,\varepsilon }\nolimits_2^{} \left( \omega \right)} \; + \;1}}\;} \right|\,\;}\nolimits^{\mathop 2\nolimits_{} } .$

光在介质中传播时, 能量会发生变化, 光在介质中传播的光强度减弱的百分比可以用吸收系数I来表示:

$I\left( \omega \right)=\sqrt{2}\omega {{\left[ \sqrt{\varepsilon _{1}^{2}\left( \omega \right)+\varepsilon _{2}^{2}\left( \omega \right)}-{{\varepsilon }_{1}}\left( \omega \right) \right]}^{1/2}}.$

光电子在均匀介质中会以某一恒定速度v传播, 其能量会发生改变, 造成一定损失, 可以用损失函数L来表示其损失量:

$L\left( \omega \right)\; = \;\frac{{\mathop \varepsilon \nolimits_2^{} \left( \omega \right)}}{{\mathop \varepsilon \nolimits_1^2 \left( \omega \right)\; + \;\mathop \varepsilon \nolimits_2^2 \left( \omega \right)}}\;.$

当光照射到材料表面时, 会引起材料电导率的改变, 这种由光照引起的电导率称为光电导, 其与介电函数的关系式为

$\sigma \left( \omega \right)\; = \; - \mathop {\rm{i}}\nolimits_{} \frac{\omega }{{4{\text{π}}}}\left[ {\varepsilon \left( \omega \right)\; - \;1} \right]\;.$

复介电函数是描述固体的能带结构和光学线性响应关系的函数, 它在晶体电子结构和能带间跃迁之间起着连接桥梁的作用, 它可以解释一些材料的光学现象. c-BN和h-BN结构的复介电函数实部和虚部随入射光能量E_in的变化如图11所示.
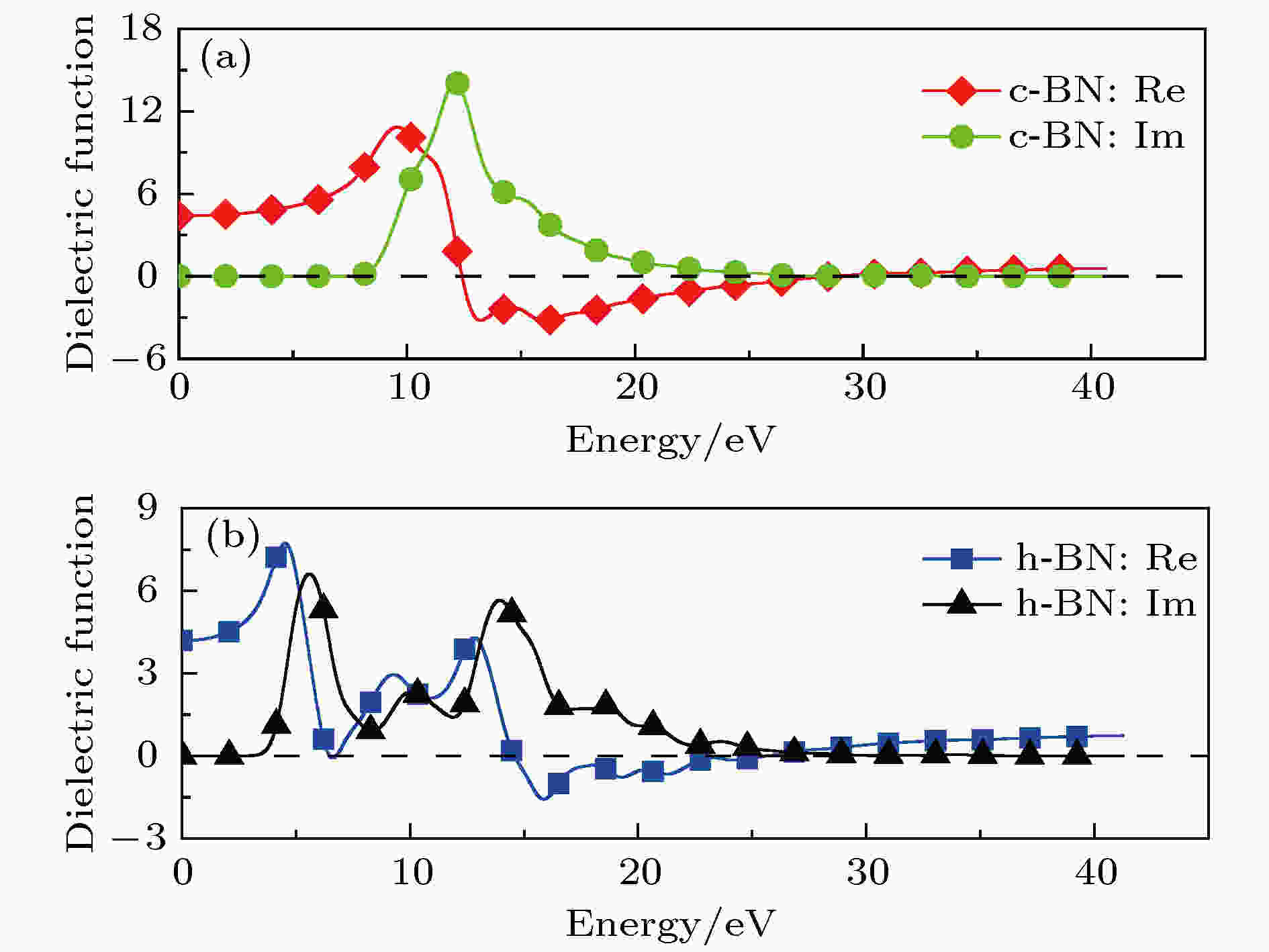图 11 0 K和0 GPa时c-BN和h-BN的复介电函数
Figure11. Complex dielectric functions of c-BN and h-BN at 0 K and 0 GPa

由图11可知, 入射光能量E_in = 0时, c-BN和h-BN的介电常数值ε₀(单位: C²·N^–1·m^–2)分别是4.385和4.180, 因此c-BN和h-BN的屏蔽性都比较强. 在低能区域, c-BN的复介电函数虚部ε₂(ω)(图11(a)中的Im)在E_in达到6.942 eV时开始上升, 即c-BN的吸收边界为6.942 eV, 这是由价带穿越费米能级E_F导致的, 说明c-BN具有一定的导电性, 这和前面电子结构的分析结果相同. h-BN的复介电函数虚部ε₂(ω)(图11(b)中的Im)和c-BN类似, 在低能区一直趋于0, h-BN的吸收边界为2.797 eV, 同样也具有一定的金属特性.
吸收系数I和复介电函数的虚部ε₂密切相关, 如图12所示. 可以看出, c-BN的吸收峰要明显高于h-BN的吸收峰. 吸收峰的较高能量主要源自于带间电子跃迁, c-BN和h-BN有如此高的吸收系数, 主要是由电子从价带向导带跃迁导致的.
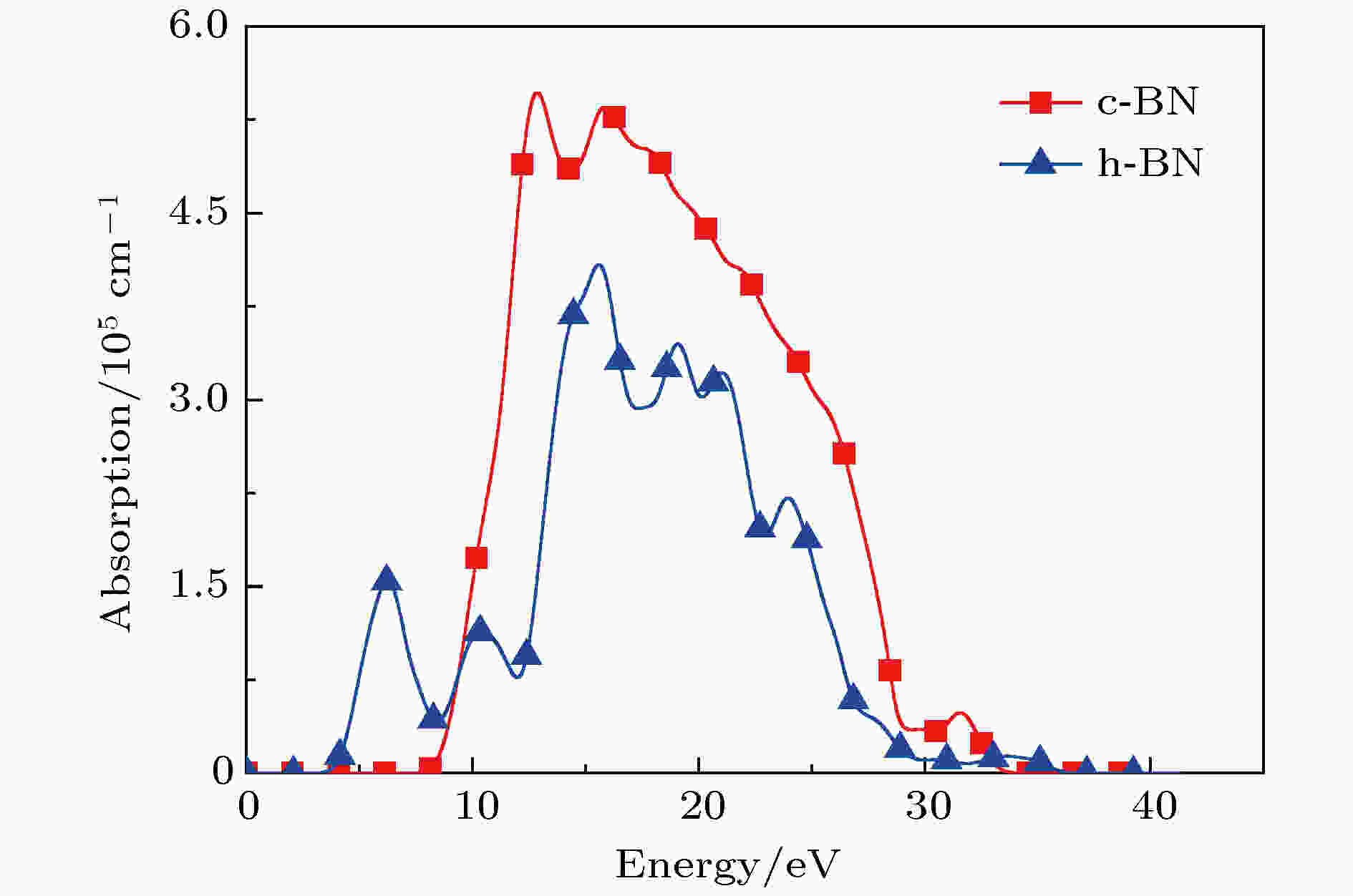图 12 0 K和0 GPa时c-BN和h-BN的吸收系数
Figure12. Absorption coefficients of c-BN and h-BN at 0 K and 0 GPa

c-BN和h-BN的反射率R如图13所示, 入射光能量E_in = 27.083 eV时, c-BN的反射率达到最大值R = 0.859. 显然, c-BN的反射能力明显优于h-BN, 在40 eV以上的高能区, c-BN和h-BN的反射率R均几乎为0. c-BN的R在29.5 eV左右急剧下降, 说明对于不同频率的入射光, 材料的响应性能变化较大.
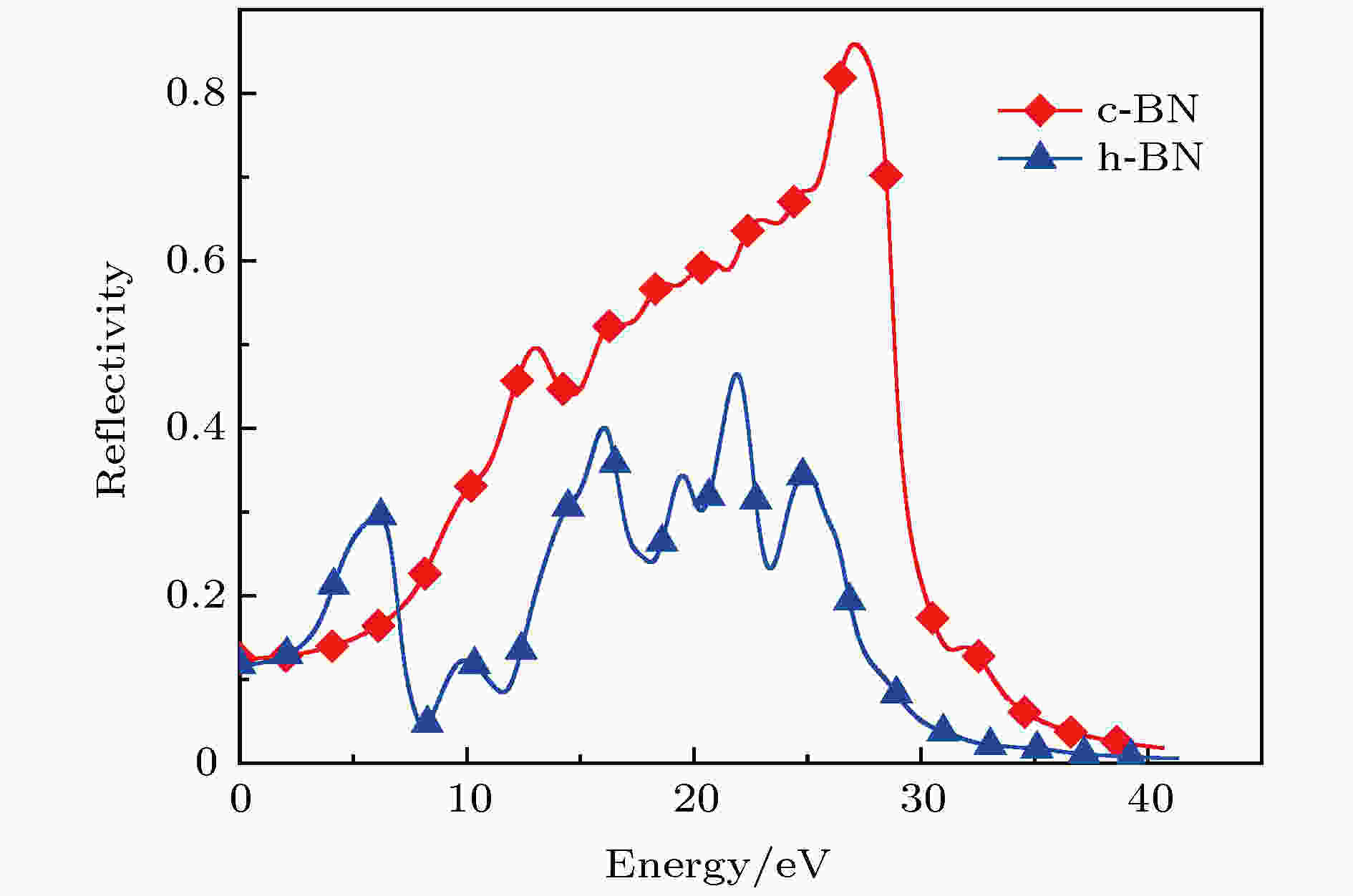图 13 0 K和0 GPa时c-BN和h-BN的反射率
Figure13. Reflectivity of c-BN and h-BN at 0 K and 0 GPa

c-BN和h-BN的光折射率n和消光系数k随入射光能量E_in的变化关系如图14所示, 可以看出与对应的复介电函数变化趋势几乎相同. E_in = 0时, c-BN和h-BN的静态折射率n(0)分别是2.094和2.045, h-BN的n(0)略小于c-BN, 这与静态介电常数类似. 由复介电函数和折射率、消光系数的关系(28)式和(29)式可知, ε₁(ω)和ε₂(ω)在上升和下降过程中斜率最大的地方分别对应着n(ω)和k(ω)的峰和谷.
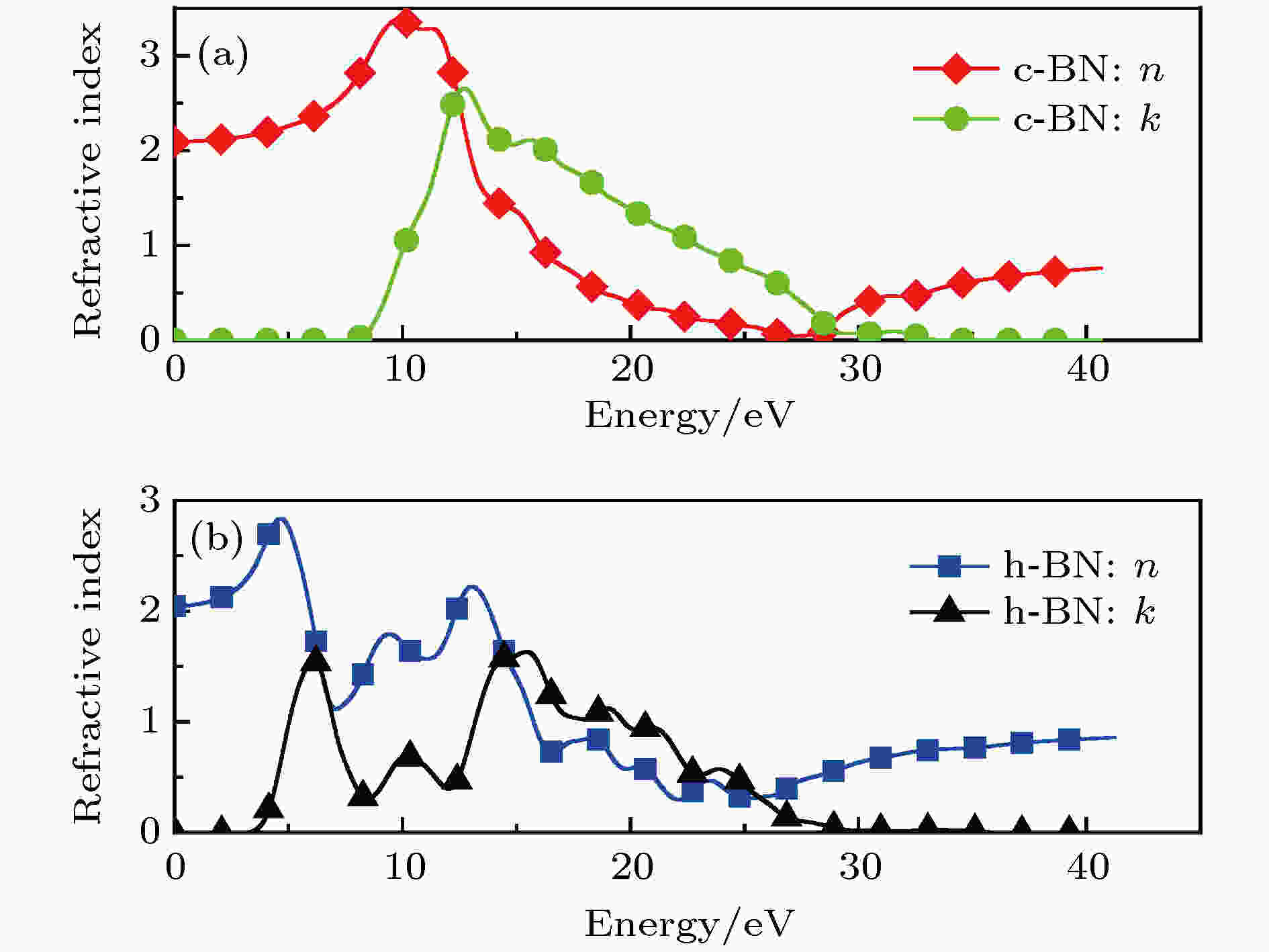图 14 0 K和0 GPa时c-BN和h-BN的折射率和消光系数
Figure14. Refractive index and extinction coefficient of c-BN and h-BN at 0 K and 0 GPa

c-BN在E_in = 12.415 eV时, n, k 相等, 约为2.6, 此时的ε₁ = 0; 当ε₁ < 0, 即n < k时, 通过对比图13中的c-BN的反射率R可知此时R比较大, 说明在此频率范围内光几乎不能在固体中传播; 当n 随着E_in的增加而增大时, c-BN表现为正常色散特性, 反之则表现为反常色散特性. 对于h-BN则比较复杂, 可以看出其n和k曲线有4次交叉, 这和h-BN有4次ε₁ = 0相符合; 在较高能量段, 当ε₁ < 0, 即n < k时, 其R也比较大, 光也很难在其内部通过. 无论是c-BN还是h-BN, 在高频能量范围内(E_in > 30 eV), k几乎为0, 这说明光在其内部传播不会衰减, 也就是说能量不会减小, 此时c-BN和h-BN在高能区内很难吸收光.
损失函数L描述的是光电子在均匀电介质中穿过时的能量损失情况, c-BN和h-BN的损失函数L如图15所示, c-BN和h-BN都有明显的能量损失峰, 分别出现在E_in = 28.648 eV和E_in = 26.232 eV处, 对应的L分别为30.112和5.662. 值得注意的是, c-BN的峰值明显大于h-BN, 且更加尖锐, 这说明c-BN在峰值处随E_in变化更加敏感. 结合图13和图14的变化曲线可以看出, 在该峰处对应的反射率R迅速下降. L的变化比较大是由于带间的相互作用比较强; 反之, 则带间相互作用较弱.
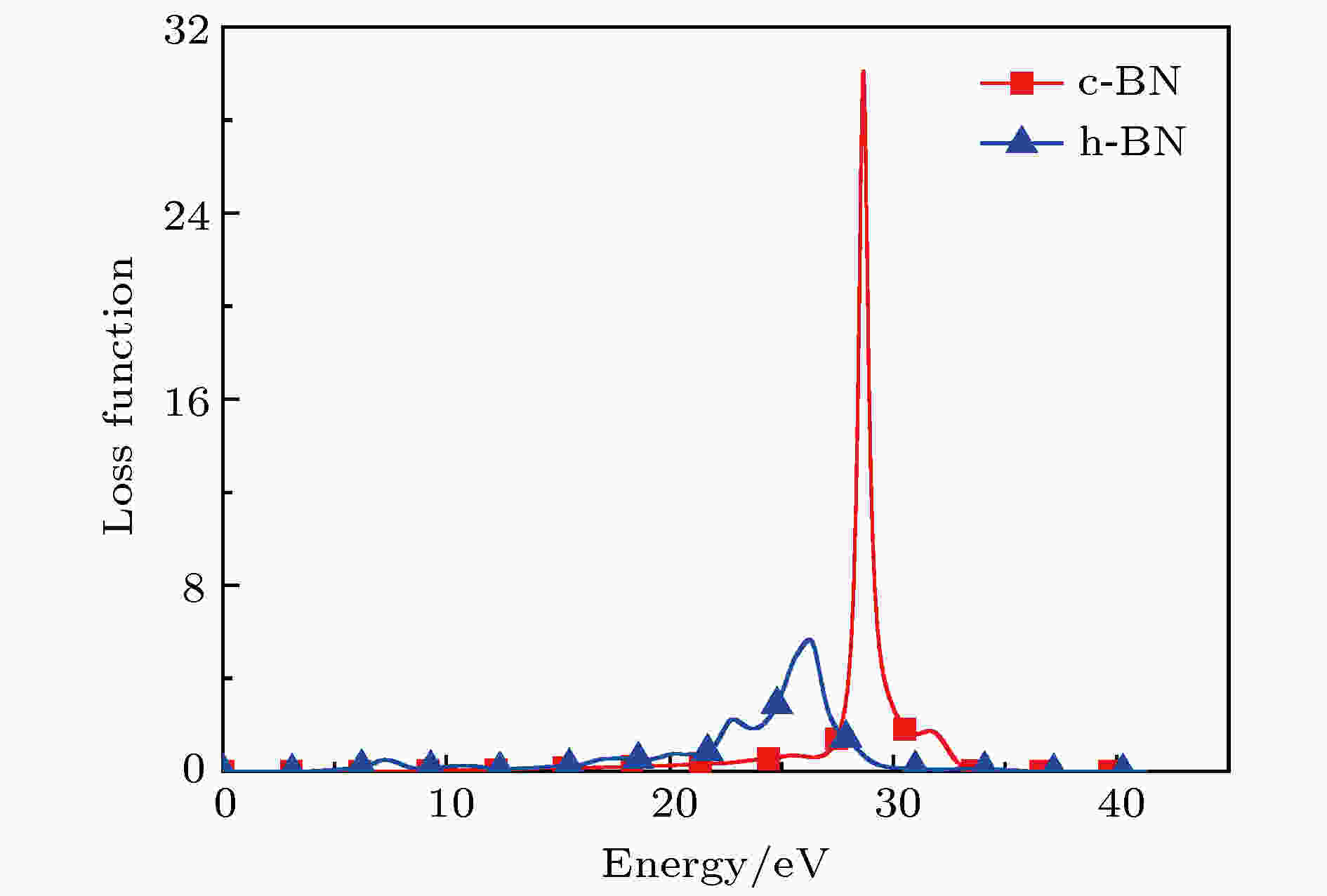图 15 0 K和0 GPa时c-BN和h-BN的损失函数
Figure15. Loss function of c-BN and h-BN at 0 K and 0 GPa

通过前面能带的分析可以知道, c-BN和h-BN均为间接带隙半导体, 在半导体的光吸收过程中, 电子的跃迁会产生光电导现象. c-BN和h-BN的光电导率σ如图16所示, c-BN和h-BN的光电导实部(Re)在低能区(c-BN: E_in < 6.961 eV, h-BN: E_in < 2.942 eV)和高能区(c-BN: E_in > 34.075 eV, h-BN: E_in > 36.679 eV)趋近于0. c-BN和h-BN分别在E_in = 12.185 eV和E_in = 14.029 eV处达到峰值20.697和9.567 fs^–1, c-BN的峰值明显大于h-BN, 而h-BN有两个较明显的峰. c-BN的虚部可以分为两部分, 在E_in < 12.286 eV时为负, E_in > 12.286 eV时为正; h-BN相对复杂, 但基本上是在E_in < 14.133 eV时为负, E_in > 14.133 eV时为正. c-BN和h-BN在正负分界处附近的变化都十分明显.
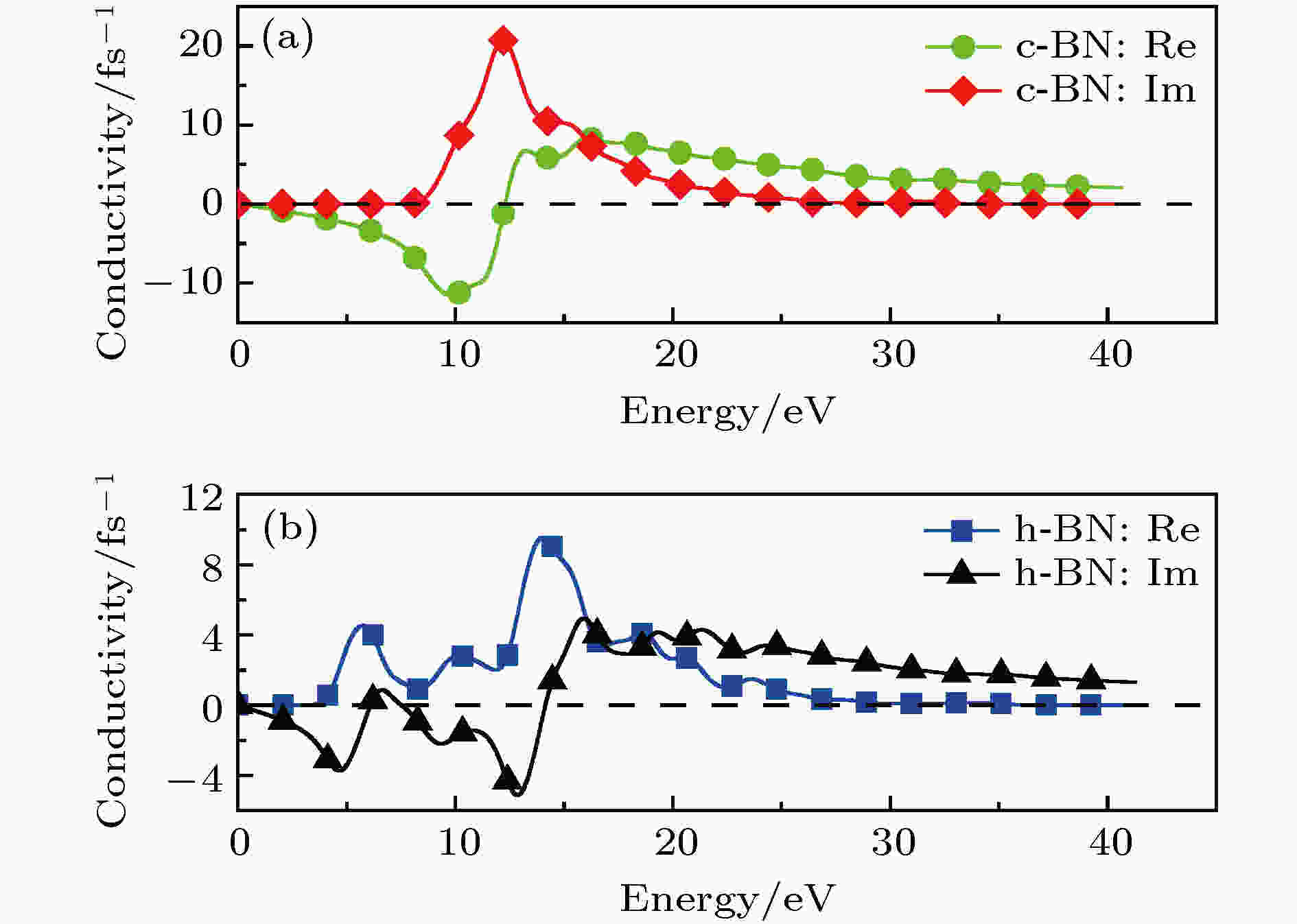图 16 0 K和0 GPa时c-BN和h-BN的光电导率
Figure16. Conductivity of c-BN and h-BN at 0 K and 0 GPa

本文采用基于DFT第一性原理和LDA近似方法, 对c-BN和h-BN的结构进行了几何优化, 得到了其能量最低结构, 并计算了两种结构的相关性质, 得到以下结论: 1)经过几何优化, c-BN和h-BN得到稳定结构的的晶格常数分别为3.576 和2.504, 6.610?; 2)通过研究零压下的力学性质可知: c-BN和h-BN的弹性常数值均满足玻恩稳定性判据, 而h-BN的声子图谱出现了虚频, 说明零温零压下c-BN为稳定结构, 而h-BN为亚稳定结构; 通过对弹性模量和泊松比的分析, 得到了c-BN和h-BN均为脆性材料且c-BN的硬度要大于h-BN; 3)通过研究c-BN在不同温度、不同压力下的热力学性质可知: c-BN的晶胞体积随着温度和压力的增大越来越难被压缩; 热熔在高温时符合德拜定律并接近Dulong—Petit极限; 4) 通过对电子结构的研究可知: c-BN和h-BN均为间接带隙半导体, 带隙宽度分别是4.391和4.071 eV; 再结合态密度可以看出, c-BN和h-BN均表现出部分金属性质; c-BN局域性要强于h-BN, 即c-BN的稳定性更好; 5)通过对光学性质的研究可知: c-BN的反射率和吸收系数在很大频率范围内都大于h-BN, 且对入射光响应性能变化较大; 同时, 由折射率、消光系数、损失函数和光电导性得知: c-BN和h-BN在高能区内很难吸收光, c-BN和h-BN在很大的频率范围内, 对入射光的通过性都很好.
感谢中原工学院材料模拟与计算中心实验室, 对本文相关计算资源的帮助和支持.