摘要:螺旋锥束计算机断层成像(CT)作为常用的临床诊断工具, 如何尽可能地减少其辐射剂量是热点研究领域之一. 局部成像利用准直器减小射线直照区域, 能够有效降低CT辐射剂量. 然而, 局部成像会造成投影数据横向截断, 产生局部重建问题. 现有螺旋反投影滤波(BPF)算法只能实现局部曲面重建, 难以实现局部体区域重建. 在圆轨迹扇束BPF算法的基础上, 通过加权修正和坐标扩展, 提出了螺旋锥束CT 倾斜扇束反投影滤波(TFB-BPF)重建算法. 该算法把重建区域按层划分, 对各层构建倾斜的扇形束几何, 并使用经过加权修正的TFB-BPF算法逐层进行重建. 该算法最大的优势是滤波线(与原始螺旋锥束BPF算法中PI线等价)在二维平面内选择, 算法更加简洁高效, 并且能够应用于局部体区域的重建. 实验结果表明, 算法能够有效重建物体局部体区域, 并且重建图像质量较好, 没有明显的截断伪影.
关键词: 锥束计算机断层成像/
螺旋轨迹/
局部成像/
反投影滤波

English Abstract

全文HTML

--> --> -->

螺旋锥束计算机断层成像(computed tomography, CT)在临床医疗诊断中具有非常广泛的应用. 然而, X射线CT对公众所造成的辐射伤害是不可忽视的^[1]. 随着人们越来越关注CT所产生的次生辐射伤害, 如何合理做到尽可能减少CT辐射剂量已成为热点研究领域之一^{[2, 3]}. CT辐射剂量受管电压(kVp)、管电流和曝光时间(mAs)和射束准直情况等很多因素的影响. 根据应用条件不同, 已有很多减少CT辐射剂量的方法, 比如低mAs成像^[4-9]、短扫描/半覆盖成像^[10-12]、不完全数据成像^[13-16]、局部成像^[17-22]和相位衬度成像^{[23, 24]}等. 局部成像利用准直器限制X射线仅对被试的感兴趣区域进行照射, 避免其他部位受到直射射线辐照, 从而减少被试受到的辐射总量. 由于对直射区域范围的限制, 局部成像图像重建所使用的投影数据通常是截断的, 这也被称为局部重建问题, 其关键是如何处理投影数据的横向截断. 螺旋轨迹作为最常用的医用扫描轨迹, 研究可适用于其局部成像的高质量和高效率的图像重建算法具有重要意义.
螺旋锥束CT源点轨迹满足精确重建条件, 对其图像重建算法的研究一直有两条主线: 近似型^[25-28]和精确型重建算法. 对于精确型重建算法, Katsevich^[29]的滤波反投影(filtered back-projection, FBP)算法和Pan等^[30-32]提出的滤波反投影 (back-projection filtration, BPF)算法是两个重要的里程碑. Katsevich的FBP算法和近似重建算法要求投影数据不存在横向截断, 否则全局滤波会产生截断误差, 并通过反投影影响重建图像. 而螺旋锥束BPF算法仅需要保证PI线投影的完整性, 便可实现整条PI线的重建, 为局部重建带来了可能. 目前BPF算法已扩展到圆轨迹扇束CT^[33]和圆轨迹锥束CT^[34], 并有明确的局部成像公式. 而对于螺旋锥束CT, 由于PI线空间分布的复杂和无规律性, 局部重建算法的研究并没有那么简单. 原始螺旋锥束BPF算法只能实现一个局部PI面的重建, 而无法重建一块连续的局部体区域, 降低了算法的实用性.
针对BPF算法在螺旋锥束CT成像中PI线及采样点设计和在局部体区域重建方面存在的困难, 本文提出了一种倾斜扇束反投影滤波(tilted fan-beam back-projection filtration, TFB-BPF)重建算法, 该算法形式简单、计算高效, 在扫描轨迹螺距较小时具有很好的成像质量, 同时能够更好地发挥BPF型算法在局部成像中的优势, 对于螺旋锥束几何下的局部体区域成像有很好的应用效果.
本文首先介绍了螺旋锥束CT成像几何和原始的螺旋锥束BPF算法; 然后, 推导了TFB-BPF重建算法; 最后, 通过实验对本文算法的性能进行了验证.

2

-->

2.1.螺旋锥束CT成像几何

如图1所示, 首先介绍螺旋锥束CT成像几何. 以物体中心为原点定义三维笛卡儿直角坐标系$(x,y,z)$. 假设物体全部位于一个半径为${R_0}$的圆柱体支撑内. 螺旋锥束CT的旋转轴位于圆柱体支撑的中心轴线, 同时与$z$轴重合. 成像几何中光源和面阵探测器同时围绕旋转轴做螺旋轨迹运动. 光源发出锥形束射线对物体进行成像. 定义光源到旋转轴的距离为$R$, 光源到探测器的距离为$D$.
图 1 螺旋锥束CT成像几何
Figure1. Imaging geometry of helical cone-beam CT.

成像几何中, 在固定坐标系$(x,y,z)$中光源的扫描轨迹可表示为

${{r}_o}(\lambda ) = {\left(R\cos (\lambda ),R\sin (\lambda ),\dfrac{h}{{2{\text{π}}}}\lambda \right)^{\rm{T}}},$

式中$\lambda $为旋转角度; $h$为螺距.
此外, 在旋转轴构建虚拟的面阵探测器, 并以虚拟探测器中心为原点定义旋转的笛卡儿坐标系$(u,v,w)$. 分别用${\hat {{e}}_{{u}}}\left( {\lambda } \right)$,${\hat {{e}}_{{v}}}\left({\lambda } \right)$和${\hat {{e}}_{{w}}}\left({\lambda } \right)$表示旋转角度为$\lambda $时三个坐标轴的方向向量. 其中, ${\hat {{e}}_{{w}}}\left({\lambda } \right)$与面阵探测器的法向量平行; ${\hat {{e}}_{{u}}}\left({\lambda } \right)$和${\hat {{e}}_{{v}}}\left({\lambda } \right)$分别沿面阵探测器的行方向和列方向. 在固定坐标系$(x,y,z)$中, $(u,v,w)$三个轴的方向向量可表示为

$\begin{split}& {\hat {{e}}_{{u}}}\left({\lambda } \right) = {(\cos (\lambda )\;,\;\sin (\lambda )\;,\;0)^{\rm{T}}},\\& {\hat {{e}}_{{w}}}\left({\lambda } \right) = {( - \sin (\lambda )\;,\;\cos (\lambda )\;,\;0)^{\rm{T}}},\\& {\hat {{e}}_{{v}}}\left({\lambda } \right) = {(0\;,\;0\;,\;1)^{\rm{T}}}.\;\end{split}$

显然${\hat {{e}}_{{u}}}\left({\lambda } \right)$和 ${\hat {{e}}_{{w}}}\left({\lambda } \right)$在$x{\text{-}}y$平面内, 而${\hat {{e}}_{{v}}}\left({\lambda } \right)$平行于$z$轴, 并且面阵探测器上任何一点都可以用二维坐标$(u,v)$表示.
2 -->

2.2.BPF重建算法

BPF算法最先由Pan等^[30]于2004年针对螺旋锥束几何提出, 对于螺旋锥束CT的精确重建具有重要意义. BPF算法是基于PI线的重建算法. PI线是算法的最小重建单元. 只要保证PI线投影的完整性, 算法便可精确重建整条PI线.
螺旋轨迹BPF算法公式可表示为

$f({x}) = \int_{{R^3}} {g({x}')} k({x},{x}'){\rm{d}}{x}',$

式中

$g({x}') = \int_{{\lambda _1}}^{{\lambda _2}} {\dfrac{{{\rm{d}}\lambda }}{{|{x}' - {{x}_0}(\lambda )|}}} {\left. {\dfrac{\partial }{{\partial q}}D({{x}_0}(q),{\beta }({x}',\lambda ))} \right|_{q = \lambda }},$

$k({x},{x}') = \dfrac{1}{{2{\text{π}}{\rm{j}}}}\int_{{R^3}} {{\rm{d}}{\nu }{\mathop{\rm sgn}} \left[ {{\nu } \cdot {{e}_{\text{π}}}\left( {x} \right)} \right]{{\rm{e}}^{2{\text{π}}{\rm{j}}{\nu }{ \cdot ({x} - {x}')}}}} ,\quad\quad\quad\quad\quad$

${{x}_0}\left( {\lambda } \right)$表示光源坐标; $D({{x}_0}\left({\lambda } \right),\beta ({x}',\lambda ))$表示投影角度为$\lambda $时穿过点${{x}}'$的射线投影值; ${{e}_{\text{π}}}\left( {x} \right)$表示由${\lambda _1}$和${\lambda _2}$确定的PI线的方向向量; ${x}$和${x}'$为PI线上两点.
具体对于PI线段$\left[ {{x_{{\text{π}}{\rm{1}}}},{x_{{\text{π}}2}}} \right]$上任意一点${x_{\text{π}}}$, 实际应用中BPF算法可根据如下四个步骤进行实现.
步骤1　对原始投影数据进行求导. 根据链式法则, 投影数据对旋转角度的求导可以转化为对探测器横纵坐标的求导:

${\left. {\frac{\partial }{{\partial q}}D({{x}_0}\left( {q} \right),\beta )} \right|_{q = \lambda }} = {\left. {\frac{{\partial P\left( {u,v,q} \right)}}{{\partial q}}} \right|_{q = \lambda }}.$

步骤2　对求导后的投影数据在PI线段进行反投影:

$\begin{split}{g_{\text{π}}}\left( {{{x'}_{\text{π}}},{\lambda _1},{\lambda _2}} \right) =\;& \int_{{\lambda _2}}^{{\lambda _1}} {\frac{{{\rm d}\lambda }}{{{{\left| {{x} - {{x}_0}\left({\lambda } \right)} \right|}^2}}}{{\left. {\frac{{\partial P\left( {u,v,q} \right)}}{{\partial \lambda }}} \right|}_{q = \lambda }}} \\ & + \left. {\frac{{P\left( {u,v,\lambda } \right)}}{{\left| {{x} - {{x}_0}\left({\lambda } \right)} \right|}}} \right|_{{\lambda _1}}^{{\lambda _2}}.\end{split}$

步骤3　对反投影后的数据沿PI线方向进行希尔伯特滤波:

${f_{\text{π}}}\left( {{x_{\text{π}}},{\lambda _1},{\lambda _2}} \right) = - \frac{1}{{2{{\text{π}}^2}}}\int_{{R^3}}^{} {\frac{{{\rm{d}}{{x}_\text{π}'}}}{{{x_{\text{π}}} - {{x}_\text{π}'}}}{g_{\text{π}}}\left( {{{x}_\text{π}'},{\lambda _1},{\lambda _2}} \right)} .$

步骤4　根据PI线坐标与$(x,y,z)$坐标的转换关系, 完成重建值从PI线坐标系到三维笛卡儿坐标系的重采样.
BPF算法初始的重建采样点并非位于笛卡儿坐标网格上, 而是位于PI线上. 所以, 算法需要从PI线坐标到三维笛卡儿坐标重采样. 实际中, 首先需要设计合适的PI线组, 并使PI线组完全覆盖待重建三维体区域. 然而, 三维空间中PI线的分布是无规律的, 并且PI线上采样点的设置也不像笛卡儿网格具有天然的均匀性. 因此, PI线设计及PI线上采样点设置很重要, 不仅会影响算法的执行效率, 而且会影响重采样后笛卡儿空间三维图像的均匀性.
BPF算法另一个重要的优势是解决投影数据存在某些横向截断时的图像重建. 目前在圆轨迹扇束CT和圆轨迹锥束CT中已经有专用的局部成像BPF算法. 而对于螺旋锥束CT, 用于局部成像BPF算法的设计并不像圆轨迹那么简单. 这主要是因为, 在实际局部成像应用中, 很难同时保证沿多个方向的PI线的数据完整性. 在圆轨迹成像中可以很容易设计PI线组完全覆盖待重建区域且方向一致, 但是在螺旋锥束成像中, 由于PI线分布的复杂性, 很难设计完全覆盖待重建区域且方向一致的PI线组.

TFB-BPF算法是Noo等^[33]提出的圆轨迹扇形束BPF算法的推广. TFB-BPF算法的数学推导与Feldkamp-Davis-Kress (FDK)算法的推导过程非常类似: 扇形束BPF算法在三维空间上的扩展. TFB-BPF算法更加简洁高效, 在扫描轨迹螺距较小时具有很好的成像质量, 同时能够发挥BPF型算法在局部成像中的优势, 对于螺旋锥束几何下的局部体区域成像有很好的应用效果.
2

-->

3.1.圆轨迹扇束BPF算法

首先介绍圆轨迹扇束BPF算法. 2004年, Noo等^[33]将BPF算法引入圆轨迹扇束成像几何中, 并在二维平面内对BPF公式做了重新推导. PI线属于螺旋轨迹成像中的专有名词, 而在圆轨迹扇束BPF算法中用滤波线代替PI线.
图2为圆轨迹扇束CT成像几何. 以物体中心为原点定义固定的笛卡儿坐标系$(x,y)$. 光源和线探测器一起围绕物体做圆轨迹运动, 旋转中心与固定坐标系原点重合. 定义光源到旋转中心的距离为R, 而光源到探测器的距离为D. 在物体中心构建虚拟探测器, 以虚拟探测器中心为原点建立旋转的坐标系$(u,w)$. 投影数据用$p(\lambda ,u)$表示, 其中, $\lambda $表示投影角度, $u$表示探元在探测器上的位置.
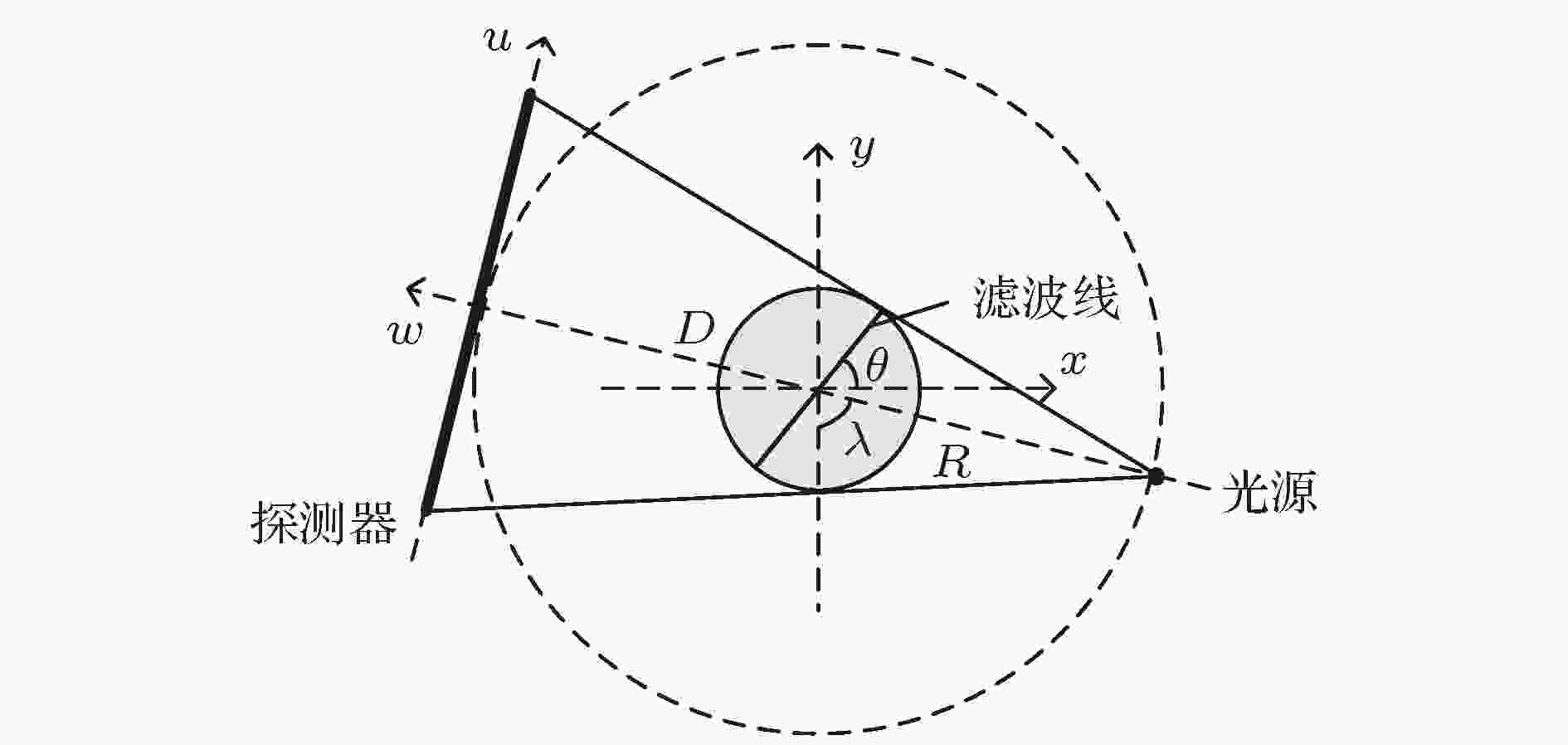图 2 圆轨迹扇束CT成像几何
Figure2. Imaging geometry of circular fan beam CT.

圆轨迹扇束BPF算法可以分解为两个步骤: 第一步, 对求导后的投影数据的进行反投影; 第二步, 对反投影后的数据沿滤波线方向做希尔伯特滤波. 其中, 第一步后得到的图像被称为偏导反投影(differentiated back projection, DBP)图像. 如何得到DBP图像是BPF算法在不同成像几何下扩展的关键. 同扇束FBP公式一样, 扇束DBP公式也是通过对平行束DBP公式进行变量替换得到的. 具体的, 扇束DBP公式为

$\begin{split}&{b_\theta }({x}) \\&= \dfrac{1}{2}\displaystyle\int_0^{2{\text{π}}} {\dfrac{{{R^2}}}{{{{(R + w)}^2}}}\displaystyle\int_{ - \infty }^{ + \infty } {\frac{R}{{\sqrt {{R^2} + {u^2}} }}p(\lambda ,u)} } \delta '(u' - u)\\&\times {\mathop{\rm sgn}} \left[{\sin \left( {\lambda - \arctan \dfrac{u}{R} - \theta } \right)} \right]{\rm{d}}u{\rm{d}}\lambda ,\end{split}$

式中${x} = (x,y)$表示待重建物体上一点; $\theta $为滤波线的方向角; $(u,w)$表示旋转后的坐标, 即

$\left[ \begin{gathered} u \\ w \\ \end{gathered} \right] = \left[ \begin{gathered} \cos \lambda \\ - \sin \lambda \\ \end{gathered} \right.\left. \begin{gathered} \sin \lambda \\ \cos \lambda \\ \end{gathered} \right]\left[ \begin{gathered} x \\ y \\ \end{gathered} \right],$

$u' = Ru/(R + w).$

DBP图像与实际图像的关系为

${b_\theta }({{x}}) = - 2{\text{π}}{H_\theta }f({{x}}),$

其中${H_\theta }f({{x}})$表示实际图像沿滤波线的希尔伯特变换, 对DBP图像沿滤波线方向做希尔伯特滤波便可以得到重建图像.
2 -->

3.2.TFB-BPF算法

TFB-BPF算法是由圆轨迹扇束BPF算法推广而来. 算法同样可以分解为两个步骤: 首先, 由投影数据得到DBP图像; 然后, 对DBP图像沿滤波线方向做希尔伯特滤波得到重建图像.
在螺旋锥束成像几何中, 光源的运动轨迹在三维空间内不能直接构成二维平面, 本文算法首先将待重建物体划分成一组平行于x-y平面的待重建平面. 如图3所示, 待重建平面与z轴垂直, 沿z轴方向均匀分布, 且完全覆盖待重建物体. 在每个待重建平面中引入虚拟滤波线的概念. 虚拟滤波线与圆轨迹扇束BPF算法中滤波线具有相同的作用. 螺旋锥束几何具有旋转对称性, 各个待重建平面的成像几何等价. 因此, 不失一般性, 以任意一个待重建平面为例继续介绍TFB-BPF算法.
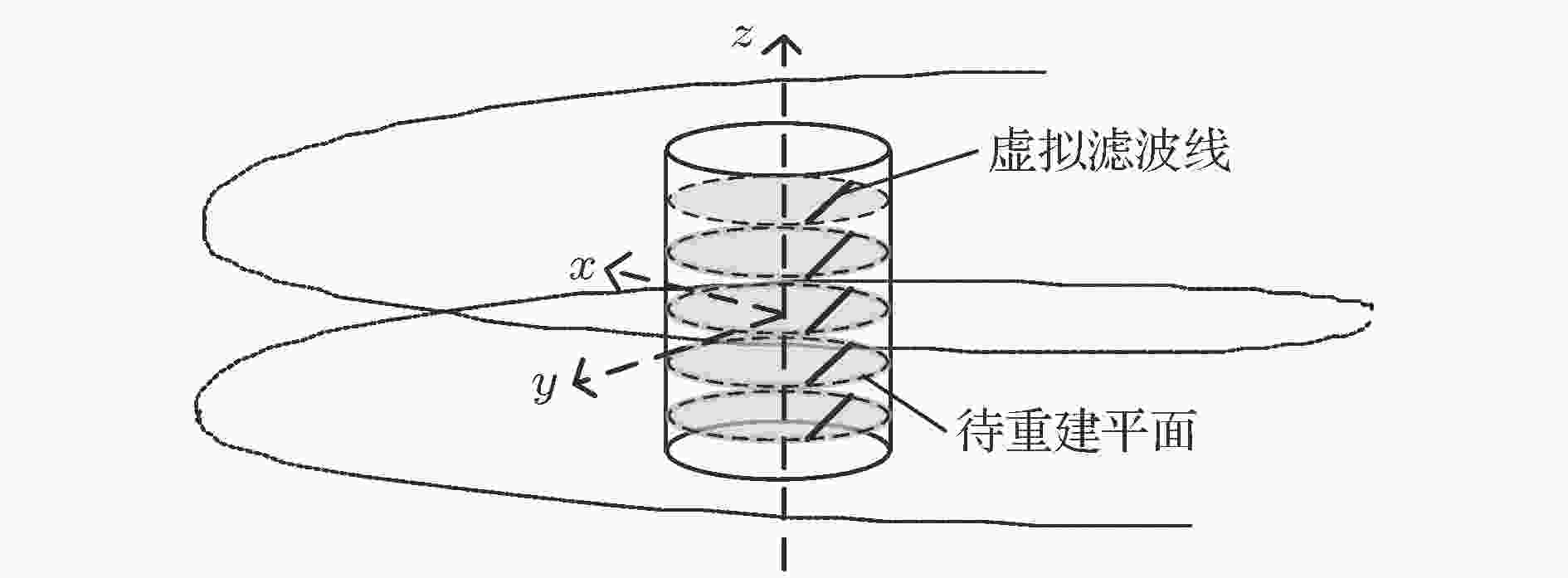图 3 螺旋锥束CT几何中的待重建平面和虚拟滤波线
Figure3. Reconstruction planes and virtual filtering lines in helical cone beam CT geometry.

将任意一个待重建平面和该平面上下各180°的螺旋轨迹提取出来, 如图4所示, 这构成了单个待重建平面的螺旋锥束成像几何. 当螺旋轨迹的螺距为0时, 图4的螺旋锥束几何退化为圆轨迹扇束成像几何, 此时, 可以直接应用扇束BPF算法对虚拟滤波线进行重建. 当螺距大于0的时候, 则需要在倾斜的扇束平面几何中对虚拟滤波线进行反投影, 并对反投影后的图像沿虚拟滤波线进行希尔伯特进而实现图像重建. 如图4所示, 对于虚拟滤波线中任何一点$({x_p},{y_p},{z_p})$的反投影是在倾斜的扇束平面中完成的, 需要构建新的倾斜扇束平面成像几何, 并对原始扇束BPF算法公式进行修正. 在图4倾斜扇束平面中定义光源到旋转中心的距离为${R_{\rm h}}$和新的旋转坐标系$({u_{\rm{h}}},{w_{\rm{h}}})$.
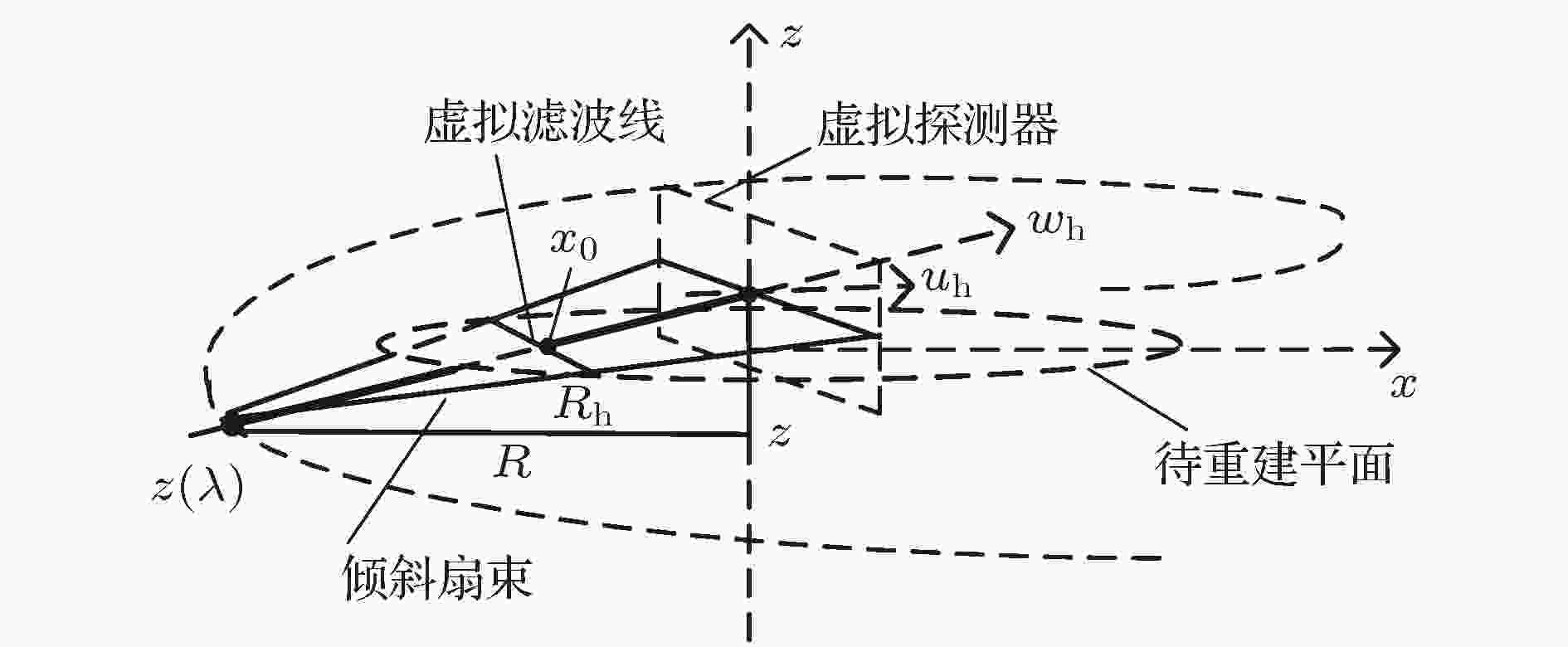图 4 单个待重建平面螺旋锥束成像几何
Figure4. Imaging geometry of single reconstruction plane.

倾斜扇束平面中光源到旋转中心${R_{\rm{h}}}$的距离的计算公式为

${R_{\rm{h}}} = \sqrt {{R_{}}^2 + {\varsigma ^2}} ,$

式中$\varsigma $为倾斜扇束平面与中心扇束平面沿z轴的高度差, 具体计算公式为

$\zeta = \frac{{R({z_p} - z(\lambda ))}}{{R + w}},$

其中$z(\lambda )$表示光源在z轴的位置; $w$表示旋转后的坐标.
此外, 倾斜平面中光源的角度增量${\rm{d}}{\lambda _{\rm{h}}}$应满足

${\rm{d}}\lambda R = {\rm{d}}{\lambda _{\rm{h}}}{R_{\rm{h}}}.$

新的旋转坐标系$({u_{\rm{h}}},{w_{\rm{h}}})$可以通过(16)式进行计算:

${u_{\rm{h}}} = u,\;\;\frac{{{w_{\rm{h}}}}}{{{R_{\rm{h}}}}} = \frac{w}{R}.$

将(13), (15)和(16)式代入圆轨迹扇束DBP公式中, 即可得到螺旋锥束几何下的TFB-DBP公式为

$\begin{split}&{{b_\theta }({{{x}}_p})} = \\ &\frac{1}{2}\int_{\lambda \left( {{z_p}} \right){\rm{ - }}{\text{π}}}^{\lambda \left( {{z_p}} \right){\rm{ + }}{\text{π}}} {\frac{{{R^2}}}{{{{(R + w)}^2}}}\int_{ - \infty }^{ + \infty } {\frac{R}{{\sqrt {{R^2} + {u^2} + {v^2}} }}P(\lambda ,u,v)} } \\&\times{\delta '(u' - u){\rm{sgn}}\left[ {\sin \left( {\lambda - \arctan \frac{u}{R} - \theta } \right)} \right]{\rm{d}}u{\rm{d}}\lambda ,}\end{split}$

式中$\lambda \left( {{z_p}} \right)$表示光源轨迹与待重建平面相交时的旋转角度. 对比(9)式和(17)式可以发现, 通过变量替换和调整积分限, 本文TFB-DBP公式对圆轨迹扇束DBP公式中的反投影部分做了修正, 而没有改变求导过程. 通过对投影图像逐行进行求导, 并对求导后的图像按(17)式进行反投影即可得到TFB-DBP图像.
与圆轨迹扇束BPF算法一样, 螺旋锥束BPF算法中DBP图像与实际图像的关系为

${b_\theta }({{x}}) = - 2{\text{π}}{H_\theta }f({{x}}),$

因此, 对(17)式得到的TFB-DBP图像沿虚拟滤波线方向做希尔伯特滤波获得重建图像.
综上, TFB-BPF算法首先通过在多个相互平行的二维平面内选则合适的虚拟滤波线组确定重建网格; 然后, 通过(17)式计算待重建物体的DBP图像; 最后, 沿虚拟滤波线方向对DBP图像做希尔伯特滤波获得三维重建图像.
TFB-BPF算法的虚拟滤波线设计与圆轨迹扇束中滤波线的设计方法相似: 只需要在二维平面内进行设计. 算法可以方便地确定重建采样点, 并可以通过选择与x轴或y轴平行的虚拟滤波线使重建采样点与三维笛卡儿网格匹配, 从而避免了原始BPF算法中重建结果从PI线坐标到笛卡儿坐标的重采样. 基于此, 可以看出TFB-BPF算法相比原始螺旋锥束BPF算法具有更简单的实现方式和更高效的执行效率.
更重要的是, TFB-BPF算法在螺旋锥束CT局部体区域成像也具有明显的优势. 对于圆轨迹扇束BPF算法, Noo等^[33]讨论了多种适用的局部断层区域成像几何结构, 其关键是设计适合的滤波线组, 使得利用(9)式计算DBP图像时所需的投影数据在角度上是不缺失的, 而与投影数据是否存在截断无关. 与圆轨迹扇束BPF算法一样, TFB-BPF算法也可以设计一组适合的虚拟滤波线, 只要保正计算该滤波线组的TFB-DBP图像所需的投影数据在角度上是完全的(可以存在截断), 便可以实现局部三维体区域重建. 如图5所示, 利用螺旋锥束CT对椭圆柱状物体进行局部成像. 如图5(b)所示, TFB-BPF算法在圆柱状重建区域内(虚线圆内)沿z轴划分一组平行x-y平面的待重建平面, 并在每个待重建平面内设计与y轴平行的虚拟滤波线. 根据(17)式, 可以看出计算此虚拟滤波线组中任意采样点TFB-DBP时, 投影数据在角度上是不缺失的, 因此可以应用本文算法进行重建. 在工业应用和医学应用中, TFB-BPF算法与圆轨迹扇束BPF算法都具有重要的实际意义.
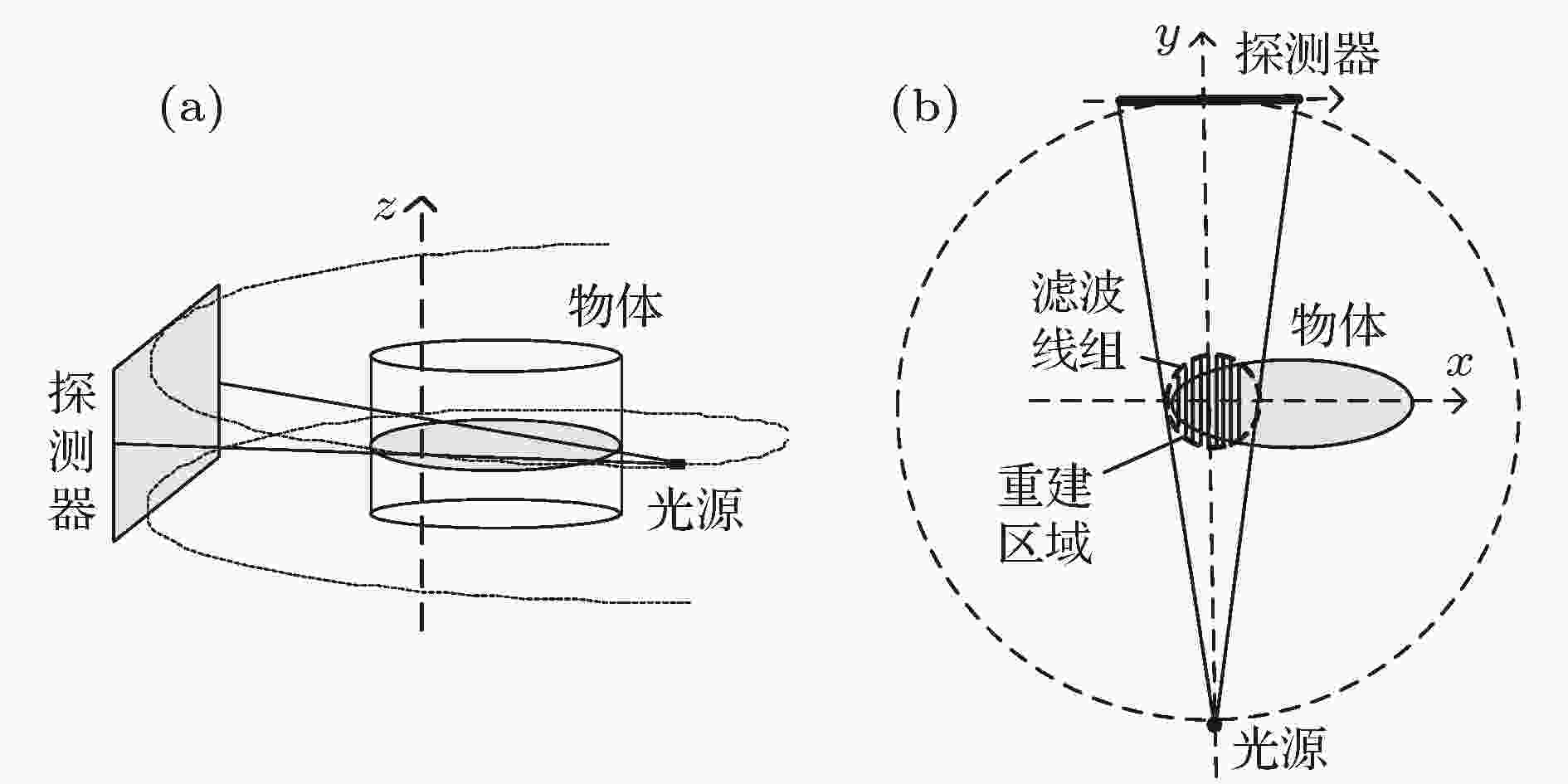图 5 局部体区域成像示意图　(a)侧视图; (b)俯视图
Figure5. Imaging schematic for local volume: (a) Side view; (b) top view.

本节通过实验验证本文算法的有效性, 同时将本文实验结果与经典的螺旋FDK算法^[35]的实验结果进行了比较.
如图1所示, 首先构建螺旋锥束CT成像几何. 光源到旋转轴的距离R = 100 mm, 光源到面阵探测器的距离D = 300 mm, 光源运动轨迹的螺距h = 7.89 mm. 面阵探测器的探元阵列为200 × 256, 其中每个探元的尺寸为0.148 mm× 0.148 mm. 在此成像几何下, 对三维Shepp-Logan^[36]体模进行数据采集. 三维Shepp-Logan体模被定义在一个半径R₀ = 6.31 mm圆柱体内. 在5.2${\text{π}}$的螺旋轨迹中共采集了1872张没有横向截断且不含噪声的投影数据, 采集的角度间隔为0.5°. 二维投影生成采用标准的体素驱动模式, 并使用二维线性插值的方式对投影点邻近的4个探测器探元进行插值. 利用此投影数据, 分别使TFB-BPF算法和螺旋FDK算法进行重建. 重建图像的规模为256 × 256 × 256. 重建结果如图6所示, 第一行为Shepp-Logan体模真值, 第二行为螺旋FDK算法重建结果, 第三行为本文算法重建结果; 第一列、第二列和第三列分别为体模沿z轴第128层、沿x轴第128层和沿y轴第128层切片. 为了定量分析重建结果, 图7给出了重建切片的剖线图.
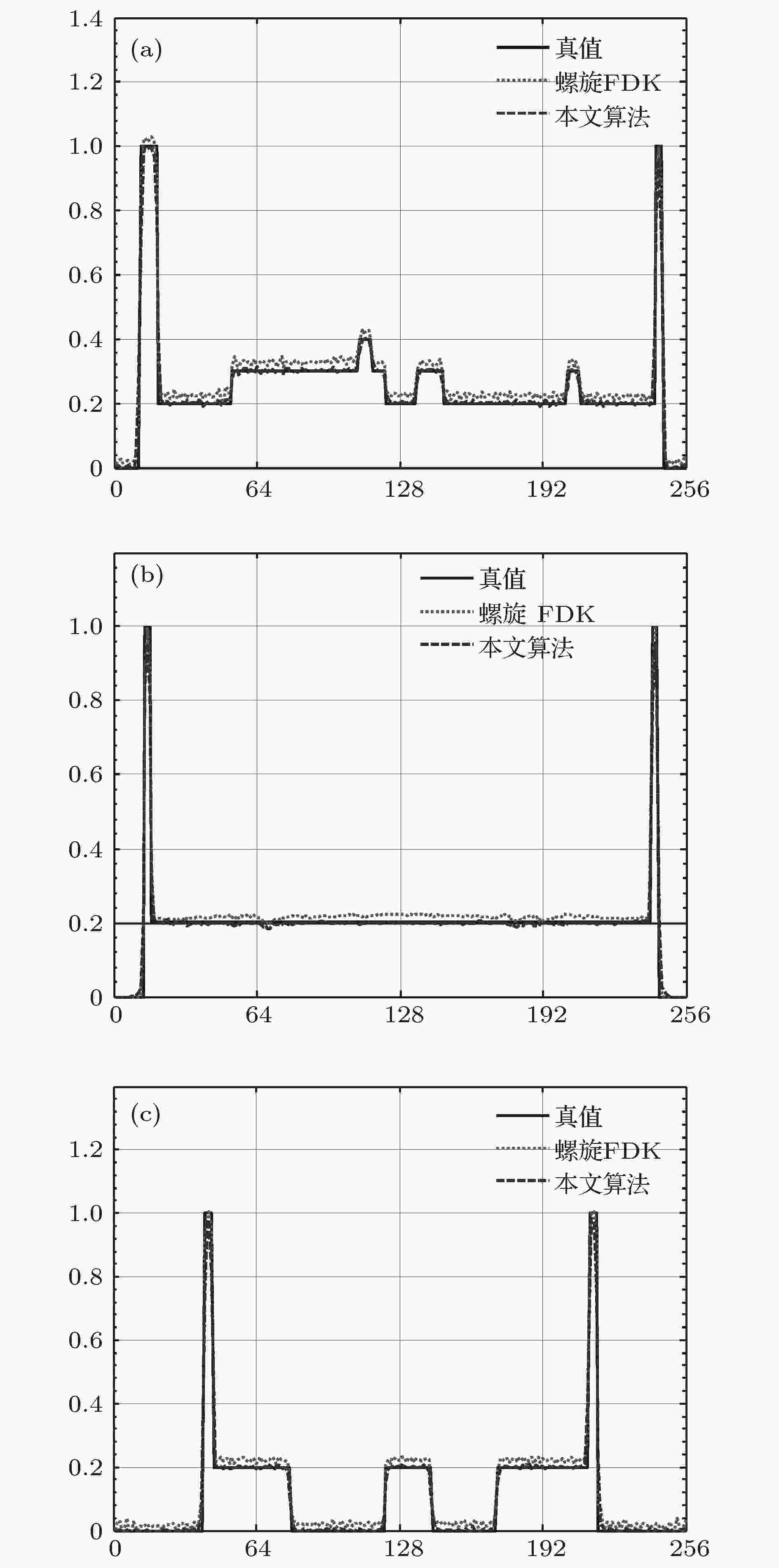图 7 无截断投影重建图像剖线图　(a), (b), (c)分别为图6第一列、第二列和第三列切片的垂直剖线
Figure7. Plots of reconstruction image without truncated projections: (a), (b), (c) the vertical plots of the first, second, and third column slices of Fig.6., respectively.

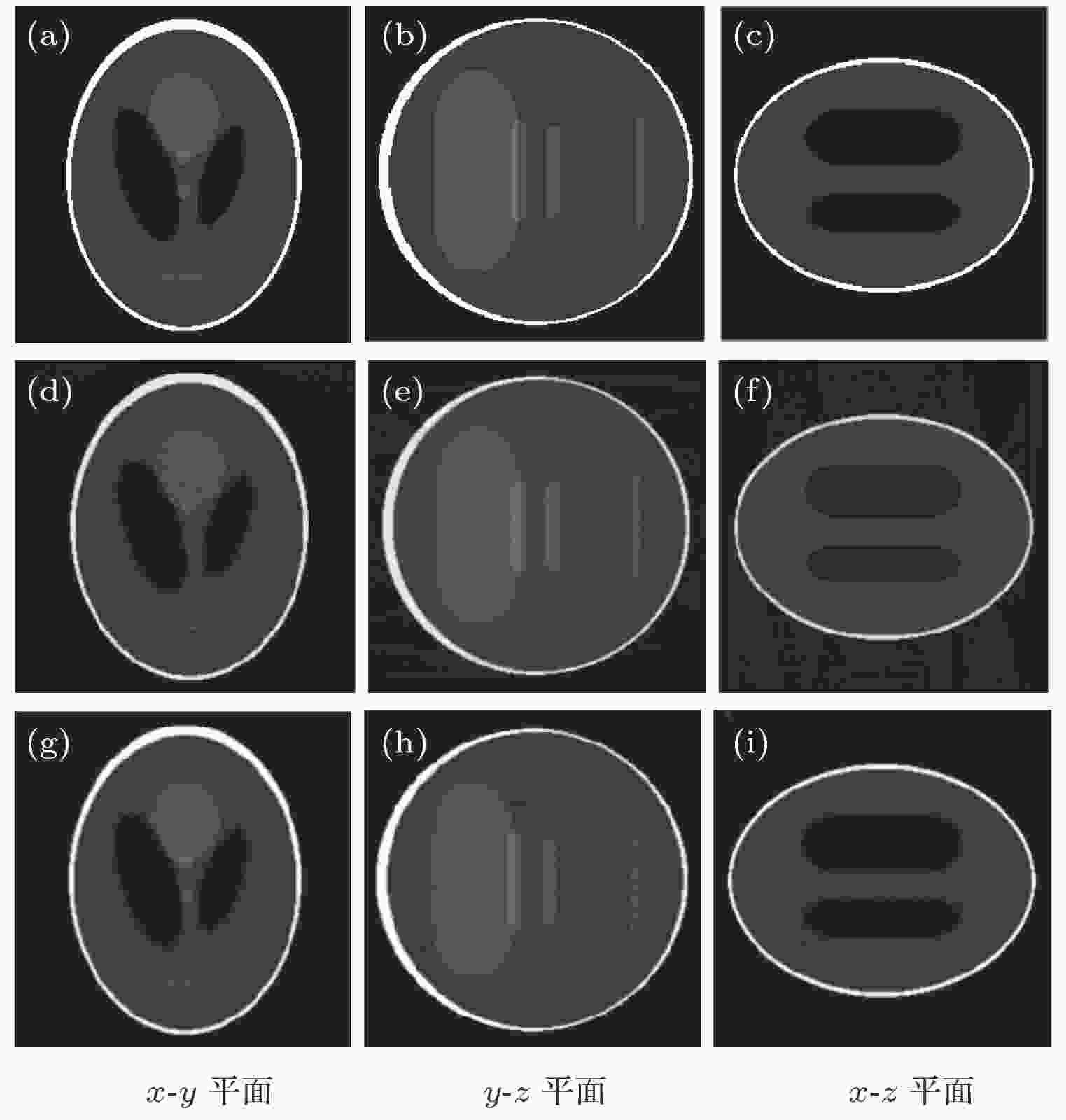图 6 无截断投影重建图像　(a), (b), (c)真值; (d), (e), (f)螺旋FDK算法; (g), (h), (i)本文算法
Figure6. Reconstruction image without truncation: (a), (b), (c) True value; (d), (e), (f) helical FDK algorithm; (g), (h), (i) the proposed algorithm.

由图6可以看出, 对于无截断的投影数据, 本文算法能够有效地实施重建, 重建图像中没有明显的伪影. 图7的数值比较表明, 本文算法的重建值与真值的偏差较小, 能够实现准确的重建. 与螺旋FDK算法重建结果的比较也说明本文算法能够有效重建无截断的投影数据, 重建图像不会引入新的误差, 重建质量与螺旋FDK算法相当.
为了验证本文算法对含噪声数据的处理性能, 本文还进行了对加噪数据的重建实验. 模拟由500000光子产生的泊松噪声, 并将噪声添加到之前采集的投影数据中生成含噪投影数据. 对含噪投影数据, 同样分别使用本文算法和螺旋FDK算法进行重建. 重建结果如图8所示.
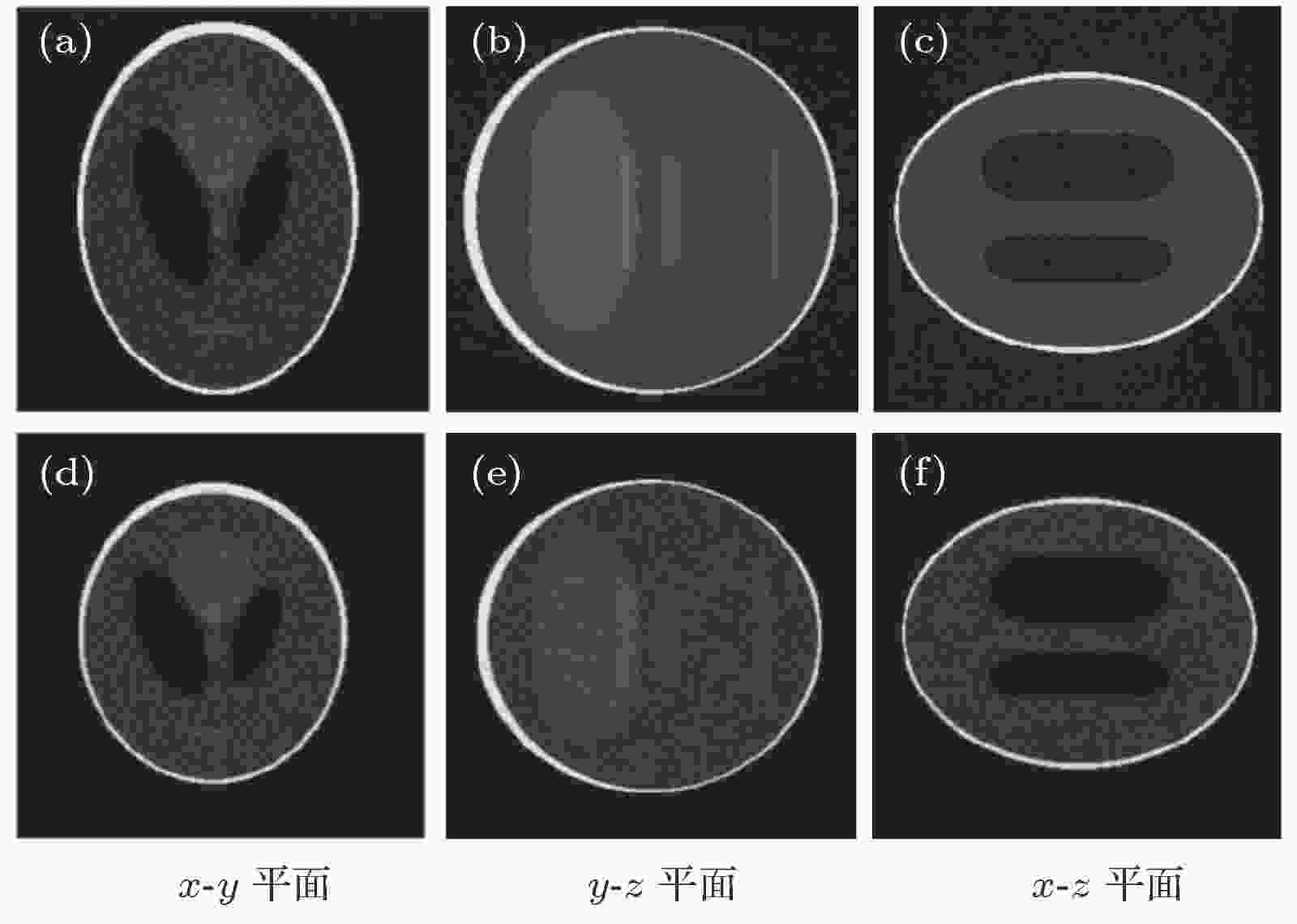图 8 带噪声无截断投影重建图像　(a), (b), (c)螺旋FDK算法; (d), (e), (f)本文算法
Figure8. Reconstruction image without truncated projections: (a), (b), (c) With helical FDK algorithm; (d), (e), (f) the proposed algorithm.

由图8算法对含噪数据的重建结果可以看出, 本文算法与螺旋FDK算法的重建图像都会受到噪声影响, 而且表现出相似的噪声特性. 这说明本文算法与螺旋FDK算法有相似的抗噪性能.
此外, 本文进一步通过模拟图5所示的局部成像实验, 验证本文算法处理有横向截断投影数据时的性能. 局部成像实验采用的是三维Popeye体模^[33]. Popeye体模由Noo等^[33]最先提出, 并同样被用于局部成像实验的仿真. Popeye体模模拟的是人体腹部, 里面包含了肝脏和胃脏等器官. 此外, 为了更好地生成横向截断投影数据, Popeye体模还包含了两个略微夸大的胳膊, 其整体形状与图5中的椭圆柱状物体相似. 为了让图像的离散化噪声在压缩的对比度下不是特别明显, 对体模中的部分数值做了微小的修改.
构建螺旋锥束成像几何, 其中光源到旋转轴的距离R = 100 mm, 光源到面阵探测器的距离D = 300 mm, 光源运动轨迹的螺距h = 7.89 mm, 面阵探测器的探元阵列为200 × 200, 探元的尺寸为0.148 mm× 0.148 mm. Popeye体模同样被定义在一个半径R₀ = 6.31 mm圆柱体内. 可以看出, 考虑放大因子, 探测器的横向尺寸小于Popeye体模的横截面直径. 因此, 螺旋投影数据会产生横向截断. 同样采用体素驱动的模式, 在0.5°的采样间隔下采集了1872张投影数据.
利用存在横向截断的投影数据, 分别使用本文算法和螺旋FDK算法进行重建. 重建结果如图9所示, 第一行左图和右图分别为螺旋FDK算法和本文算法使用无截断投影数据对Popeye体模的重建结果; 第二行分别为螺旋FDK算法和本文算法使用存在截断的投影数据对Popeye体模的重建结果.
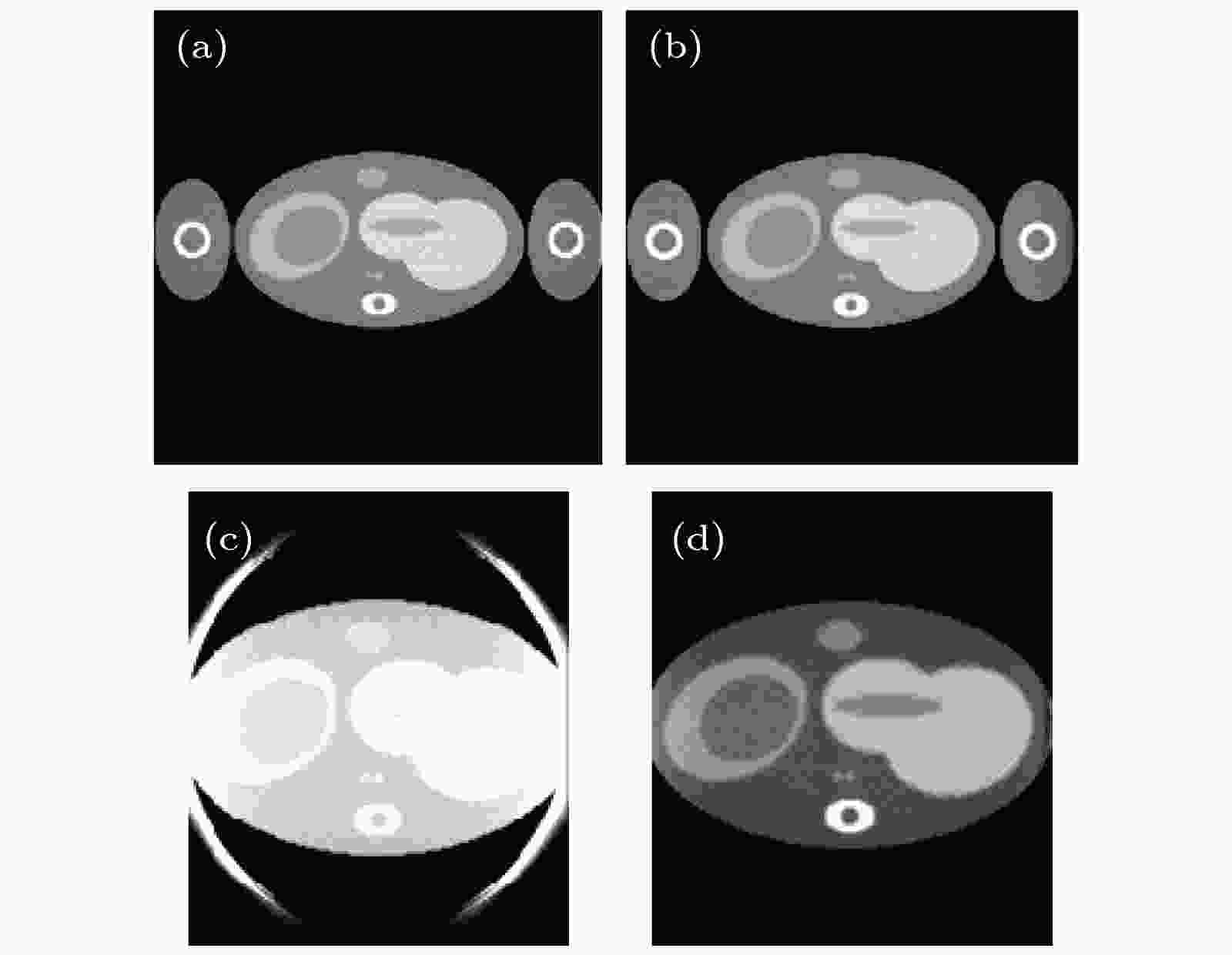图 9 Popeye体模局部成像实验结果　(a)无截断投影数据, 螺旋FDK算法; (b)无截断投影数据, 本文算法; (c)有截断投影数据, 螺旋FDK算法; (d)有截断投影数据, 本文算法
Figure9. Local reconstruction results for the Popeye phantom: (a) Without the truncated projection data, the helical FDK algoritm; (b) without the truncated projection data, the proposed algorithm; (c) with the truncated projection data, the helical FDK algoritm; (d) with the truncated projection data, the proposed algorithm.

图9是对Popeye体模的重建结果, 由第一行无截断投影数据的重建结果可以看出, 螺旋FDK算法和本文算法在投影数据无截断的情况下都能较好地重建出Popeye体模, 由于压缩了对比度, 图中离散化噪声比较明显. 而对于有截断投影数据的重建, 螺旋FDK算法的重建结果中有明显的截断伪影, 表现为x-y切片中横向边缘处有高亮的圆弧伪影, 影响了对整个图像的阅读. 而本文算法的重建结果几乎不受数据截断的影响, 与无截断投影的重建结果相似, 能够准确地重建出Popeye体模的局部三维体区域.

针对BPF算法在螺旋锥束CT成像中PI线及采样点设计和局部重建方面存在的困难, 本文提出了TFB-BPF算法. 该算法是Noo提出的圆轨迹扇形束BPF算法在螺旋锥束几何下的扩展. 算法的虚拟滤波线设计方式与圆轨迹扇束中滤波线的选择方式相似: 只需要在二维平面内设置. 算法最大的特点是能够在投影数据存在横向截断的情况下重建物体的局部体区域. 此外, 算法可以很方便地确定重建网格, 并使重建网格与三维笛卡儿网格匹配, 从而避免了原始BPF算法中重建结果从PI线坐标到笛卡儿坐标的重采样, 提高算法的执行效率.