摘要:为了得到最长有效余辉时间的Sr₂MgSi₂O₇:Eu²⁺, Dy³⁺荧光粉, 应用二次通用旋转组合设计对实验进行全程优化, 建立了稀土离子掺杂浓度Eu²⁺, Dy³⁺和有效余辉时间的二元二次回归方程模型, 应用遗传算法计算得到有效余辉时间的理论最大值. 采用高温固相法合成了最优掺杂浓度Sr₂MgSi₂O₇:0.5 mol%Eu²⁺, 1.0 mol%Dy³⁺的荧光粉, 在370 nm激发下观察到了465 nm的特征发射, 这归因于Eu²⁺的4f⁶5d¹—4f⁷跃迁. 测量了最优荧光粉的热释发光特性, 计算得到了陷阱深度为0.688 eV, 讨论了长余辉发光的特性.
关键词: 实验优化设计/
长余辉/
硅酸锶镁/
Eu²⁺/Dy³⁺

English Abstract

全文HTML

--> --> -->

近年来, 随着科技的不断发展, 长余辉发光材料由于被紫外光进行激发后可以获得长久黑暗环境的发光而受到广泛关注^[1]. 正是因为长余辉材料在黑暗环境中的蓄能发光优点, 可广泛应用于汽车和航空仪表显示、安全防伪技术、应急照明技术和交通安全标志等多个领域. 根据陷阱能级可以划分为浅陷阱和深陷阱^[2-11]. 长余辉材料属于浅陷阱材料, 在室温下材料能够将能量缓慢地以光的形式进行释放. 较深陷阱材料应用于光激励发光材料, 最早是在1988年由Lindmayer^[2]提出并率先应用在光存储材料上. 光存储材料中的深陷阱由于在常温下不易释放出来, 所以适用于做光信息传递、第四代相变存储器、高密度高速存储器、红外线探测等的材料^[7-14].
长余辉材料的研究时间较长, 其发现更是可以追溯到古代. 对于长余辉发光的模型, 不同的科学家给出了不同的见解, 发光过程和机理本身也较为复杂, 且长余辉的各种发光性质易受到合成温度、稀土离子掺杂浓度、还原气氛和基质材料等的影响^[14-18], 其中稀土离子的不同浓度对余辉时间影响最为显著, 稀土离子的浓度范围广, 且双掺杂的稀土离子在尽可能少的实验中寻找最优的样品更加困难. 因此急需寻找一种高效、快捷的方式获得最佳样品, 也是科研人员研究的重点之一.
在长余辉材料中, 硅酸盐体系优于铝酸盐体系不具有的防水性能, 其优异的物理和化学性质, 低的成本等受到科研人员的广泛关注. 其中, Sr₂MgSi₂O₇体系的蓝色荧光粉在Eu²⁺和Dy³⁺共掺杂时具有显著的余辉性能. 虽然稀土掺杂的Sr₂MgSi₂O₇体系已经有大量报道, 但是应用实验优化的方法对该体系进行研究, 是更为科学的一种方法^[14-21].
为了进一步延长Sr₂MgSi₂O₇体系的有效余辉时间, 需要确定Eu²⁺和Dy³⁺共掺杂的最优浓度. 文献[22]选用试验优化设计的方法对实验进行全程优化. 本文应用试验优化设计中的二次通用旋转组合设计^[15-24], 建立了Sr₂MgSi₂O₇:Eu²⁺, Dy³⁺掺杂浓度和有效余辉时间的二次回归方程^[23]. 再应用遗传算法, 计算得到Sr₂MgSi₂O₇:Eu²⁺, Dy³⁺最优稀土离子掺杂浓度的理论最优值^[25]. 高温固相法进行最优样品制备. 用X射线衍射(XRD)表征最优样品的物相, F-4600测试样品的余辉衰减, 大连海事大学自主研制的DMU-450自动加热控温系统测量样品的热释发光谱, 探讨了长余辉发光的机理.

2

-->

2.1.样品的合成与表征

将上述化学原料试剂按照精确的化学计量比进行称量用于合成目标产物Sr₂MgSi₂O₇, 称量后的试剂放进玛瑙研钵中各研磨30 min混合均匀, 将研磨后的材料放在Al₂O₃坩埚内并置于装有碳粉的大坩埚中, 并置于马弗炉中, 在CO气氛下1250 ℃保持3 h. 待样品随炉冷却至室温后取出, 研磨成粉末.
应用日本岛津XRD-6000粉末衍射仪对样品的纯度和结构进行分析, X射线波长为1.5406 ?, 辐射源为Cu靶K$\alpha$辐射. 日本日立F-4600光谱仪测量样品的荧光激发和发射光谱. 测量长余辉衰减曲线应用UV365 nm紫外线激发5 min后, 进行衰减测试. 热释发光测量采用DMU-450自动控温系统, 在UV365 nm紫外线激发5 min, 停止4 min后进行测试, 实验中F-4600光谱仪所用电压为400 mV和激发和发射狭缝为 5 nm.
2 -->

2.2.二次通用旋转组合设计

通过查阅文献对Sr₂MgSi₂O₇体系中Eu²⁺和Dy³⁺的掺杂浓度范围初步确定为0.5 mol%—5 mol%和1 mol%—10 mol%^[23], 完成二次通用旋转组合设计. 在编码空间中二次通用旋转组合设计由于其具有旋转性和通用性等优点, 因此在应用二次通用旋转组合设计进行实验优化时需要将各因素先进行编码, 得到的Sr₂MgSi₂O₇:Eu²⁺, Dy³⁺的自然因素水平编码表, 如表1. 从表1可知本次实验的全程优化选取Eu²⁺和Dy³⁺掺杂浓度的5个水平. 其中编码水平分别为0, ±1和±r.

Zj(xj)	x1(Eu2+)/%	x2(Dy3+)/%
Z2j(r)	5	10
Z0j + $\varDelta_j$(1)	4.341	8.682
Z0j(0)	2.75	5.5
Z0j – $\varDelta_j$(–1)	1.159	2.318
Z1j(–r)	0.5	1
$\varDelta_j$ = (Z2j – Z1j)/2r	1.591	3.182
xj = (Zj – Z0j)/$\varDelta_j$	x1 = (Z1 – 2.75)/1.591	x2 = (Z2 – 5.5)/3.182

表1自然因素水平编码表
Table1.Natural factor level coding table

根据表1自然因素水平编码表进行二次通用旋转组合设计共进行13组实验, 实验方案和有效余辉时间的结果列于表2.

Number	x0	x1	x2	x1x2	x12	x22	Afterglow time/s
1	1	1	1	1	1	1	132
2	1	1	–1	–1	1	1	80
3	1	–1	1	–1	1	1	212
4	1	–1	–1	1	1	1	184
5	1	r	0	0	r2	0	116
6	1	–r	0	0	r2	0	290
7	1	0	r	0	0	r2	172
8	1	0	–r	0	0	r2	138
9	1	0	0	0	0	0	141
10	1	0	0	0	0	0	104
11	1	0	0	0	0	0	102
12	1	0	0	0	0	0	101
13	1	0	0	0	0	0	105

表2二次通用旋转组合设计实验方案及余辉时间
Table2.Quadratic general rotation combination design experimental scheme and afterglow time.

2

-->

3.1.二次通用旋转组合设计有效余辉时间分析

图1为Sr₂MgSi₂O₇体系的Eu²⁺和Dy³⁺在经过UV365 nm紫外线激发5 min后测试得到的衰减曲线, 可以看出所有样品在50 s内呈现快速衰减, 其中6号样品和3号样品的有效余辉光时间最长, 将余辉衰减曲线按照初始强度衰减的10%作为有效余辉时间填入表2第8列.
图 1 Eu²⁺/Dy³⁺的余辉衰减曲线
Figure1. Afterglow attenuation curve of Eu²⁺/Dy³⁺.

2 -->

3.2.二次通用旋转组合实验设计数据分析

根据以上二次通用旋转组合设计的实验结果及分析, 可以通过自然因素编码空间得到有效余辉时间的二元二次回归方程:

$\begin{split}{Y_1} = \; & 110.6 - 53.7545{x_1} + 16.0095{x_2} + 6{x_1}{x_2} \\ & - 39.5824x_1^2 + 15.5824x_2^2.\end{split}$

应用F-检验和T-检验来检验二元二次回归方程各个系数的显著性以及方程是否失拟, 可以得到如下结果:

${F_{{\text{回}}1}}{\rm{ = }}\frac{{S_{{{\text{回}}1}/{{{\text{回}}1}_1}}}}{{{S_{R1}}/{f_{R1}}}} \approx 18.07 > {F_{0.01}}(5, 7) = 7.46, $

$ \begin{split}{F_{lf}}\; & = \frac{{{S_{lf}}/{f_{lf}}}}{{{S_{\rm{e}}}/{f_{\rm{e}}}}} = \frac{{1720.6019/3}}{{1165.2/4}} \\ & = 1.9689 < {F_{0.25}}(3, 4) = 2.05.\end{split}$

F-检验和T-检验结果列于表3. 从(3)式中可以看出回归方程不失拟, 证明回归方程与实际情况相符, 可以合理地对样品的有效余辉时间进行预测. 由方程(2)可以得到方程的显著性水平为0.01, 证明回归方程的置信度都为99%. 余辉时间回归系数的T-检验说明除了x₁x₂不显著外, 其他二元二次回归方程各项均表现出不同程度的显著性.

	Afterglow time/s
	方差或 t 统计量	显著性水平$\alpha$	显著性水平$\alpha$
x0	14.490	0.001	***
x1	5.193	0.01	**
x2	1.546	0.2	*
x1x2	0.703	0.6	Insignificant
x12	6.116	0.01	***
x22	2.408	0.2	*
F回	18.07	0.001	***
注: ***极显著水平($\alpha$ ≤ 0.01); **显著水平($\alpha$ ≤ 0.1); *较显著水平($\alpha$ ≤ 0.25).

表3显著性检验分析
Table3.Significant test analysis.

因此编码空间中有效余辉时间Eu²⁺和Dy³⁺的二元二次回归方程可以优化为

$\begin{split}{Y_1} = \; & 110.6 - 53.7545{x_1} + 16.0095{x_2} \\ & - 39.5824{x_1}^2 + 15.5824{x_2}^2.\end{split}$

将自然因素编码空间中的二元二次回归方程转化为在实际空间中的二元二次回归方程, 可以得到有效余辉时间Eu²⁺和Dy³⁺的方程为

$ \begin{split}{Y_1} =\; & - 6.0951 + 0.48175{z_1} + 34.0132{z_2} \\ & - 15.6373{z_1}^2 + 1.5390{z_2}^2.\end{split}$

最终, 通过遗传算法解出二元二次回归方程Y₁最长有效余辉时间所对应的样品Eu²⁺和Dy³⁺浓度分别是0.500326 mol%, 1.000652 mol%. 计算得到理论有效余辉时间321.28 s. 我们在相同的实验条件下制备出最优掺杂浓度样品, 同时受实验室天平精度的限制, 实际制备的样品Eu²⁺和Dy³⁺掺杂浓度为浓度分别是0.5 mol%, 1.0 mol%.
2 -->

3.3.最优样品的晶体结构特性

图2为Sr₂MgSi₂O₇:0.5 mol%Eu²⁺/1.0 mol%Dy³⁺和数据库中标准数据卡片Sr₂MgSi₂O₇的JCPDS#75-1736的XRD图谱. 从图中可以看出制备的最优样品的衍射峰位置与标准数据卡片相比基本一致, 且无其他杂相出现, 这说明本文中制备的最优样品为纯相, 也说明Eu²⁺和Dy³⁺的共掺杂被Sr₂MgSi₂O₇中的Sr²⁺离子完全取代格位, 且样品最优的掺杂浓度并未对Sr₂MgSi₂O₇的晶体结构造成显著的影响.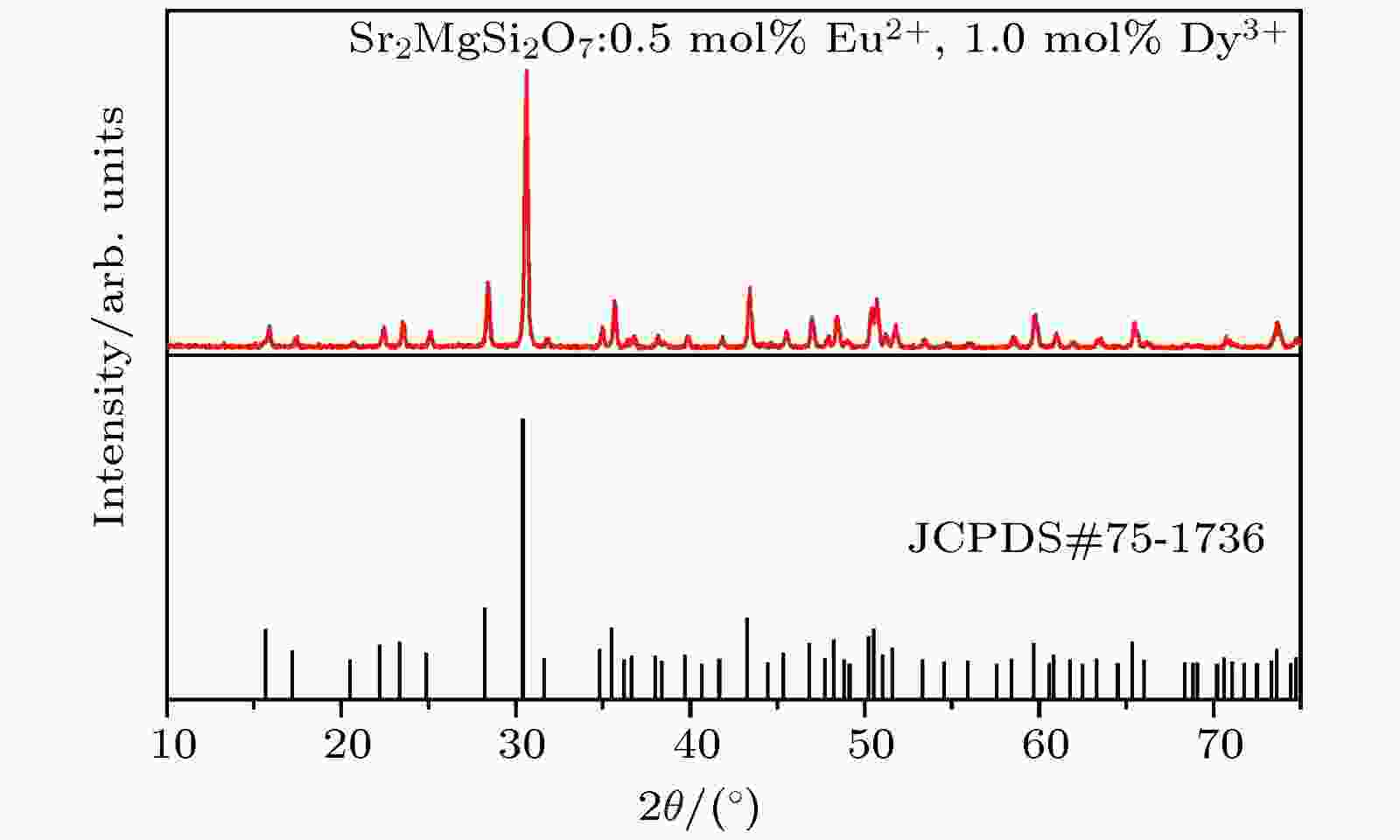
图 2 Sr₂MgSi₂O₇:0.5 mol% Eu²⁺, 1.0 mol% Dy³⁺和标准数据卡卡片JCPDS#75-1736的XRD图谱
Figure2. XRD pattern of Sr₂MgSi₂O₇:0.5 mol% Eu²⁺, 1.0 mol%Dy³⁺ and standard data card card JCPDS#75-1736.

2 -->

3.4.最优样品的荧光激发和发射光谱

图3为最优样品Sr₂MgSi₂O₇:0.5 mol%Eu²⁺, 1.0 mol% Dy³⁺的荧光激发和发射光谱, 样品的激发和发射光谱由宽带构成, 激发光谱位于250—450 nm, 其峰值位置位于370 nm, 样品在370 nm激发下具有强烈的蓝色发射, 发射中心位于465 nm, 这归因于Eu²⁺的4f⁶5d¹—4f⁷跃迁^[26].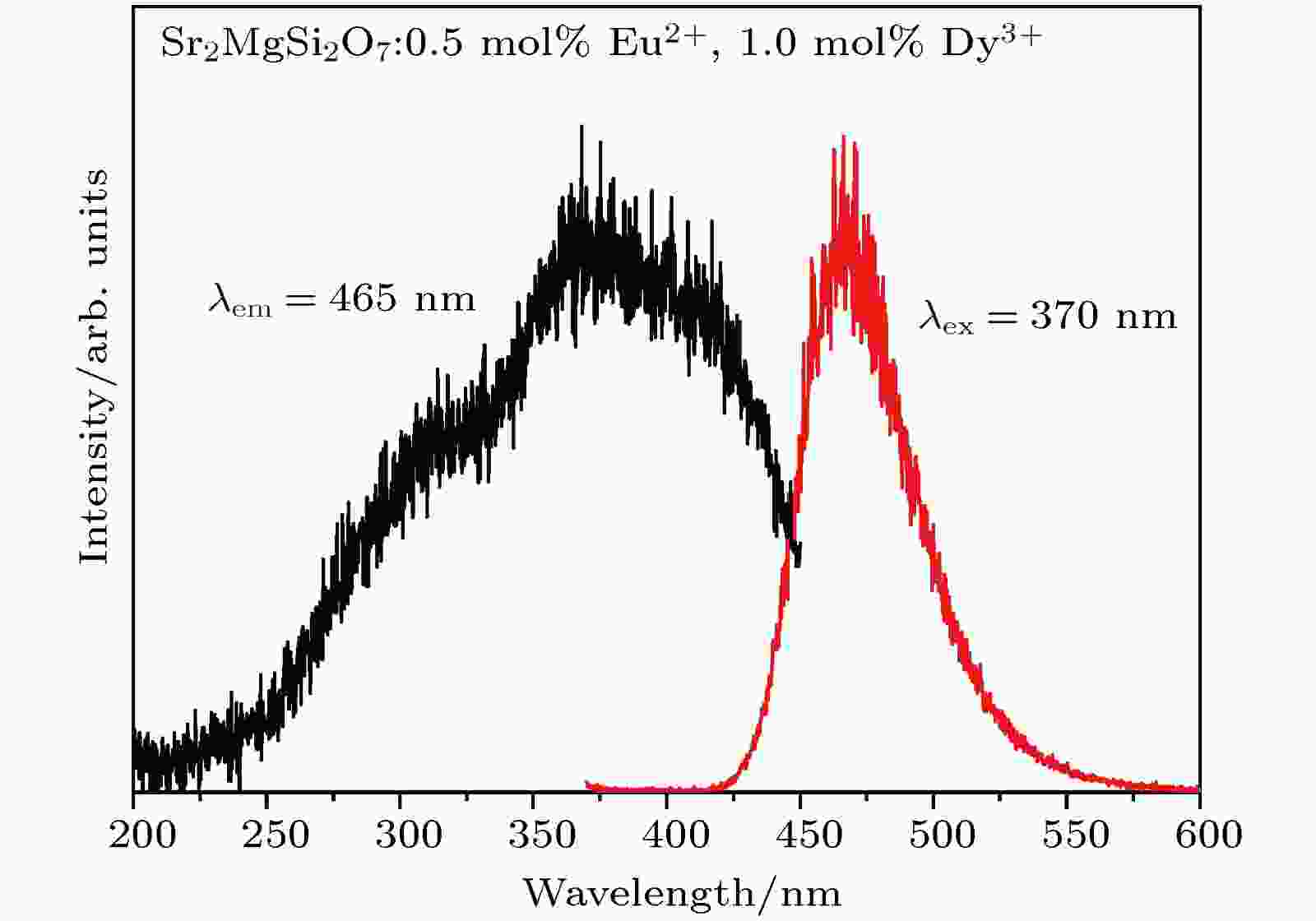
图 3 Sr₂MgSi₂O₇:0.5 mol% Eu²⁺, 1.0 mol% Dy³⁺的荧光激发和发射光谱
Figure3. Fluorescence excitation and emission spectroscopy of Sr₂MgSi₂O₇:0.5 mol% Eu²⁺, 1.0 mol% Dy³⁺.

2 -->

3.5.最优样品的余辉衰减曲线

图4为最优样品的余辉衰减曲线以及应用华为相机在感光度ISO3200, 曝光时间1/20 s下拍摄的样品在紫外灯下照射5 min和停止照射1, 3和6 min的照片. 从图中可以计算出有效余辉时间为333 s, 与应用二次通用旋转组合设计计算得到的理论值321 s接近, 这也证明了实验优化设计在本工作中的应用是合理的. 为进一步得到最优样品的余辉性能参数, 我们应用单指数方程$I = A{t^{ - \alpha }}$, 其中I代表余辉初始发光强度, A代表常数, t代表时间, $\alpha$表示衰减速率, 对曲线进行拟合, 得到常数A = 1.78, 衰减速率$\alpha=0.52$.
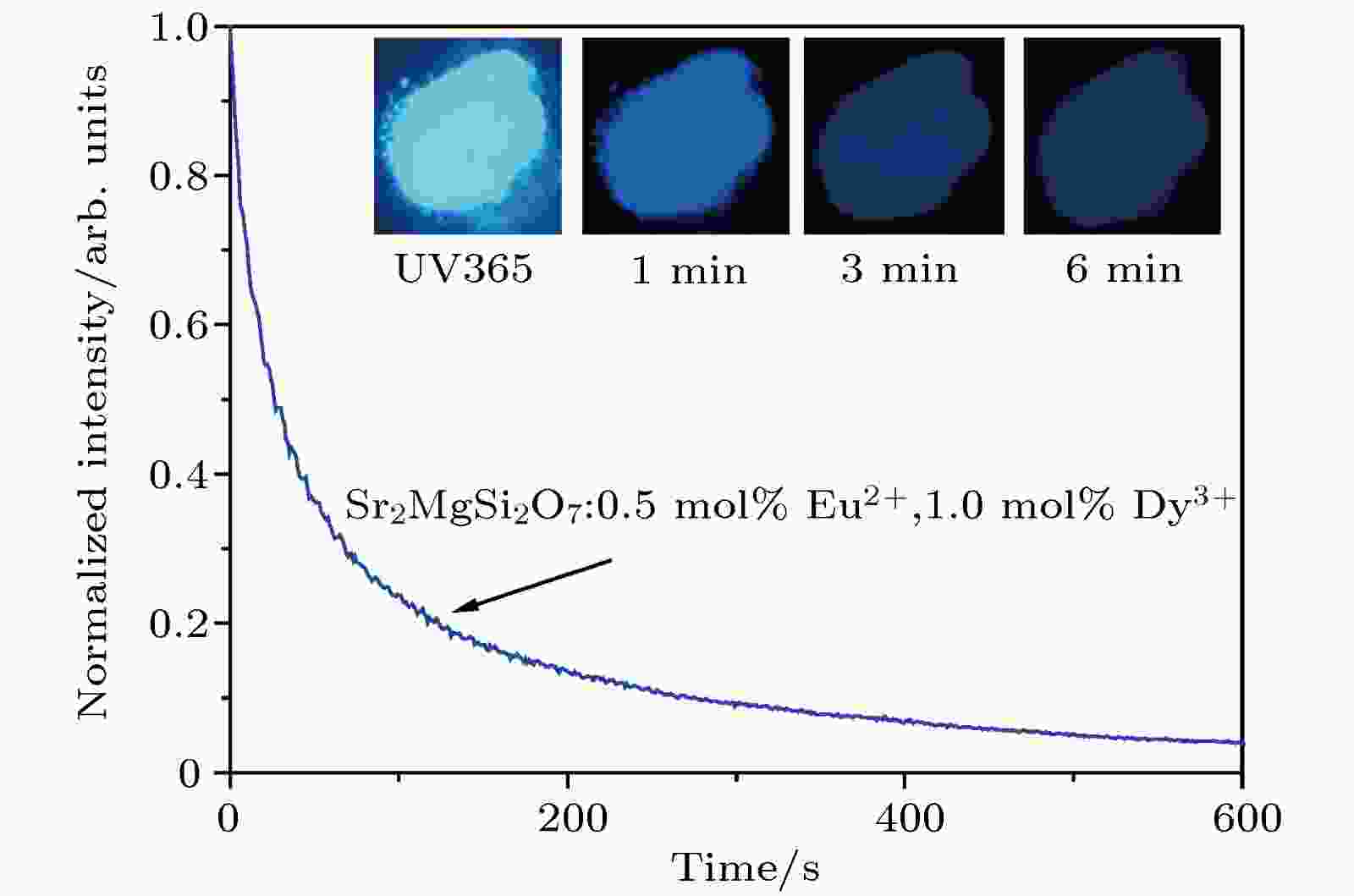图 4 Sr₂MgSi₂O₇:0.5 mol%Eu²⁺, 1.0 mol% Dy³⁺的余辉衰减曲线
Figure4. Afterglow decay curve of Sr₂MgSi₂O₇:0.5 mol% Eu²⁺, 1.0 mol% Dy³⁺.

2 -->

3.6.最优样品的热释发光光谱

根据文献[27, 28]建立的模型, 对样品的热释发光谱进行计算得到样品的陷阱深度为

$E = {C_\alpha }\left(\frac{{kT_{\rm m}^2}}{\alpha }\right) - {B_\alpha }(2k{T_{\rm m}}), $

其中$\alpha$代表$\delta$, $\tau$和$\omega$; k代表玻尔兹曼常数8.617 × 10^–5 ${\rm eV}\cdot {\rm K^{-1}} $; $\delta$ = T₂ – T_m代表热释光谱下降沿半峰宽; $\tau$ = T – T₁代表热释光谱上升沿半峰宽; $\omega$ = T₂ – T₁代表热释光谱半峰全宽. 光谱学因子${\mu _{\rm g}}$可以表示为${\mu _{\rm{g}}} = \dfrac{\delta }{\omega } = \dfrac{{{T_2} - {T_{\rm m}}}}{{{T_2} - {T_1}}}$.
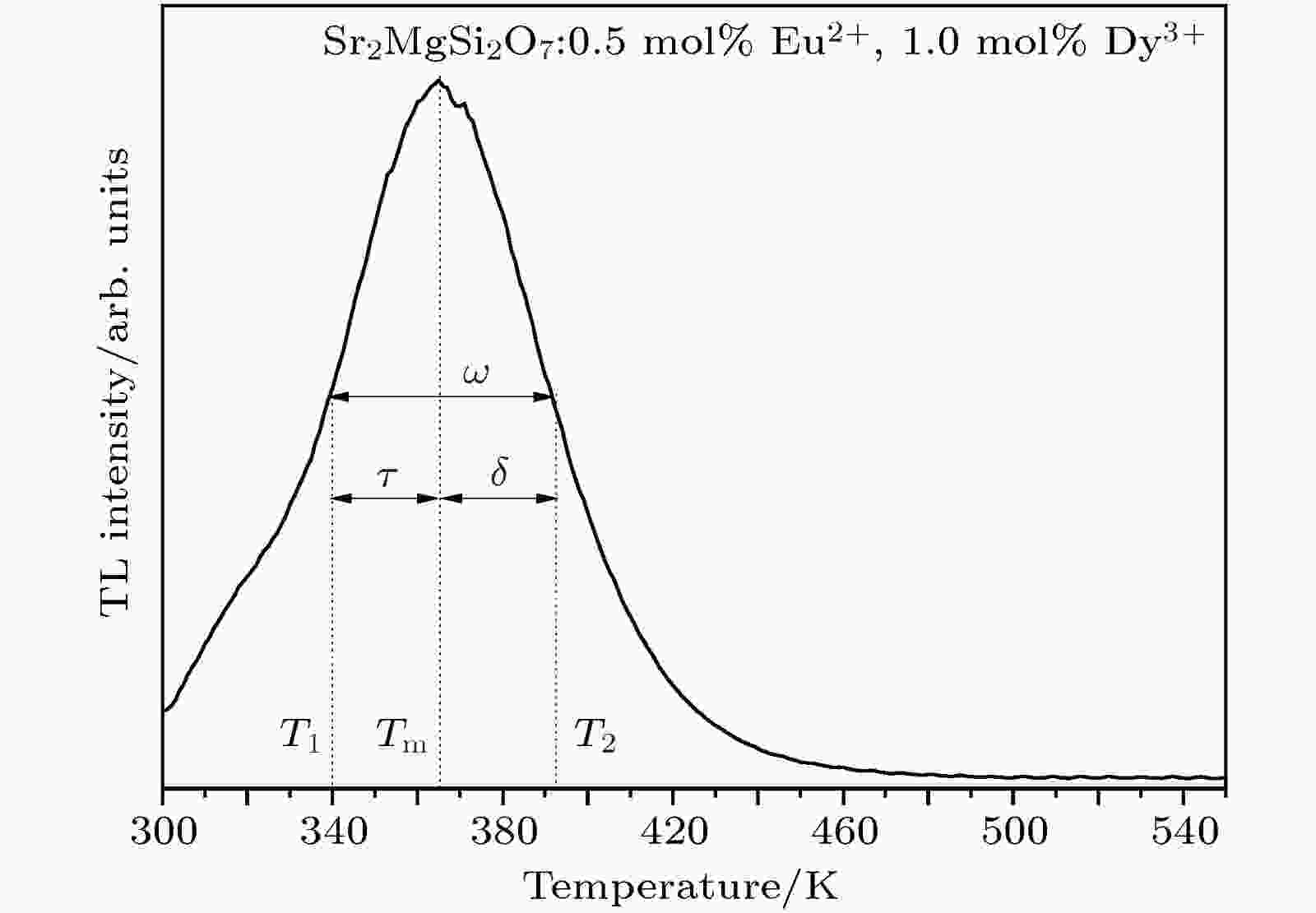图 5 Sr₂MgSi₂O₇:0.5 mol%Eu²⁺, 1.0 mol% Dy³⁺的热释发光光谱
Figure5. Thermoluminescence spectroscopy of Sr₂MgSi₂O₇:0.5 mol% Eu²⁺, 1.0 mol% Dy³⁺.

根据文献[27, 28]建立的模型, 可以得到表3数据, 由(5)式可以计算得到表4数据.

T1/K	Tm/K	T2/K	$\tau$/K	$\delta$/K	$\omega$/K	${\mu _{\rm g}}$/K	${E_\tau }$/eV	${E_\delta }$/eV	${E_\omega }$/eV	E/eV
339*	365	393	26	28	54	0.528	0.673	0.701	0.690	0.688

表5Sr₂MgSi₂O₇:0.5 mol% Eu²⁺, 1.0 mol% Dy³⁺的陷阱深度参数
Table5.Trap depth parameter of Sr₂MgSi₂O₇:0.5 mol% Eu²⁺, 1.0 mol% Dy³⁺.

	$\tau$	$\delta$	$\omega$
${c_\alpha }$	1.81	1.71	3.54
${b_\alpha }$	2	0	1

表4文献[27, 28]的模型陷阱深度参数
Table4.Model trap depth parameter in Refs. [27, 28].

通常认为, 当热释发光谱主峰的峰值位置位于350 K左右时, 在室温下易于表现出优异的长余辉现象. 当陷阱深度比较低时, 同样载流子会迅速释放, 因而不易产生优秀的长余辉现象^[25,29]. 其中最优样品Sr₂MgSi₂O₇:0.5 mol% Eu²⁺, 1.0 mol% Dy³⁺的热释光谱峰值位置为365 K, 计算得出陷阱深度为0.688 eV (见图5和表5). 这与文献中给出的产生优异长余辉现象一致, 也充分证明应用二次通用旋转组合计算并制备得到的最优样品Sr₂MgSi₂O₇:0.5 mol%Eu²⁺, 1.0 mol%Dy³⁺是可信的.
2 -->

3.7.长余辉光发光过程

根据以上实验分析及得出的优异效果, 根据能级结构, 提出了Eu²⁺作为Sr₂MgSi₂O₇基质发光中心的长余辉发光过程, 如图6所示, 为稀土离子掺杂基质作为发光中心以及表现出长余辉的现象的电子俘获过程提供参考.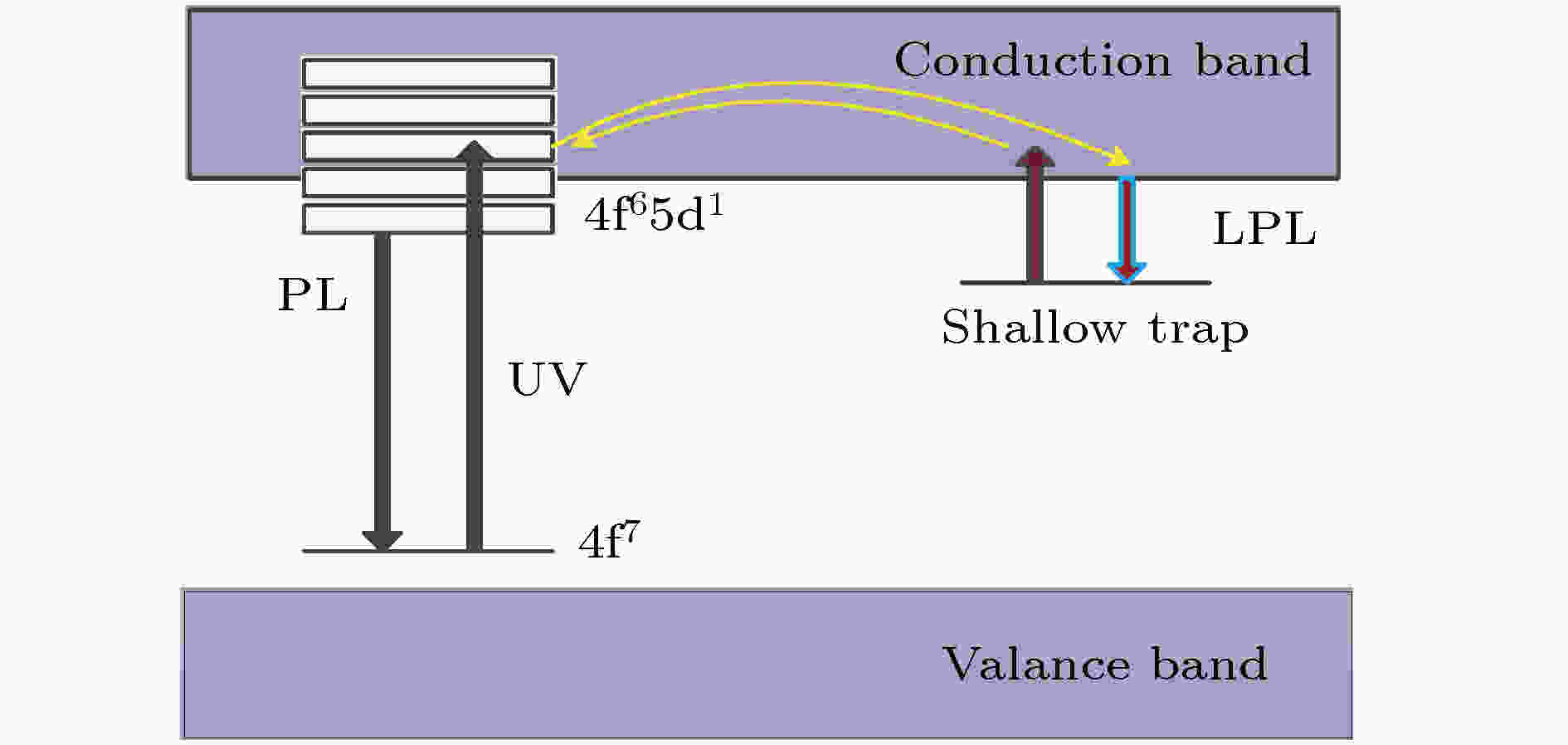
图 6 长余辉发光过程的简单模型
Figure6. Simple model of long afterglow luminescence process.

当样品受到外界UV辐射时, 通过跃迁的方式到激发态产生电子, 一部分电子返回到Eu²⁺的基态与空穴进行复合从而产生Eu²⁺的特征发射峰; 剩下的电子被陷阱俘获并暂时存储在其中. 受到热扰动时, 电子逸出陷阱并到达发光中心以一定波长的方式释放出来, 产生长余辉现象.

应用二次通用旋转组合设计方法, 对Eu²⁺和Dy³⁺掺杂的Sr₂MgSi₂O₇有效长余辉时间进行优化, 获得了Eu²⁺和Dy³⁺的最优掺杂浓度. 建立了有效长余辉发光时间和最优离子浓度Eu²⁺和Dy³⁺二元二次回归方程, 采用遗传算法对方程进行了理论计算和求解, 得到样品离子Eu²⁺和Dy³⁺的最优掺杂浓度分别为0.5 mol%和1.0 mol%. 最大有效余辉时间为321 s. 最终采用高温固相的方法制备了最优掺杂样品Sr₂MgSi₂O₇:0.5 mol% Eu²⁺, 1.0 mol%Dy³⁺, 测量余辉衰减并得到了有效余辉时间为333 s,与理论计算值321 s相符. 应用文献[27, 29]的模型计算了热释发光的陷阱深度为0.688 eV. 结合能级图讨论了Eu²⁺作为Sr₂MgSi₂O₇基质发光中心的长余辉发光过程.