摘要:夹心式换能器应用极为广泛, 但当其横向尺寸过大时, 存在耦合振动, 影响其辐射面的位移分布. 本文通过在大尺寸夹心式换能器的前盖板中加工周期排列的槽, 来形成一种二维声子晶体结构. 随后, 采用有限元法对基于二维声子晶体的大尺寸夹心式换能器的振动传输特性、共振频率以及发射电压响应进行仿真模拟, 讨论了开槽高度和开槽宽度对其带隙、共振与反共振频率、带宽以及辐射面位移分布的影响. 研究结果表明, 通过在大尺寸夹心式换能器中应用声子晶体结构可对其进行优化设计. 当大尺寸夹心式换能器的工作频率位于其带隙范围内时, 二维声子晶体结构能有效地抑制其横向振动, 从而改善换能器辐射面位移分布的均匀程度. 此外, 在大尺寸夹心式换能器的前盖板中加工二维声子晶体结构, 能有效提升换能器的带宽, 进而拓宽大尺寸夹心式换能器的工作频带.
关键词: 声子晶体/
夹心式压电换能器/
横向振动/
宽带

English Abstract

全文HTML

--> --> -->

在功率超声以及水声领域中, 夹心式换能器(又称为朗之万型换能器)的应用极为广泛, 其主要组成部分为前后金属盖板、压电陶瓷晶堆、金属电极和预应力螺栓^[1?3]. 在设计夹心式换能器时, 通常要求其横向尺寸小于1/4波长, 以便满足一维纵向振动理论的要求^[4?7]. 但随着夹心式换能器应用范围的扩大, 在某些大功率、高声强的超声应用中, 例如超声冷拔金属管、超声焊接等, 需要增大其横向尺寸^[8,9]. 当大尺寸夹心式换能器处于工作状态时, 由于材料的泊松效应, 考虑到其纵向振动与横向振动的耦合, 长度与直径的纵横比决定其共振频率和振动位移分布, 导致换能器辐射面的振动位移分布不均匀, 因此如何抑制横向振动对大尺寸夹心式换能器的研究具有重要的意义.
Kushwaha等^[10]在研究镍/铝二维固体周期复合介质时, 首次明确提出了声子晶体的概念. 声子晶体是一种具有周期性结构的功能材料, 当弹性波穿过声子晶体时, 受材料周期性排列结构特点的影响, 某些频率的波在周期结构中不能传播, 进而产生带隙^[11?13]. 声子晶体独特的振动带隙特性使其在带隙范围内的振动可以被禁止传播(无限周期结构)或被抑制(有限周期结构)^[14,15]. 这一特性使得其在抑制振动领域具有广泛的应用. 例如, Ronda等^[16]和Aragón等^[17]在谐振器中应用声子晶体来抑制横向振动; Wen等^[18,19]将声子晶体应用于直梁结构以抑制弯曲振动; Zhao等^[20]则提出基于声子晶体的管道结构的减振机制, 并表明声子晶体结构可以有效减少管道振动.
基于二维声子晶体结构的带隙理论, 本文设计了一种新型的基于二维声子晶体的大尺寸夹心式换能器, 通过在大尺寸前盖板上加工周期排列的槽来形成二维声子晶体. 由于周期性的槽沿径向形成, 使得径向波无法传播, 进而有效抑制横向振动, 改善换能器辐射面纵向振动位移分布. 此外, 周期排列的槽结构对大尺寸夹心式换能器的带宽有一定的影响, 可拓宽其工作频带.

传统的大尺寸夹心式换能器主要由圆柱形后盖板、压电陶瓷晶堆和喇叭形前盖板组成, 其示意图如图1(a)所示, 当其处于工作状态时, 由于其过大的横向尺寸, 存在强烈的耦合振动, 导致其辐射面的位移分布不均匀. 为此, 我们设计了一种新型的基于二维声子晶体的大尺寸夹心式换能器, 如图1(b)所示, 通过在喇叭形前盖板上沿半径方向加工周期排列穿透式的槽, 来形成二维声子晶体结构, 进而有效地抑制横向振动, 其开槽方式如图1(b)插图所示. 本研究中, 我们所设计的槽与槽之间的间隔角度为60°.
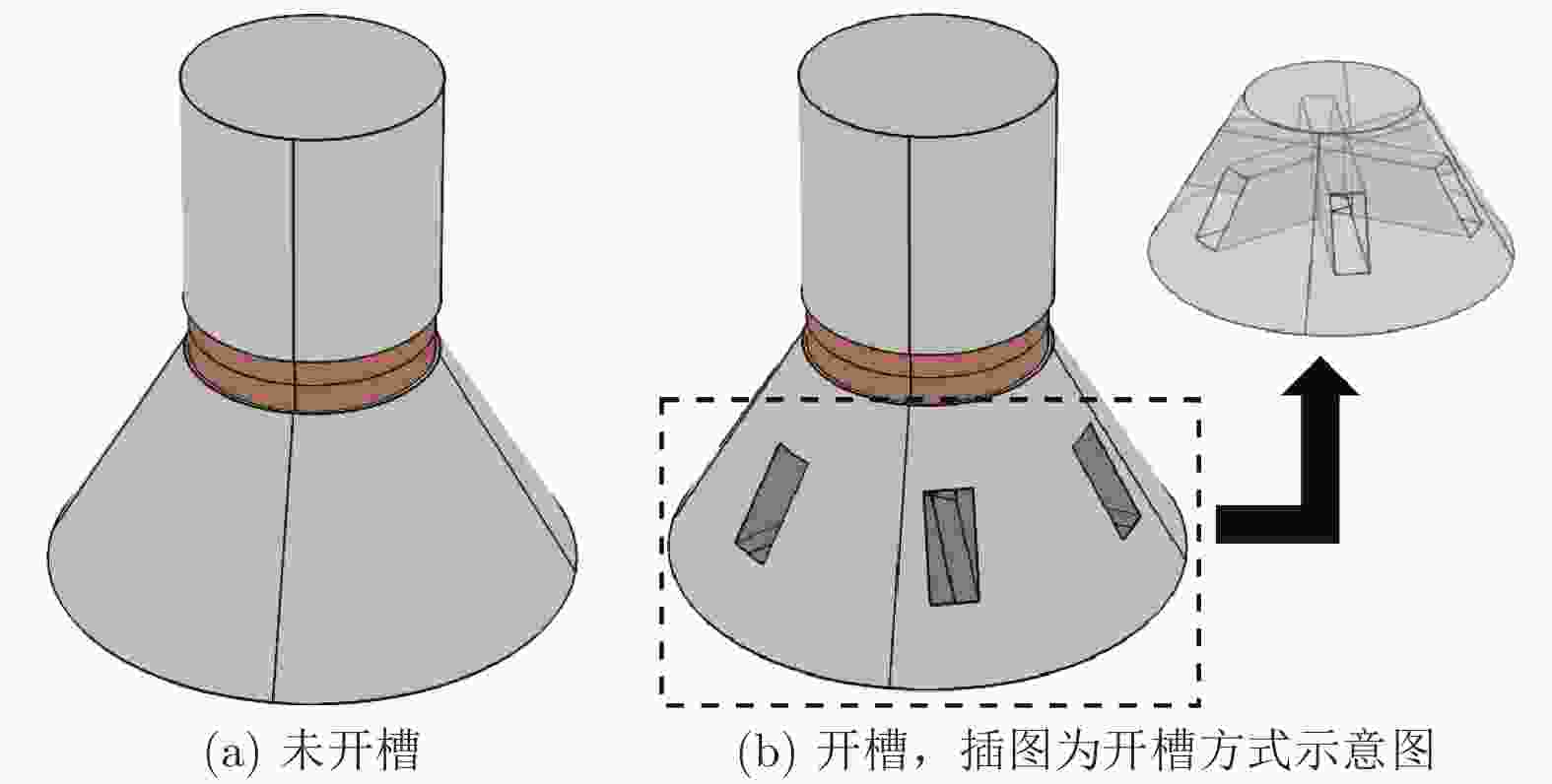图 1 大尺寸夹心式换能器示意图　(a)未开槽; (b)开槽, 插图为开槽方式示意图
Figure1. Schematic diagram of a large-size sandwich transducer: (a) Not grooved; (b) grooved. Inset is a schematic diagram of the grooved method.

为了分析大尺寸夹心式换能器的共振频率, 在有限元软件COMSOL Multiphysics的固体力学模块中建立大尺寸夹心式换能器的模型, 其中圆柱形后盖板的半径和高度分别为26 mm和50 mm, 选取Steel AISI 4340作为后盖板材料, 压电陶瓷晶堆的半径和高度分别为25 mm和6 mm, 数量为2, 材料为PZT-4, 喇叭形前盖板的上底面半径、下底面半径和高度分别为26, 55和50 mm, 选取Aluminum 6063-T83作为前盖板材料. 通过计算得到图1(a)换能器的振型图, 如图2所示.
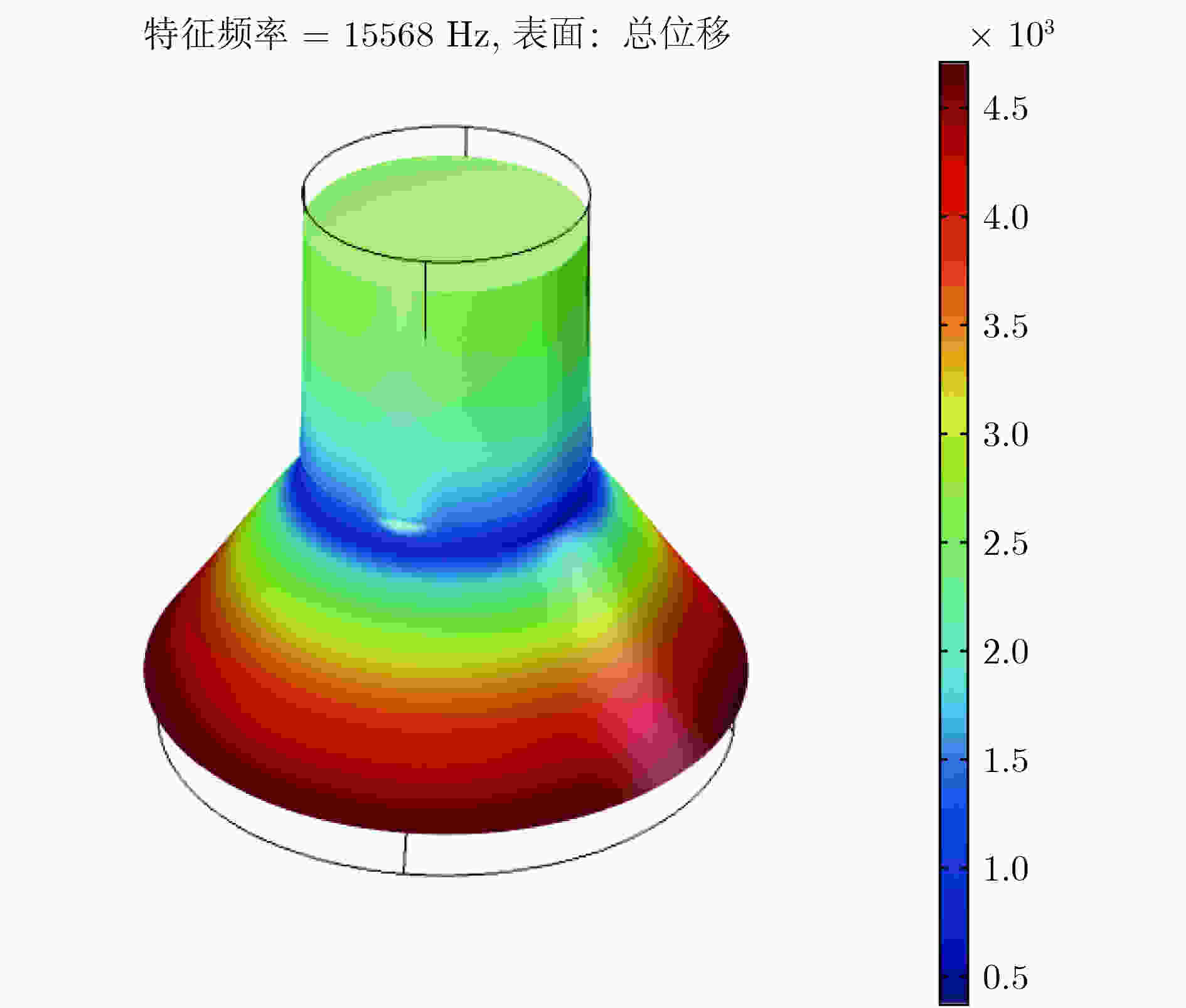图 2 大尺寸夹心式换能器振型图
Figure2. Large-size sandwich transducer vibration diagram.

图2给出了大尺寸夹心式换能器的振型图. 通过观察振型图, 可以发现其共振频率为15568 Hz. 因此, 本文分析换能器前盖板的带隙时, 可以选择性地分析15 kHz附近的带隙.
在实际情况下的声子晶体皆为有限周期性结构, 该结构仅对带隙频率范围内的振动传播起到明显的抑制作用. 可根据振动传递特性曲线, 来确定振动带隙是否存在以及带隙的位置和宽度. 本文利用有限元分析软件COMSOL Multiphysics 模拟了具有有限周期结构的基于二维声子晶体夹心式换能器的振动传递特性.
首先, 在COMSOL Multiphysics中建立6个换能器的模型, 分别为: 当槽宽为8 mm时, 改变槽高, 所设计槽高依次为10, 15, 20和25 mm; 当槽高为20 mm时, 改变槽宽, 所设计槽宽依次为6, 8和10 mm. 随后, 对二维声子晶体的振动传输特性进行模拟仿真. 在有限周期的二维声子晶体一侧沿半径方向均匀地加上1 m/s²的加速度激励, 使得振动在二维声子晶体中传播, 计算另一侧的输出响应, 可以得到该有限周期二维声子晶体的振动传输特性曲线. 通过计算, 得到基于不同开槽高度和宽度的二维声子晶体换能器的振动传递特性曲线. 最后, 经对比分析, 得出开槽高度及宽度对二维声子晶体带隙的影响情况, 如图3所示.
图3中给出了具有不同开槽尺寸的夹心式换能器的振动传输特性曲线. 将振动传输率小于1确定为振动传输衰减频率范围的标准, 从图3可以看出, 开槽高度及宽度的变化对二维声子晶体的带隙有很大的影响. 根据带隙的定义, 在所考虑的频率范围内存在许多方向带隙. 由此可以在任何带隙处设计换能器的工作频率, 并保证其可有效地抑制相应的横向振动. 考虑到该大尺寸夹心式换能器的共振频率在15 kHz附近, 故选择性地分析该频率附近的带隙. 不同开槽高度和宽度的大尺寸夹心式换能器的带隙范围如表1所列.
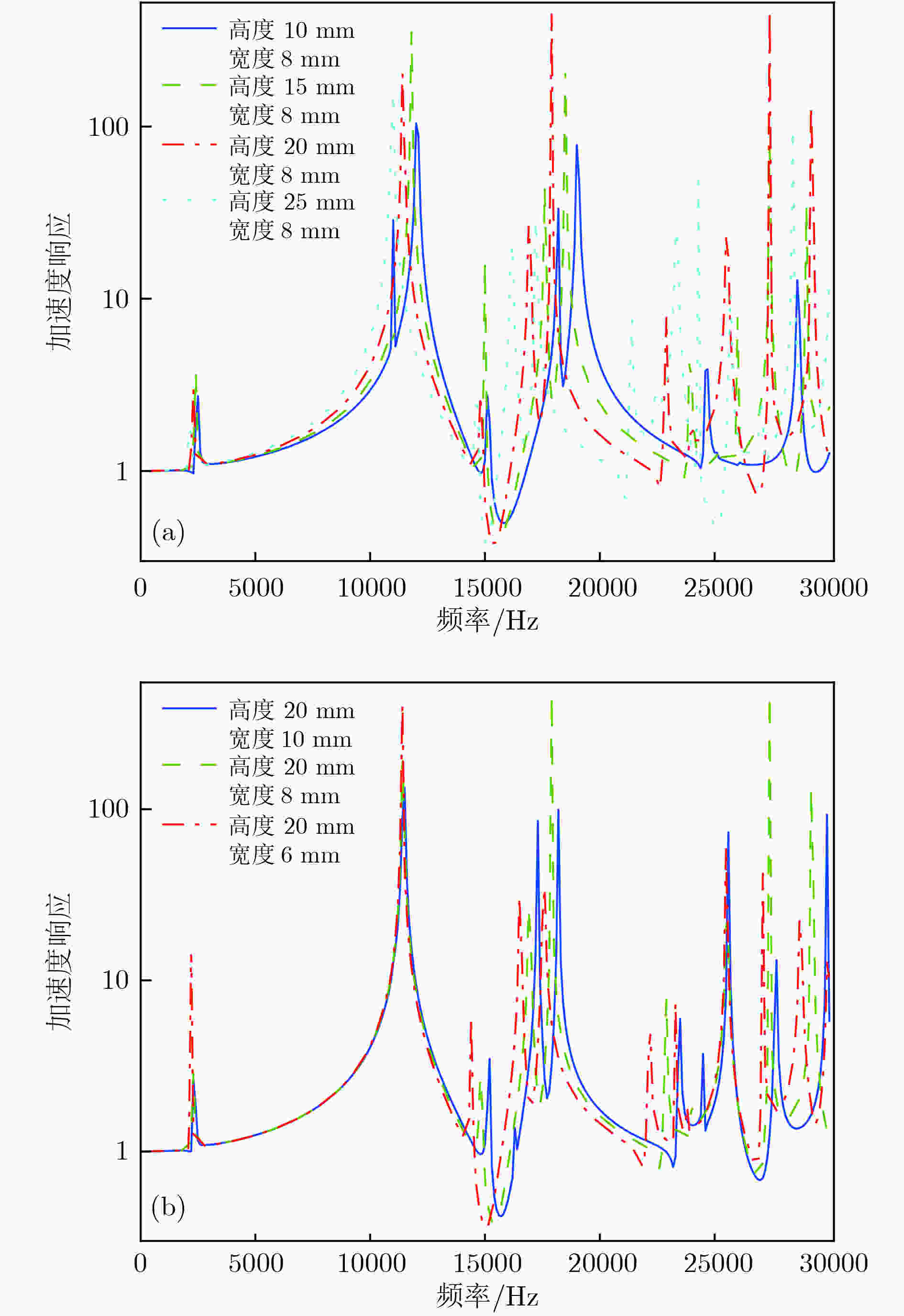图 3 大尺寸夹心式换能器的振动传输特性曲线　(a)改变槽高; (b)改变槽宽
Figure3. Vibration transmission characteristic curves of large-size sandwich transducer: (a) Change the groove height; (b) change the groove width.

开槽高度/mm	开槽宽度/mm	带隙范围/kHz
10	8	15.3—16.8
15	8	15.1—16.5
20	8	14.9—16.1
25	8	14.8—15.6
20	6	15.3—16.3
20	8	14.9—16.1
20	10	14.5—15.7

表1大尺寸夹心式换能器的带隙分布情况
Table1.Band gap distribution of large-size sandwich transducers.

从表1中可以看出, 在15 kHz附近, 具有不同槽高及槽宽的换能器均存在方向带隙, 并且随着高度的增加, 带隙向低频方向移动, 带隙的宽度减小, 但衰减幅值增大. 同样地, 随着开槽宽度的增加, 带隙对应的频率有所减小, 其衰减幅值变大.

本文利用COMSOL Multiphysics模拟大尺寸夹心式换能器的振动特性, 虽然预应力螺栓对换能器有一定影响, 但为了简化模型, 暂不考虑预应力螺栓的影响. 根据尺寸以及开槽方式的不同, 在COMSOL Multiphysics中建立7个模型, 分别对应未开槽、相同槽宽(8 mm)下不同开槽高度(10, 15, 20和25 mm)以及相同槽高(20 mm)不同开槽宽度(6, 8和10 mm). 通过计算, 得到如图4所示的大尺寸夹心式换能器的共振及反共振频率.
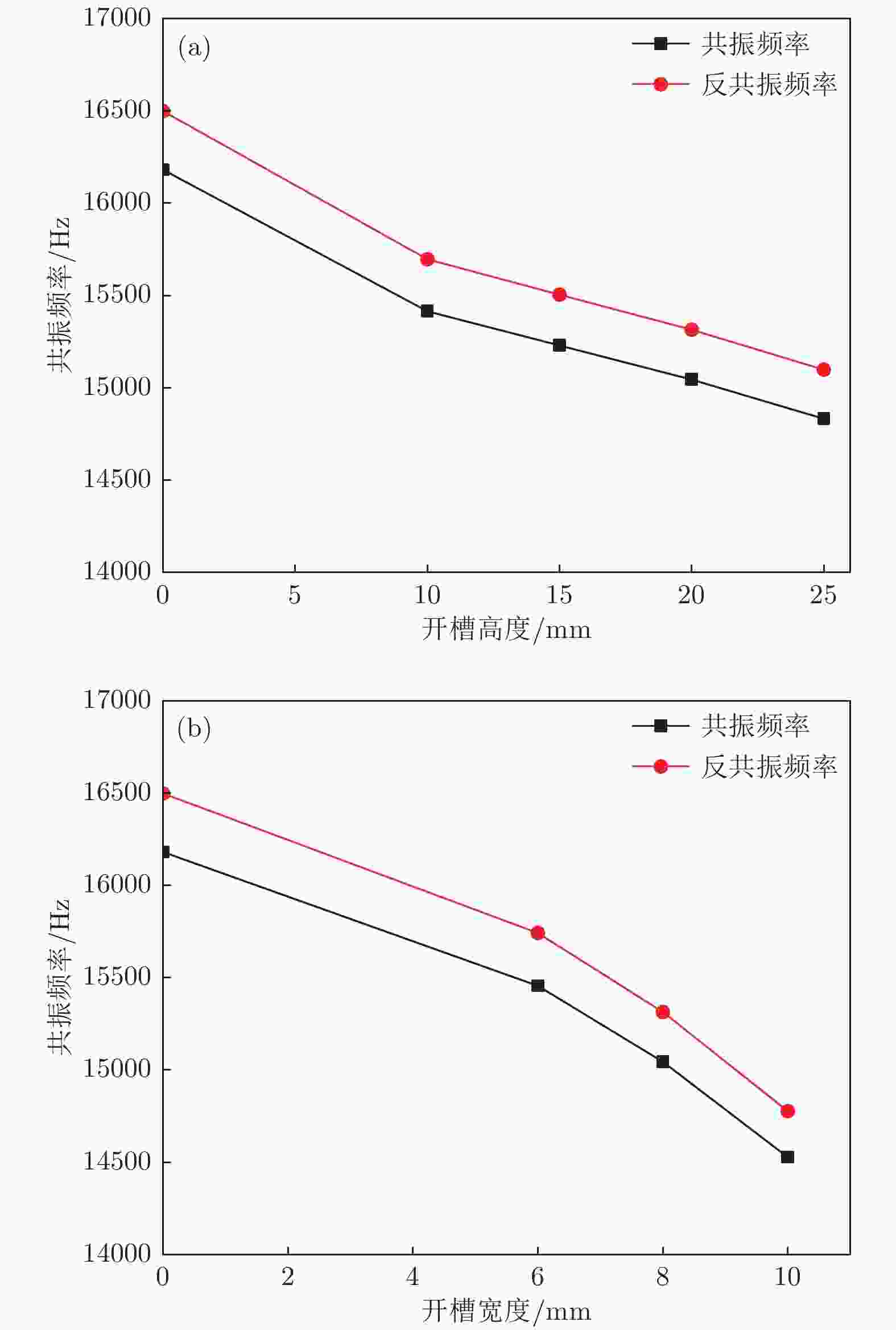图 4 大尺寸夹心式换能器的共振及反共振频率　(a)改变槽高; (b)改变槽宽
Figure4. Resonance and anti-resonance frequency of a large-size sandwich transducer: (a) Change the groove height; (b) change the groove width.

本研究发现通过在前盖板上加工周期性排列的槽, 对换能器的机械性能产生了一定的影响, 换能器的共振频率与反共振频率有了相应的变化. 开槽宽度一定, 随着开槽高度增加, 换能器的共振以及反共振频率都有相应的减少, 如图4(a)所示. 同样地, 开槽高度一定, 随着开槽宽度的增加, 换能器的共振以及反共振频率也都有相应的减少, 如图4(b)所示. 通过对比大尺寸夹心式换能器的共振频率及其带隙范围发现, 开槽后换能器的共振频率均在其带隙范围内, 说明当换能器处于工作状态时, 声子晶体结构可以对其横向振动有抑制作用.
为了分析大尺寸夹心式换能器的带宽, 通过发射电压响应曲线来计算其带宽. 换能器的发射电压响应是指换能器在某频率下, 在指定方向上的远场中, 离换能器等效声中心1 m处的声压值与加到输入端的电压的比值. 采用有限元法, 在COMSOL Multiphysics中建立与上述相同的7个模型, 选用水作为负载, 求得基于二维声子晶体的大尺寸夹心式换能器的发射电压响应曲线. 图5给出了换能器的发射电压响应曲线示意图, 根据带宽的定义, 发射电压响应下降3 dB时, 两频率之差为频带宽度, 即$\Delta f = {f_2} - {f_1}$. 由此可以计算其带宽, 得到如图6所示的大尺寸夹心式换能器的带宽.
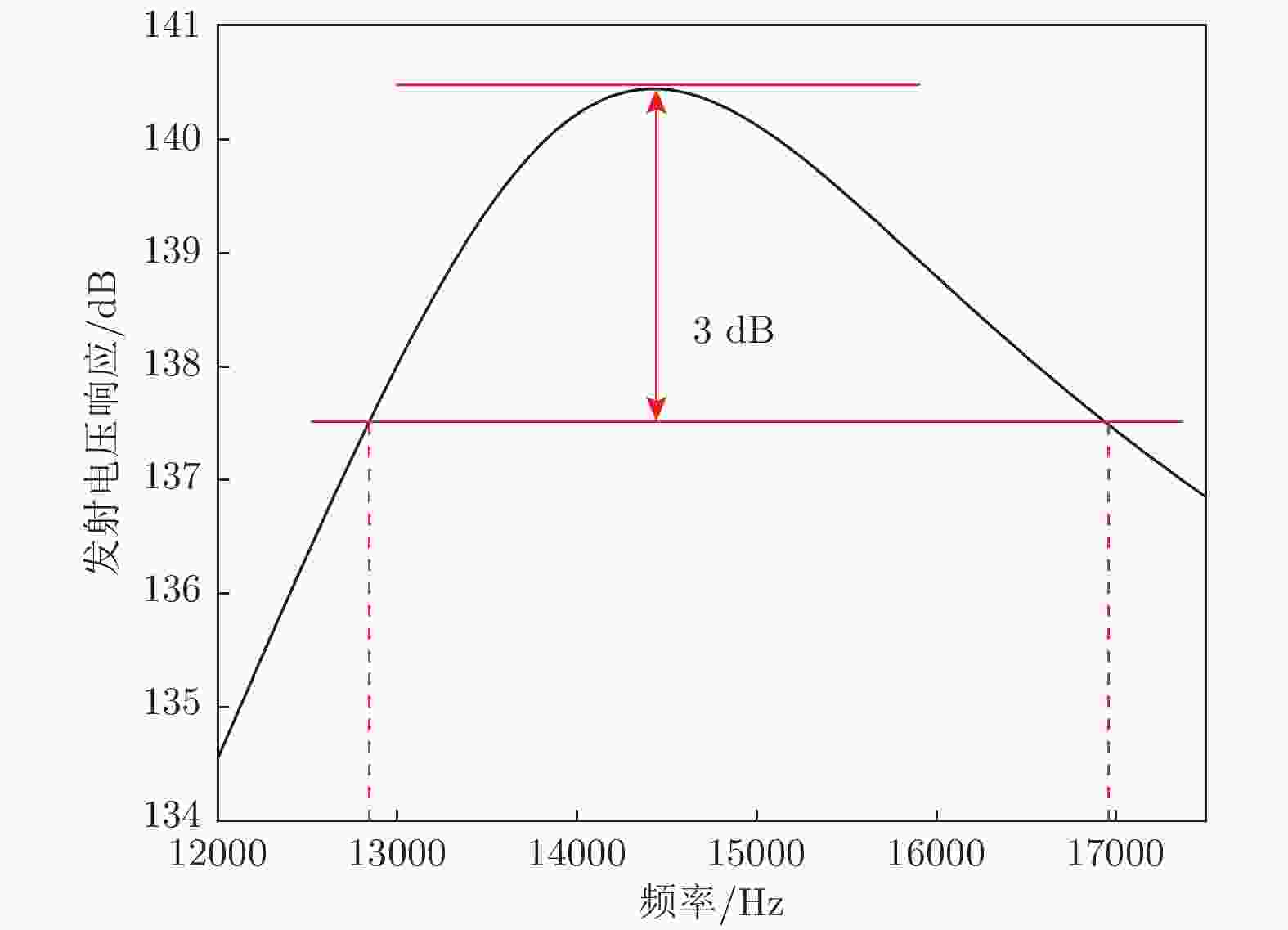图 5 换能器的发射电压响应曲线示意图
Figure5. Schematic diagram of the emission voltage response curve of the transducer.

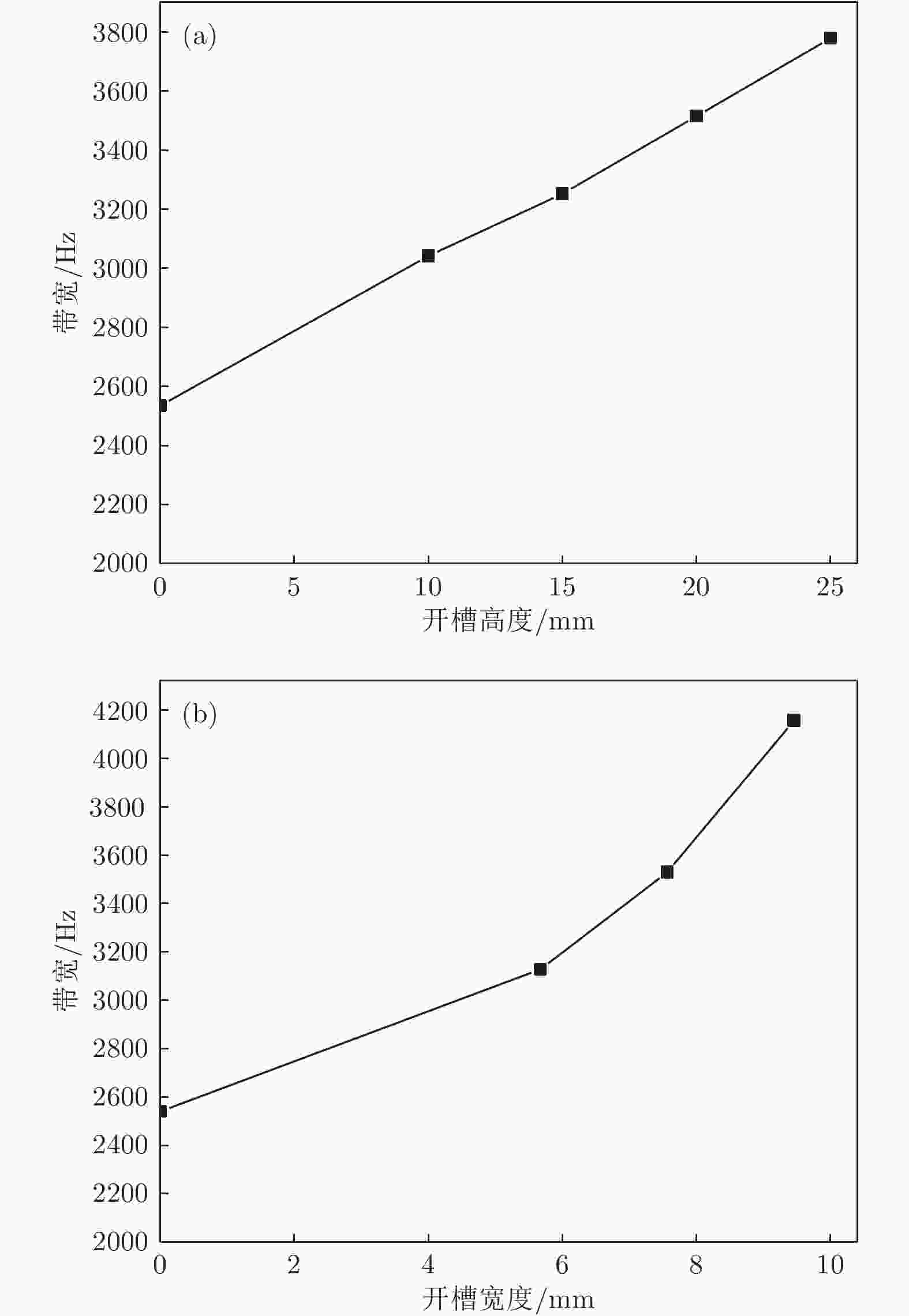图 6 大尺寸夹心式换能器的带宽　(a)改变槽高; (b)改变槽宽
Figure6. Bandwidth of a large-size sandwich transducer: (a) Change the groove height; (b) change the groove width.

图6给出了大尺寸夹心式换能器的带宽. 在大尺寸夹心式换能器的前盖板上加工周期排列的槽结构, 对其带宽有一定的影响. 当开槽宽度一定, 改变槽高的换能器带宽如图6(a)所示, 可以发现随着开槽高度的增加, 换能器的带宽不断增大. 当开槽高度一定, 随着开槽宽度的增加, 换能器的带宽也不断地增大, 如图6(b)所示. 说明在大尺寸夹心式换能器的前盖板上加工声子晶体结构可有效拓宽换能器的工作频带.
在计算换能器的振动特性后, 为了清楚地分析其前盖板的辐射面的位移分布, 在其端面处, 定义一条沿x轴正方向的截线(ab), 如图7所示. 采用有限元法, 分别计算出上述7个换能器在其工作频率下ab线上的纵向位移分布, 如图8所示.
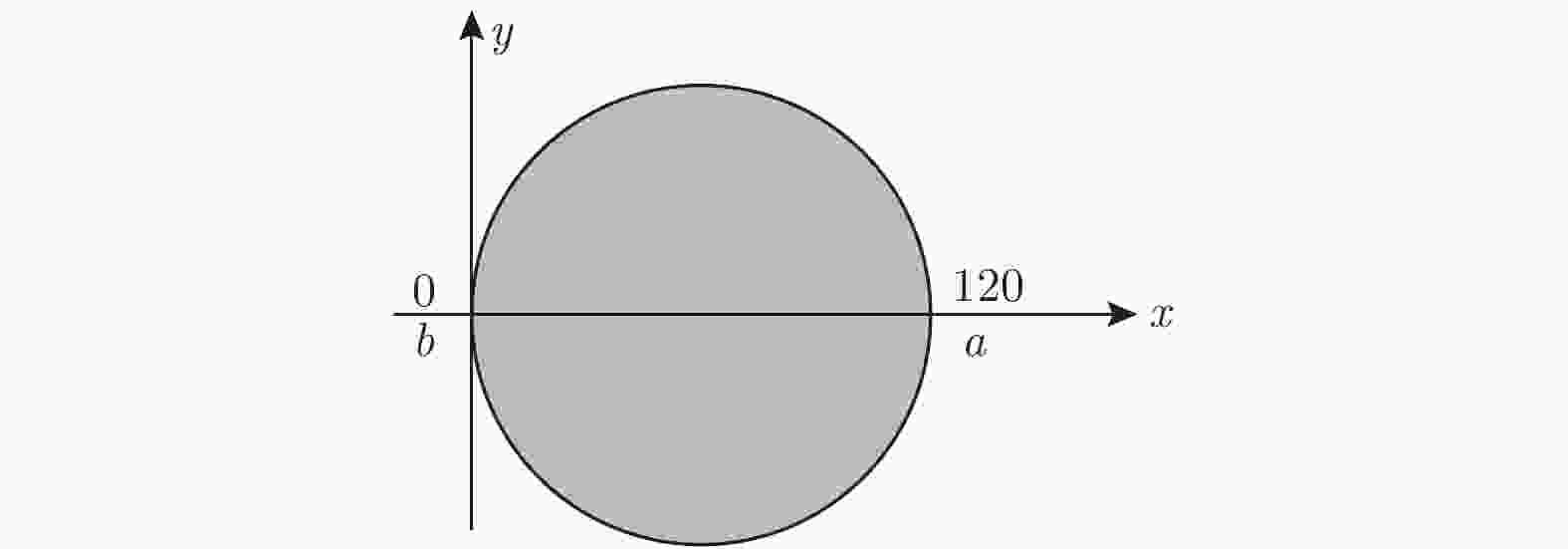图 7 大尺寸夹心式换能器辐射面截线示意图
Figure7. Schematic diagram of the radiation surface section of the large-size sandwich transducer.

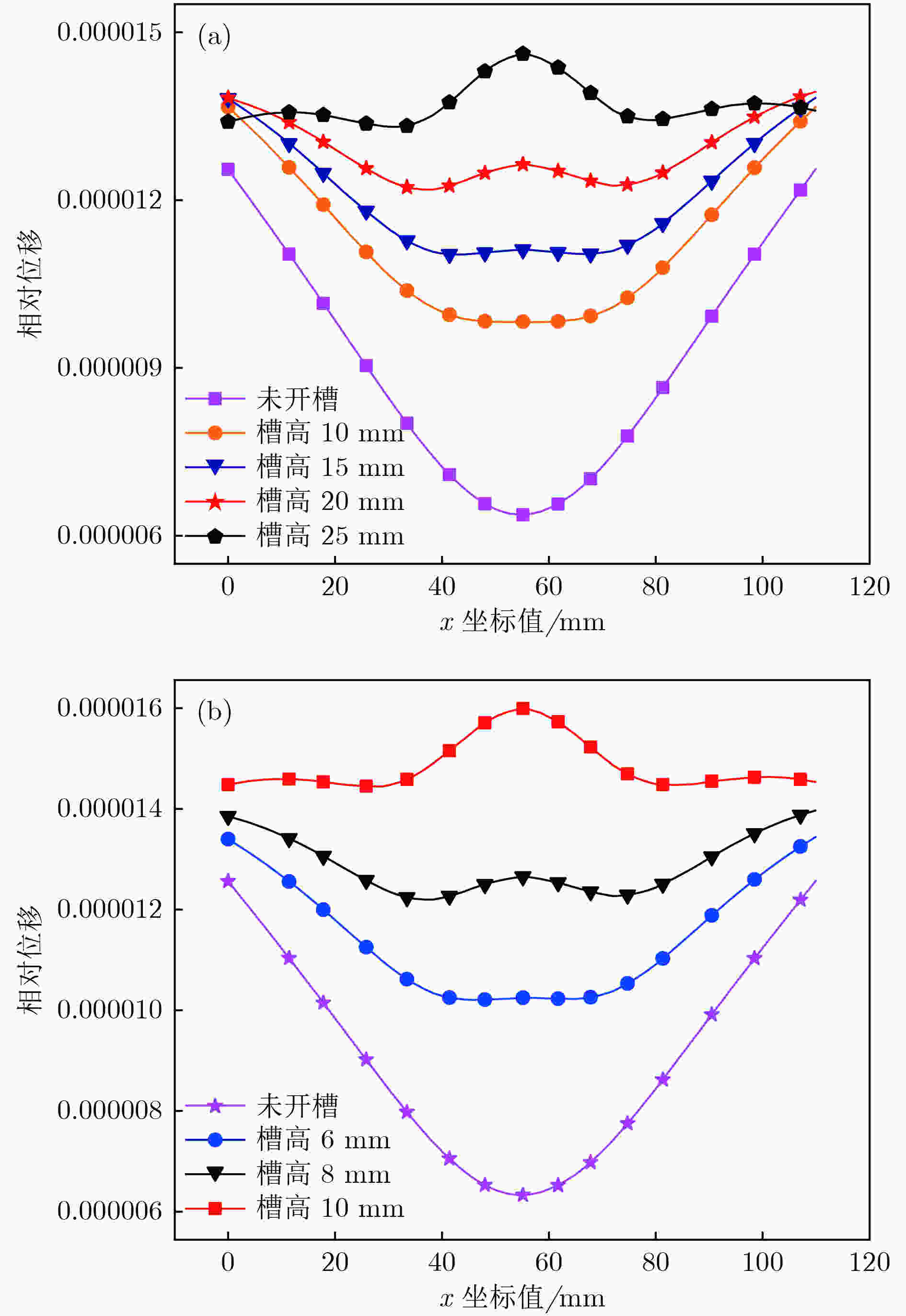图 8 大尺寸夹心式换能器的端面位移分布　(a)改变槽高; (b)改变槽宽
Figure8. End face displacement distribution of large-size sandwich transducer: (a) Change the groove height; (b) change the groove width.

图8中给出了大尺寸夹心式换能器的端面位移分布情况, 可以看出, 与未开槽相比, 开槽后换能器的端面的位移分布更加均匀, 并且开槽宽度以及高度的改变, 对大尺寸换能器端面的位移分布具有一定的影响. 当开槽宽度一定时, 改变开槽高度, 随着高度的增加, 前盖板辐射面的位移分布更加均匀, 但当高度过大时, 端面的中心位置容易出现强烈的振幅, 如图8(a)所示. 同样地, 对于开槽宽度过大的换能器同样出现了该现象, 如图8(b)所示. 通过对比不同开槽高度及宽度的带隙与共振频率, 开槽高度和宽度分别为20 mm和8 mm的大尺寸夹心式换能器的共振频率在带隙处的衰减程度最大, 故辐射面的位移分布最为均匀. 当基于二维声子晶体的大尺寸夹心式换能器的工作频率在其方向带隙范围内时, 该方向上弹性波的传播会受到一定的抑制. 这说明在大尺寸夹心式换能器前盖板上加工槽, 形成二维声子晶体, 能有效地抑制其横向振动, 从而使其辐射面的位移分布更加均匀. 本研究表明, 将声子晶体结构应用于大尺寸夹心式换能器中, 可显著提升换能器性能, 为实现大尺寸夹心式换能器的优化设计提供理论支撑.
由于二维声子晶体的结构能抑制大尺寸前盖板的横向振动, 从而均匀其辐射面的位移分布, 同时对共振与反共振频率以及带宽都有一定的影响, 能有效提升大尺寸夹心式换能器的性能及工作带宽. 本研究通过在前盖板上加工二维声子晶体结构, 最终实现了对大尺寸夹心式换能器的优化设计.

对基于二维声子晶体的大尺寸夹心式换能器进行了研究. 利用前盖板上加工槽的方式形成二维声子晶体, 使其横向耦合振动得到有效的抑制, 从而使得纵向的振动模态更加单一. 分别讨论了开槽高度和开槽宽度对大尺寸夹心式换能器的带隙、共振与反共振频率、带宽以及辐射面的位移分布的影响, 得出以下结论.
1) 基于二维声子晶体的大尺寸夹心式换能器存在横向带隙.
2) 在开槽宽度一定时, 基于二维声子晶体的大尺寸夹心式换能器的带宽随着开槽高度的增加而增大. 同样地, 在开槽高度一定时, 基于二维声子晶体的大尺寸夹心式换能器的带宽随开槽宽度的增加而增加.
3) 将二维声子晶体结构应用于大尺寸夹心式换能器前盖板中, 能有效地抑制横向振动, 均匀前盖板辐射面的位移分布.
总之, 二维声子晶体结构应用于大尺寸夹心式换能器中, 能有效地抑制换能器的横向振动, 并拓宽换能器的工作频带, 可以对大尺寸夹心式换能器的性能进行优化设计.