摘要:针对传统基线相减成像方法受环境温度影响的问题, 考虑到反转路径下超声波在缺陷处散射场的差异性, 提出了一种基于反转路径差信号的兰姆波稀疏阵列成像方法. 通过数值仿真, 对反转路径差信号的来源进行了分析, 并研究了缺陷与两个传感器的夹角及路径差对反转路径差信号幅值的影响规律. 在此基础上, 通过数值仿真及检测实验, 研究了基于反转路径差信号的兰姆波成像方法对板中缺陷检测的有效性. 结果表明, 基于反转路径差信号的兰姆波成像方法可以很好地消除直达波对缺陷成像的影响, 实现板中不同位置的圆孔和矩形缺陷成像, 且成像分辨率较高, 定位较准确. 本文为板结构大范围健康监测提供了一种可行的新方案.
关键词: 兰姆波/
板结构/
反转路径差信号/
稀疏阵列

English Abstract

全文HTML

--> --> -->

因具有检测范围广、检测效率高等优势, 兰姆波技术已广泛应用于板、管等结构的无损检测及健康监测^[1-3]. 利用稀疏分布^[4]在板结构上的传感器阵列, 还可以实现板结构大范围成像. 在兰姆波检测中, 其检测信号波形复杂, 蕴含信息丰富, 既包括直达波和缺陷回波, 又包括边界回波等特征体回波. 与直达波和边界回波相比, 缺陷回波幅值较小, 易被其他回波及噪声所淹没, 而兰姆波的频散^[5]和多模态^[6]特性更增加了检测信号分析和识别的难度.
针对兰姆波检测信号分析与识别难题, 国内外****对兰姆波检测信号分析与识别技术开展了大量卓有成效的研究, 发展了多种兰姆波信号分析与处理方法, 如时频分析^[7,8]、时间-空间变换^[9,10]等; 此外, 针对弱缺陷回波提取问题, 也发展了一些相对简单、高效的信号处理手段, 而基线相减法就是其中最典型、最有效的缺陷信息提取手段^[11,12], 被广泛应用于兰姆波检测信号处理中. 该方法通过将检测信号与预先获取的无缺陷状态下的基线(参考)信号进行相减, 达到抵消直达波和边界回波、凸显缺陷回波的目的^[13,14]. 例如, Zhao等^[14]将压电陶瓷传感器稀疏地粘贴到飞机机翼不同部位, 将基线相减法应用于其兰姆波监测信号的分析处理, 实现飞机机翼上裂缝和腐蚀缺陷的检测.
在实际使用中, 由于检测信号与基线信号获取的环境条件一般是不同的, 当环境条件变化较大时, 基线相减法就无法准确、有效地去除检测信号中的直达波和界面回波. 影响检测的环境因素主要包括载荷和边界条件^[15], 湿度和湿度^[16,17]等. 已有研究表明, 环境温度是对结构健康监测方法影响最大的外部因素之一^[18]. 针对基线相减法主要受环境温度影响的问题, 国内外****对其补偿及改进方法开展了大量的研究. 例如, 在传统基线相减法的基础上, Clarke等^[19]和Konstantinidis等^[20]提出了一种最佳基线相减法, 并通过实验研究了温度变化率对最佳基线相减法的适用性和鲁棒性的影响, 结果表明, 与基线减法相比, 最佳基线相减法的适用性较强, 其信噪比比常规基线法高近20 dB.
针对传统基线相减法需要预先获取结构健康状态下的基线参考信号问题, 国内外****对基线信号获取的方法进行了改进. Park等^[21]对时间反转激励下的损伤响应进行了分析, 利用重建波源信号和初始波源信号来确定损伤存在的路径, 从而估计出损伤位置. 该方法不再需要结构健康状态的基线信号, 但由于监测路径的限制, 其定位精度较低. Jan等^[22]和Tabatabaeipour等^[23]提出了一种基于瞬时基准的疲劳裂纹损伤识别方法. 该方法通过将结构在不同激励幅值下的非线性超声响应进行比例相减, 来实现结构中非线性损伤源(如疲劳裂纹)的检测. 基于分层缺陷产生的二次谐波非线性响应, Ciampa等^[24]提出了一种基于二次相位耦合信息的双相干系数成像方法, 该方法无需基线参考信号, 但需要在结构上布置较多数量的传感器.
以上缺陷信号提取方法大多针对缺陷的反射信息, 未考虑超声波在缺陷处产生的散射信号. 实际上, 超声波传播到缺陷时, 会产生散射现象, 其散射场中包含有更丰富的缺陷信息. 因此, 若利用传感器阵列接收其散射场信号, 从中可以提取出更为精确的缺陷状态信息, 如缺陷的类型^[25]、尺寸^[26]、形状^[27]等. 例如, Zhang等^[28]对线性相控阵探头接收到的超声信号进行全聚焦成像, 利用提取出缺陷位置的散射系数矩阵, 很好地实现了缺陷类型(裂纹、孔)及方向表征. 郑阳等^[29]利用环形分布的电磁声传感器阵列进行了板结构大范围缺陷检测研究, 通过提取的散射系数矩阵实现板结构中裂纹长度及角度表征.
针对传统基线相减方法受环境温度影响的问题, 考虑到反转路径下超声波在缺陷处散射场的差异性, 本文提出了一种基于反转路径差信号的兰姆波稀疏阵列成像方法. 通过数值仿真, 对反转路径差信号的来源进行了分析, 并研究了缺陷与两个传感器的夹角及路径差对反转路径差信号幅值的影响规律. 在此基础上, 通过数值仿真及检测实验, 验证了该方法的有效性.

2

-->

2.1.反转路径差信号分析

图1给出了无限大各向同性薄板中兰姆波检测原理. 两圆形压电传感片用于兰姆波的激励和接收, 其中心距离为d₀. 假设两压电片的性能一致, 均能周向一致地向空间各方向激励和接收超声波. 圆形缺陷的半径为r, 位于远场. 若考虑缺陷的尺寸效应, 则激励传感器发射的多束声波会传播到缺陷处, 并在缺陷处产生反射及散射, 这些反射波及散射波的一部分又会被接收传感器所接收, 如图1所示. 考虑到两个传感器接收到的缺陷回波以传感器主声束方向上的散射波为主(传感器1激励、传感器2接收时, 传播路径为d₁和d₂; 传感器2激励、传感器2接收时, 传播路径为d₃和d₄), 则以其中一个传感器作为激励, 另外一个传感器接收信号的频域表达式可简化为^[30]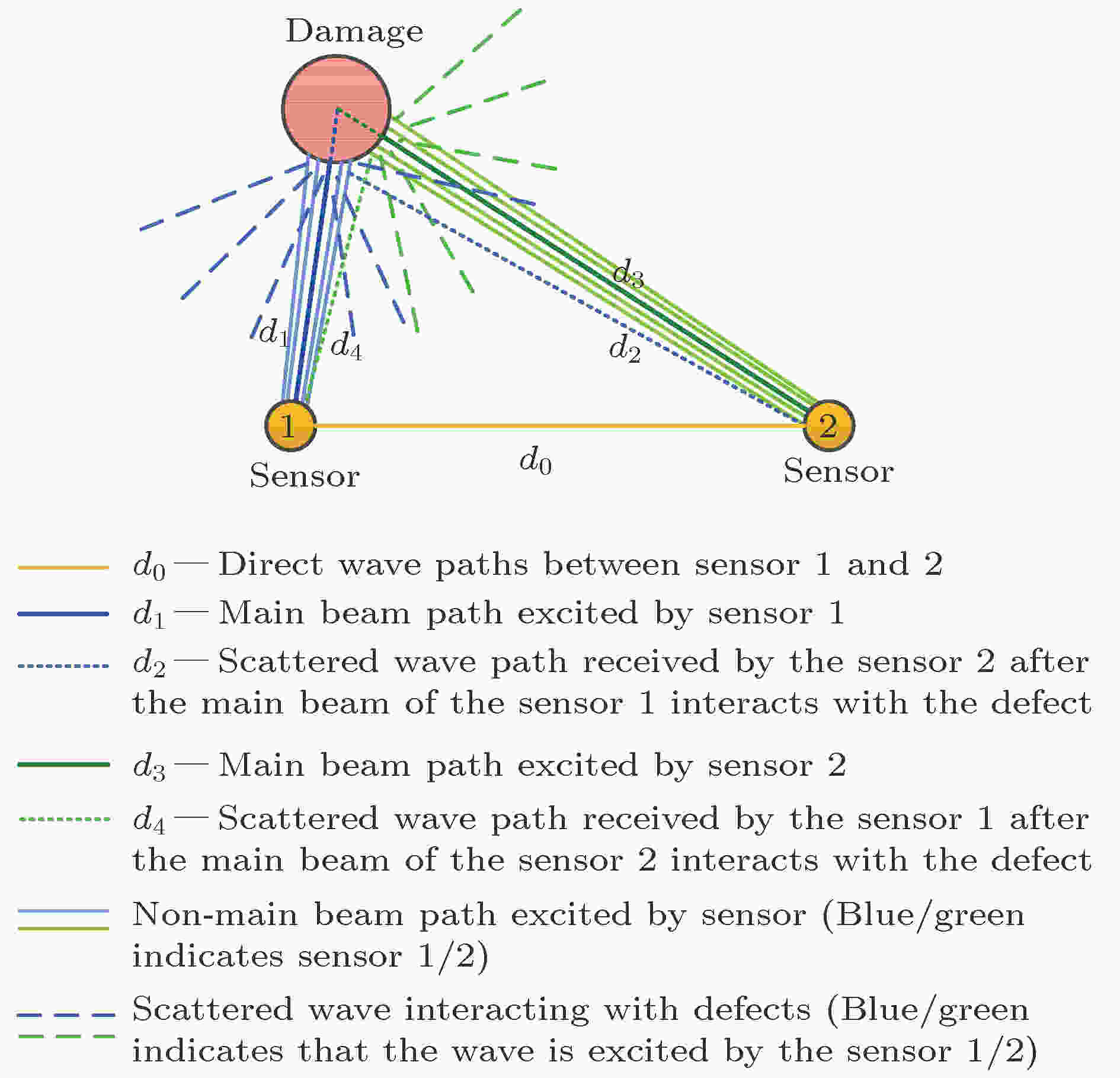
图 1 无限大薄板中兰姆波传播模型示意图
Figure1. Schematic diagram of Lamb wave propagation model in an infinite plate.

$\begin{split}&{X_{12}}(\omega ) \\= \;& T(\omega )R(\omega )\sqrt {\frac{1}{{k{d_1}}}} D({\alpha _{12}}, \omega )\sqrt {\frac{1}{{k{d_2}}}} \tilde G(\omega ){{\rm e}^{ - {\rm{j}}(k{d_1} + k{d_2})}} \\& + T(\omega )R(\omega ) \sqrt {\frac{1}{{k{d_0}}}} \tilde G(\omega ){{\rm{e}}^{ - {\rm{j}}(k{d_0})}}, \\& {X_{21}}(\omega ) \\=\;& T(\omega )R(\omega )\sqrt {\frac{1}{{k{d_3}}}} D({\alpha _{21}}, \omega )\sqrt {\frac{1}{{k{d_4}}}} \tilde G(\omega ){{\rm{e}}^{ - {\rm{j}}(k{d_3} + k{d_4})}} \\ &+ T(\omega )R(\omega )\sqrt {\frac{1}{{k{d_0}}}} \tilde G(\omega ){{\rm{e}}^{ - {\rm{j}}(k{d_0})}},\end{split} $

其中${X_{12}}(\omega )$和${X_{21}}(\omega )$为两压电片分别作为激励传感器, 另一传感器接收信号的频谱; $\tilde G(\omega )$为位移响应幅值^[31]; T(ω)和R(ω)为传感器的激励和接收传递函数; k为兰姆波的波数; D(α, ω)为兰姆波与缺陷相互作用后在α方向的散射系数. 式中第一项为缺陷散射回波, 第二项为直达波, 若令$G(\omega ) = T(\omega )R(\omega )\tilde G(\omega )$, 则(1)式可表示为

$\begin{split} {X_{12}}(\omega ) = \;& \sqrt {\frac{1}{{k{d_1}}}} D({\alpha _1}, \omega )\sqrt {\frac{1}{{k{d_2}}}} G(\omega ){{\rm e}^{ - {\rm{j}}(k{d_1} + k{d_2})}}\\ & + \sqrt {\frac{1}{{k{d_0}}}} G(\omega ){{\rm{e}}^{ - {\rm{j}}(k{d_0})}}, \\ {X_{21}}(\omega ) = \;& \sqrt {\frac{1}{{k{d_3}}}} D({\alpha _2}, \omega )\sqrt {\frac{1}{{k{d_4}}}} G(\omega ){{\rm{e}}^{ - {\rm{j}}(k{d_3} + k{d_4})}} \\ & + \sqrt {\frac{1}{{k{d_0}}}} G(\omega ){{\rm{e}}^{ - {\rm{j}}(k{d_0})}}. \end{split} $

将(2)式中两个表达式作差, 并称其为反转路径差信号:

$\begin{split}&\; \Delta {X_{12}}(\omega ) = {X_{12}}(\omega ) - {X_{21}}(\omega ) \\ = & \;\sqrt {\frac{1}{{k{d_1}}}} D({\alpha _1}, \omega )\sqrt {\frac{1}{{k{d_2}}}} G(\omega ){e^{ - {\rm{j}}(k{d_1} + k{d_2})}} \\ &- \sqrt {\frac{1}{{k{d_3}}}} D({\alpha _2}, \omega )\sqrt {\frac{1}{{k{d_4}}}} G(\omega ){{\rm{e}}^{ - {\rm{j}}(k{d_3} + k{d_4})}} \\ = & \;G(\omega )\frac{1}{k}\left(D({\alpha _1}, \omega )\sqrt {\frac{1}{{{d_1}{d_2}}}} {{\rm e}^{ - {\rm{j}}k({d_1} + {d_2})}}\right. \\ & \left.- D({\alpha _2}, \omega )\sqrt {\frac{1}{{{d_3}{d_4}}}} {{\rm{e}}^{ - {\rm{j}}k({d_3} + {d_4})}}\right) .\end{split} $

由(3)式可以看出, 反转路径差信号中的直达波被消除了, 仅保留下能够反映缺陷状态信息的缺陷散射回波的差, 如无特别说明, 文中差信号指反转路径下接收信号的差信号. 同时观察到, 反转激励下缺陷散射回波的差信号与散射系数D和传播距离有关. 正是由于这两个因素, 造成了反转激励下缺陷散射回波的幅值和相位的不同.
2 -->

2.2.基于反转路径差信号的延时叠加成像方法

基于以上分析得到的单对传感器的反转路径差信号, 利用稀疏分布在板结构的压电阵列对其进行兰姆波检测, 也可以实现整个板结构成像. 若稀疏阵列中包含的阵元个数为N, 则可以组成N(N–1)/2个传感器对, 得到N(N–1)组检测信号${s_{ij}}$, 其中, 下标i, j分别表示激励接收传感器的序号, 且i≠j. 相应地, 也可以得到N(N–1)组反转路径差信号$\Delta {s_{ij}}={s_{ij}} - {s_{ji}}$. 利用这些反转路径差信号$\Delta {s_{ij}}$可以得到板中任意点$(x, y)$处散射声场强度:

$I(x, y) = \sum\limits_{i = 1}^N {\sum\limits_{j = 1, j \ne i}^N {\Delta {s_{ij}}({t_{ij}}(x, y))} } , $

其中, ${t_{ij}}(x, y)$为兰姆波由激励传感器(坐标为$({x_i}, {y_i})$)传播到该点(坐标为$(x, y)$), 再传播到接收传感器(坐标为$({x_j}, {y_j})$)所用的时间, 其表达式为

$\begin{split}&{t_{ij}}\left( {x, y} \right) = \\&\;\;\frac{{\sqrt {{{\left( {{x_i} - x} \right)}^2} + {{\left( {{y_i} - y} \right)}^2}} + \sqrt {{{\left( {{x_j} - x} \right)}^2} + {{\left( {{y_j} - y} \right)}^2}} }}{{{c_{\rm{g}}}}}, \end{split}$

其中, ${c_{\rm{g}}}$为检测频率下兰姆波传播的群速度.
显然, (4)式所示的散射场空间分布可以实现板结构损伤检测及成像. 值得注意的是, 上述成像中通过反转传感器对的激励和接收位置, 来达到消除直达波的影响, 突出缺陷散射波的效果. 同时, 该方法无需无缺陷情况下的参考信号, 可以很好避免由此带来的环境温度等因素的影响.

通过数值仿真, 对反转路径差信号的来源进行研究, 分析反转路径差信号存在的条件, 并研究传播距离和散射系数对反转路径差信号的影响规律.
2

-->

3.1.缺陷反射信号的导波模态分析

为说明散射信号的主要模态类型, 利用图2所示的模型, 基于商用有限元分析软件PZFlex进行了一系列不同条件下板中兰姆波数值仿真研究. 在仿真模型中, 铝板尺寸为600 mm × 500 mm × 1 mm. 缺陷为直径2r = 8 mm的圆形通孔, 其中心位于(180 mm, 320 mm)处. 激励接收位置为直径10 mm的圆形区域, 激励时对该圆形区域施加垂直于板面的力, 信号接收点为圆形区域中心, 为方便叙述, 将数值仿真模型中的圆形激励接收区域称为传感器. 传感器1中心位于(200 mm, 320 mm), 其与缺陷中心的距离D₁ = 126.5 mm. 在仿真过程中, 保持传感器1与缺陷的位置不变, 传感器2的初始位置为(200 mm, 320 mm), 以1 mm的步长间隔, 依次沿水平方向(x方向)移动传感器2, 直到传感器2与缺陷中心的距离D₃ = 300 mm为止(即传感器2到(500 mm, 320 mm)位置处). 在以上不同条件下, 分别进行有缺陷和无缺陷情况下板结构中兰姆波传播的数值仿真, 其中传感器1作为激励, 传感器2用于接收, 激励信号为中心频率为200 kHz、汉宁窗调制的5周期单音频信号.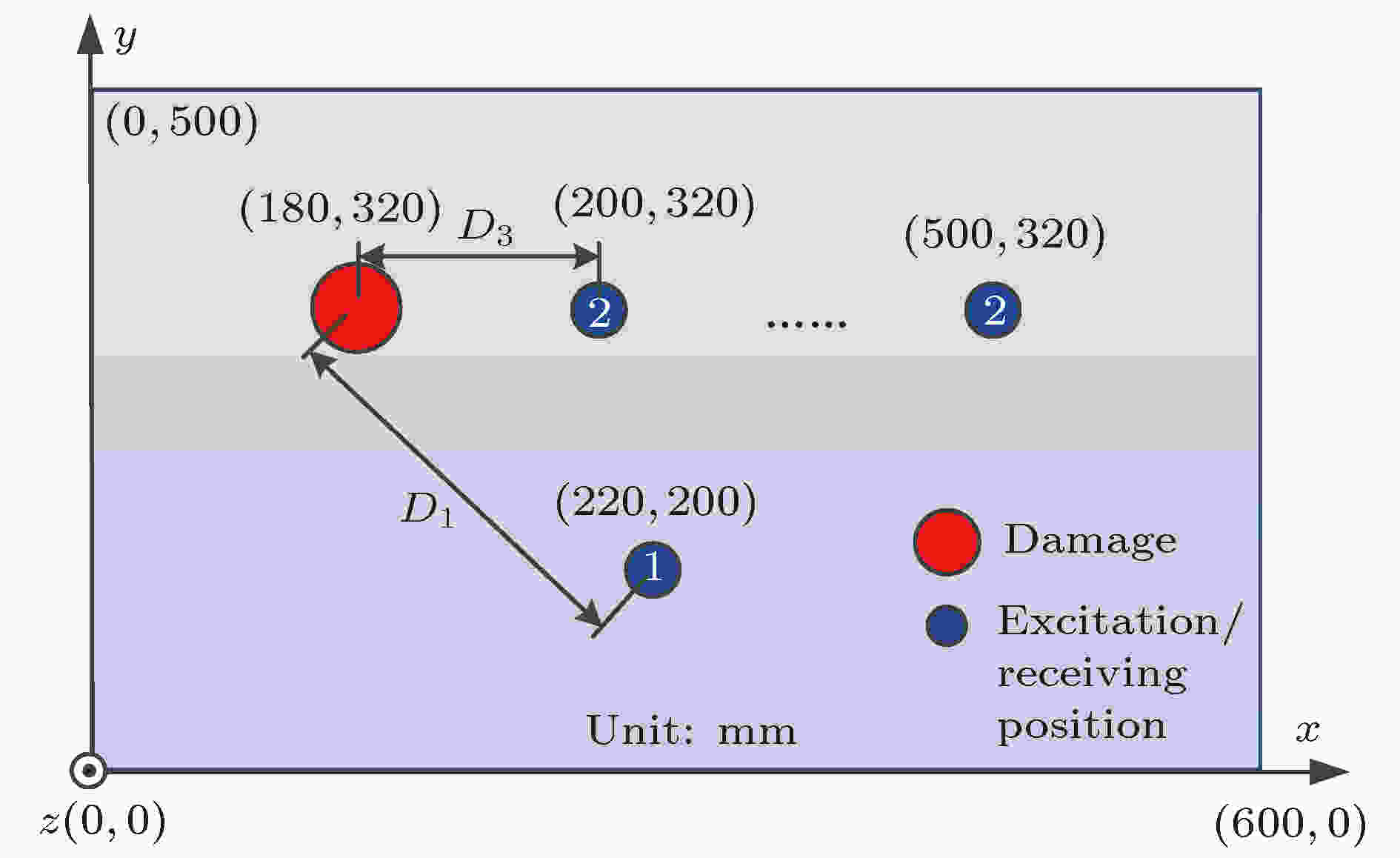
图 2 接收信号模态分析数值仿真模型
Figure2. Numerical simulation model of modal analysis of received signals.

分别提取有缺陷和无缺陷条件下传感器2接收到的z方向的离面位移和x方向的面内位移, 以无缺陷板中获得的仿真信号作为参考信号, 对有缺陷板中获得的仿真信号进行去参考处理, 即将有缺陷条件下的获得数值仿真信号减去对应条件下的无缺陷板中获得的数值仿真信号. 图3和图4给出了不同空间位置接收到的两个方向上去参考信号的典型波形. 可以看出, z方向的去参考信号中只包含单个波包, 且随传播距离增加, 波包宽度明显增加, 说明其频散较为严重; x方向的去参考信号中包含多个波包, 说明该方向上的缺陷散射信号中包含多个模态的兰姆波, 且波包宽度亦随传播距离增加而展宽. 图5和图6为对不同空间位置上接收到的两个方向上去参考信号进行二维快速傅里叶变换(two dimensional fast Fourier transform, 2D-FFT)的结果. 可以看出, z方向接收信号的仅包含单一A0模态兰姆波, 而x方向接收信号中除了包含A0模态兰姆波外, 还出现了明显的S0模态兰姆波.
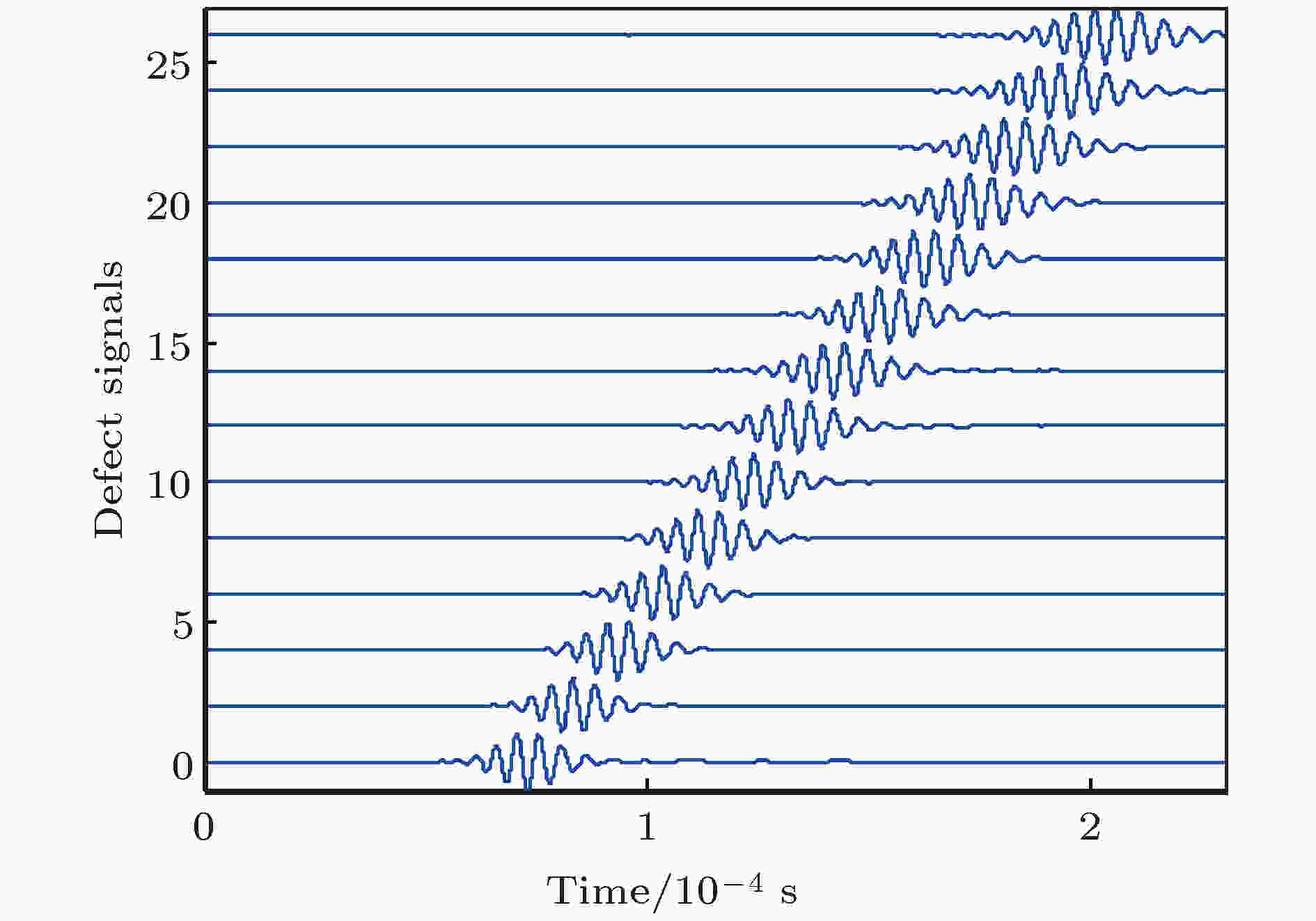图 3 不同位置接收到的z方向的去参考信号
Figure3. Dereference signals in the z direction received at different positions.

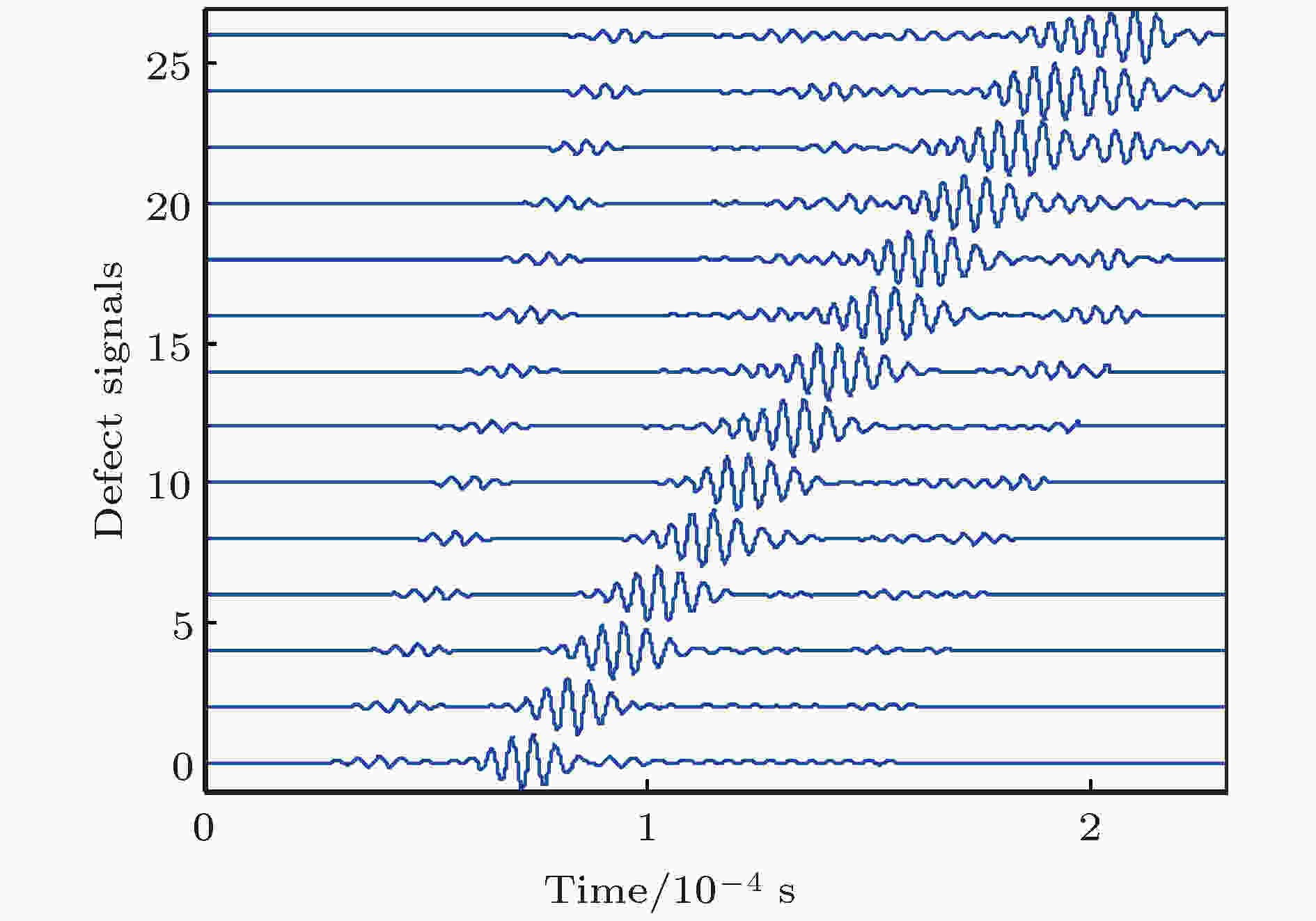图 4 不同位置接收到x方向的去参考信号
Figure4. Dereference signal in the x direction received at different positions.

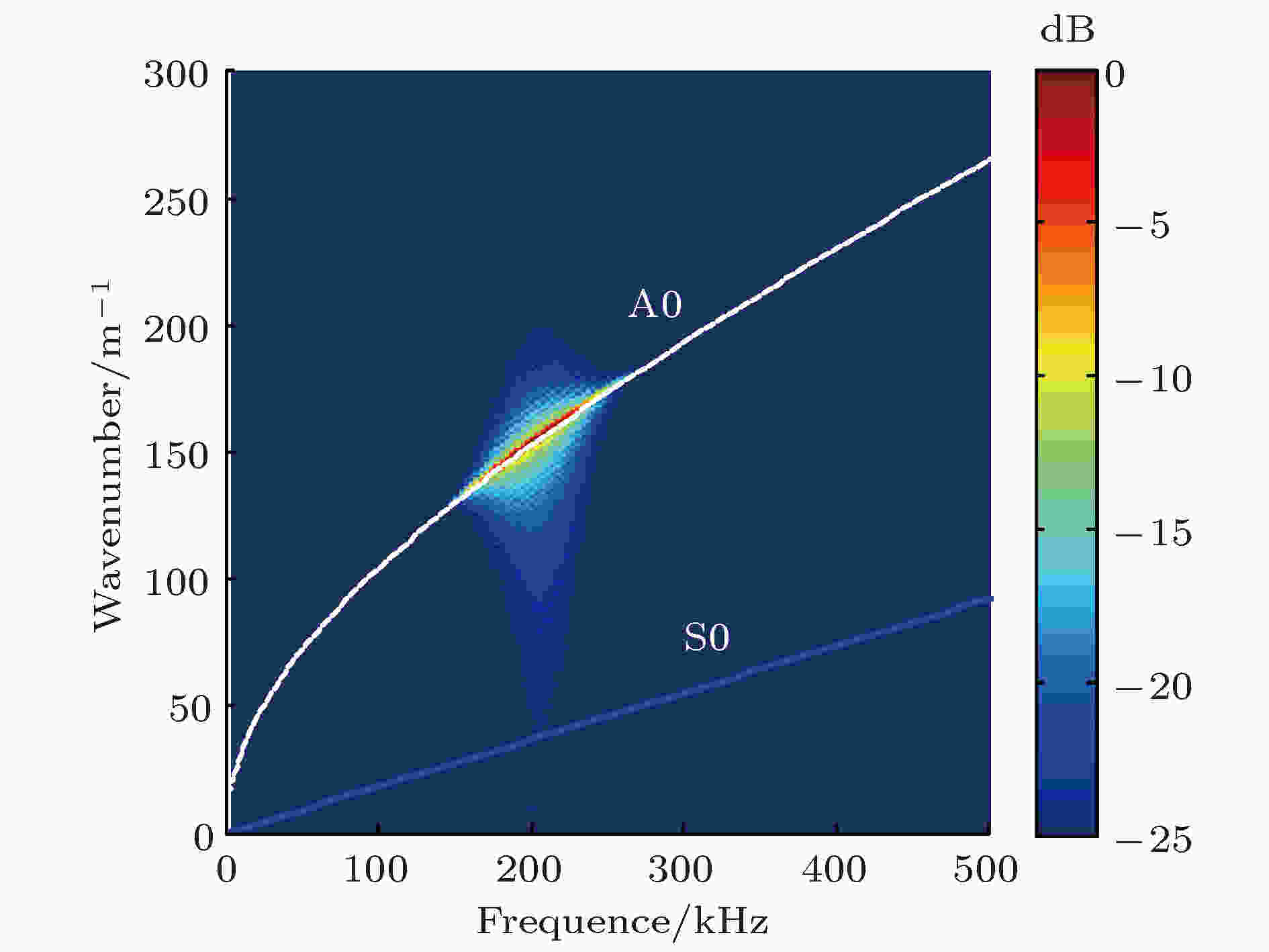图 5 z方向去参考信号的2D-FFT
Figure5. 2D-FFT of the reference signal in the z direction.

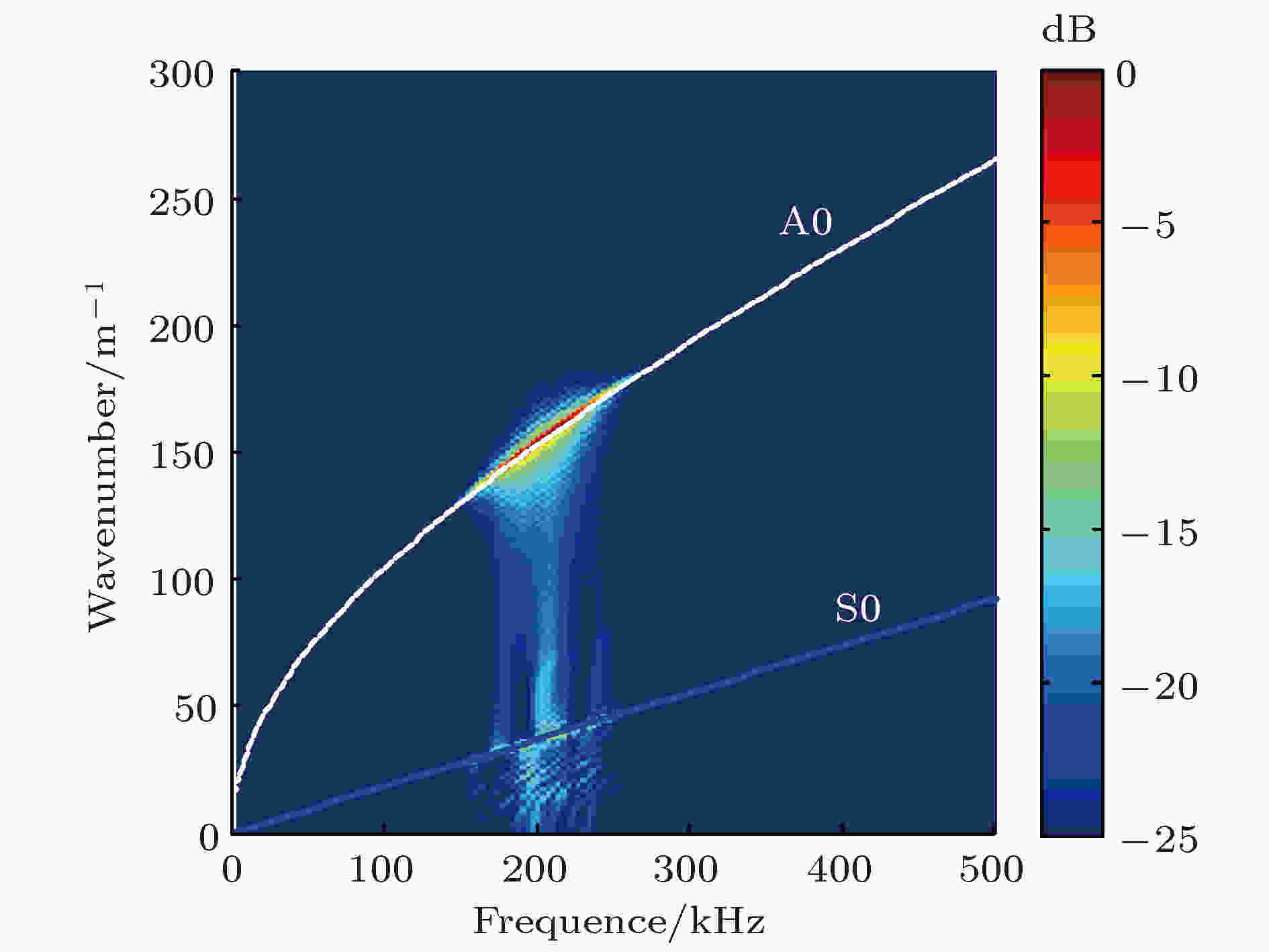图 6 x方向去参考信号的2D-FFT
Figure6. 2D-FFT of the reference signal in the x direction.

根据图3和图5所示z方向上的仿真结果可知, 缺陷散射波以A0模态为主, 其他类型的散射波(包括激励出的其他模态及A0模态在缺陷发生模态转换产生的其他模态)可以忽略不计. 同时, 在本文后续数值仿真中, 仅对z方向的离面位移进行分析.
2 -->

3.2.反转路径差信号的影响因素分析

分析(3)式所示的反转激励下薄板中兰姆波传播简化模型可知, 反转路径下缺陷散射回波的差信号与散射系数D和传播距离有关. 具体而言, 反转路径差信号的幅值直接和传感器与缺陷的夹角α及两传感器与缺陷距离的乘积有关. 为说明反转路径差信号幅值与这些参数的关系, 利用图7所示的两个模型进行了一系列反转激励(包括: 传感器1作为激励, 传感器2作为接收; 传感器2作为激励, 传感器1作为接收)下板中兰姆波传播的数值仿真. 模型中, 铝板尺寸为600 mm × 500 mm × 1 mm.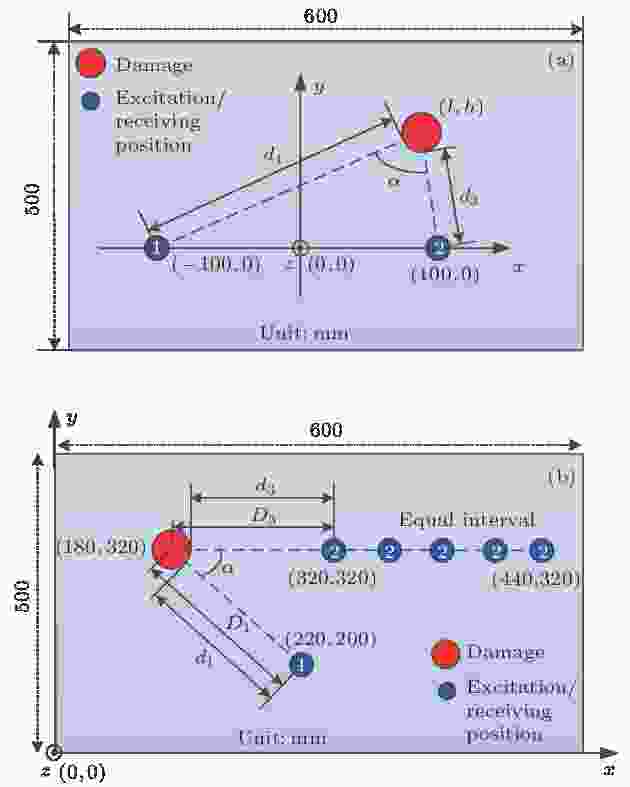
图 7 影响因素分析数值仿真模型　(a) 双因素综合影响模型; (b) 距离差影响因素模型
Figure7. Numerical simulation model of influencing factor analysis: (a) A model of two-factor comprehensive impact; (b) model of distance difference influencing factor.

在图7(a)所示模型中, 两传感器关于原点对称, 其间距为200 mm, 保持两传感器位置不变. 当缺陷位于不同位置时, 进行反转激励下板中兰姆波传播数值仿真. 缺陷的形状、尺寸和激励信号的类型及参数与3.1节中相同. 表1列出了数值仿真中缺陷的具体位置(l, h)及两传感器与缺陷中心相应的夹角α. 该模型能综合反映缺陷与两传感器的距离差及夹角对反转路径差信号的影响.

h	l
	0	10	20	30	40	50	60	70	80	90
60	118.1	117.7	116.6	114.62	111.8	108.0	103.1	97.1	90.0	81.93
72	102.7	102.3	101.3	99.6	97.1	93.9	90.0	85.35	80.1	74.3
80	108.5	108.1	107.0	105.2	102.6	99.1	94.8	89.6	83.7	77.2
100	90.0	89.7	88.8	87.4	85.4	82.8	79.8	76.2	72.2	68.0

表1不同位置缺陷的坐标(单位mm)以及相应的夹角α (单位(°))
Table1.Coordinates (unit: mm) of defects at different locations and corresponding angles α (unit: (°))

对反转激励下得到的数值仿真结果进行相减运算, 获得不同缺陷位置处的反转路径差信号$\Delta {s_{12}}={s_{12}} - {s_{21}}$. 下面分三种情形研究反转路径差信号随缺陷与传感器位置的变化规律.
3 -->

3.2.1.反转路径信号差异的来源分析

根据缺陷与两个传感器的位置关系, 可将表1列出的40种缺陷分布情形分为两类: 缺陷位于纵轴上(即l = 0)及缺陷偏离纵轴(即l ≠ 0). 图8和图9给出了两种情形下, 数值仿真得到的检测信号(${s_{12}}$和${s_{21}}$)及对应的反转路径差信号$\Delta {s_{12}}$的典型波形. 可以看出, 当l = 0时, 反转路径差信号中无法观察到明显的回波信号; 而当l ≠ 0时, 反转路径差信号中会出现明显的波包, 需要指出的是, 本文仿真中的反转路径差信号均被放大5000倍. 这一现象可以利用(3)式加以解释: 当l = 0时, 两个传感器与缺陷距离相等, 且与纵轴呈对称分布. 此时, (3)式中两个相减项近似相等. 因此, 得到的反转路径差信号近似为零; 当l ≠ 0时, 两个传感器与缺陷距离不相等, 与纵轴呈非对称分布. 此时, (3)式中两个相减项不相等. 因此, 得到的反转路径差信号中能观察到明显的波包.
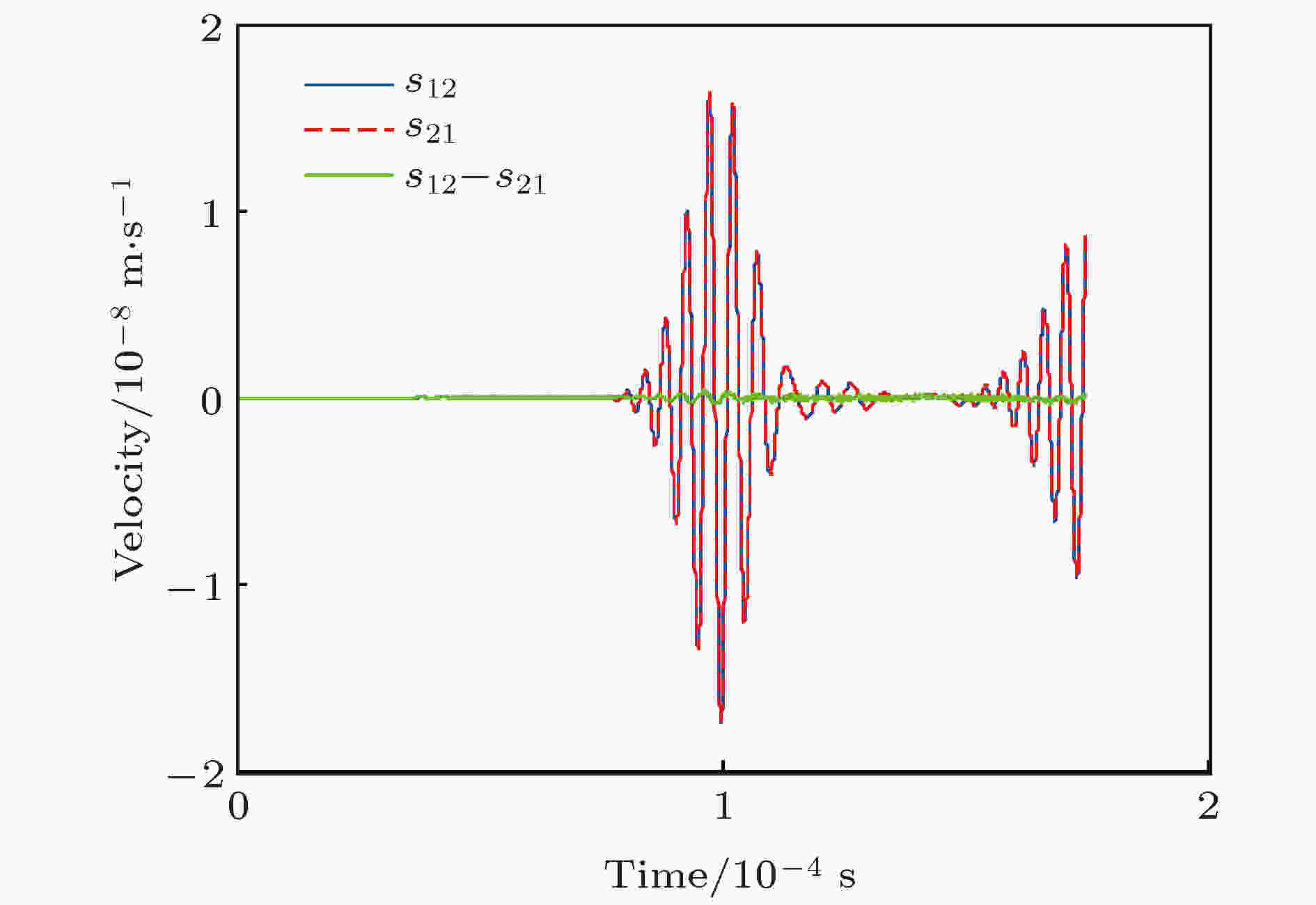图 8 当l = 0时接收信号及反转路径差信号
Figure8. Received signal and reverse path delta signal when l = 0.

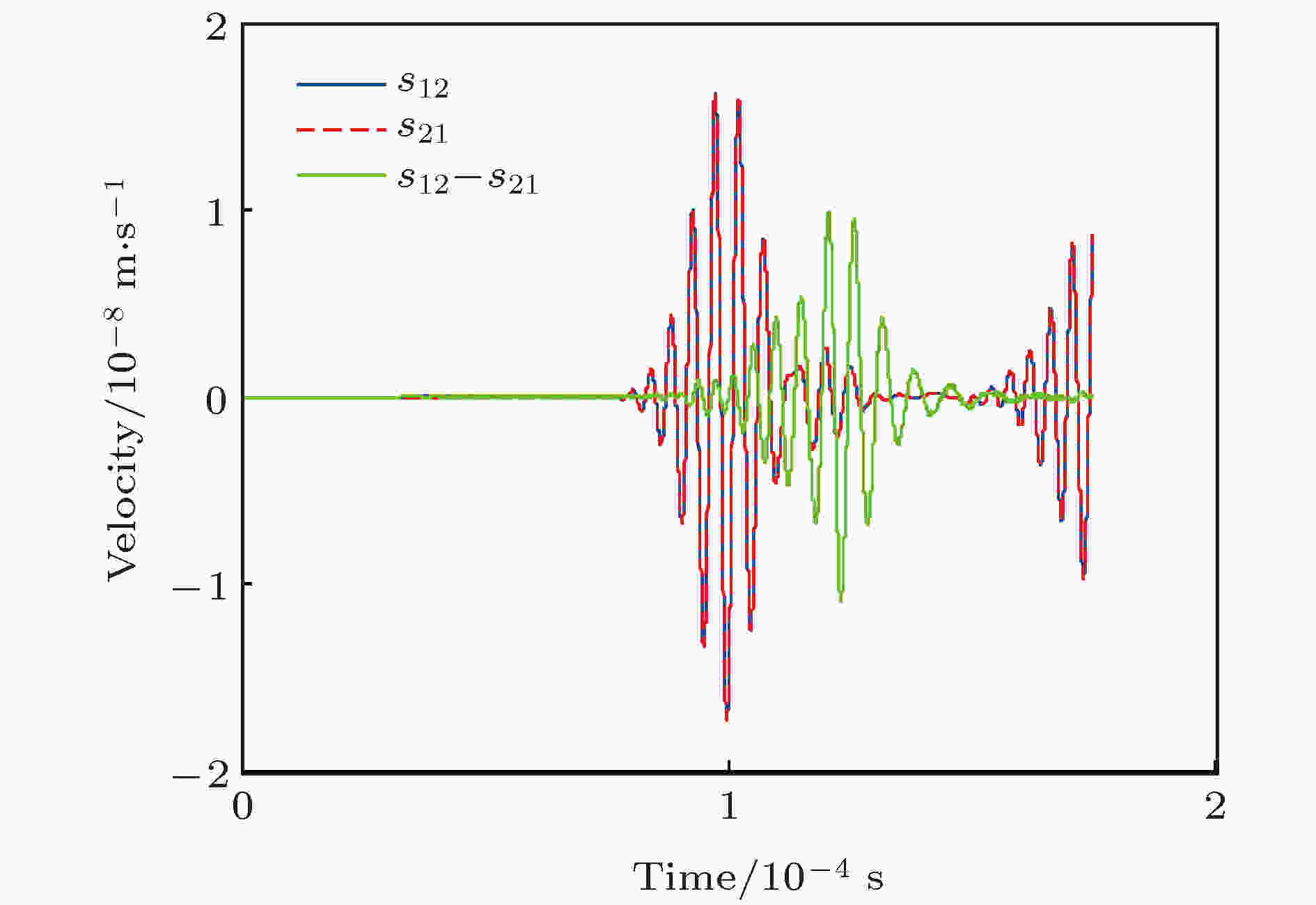图 9 当l ≠ 0时接收信号及反转路径差信号
Figure9. Received signal and reverse path delta signal when l ≠ 0.

3 -->

3.2.2.两传感器与缺陷的距离差对反转路径差信号的影响规律

为了反映两传感器与缺陷距离差这单一因素对反转路径差信号的影响, 参照图2所示仿真模型, 建立了图7(b)所示的仿真模型. 缺陷形状、位置及传感器1位置与图2模型中一致, 传感器2的初始位置为(320 mm, 320 mm). 保持传感器1与缺陷的位置不变, 将传感器2沿水平方向逐步移动(步长为30 mm), 增加两个传感器与缺陷的距离差. 在这些情况下, 进行反转激励下板结构中兰姆波传播的数值仿真.
图10给出了归一化后反转路径差信号随距离差的变化规律. 可以看出, 随着缺陷与两传感器距离差的增加, 反转路径差信号幅值呈递增趋势. 这与图11给出的根据(3)式计算出的归一化后反转路径差信号幅值($\Delta A = \sqrt {{1 / {\left( {{d_1}{d_2}} \right)}}} - \sqrt {{1 / {\left( {{d_3}{d_4}} \right)}}} $, 此时$D({\alpha _1}, \omega )=D({\alpha _2}, \omega )$)随距离差的变化规律相一致.
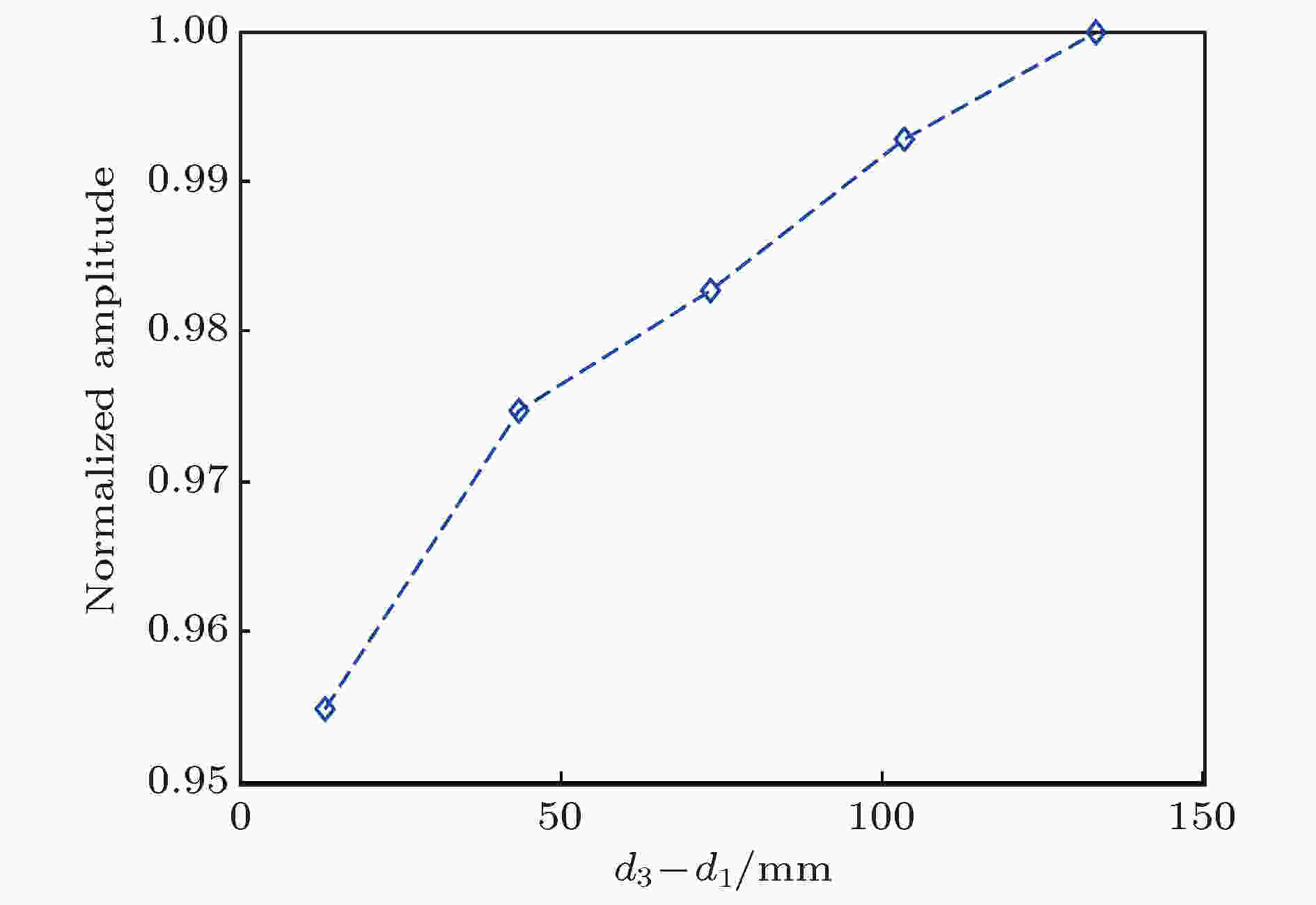图 10 不同传播距离差下的差信号最大幅值
Figure10. Maximum amplitude of the delta signals under different propagation distance differences.

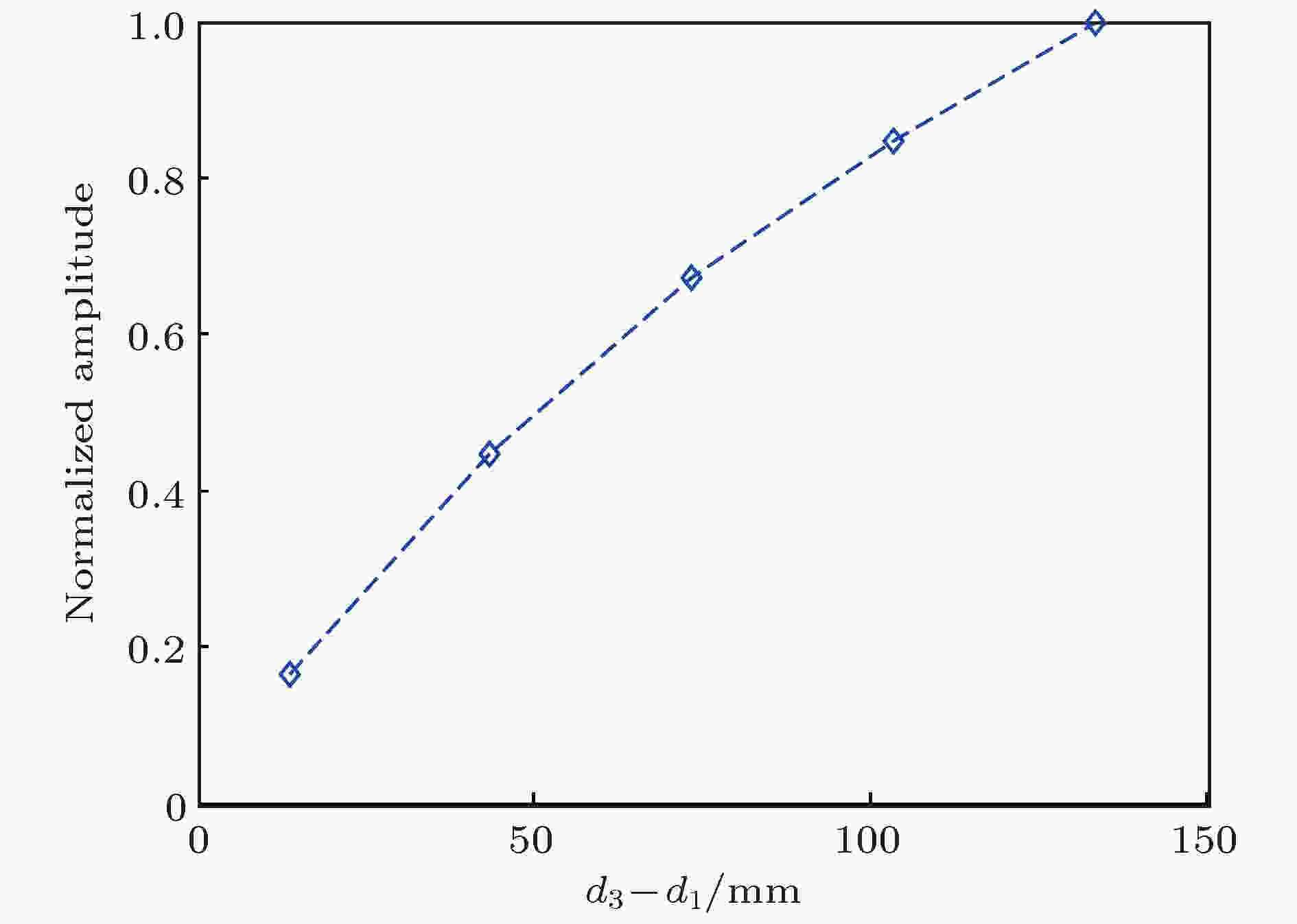图 11 不同传播距离差下的$\Delta A$计算结果
Figure11. Calculation results of $\Delta A$ under different propagation distance differences.

3 -->

3.2.3.夹角和距离差对反转路径差信号的综合影响

为说明缺陷与两传感器夹角及路径差对反转路径差信号的综合影响, 对不同缺陷位置(按照表1变化)处获得的反转路径差信号进行了分析. 图12给出了反转路径差信号$\Delta {s_{12}}$幅值随缺陷空间位置的变化规律. 可以看出, 当h = 60, 72 和80 mm时, 随着缺陷与对称轴(纵轴)之间距离l的增加, 反转路径差信号幅值变化规律较类似, 呈振荡变化, 先增加、后减小、再增加的规律; 当h = 100 mm时, 反转路径差信号幅值呈现单调递增趋势.
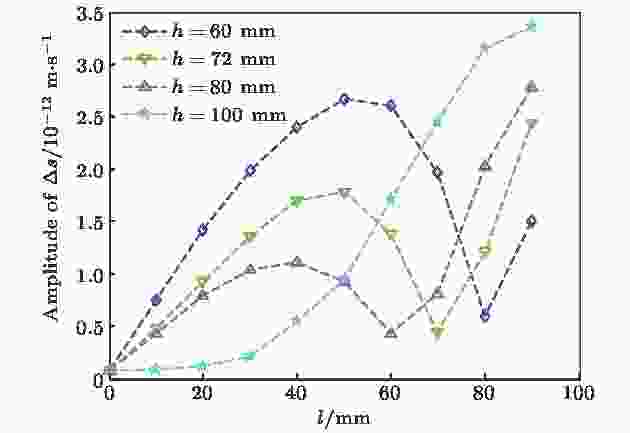图 12 不同缺陷位置下的差信号幅值
Figure12. Amplitude of delta signals at different defect locations.

直观上难以理解上述反转路径差幅值随缺陷位置的变化规律, 更难以建立其与夹角及路径差的联系. 为此, 对薄板中兰姆波在圆形通孔缺陷处的散射特性进行了数值仿真^[32], 得到了圆形通孔的散射系数分布, 如图13所示. 由于散射系数关于入射方向的对称性, 图中仅给出了0—180°范围内的散射系数. 可以看出, 当α = 90° (即入射方向与散射方向垂直)时, 散射系数最小.
根据表1中不同位置缺陷对应的夹角α和图13所示的散射系数分布, 可以插值出不同缺陷位置所在方向上的散射系数, 结果如图14所示. 可以看出, 不同缺陷位置的散射系数分布与其反转路径差信号幅值的变化规律有一定的相似性. 具体来说, 在h = 60, 72和80 mm条件下, 散射信号幅值呈振荡变化, 呈先减小后增加的趋势. 当缺陷位置接近对称轴(纵轴)时, 随缺陷位置远离对称轴, 散射系数数值较大, 且呈减小趋势, 这与反转路径差信号幅值变化规律相反; 但当缺陷位置远离对称轴到一定距离(50 mm)时, 散射系数和反转路径差信号幅值随缺陷位置变化规律相一致, 且极小值对应的缺陷位置相同, 即在α接近90°附近. 当h = 100 mm时, 散射信号幅值随缺陷位置远离对称轴呈单调递增, 这与图12中反转路径差信号幅值的变化规律一致.
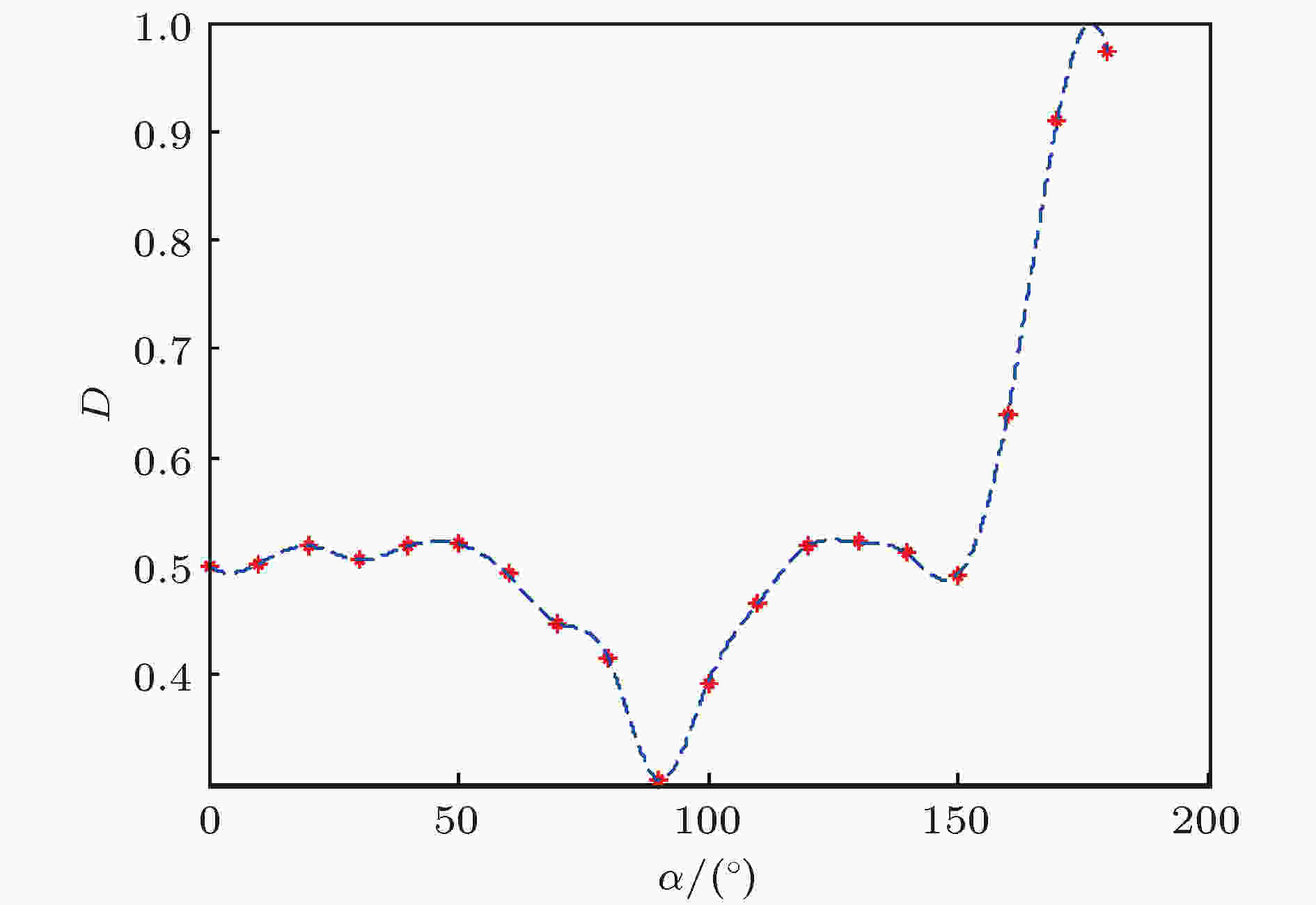图 13 圆形通孔缺陷的散射系数
Figure13. Scattering coefficient of the circular through hole defect

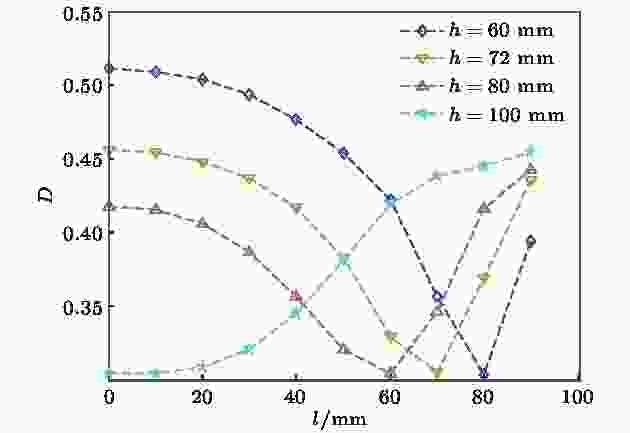图 14 不同缺陷位置下的散射系数
Figure14. Scattering coefficients at different defect locations.

若忽略不同方向缺陷散射性能的差异, 根据表1列出的缺陷位置和(3)式, 可以计算出不同位置缺陷对应的$\Delta A$值, 图15给出了其归一化后数值随缺陷位置的变化规律. 可以看出, 随着缺陷与对称轴(纵轴)距离的增加, 反转路径差信号幅值整体呈增加趋势, 但当距离大于80 mm后, 呈递减变化.
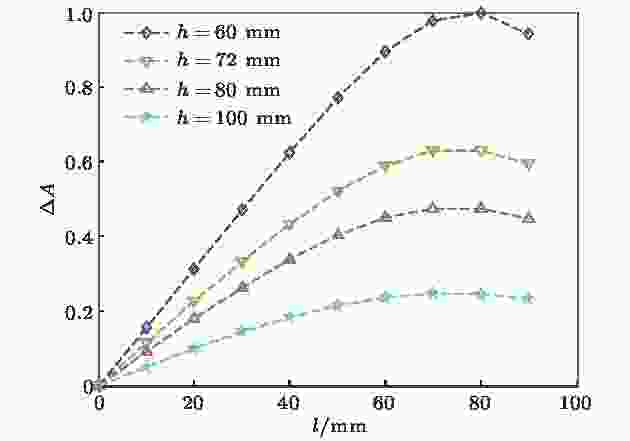图 15 不同缺陷位置下的$\Delta A$值
Figure15. Values of $\Delta A$ at different defect locations.

综上可知, 图14实际上是缺陷与两个传感器夹角变化导致的其散射系数性能的变化规律, 图15是缺陷与两个传感器距离变化(忽略了不同方向的散射性能的差异)导致的反转路径差信号的变化规律. 将二者相结合, 可以很好地解释图12所示的缺陷与两传感器夹角及路径差对反转路径差信号幅值的变化规律.
需要特别说明的是, 当缺陷位置接近对称轴(纵轴)时, 因传播方向变化引起的散射系数的数值较大, 而因距离差变化引起的传播路径差信号的幅值较小, 且二者随缺陷与对称轴之间距离的增加呈相反变化趋势(距离小于50 mm时), 而图12则反映了二者对传播路径差信号幅值的综合影响; 此外, 当缺陷与两传感器夹角α接近90°时, 其散射系数取极小值, 使得对应位置的反转路径差信号也出现极小值.
综上所述, 反转路径激励下两接收信号存在差异的前提条件是两传感器关于缺陷呈非对称分布, 反转路径差信号幅值受缺陷与两传感器间的夹角及传播距离差综合影响.

本节通过有限元仿真和检测实验, 验证基于反转路径差信号的稀疏阵列兰姆波成像方法对板结构缺陷检测的有效性.
2

-->

4.1.仿真数据分析

基于PZFlex有限元仿真软件, 建立板结构稀疏阵列兰姆波检测仿真模型, 如图16所示. 其中, 待检测构件为尺寸500 mm × 500 mm × 1 mm的铝板, 板上布置有4个压电传感器, P处有一通透型缺陷, 激励信号与3.1节相同. 利用反转激励下数值仿真得到的数据, 研究基于反转路径差信号成像方法对于板中不同位置的两类通透型缺陷(圆孔、矩形)检测的有效性, 并分析板边界回波对成像方法的影响; 同时, 作为对比, 也进行了基于基线相减的椭圆成像数值仿真研究.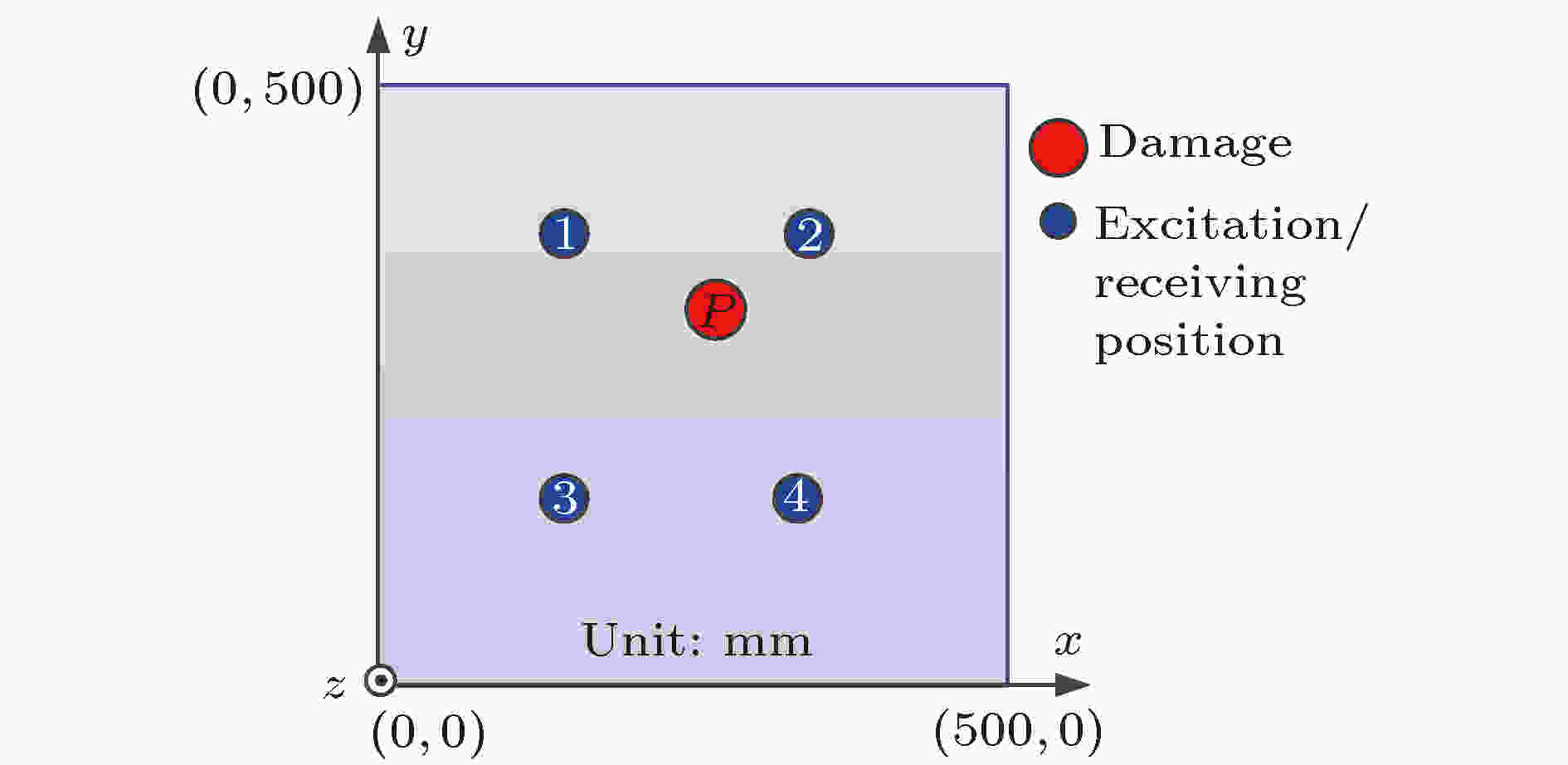
图 16 板结构稀疏阵列兰姆波检测仿真模型
Figure16. Simulation model of lamb waves detection for sparse array of plate structure.

3 -->

4.1.1.不同缺陷成像结果

针对圆形和矩形两类通透性缺陷检测, 表2和表3分别列出了数值仿真模型中传感器及缺陷的位置. 数值仿真中, 缺陷的几何尺寸固定, 圆孔缺陷的直径为8 mm, 矩形缺陷尺寸为8 mm × 4 mm.

序号	传感器1	传感器2	传感器3	传感器4	缺陷P位置	定位结果	定位误差
1 (基于参考信号)	(150, 350)	(350, 350)	(150, 150)	(350, 150)	(280, 280)	(284, 281)	4.1
2	(150, 350)	(350, 350)	(150, 150)	(350, 150)	(280, 280)	(285, 285)	7.1
3	(150, 340)	(350, 340)	(150, 150)	(350, 150)	(240, 280)	(239, 282)	2.2
4	(170, 350)	(350, 335)	(140, 150)	(345, 160)	(240, 280)	(239, 281)	1.4

表2圆形缺陷检测时仿真参数及定位结果(单位: mm)
Table2.Simulation parameters and positioning results for circular defect detection (unit: mm).

序号	传感器1	传感器2	传感器3	传感器4	缺陷P位置	定位结果	定位误差
1	(150, 340)	(350, 340)	(150, 150)	(350, 150)	(240, 280)	(239, 279)	1.4
2	(170, 350)	(350, 335)	(140, 150)	(345, 160)	(240, 280)	(241, 279)	1.4

表3矩形缺陷检测时仿真参数及定位结果(单位: mm)
Table3.Simulation parameters and positioning results for rectangular defect detection (unit: mm).

基于数值仿真结果, 计算各相邻传感器对的反转路径差信号$\Delta {s_{ij}}$, 按照(4)式得到的两种缺陷成像结果分别如图17和图18所示. 表2和表3同时列出了成像结果的定位误差. 本文所采用定位误差的定义为
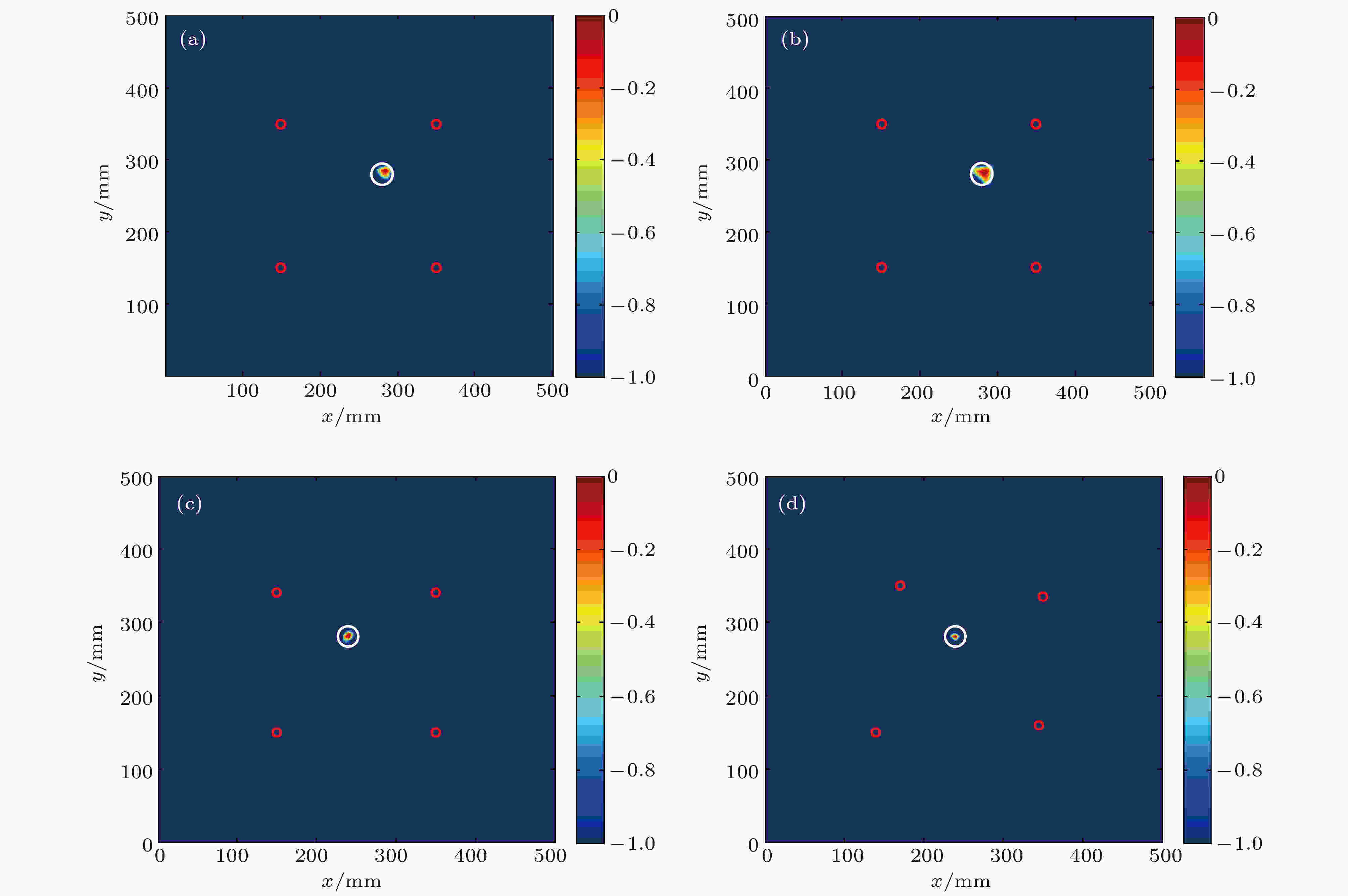图 17 圆形通孔缺陷成像结果　(a) 序号1 (基于参考信号); (b) 序号2; (c) 序号3; (d) 序号4
Figure17. Imaging results of circular through hole defects: (a) Number 1 (based on reference signal); (b) number 2; (c) number 3; (d) number 4.

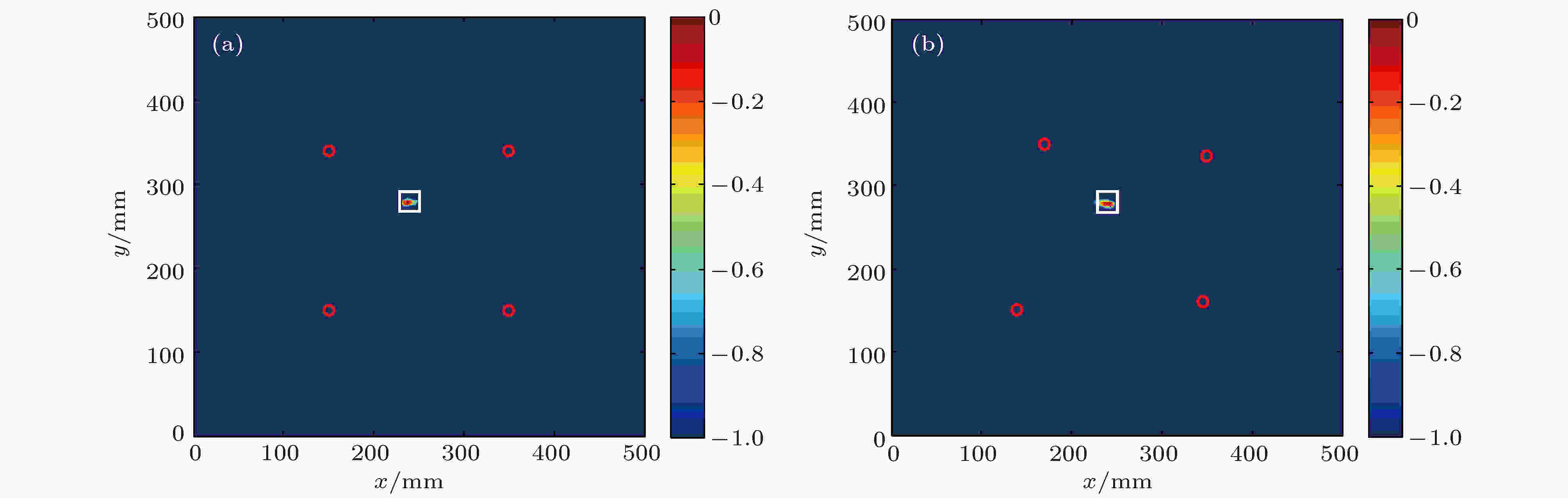图 18 矩形缺陷成像结果　(a) 序号; (b) 序号2
Figure18. Imaging results of rectangular defect: (a) Number 1; (b) number 2.

$\delta =\sqrt {{{({x_p} - {x_r})}^2} + {{({y_p} - {y_r})}^2}} , $

其中, $({x_p}, {y_p})$为缺陷中心位置坐标; $({x_r}, {y_r})$为成像结果中幅值最大点对应位置坐标. 虽然反转路径差信号来自于兰姆波在缺陷边缘处的反射及散射, 但由于缺陷位于稀疏阵列所组成多边形的内部, 认为兰姆波在缺陷四周均会发生反射和散射, 并被周围的稀疏阵列所接收. 同时, 鉴于本文尚未考虑缺陷尺寸的定量化, 因此, 缺陷定位误差表达式中忽略了缺陷尺寸对其定位误差的影响.
图17(a)给出了与本文提出的成像方法做对比的基于参考信号的成像结果. 可以看出, 基于反转路径差信号的兰姆波成像方法可以很好地实现板结构中圆形和矩形通透缺陷检测, 定位准确. 与传统成像方法相比, 本文提出的成像方法的成像分辨率更高, 定位误差较小, 且均小于实际缺陷的尺寸. 特别需要指出的是, 不同条件下缺陷成像的高信噪比说明, 基于反转路径差的兰姆波成像方法可以很好地消除直达波和边界回波的影响.
需要说明的是, 对于各对激励接收传感器, 布置在板上的其他传感器也可以被视为缺陷, 各传感器的反转路径差信号中也包含超声波与这些传感器相互作用产生的散射波, 会对反转路径差信号中缺陷散射波的分析带来不利的影响. 为尽量减小其他传感器产生的散射波对缺陷波的影响, 本文成像中仅采用相邻传感器对间的差信号进行延时叠加成像.
3 -->

4.1.2.边界回波对缺陷成像的影响

为了进一步说明本文提出的成像方法不受边界回波的影响, 将稀疏传感器阵列的布置位置靠近板边缘, 使得部分检测信号中的缺陷反射回波与边界反射回波重叠在一起. 表5列出了数值仿真中4个传感器及缺陷的位置. 图19给出了两组传感器对接收到的信号波形和反转路径差信号及其对成像的贡献. 可以看出, 两组传感器接收信号中缺陷回波与板边界回波存在叠加, 且边界回波幅值明显大于缺陷散射波幅值. 但通过将反转激励下接收信号做相减后, 得到的反转路径差信号中边界回波被极大地去除, 而保留下了缺陷散射波信息. 这也可以从反转路径差信号对成像的贡献中得到体现. 图20给出了基于反转路径差信号的兰姆波成像结果, 可以看出, 这种情况下同样可以实现缺陷定位, 不受边界回波影响, 且成像分辨率高.

序号	传感器1	传感器2	传感器3	传感器4	缺陷位置	定位结果	定位误差
1	(140, 370)	(380, 3355)	(130, 140)	(360, 150)	(240, 280)	(240, 284)	4

表4考虑边界影响时仿真参数及定位结果(单位: mm)
Table4.Simulation parameters and positioning results when considering boundary effects (unit: mm).

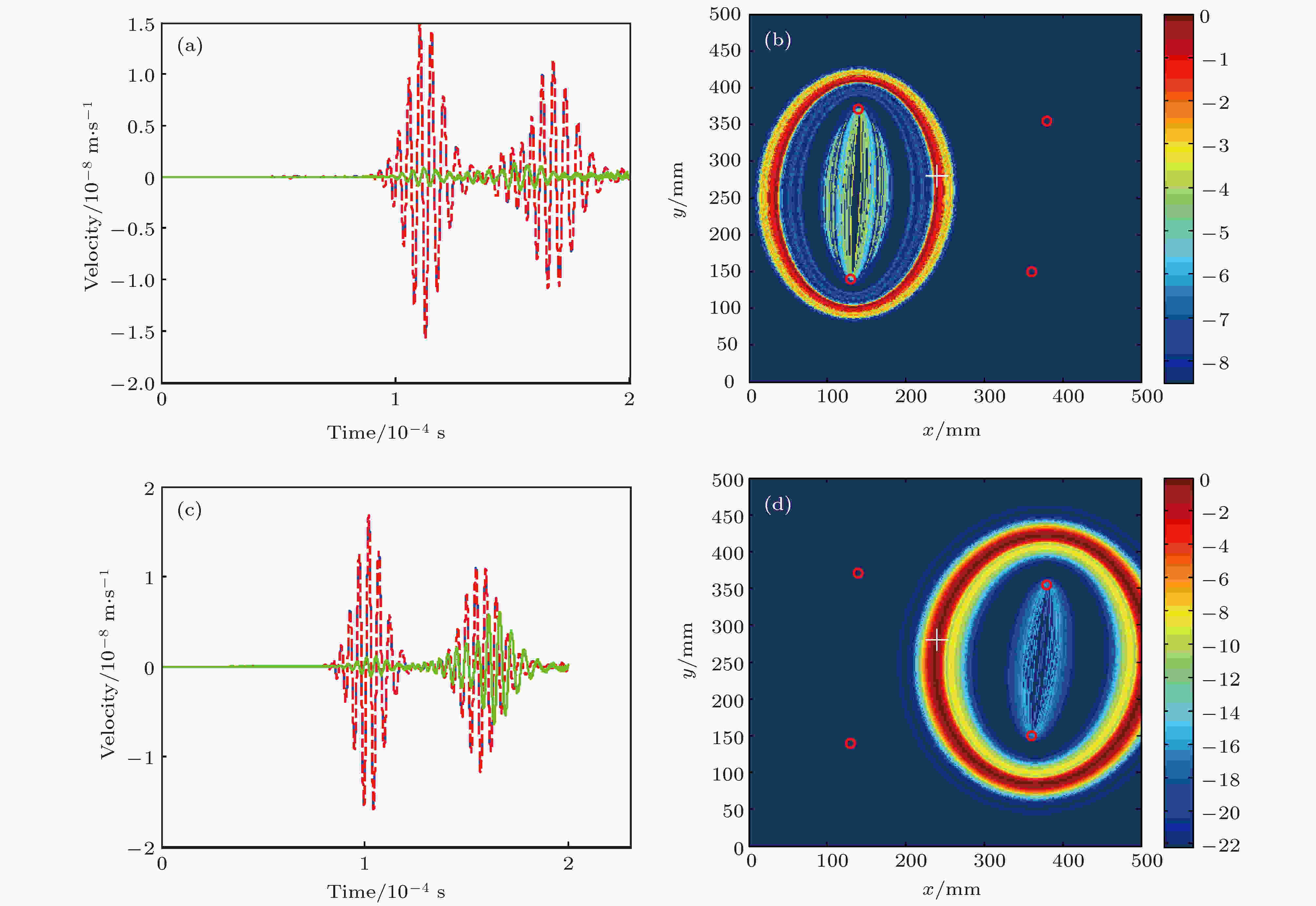图 19 典型传感器对的反转路径差信号及其对成像的贡献　(a) 1号和3号传感器对的反转路径差信号; (b) 1号和3号传感器对的反转路径差信号对成像的贡献; (c) 2号和4号传感器对的反转路径差信号; (d) 2号和4号传感器对的反转路径差信号对成像的贡献
Figure19. Inverted path delta signal of a typical sensor pairs and its contribution to imaging: (a) Inverted path delta signal of sensor pairs of number1 and number 3; (b) contribution to imaging of inverted path delta signal of sensor pairs of number1 and number 3; (c) inverted path delta signal of sensor pairs of number 2 and number 4; (d)contribution to imaging of inverted path delta signal of sensor pairs of number 2 and number 4.

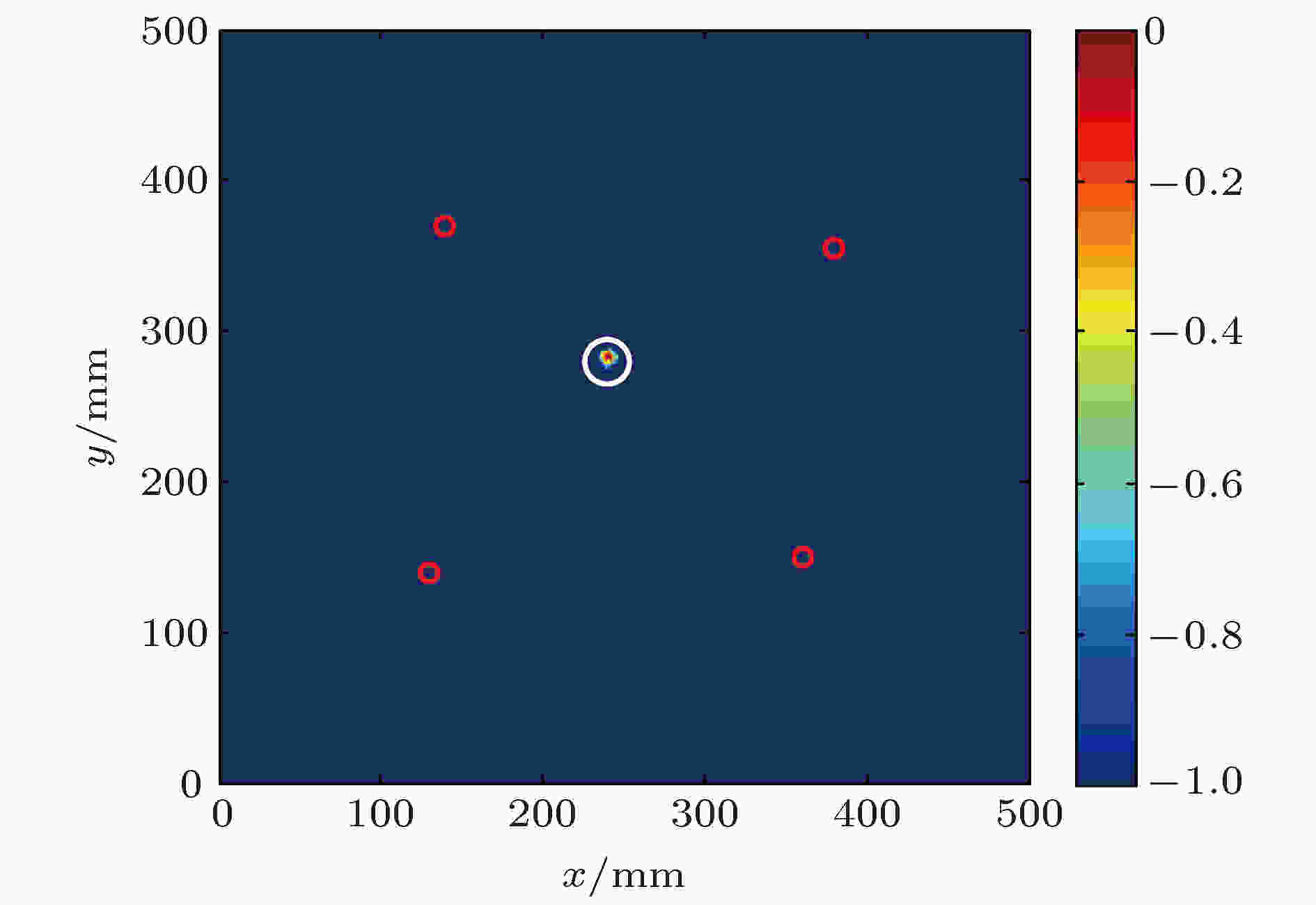图 20 基于反转路径差信号的成像结果
Figure20. Imaging results based on the inverted path delta signal.

2 -->

4.2.试验数据分析

本部分通过检测试验, 验证提出的成像方法对于板结构中缺陷检测的有效性. 图21给出了检测试验系统图. 检测系统主要包括任意函数发生器、电压放大器、示波器、待测铝板试件以及稀疏传感器阵列. 待检测板结构为800 mm × 800 mm × 1 mm的铝板, 在板上P处有一个直径8 mm的圆形通孔缺陷. 板上稀疏布置有4—6个压电片, 其尺寸为Φ8 mm × 1 mm, 该传感器为长度伸缩型的压电陶瓷, 激励出的兰姆波模态主要为S0模态, 因此在实验中只考虑了S0模态的兰姆波. 缺陷位置为(350 mm, 370 mm), 根据所用尺寸压电片的压电性能, 激励信号选择中心频率270 kHz汉宁窗调制的5周期单音频信号, 激励电压为100 Vpp (Vpp为峰峰值电压), 采样频率为50 MHz. 分别将相邻两个压电片构成传感器对, 进行反转激励兰姆波检测试验. 对每对相邻传感器得到的反转路径信号相减, 将得到的反转路径差信号按照(4)式进行处理, 可以计算出整个板结构散射声场的强度.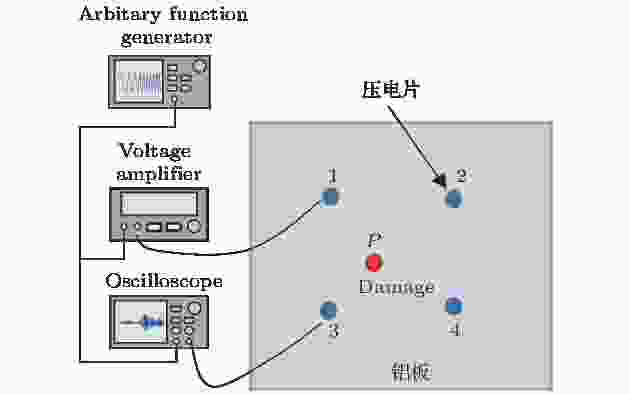
图 21 实验系统示意图
Figure21. Schematic diagram of the experimental system.

反转激励下某对传感器的接收信号波形及放大后的反转路径差信号波形如图22所示, 可以看出, 在反转路径差信号中, 直达波和边界回波被大大减弱, 而缺陷散射波则被凸显出来. 图23给出了基于反转路径差的兰姆波成像结果, 可以看出该方法的实验验证可以实现缺陷的检测和定位, 定位误差分别为19.8 mm和31.3 mm.
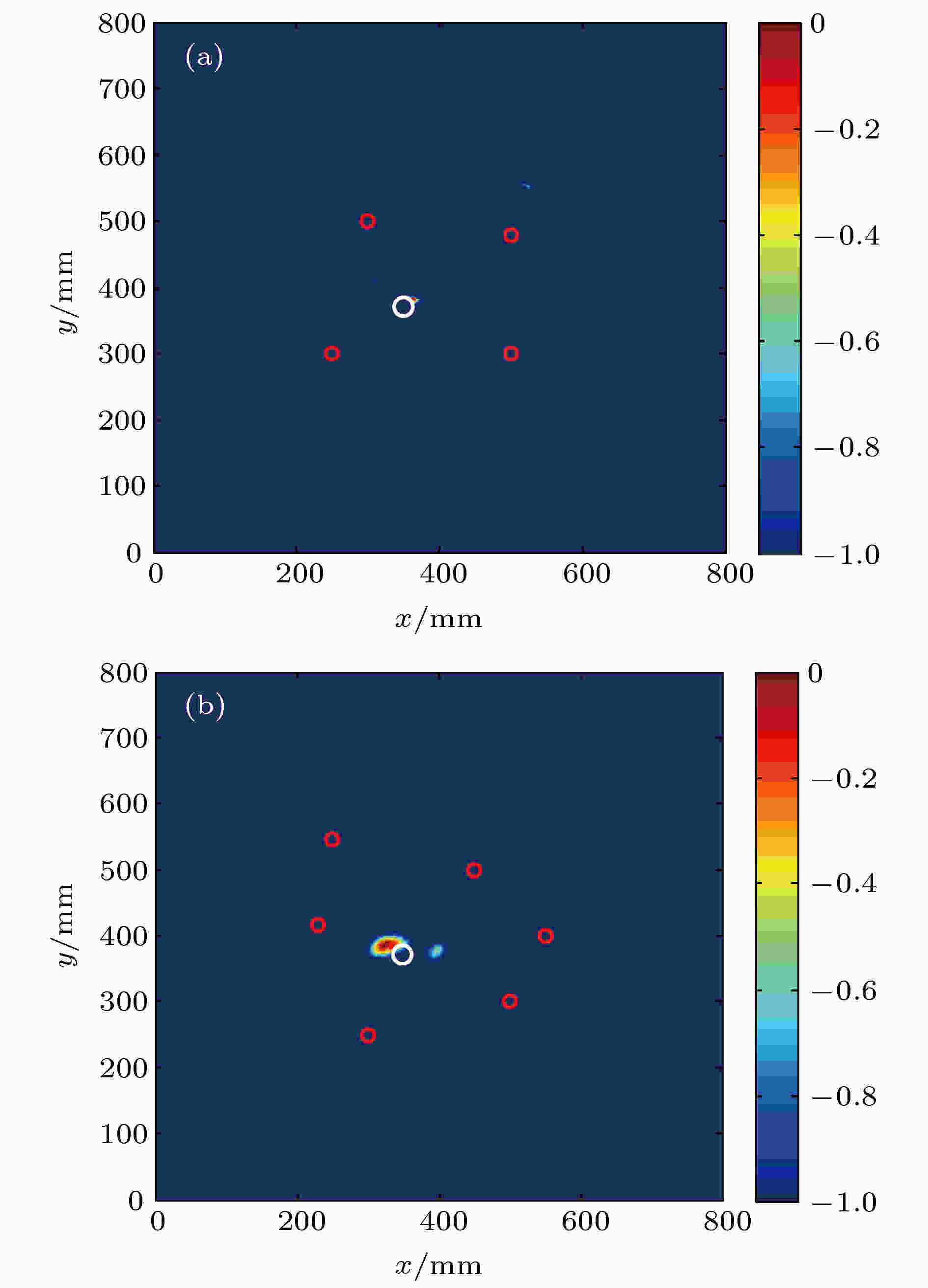图 23 实验成像结果　(a) 4个传感器; (b) 6个传感器
Figure23. Imaging results of the experiment: (a) Four sensors; (b) six sensors.

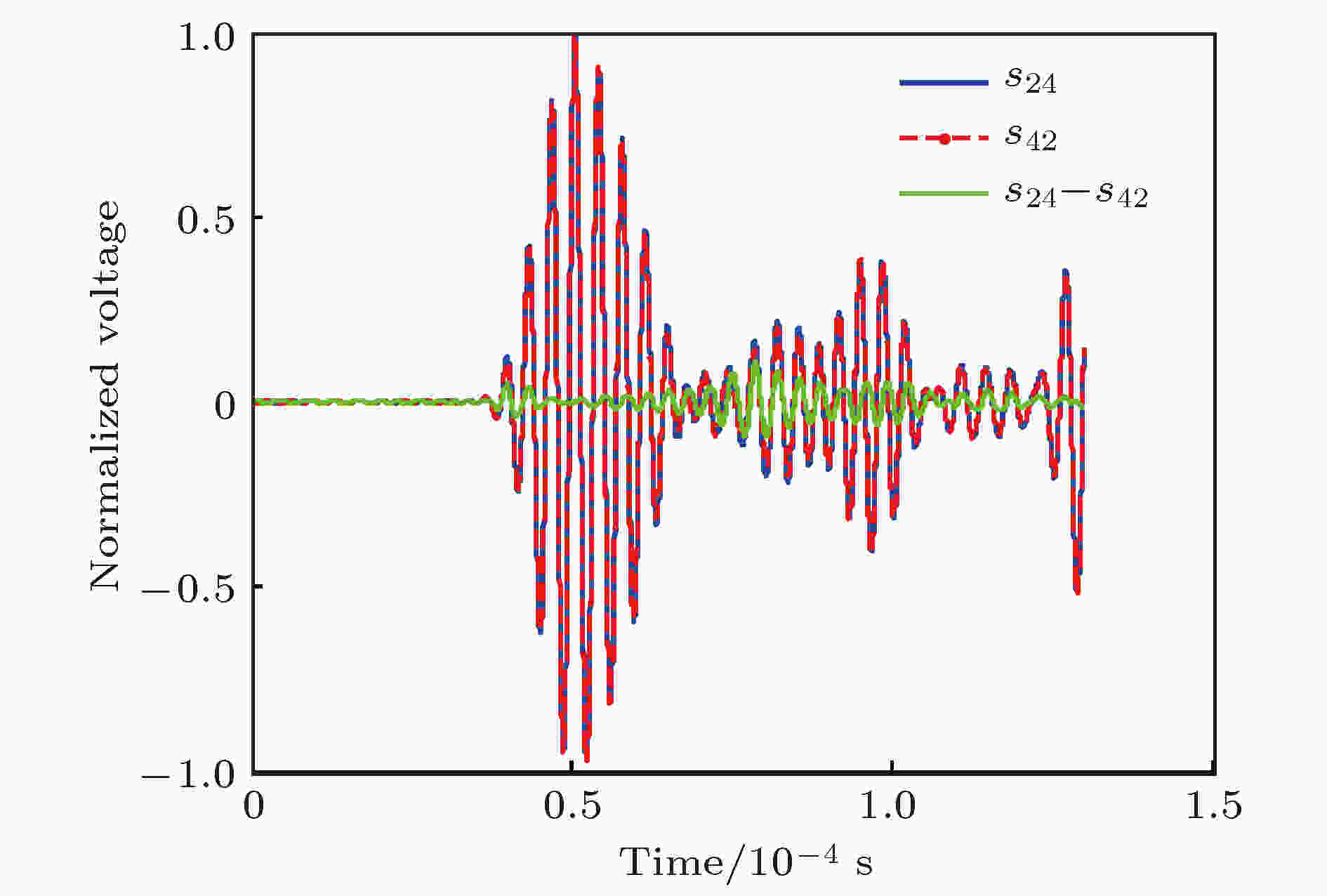图 22 2号和4号传感器对的接收信号及差信号
Figure22. Receiving signals and delta signal for sensor pairs 2 and 4.

本文提出了一种基于反转路径差信号的兰姆波成像方法, 用于板中通透型缺陷的检测, 得到以下结论:
1)反转路径激励下两接收信号存在差异的前提条件是, 两传感器关于缺陷呈非对称分布, 反转路径差信号幅值受缺陷与两传感器间的夹角及传播距离差的综合影响;
2)基于反转路径差信号的兰姆波成像方法可以消除直达波和边界回波的影响, 实现板结构中缺陷检测及定位, 且成像分辨率高.
本文提出的成像方法的一个前提假设是, 每对传感器的激励接收性能具有很好的一致性. 在实际兰姆波检测试验中, 由于传感器自身性能、传感器与被测结构间的耦合不可避免地存在一定的不一致性, 使得各传感器对的激励接收性能不可避免地存在一定的差异性, 同时环境噪声和系统噪声也会干扰接收信号, 使得成像结果受到一定的影响. 后续工作将进一步分析并减弱这些因素对成像结果的影响, 提高成像方法的可靠性和鲁棒性.