摘要: 为了研究高斯光束在湍流等离子体鞘套中的传输特性, 根据广义惠更斯-菲涅耳原理, 采用基于快速傅里叶变换的功率谱反演法, 用多随机相位屏来模拟湍流带来的影响. 根据超声速飞行器绕流等离子体流场厚度在厘米级别的特点, 光束在两个相位屏之间的传输过程中采用菲涅耳衍射积分的两次快速傅里叶变换算法(double fast Fourier transform algorithm), 利用多随机相位屏模拟等离子体鞘套湍流对光束传输产生的影响, 解决了多随机相位屏模拟湍流研究中的超短距离传输问题. 当飞行高度为45 km, 飞行速度为18马赫时, 通过对超声速飞行器绕流等离子体流场的统计分析, 发现在此飞行条件下折射率起伏方差的强度范围10
–11 —10
–14 . 对高斯光束在湍流等离子体流场中的传输特性进行了数值仿真. 结果表明: 在等离子体鞘套湍流中折射率起伏强度、波长、传输距离等都是影响高斯光束质量的重要因素. 折射率方差越大, 传输距离越长, 光斑弥散越严重, 光强起伏越大, 光强减弱也越明显. 光束的波长越长, 高斯光束抑制湍流的能力越强, 光斑弥散程度越小, 光强起伏也越小.
关键词: 光传输 /
随机介质 /
随机相位屏 English Abstract Analysis of propagation characteristics of Gaussian beams in turbulent plasma sheaths Lü Chun-Jing 1 ,Han Yi-Ping 2 1.School of Telecommunitions Engineering, Xidian University, Xi’an 710071, China Fund Project: Projiect supported by the National Natural Science Foundation of China (Grant No. 61431010).Received Date: 10 December 2018Accepted Date: 10 February 2019Available Online: 01 May 2019Published Online: 05 May 2019Abstract: In this paper, the characteristics of Gaussian beam propagation through turbulent plasma sheath are studied. According to the generalized Huygens-Fresnel principle, the random phase screen is generated by power spectrum inversion method based on the fast Fourier transform. The random phase screen is used to simulate turbulence effect. The thickness of the plasma sheath is of about centimeter order of magnitude. Compared with the single fast Fourier transform algorithm, the double fast Fourier transform algorithm is not prone to under-sampling and can obtain good image results, even if the diffraction distance is 1 mm. Therefore, double fast Fourier transform algorithm is used for investigating the beam propagation between two phase screens. The turbulence effect of the plasma sheath surrounding a hypersonic vehicle is simulated by the multi-random phase screens. When the flight altitude is 45 km and the flight speed is 18 Mach, the intensity of refractive index fluctuation variance ranges from ${10}^{ - 11} $ to $ {10}^{ - 14} $ indicated by analyzing the plasma flow field around the hypersonic vehicle. The characteristics of the Gaussian beam propagation through the turbulent plasma are numerically simulated. The results show that the refractive index fluctuation, wavelength and transmission distance are important factors affecting the Gaussian beam quality. The larger the refractive index variance, the more severe the spot dispersion and the more obvious the light intensity fluctuation. As wavelength is longer, the ability of the Gaussian beam to resist turbulence becomes stronger and the dispersion of the light spot and the intensity fluctuation are smaller. The beam distortion and the spot dispersion become more severe as the transmission distance is longer.Keywords: light propagation /random media /random phase screen 全文HTML --> --> --> 1.引 言 当飞行器以高超声速在大气中飞行时, 其动能会迅速转化为大量的热能导致飞行器周围的空气产生离解和电离, 最终形成等离子体包覆的流场[1 -4 ] . 等离子体的存在对于电磁波信号有很大的衰减作用, 甚至导致信号中断形成“黑障效应”[5 ,6 ] . 目前已经提出几种有希望解决这一难题的几种方法[7 -11 ] , 例如通过提高电磁波频率来减小信号衰减, 或者在鞘套层中加入亲电材料, 这两种方法的目的都是为了提高电磁波频率与等离子体频率的比值. 同时有研究表明等离子体鞘套层是不稳定的[12 ,13 ] , 所以湍流也是影响“黑障效应”的重要因素. 近些年, 国内外也早对湍流等离子体流场进行了较多的研究, 例如Shi等[14 ] 为了研究等离子体鞘套在无线信道上的动态效应, 分析飞行条件变化(例如攻角、小尺度湍流)对介质传输性能的影响, 提出了一种新的自适应马尔可夫信道建模方法, 利用该方法建立的信道的一阶统计特性与无线电波的可变衰减具有良好的一致性, 而且该方法具有良好的自适应能力. He等[15 ] 从通信角度采用透射矩阵法研究了再入等离子体鞘套对电磁波传播的动态影响, 所建立的模型中包含空间湍流和等离子体电子密度的变化, 并对由等离子体的非线性特性引起的幅度和相位变化进行了数值仿真, 发现幅度变化服从对数正态分布, 相位变化服从瑞利分布. Yao等[16 ] 针对等离子体流场的不稳定性, 首先在时-空-频域揭示了电子密度的波动的规律, 并基于这些规律提出了时变电子密度分层模型, 利用Monte Carlo准静态电磁波数值方法计算了动态等离子鞘套层对Ka波段电磁波的影响. Lin和Sproul[17 ] 重点研究了电子密度波动对电磁波传播的影响, 利用Navier-Stokes模型、三维抛物化Navier-Stokes模型、耦合边界层和非黏性流动代码估算了截头锥体的电子密度的均值和方差. Li等[18 ] 基于在高超声速湍流实验中测量的分维数, 建立了分形模型和等离子鞘套湍流功率谱, 为研究等离子体鞘套湍流中的光束传输特性提供了重要参考.[19 -21 ] , 但是这种菲涅耳衍射积分的S-FFT算法适用于长距离传输, 例如大气湍流[22 -24 ] 和海洋湍流[25 -27 ] . 飞行器周围等离子体包覆的流场的厚度很小, 在厘米或毫米级别[28 ,29 ] . 对于厘米和毫米级别的短距离传输问题, S-FFT算法会出现欠采样的问题, 最终将会导致信号失真. 针对等离子体鞘套厚度较小这一特点, 采用菲涅耳衍射积分的两次快速傅里叶变换(double fast Fourier transform, D-FFT)算法研究光束在两个相位屏之间的传输过程. 本文第2部分首先在高度为45 km、飞行速度为18马赫和0攻角的飞行条件, 数值模拟了钝头体飞行目标的高超音速等离子体鞘套湍流流场. 然后利用Gladstone-Dale公式根据等离子体密度计算折射率, 并对折射率的方差进行了估算; 第3部分对比研究了菲涅耳衍射积分的D-FFT算法和S-FFT算法, 说明D-FFT算法在厘米级别的短距离传输问题中的显著优势, 并利用多随机相位屏模拟了高斯光束在等离子体鞘套湍流中的传输特性.2.高超声速钝头体等离子体鞘套湍流流场计算 22.1.钝头体飞行目标绕流流场数值模拟 2.1.钝头体飞行目标绕流流场数值模拟 利用三维Navier-Stokes (N-S)方程和湍流两方程$k $ -$\varepsilon $ 模型数值模拟湍流流场. 在笛卡尔坐标系中, 考虑1989年提出的双温热力学模型[30 ] 和7组分空气化学反应模型(七组分化学反应模型如表1 所列), 并对三维N-S方程进行适当封闭, 相应模型如下[31 -33 ] :No. Reaction 1 ${\rm {N_2} + M \rightleftharpoons N + N + M}$ 2 ${\rm {O_2} + M \rightleftharpoons O + O + M}$ 3 ${\rm NO + M \rightleftharpoons N + O + M}$ 4 ${\rm O + {N_2} \rightleftharpoons NO + N}$ 5 ${\rm NO + O \rightleftharpoons {O_2} + N}$ 6 ${\rm N + O \rightleftharpoons N{O^ + } + e}$
表1 化学反应模型中的方程Table1. Reactions considered in chemistry modelQ S $x$ 方向为例, E ${{E}}_v $ 分别是对流通量矢量和黏性通量矢量; $\kappa $ 和$\kappa_ t$ 分别是热传导系数和湍流热传导系数; $u$ , $v$ 和$w$ 分别是3个方向的瞬时速度分量; $k$ 是湍动能; ${\dot \omega }_{{\rm{int}}} $ 是振动源项, ${\dot \omega }_i $ 是每个组分所占的质量分数; $\tau _{ij}\; (ij = x,y,z)$ 为各个方向的剪应力张量, 需要利用湍流模型进行封闭[34 ] ; $e _{v,i} $ ,$h _i $ 和$\rho _i $ 分别是每一种组分的振动能量、显焓和密度, 下标$i$ 代表每一种组分$(i = 1,\;2,\;3,\cdots, 7)$ ; $\rho $ , $p$ 和$U _{\rm{a}} $ 分别为混合物的密度、压强和平均速度; $E _{{\rm{int}}} $ , $E _t $ 和$T _{{\rm{int}}} $ 分别是混合物的内部能量、湍流内部能量和内部温度.[35 ] 求解N-S方程, 其中时间推进采用LU-SGS (lower-upper symmetric Gauss-Seidel relaxation)方法[36 ] . 值得注意的是, 文中采用的湍流$k $ -$\varepsilon $ 模型是利用不同的方程来控制湍流能量传输并适合高雷诺数环境的两方程模型, 其中控制湍动能$k$ 和湍动能耗散率$\varepsilon $ 的两方程分别为${\mu} $ , ${\mu}_t $ , ${\mu}_i $ 分别是等离子体的动力学黏性系数、湍流黏性系数和质量平均速度; 常数$C _{\varepsilon _1 } = $ $ 1.44,\;C _{\varepsilon _2 } = 1.92,\;\sigma _k = 1.0,\;\sigma _\varepsilon = 1.3$ ; $P$ 被定义为 $P = {\mu}_t \left( {\dfrac{{\partial u _i }}{{\partial x _j }} + \dfrac{{\partial u _j }}{{\partial x _i }} - \dfrac{2}{3}\dfrac{{\partial u _m }}{{\partial x _m }}\delta _{ij} } \right)\dfrac{{\partial u _i }}{{\partial x _j }} - \dfrac{2}{3}k\dfrac{{\partial u _m }}{{\partial x _m }},$ $u _i $ , $u _j $ 和$u _m $ 为张量表示法中时均速度, $\delta _{ij} $ 是克罗内克尔符(当$i = j$ 时, $\delta _{ij} = 1$ , 否则$\delta _{ij} = 0$ ).2.2.对流场数据做统计分析, 估算等离子体折射率起伏方差 -->2.2.对流场数据做统计分析, 估算等离子体折射率起伏方差 基于Gladstone-Dale公式[37 ] , 根据2.1节中计算的等离子体密度求解其折射率, Gladstone-Dale公式为$\lambda $ 为光波波长, $G(\lambda )$ 为Gladstone-Dale常数, 被定义为图1(a) 和图1(b) 分别为飞行目标的区域划分图和五个区域的折射率统计方差$\left\langle {n_1^2 } \right\rangle $ 图. 图2(a) 和图2(b) 分别为飞行目标头部和侧部选取的一条传输路径, 头部路径三维坐标范围分别为: x = [0.0047 m, 0.0170 m], y = [–0.0581 m, –0.0475 m], z = [0.0627 m, 0.0512 m], 侧部路径三维坐标范围分别为: x = [0.0674 m, 0.0788 m], y = [–0.1555 m,–0.1225 m], z = [0.0628 m, 0.0527 m]. 对两条传输路径上的折射率进行方差统计, 统计方法为: 以传输路径中的每个三维流场坐标点为中心, 以超声速湍流中典型的相关长度[38 ] —${L / {10}}$ 为半径($L$ 为等离子体鞘套的厚度)建立球模型, 对球内所有数据进行统计, 计算每个网格点处的折射率方差, 流场边界值采用外推法求解. 通过对比图2(a) 和图2(b) 发现, 在接近飞行目标壁面时, 头部折射率方差较大, 比两侧的折射率方差要高出一个数量级, 这是因为等离子鞘套中的湍流状态还会受到激波、高温、高压等因素的影响, 在靠近头部的区域内温度、压强较高且起伏较大. 由图1 和图2 的计算结果显示, 在高度为45 km、飞行速度为18马赫和0攻角的飞行条件下, 飞行目标的绕流流场中折射率起伏方差的强度的为10–11 —10–14 .图 1 (a)五个区域; (b)五个区域的折射率方差$\left\langle { n_1^2 } \right\rangle $ Figure1. (a) Five regions; (b) refractive index variance $\left\langle {n_1^2 } \right\rangle $ in five regions.图 2 折射率方差$\left\langle {n_1^2 } \right\rangle $ (a)头部区域1; (b)侧部区域2Figure2. Refractive index variance $\left\langle {n_1^2 } \right\rangle $ in different regions: (a) Head area 1; (b) side area 2.3.湍流等离子体鞘套中的随机相位屏模拟 23.1.相邻两屏之间传输算法讨论及仿真实验验证 3.1.相邻两屏之间传输算法讨论及仿真实验验证 S-FFT算法和D-FFT算法都是从菲涅耳衍射公式出发, 但对于衍射距离$d$ 的要求不同. S-FFT算法主要适用于衍射距离较大的情况, 而D-FFT算法可适用于衍射距离较小的问题, 下面对两种算法进行理论分析和数值仿真, 说明选用D-FFT算法的原因.3.1.1.菲涅耳衍射积分的S-FFT算法 -->3.1.1.菲涅耳衍射积分的S-FFT算法 在傍轴近似情况下, 菲涅耳衍射积分可以表示为$\lambda $ 为光波波长, $k _\lambda = {{2{\text{π}}} / \lambda }$ 为波数, $d$ 是观察面到衍射屏的距离, ${\tilde U}_0 \left( {{x_0},{y_0}} \right)$ 和$\tilde U\left( {x,y} \right)$ 分别是光场在衍射面上和观察面上某一点的复振幅分布. 对(10 )式进行适当变换, 并根据傅里叶变换法则, 上式可改写为11 )式可知其空间频率为$ f_{\mu} = \dfrac{x}{{\lambda d}}, f_v = \dfrac{y}{{\lambda d}}$ , 即观察屏上不同的点$\left( {x,y} \right)$ 其实对应不同的空间频率(方向)的光. 又因为光传播方向与空间频率的关系为$f _{\mu} = {1 / {X = {{\cos \alpha } / \lambda }}}$ , 所以$f _{\mu} = {{\sin \left( {{\text{π}}/2 - \alpha } \right)} / {\lambda \approx {1 / {\lambda \cdot {{(x} / d}}}}})$ .$x$ 方向为例进行讨论说明, $y$ 方向的情况与之类似. 设衍射面在$x$ 方向上的宽度为$L _{x _0 } $ , 共有${N_x}$ 个抽样点, 则按照抽样定理, 在用FFT变换计算时得到的空间频率最高为${f}_{{{\mu} _{{\rm{max}}}}} = {{{N_x}} / {2{L_{x _0 }}}}$ , 空间频率为$f _{{{\mu} _{{\rm{max}}}}} $ 的这些衍射光对应的传播方向为$f _{{{\mu} _{{\rm{max}}}}} = {1 / X} = {{\cos {\alpha _{{\rm{max}}}}} / \lambda }$ . 这些衍射光出现在衍射观察屏上坐标的位置为$f _{{{\mu} _{{\rm{max}}}}} = {{\sin \left( {{\text{π}}/2 - \alpha } \right)} / \lambda } \approx {1 / \lambda } \cdot ({{{{{L_{x{\rm{max}}}}} / 2}} / d})$ , 即衍射屏上的最大坐标为${L_{x{\rm{max}}}} = {{{N_x}\lambda d} / {{L_{x0}}}}$ . 由此可见在使用S-FFT算法时, 衍射观察屏的大小不仅是波长的函数, 而且还是再现距离和抽样数的函数, 当$d$ 很小, 如果保持取样数不变, 则观察屏上的再现结果只是邻近光轴的很小区域, 所以该算法主要适用于衍射距离较大的情况.3.1.2.菲涅耳衍射积分D-FFT算法 -->3.1.2.菲涅耳衍射积分D-FFT算法 同S-FFT算法相类似, 在直角坐标系中, 傍轴近似下, 当衍射距离满足菲涅耳衍射条件时, 根据衍射积分表达式(10 )可以得到其脉冲响应:$\tilde H\left( {f _{\mu},f _v } \right)$ , 则菲涅耳积分可以分为两次傅里叶变换完成, 所以称其为D-FFT算法. 可以通过傅里叶变换的性质直接得到菲涅耳衍射传递函数$\tilde H\left( {f _{\mu},f _v } \right)$ 的解析表达式:$\tilde H\left( {f _{\mu},f _v } \right)$ 的解析表达式, 只需要将频域中$x$ 方向和$y$ 方向的频率$f _{\mu} $ 和$f _v $ 代入解析式, 就可以得到传递函数的数值. 假设实际问题是在宽度为${L_{x0}} \times {L_{y0}}$ 的空间采样, 并且有${N_x} \times {N_y}$ 个抽样点, 最高空间频率分别为$f _{{{\mu} _{{\rm{max}}}}} = {{{N_x}} / {2{L_{x0}}}},f _{{\nu _{{\rm{max}}}}} = {{{N_y}} / {2{L_{y0}}}}$ . 所以, $f _{\mu} $ 的取值范围从$ { - f}_{{{\mu} _{{\rm{max}}}}} $ 到$f _{{{\mu} _{{\rm{max}}}}} $ 取${N_x}$ 个点, 同样, $f _v $ 的取值范围从$ - f_{{\nu _{{\rm{max}}}}} $ 到$ f_{{\nu _{{\rm{max}}}}} $ 取${N_y}$ 个点.3.2.S-FFT算法和D-FFT算法的数值模拟结果的比较 -->3.2.S-FFT算法和D-FFT算法的数值模拟结果的比较 在衍射计算过程中, 应该特别注意欠采样的问题, 在保证抽样数和光束波长不变的情况下, 改变衍射距离$d$ , 比较S-FFT算法和D-FFT算法抑制欠采样发生的能力, 说明D-FFT算法在处理短距离衍射积分问题的优势.图3(a) 和图3(b) 分别为衍射距离为100 mm时利用S-FFT算法和D-FFT算法得到的衍射光强分布, 图3(c) 和图3(d) 分别为衍射距离为10 mm时利用S-FFT算法和D-FFT算法得到的衍射光强分布. 通过对比图3(a) 和图3(b) 发现: 当衍射距离为100 mm时, 利用S-FFT和D-FFT两种算法得到的衍射光强分布均未出现欠采样现象. 通过对比图3(c) 和图3(d) 可知: 随着衍射距离的减小, 采用S-FFT算法得到的衍射光强出现了明显的欠采样现象, 但是D-FFT算法未出现, 可见D-FFT算法的抗欠采样能力要明显高于S-FFT算法. 结果表明, D-FFT算法不惧怕计算衍射距离近的问题, 即使衍射距离$d$ = 1 mm时, 用D-FFT算法依然可以得到很好的结果. 超高音速飞行器周围形成的等离子体鞘套的厚度属于厘米数量级. 由此可见, 用FFT算法数值模拟光束在相邻两屏之间的传输过程时, 选用D-FFT算法更合适.图 3 在不同衍射距离下S-FFT和D-FFT两种算法的光强分布 (a) S-FFT, $d$ = 100 mm; (b) D-FFT, $d$ = 100 mm; (c) S-FFT, $d$ = 10 mm; (d) D-FFT, $d$ = 10 mmFigure3. Intensity distribution of S-FFT and D-FFT algorithm at different diffraction distances: (a) S-FFT, $d$ = 100 mm; (b) D-FFT, $d$ = 100 mm; (c) S-FFT, $d$ = 10 mm; (d) D-FFT, $d$ = 10 mm.$N \times N$ 复随机矩阵$H\left( {{k_x},{k_y}} \right)$ , 利用等离子体鞘套湍流功率谱[18 ] 对其进行滤波, 然后再进行傅里叶逆变换便可以得到等离子体鞘套湍流的随机相位屏$\varPhi \left( {{k_x},{k_y}} \right)$ . 等离子体鞘套湍流功率谱为$\langle n_1^2\rangle $ 为折射率方差, $L _0 $ 为湍流外尺度, ${k_x}$ 和${k_y}$ 分别为不同方向的频率. 由折射率频谱可得到相位频谱为$\varPhi \left( {{k_x},{k_y}} \right) = 2{\text{π}}{k^2}{\varPhi _n}\left( {{k_x},{k_y}} \right)$ , 则相位频谱的方差为${\sigma ^2}\left( {{k_x},{k_y}} \right) = {\left( {{{2{\text{π}}d} / {N{\Delta}x}}} \right)}^2 \varPhi \left( {{k_x},{k_y}} \right)$ , 其中$d$ 是每两个随机相位屏的间距, $N$ 为采样数, $\Delta x$ 是栅格间距. 通过傅里叶变化便可得到空域中的随机相位屏[39 ] : $\varPhi \left( {x,y} \right) = {\cal F}\left[ {H\left( {{k_x},{k_y}} \right)\sigma \left( {{k_x},{k_y}} \right)} \right]$ .图4 所示.图 4 多随机相位屏示意图Figure4. Schematic diagram of multi-random phase screen.3.3.等离子体鞘套湍流中影响高斯光束质量的因子分析 -->3.3.等离子体鞘套湍流中影响高斯光束质量的因子分析 图5 的传输参数为: 束腰半径$ \omega _0$ = 40 mm, 相位屏间隔$d$ = 0.013 m, 相位屏采样数为$1024 \;\times $ 1024. 分析折射率方差、波长和传输距离对高斯光束质量的影响.图 5 不同传输条件时的高斯光束光强数值仿真 (a) λ = 1.55 × 10–6 m, ω 0 = 40 mm, d = 13 mm; (b) ω 0 = 40 mm, d = 13 mm, $\langle n_1^2\rangle$ = 10–12 ; (c) λ = 1.55 × 10–6 m, ω 0 = 40 mm, $\langle n_1^2\rangle$ = 10–12 Figure5. Numerical simulation of intensity of Gaussian beam in different propagation conditions: (a) λ = 1.55 × 10–6 m, ω 0 = 40 mm, d = 13 mm; (b) ω 0 = 40 mm, d = 13 mm, $\langle n_1^2\rangle$ = 10–12 ; (c) λ = 1.55 × 10–6 m, ω 0 = 40 mm, $\langle n_1^2\rangle$ = 10–12 .图5(a) 是高斯光束在折射率起伏方差分别为$\langle n_1^2\rangle = {10^{ - 13}},\,{10^{ - 12}},\;{10^{ - 11}}$ 时通过10个随机相位屏后系统归一化的三维(3D)和二维(2D)光强数值仿真结果. 由图5(a) 可知, 在湍流折射率方差不断增大的过程中, 光斑分裂成形状不规则的若干小光斑, 光斑弥散程度加剧, 而且光强起伏逐渐增大, 强度逐渐减小.图5(b) 是高斯光束波长分别为$\lambda = 0.6328\; \times$ $ {10^{ - 6}},\; 1.05 \times {10^{ - 6}},\; 1.55 \times {10^{ - 6}}$ m时通过10个随机相位屏后系统归一化的3D和2D光强数值仿真结果. 通过对比分析可知, 随着波长的不断增加, 高斯光束抵抗湍流的能力逐渐增强, 具体表现在光斑弥散程度减小、光强起伏减弱上, 所以在等离子体鞘套通信系统中选用波长较长的激光光束作为信息载体比较好.图5(c) 是高斯光束沿z 轴传输时距离分别为6.5, 13, 19.5 cm, 即分别通过5, 10, 15个随机相位屏后系统归一化的3D和2D光强数值仿真结果. 结果反映出: 传输距离越大, 光斑弥散越严重, 光强起伏也越明显.4.结 论 首先利用菲涅耳衍射积分的D-FFT算法解决了湍流问题中的短距离传输问题, 然后利用多随机相位屏数值模拟了高斯光束在等离子体鞘套湍流中的传输特性. 研究表明折射率方差越大, 高斯光束的光斑弥散程度越大, 光强越弱, 光强起伏越明显; 随着波长的不断增加, 高斯光束抵抗湍流的能力逐渐增强, 所以在等离子体鞘套通信系统中选用波长较长的激光光束作为信息载体比较好; 传输距离越大, 光斑弥散越严重, 光强起伏也越明显. 综上所述, 高斯光束在等离子体鞘套湍流中的传输质量与外界因素折射率起伏方差、传输距离及自身因素波长、束腰半径等密切相关. 本文对研究激光在湍流等离子体鞘套中的传输问题具有一定的意义. 
















































 图 1 (a)五个区域; (b)五个区域的折射率方差
图 1 (a)五个区域; (b)五个区域的折射率方差

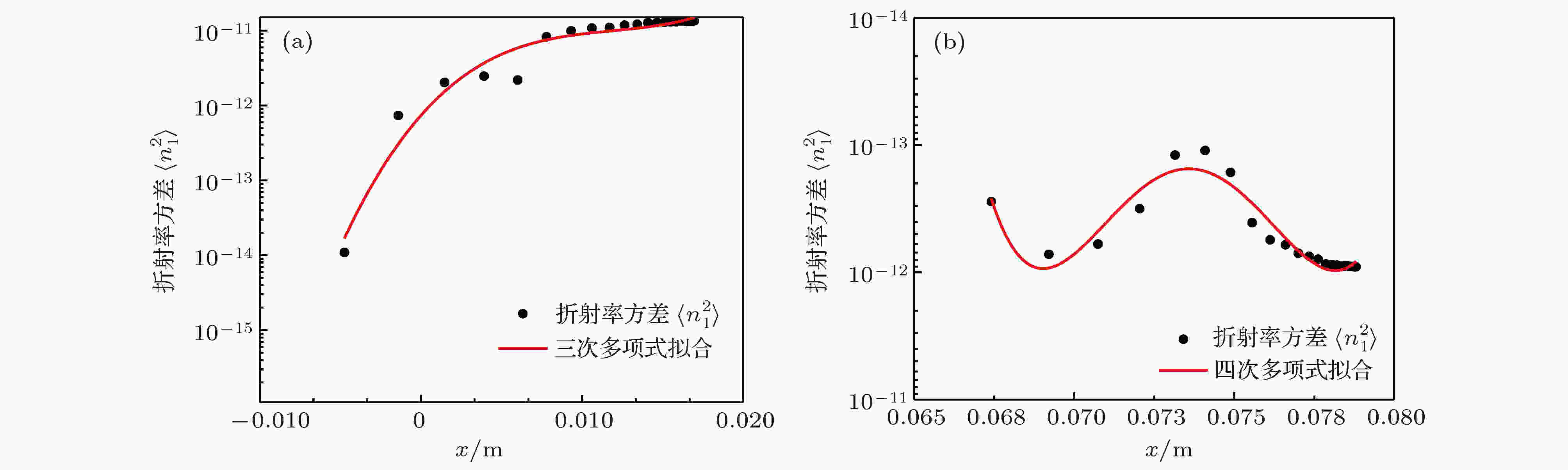 图 2 折射率方差
图 2 折射率方差


















































 图 3 在不同衍射距离下S-FFT和D-FFT两种算法的光强分布 (a) S-FFT,
图 3 在不同衍射距离下S-FFT和D-FFT两种算法的光强分布 (a) S-FFT, 












































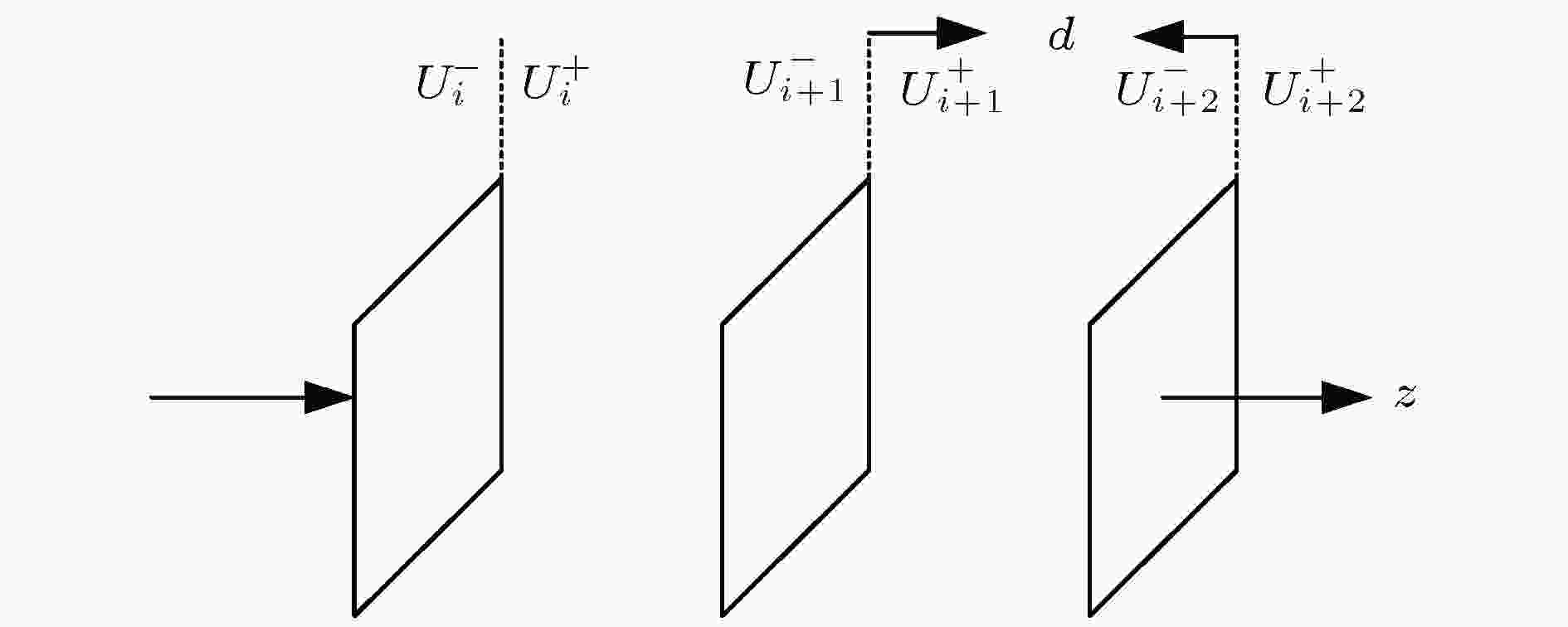 图 4 多随机相位屏示意图
图 4 多随机相位屏示意图


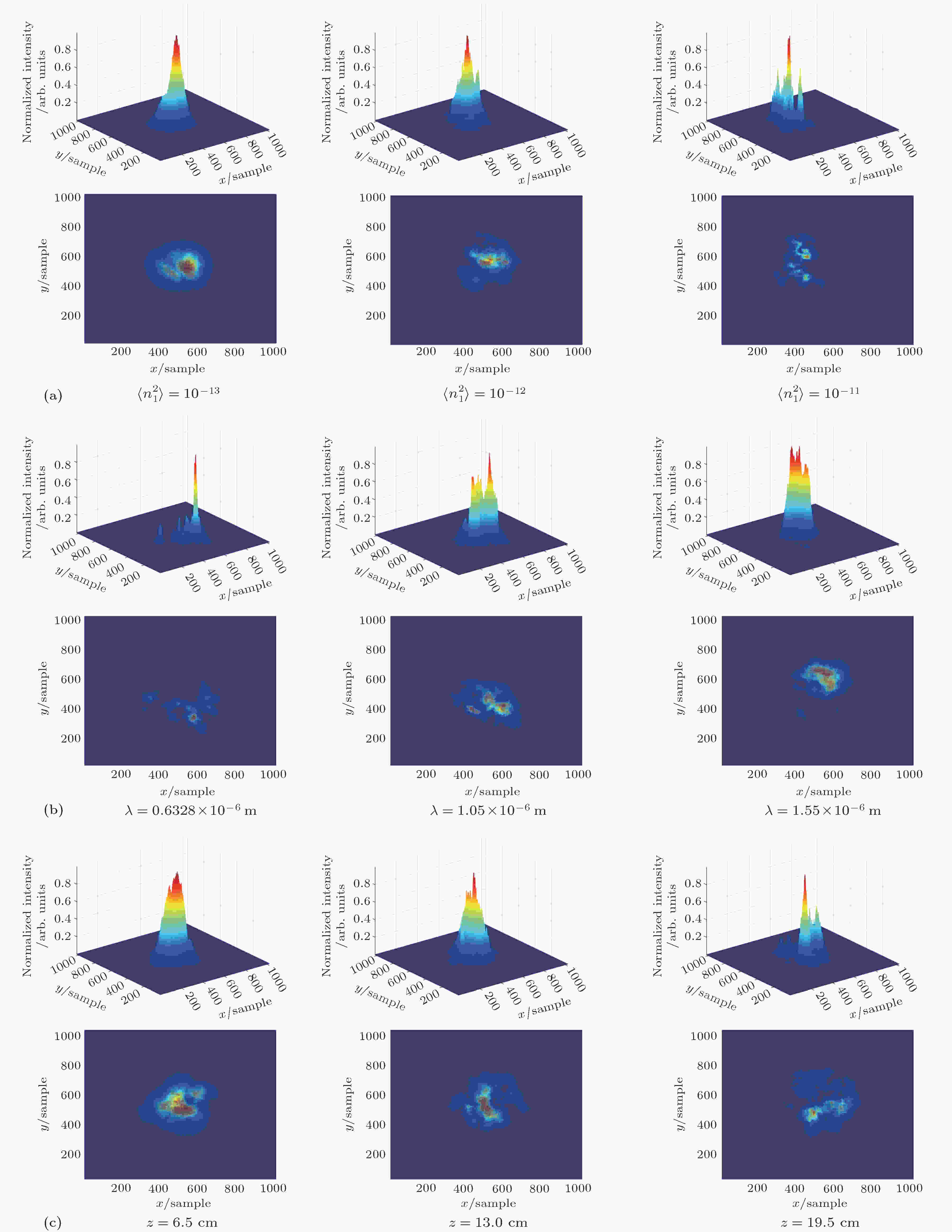 图 5 不同传输条件时的高斯光束光强数值仿真 (a) λ = 1.55 × 10–6 m, ω0 = 40 mm, d = 13 mm; (b) ω0 = 40 mm, d = 13 mm,
图 5 不同传输条件时的高斯光束光强数值仿真 (a) λ = 1.55 × 10–6 m, ω0 = 40 mm, d = 13 mm; (b) ω0 = 40 mm, d = 13 mm, 












