全文HTML
--> --> -->多激子效应通常是指吸收单个光子产生多个激子的过程[7]. 一般来讲, 半导体中的多激子效应效率低且阈值较高[8-10]. 相比之下, 最近在PbX(X = S, Se, Te)[11-14], CdSe[15,16], InAs[17,18], Si[19,20]量子点和碳纳米管[21,22]中发现的高效多激子效应具有较低阈值的光子能量. 其中, PbSe量子点在激发能量为7.8 Eg(带隙能量, 为量子点中的1S激子能量)时, 每个光子可以产生多达七个激子[23]. 如果能够将这些发现成功应用到太阳能电池上, 量子点的高效多激子效应将是一个革命性的发现, 因为它提供了改善基于量子点太阳能电池转换效率的新方法[24]以及设计基于多激子效应量子点材料的新思路[25,26].
然而, 到目前为止, 多激子效应的激子产生以及复合机制仍然晦暗不清、备受争议[27,28]. 很明显, 对量子点多激子效应的激子生成和复合动力学探究是不完善的.
本文以CdSeS合金结构量子点为研究对象. 首先, 利用双光束分光光度计得到其稳态吸收光谱, 发现510, 468和430 nm附近的稳态吸收峰, 分别对应1S3/2(h)-1S(e) (或1S), 2S3/2(h)-1S(e) (或2S)和1P3/2(h)-1P(e) (或1P)激子的吸收带. 然后, 利用飞秒抽运-探测技术得到样品的飞秒时间分辨瞬态吸收光谱, 结果显示, 1S激子的双激子复合时间大概是80 ps, 这一时间比传统量子点的双激子复合时间(小于50 ps)[29,30]延长了近一倍, 结合最近发展的超快界面电荷分离技术[31-34], 这一时间的延长将有很大应用前景. 此外, 在2S和1P激子中除了上述双激子复合外, 还存在一个空穴转移过程, 时间大概是5—6 ps. 最后, 利用纳秒时间分辨荧光光谱得到该样品体系的单激子复合时间约为200 ns.
2.1.实验药品与试剂
实验药品与试剂: 氧化镉(CdO), 单质硫(S, 99.98%), 单质硒(Se, 99.99%), 三正辛基膦(TOP, 90%), 二苯基膦(DPP), 十八烯(ODE, 90%), 油酸(OA, 90%), 辛烷(n-Octane, 99%).2
2.2.样品的合成
TOPSe/S前驱体的制备: 在手套箱中配制Se(Se:TOP = 1:1.5)和S(S:TOP = 1:1.5)溶液, 并在氮气环境下搅拌直至澄清.CdSeS合金量子点的合成: 1 mmol CdO, 8.7 mL ODE, 1.3 mL OA混合加入到25 mL 的三颈瓶中, 在氮气环境下升温至120 ℃, 排气15 min, 然后升温至240 ℃, 直至溶液澄清; 再降温至150 ℃, 将0.5 mL DPP溶液快速注入上述混合溶液, 保持5 min后, 加入Se/S摩尔比例为1:8的TOPSe/S(0.25 mmol Se和2 mol S)混合溶液, 240 ℃反应60 min, 冷却至室温, 使用正己烷和乙醇离心纯化后分散于辛烷中.
2
2.3.实验设备信息
稳态吸收光谱和稳态荧光光谱分别通过双光束分光光度计(Cary-5000, Agilent)和光纤光谱仪(USB-4000, Ocean Optics)测量. 飞秒时间分辨瞬态吸收光谱是Helios抽运-探测系统(Ultrafast Systems LLC)与飞秒激光器系统(Coherent)组合进行测量的. 其中365 nm抽运激光脉冲由光学参量放大器(TOPAS-800-fs)提供, 探测用的超连续白光(390—650 nm)是将800 nm光束(从激光器产生的激光中分离出一小部分光束, 约400 nJ/脉冲)聚焦到氟化钙晶体上产生的. 电动光学延迟线用于改变抽运激光脉冲和探测激光脉冲之间的时间延迟(延迟范围为0—8 ns), 仪器响应函数(IRF)约为100 fs. 纳秒时间分辨荧光光谱也是由上述365 nm激光激发, 并通过光栅单色仪(Omni-λ300, Zolix)和示波器(GDS-3354, GWINSTEK)获得各个波长下的荧光衰减信息.3.1.稳态吸收和荧光发射光谱
图1显示了样品的稳态吸收(实线)和稳态荧光光谱(虚线). 从图1可以看出, 样品的稳态吸收在510和468 nm有两个明显的峰, 这两个峰分别对应1S3/2(h)-1S(e) (或1S)和2S3/2(h)-1S(e) (或2S)激子的吸收[35]. 另外, 通过与后面要讨论的瞬态吸收基态漂白峰比较, 可以推断430 nm附近也存在一个较为微弱的稳态吸收峰, 它对应1P3/2(h)-1P(e) (或1P)激子的吸收. 从样品的光致发光光谱可以得到荧光峰在530 nm附近, 并且荧光光谱对称性良好, 峰宽在80 nm以下, 这间接证明了量子点样品粒径分布均匀[36]. 为了进一步探讨量子点的荧光平均寿命, 我们还利用纳秒时间分辨荧光光谱对样品的纳秒荧光动力学做了探究, 具体结果将在后面给出.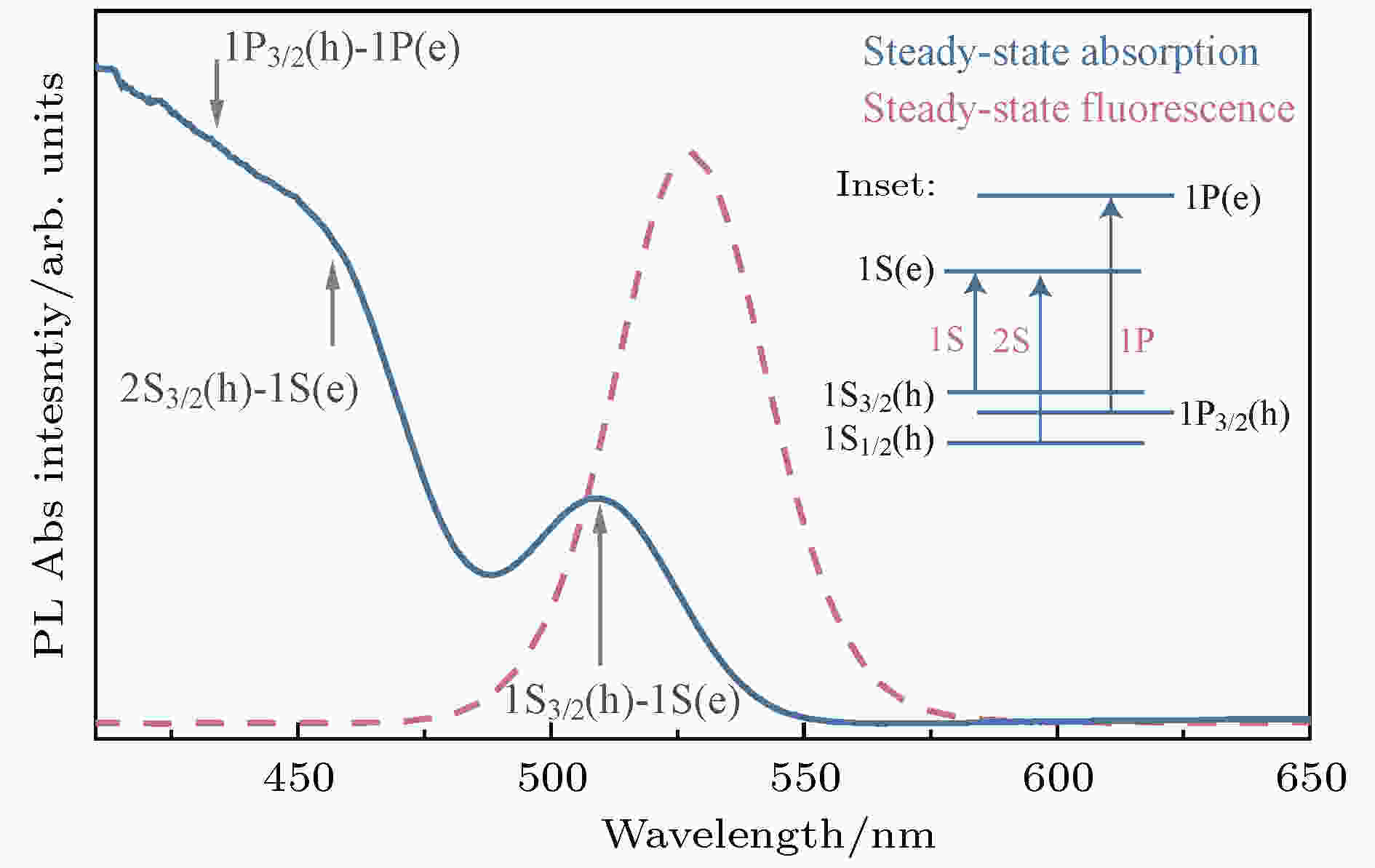
图 1 样品的稳态吸收光谱(实线)和稳态荧光光谱(虚线), 其中插图部分为样品的能带跃迁示意图Figure1. Steady-state absorption (solid-line) and fluorescence (dash-line) spectrum of QDs sample. Inset: energy level diagram illustrating the relevant energy of electron/hole states and allowed optical transitions (diagram not drawn to scale).
2
3.2.飞秒时间分辨瞬态吸收光谱分析
稳态光谱只能对电子跃迁的整体情况做一个宏观的描述, 为了研究样品的超快激子产生和复合动力学, 我们做了飞秒时间分辨瞬态吸收实验, 实验结果如图2所示.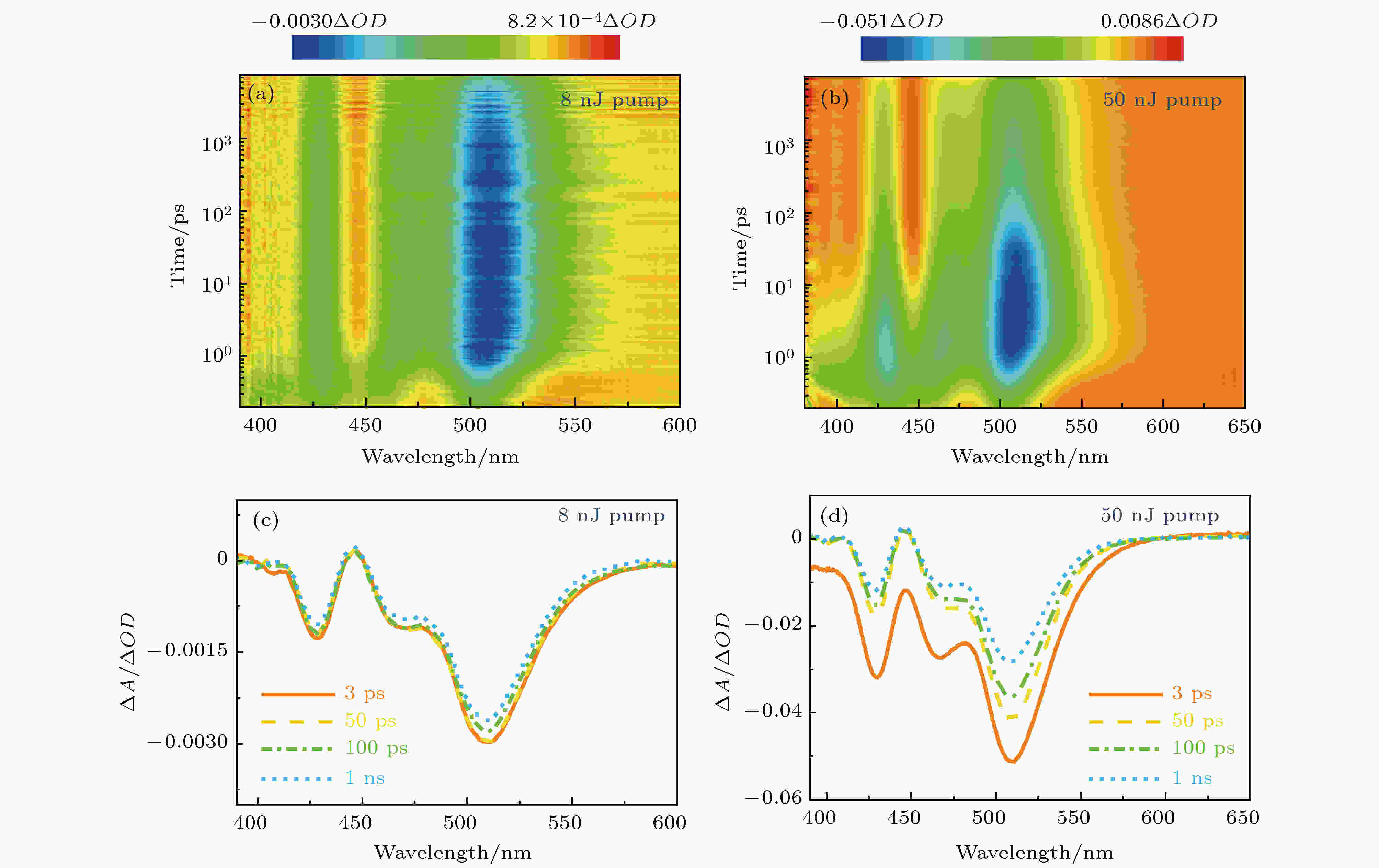
图 2 365 nm不同光强激发下的飞秒时间分辨瞬态吸收光谱 (a) 激发脉冲能量为8 nJ的瞬态吸收光谱彩图; (b) 激发脉冲能量为50 nJ的瞬态吸收光谱彩图; (c) 激发脉冲能量为8 nJ的演变相关差分光谱; (d) 激发脉冲能量为50 nJ的演变相关差分光谱Figure2. Femtosecond time-resolved transient absorption (TA) spectra at 365 nm excitation with different intensities: (a) TA color map with excitation pulse energy of 8 nJ; (b) TA color map with excitation pulse energy of 50 nJ; (c) evolution-associated difference spectrum (EADS) with excitation pulse energy of 8 nJ; (d) EADS with excitation pulse energy of 50 nJ.
图2 (a)和图2 (c)分别给出了波长为365 nm, 能量为8 nJ的飞秒激光脉冲激发下的飞秒时间分辨瞬态吸收光谱和随时间演变的差分光谱, 图2 (b)和图2 (d)是波长为365 nm, 能量为50 nJ的飞秒激光脉冲激发时所测得的时间分辨瞬态吸收光谱和随时间演变的差分光谱. 从图2 (a)和2 (c)可以观察到, 在激发脉冲作用下, 510, 468 和430 nm附近出现了三个基态漂白峰, 这三个峰与稳态吸收峰相对应, 分别是1S3/2(h)-1S(e) (或1S), 2S3/2(h)-1S(e) (或2S)和1P3/2(h)-1P(e) (或1P)激子的吸收带[35]. 其中, 以低能量脉冲激发(8 nJ)是为了确保处于多激子态的激子数目可以忽略. 在低能量激发下, 激子的漂白幅度在1 ns中衰减了约10%. 相比之下, 如图2 (d)所示, 在较高能量脉冲(50 nJ)激发下, 激子的漂白幅度在1 ns时恢复了约50%, 这一快速的激子漂白恢复表明在该条件下存在一个快速的激子-激子湮灭过程(双激子复合/俄歇复合). 此外, 2S和1P激子漂白幅度相比于低激发能量也有所增加(对比图2 (c)和图2 (d)), 这是由于随激发能量增大, 激子数目增多, 1S激子布居饱和后激子布居至更高能态.
以上数据表明, 在低激发能量下激子寿命很长, 且多激子态数目可以忽略不计. 为了进一步探究量子点多激子产生和复合动力学对激发能量的依赖关系, 进一步增大了飞秒时间分辨瞬态吸收实验中的激发光强(图3). 图3 (a)和图3 (c)分别是波长为365 nm, 能量为100 nJ的飞秒激光脉冲激发下的飞秒时间分辨瞬态吸收光谱和随时间演变的差分光谱, 图3 (b)和图3 (d)分别是波长为365 nm, 能量为500 nJ的飞秒激光脉冲激发下的飞秒时间分辨瞬态吸收光谱和随时间演变的差分光谱. 对比图3 (c)和图3 (d)可以发现, 激子基态漂白峰位置与低激发光强相比没有发生改变, 仍在510, 468和430 nm附近. 其中100 nJ激发脉冲下的瞬态吸收光谱(图3 (c))与50 nJ(图2 (d))的相比, 没有发生明显变化, 考虑是激发脉冲能量改变较小的原因. 不同的是, 随着激发光强进一步增加, 2S和1P激子峰的基态漂白幅度和动力学发生了很大变化, 特别是1P激子, 如图3 (d)所示, 当激发脉冲光强增加至500 nJ时, 1P激子峰(430 nm)基态漂白幅度大幅增加, 基本跟1S激子峰(510 nm)的基态漂白幅度相持平. 这一点也证实了激子优先布居1S态, 随激发光强的增大, 1S激子布居逐渐趋于饱和状态, 而后激子布居至更高能态(2S和1P态). 此外, 通过比较图3 (c)和图3 (d), 可以发现2S(468 nm)和1P(430 nm)激子峰基态漂白的恢复随光强增大而变快.
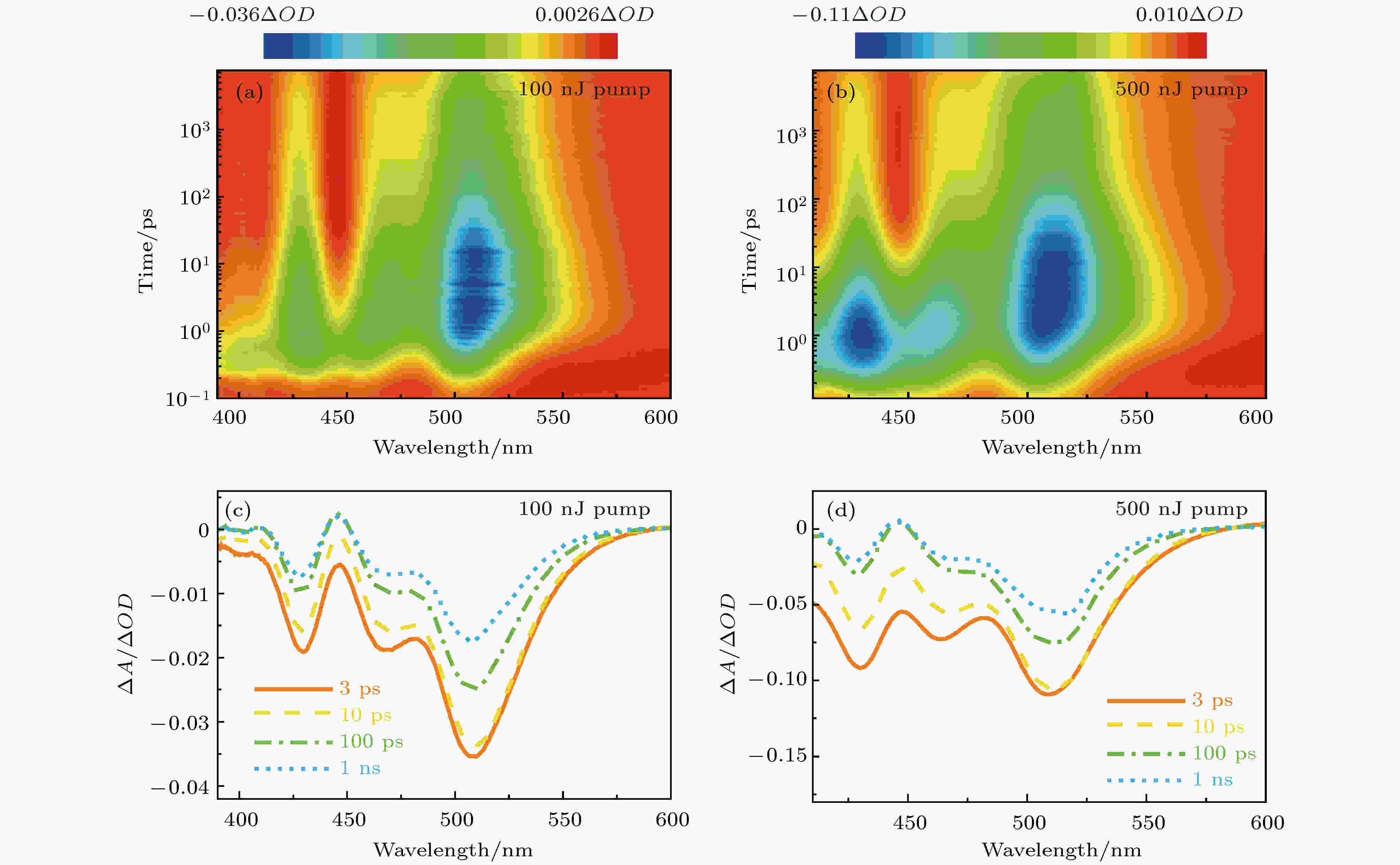图 3 365 nm不同光强激发下的飞秒时间分辨瞬态吸收光谱 (a) 激发脉冲能量为100 nJ的瞬态吸收光谱彩图; (b)激发脉冲能量为500 nJ的瞬态吸收光谱彩图; (c) 激发脉冲能量为100 nJ的演变相关差分光谱; (d)激发脉冲能量为500 nJ的演变相关差分光谱Figure3. Femtosecond time-resolved transient absorption (TA) spectra at 365 nm excitation with different intensities: (a) TA color map with excitation pulse energy of 100 nJ; (b) TA color map with excitation pulse energy of 500 nJ; (c) EADS with excitation pulse energy of 100 nJ; (d) EADS with excitation pulse energy of 500 nJ.
为了更深入地分析量子点的多激子形成和复合动力学以及其随光强的变化, 将这四个光强的激子基态漂白动力学曲线提取出来, 并进行了拟合和归一化处理(图4). 其中1S激子动力学曲线的拟合公式为ΔA(t) = a1exp(–t/τ1) + a2exp(-t/τ2) – c1exp(-t/τet); 2S和1P激子的动力学曲线拟合公式为ΔA(t) = a1exp(–t/τ1) + a2exp(–t/τ2) + a3exp(–t/τ3) – c1exp(–t/τet). 其中a1, a2, a3和c1是幅度; τ1, τ2, τ3对应衰减时间常数; τet对应形成时间常数.
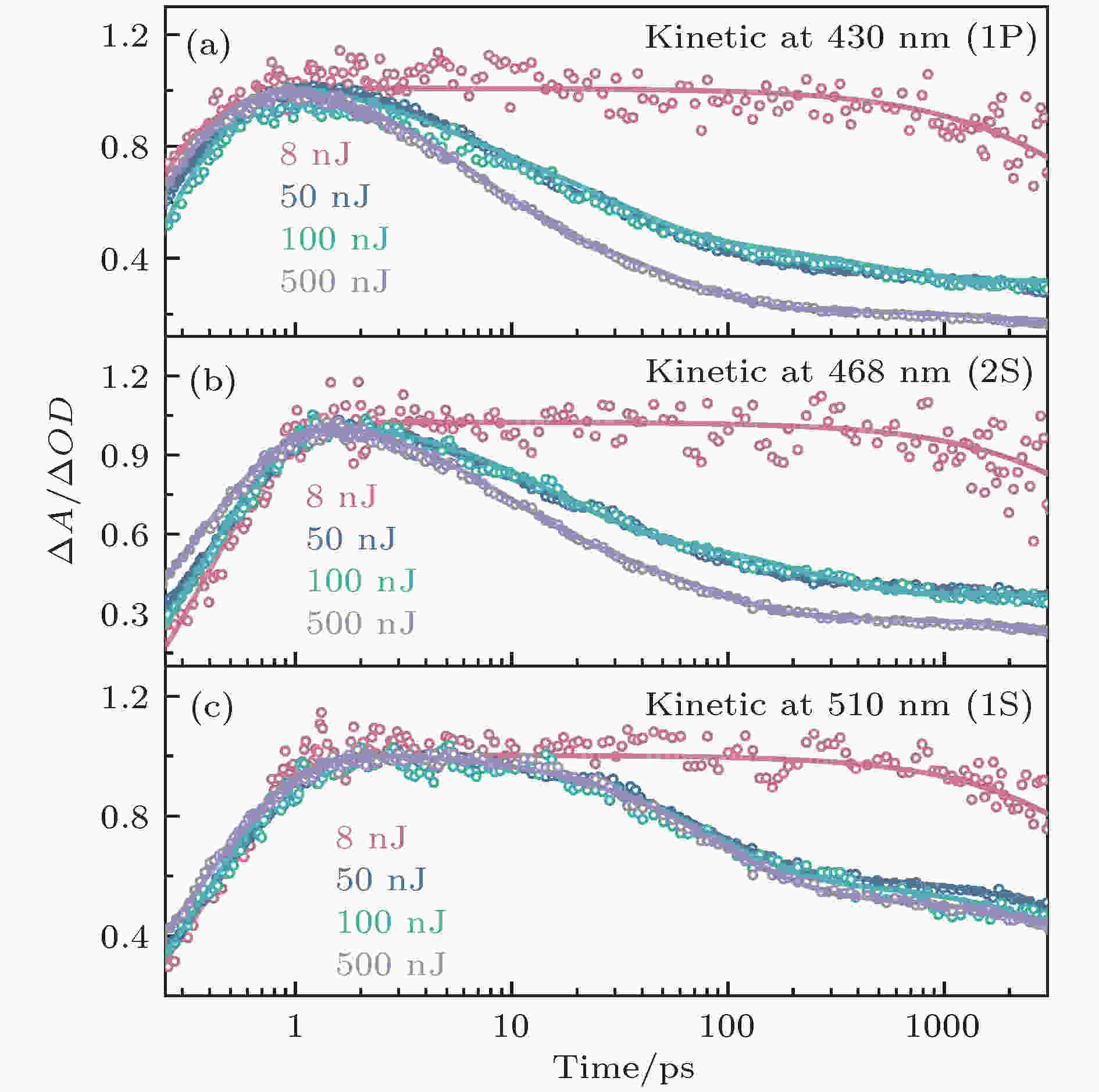图 4 不同激发能量的瞬态吸收光谱数据在各个激子峰处的漂白动力学曲线 (a) 1P激子漂白峰(430 nm); (b) 2S激子漂白峰(468 nm); (c) 1S激子漂白峰(510 nm). 所有动力学曲线已经归一化至最大振幅Figure4. The kinetics of TA with different excitation intensities at exciton peaks: (a) 1P exciton bleach recovery (at 430 nm); (b) 2S exciton bleach recovery (at 468 nm); (c) 1S exciton bleach recovery (at 430 nm). All kinetic traces have been normalized to the same maximum amplitude.
图4是分别将8, 50, 100和500 nJ的能量脉冲激发瞬态吸收光谱的1P(图4 (a)), 2S(图4 (b))和1S态(图4 (c))激子的漂白动力学曲线提取出来并进行了拟合, 拟合的参量见表1、表2和表3(其中τ1, τ2, τ3所占权重为其对应幅度a1, a2, a3与总幅度的比值, τet为形成时间常数, 其权重为100%). 为了便于对比, 在最大振幅位置进行了归一化处理. 首先, 由图4 (c)可以发现, 当激发脉冲能量为8 nJ时(多激子态激子数目可以忽略), 1S激子呈现出一个远大于10 ns的长衰减寿命(见表1), 反映了单激子复合时间. 随激发脉冲能量的增加, 1S激子多了一个寿命约为80 ps的衰减成分, 对应激子-激子湮灭过程(双激子复合/俄歇复合). 并且, 双激子复合时间随激发光强的增大而减小, 这是由于多激子态密度增大导致了俄歇复合变快[25]. 与先前报道不同的是, 本样品双激子复合时间比传统量子点的双激子复合时间(小于50 ps)[29,30]延长了近一倍. 结合最近发展的超快界面电荷分离技术[31-34], 在双激子复合之前将激子吸附解离出来便可以避免激子-激子湮灭, 规避能量损失, 因此该样品双激子复合时间的提升将有很好的应用前景.
| 激发脉冲能量 | 寿命值 | ||
| τet/ps (权重/%) | τ1/ps (权重/%) | τ2/ns (权重/%) | |
| 8 nJ | 0.391 (100) | – | $\gg$10 (100) |
| 50 nJ | 0.431 (100) | 82.6 (52.5) | $ \gg$10 (47.5) |
| 100 nJ | 0.374 (100) | 82.5 (55.6) | $ \gg$10 (44.4) |
| 500 nJ | 0.381 (100) | 80.9 (54) | $ \gg$10 (46) |
表1样品的瞬态吸收数据在510 nm(1S激子)处动力学曲线的拟合参数
Table1.Best-fit parameters of the kinetic curve of the transient absorption data of the QDs at 510 nm (1S exciton).
| 激发脉冲能量 | 寿命值 | |||
| τet/ps (权重/%) | τ1/ps (权重/%) | τ2/ps (权重/%) | τ3/ns (权重/%) | |
| 8 nJ | 0.353 (100) | – | – | $ \gg$10 (100) |
| 50 nJ | 0.429 (100) | 6.0 (67.7) | 59.1 (8.5) | $ \gg$10 (23.8) |
| 100 nJ | 0.362 (100) | 5.5 (32.7) | 59.8 (43.5) | $ \gg$10 (25) |
| 500 nJ | 0.340 (100) | 5.1 (50.1) | 53.7 (41.3) | $ \gg$10 (8.3) |
表2样品的瞬态吸收数据在468 nm(2S激子)处动力学曲线的拟合参数
Table2.Best-fit parameters of the kinetic curve of the transient absorption data of the QDs at 468 nm (2S exciton).
| 激发脉冲能量 | 寿命值 | |||
| τet/ps (权重/%) | τ1/ps (权重/%) | τ2/ps (权重/%) | τ3/ns (权重/%) | |
| 8 nJ | 0.188 (100) | – | – | $ \gg$10 (100) |
| 50 nJ | 0.269 (100) | 8.2 (27.1) | 57.0 (22.9) | $ \gg$10 (50) |
| 100 nJ | 0.213 (100) | 6.8 (27.2) | 52.8 (47.7) | $ \gg$10 (21.9) |
| 500 nJ | 0.207 (100) | 6.3 (49.5) | 51.4 (33.3) | $ \gg$10 (17.1) |
表3样品的瞬态吸收数据在430 nm(1P激子)处动力学曲线的拟合参数
Table3.Best-fit parameters of the kinetic curve of the transient absorption data of the QDs at 430 nm (1P exciton).
除了衰减的寿命成分, 1S激子还存在一个约400 fs的增加寿命成分, 对应热激子的冷却过程, 即光激发样品后生成的处于高能态激子 (未冷却到导带底)冷却至导带底部的过程. 同样地, 2S和1P激子也存在热激子冷却过程, 冷却时间大概是350 fs(具体时间见表2)和200 fs(具体时间见表3), 该结果表明随激子能量的增加, 热激子冷却时间呈缩短趋势.
对比图4 (b)和图4 (c)可以发现, 2S激子相对1S激子还多了一个快速衰减的寿命成分, 表2的拟合结果显示该寿命大概是5—6 ps. 这一寿命成分来源于2S激子的空穴至1S激子态的弛豫, 与先前报道通过声子耦合路径的空穴弛豫时间(7 ± 2 ps)相吻合[37]. 同样地, 1P激子同量级的快速衰减成分也来源于此(表3). 此外, 2S和1P激子50—60 ps的弛豫过程(表2和表3)对应双激子复合, 该复合过程随激发光强的增大而变快, 这也是增大光强后多激子态密度增大导致的. 相比之下, 2S和1P激子的双激子复合时间比1S的短, 考虑是由于激子种类不同, 双激子复合时间不同造成的.
通过以上数据可以得到, 样品的多激子态在光强较强时开始出现, 其复合本质是激子-激子湮灭. 随激发脉冲能量的增大, 俄歇复合变快(多激子态密度增加), 1S激子布居逐渐趋于饱和状态, 而后激子布居至更高能态(2S和1P态). 本样品1S激子的俄歇复合时间大概是80 ps, 而在2S和1P激子中除了上述俄歇复合, 还存在一个约5—6 ps的空穴转移过程.
2
3.3.纳秒时间分辨荧光光谱分析
飞秒时间分辨瞬态吸收光谱的优势在于分析较快的动力学过程(< 10 ns), 因此对于单激子复合这一较慢弛豫过程(
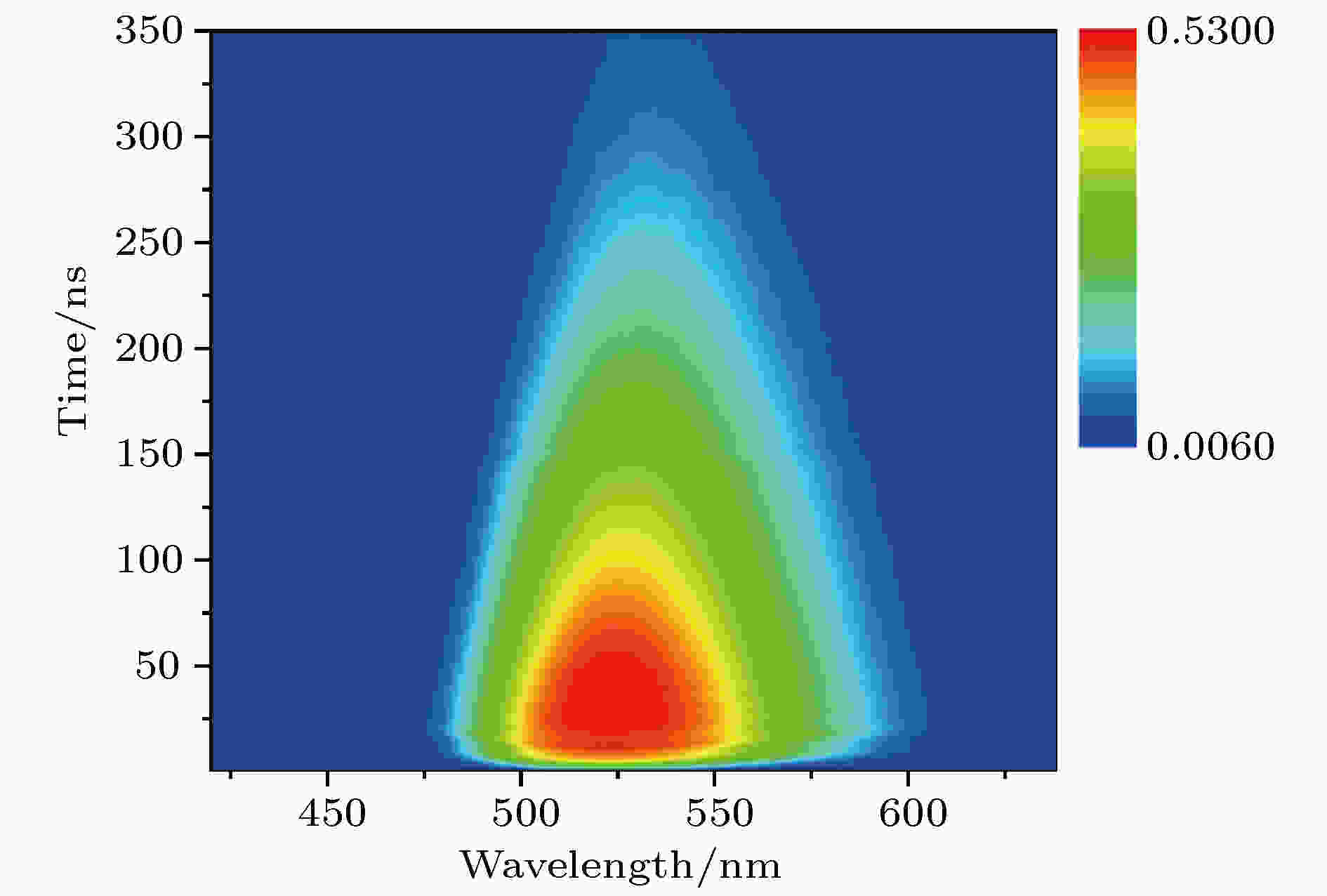图 5 时间分辨荧光光谱图Figure5. Time-resolved photoluminescence color map.
图5为样品的纳秒时间分辨荧光光谱彩图, 通过对数据进一步处理拟合, 可以得到样品的单激子复合时间约为200 ns.
