摘要:非线性、非平稳探地雷达数据常掺杂各种复杂噪声源, 其对精确提取弱反射波信号、识别绕射波双曲线同相轴特征具有严重影响, 忽略噪声影响给探地雷达探测数据全波形偏移成像及后续解译造成较大误差. 采用传统阈值函数的曲波变换去噪需要根据数据噪声水平人为确定合理阈值控制系数. 对此, 本文开展自适应阈值函数的曲波变换去噪算法研究. 引入块状复数域阈值函数算法, 分析传统阈值函数曲波变换去噪的效果随阈值控制系数变化的规律; 利用高阶统计量理论, 对曲波变换系数在尺度、方向上进行相关性叠加, 通过相关性统计量自适应确定有效信号在曲波变换系数分布尺度、旋转方向, 由此确定清除噪声成分阈值范围, 构建统计量自适应阈值函数曲波变换去噪算法. 针对包含随机噪声、相关噪声合成探地雷达数据及实测探地雷达数据, 采用传统阈值函数曲波变换去噪与本文提出去噪算法处理结果对比分析, 检验了本文算法的有效性及可行性. 研究成果对复杂探地雷达数据精确推断解译具有指导意义.
关键词: 探地雷达去噪/
自适应阈值/
统计量/
曲波变换

English Abstract

全文HTML

--> --> -->

探地雷达勘探采用天线发射不同频率电磁波, 利用地下介质的电磁性质差异, 根据接收回波的幅值、波形等运动学及动力学特征推断目标介质的空间、物性分布, 广泛应用于地质灾害监测、工程与环境地质勘察、水文地质勘查及军事侦查等领域. 然而, 随着探地雷达勘探环境越来越复杂、目标探测要求越来越精细^[1,2], 如何在强能量的各种复杂干扰噪声湮没环境中提取微弱的目标信号是一项艰巨的任务^[3,4].
常规中值滤波法^[5]、S变换去噪^[6-8]及F-K (频率-波速)滤波方法^[9,10]等探地雷达勘探数据去噪技术多基于简单最优化或正交变换算法, 构建固定滤波窗口, 去噪过程导致时频域重叠微弱有效信号失真, 具有特定噪声处理的局限性. 由于各种噪声源掺杂, 探地雷达数据常为非线性、非平稳信号序列^[11]. 基于傅里叶变换理论研发的信号处理技术可有效解决平稳信号分析处理问题, 但非自适应时频窗口局限性使其无法解决探地雷达复杂数据的去噪问题. 小波变换用于探地雷达数据去噪的假设前提是有效信号与噪声信号频谱分离, 通过采用具有伸缩和平移特性基函数在特定频段的稀疏表示, 设置噪声频段阈值以达到保真去噪的目的^[12]. 如利用高频阈值函数小波变换去噪理论开展探地雷达弱信号提取, 为推断异常位置提供依据^[13]. 改进阈值的提升小波变换用于混凝土脱空探地雷达数据去噪, 提高了解释推断精度^[14]. 可协调方向阈值函数的小波变换用于考古学和岩土勘察探地雷达数据去噪及杂波压制, 改善了数据信噪比等^[15,16]. 因而, 高效的阈值函数可有效提升去噪效果, 实现保真去噪的目的.
为突破小波变换采用矩形时频窗口去噪的局限性, 曲波变换采用小波域伸缩及平移特性, 并且引入一个方向参量从而具有更好的方向识别能力^[17,18]. 曲波变换自提出便迅速广泛应用于地球物理数据处理领域, 特别是在地震数据噪声压制、多次波分离等领域, 研究成果不断涌现^[19-22]. 其中, Neelamani等^[23]将曲波变换应用于三维地震数据, 通过设定阈值函数有效地清除随机噪声、相关噪声, 提高了地震资料的信噪比; 张金良等^[24]研究快速曲波变换域的SAR (synthetic aperture radar)图像去噪算法, 使用均值阈值滤波器使得图像的可视化和解译变得精确; Terrasse等^[25]通过人工挑选探地雷达数据曲波变换域系数, 明确需要去除杂乱回波及噪声源的尺度、方位信息, 利用硬阈值函数实现去噪处理. 可见, 曲波变换应用于探地雷达数据噪声压制的前提条件是获取较为准确的噪声阈值参数及其所属曲波系数在尺度、方位上分布范围.
实测复杂探地雷达数据常包含随机噪声、相关噪声及其他未知噪声类型, 所需阈值参数及所属曲波系数在尺度、方位上分布范围亦有所不同. 如朱自强等^[26]在曲波变换域中将选择的角度窗函数方向因子设置为零, 同时估计噪声方差确定阈值函数, 实现去除表层直达波、噪声源, 在幅值强度较高的直达波背景下提取了钢筋层和裂隙水层的弱化反射信号. Bao等^[27]认为背景噪声主要能量集中在曲波变换域方向90°区域附近, 而随机噪声会相对均匀地分布在整个曲波域, 采用二维滤波器估计噪声分布. Tzanis^[28]通过数值模拟人为地建立了不同裂隙构造对应探地雷达数据曲波变换域尺度、方位分布范围, 继而实现特定方向发育裂隙结构探地雷达反射波信号提取. 因而, 如何有效地确定目标体引起的探地雷达数据曲波变换域尺度、方位上分布范围是实现高效去噪、精确偏移成像的关键^[29]. 当前, 曲波变换配置研发了诸多计算阈值的方法, 如分段线性滤波方法、L2标准差法、曲波正变换法、对角实数及复数阈值法等, 实测数据去噪需根据噪声类型选用, 总体上无法满足自适应保真去噪的目的. 因而, 曲波域自适应阈值的构建是****关注的研究热点. 基于此, 结合曲波变换与高阶相关统计分析的优势, 本文提出在曲波变换多尺度、多方向分析理论基础上采用高阶相关统计量构建自适应阈值算法, 探索探地雷达数据曲波域自适应保真去噪方法技术.

2

-->

2.1.曲波变换

拟采用第二代截断离散曲波变换算法^[17,18]开展去噪算法研究. 曲波变换变量包含频率、尺度及方位(角度), 其变换表达式为

${{\varphi }_{j,m,k}}\left( x \right)={{\varphi }_{j}}\left[ {{R}_{j,m}}\left( x-x_{k}^{j,m} \right) \right].$

定义频率窗口$U$、尺度窗口$W$和角度窗口$V$为

${{U}_{j}}\left( r,\theta \right)={{2}^{-3/4}}W\left( {{2}^{-j}}r \right)V\left(\frac{2\left[ j/2 \right]\cdot \theta }{2\text{π}}\right),$

$\sum\limits_{ - \infty }^\infty {{W^2}\left( {{2^j}r} \right)} = 1,\begin{array}{*{20}{c}}&{r \in \left( {3/4,\;3/2} \right)},\end{array}$

$\sum\limits_{ - \infty }^\infty {{V^2}\left( {t - m} \right)} = 1,\begin{array}{*{20}{c}}&{t \in \left( { - 1/2,\;1/2} \right)},\end{array}$

式中, $j$为尺度, $m$为旋转方向, $r$和$t$为空间及时间域参数. 其中, 角度窗口$V$为环形域, 并满足$\left| x \right| \in \left[ {{2^j},\;{2^{j + 1}}} \right]$及极坐标定义${\theta _{j,m}} = 2{\text{π}}m \cdot {2^{ - \left[j/2\right]}}$. 对尺度$j$、旋转角度${\theta _{j,m}}$及空间位置

$x_k^{j,m} = R_{j,m}^{ - 1}\left({k_1} \cdot {2^{ - j}},\;{k_2} \cdot {2^{ - j/2}}\right),$

$R_{j,m}= \cos \theta \cdot \left(\!\!{\begin{array}{*{20}{c}} 1&{\tan \theta }\\ { - \tan \theta }&1 \end{array}}\!\!\right).$

对$f\left( x \right) \in {L^2}\left( {{R^2}} \right)$, 曲波系数定义为

$Cv\left( {j,m,k} \right) = \left\langle {f,{\varphi _{j,m,k}}} \right\rangle = \int_{{R^2}} {f\left( x \right)} \overline {{\varphi _{j,m,k}}\left( x \right)} {\rm{d}}x.$

曲波域噪声压制主要思路为: 1)对探地雷达数据进行二维快速傅里叶正变换获取系数分布; 2)按(2)—(4)式配置频率、尺度和角度窗口; 3)根据给定阈值函数截断去噪, 或将噪声所属系数范围设置为零实现噪声压制; 4)对3)部分处理剩余曲波系数利用二维快速傅里叶反变换算法获取处理后的数据结果. 曲波域噪声压制技术的关键是获取较为准确的阈值函数及其所属系数范围. 对于合成探地雷达数据, 可根据加入的噪声类型、强度给出准确的阈值函数及确定其所属系数范围; 对于实测探地雷达数据, 常规操作是根据实际情况, 人为选取合适的估计阈值函数及所属系数范围.
利用第二代曲波变换算法^[17,18]开展含噪数据处理对比研究, 其中曲波变换涉及的阈值窗口在所有尺度设置为$\tilde \delta = \delta \cdot {E_{\rm{c}}}$, $ \delta$为阈值分布范围控制系数, 可人为设定; ${E_{\rm{c}}}$为曲波变换系数L2范数. $\delta $值越大, 过滤窗口越大, 残余信息越少; 反之, $ \delta$值越小, 噪声及有效信息量越多. 关于数据过滤判断范围的估计, 有多种方法供参考, 如计算数据L2范数、块状复数阈值估计等^[30]. 对于复杂数据处理, 块状复数阈值函数更具有优势, 并将其用于曲波变换去噪过程, 如(6)式所示:

$\varPhi = \left\{\begin{aligned}& 1,\quad {\varPsi /{\rm{sqrt}}\left( {1 + 4 \cdot {\varGamma _1} \cdot {\varGamma _2}} \right)} > \tilde \delta,\\& 0,\quad\varPsi /{\rm{sqrt}}\left( {1 + 4 \cdot {\varGamma _1} \cdot {\varGamma _2}} \right) < \tilde \delta,\end{aligned}\right.$

式中, $\varPsi $为复数域阈值函数, 用于估计判断滤除范围, 具体推导请参考文献[30]; ${\varGamma _1}$为相邻道曲波系数权重值, ${\varGamma _2}$为曲波系数开平方归一化和权重值.
2 -->

2.2.曲波域统计量自适应阈值去噪

对探地雷达数据做二维的曲波正变换获取不同尺度、不同选择角度的系数分布; 对每一道探地雷达数据在不同尺度、不同角度下计算高阶相关统计量, 根据统计量分布明确阈值分布权重, 实现噪声滤除; 最后采用二维的曲波反变换重建去噪后的探地雷达数据. 其中, 未偏移的三阶相关函数表示为

$h_{i,i + 1,i}^{j,\theta }\left( t \right) = \sum\limits_{p = t - q}^{t + q} {\frac{{{{\left\| {F_i^{j,\theta }\left( p \right)} \right\|}_2}}}{{{{\left| {F_{i + 1}^{j,\theta }\left( p \right)} \right|}^{ - 1}}}}} ,$

归一化加权系数为

$\overline F _i^{j,\theta }\left( t \right) = F_i^{j,\theta }\left( t \right) \cdot h_{i,i + 1,i}^{j,\theta }\left( t \right) \cdot {\rm{sqrt}}\left( {\frac{{\left\| {h_{i,i}^{j,\theta }\left( t \right)} \right\|_2^{ - 1}}}{{h_{i + 1,i + 1}^{j,\theta }\left( t \right)}}} \right),$

式中, $i$为探地雷达数据接收点; $t$为时间采样点; $q$为平移因子, 取值为1; $F_i^{j,\theta }$为第$i$道探地雷达数据曲波域第$j$个尺度、第$\theta $个方向正变换系数.
该算法的优势在于不需要估计曲波变换阈值函数及其所属系数范围, 而是通过统计理论建立目标体引起的探地雷达有效信息所属的尺度及旋转角度范围. 其基本步骤如下.
步骤1, 对原始探地雷达数据做曲波正变换获取所有尺度$j$和选择角度$\theta $系数分布, 并提取大尺度和小尺度的曲波系数$Cv_{j,\theta }^d$和$Cv_{j,\theta }^a$.
步骤2, 采用曲波变换数值分析确定参与高阶相关统计量计算的尺度范围.
步骤3, For $j = 1,\; \cdots ,\;J$ do,
$ {\rm{For}} \ \theta = 1,\; \cdots,\;\vartheta \ {\rm{do}}.$
${\rm{For}}\ i = 1,\; \cdots ,\;M - 1\ {\rm{do}}.$
过程I, 按(7)式计算相关系数$h_{i,i + 1,i}^{j,\theta }\left( t \right)$;
按(8)式进行探地雷达数据归一化叠加获取$\overline F _i^{j,\theta }\left( t \right)$系数;
对$Cv_{j,\theta }^a$重复I过程, 获取$Cv_{j,\theta }^a$的高阶相关统计叠加系数;
end.
$i = i + 1$; $\theta = \theta + 1;\;j = j + 1$;
end.
步骤4, 对经过曲波域高价统计的变换系数$Cv_{j,\theta }^d$和$Cv_{j,\theta }^a$采用曲波反变换获取最终噪声压制的探地雷达数据.

2

-->

3.1.传统曲波变换去噪

建立理论模型并采用二维有限差分程序计算合成模拟数据. 矩形目标体规模为2 m × 1 m, X轴分布–1—1 m, Z轴分布为2—3 m; 电阻率为10 Ω·m、介电常数为30 F/m; 背景介质电阻率为1000 Ω·m、介电常数为3 F/m; 探地雷达观测系统频率为100 MHz, 点距为0.1 m, X轴方向设置测点数为101, 时间域采集点数为241. 文中峰值信噪比(PSNR)定义为$PSNR = 20\;{\log _{10}}\left(\dfrac{{{\rm max} \left( s \right)}}{{MSE}}\right)$, 其中MSE为数据均方差, 表示原始信号和噪声(或去噪后)信号的近似程度, max(s)为原始信号的峰值.
图1(a)所示为无噪声模拟合成探地雷达原始时间域数据, 可见在空间域设定矩形目标模型边界引起的探地雷达反射波信号分布于不同时间范围. 图1(b)和图1(c)分别为加入随机噪声(PSNR = 17 dB)、相关噪声后的探地雷达数据(PSNR = 15.51 dB). 椒盐式无规律的随机噪声分布于整个探地雷达剖面, 目标弱反射信号完全被噪声淹没; 相关噪声根据有效反射信号范围比例分布, 可见部分假反射信号. 采用(6)式阈值函数曲波变换去噪数据的PSNR值随阈值控制系数$\delta $的变化如图1(d)所示. 随着阈值控制系数$\delta $取值由小变大, 去噪数据PSNR值趋于极值后逐渐降至原噪声数据PSNR值水平, 其中含随机噪声数据去噪结果PSNR值在阈值控制系数$\delta $ = 0.15 (与原始数据噪声水平一致)附近取得PSNR极值(27.33 dB), 含相关噪声数据去噪结果对应在$\delta $ = 0.35附近取得PSNR极值(23.27 dB). 上述结果分析表明, 采用阈值函数曲波变换去噪效果的好坏取决于阈值控制系数(原始数据噪声水平)取值是否合理. 同时, 含随机噪声与相关噪声数据采用阈值函数曲波变换去噪的合理阈值控制系数规律不同, 前者阈值控制系数取噪声水平值($\delta $ = 0.10—0.20), 而后者取略高于阈值控制系数值($\delta $ = 0.3—0.4).
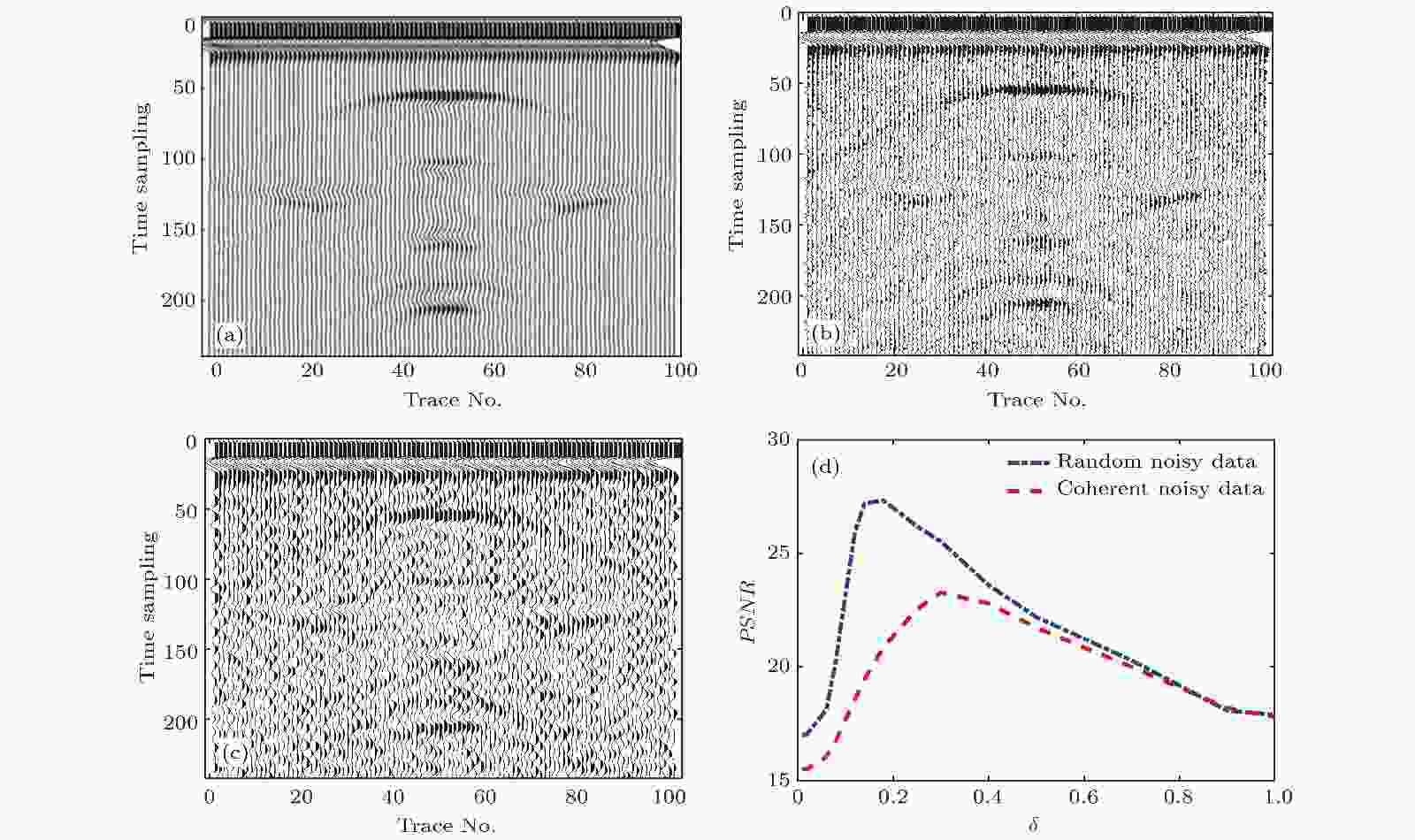图 1 含噪声模拟合成探地雷达数据的曲波变换阈值去噪结果　(a)原始合成数据; (b)含随机噪声数据, PSNR = 17 dB; (c)含相关噪声数据, PSNR = 15.51 dB; (d)去噪数据PSNR值随阈值控制系数δ的变化
Figure1. Denoised results for the synthetic ground penetrating radar (GPR) data with random and coherent noise using traditional curvelet transform: (a) Original GPR data; (b) data with random noise, PSNR = 17 dB; (c) data with coherent noise, PSNR = 15.51 dB; (d) the δ value vs. PSNR value curves

针对含噪模拟数据阈值函数曲波变换去噪问题, 预先获取的准确阈值控制系数范围可有效用于含噪数据处理. 但实测数据常常被不同类型、不同强度的噪声源污染, 合理的阈值控制系数范围难以确定. 为了有效使用阈值函数曲波变换去噪算法, 需要通过特定方式人为估计阈值控制系数范围, 如L2标准方差算法. 图2所示为含噪声数据(图1(b)和图1(c))采用L2标准方差估计方法确定阈值控制系数为0.08时的曲波变换去噪结果. 相比原始含噪数据(图1(b)和图1(c)), 阈值函数曲波变换去噪清除了部分噪声成分信号, 但矩形目标模型引起的有效反射波信号仅依稀可辩, 无法有效用于全波形反演成像计算及后续推断解译过程(见图2).
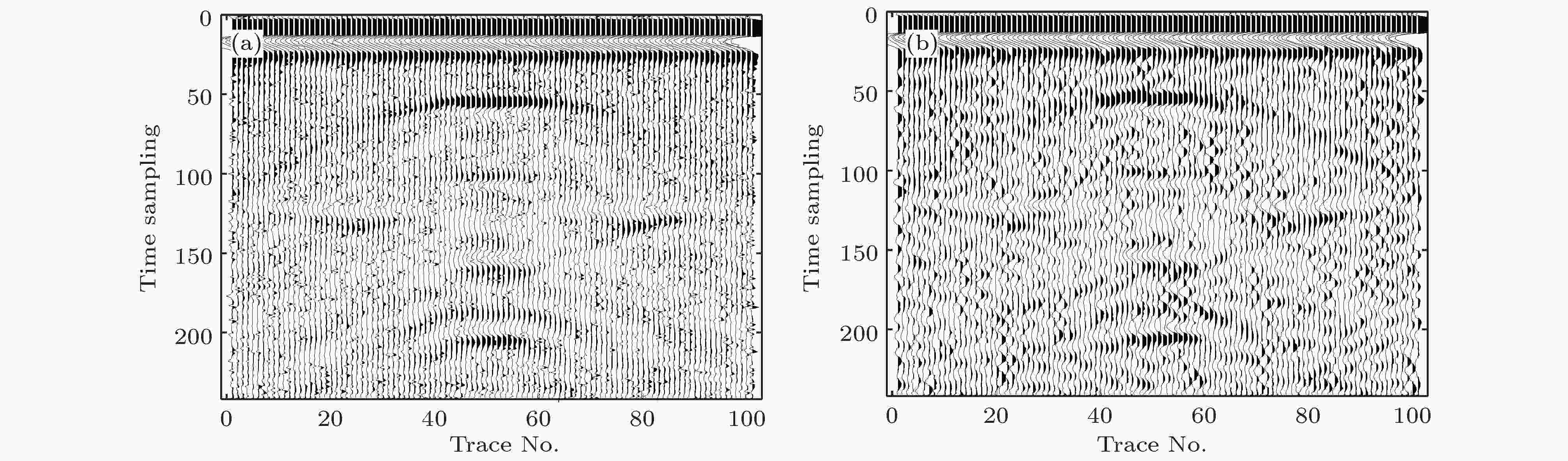图 2 δ = 0.08时含噪声数据(图1(b)和图1(c))曲波变换去噪结果　(a)随机噪声数据去噪结果, PSNR = 20.23 dB, 提高3.23 dB; (b)相关噪声数据去噪结果, PSNR = 16.75 dB, 提高1.24 dB
Figure2. Denoised results for the synthetic GPR data (Fig. 1. (b) and Fig. 1. (c)) with δ = 0.08 using traditional curvelet transform: (a) Result for random noise, PSNR = 20.23 dB; (b) result for coherent noise, PSNR = 16.75 dB.

2 -->

3.2.统计量自适应阈值曲波变换去噪

为解决传统曲波变换去噪需要估计合理阈值函数范围的问题, 采用统计量自适应阈值曲波变换去噪方法对图1所示含随机噪声、相关噪声数据进行处理. 去噪结果如图3所示, 基于统计量自适应阈值曲波变换去噪方法不仅可有效衰减随机噪声(PSNR值提高8.3 dB)、相关噪声(PSNR值提高6.41 dB), 同时较好地还原剖面中有效反射波信号时空域分布特征. 在噪声处理过程中, 本文提出的去噪算法无需估计阈值函数范围, 而是采用(8)式计算统计量自适应阈值权重, 达到了保真去噪的目的. 其中, 随机噪声数据去噪效果优于相关噪声数据去噪效果, 究其缘由, 低信噪比相关噪声数据(PSNR = 15.51 dB)导致噪声信号相关性统计量计算误差, 残留部分相关性较强的噪声信号. 总体上, 统计量自适应阈值曲波变换去噪结果可有效地用于探地雷达数据全波形偏移成像处理及后续解释推断过程.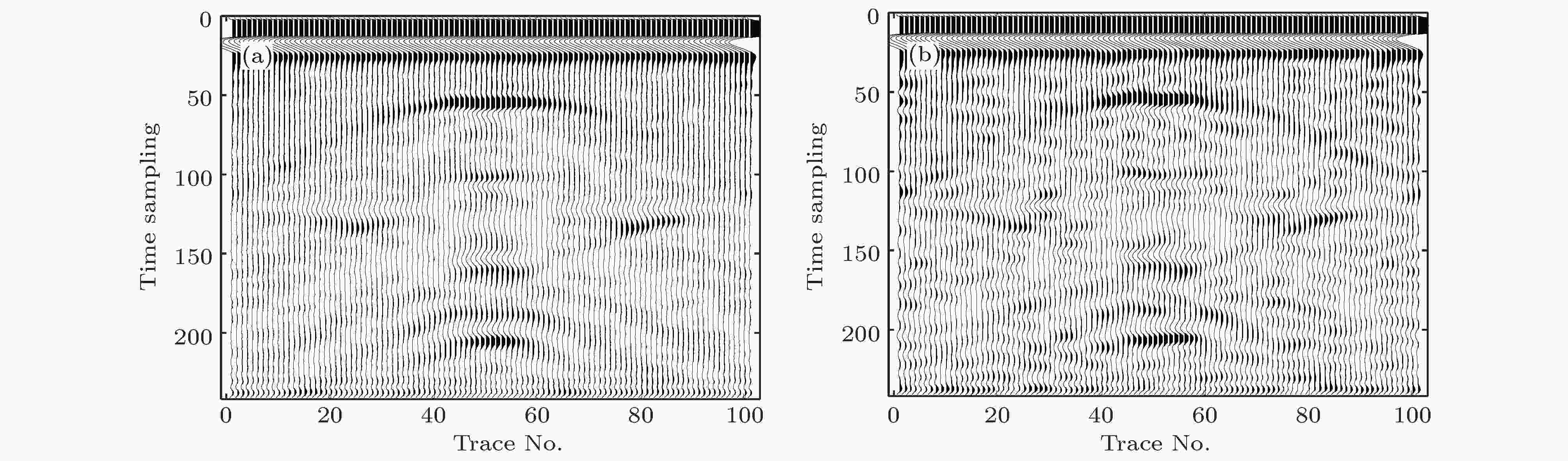
图 3 含噪声数据(图1(b)和图1(c))的统计量自适应阈值曲波变换去噪结果　(a)随机噪声数据去噪结果, PSNR = 25.3 dB, 提高8.3 dB; (b)相关噪声数据去噪结果, PSNR = 21.92 dB, 提高6.41 dB
Figure3. Denoised results for the synthetic GPR data (Fig. 1. (b) and Fig. 1. (c)) using curvelet transform with statistical self-adaption: (a) Result for random noise, PSNR = 25.3 dB; (b) result for coherent noise, PSNR = 21.92 dB.

进一步, 设计双矩形目标体规模为1 m × 1 m, 水平位置分别为–2至–3 m及2至3 m, 埋深范围分别为2至3 m及3至4 m; 其他物性参数及探地雷达观测系统与前述单个矩形目标模型一致. 数值模拟的双矩形目标体探地雷达时间剖面如图4(a)所示, 加入随机噪声及相关噪声数据如图4(b)和图4(c)所示. 含随机噪声数据(PSNR = 16.04 dB)及相关噪声数据(PSNR = 15.7 dB)完全淹没双矩形目标体引起的有效反射波信号, 无法用于双矩形目标体时空域分布推断解释.
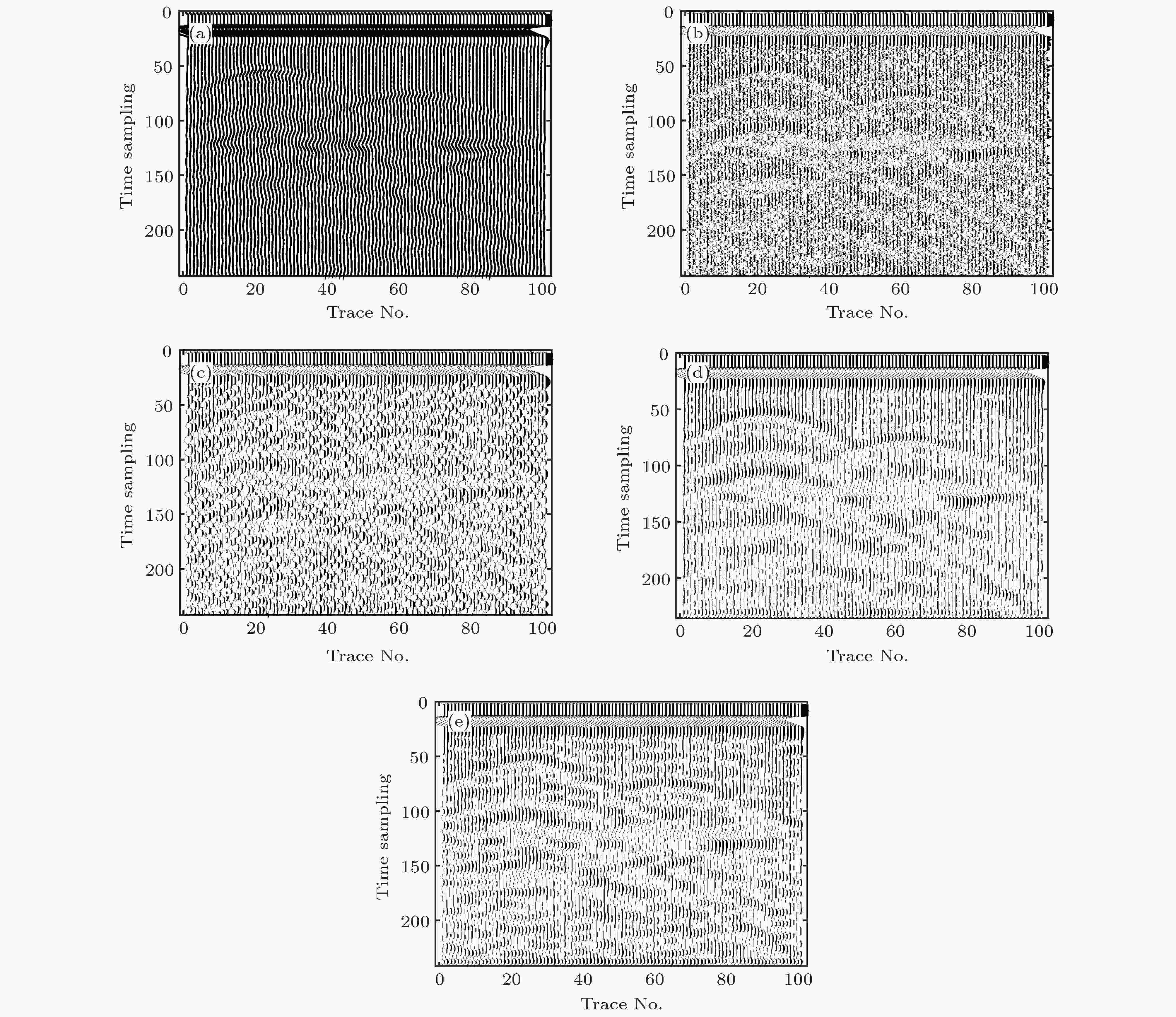图 4 双矩形目标模型含噪声数据统计量自适应阈值曲波变换去噪结果　(a)原始合成数据; (b)含随机噪声数据, PSNR = 16.04 dB; (c)含相关噪声数据, PSNR = 15.7 dB; (d)随机噪声数据去噪结果, PSNR = 23.97 dB; (e)相关噪声数据去噪结果, PSNR = 21.05 dB
Figure4. Denoised results for the synthetic GPR data of complex model with random and coherent noise using curvelet transform with statistical self-adaption: (a) Original GPR data; (b) data with random noise, PSNR = 16.04 dB; (c) data with coherent noise, PSNR = 15.7 dB; (d) result for random noise, PSNR = 23.97 dB; (e) result for coherent noise, PSNR = 21.05 dB.

图4(d)和图4(e)为采用本文提出的去噪算法处理结果. 由去噪结果可见, 含随机噪声时间剖面内双矩形目标体引起复杂有效反射波信号被完全恢复, PSNR值较原始含噪数据提高7.93 dB; 含相关噪声数据处理结果基本重建目标体引起有效反射波信号时空分布, 但仍残余部分相关噪声成分, PSNR值较原始含噪数据提高6.65 dB. 抽取图4所示去噪结果第50道数据, 绘制原始无噪声数据、含噪数据及去噪数据信号局部细节对比曲线, 如图5所示. 可见, 本文提出的去噪算法有效清除了全局椒盐式随机噪声分布(图5(a))、可有效分辨相关噪声环境下微弱有效反射波信号(图5(b)), 去噪数据曲线与原始无噪声数据曲线吻合较好, 验证了本文提出的去噪算法有效性及可行性.
图 5 双矩形目标模型含噪声数据第50道统计量自适应阈值曲波变换去噪结果　(a)随机噪声数据去噪结果; (b)相关噪声数据去噪结果
Figure5. Denoised results for the synthetic GPR data (Fig. 4.) in the 50th receiver using curvelet transform with statistical self-adaption: (a) Result for random noise; (b) result for coherent noise.

数值模拟实验结果表明, 传统曲波变换去噪效果依赖于阈值控制系数选取范围是否符合含噪数据噪声水平范围, 而不同信噪比含噪数据噪声水平各异, 因此采用传统阈值函数的曲波去噪算法抗噪性能与估计阈值控制系数范围准确度具有直接关系. 对于含有弱信号成分探地雷达数据的去噪处理, 普遍应用于传统曲波变换去噪算法理论与实践研究的L2标准差估计的噪声水平导致伪异常信号问题. 本文提出的统计量自适应阈值曲波变换去噪算法可有效确定含噪数据噪声水平范围, 在单一以及多个异常信号叠加的探地雷达数据处理方面显示了较好的应用效果. 需要指出的是, 本文考虑数据噪声水平为15%, 远远高于地球物理勘探数据采集质量控制误差水平5%, 数值算例结果可见, 含随机噪声、相关噪声数据处理结果可有效地用于后续成像及解译; 而高于15%含噪数据通常视为无效数据, 其相应去噪处理分析研究不在本文讨论范围.

图6(a)所示为某地探地雷达实测某测线原始时间剖面图, 由于受场地环境影响, 椒盐式随机噪声遍布整个剖面数据; 部分采集道数据受局部不均匀体影响, 出现相邻观测道数据幅值畸变. 原始数据剖面浅部(100—250时间采样点)介质的反射波能量非常微弱, 依稀可见几处绕射波同相轴, 但受噪声淹没, 双曲线特征不明显; 在250—300时间采样范围内出现较强幅值的似平行反射波组能量, 同相轴断断续续并不连续; 强幅值反射波组下部(300—400时间采样点)出现较弱的零散反射波组, 难以识别强幅值反射波组下边界.
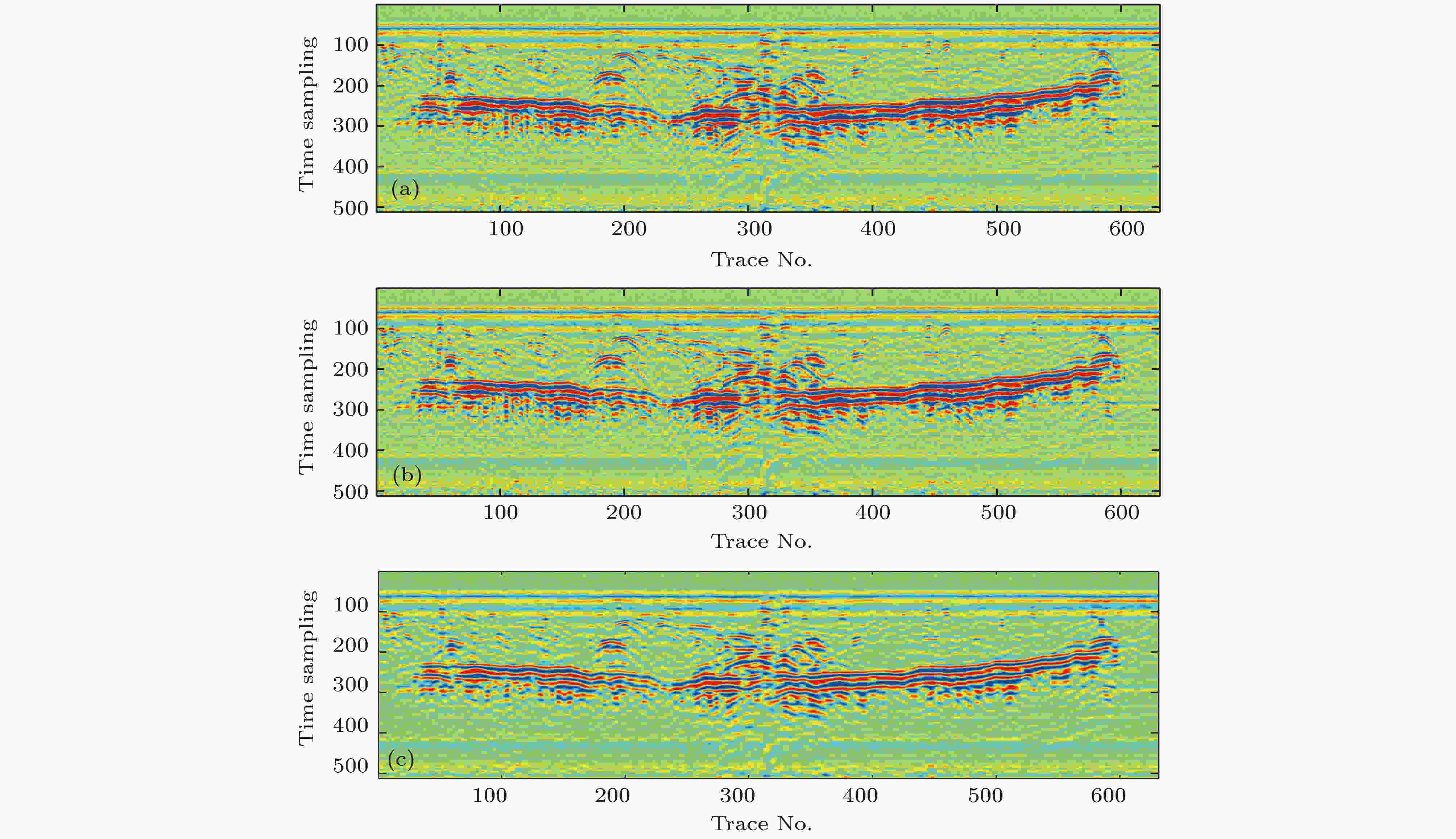图 6 实测探地雷达时间剖面传统曲波变换去噪和本文去噪算法处理结果　(a)实测时间剖面; (b)采用L2标准方差估计阈值曲波去噪结果; (c)统计量自适应阈值曲波去噪结果
Figure6. Denoised results for field GPR data using curvelet transform with L2 standard deviation and statistical self-adaption respectively: (a) Original field GPR data; (b) result using curvelet transform with L2 standard deviation; (c) result using curvelet transform with statistical self-adaption.

利用上述传统曲波变换去噪处理方法对图6(a)进行数据处理, 通过L2标准方差估计阈值范围, 去噪获得的探地雷达时间剖面如图6(b)所示. 由去噪结果可见, 部分地下反射波组能量信号得以加强, 清除了部分随机噪声信号. 但原始数据内有效绕射波双曲线特征、错动反射波组依然无法有效识别, 去噪数据信噪比提高并不显著. 究其原因, 实测数据中随机噪声、相关噪声及其他类型噪声源掺杂, 同时, 原始数据包含幅值强度各异的反射波组, L2标准方差估计阈值范围无法有效涵盖上述噪声特点的数据去噪范围. 人工试错法确定最佳阈值范围或能有效清除噪声, 但最佳去噪效果评价缺乏科学依据. 因此, 基于传统阈值函数曲波变换去噪数据处理后的探地雷达时间剖面进行分析解释, 无法保证资料解译的准确度.
采用本文提出的统计量自适应阈值曲波变换去噪算法对图6(a)原始数据进行处理, 去噪结果如图6(c)所示. 由于随机噪声源在曲波变换系数尺度、方向上并不具备统计相关特性; 相关噪声源变换系数在尺度、方向上虽具备一定相关性, 但相对有效反射波组信号相关性仍然较小, 因而统计量自适应阈值可有效分辨反射波组能量, 去除噪声信号, 达到保真去噪的目的. 由图6(c)可见, 地下反射波能量得到显著增强, 特别是浅部多个绕射波双曲线同相轴特征的信噪比得到有效提高; 中深度多层介质的反射组同相轴连续、分界面明显; 且分布于强幅值反射波组下部的弱幅值反射波组清晰可辩. 经过统计量自适应阈值曲波变换数据处理后的探地雷达时间剖面进行分析解释, 有助于资料解译的准确度.
抽取图6所示实测探地雷达数据第200道数据, 绘制传统曲波变换去噪结果与本文提出的去噪结果局部细节对比曲线, 如图7所示. 由曲线对比图可见, 在0—100时间采样范围内地面回波、弱幅值绕射波(100—150时间采样)、强幅值绕射波(150—230时间采样)及强幅值反射波组(230—350时间采样)受到随机噪声及相关噪声污染, 在第350时间采样范围以外的弱反射波信号受到较强幅值的上述噪声源淹没. 相比传统曲波变换去噪结果, 本文提出的去噪算法可有效恢复弱幅值绕射波、强幅值绕射波及强幅值反射波组的同相轴特征, 同时可清晰分辨弱幅值反射波信号, 验证了本文提出的去噪算法在实测探地雷达时间剖面数据处理应用中的可行性及有效性.
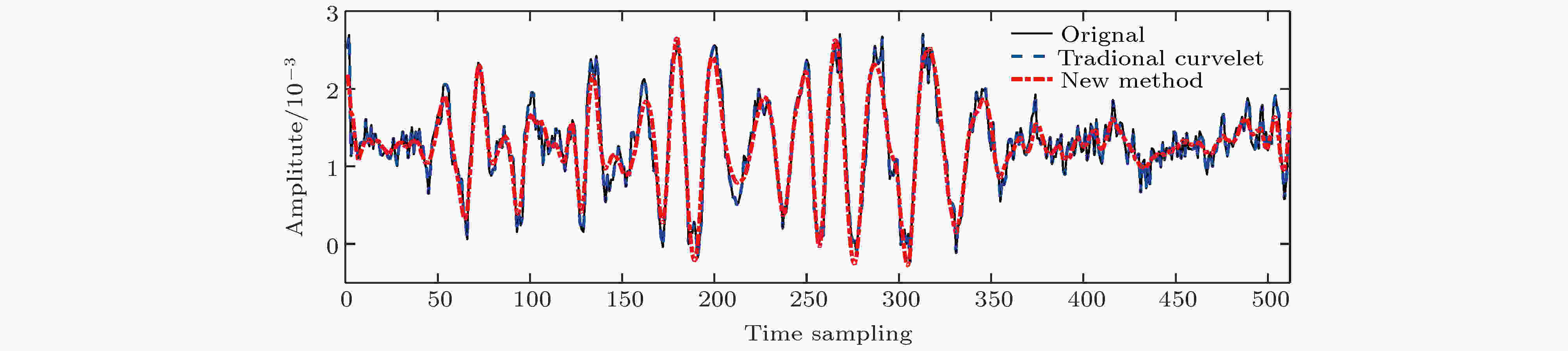图 7 实测探地雷达时间剖面第200道传统曲波变换去噪和本文去噪算法处理结果
Figure7. Denoised results for field GPR data (Fig. 6) in the 200th receiver using curvelet transform with L2 standard deviation and statistical self-adaption respectively.

1)针对传统曲波变换探地雷达数据去噪需估计阈值函数问题, 对探地雷达数据做二维曲波正变换获取不同尺度、不同选择角度下的系数分布; 对每一道探地雷达数据在不同尺度、不同角度下计算高阶相关统计量, 根据统计量分布明确阈值分布权重, 开展了统计量自适应函数算法研究, 实现无需估计曲波变换阈值函数及其所属系数范围, 而是通过统计理论明确目标体探地雷达有效信息所属的尺度及旋转角度范围, 从而构建了统计量自适应阈值函数曲波变换去噪算法.
2)基于块状复数域阈值函数理论, 设计简单矩形及埋深不同双矩形模型, 并合成随机噪声、相关噪声合成探地雷达数据. 由传统阈值函数曲波变换去噪分析表明: 块状复数域阈值范围的计算需给定阈值控制系数, 去噪效果的优劣取决于与含噪数据是否匹配的阈值控制系数; 合成含噪数据可通过给定的估计阈值函数实现高效去噪, 但实测含噪数据无法准确估计阈值函数, 因而难以实现高效保真的去噪目的.
3)对复杂噪声源环境下采集的探地雷达实测数据进行去噪分析处理, 提取了微弱幅值绕射波双曲线同相轴特征, 恢复了中深部不同幅值似平行非连续性反射波组及弱幅值错动反射波组, 获得了相应去噪结果. 将相应结果与传统阈值函数曲波变换去噪结果对比, 验证了统计量自适应阈值曲波变换去噪算法在复杂噪声背景下探地雷达弱信号提取方面的独特优势, 有助于对探地雷达探测资料进行可靠、准确的解译.