摘要:节点重要性对于分析网络结构具有重要意义. 为了充分刻画网络全局和局部特性, 本研究基于网络拓扑结构对疾病传播过程进行了抽象, 分别设置各个节点为传染源, 在经历传播时长K后, 将网络中已感染节点的数量定义为K-阶传播数, 最终基于不同K值下的K-阶传播数得到节点重要性结果. 对Watts-Strogatz小世界网络和海豚网络的仿真实验表明, 加权K-阶传播数法对节点重要性的评估较其他方法更为合理, 能够细致地刻画小世界网络中长程连接对信息传输的影响, 提高海豚网络中对社区交流起关键作用的节点的重视程度. 本文利用蓄意攻击策略对美国西部电网、芝加哥公路网络、网络科学家合著网络以及小鼠神经纤维束网络进行了研究, 即依照节点重要性由高到低的排序依次攻击网络. 结果显示, 相较于其他方法, 基于加权K-阶传播数法仅需移除少量重要节点便可实现对网络结构的充分破坏.
关键词: 复杂网络/
节点重要性/
传播模型

English Abstract

全文HTML

--> --> -->

复杂网络是现实系统的抽象表达. 网络节点依靠边相互联系, 通常存在着重要性差异. 节点重要性是分析设计网络结构、提升系统鲁棒性等研究的重要基础^[1-3]. 目前, 已有诸多研究各自从不同的角度提出了节点重要性评价指标.
度中心性法^[4]认为节点拥有的邻居数越多, 其直接影响力越强. 对食物链网络^[5]、P2P网络^[6]、电子邮件网络^[7]以及蛋白质网络^[8]的研究指出, 当度值较大的节点被移除后, 网络结构将变得更加脆弱. 此外, 度中心性法计算简便, 其时间复杂度为$O(N)$, 适用于网络规模较大的情况. 然而, 度中心性法未考虑非邻居节点的影响, 利用的信息较为有限, 不能充分地反映网络的全局特性和桥连接节点的重要性. 任卓明等^[9]在度中心性法的基础上, 将邻居节点相互连接的紧密程度, 即局部聚类系数也纳入了评价体系(下文简称Ren法), 结果虽优于度中心性法, 但其反映网络全局特性的能力仍然有限. 此外, Ren法利用趋同化函数将度与聚类系数处理后直接加和, 并未设置比例系数, 即该方法认为二者同等重要, 其合理性有待商榷. 为了更充分地利用网络结构信息, Chen等^[10]提出了一种基于多级邻居信息指标的半局部中心测度的方法(下文简称Chen法), 首先确定节点的一级重要性为最近邻与次近邻节点的个数之和, 再计算节点的二级重要性为所有邻居节点的一级重要性之和, 最后定义节点的三级重要性为所有邻居节点的二级重要性之和, 并作为最终的重要性评价指标. 但为了保证较低的算法复杂度, Chen法仅将分析范围扩展到了次近邻节点, 因而对网络全局特性的挖掘也并非十分充分. 介数中心性^[11]指网络中所有最短路径通过某节点的占比, 是节点对网络传播信息的影响或对节点预期负载的度量. 紧密度^[12,13]指由某节点出发, 到达其余节点的最短路径的和的倒数, 是将信息从给定节点传播到网络中其他可达节点的时间的度量. 介数中心性与紧密度虽提高了对桥节点的重视程度, 但需要计算任意一对节点之间的最短路径, 其时间复杂度为$O({N^3})$, 不适用于大型网络, 且对随机网络的解释也不够充分. 特征向量法^[14,15]将网络邻接矩阵最大特征值对应特征向量的元素作为各个节点的重要性指标, 本质上是将单个节点的拓扑性质线性叠加, 结果较为片面. Katz^[16]认为节点的重要性正比于网络邻接矩阵A的幂级数$\sum\limits_{k = 0}^\infty {{a^k}{{{A}}^k}} $与单位阵E的差的各列元素之和, 其中α为权重衰减因子. Katz指标虽充分利用了网络的全局特性, 但α却无法定量计算, 只能根据不同的网络进行人为设置, 且该方法还认为节点影响力随路径的增加呈指数形式衰减, 较为主观. 此外, 现实世界中的网络均是有限的, 而Katz指标为了得到收敛形式, 使路径长度取值无穷大, 其结果包含了大量的冗余信息. 为了解决Katz指标存在的问题, Zhang等^[17]以网络节点为变量, 将其余所有节点对当前节点的影响力进行加和, 并假设节点的影响力随路径的增加呈高斯形式衰减. 该方法在一定程度上解决了Katz指标的信息冗余等问题, 但节点影响力的衰减形式仍较为主观. K-核分解法^[18,19]试图递归地移去网络中度中心性的值小于等于K的节点, 其时间复杂度为$O(N)$, 相比于度中心性、介数等指标更能反映诸如演员网络、社交网络等实际网络的节点重要性. 但K-核分解法对节点的排序并不细致, 常常赋予大量节点相同的重要度, 不适合于树状网络和无标度网络的分析. PageRank算法^[20]认为节点的重要性与随机浏览者访问的频率成正比, 被广泛地应用在了网页排名等领域, 但该算法对含孤立节点或社团结构的网络会出现重要性排序不唯一等问题. 为了解决该弊端, Lü等^[21]提出了LeaderRank算法, 在原始网络的基础上, 增加了一个与所有节点双向连接的Ground节点. 这一操作使网络变为强连通的, 其结果比PageRank算法更加准确, 但LeaderRank算法不适用于无向网络. Zhong等^[22]利用网络节点被移除前后流行阈值的差来表征节点的全局重要性, 并利用度中心性来表征节点的局部重要性, 最后将归一化后的全局和局部重要性结果进行加权求和(下文简称CI法), 并利用美国航空网络等九个真实网络证明了CI法的有效性. 然而CI法中全局和局部重要性的加权系数对最终结果的影响较大. 虽然文献[22]经仿真分析归纳指出当加权系数近似为0.5时得到的节点重要性结果较好, 但缺乏更为深入的理论证明. 此外, CI法为何选择度中心性而非其他局部重要性指标有待进一步说明.
以上方法均存在各自的不足, 本研究将提出一种新的节点重要性评价方法, 即加权K-阶传播数法, 并试图利用WS (Watts-Strogatz)小世界网络、海豚网络、美国西部电网、芝加哥公路网络、网络科学家合著网络以及小鼠神经纤维束网络进行仿真分析, 以证明该方法的有效性.

SI (susceptible-infective), SIS (susceptible-infective-susceptible)和SIR (susceptible-infective-removed)等模型^[23]被广泛地应用在疾病以及信息传播等领域, 最初均是对某地区疾病传播过程的抽象. 其中, 个体能否恢复健康和是否具有免疫力是造成上述模型差异的重要因素. SI和SIS模型假设个体不具备免疫力, 将人群分为易感染者和已感染者两类. 此外, SI模型认为个体一旦被传染便永久处于已感染状态, 而SIS模型则认为个体被传染后将以一定概率恢复为易感状态, 并会被再次传染. SIR模型假设已感染者可被治愈且将具有终身性的免疫力, 将人群分为易感染者、已感染者和免疫移出者三类. 然而, 以上模型均假设疾病传播为随机接触, 并未考虑个体间的拓扑关系. 受上述模型启发, 本文将结合复杂网络对已感染者无法恢复健康且不具有免疫力的最为简单的疾病传播过程进行抽象, 最终得到加权K-阶传播数法来评价节点的重要性, 描述如下.
首先给定无向网络图$G(V,E)$, 其中, V = $ \{ {v_1},{v_2}, \cdots,{v_n}\} $为节点集, 共n个节点, 代表个体; E为边集, ${e_{ij}}$表示节点${v_i}$与${v_j}$之间的边. 这里假设疾病传播过程中该网络的结构不会发生变化, 且已感染者只能传染给与其直接接触的易感染者. 现假设某节点${v_i}$为已感染者, 与其相邻的易感染者集合记为$\varGamma ({v_i})$. 对节点${v_j} \in \varGamma ({v_i})$而言, ${v_i}$将以一定概率$0 \leqslant {p_{ij}} \leqslant 1$向${v_j}$传播疾病. 同时, ${v_i}$向${v_j}$传播疾病需要耗费一定时间${t_{ij}}$, 通常受到边${e_{ij}}$的影响. 若除${v_i}$外, ${v_j}$同时受到其他相邻的已感染者的传播, 还需进行综合考量. 以上描述考虑到了节点间疾病传播的概率以及耗时等因素, 但若网络边是无权的, 且不考虑节点以及边的意义, 则可进一步抽象, 作出以下假设:
1)已感染者会向其相邻的所有易感染者传播疾病;
2)已感染者向其相邻的易感染者传播疾病的耗时相等, 并设为1;
3)易感染者一旦受到其任一相邻的已感染者的传播, 便转化为已感染者.
在衡量节点的重要性时, 较为常用的方法是分别将各个节点设置为传染源进行疾病传播, 并以网络中所有节点被转化为已感染者的总耗时作为节点重要性的评价指标, 总耗时越少, 则证明节点越重要. 然而, 当网络非连通时, 从不同节点出发最终能够传播到的节点总数未必相同. 为了保证一致性, 另一种节点重要性衡量方法仍是将各个节点设置为传染源, 但比较的是在经历相同的传播时长K后网络中已感染者的数量, 数量越大则证明该节点越重要. 基于假设2可将传播时长K取值离散, 并规定为非负整数, 这与SI等模型中时间取值连续的假设略有不同. 其中, 当$K = 0$时可认为只有传染源节点已被感染, 但尚未开始传播.
此外, 基于假设1和3可以得到以${v_i}$为传染源, 传播了时长K后网络中已感染者的数量为

$N_{{v_i}}^K = {\left\| {\left( {\sum\limits_{k = 0}^K {{{A}^k}} } \right) \cdot {{e}_i}} \right\|_0} = {\left\| {\sum\limits_{k = 0}^K {{{A}^k}} \cdot {{e}_i}} \right\|_0}, $

这里, 将$N_{{v_i}}^K$命名为K-阶传播数; A为网络的邻接矩阵; ${\left\| \cdot \right\|_0}$表示向量的${L_0}$范数; ${{e}_i}$表示第i个分量为1, 其余分量为0的n维向量. 事实上, (1)式表示的是矩阵多项式${{A}^0} + {{A}^1} + \cdots + {{A}^K} = \sum\limits_{k = 0}^K {{{A}^k}} $中第i行或列向量(无向图的邻接矩阵A为对称阵, 其多项式亦对称)的${L_0}$范数, 即非零元素的个数. (1)式与文献[24]中定义的K-阶邻居数相同, 同样可以衡量K步内可达的节点总数. 此外, 文献[24]指出当K大于网络最大连通部分的直径d时, 任意节点的$N_{{v_i}}^K$均不再随K值变化, 因此有$K \in \{ 0,1, \cdots,d\} $.
传播时长K的取值是影响节点重要性评价结果的关键. 文献[24]利用$N_{{v_i}}^K$并基于信息熵定义了K-阶结构熵${H^K}$, 衡量了网络的异构性:

${H^K} \!=\! - \sum\limits_{i = 1}^n {\frac{{N_{{v_i}}^K}}{{\sum\limits_{j = 1}^n {N_{{v_j}}^K} }}} \log \!\left(\!\frac{{N_{{v_i}}^K}}{{\sum\limits_{j = 1}^n {N_{{v_j}}^K} }}\!\right)\!,\; K \in \{ 0,1, \cdots\!,d\} .$

结构熵${H^K}$取值越小, 网络的异构性越强, 并以结构熵序列为依据研究了WS小世界、BA无标度等网络的异构性. 若从疾病传播的角度出发, 可认为${H^K}$取值越大, 以各个节点$\{ {v_1},{v_2}, \cdots,{v_n}\} $分别作为传染源的网络K-阶传播数$\{ N_{^{{v_1}}}^K,N_{^{{v_2}}}^K, \cdots,N_{^{{v_n}}}^K\} $之间的差异越小, 即可认为各节点重要性的差异越小, 反之差异越大. 若仅仅以某单一传播时长下网络中已感染者的数量来衡量节点的重要性, 可能会遗漏其他传播时长下的有用信息. 因此, 本文将对K取从0至d间的所有时刻进行综合考察, 定义节点${v_i}$的重要性${Q_{{v_i}}}$为

${Q_{{v_i}}} = \sum\limits_{K = 0}^d {{c^K} \cdot S_{{v_i}}^K} , $

其中

$S_{{v_i}}^K = \frac{{N_{{v_i}}^K - \min ({N^K})}}{{\max ({N^K}) - \min ({N^K})}}, $

这里${N^K} = \{ N_{^{{v_1}}}^K,N_{^{{v_2}}}^K, \cdots,N_{^{{v_n}}}^K\} $, $S_{{v_i}}^K$是$N_{{v_i}}^K$归一化后的结果, $N_{{v_i}}^K$通常会随着K的增大而增大, 为了避免较大的$N_{{v_i}}^K$掩盖取值较小时的信息, 本文将${N^K}$映射至[0, 1]区间, 仅考虑节点重要性的相对顺序. 此外, 权重系数${c^K}$为

${c^K} = 1 - \frac{{{H^K} - \min (H)}}{{\max (H) - \min (H)}}, $

其中$H = \{ {H^0},{H^1}, \cdot \cdot \cdot,{H^d}\} $, ${H^K}$越小, 权重系数${c^K}$越大. 本文对(3)式中节点重要性差异较大的时刻更为关注并进行放大, 相对忽略差异较小的时刻. 最终可利用$Q = \{ {Q_{{v_1}}},{Q_{{v_2}}}, \cdot \cdot \cdot,{Q_{{v_n}}}\} $来衡量各个节点的重要性.

为了验证加权K-阶传播数法在节点重要性评估方面的优势, 本文将利用WS小世界网络、海豚网络、美国西部电网、芝加哥公路网络、网络科学家合著网络以及小鼠神经纤维束网络进行仿真分析.
2

-->

3.1.WS小世界网络

小世界网络是指同时具有较短特征路径长度以及较大平均聚类系数的一种网络类型. Watts和Strogatz^[25]最早提出了一种构造小世界网络的方法, 即将最近邻耦合网络中的边依概率进行随机重连, 通常将这种网络称为WS小世界网络. 图1(a)基于100节点最近邻耦合网络随机生成了一个WS小世界网络, 该最近邻耦合网络中每个节点与其邻近的左右两侧各两个节点相连. 在随机重连后, 边31-33和95-96分别被改连为31-72和95-53, 见图1(b)和图1(c), 其余边的位置不变.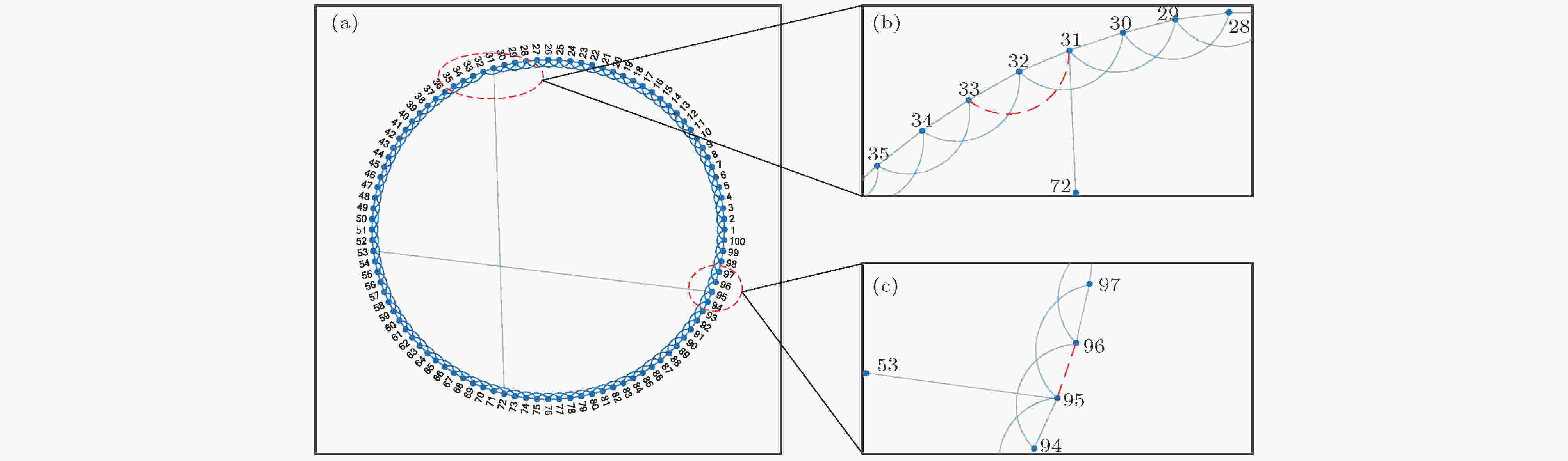
图 1 随机生成的100节点WS小世界网络　(a) 网络结构; (b) 边31-33被改连至边31-72; (c) 边95-96被改连至边95-53
Figure1. A random WS small-world network with 100 nodes: (a) Network structure; (b) the edge 31-33 is rescheduled to the edge 31-72; (c) the edge 95-96 is rescheduled to the edge 95-53.

表1列出了该WS小世界网络与同规模随机网络的平均聚类系数、特征路径长度等参数. 可见, 该网络的特征路径长度为随机网络的2.49倍, 但其平均聚类系数为随机网络的近20倍, 这是由于边31-72和95-53的长程连接提高了网络的连通性.

网络类型	节点数	边数	平均聚类 系数	特征路径 长度
WS小世界网络	100	200	0.486	8.4891
随机网络	100	200	0.0254	3.4158

表1WS小世界网络以及同规模随机网络的网络参数
Table1.Network features of the WS small-world network and random networks.

现利用加权K-阶传播数法对该网络节点的重要性进行分析. 图2(a)为网络的K-阶结构熵${H^K}$, 图2(b)为权重系数${c^K}$, 图2(c)为归一化的节点重要性. 此外, 图2(c)中的小图按色度对重要性进行了标注.
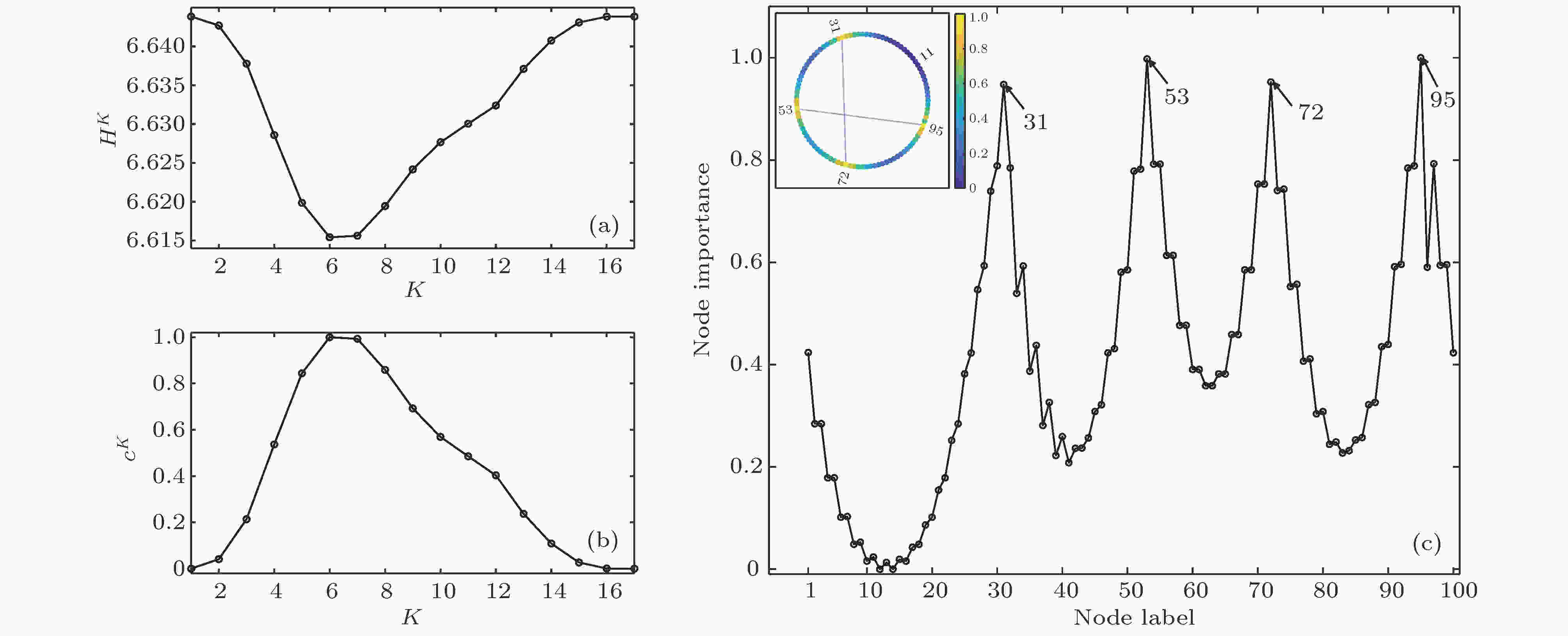图 2 基于加权K-阶传播数法的WS小世界网络节点重要性结果　(a) K-阶结构熵; (b) 权重系数; (c) 节点重要性
Figure2. Node importance of the WS small-world network based on the weighted K-order propagation number algorithm: (a) The K-order structure entropy; (b) the weight coefficient; (c) the importance of nodes.

由前文所述, 节点95和53, 31和72之间的长程连接提高了网络的连通性, 若移除上述任一节点, 网络的特征路径长度将大为增加, 因此加权K-阶传播数法认为以上四个节点的重要性最高是较为合理的. 由于该网络是基于最近邻耦合网络构造的, 而最近邻耦合网络中每个节点与其邻近的左右两侧各两个节点相连. 因此, 与95, 53, 31, 72距离相近的左右各两个节点的重要性应当相似, 且距离95, 53, 31, 72越远, 节点的重要性越低. 例如, 移除91, 92, 99或98中的任一节点对网络结构造成的影响是相似的; 此外, 同时移除99和98相较同时移除100和1, 会有更多的节点难以通过95进行长程通信, 因此99和98的重要性高于100和1是较为合理的. 值得注意的是, 图2(c)中97的重要性显著高于96, 这是由于边96-95被断开, 若依赖96进行长程通信需要借助边95-94, 而97与95直接相连, 因此通过97进行长程通信更为便捷. 此外, 由于边33-31被断开, 33, 34, 35等节点向30, 29, 28等节点进行短程通信, 或经由31向72等节点进行长程通信, 均需要依赖节点32, 因此其重要性应当较高. 最后, 35, 36, 37, 38等节点进行长短程通信时需要依赖33或34; 对35, 37等奇数节点而言, 通过33或34进行通信的效果相同, 但对36, 38等偶数节点而言, 通过34进行通信的效率更高, 可见34的重要性大于33, 这也可以解释图2(c)中36的重要性略高于35等现象.
为了进一步证明加权K-阶传播数法的有效性, 图3绘制了度中心性、Ren法、Chen法、介数中心性、特征向量法、Katz指标(权重衰减因子取1.5倍邻接矩阵最大特征值的倒数)、PageRank算法(阻尼系数取0.85)以及CI法(权重系数取0.5)得出的节点重要性结果. 由于K-核分解法得到的所有节点的重要性相同, 因此其结果未在图3给出.
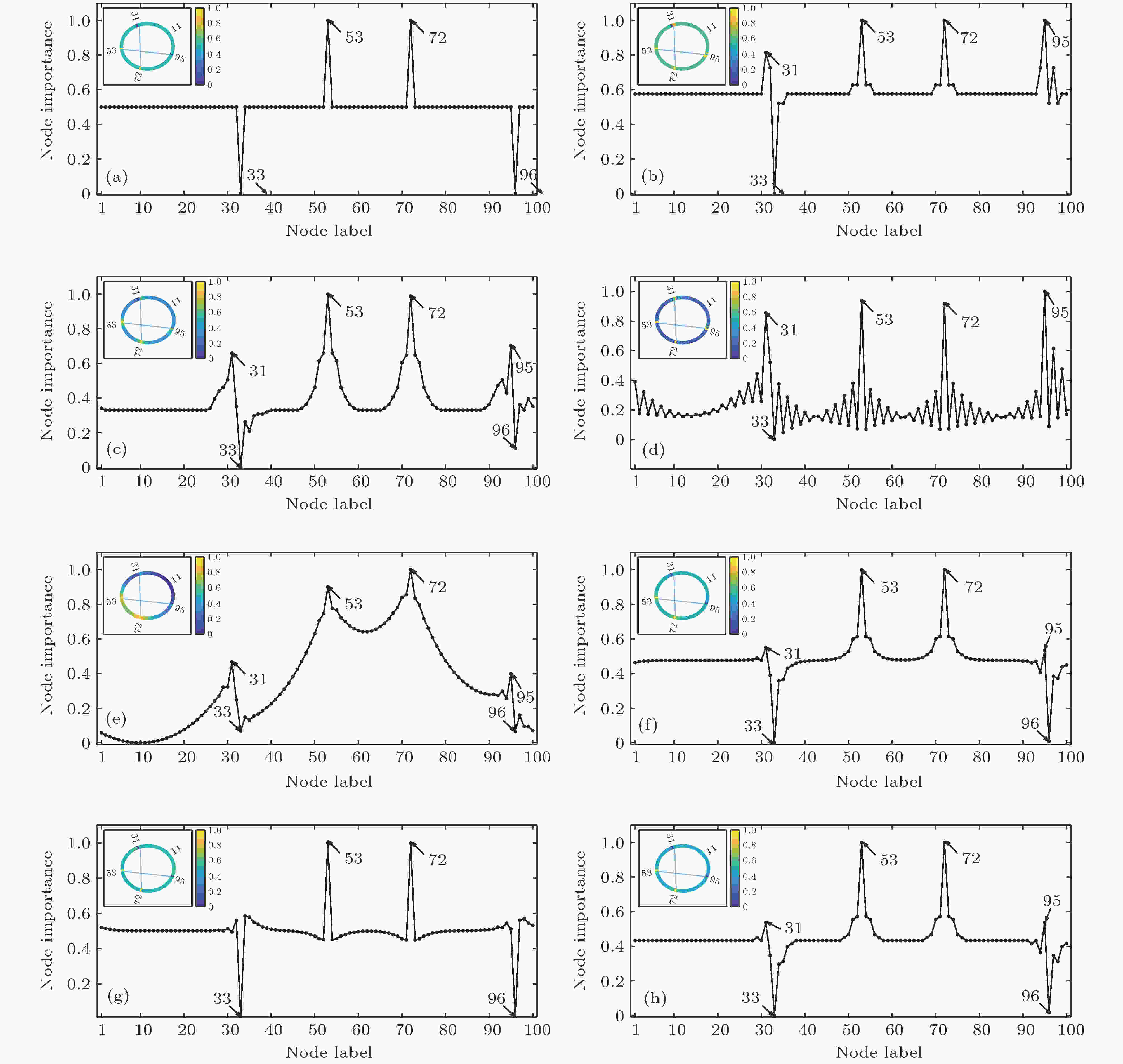图 3 基于若干传统算法的WS小世界网络节点重要性评价结果　(a) 度中心性; (b) Ren法; (c) Chen法; (d) 介数中心性; (e) 特征向量法; (f) Katz指标法; (g) PageRank算法; (h) CI法
Figure3. Node importance of the WS small-world network based on some traditional algorithms: (a) Degree centrality; (b) Ren method; (c) Chen method; (d) betweenness centrality; (e) eigenvector method; (f) Katz index; (g) PageRank; (h) CI method.

由图3可知, 以上方法认为33或96的重要性最低, 而加权K-阶传播数法却认为33和96的重要性较高. 由前文分析可知, 虽然在33节点移除后, 网络的长短程通信不会受到显著影响, 但27, 28, 29等节点与34, 35, 36等节点间的短程通信, 或34, 35, 36等节点依靠31进行长程通信只能依赖边32-34进行; 同样, 当96被移除后, 边95-97将参与所有通信, 可见33和96的存在降低了其余重要节点或边的负载, 起到了分流的作用, 因此认为33或96在所有节点中重要性最低是值得商榷的; 度中心性、特征向量法、Katz指标、PageRank算法和CI法认为72和53的重要性远高于31和95, 但长程通信需要同时依赖以上4个节点进行, 因此节点31和72或95和53的重要性应当是相似的; 度中心性、Ren法、Chen法、Katz指标、PageRank算法和CI法, 尤其是K-核分解法对节点的排序并不细致, 存在节点重要性相同的情况; 此外, 介数中心性认为10, 11, 12等节点的重要性高于52, 54, 71, 73等节点, 49, 51, 55, 57, 74, 76等节点的重要性高于50, 52, 54, 56, 73, 75等节点, PageRank算法认为61, 62, 63等节点的重要性高于52, 54, 71, 73等节点, 均缺乏较为合理的解释. 可见, 加权K-阶传播数法对网络通信的刻画更为细致, 节点重要性的评估优于以上传统方法.
2 -->

3.2.海豚网络

为了进一步验证加权K-阶传播数法的有效性, 本文以海豚网络为例进行研究. Lusseau等^[26,27]对新西兰道特富尔峡湾(Doubtful Sound) 62只宽吻海豚进行研究并构建了海豚社会网络. 基于加权K-阶传播数法的海豚网络节点重要性结果如图4所示, 图4(a)为网络的K-阶结构熵${H^K}$, 图4(b)为权重系数${c^K}$, 图4(c)为归一化后的节点重要性. 网络中节点代表海豚, 边表示海豚间的相关接触.
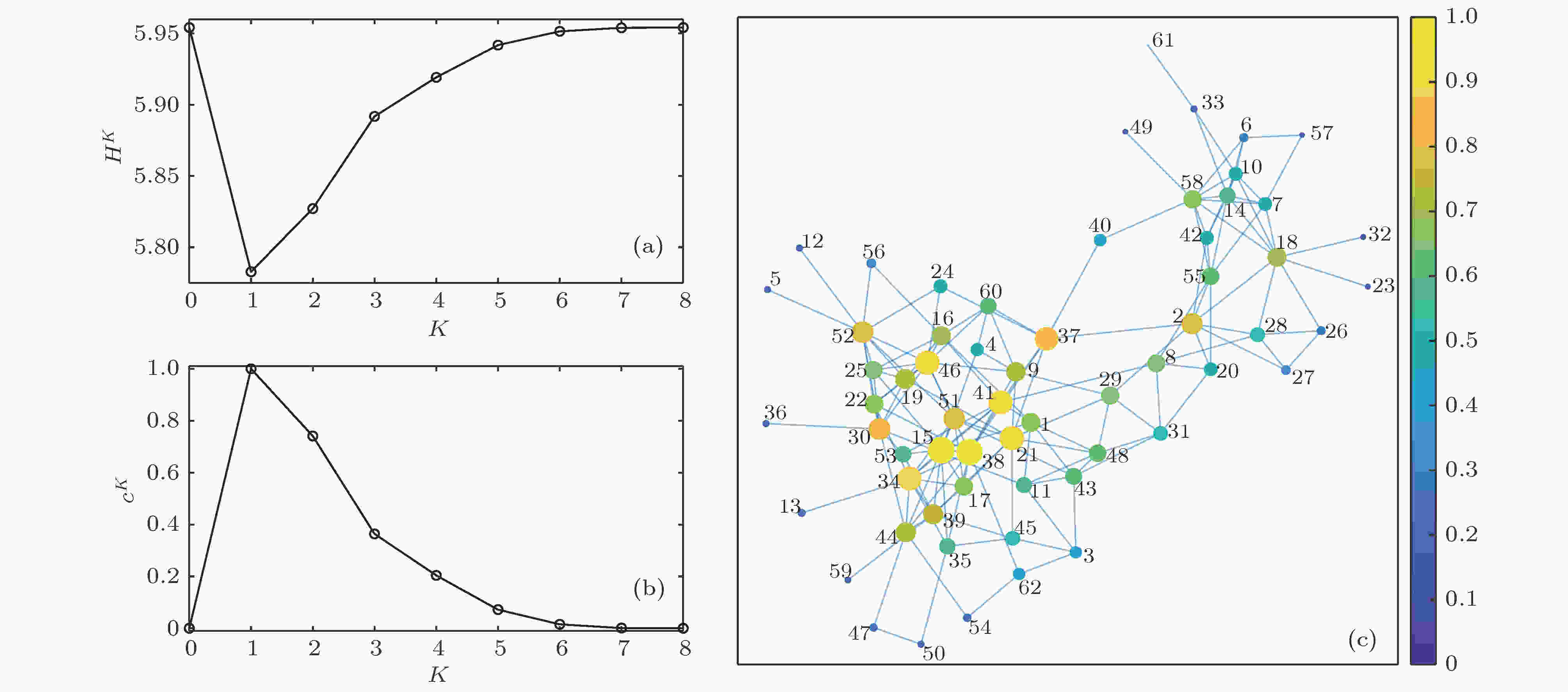图 4 基于加权K-阶传播数法的海豚网络节点重要性结果　(a) K-阶结构熵; (b) 权重系数; (c) 节点重要性
Figure4. Node importance of the dolphin network based on the weighted K-order propagation number algorithm: (a) The K-order structure entropy; (b) the weight coefficient; (c) the importance of nodes.

表2列出了基于加权K-阶传播数法、Ren法、Chen法、介数中心性、特征向量法、Katz指标(权重衰减因子为1.5倍邻接矩阵最大特征值的倒数)、PageRank算法(阻尼系数0.85)、CI法(权重系数取0.5)得出的前15个重要节点的排序结果. 由于度中心性和K-核分解法存在节点重要性相等的情况, 其排序结果未在表2列出. 其中, 基于度中心性法得到的节点重要性排序结果(前20个重要节点)为15 > 38 = 46 > 34 = 52 > 18 = 21 = 30 = 58 > 2 = 14 = 39 = 41 > 10 = 16 = 19 = 37 = 44 = 51 = 55; K-核分解法认为1, 2, 7, 8, 9等37个节点的重要性最高且相等.

节点重要性	加权K-阶传播数法	Ren法	Chen法	介数中心性法	特征向量法	Katz指标法	PageRank算法	CI法
1	15	15	15	37	15	15	15	15
2	38	38	38	2	38	38	18	38
3	46	46	46	41	46	46	52	46
4	21	34	34	38	34	34	58	34
5	41	51	51	8	51	52	38	41
6	34	41	41	18	30	30	46	30
7	37	21	17	21	52	41	34	52
8	30	30	22	55	17	21	30	21
9	52	52	19	52	41	51	14	51
10	51	44	30	58	22	39	2	19
11	2	39	21	40	19	19	21	39
12	39	19	25	29	39	17	39	17
13	19	37	39	30	25	22	10	22
14	44	22	52	44	44	44	41	44
15	9	18	44	15	21	25	55	25

表2海豚网节点重要性排序结果
Table2.Node importance ordering result of the dolphin network.

与度中心性、Ren法、Chen法、特征向量法、Katz指标、PageRank算法和CI法不同, 加权K-阶传播数法认为节点37相对重要, 排在第7位. 文献[27]将该海豚网络划分成了若干小社区, 指出37号海豚曾消失了一段时间, 此时不同海豚社区间的互动受到了限制, 当37号海豚再次出现时, 社区又恢复了普遍联系, Lusseau等^[27]指出37号海豚是社区间信息交流的关键个体. 因此, 加权K-阶传播数法认为节点37相对重要的结论是较为合理的. 然而, 37号海豚处于社区边缘, 因此介数中心性认为节点37重要性最高的结论是值得商榷的.
此外, 加权K-阶传播数法提高了对节点2和21的重视程度, 分别排在第11和第4位, 而2和21处于各自海豚社区偏中心位置, 又与37等负责信息交流的节点直接相连, 因此该结论是较为合理的; Ren法、Chen法、特征向量法、Katz指标法和CI法认为节点22相对重要, 但该节点的度中心性与介数均是较低的; 最后, 度中心性法和K-核分解法存在节点重要性相同的情况, 排序不细致. 可见, 加权K-阶传播数法在评价海豚网络节点重要性时适当地提高了对海豚社区间信息交流起到关键作用的节点的重视程度, 结果更为合理.
2 -->

3.3.基于节点重要性的蓄意攻击研究

为了进一步验证加权K-阶传播数法的优越性, 本文对美国西部电网^[25]、芝加哥公路网络^[28]、网络科学家合著网络^[29]以及小鼠神经纤维束网络(Kasthuri_graph_v4)^[30]进行了节点重要性研究. 其中美国西部电网共有4941个节点和6594条边, 描述了美国西部的高压输电电网结构; 芝加哥公路网络共有1467个节点和1298条边, 描述了美国芝加哥地区的公路运输情况; 网络科学家合著网络共有1589个节点和2742条边, 描述了从事网络理论和实验的科学家合著关系; 小鼠神经纤维束网络共有1029个节点和1700条边, 描述了小鼠部分脑皮层中神经元间的轴突束连接. 美国西部电网、芝加哥公路网络和网络科学家合著网络均是无权无向的; 小鼠神经纤维束网络是有权无向的, 为了适应加权K-阶传播数法, 本文忽略了该网络的边权信息. 以上网络的K-阶结构熵H^K如图5所示.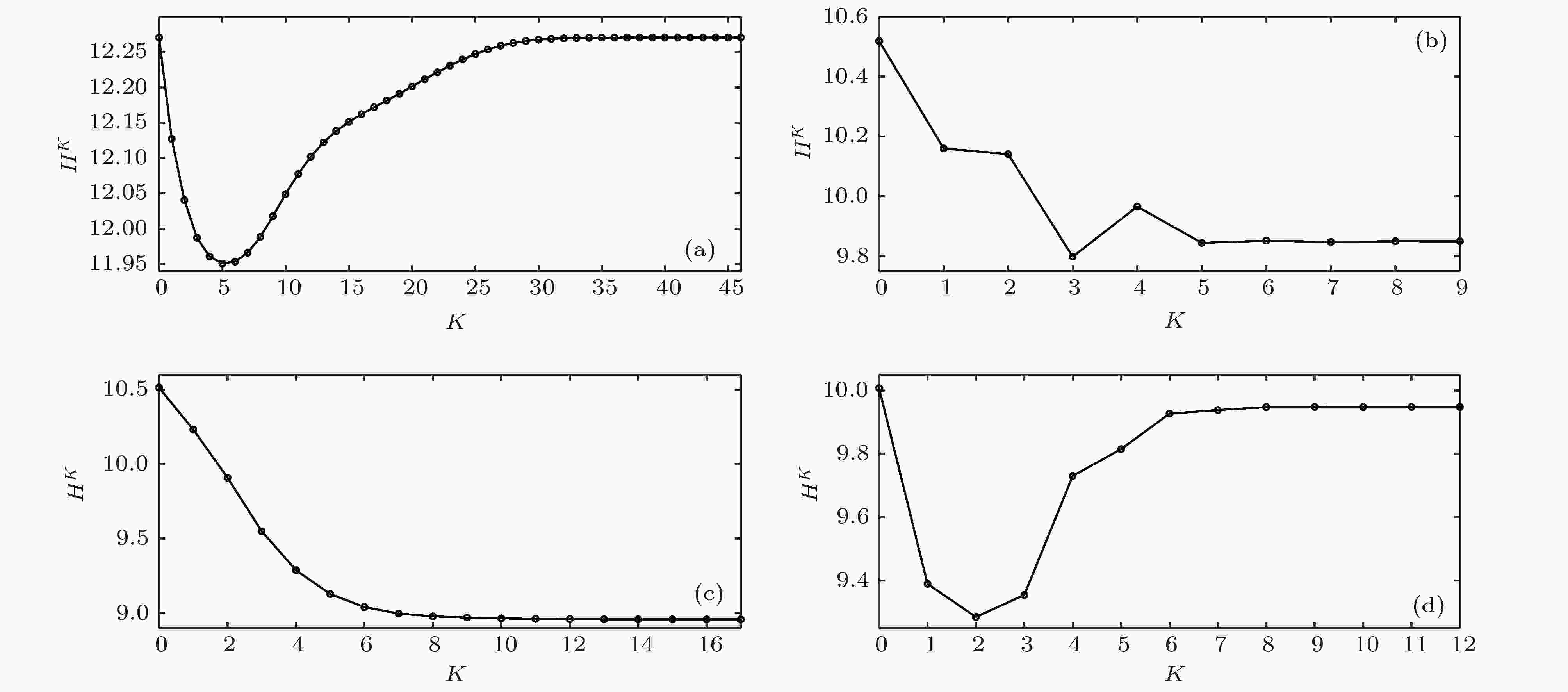
图 5 K-阶结构熵　(a) 美国西部电网; (b) 芝加哥公路网络; (c) 科学家合作网络; (d) 小鼠神经纤维束网络
Figure5. The K-order structure entropy: (a) The western power grid of the United States; (b) the road transportation network of the Chicago region; (c) the co-authorship network in network science; (d) the axonal tracts network between neurons of mouse.

由于以上四个网络的节点数较多, 本文拟采用蓄意攻击策略对节点重要性进行研究^[31-33]. 蓄意攻击策略是指基于节点重要性由高到低的排序依次攻击网络, 即移除与节点相连的所有边, 通过网络结构随攻击次数的变化情况来评价节点重要性算法的各自特点. 由于在蓄意攻击后网络结构发生了变化, 因此仅仅依据原始网络的节点重要性进行研究会存在偏差. 为了解决此问题, 本文在每次蓄意攻击后更新节点排序结果. 此外, 若存在重要性相等的情况, 将选择编号最小的节点进行攻击.
由于网络被攻击后可能会出现孤立节点, 因此选用网络效率来评价网络的连通性. 网络效率的表达式为

$e = \frac{1}{{n(n - 1)}}\sum\limits_{{v_i} \ne {v_j}} {\frac{1}{{{d_{{v_i}{v_j}}}}}} , $

其中${d_{{v_i}{v_j}}}$是指节点${v_i}$和${v_j}$之间的最短路径长度. 由(6)式可知, e值越大, 网络效率越高; 当网络由孤立节点组成时$e = 0$, 取值最小. 攻击节点可能造成网络连接通路的中断, 节点间的最短路径将有所增大, 网络效率则会随之降低. 为了更为直观地反映被攻击后网络效率的降低情况, 依照文献[9]定义网络效率下降率$\varepsilon $为

$\varepsilon = 1 - \frac{e}{{{e_0}}}, $

其中${e_0}$为未被攻击的原始网络的网络效率. 由(7)式可见, ε的取值为$[0,\;1]$, 当网络未被攻击时$\varepsilon = 0$, 当网络被攻击时ε会随之升高; 最终, 当所有的边被删除时网络效率降至最低, 此时$\varepsilon = 1$. 此外, 为了进一步分析攻击前后网络拓扑结构的变化情况, 依照文献[33]将网络最大子图节点数设为γ. 图6和图7分别绘制了美国西部电网、芝加哥公路网络、网络科学家合著网络以及小鼠神经纤维束网络基于不同节点重要性的排序方法, 其网络效率下降率ε和最大子图节点数γ随攻击次数的变化曲线. 其中, Katz指标的权重衰减因子为1.5倍邻接矩阵最大特征值的倒数; PageRank算法的阻尼系数取0.85; CI法的权重系数取0.5.
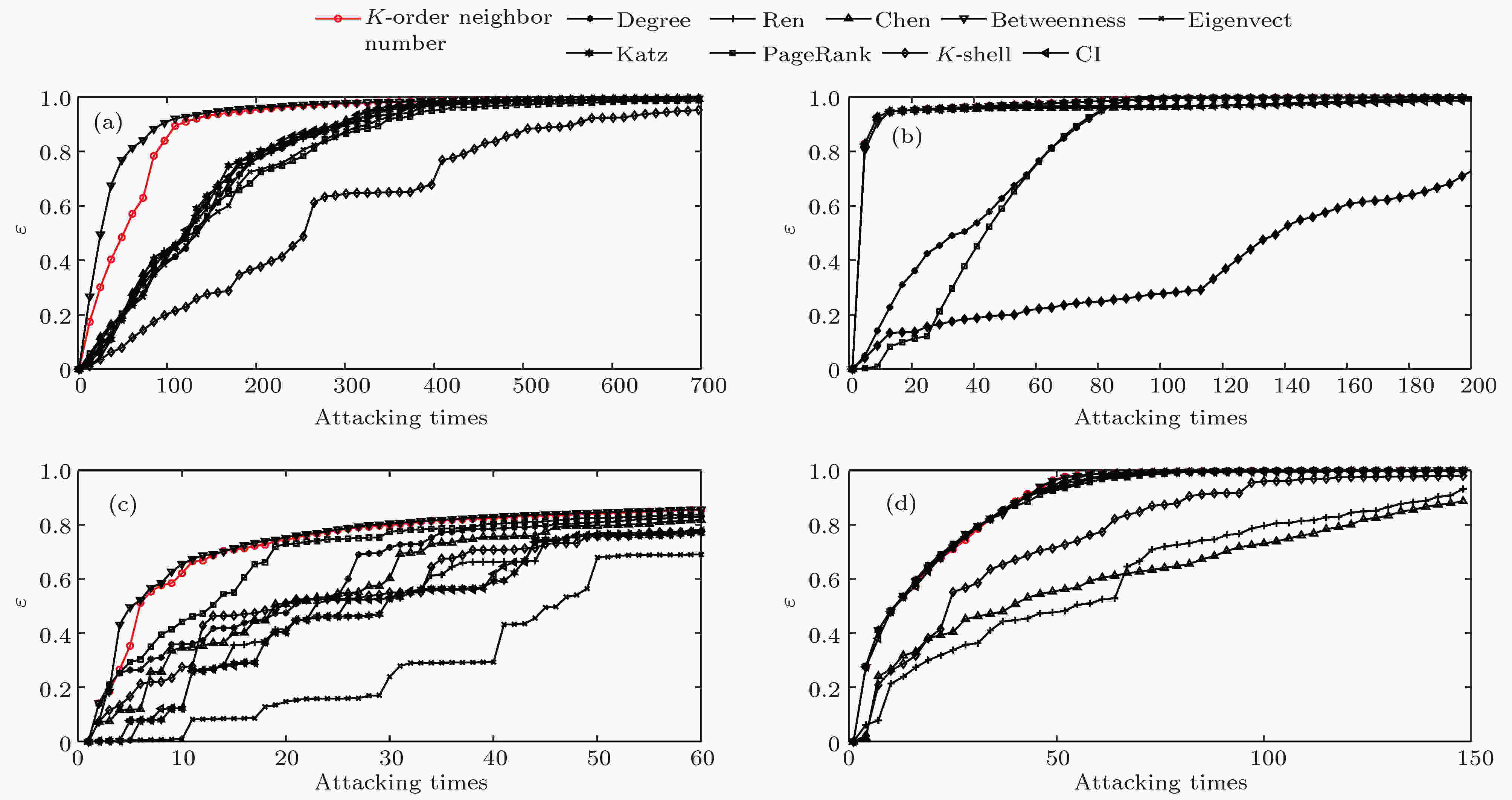图 6 网络效率下降率ε随攻击次数的变化情况　(a) 美国西部电网; (b) 芝加哥公路网络; (c) 网络科学家合著网络; (d) 小鼠神经纤维束网络
Figure6. Change of the network efficiency decrease rate ε with attacking times: (a) The western power grid of the United States; (b) the road transportation network of the Chicago region; (c) the co-authorship network in network science; (d) the axonal tracts network between neurons of mouse.

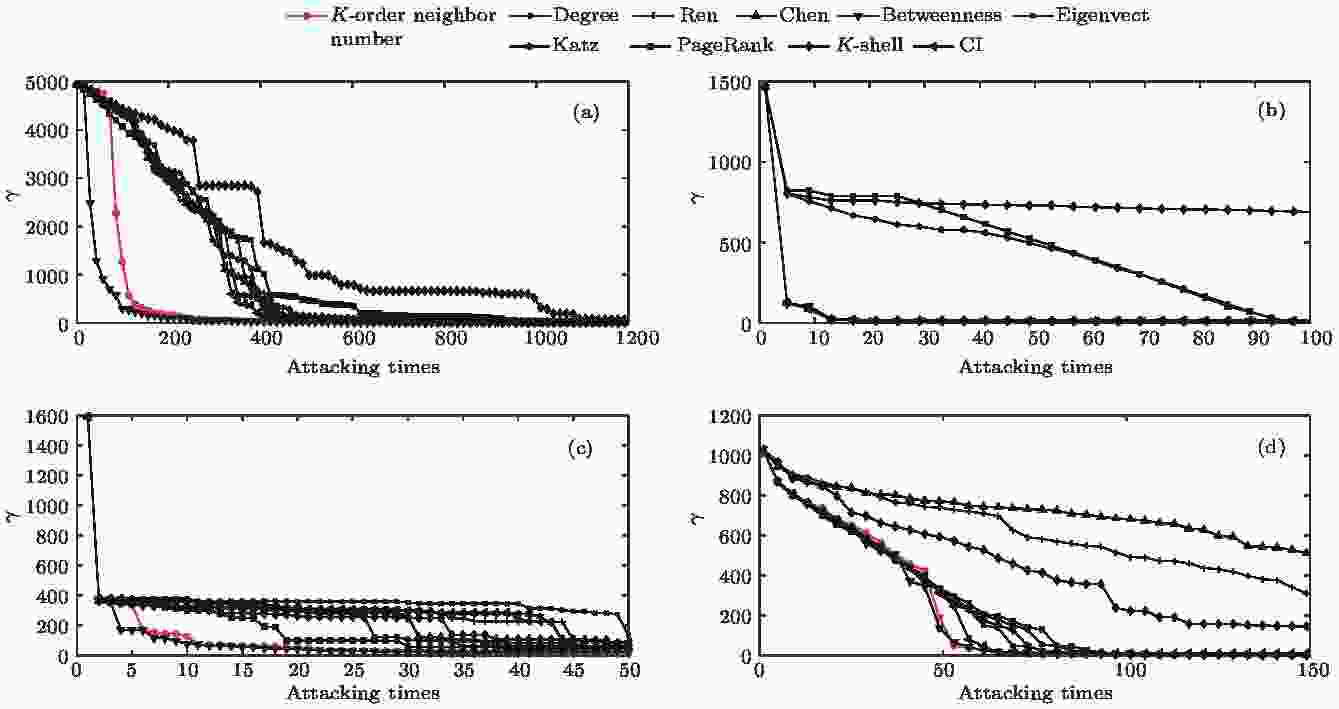图 7 最大子图节点数γ随攻击次数的变化情况　(a) 美国西部电网; (b) 芝加哥公路网络; (c) 网络科学家合著网络; (d) 小鼠神经纤维束网络
Figure7. Change of the node number of the maximum sub-graph ε with attacking times: (a) The western power grid of the United States; (b) the road transportation network of the Chicago region; (c) the co-authorship network in network science; (d) the axonal tracts network between neurons of mouse.

对美国西部电网而言, 依照加权K-阶传播数法和介数中心性法的排序结果进行攻击, 网络效率下降得最为迅速, 仅攻击约100次后, 网络效率便下降了近90%; 而依据度中心性、Ren法、Chen法、特征向量法、Katz指标、PageRank算法和CI法则需约300次, K-核分解法需约550次, 才能达到同等效果. 此外, 基于加权K-阶传播数法和介数中心性对网络进行攻击, 最大子图节点数降低的速率远远高于其他方法. 以加权K-阶传播数法为例, 当网络被攻击200次后, 最大子图节点数仅为154, 为原始网络节点数的3%, 可认为网络基本瘫痪. 而度中心性、Ren法、Chen法、特征向量法、Katz指标和CI法则需攻击近400次, PageRank算法需650次, K-核分解法需1000次才能达到相同效果; 对芝加哥公路网络而言, 依据加权K-阶传播数法、介数中心性、Chen法、特征向量法、Katz指标和CI法进行蓄意攻击, 网络被破坏的程度较为接近, 且优于度中心性、Ren法、PageRank算法和K-核分解法. 其中, 依据加权K-阶传播数法进行蓄意攻击, 网络效率下降得最为迅速; 对网络科学家合著网络而言, 依照加权K-阶传播数法和介数中心性进行蓄意攻击, 网络被破坏的程度较为接近, 且优于其他算法; 对小鼠神经纤维束网络而言, 依据加权K-阶传播数法、度中心性、介数中心性、特征向量法、Katz指标、PageRank算法和CI法进行蓄意攻击, 网络被破坏的程度较为接近, 且优于Ren法、Chen法和K-核分解法. 其中, 依据加权K-阶传播数法和介数中心性进行蓄意攻击, 网络最大子图节点数下降得最为迅速, 略优于其他算法.
综上所述, 无论对美国西部电网、芝加哥公路网络、网络科学家合著网络还是小鼠神经纤维束网络而言, 基于加权K-阶传播数法进行蓄意攻击, 仅需移除少量重要节点便可实现对网络结构的充分破坏.

本文考虑到个体间的相关关系, 基于网络拓扑结构重新描述了传染病模型, 并将各个节点分别设置为传染源进行疾病传播, 提出了加权K-阶传播数法. 通过对WS小世界网络的仿真分析发现, 加权K-阶传播数法相较于传统的节点重要性评价指标能够更为综合地考量长程连接对网络长、短程通信的影响; 此外, 加权K-阶传播数法不仅认为海豚网络社区中心的重要性较高, 且适当地提高了对社区间的信息交流起到关键作用的海豚的受重视程度. 最后, 本文还基于蓄意攻击策略以美国西部电网、芝加哥公路网络、网络科学家合著网络以及小鼠神经纤维束网络为实例进行了研究. 然而, 由于目前加权K-阶传播数法的求解依赖于网络邻接矩阵的K-阶多项式, 需要进行K–1次矩阵乘法和K次矩阵加法, 时间复杂度较高. 因此需要进一步探索K-阶传播数的物理意义以提出更为便捷的求解方案. 此外, 小鼠神经纤维束网络原为有权网络, 为了适应加权K-阶传播数法, 本文忽略了该网络的边权信息. 因此将加权K-阶传播数法进行改进, 使其适用于有向有权网络, 也是后续研究的重点.