摘要: 复杂网络的同步作为一种重要的网络动态特性, 在通信、控制、生物等领域起着重要的作用. 谱粗粒化方法是一种在保持原始网络的同步能力尽量不变情况下将大规模网络约简为小规模网络的算法. 此方法在对约简节点分类时是以每个节点对应特征向量分量间的绝对距离作为判断标准, 在实际运算中计算量大, 可执行性较差. 本文提出了一种以特征向量分量间相对距离作为分类标准的谱粗粒化改进算法, 能够使节点的合并更加合理, 从而更好地保持原始网络的同步能力. 通过经典的三种网络模型(BA无标度网络、ER随机网络、NW小世界网络)和27种不同类型实际网络的数值仿真分析表明, 本文提出的算法对比原来的算法能够明显改善网络的粗粒化效果, 并发现互联网、生物、社交、合作等具有明显聚类结构的网络在采用谱粗粒化算法约简后保持同步的能力要优于电力、化学等模糊聚类结构的网络.
关键词: 复杂网络 /
同步能力 /
谱粗粒化 /
相对距离 English Abstract A spectral coarse graining algorithm based on relative distance Yang Qing-Lin Wang Li-Fu Li Huan Yu Mu-Zhou School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China Fund Project: Project supported by the Nature Science Foundation of Hebei Province, China (Grant Nos. F2016501023, F2017501041), Fundamental Research Funds for the Central Universities, China (Grant No. N172304030), and the National Natural Science Foundation of China (Grant No. 61402088).Received Date: 15 October 2018Accepted Date: 14 March 2019Available Online: 01 May 2019Published Online: 20 May 2019Abstract: As a key approach to understanding complex systems (e.g. biological, physical, technological and social systems), the complex networks are ubiquitous in the whole world. Synchronization in complex networks is significant for a more in-depth understanding of the dynamic characteristics of the networks, where tremendous efforts have been devoted to their mechanism and applications in the last two decades. However, many real-world networks consist of hundreds of millions of nodes. Studying the synchronization of such large-scale complex networks often requires solving a huge number of coupled differential equations, which brings great difficulties to both computation and simulation. Recently, a spectral coarse graining approach was proposed to reduce the large-scale network into a smaller one while maintaining the synchronizability of the original network. The absolute distance between the eigenvector components corresponding to the minimum non-zero eigenvalues of the Laplacian matrix is used as a criterion for classifying the nodes without considering the influence of the relative distance between eigenvector components in an original spectral coarse graining method. By analyzing the mechanism of the spectral coarse graining procedure in preserving the synchronizability of complex networks, we prove that the ability of spectral coarse graining to preserve the network synchronizability is related to the relative distance of the eigenvector components corresponding to the merged nodes. Therefore, the original spectral coarse graining algorithm is not satisfactory enough in node clustering. In this paper, we propose an improved spectral coarse graining algorithm based on the relative distance between eigenvector components, in which we consider the relative distance between the components of eigenvectors for the eigenvalues of network coupling matrix while clustering the same or similar nodes in the network, thereby improving the clustering accuracy and maintaining the better synchronizability of the original network. Finally, numerical experiments on networks of ER random, BA scale-free, WS small-world and 27 different types of real-world networks are provided to demonstrate that the proposed algorithm can significantly improve the coarse graining effect of the network compared with the original algorithm. Furthermore, it is found that the networks with obvious clustering structure such as internet, biological, social and cooperative networks have better ability to maintain synchronization after reducing scale by spectral coarse-grained algorithm than the networks of fuzzy clustering structure such as power and chemical networks.Keywords: complex network /synchronizability /spectral coarse graining /relative distance 全文HTML --> --> --> 1.引 言 从20世纪末开始, 复杂网络理论逐步成为社会、经济、化学和信息系统等领域的重要研究方法, 对复杂网络静态特性和动态特性的定量定性描述, 已经成为网络时代一个极其重要的挑战性课题, 被称为“网络的新科学(new science of network)”[1 ] . 复杂网络的同步作为一种重要的网络动态行为, 在激光系统、超导材料和通信等领域有重要的意义. 同步现象在自然界中也广泛存在, 例如萤火虫有规律地闪光、心脏细胞同步震荡、挂在同一横梁上的钟摆同步摆动等. 近20多年来, 研究人员对复杂网络的同步研究取得了丰硕的成果[2 -15 ] . 其中, 对于一般连续时间耦合网络最常用的方法是将网络的状态方程线性化后转化成主稳定函数来研究[2 ,3 ] . 然而对于实际网络动辄成千上万的节点来说, 判断他们是否同步需要求解大量耦合微分方程, 并且小规模网络得到的同步判据或定理不能直接推广到大规模网络[16 ] . 因此, 如何将复杂网络进行约简并保留其同步能力不变, 对大规模网络的同步分析和仿真至关重要. Gfeller和Rios[17 ,18 ] 提出的谱粗粒化(spectral coarse graining, SCG)算法通过分析网络的结构矩阵, 把特征向量分量相同或相近的节点合并, 从而保证了约简后网络的同步能力不变. 周建等[19 ] 提出的改进谱粗粒化(improved spectral coarse graining, ISCG)算法采用了不同的分类方式, 改善了在特征向量分量分布极不均匀时的粗粒化效果, 并且降低了算法的复杂度. Chen等[20 ] 进一步研究了网络的聚类结构对谱粗粒化效果的影响. Wang和Xu[21 ] 发现采用SCG算法对网络约简后, 其可控性也能很好地保留下来.2.同步能力的刻画 主稳定方程法是研究一般连续时间耦合网络同步的常用方法[2 ,3 ] . 考虑由$N$ 个节点构成的复杂网络, 其中第$i$ 个节点的动力学方程为${x_i} \in {{{R}}^m}$ 为节点i 的m 维状态变量; ${f}\left( {x_i} \right)$ 为第i 个节点自身的状态方程; 常数$\mu > 0$ 是网络的耦合强度; ${H}\left( \bullet \right):{{{R}}^m} \to {{{R}}^m}$ 表示各个节点之间的内部耦合函数; Laplacian矩阵${L} = \left( {{l_{ij}}} \right) \in$ $ {{{R}}^{N \times N}}$ 是外部耦合矩阵, 表示网络的拓扑结构, 满足耗散条件$\displaystyle\sum\limits_{j = 1}^n {{l_{ij}} = 0} $ . 特别的, 当Laplacian矩阵${{L}}$ 表示一个无向无权的网络时, 有如下定义:${k_i}$ 为节点$i$ 的度数. 此时, 外部耦合矩阵${L}$ 是一个不可约的对称阵, 具有非负特征根并且特征根满足$0 = {\lambda _1} \leqslant {\lambda _2} \leqslant \cdots \leqslant {\lambda _N}$ . 如果在$t \to \infty $ 时有${x_1}\left( {t} \right) = {x_2}\left( {t} \right) = \cdots = {x_N}\left( {t} \right) = s\left( {t} \right)$ , 那么就称动态网络(1 )式能够达到完全同步, 其中同步流形$s\left( {t} \right)$ 满足$\dot s\left( t \right) = {{f}}\left( {s\left( t \right)} \right)$ . 对(1 )式在同步状态$s\left( t \right)$ 处线性化, 令${\xi _i}\left( {t} \right) = {x_i}\left( {t} \right) - s\left( {t} \right)$ , 可以得到如下线性动力学方程:${{Df}}\left( {s} \right)$ 和 ${DH}\left( {s} \right)$ 分别是${{f}}\left( {s} \right)$ 和${{H}}\left( {s} \right)$ 在同步$s\left( t \right)$ 处的Jacobi(雅可比)矩阵, 令$ {\xi} = \left[ {{\xi _1},{\xi _2} \cdots {\xi _N}} \right] $ , 则(4 )式可以写为${{L}^{\rm{T}}} = {J\Lambda }{{J}^{ - 1}}$ 为Laplace矩阵${L}$ 的Jordan分解, $ \Lambda = {\rm{diag}}\left[ {{\lambda _{\rm{1}}},{\lambda _{\rm{2}}}, \cdots ,{\lambda _N}} \right] $ 为${L}$ 的特征值矩阵. 再令$ {\psi } = [\psi _{\rm{1}},\psi _{\rm{2}}, \cdots \psi _{\rm{N}}] = {\xi J} $ , 将(5 )式对角化可得6 )式是一个关于${\lambda _k}$ 的N 维微分方程组, 展开后可以写成7 )式一般化后即可得到主稳定方程:$\alpha = \mu {\lambda _k}$ . (8 )式的最大Lyapunov指数${L_{\max }}$ 是变量 $\alpha $ 的函数, 称为动力学网络(1 )式的主稳定函数. 给定一耦合强度$\mu $ , 在坐标轴上可以相应地找到一点$\mu {\lambda _k}$ , 若该点对应的${L_{\max }}$ 为负数时, 则该特征模态为稳定态; 反之, 则该特征模态为不稳定态. 如果与特征值${\lambda _k}\left( {k = 2,3, \cdots,N} \right)$ 对应的最大Lyapunov指数${L_{\max }}$ 均为负数, 那么在该耦合强度$\mu $ 下, 整个网络的同步流形是渐近稳定的. 我们把使得 ${L_{\max }} < 0$ 的 $\alpha $ 取值范围$S$ 称为动态网络(1 )式的同步化区域, 它由孤立节点的动力学函数 ${{f}}\left( {x_i} \right)$ 和内部耦合函数${H}\left( \bullet \right)$ 决定. 如果耦合强度$\mu $ 与Laplacian矩阵的每个非零特征值之积都在同步区域$S$ 内, 即$\mu {\lambda _k} \in S \left( {k = 2,3, \cdots,N} \right)$ , 那么动态网络(1 )式的同步流形是渐近稳定的, 网络就能达到同步[2 ,3 ] . 同步区域$S$ 可以分为以下4种类型: Ⅰ. $S = \left( {{\alpha _1}, + \infty } \right)$ ; Ⅱ. $S = \left( {{\alpha _1},{\alpha _2}} \right)$ ; Ⅲ. S =$\left( {{\alpha _1},{\alpha _2}} \right) \cup $ $ \left( {{\alpha _2},{\alpha _3}} \right) \cup \cdots $ ; Ⅳ. $S = \varnothing$ . 其中, 类型Ⅰ网络的同步化能力可以用Laplacian矩阵${{L}}$ 的最小非零特征值 ${\lambda _2}$ 来刻画, ${\lambda _2}$ 越大, $\mu {\lambda _2}$ 越容易大于 ${\alpha _1}$ , 网络的同步化能力越强; 类型Ⅱ网络的同步能力可以用Laplacian矩阵${{L}}$ 的最大特征值${\lambda _N}$ 与${\lambda _2}$ 的比值 ${{{\lambda _N}}/ {{\lambda _2}}}$ 来刻画, ${{{\lambda _N}}/ {{\lambda _2}}}$ 越小, 网络的同步能力越强; 类型Ⅲ网络需要所有特征值都满足一定的条件, 很难达到同步; 类型Ⅳ网络无论耦合强度$\mu $ 和Laplacian矩阵${{L}}$ 的特征值为何值, 网络都不能达到同步. 大多数网络都属于Ⅰ或Ⅱ两种类型, 因此在分析网络的同步能力时, 通常考虑${\lambda _2}$ 和${{{\lambda _N}} /{{\lambda _2}}}$ 两个指标[22 ] .3.网络同步的SCG算法和ISCG算法 23.1.SCG方法与ISCG方法的原理 3.1.SCG方法与ISCG方法的原理 由主稳定方程法可知, 当动态网络节点间的耦合强度、孤立节点的动力学方程和内部耦合函数固定后, 网络的同步能力由Laplacian矩阵的${\lambda _2}$ 或${{{\lambda _N}} /{{\lambda _2}}}$ 决定. 所以要想保持网络的同步能力不变, 需要尽量保持网络在粗粒化前后的${\lambda _2}$ 或${{{\lambda _N}} /{{\lambda _2}}}$ 不变. Dffller和Rios[17 ,18 ] 提出的SCG算法较好地保留了约简前后网络的${\lambda _2}$ 和${{{\lambda _N}} /{{\lambda _2}}}$ 值, 从而保持了约简前后网络的同步能力不变. 这种算法主要解决了合并过程中的两个主要问题, 一是如何合并节点及更新边, 即如何更新约简后网络的Laplacian矩阵; 二是确定哪些节点可以被合并.图1(a) 是一个无向无权的网络, 如果把节点c 、d 、e 合并为图1(b) 中的节点g , 则称节点c 、d 、e 组成了团${C_g}$ , 记${\omega _{x \to y}}$ 是节点x 到节点y 的权值, 我们有:图 1 合并节点的过程Figure1. The processing of merging nodes.$ \left| {C_g} \right| $ 表示团${C_g}$ 中包含的节点个数. 同理, 我们也可以求出其他的边权. 在大型网络中, 记初始节点的标号$i = 1,2, \cdots,N$ . 约简后的节点标号为$C = 1,2, \cdots,\tilde N$ , $\tilde N$ 为约简之后网络的节点数, $C$ 也可以表示原始网络中要约简的节点所在的团, 同属于一个团的节点被合并成一个节点. 约简之后网络的Laplacian矩阵${\tilde L}$ 可以用以下公式求解${K} \in {{\bf{R}}^{\tilde N \times N}}$ 和${R} \in {{\bf{R}}^{N \times \tilde N}}$ 分别为${C_i}$ 表示原始网络节点i 所在团的标号; $\left| C \right|$ 表示团$C$ 中节点的个数, $\delta $ 是常用的Kronecker函数.${\lambda _2}$ 和 ${{{\lambda _N}} /{{\lambda _2}}}$ 两 种情况进行讨论. 若要保持网络(1 )式的Laplacian矩阵L ${\lambda _2}$ 不变, SCG方法的原理是将 ${\lambda _2}$ 所对应特征向量 ${{P}_2}$ 中分量相同或相近的节点合并在一起, 这样得到合并后网络的Laplacian矩阵${\tilde L}$ 的最小非零特征值 ${\tilde \lambda _2}$ 与原来网络的 ${\lambda _2}$ 相同或相近. 通常, 我们定义特征向量${{P}_2}$ 所对应的两个分量 ${p_{2i}}$ 和 ${p_{2j}}$ 相近是指$\left\| {{p_{2i}} - {p_{2j}}} \right\|/\left\| {{p_{2\max }} - {p_{2\min }}} \right\| \ll 1$ , 其中${p_{2\max }}$ 和${p_{2\min }}$ 分别是特征向量分量中的最大值和最小值. 具体的操作步骤为, 先把区间$\left[ {{p_{2\min }},{p_{2\max }}} \right]$ 平均分成$i$ 个区间, 再把分在同一个区间内的特征向量分量对应的节点合并为一个节点, 最后利用(11 )式求解约简后网络的Laplacian矩阵${\tilde L}$ . 类似地, 当要保持网络(1 )的Laplacian矩阵L ${{{\lambda _N}} /{{\lambda _2}}}$ 时, 需要同时保持${\lambda _2}$ 和${\lambda _N}$ 不变. 具体的步骤为: 先把${\lambda _2}$ 所对应的特征向量分量分为i 个等分区间, 再把 ${\lambda _N}$ 所对应的特征向量分量分为i 个等分区间, 找出${{P}_2}$ 和${{P}_N}$ 中同时落入等分区间的分量, 将这些分量对应的节点合并, 最后利用(11 )式更新合并后的Laplacian矩阵, 便可以得到约简后的网络.图1 表明, 采用谱粗粒化思想把外部连接相同的节点合并, 网络的第二小特征值${\lambda _2}$ 不变, 即约简后网络的同步能力不发生改变.[19 ] , 也是通过合并特征向量${{P}_2}$ 中相同或相近的分量达到约简网络的目的. 但与SCG算法不同的是, ISCG算法不是把特征向量分量等间距平分, 而是采用分裂聚类的方法对节点进行分类. 具体操作为, 当要保持 ${\lambda _2}$ 不变时, 先把 ${\lambda _2}$ 所对应的特征向量分量从小到大排列, 算出两两相邻分量间的距离, 找出最大的前 $\tilde N - 1$ 个间距, 在这 $\tilde N - 1$ 个间距设置分割点, 将特征向量分量分裂为$\tilde N$ 个聚类, 把属于同一聚类的节点合并为一个节点, 最后更新Laplacian矩阵, 就得到了节点数为 $\tilde N$ 的粗粒化网络. 同理, 当要保持 ${{{\lambda _N}} /{{\lambda _2}}}$ 不变时, 先根据特征向量分量的间距分别将${{P}_2}$ 的分量和${{P}_N}$ 的分量分裂为 $\tilde N$ 个聚类, 找出同时被分裂到同一聚类里的分量, 把分量对应的节点合并, 最后按照(11 )式来更新合并后网络的Laplacian矩阵. ISCG算法的优点在于可以将原始网络约简为任意指定规模 $\tilde N$ 的粗粒化网络, 复杂度为$ O\left( {{N^2}} \right) $ , 要低于SCG算法的复杂度 $ O\left( {{N^3}} \right) $ , 并且在特征向量分量分布不均匀时, 使用ISCG算法的粗粒化效果要明显优于SCG算法[19 ] .3.2.SCG算法和ISCG算法的局限 -->3.2.SCG算法和ISCG算法的局限 SCG算法和ISCG算法在保持网络的同步能力时都有着得天独厚的优势. 现实世界中大部分特征向量分量分布非常集中, 少数特征向量分量分布特别分散, 对于这种特征向量分量分布不均匀的网络采用SCG算法一方面会出现距离很近的特征向量分量被分到两个聚类里面, 另一方面由于少数特征向量分布较为分散, 导致得到的聚类数$\tilde N$ 随$i$ 变化不大, 不容易得到任意规模的粗粒化网络[19 ] . 而ISCG方法采用分裂聚类的方式对节点分类, 因此, 在特征向量${{P}_2}$ 的分量极不均匀时, 采用ISCG算法约简网络更能保持其同步能力.${\lambda _2}$ 对应的特征向量${{P}_2}$ 的第$i$ 个分量和第$j$ 个分量相等, 即${p_{2i}} = {p_{2j}}$ , 按照SCG算法或ISCG算法把这两个节点合并, ${\lambda _2}$ 的值在网络约简前后不发生改变. 而当${{P}_2}$ 的两个分量有较小的距离时, 两种算法的分类方式都遵循两个分量间距离越小, 被分在一起的几率越大, 而没有考虑分量间相对距离的因素. 如果设分量${p_{2i}}$ 与${p_{2j}}$ 之间的间距为$\varepsilon $ , 则${p_{2i}}$ 与${p_{2j}}$ 间的相对距离就是指$\varepsilon $ 占$\min \left\{ {\left. {\left| {{p_{2i}}} \right|,\left| {{p_{2j}}} \right|} \right\}} \right.$ 的比例$\rho = \varepsilon /\min \left\{ {\left. {\left| {{p_{2i}}} \right|,\left| {{p_{2j}}} \right|} \right\}} \right.$ . 下面我们通过一个例子说明在分类时只考虑绝对距离是不合理的.图2 所示, 网络的Laplacian矩阵为图 2 15个节点并为14个节点的两种方案Figure2. Two schemes of merging 15 nodes into 14 nodes.${\lambda _2} = 0.4130$ , 对应的特征向量$ {{P}_2} =[-4.19,2.87,-1.92,3.61,-2.80,2.87,-1.14,0.11, $ $1.51,1.00,2.80,-3.85,1.71,0.70,-3.27]^{\rm{T}}, $ ${{{P}}_2}$ 的第9 个与第10个分量分别是1.51和1.00, 相差0.51; 第 12个与第15个分量分别是$-3.85$ 和$-3.27$ 相差0.58. 如果以绝对距离作为合并节点的依据, 则合并节点9和10后${\lambda _2}$ 的变化量会更小. 实际上, 由(11 )式得到合并节点9和10后的Laplacian矩阵${{\tilde L}_1}$ 为${{\tilde L}_1}$ 的最小非零特征值${\tilde \lambda ^1}_2 = 0.4173$ , 比原始网络增加了1.04%. 如果合并节点12和15后网络的Laplacian矩阵${{\tilde L}_2}$ 为${{\tilde L}_2}$ 的最小非零特征值${\tilde \lambda ^2}_2 = 0.4141$ , 比原始网络增加了0.27%. 接下来计算分量间的相对距离, 第9个和第10个分量的相对距离ρ 1 = 0.51/1.00 = 0.51, 第12个与第15个分量的相对距离ρ 2 = 0.58/$\left| { - 3.27} \right| = 0.1774$ . 可见, 虽然第12个和第15个分量间的绝对距离比第9个和第10个间的大, 但相对距离比较小. 合并节点12和15后网络${\lambda _2}$ 的变化量比合并节点9和10后的更小, 更能保持原始网络的同步能力.${\lambda _2}$ 的变化量与所合并节点对应的特征向量分量间相对距离的关系.定理1: 在进行谱粗粒化过程合并两个节点时, 如果同一个特征值对应的两个特征向量分量${p_{2i}}$ 和${p_{2j}}$ 的间距$\varepsilon $ 远远小于$\min \left\{ {\left. {\left| {{p_{2i}}} \right|,\left| {{p_{2j}}} \right|} \right\}} \right.$ , 则合并节点$i$ 和节点$j$ 后网络特征值的变化量$\delta $ 与${p_{2i}}$ 和${p_{2j}}$ 间的相对距离$\varepsilon /\min \left\{ {\left. {\left| {{p_{2i}}} \right|,\left| {{p_{2j}}} \right|} \right\}} \right.$ 成正比.证明: 假设${\lambda _2}$ 对应的两个正的特征向量分量分别为为${p_{2i}}$ 与${p_{2j}}\left( {{p_{2i}} < {p_{2j}}} \right)$ , 第$j$ 个分量与第$i$ 个分量之间的距离为$\varepsilon $ , 即${p_{2j}} = {p_{2i}} + \varepsilon $ , 且$\varepsilon \ll {p_{2i}}$ . 合并节点$i$ 和节点$j$ 后${\lambda _2}$ 的改变量设为$\delta $ , 写出原始网络Laplacian矩阵的特征方程13 )式的第$i$ 个等式和第$j$ 个等式两边相加得到$\varepsilon \ll {p_{2i}}$ , 所以可以忽略$\varepsilon $ 的大小, 把合并后得到新节点所对应的特征向量分量近似为${p_{2i}}$ . 按照(11 )式求出合并后网络的Laplacian矩阵并写出特征方程15 )式的第i 个等式为14 )式和(16 )式联立可以得到17 )式表明, 约简网络后${\lambda _2}$ 的改变量$\delta $ 不仅与特征向量分量间的绝对距离$\varepsilon $ 有关, 还与特征向量分量${p_{2i}}$ 的大小有关. 在$\varepsilon $ 相对于${p_{2i}}$ 足够小时, $\delta $ 与绝对距离占$\min \left\{ {\left. {{p_{2i}},{p_{2j}}} \right\}} \right.$ 的比率$\rho = \varepsilon /\min \left\{ {\left. {{p_{2i}},{p_{2j}}} \right\}} \right.$ 成正比例关系. 同理, 可以得到当${p_{2i}}$ 为负值时$\delta $ 与$\varepsilon /\min \left\{ {\left. {\left| {{p_{2i}}} \right|,\left| {{p_{2j}}} \right|} \right\}} \right.$ 成正比. 因此, 合并节点$i$ 和$j$ 后网络特征值的变化量$\delta $ 与${p_{2i}}$ 和${p_{2j}}$ 间的相对距离$\varepsilon /\min \left\{ {\left. {\left| {{p_{2i}}} \right|,\left| {{p_{2j}}} \right|} \right\}} \right.$ 成正比. 证毕.4.ISCGR算法 与SCG和ISCG算法不同, ISCGR算法以相对距离作为分类依据, 从而更合理地对节点分类, 改善了网络的粗粒化效果, 使所得粗粒化网络保持同步的能力增强.$\varepsilon /\min \left\{ {\left. {\left| {{p_{2i}}} \right|,\left| {{p_{2j}}} \right|} \right\}} \right.$ 的大小作为设置分割点的判断标准, 因为接近0的分量不满足分量间的距离$\varepsilon $ 远远小于$\min \left\{ {\left. {\left| {{p_{2i}}} \right|,\left| {{p_{2j}}} \right|} \right\}} \right.$ 这一条件, 从而$\varepsilon /\min \left\{ {\left. {\left| {{p_{2i}}} \right|,\left| {{p_{2j}}} \right|} \right\}} \right.$ 会得出很大的距离比率. 这里用 $\dfrac{\varepsilon }{{\min \left\{ {\left. {\left| {{p_{2i}}} \right|,\left| {{p_{2j}}} \right|} \right\}} \right. + \left| {\overline {{p_2}} } \right|}}$ 来代替$\varepsilon /\min \left\{ {\left. {\left| {{p_{2i}}} \right|,\left| {{p_{2j}}} \right|} \right\}} \right.$ 作为设置分割点的标准, 其中$\left| {\overline {{p_2}} } \right|$ 是${\lambda _2}$ 对应的所有特征向量分量绝对值的平均值. 以$\dfrac{\varepsilon }{{\min \left\{ {\left. {\left| {{p_{2i}}} \right|,\left| {{p_{2j}}} \right|} \right\}} \right. + \left| {\overline {{p_2}} } \right|}}$ 代替$\varepsilon /\min \left\{ {\left. {\left| {{p_{2i}}} \right|,\left| {{p_{2j}}} \right|} \right\}} \right.$ 一方面避免了靠近0的分量算出过大的比率值, 另一方面此指标包含了相对距离的影响因素, 比采用绝对距离$\varepsilon $ 作为分类标准有更好的粗粒化效果. 与ISCG算法相比, ISCGR算法在对特征向量分量进行分类时, 越靠近0的分量分得越细化, 聚类区间的长度越小, 越远离0的分量分得越粗糙, 聚类区间的长度越大.${\lambda _2}$ 对应的特征向量分量从小到大进行排序为$\left\{ {\left. {{{\tilde p}_{21}},{{\tilde p}_{22}} \cdots {{\tilde p}_{2N}}} \right\}} \right.$ , 计算两两相邻分量之间的距离${\varepsilon _i}(i = 1,2, \cdots,N - 1)$ ; 2)用这个距离除以对应分量绝对值与所有分量绝对值平均值的和, 即计算出${\eta _i} = \dfrac{{{\varepsilon _i}}}{{\min \left\{ {\left. {\left| {{{\tilde p}_{2i}}} \right|,\left| {{{\tilde p}_{2,i + 1}}} \right|} \right\}} \right. + \overline {\left| {{p_2}} \right|} }},(i = 1,2, \cdots\!,N -\! 1)$ ; 3)根据${\eta _i}$ 的大小设置分割点, 将分量分裂成若干个聚类; 4)把同一聚类中的节点合并为一个节点, 利用(11 )式得到粗粒化网络的Laplacian矩阵.${\lambda _2}$ 对应的特征向量${P_2}$ 的分量为$\left\{ {\left. {{p_{21}},{p_{22}} \cdots {p_{2N}}} \right\}} \right.$ , 要将其分为3类. 首先把特征向量分量从小到大排列为$\left\{ {\left. {{{\tilde p}_{21}},{{\tilde p}_{22}} \cdots {{\tilde p}_{2N}}} \right\}} \right.$ , 相邻分量之间的间距为$\left\{ {\left. {{\varepsilon _1},{\varepsilon _2} \cdots {\varepsilon _{N - 1}}} \right\}} \right.$ , 再通过公式计算出$\left\{ {\left. {{\eta _1},{\eta _2} \cdots {\eta _{N - 1}}} \right\}} \right.$ , 选出最大的两个相对距离记为${\eta _j},{\eta _k}\left( {j < k} \right)$ , ${\eta _j}$ 对应着${\tilde p_{2j}}$ 和${\tilde p_{2,j + 1}}$ 之间的相对距离, ${\eta _k}$ 是${\tilde p_{2k}}$ 和${\tilde p_{2,k + 1}}$ 之间的相对距离. 接着在这两个间距处设置分割点, 把分量分裂成3类, 分别为$\left[ {{{\tilde p}_{21}}, {{\tilde p}_{2j}}} \right], \left[ {{{\tilde p}_{2,j + 1}},{{\tilde p}_{2k}}} \right]$ 和$\left[ {{{\tilde p}_{2,k + 1}},{{\tilde p}_{2N}}} \right]$ . 最后将落入同一区间内的点合并为一个节点, 利用(11 )式更新合并后的Laplacian矩阵, 就可以获得节点数为3的粗粒化网络. ISCGR算法对节点分类时考虑了特征向量分量间的相对距离, 在两组分量间距相同的情况下, 由于靠近0的分量相对距离大, 所以会优先在靠近0的两个向量间设置分割点, 把相对距离小的分量所对应的节点合并. 由此可见, ISCGR算法在区分不同节点的相似程度时更加合理, 保证了分在同一聚类的节点相似程度高于不同聚类的节点, 因此粗粒化效果较ISCG算法更好.${\lambda _2}$ 类似, 对于类型II网络, 当考虑${{{\lambda _N}} /{{\lambda _2}}}$ 作为同步能力衡量指标时, 先用ISCGR算法分别对${\lambda _N}$ 和${\lambda _2}$ 对应的特征向量分量进行分类, 将同时分裂在同一聚类的节点合并为一个节点, 最后更新Laplacian矩阵, 得到约简后的粗粒化网络.5.仿真分析 本节将对一般连续时间的动态网络模型和27种现实世界网络进行数值仿真, 分别应用ISCG方法和ISCGR方法对网络进行约简, 比较两种算法对网络约简后同步能力的保持效果.5.1.模型网络仿真 5.1.模型网络仿真 首先对连续时间动态网络模型进行数值仿真, 这里选取三种典型的网络模型, 即BA无标度网络[23 ] 、ER随机网络[24 ] 、和NW小世界网络[25 ,26 ] , 分别应用ISCG算法和ISCGR算法对其进行约简, 分析比较没有考虑相对距离和基于相对距离的算法的粗粒化效果.${\lambda _2}$ 不变即可. 图3 展示了分别采用ISCG算法和ISCGR算法对1000个节点的BA、ER、NW网络约简后${\lambda _2}$ 的变化情况. 图3(a) 是对1000个节点的BA网络的粗粒化过程仿真, 原始网络的${\lambda _2}$ 为2.95. 采用ISCG方法将网络约简至200, 102, 72个节点时, 网络的${\tilde \lambda _2}$ 分别变为2.96, 3.13, 3.26, 比原网络增加了0.34%, 6.10%, 10.51%; 采用ISCGR方法将网络约简至200, 102, 72个节点时, 网络的${\tilde \lambda _2}$ 为别是2.95, 2.95, 2.98, 变化了0, 0, 1.02%. 由此可见, 采用ISCGR算法保持BA网络${\lambda _2}$ 的能力要优于ISCG算法. 对于图3(b) 1000个节点的ER随机网络和图3(c) 1000个节点的NW小世界网络也能得出同样的结论, 即在网络约简至相同的节点时, 采用ISCGR算法${\lambda _2}$ 值的变化量要小于ISCG算法, 这表明采用ISCGR算法保持类型Ⅰ网络同步能力的效果要优于ISCG算法.图 3 采用ISCG与ISCGR算法获得谱粗粒化网络对${\lambda _2}$ 的保持情况 (a) BA无标度网络; (b) ER随机网络; (c) NW小世界网络Figure3. The maintaining of ${\lambda _2}$ obtained by using ISCG and ISCGR algorithms in coarse graining metwork: (a) BA network; (b) ER network; (c) NW network.${{{\lambda _N}} /{{\lambda _2}}}$ 衡量. 图4 展示了分别采用ISCG算法和ISCGR算法对1000个节点的BA无标度网络、ER随机网络、NW小世界网络约简后保持${{{\lambda _N}} /{{\lambda _2}}}$ 情况的对比. 从图中可以看出, 采用这两种算法对网络进行约简后, ${{{\lambda _N}} /{{\lambda _2}}}$ 都是随着约简后网络节点数$\tilde N$ 的减少而减小, 但在$\tilde N$ 相同的情况下, 用ISCGR算法得到粗粒化网络的${{{\lambda _N}} /{{\lambda _2}}}$ 变化更小, 这表明了ISCGR算法保持类型Ⅱ网络的同步能力比ISCG算法更强.图 4 采用ISCG算法与ISCGR算法获得谱粗粒化网络对${{{\lambda _N}} /{{\lambda _2}}}$ 的保持情况 (a) BA无标度网络; (b) ER随机网络; (c) NW小世界网络Figure4. The maintaining of ${{{\lambda _N}} /{{\lambda _2}}}$ obtained by using ISCG and ISCGR algorithms in coarse graining metwork: (a) BA network; (b) ER network; (c) NW network.5.2.实际网络仿真 -->5.2.实际网络仿真 下面应用一些真实网络进行粗粒化过程仿真, 进一步比较ISCG算法和ISCGR算法保持实际网络同步能力的效果. 我们选取了协作、沟通、计算机、基础设施、社会、生物、词汇和电力等不同领域的网络[27 -29 ] . 这些网络的规模从几百个到几千个节点不等, 既包括稀疏网络又包括致密网络. 表1 给出了这些网络的基本数据及分别采用ISCG和ISCGR算法约简到原始节点数$N$ 的30%, 20%, 10%, 2%时, 网络Laplacian矩阵${{L}}$ 的最小非零特征值${\lambda _2}$ 的变化量. 图5 展示了分别采用ISCG和ISCGR算法对这些实际网络约简后${\lambda _2}$ 的变化情况, 其中图5(a) 是从表1 中挑选了一些随着节点数$\tilde N$ 减少, ${\lambda _2}$ 变化比较大的网络, 图5(b) 挑选了一些随着节点数$\tilde N$ 减少, ${\lambda _2}$ 变化不太明显的网络. 图5 可以看出约简后网络节点数$\tilde N$ 越小, ${\lambda _2}$ 的变化量越大, 但是在$\tilde N$ 相同的情况下, 采用ISCGR方法约简网络后得到的${\lambda _2}$ 误差比采用ISCG方法要小. 这表明对于实际网络, 采用ISCGR方法比ISCG方法更能保持网络的同步能力.种类 网络 节点 边 文献 Δλ 2 (30%N ) Δλ 2 (20%N ) Δλ 2 (10%N ) Δλ 2 (2%N ) ISCG ISCGR ISCG ISCGR ISCG ISCGR ISCG ISCGR 化学 DD_g1 327 899 [27 ] 2.06% 1.77% 7.66% 7.17% 34.90% 23.46% 187% 173% DD_g1046 707 1646 [27 ] 1.40% 1.31% 7.27% 6.62% 42.92% 17.81% 191% 94% 合作 netscience 379 914 [27 ] 0.13% 0.13% 1.05% 1.05% 5.79% 5.46% 49.74% 39.41% ca-GrQc 4158 13422 [27 ] 0 0 0 0 0.03% 0.03% 0.34% 0.20% 社交 ia-infect-dublin 410 2765 [27 ] 0.91% 0.95% 3.59% 2.46% 13.47% 14.37% 104% 51% moreno_crime 829 1473 [28 ] 0.01% 0.01% 0.39% 0.24% 3.02% 2.32% 13.34% 13.05% socfb-Sim81 1518 32988 [28 ] 0 0 0 0 0 0 23.65% 11.82% ia-email-univ 1133 5451 [27 ] 0 0 0 0 0.07% 0.06% 0.26% 0.16% 电力 东北电网 58 70 [29 ] 8.14% 5.78% 24.36% 18.63% 54.65% 54.65% — — IEEE162 162 280 [29 ] 2.35% 2.10% 16.94% 8.68% 27.70% 25.65% 113% 113% IEEE145 145 422 [29 ] 0.85% 0.80% 4.14% 3.16% 17.85% 14.22% 240% 230% 生物 diseasome 516 1188 [27 ] 0.22% 0.11% 0.79% 0.67% 2.58% 2.02% 33.45% 15.82% 互联网 Route views 6474 12572 [28 ] 0 0 0 0 0.07% 0.07% 1.07% 0.57% Wiki-vote 889 2914 [27 ] 0.02% 0.01% 0.07% 0.05% 0.17% 0.17% 0.61% 0.49% 技术 bibd_12_4 495 2951 [27 ] 0.02% 0.01% 0.20% 0.06% 0.80% 0.41% 29.02% 19.73% G1 800 19176 [27 ] 0 0 0 0 0.27% 0.19% 0.56% 0.55% GD00_c 638 1020 [27 ] 0.02% 0.02% 0.27% 0.27% 1.50% 1.15% 4.29% 2.75% dwt_1005 1005 3808 [27 ] 2.17% 0.49% 4.25% 1.61% 23.93% 10.83% 129% 92% dwt_503 503 2762 [27 ] 4.94% 3.68% 9.33% 6.18% 44.00% 21.32% 138% 117% 数学 130bit 584 6058 [27 ] 0.01% 0 0.02% 0.01% 0.68% 0.36% 1.51% 1.15% ash608 608 1212 [27 ] 0.74% 0.40% 6.95% 1.10% 18.29% 13.73% 51.99% 30.57% bibd_12_5 792 7860 [27 ] 0.02% 0 0.07% 0.03% 0.35% 0.11% 25.14% 5.84% jagmesh3 1089 3136 [27 ] 0.31% 0.10% 1.44% 1.13% 16.86% 9.25% 192% 127% frb45-21-1 945 386854 [27 ] 0.03? 0 0.23? 0.04? 0.51? 0.28? 1.39? 1.34? kneser_6_2_1 676 2017 [27 ] 0.03% 0.01% 0.16% 0.13% 1.83% 0.44% 81% 30% EX1 560 4368 [27 ] 0 0 0.03% 0.03% 3.08% 0.41% 123% 26% 随机 G43 1000 9990 [27 ] 0 0 0.01% 0 0.13% 0.11% 0.95% 0.50%
表1 分别采用ISCG和ISCGR算法对实际网络约简后${\lambda _2}$ 的保持情况统计表Table1. The Statistics table of maintaining ${\lambda _2}$ obtained by using ISCG and ISCGR algorithms for some real-world networks in coarse graining network.图 5 分别采用ISCG与ISCGR算法对实际网络进行粗粒化后保持${\lambda _2}$ 情况的对比图Figure5. The maintaining of ${\lambda _2}$ obtained by using ISCG and ISCGR algorithms for real-world networks in coarse graining network.表1 中平均度和约简后${\lambda _2}$ 值变化量的关系发现, 在约简程度相同时, 网络的平均度越大, 约简后网络${\lambda _2}$ 的变化量越小, 保持同步的能力越强. 这是因为网络的度越大, 越接近于全局耦合网络, 网络中外部连接相同或相似的节点越多, 所以合并这些节点后对网络的特征值影响不大; 而平均度越小, 网络越稀疏, 网络中外部连接相同或相似的节点越少, 约简后网络的特征值变化量就越大.表1 的数据表明, ISCGR算法对互联网、生物、社交、合作等网络的同步保持能力更强一些, 对电力、化学等网络的同步保持能力则弱一些. 这是因为互联网[30 ] 具有模块性, 生物网络(如新陈代谢网络)中的拓扑结构是按等级组织起来的[31 ] , 社交网络与合作网络都具有“物以类聚, 人以群分”的特点[32 ] , 即这类网络都具有高聚类的特性, 网络中包含大量外部连接相同或相似的节点, 所以ISCGR算法对这类网络的约简效果更好. 相反, 电力网络、化学网络中的节点大都是链状式排列, 这类网络聚类特性不明显, 外部连接相同的节点很少, 所以采用SCG算法对网络约简到一定程度时很难保持网络的同步能力.6.结 论 小规模网络中的一些性质不能直接应用在大规模网络中, 所以复杂网络的约简成为了复杂网络理论中的重要课题. 通过对网络约简, 不仅可以把小规模网络中已经研究过的性质应用到大规模网络中, 且简化了分析和计算. SCG算法是一种保持类型I和类型II复杂网络同步能力不变的约简方法. 本文在原始谱粗粒化方法基础上提出了一种基于相对距离的谱粗粒化方法, 使应用特征向量分量分类时比原算法更加合理, 约简后的网络保持同步的能力得到增强, 为大型网络的谱粗粒化提供了一种更加精准的约简算法; 并通过对3种经典网络模型和27种实际网络的仿真分析表明, ISCGR算法比原算法粗粒化效果更好, 进一步发现SCG算法对具有明显聚类结构的实际网络(互联网、生物、社交、合作等)比模糊聚类结构的实际网络(电力、化学等)更容易保持粗粒化网络的同步能力. 








































































































































 图 1 合并节点的过程
图 1 合并节点的过程











































































































































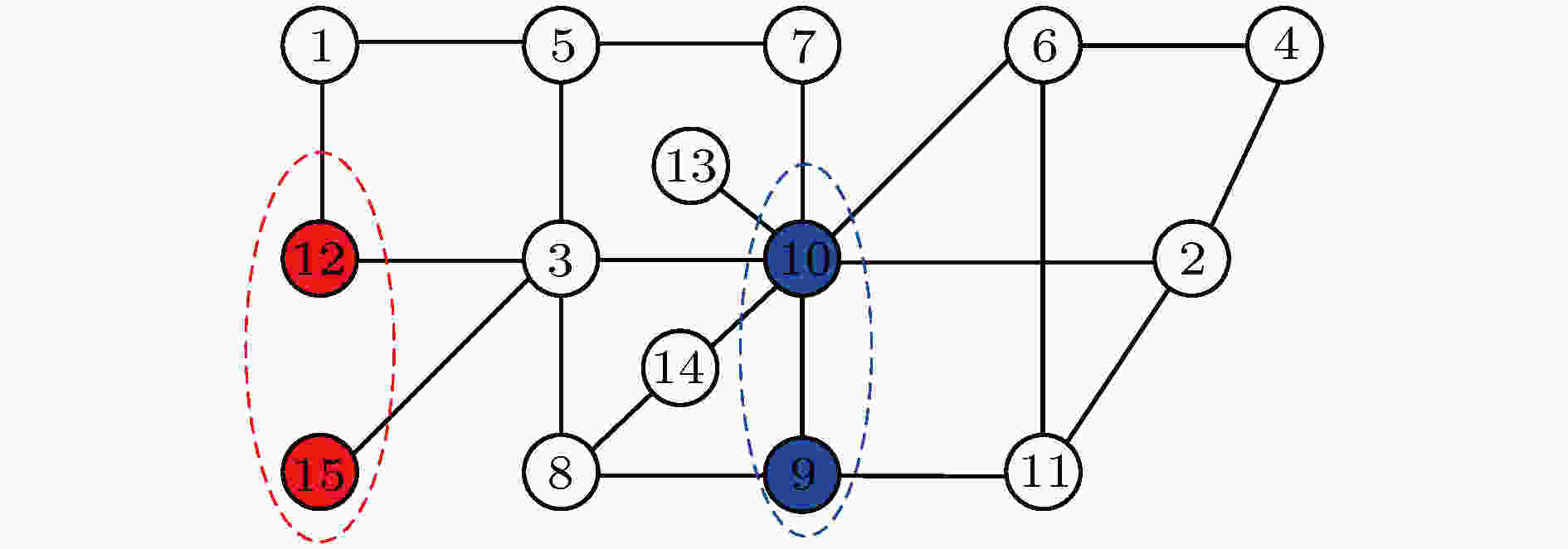 图 2 15个节点并为14个节点的两种方案
图 2 15个节点并为14个节点的两种方案




















































































































































































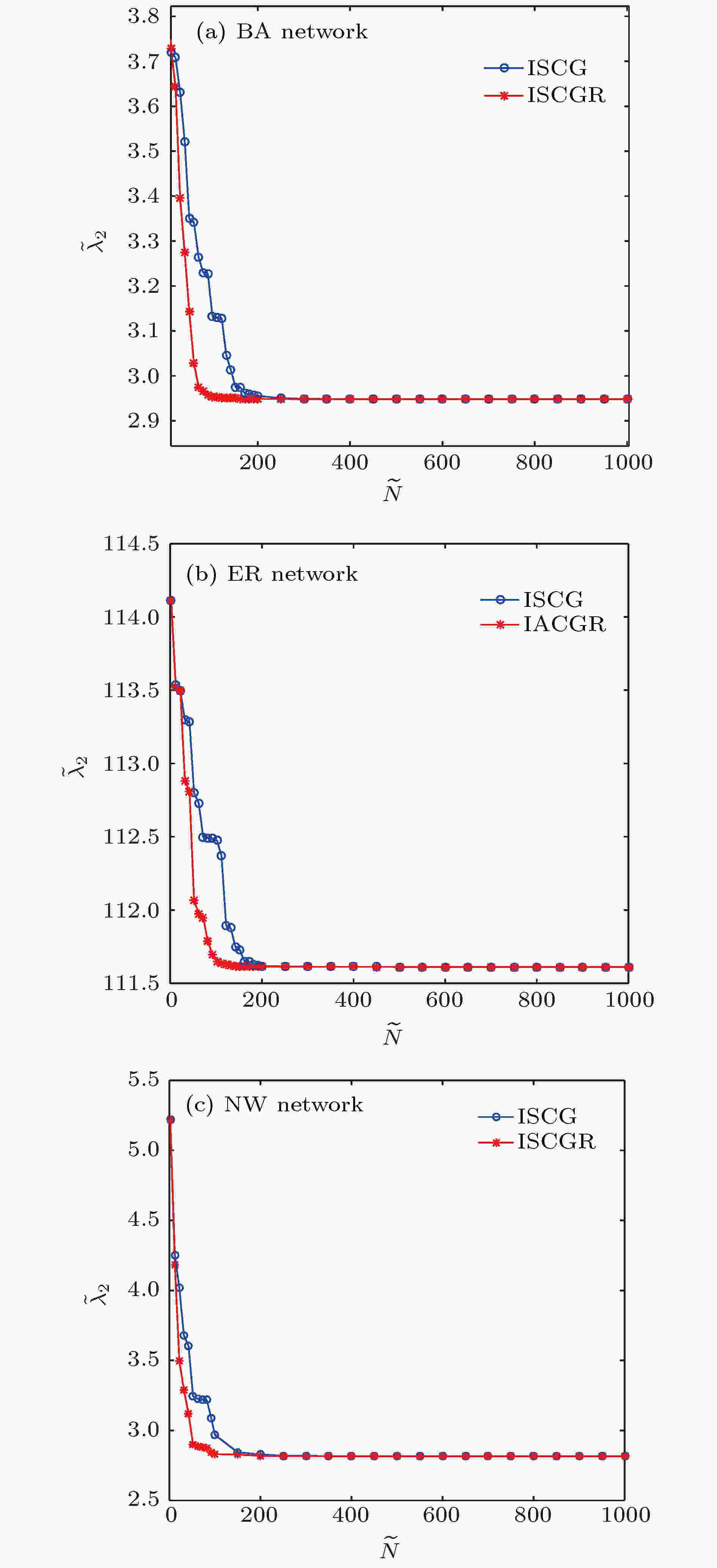 图 3 采用ISCG与ISCGR算法获得谱粗粒化网络对
图 3 采用ISCG与ISCGR算法获得谱粗粒化网络对





















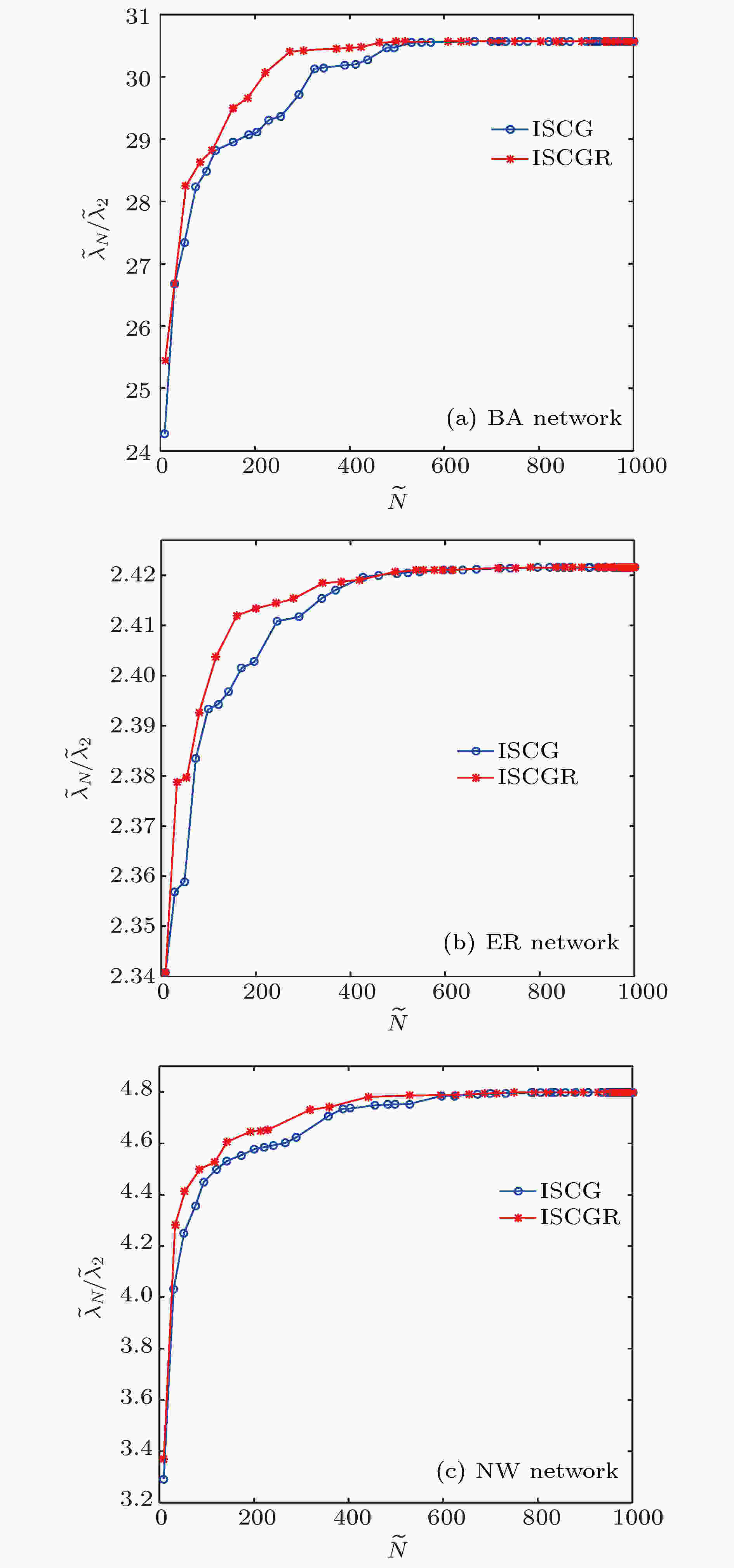 图 4 采用ISCG算法与ISCGR算法获得谱粗粒化网络对
图 4 采用ISCG算法与ISCGR算法获得谱粗粒化网络对

























































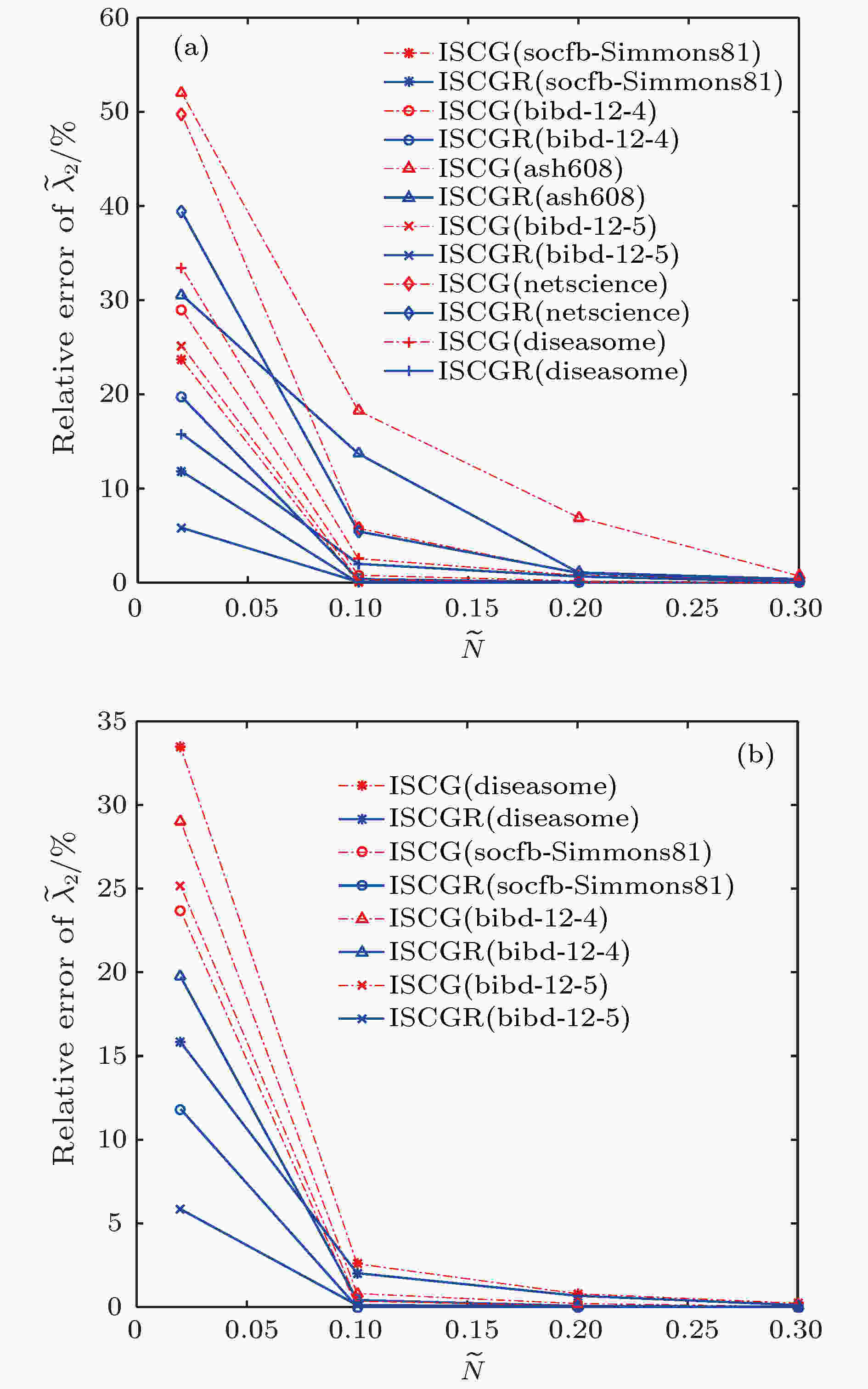 图 5 分别采用ISCG与ISCGR算法对实际网络进行粗粒化后保持
图 5 分别采用ISCG与ISCGR算法对实际网络进行粗粒化后保持





