摘要: 锂离子电池的电化学模型对于电池特性分析和电池管理具有重要意义, 但是准二维(P2D)模型复杂度太高, 为了在保证模型精度的基础上尽量降低复杂度, 本文提出了一种包含液相简化的P2D (LSP2D)模型, 该模型首先基于电化学平均动力学将电池端电压化简成为仅耦合固相Li
+ 浓度
c s 和液相Li
+ 浓度
c e 的方程, 然后进一步对表达
c s 和
c e 演化规律的偏微分方程进行抛物线近似化简, 使得最终的模型由多项式组成. COMSOL仿真表明在放电倍率为1C时该模型与单粒子(SP)模型的估算精度和速度相当, 但在放电倍率为3C时, 该模型的估算时间比P2D模型减少了99.73%, 与SP模型相当, 估算精度相比SP模型有大幅度提升.
关键词: 电化学模型 /
电池管理系统 /
液相扩散方程 /
抛物线近似 English Abstract Electrochemical model of lithium ion battery with simplified liquid phase diffusion equation Liu Zheng-Yu 1,2 ,Yang Kun 1 ,Wei Zi-Hong 1 ,Yao Li-Yang 1 1.School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China Fund Project: Project supported by the Natural Science Foundation of Anhui Province, China (Grant No. 1808085MF200) and the Ministry of Industry and Information Technology Civil Aircraft Special Scientific Research Project, China (Grant No. MJ-2017-D-26).Received Date: 27 January 2019Accepted Date: 03 March 2019Available Online: 01 May 2019Published Online: 05 May 2019Abstract: The pseudo-two-dimensional (P2D) model is the most widely used electrochemical model for lithium-ion batteries. Because of the complexity and the difficulty in using the complete P2D model, many simplified P2D models, such as the single particle model (SP model) and the parabolic profile approximation model (PP model), have been proposed. However, the using of the SP model can cause a large amount of precision to lose in its simplified process, while the PP model has a high complexity. In this paper, we propose a liquid phase simplification P2D (LSP2D) model. The using of the LSP2D model has a small precision loss and a relatively low complexity. The LSP2D model is based on the electrochemical average kinetics of the lithium ion battery. We first simplify the terminal voltage into an equation containing only the solid phase concentration c s and the liquid phase concentration c e . Then we use the partial differential equation to represent the solid phase concentration c s and the liquid phase concentration c e , and then obtain a final model. The simulation environment is based on COMSOL, and the simulation results show that when the discharge rate is 1C, the estimation accuracy and speed from the LSP2D model are similar to those from the SP model. But when the discharge rate is 3C, the estimation time from the LSP2D model is reduced by 99.73% compared with that from the P2D model, and the estimation accuracy is greatly improved compared with the estimation accuracy from the SP model.Keywords: electrochemical model /battery management system /liquid phase diffusion equation /parabolic approximation 全文HTML --> --> --> 1.引 言 锂离子电池由于具有良好的电化学稳定性、较大的能量密度、较长的电池寿命和无需维护等特点被广泛用于电动汽车以及各种储能设备中[1 ] . 锂离子电池模型对于提升能量利用效率和保障使用安全具有重要意义. 锂电池模型可按建模方法分为两大类, 即经验模型和电化学模型[2 ,3 ] . 经验模型是依据样本数据和系统辨识方法所获取的电池动力学替代模型, 其优点是复杂度可控和建模代价低, 缺点是模型参数的物理化学意义不明显且鲁棒性较差[4 ,5 ] ; 电化学模型是通过机理分析方法所获取的电池动力学特性的数学表达, 其优点是模型精度高且可深层次揭示电池特性演化机制, 缺点是模型复杂度高, 不利于其工程化应用.[6 ,7 ] . 为解决经验模型的上述缺陷, 对电化学模型进行简化已经成为当前研究的热点. 基本思路是增加前置假设条件, 近似模型的数学表达公式, 降低计算复杂度, 从而在精度损失可容忍的前提下匹配实时性要求, 以期提高实用性. 目前应用最广的电化学模型是由Doyle等[8 ] 开发的准二维(pseudo-two- dimensions, P2D)模型, P2D模型具有很高的精度, 但是由于是由复杂的耦合非线性偏微分方程组成的, 导致标准的P2D模型在实际中很难直接应用. 为了简化标准的P2D模型, 很多简化模型已经被提出, 其中最流行的是单粒子(single particle, SP)模型[9 ,10 ] 和抛物线近似(parabolic profile approximation, PPA)模型[11 ] . SP模型主要基于两个假设: 1)假设电解质中Li+ 浓度和电位保持不变; 2)假设正负极中只有单个活性颗粒. SP模型认为电池在充放电过程中锂离子从一个电极瞬间转移到另一个电极, 锂离子在电解质中的动力学分析完全被忽略, 同时SP模型用平均转移电流密度代替局部体积转移电流密度进行方程的化简. 尽管SP模型的计算时间与等效电路模型相当, 但SP模型仅对较低放电倍率(≤ 1C)有效[10 ,12 ] . PPA模型通过使用多项式函数近似表达电极颗粒内的Li+ 浓度来达到化简固相扩散方程的目的, 电极颗粒内的Li+ 浓度变化规律是非常接近抛物线的, 所以PPA模型对固相Li+ 浓度的简化精度比SP模型高. PPA模型沿着电极颗粒半径r 的方向简化了P2D模型, 虽然计算速度有所加快, 但是沿着电池的x 方向还有大量的耦合非线性偏微分方程需要计算[13 ] , 不满足实际应用的条件.${\phi _{\rm{e}}}$ 进行化简, 将电池的端电压表示成只耦合固相浓度${c_{\rm{s}}}$ 和液相浓度${c_{\rm{e}}}$ 的方程, 降低了方程的耦合度. 之后再用固相表面浓度${c_{{\rm{s,e}}}}(t)$ 以及固相体积平均浓度$\overline {{c_{\rm{s}}}} (t)$ 来表示电池的固相浓度${c_{\rm{s}}}$ , 用抛物线方程结合锂离子电池的边界条件化简液相浓度${c_{\rm{e}}}$ . 化简之后的模型不含有偏微分方程, 且化简过程是基于边界条件的, 所以该模型能够在保证精度的前提下大幅度降低模型的复杂度, 对于将电化学模型用于电池管理系统(battery management system, BMS)研究具有重要的意义.2.P2D模型 在恒流等温的前提下, 模型输入为负载电流, 输出为端电压. 图1 显示了简化的锂离子电池的结构, 包含三个部分: 具有球形石墨颗粒的阳极、多孔隔膜和具有球形活性颗粒的阴极. 多孔隔膜只允许Li+ 通过, 正负极的表面分别接铝箔和铜箔集电极.图 1 锂离子电池示意图Figure1. Lithium ion battery schematic.[10 ,14 ] .${D_{\rm{s}}}$ 代表固相浓度扩散系数, r 代表活性颗粒的有效半径$0 \leqslant r \leqslant {R_{\rm{s}}}$ (${R_{\rm{s}}}$ 代表活性材料颗粒半径).${\varepsilon _{\rm{e}}}$ 代表不同区域的液相体积分数, 液相浓度有效扩散系数$D_{\rm{e}}^{{\rm{eff}}} = {D_{\rm{e}}}\varepsilon _{\rm{e}}^{{\rm{Brug}}}$ (${D_{\rm{e}}}$ 代表液相浓度扩散系数, Brug代表锂电池不同区域的Bruggman系数), $t_ + ^0$ 代表Li+ 迁移数量.${\sigma ^{{\rm{eff}}}} = \sigma \varepsilon _{\rm{s}}^{{\rm{Brug}}}$ ($\sigma $ 表示固相电导率, ${\varepsilon _{\rm{s}}}$ 表示不同区域的固相体积分数).${k^{{\rm{eff}}}} = k\varepsilon _{\rm{e}}^{{\rm{Brug}}}$ (k 表示电解液电导率); $k_{\rm{d}}^{{\rm{eff}}}$ 代表有效扩散传导性,${j^{{\rm{Li}}}}$ 可以表示成:$\eta $ 表示表面过电位,${i_0}$ 表示交换电流密度, 大小取决于固体颗粒表面浓度${c_{{\rm{s,e}}}}$ 和电解质浓度${c_{\rm{e}}}$ ,3.P2D模型的简化 对于标准的P2D模型, 锂离子电池端电压的求解公式耦合了${c_{\rm{s}}},\;{c_{\rm{e}}}\text{和}{\phi _{\rm{e}}}$ 三个参数[15 ] , 由(4 )和(6 )式可知${\phi _{\rm{e}}}$ 由${c_{\rm{s}}}\text{和}{c_{\rm{e}}}$ 表示, 所以首先将模型的端电压方程化简成为只耦合${c_{\rm{s}}}\text{和}{c_{\rm{e}}}$ 两个参数的方程[16 ] , Subramanian等[11 ] 基于体积平均方程和抛物线近似方程来简化固相浓度, 仿真结果表明该简化方法具有较高的精度. 本文前期的COMSOL仿真表明锂离子电池的液相浓度曲线与抛物线十分类似, 在这个前提下, 用抛物线方程对锂离子电池的正极、隔膜和负极的液相锂离子浓度进行化简, 使得${c_{\rm{s}}}\text{和}{c_{\rm{e}}}$ 的计算量大幅度减小. LSP2D模型只包含电池端电压求解公式和经过抛物线近似化简的(1 )和(2 )式, 而不再有偏微分方程. 图2 是LSP2D模型的简化示意图.图 2 LSP2D模型简化示意图Figure2. Simplified schematic diagram of the LSP2D model.3.1.电池端电压的计算 3.1.电池端电压的计算 由(7 )及(9 )式可以推导出电池的端电压为${\alpha _{\rm{a}}} = {\alpha _{\rm{c}}} = 0.5$ . 假设在任一时刻, Li+ 的电流密度为常数, 那么就可以用$\overline {j_{\rm{n}}^{{\rm{Li}}}} $ 和$\overline {j_{\rm{p}}^{{\rm{Li}}}} $ 代替$j_{\rm{n}}^{{\rm{Li}}}$ 和$j_{\rm{p}}^{{\rm{Li}}}$ 代入(6 )式中得到13 )和(14 )式得到正负极的表面过电位可以表示为[17 ] 4 )式分析求解可以推导出电解质电势[18 ] 为10 ), (15 ), (16 )和(19 )式可得到端电压为${c_{\rm{s}}},{c_{\rm{e}}}$ 和${\phi _{\rm{e}}}$ 的电池端电压求解方程化简成了耦合${c_{\rm{s}}}$ 和${c_{\rm{e}}}$ 的(20 )式, P2D模型化简成为包含(1 ), (2 )和(20 )式的电化学系统. 想要求解(20 )式必须先用(1 )和(2 )式求出固相Li+ 浓度和液相Li+ 浓度, 但是(1 )和(2 )式是偏微分方程, 求解过程相对比较复杂, 必须进一步化简.3.2.固相Li+ 浓度的简化 -->3.2.固相Li+ 浓度的简化 假设粒子内的浓度分布为抛物线[11 , 19 ] [11 ] 利用固相表面浓度${c_{{\rm{s,e}}}}(t)$ 以及固相体积平均浓度$\overline {{c_{\rm{s}}}} (t)$ 来表示${c_{\rm{s}}}(r,t)$ :$\overline {{c_{\rm{s}}}} (t)$ 和${c_{{\rm{s,e}}}}(t)$ 由下列公式求出:1 )就化简成为(22 )—(24 )式.3.3.液相Li+ 浓度的简化 -->3.3.液相Li+ 浓度的简化 由于不同区域的${\varepsilon _{\rm{e}}},{D_{\rm{e}}}$ 不同, 液相扩散方程(2 )又可以表示为25 ), (26 )和(27 )式可改写为$\tau = 0$ 时,+ 浓度可以用抛物线轮廓描述, 以获得相同问题更简单的描述方法, 令39 )式代入边界控制条件(33 )—(38 )式中可得29 )—(31 )式两边同时对$x$ 从0到1积分:11 )和(12 )式中的$\overline {j_{\rm{n}}^{{\rm{Li}}}} $ 和$\overline {j_{\rm{p}}^{{\rm{Li}}}} $ 代替(48 )—(50 )式中的$j_{\rm{n}}^{{\rm{Li}}}$ 和$j_{\rm{p}}^{{\rm{Li}}}$ 可得51 )—(53 )式和(32 )式得到45 )—(47 )式和(56 )—(58 )式可得到40 )—(44 )式,可以求出(39 )式中的各系数, 参数值见表1 .${a_1}$ ${b_1}$ ${c_1}$ ${a_2}$ ${b_2}$ ${a_3}$ ${b_3}$ ${c_3}$ $\displaystyle\frac{1}{8} + \alpha \tau $ $\displaystyle\frac{{15}}{4}$ $ - \displaystyle\frac{{15}}{8}$ $1$ 0 1 $\displaystyle\frac{{30}}{7}\beta \tau $ $ - \displaystyle\frac{{15}}{7}\beta \tau $
表1 各参数的值Table1. Values of parameters.+ 浓度表示为+ 浓度利用抛物线近似化简成了(62 )式.20 )式、(22 )—(24 )式和(62 )式. 其中(22 )—(24 )式用于求解固相Li+ 浓度. 化简之后的LSP2D模型不再包含偏微分方程.4.模型的对比分析 本文用于锂离子电池实验仿真的参数如表2 所列[13 , 20 ] , 仿真软件是Windows操作系统下的COMSOL软件, 设置温度为25 ℃. 由于PPA模型的简化程度达不到实际应用的标准, 所以本文以P2D模型作为标准, 从准确性和快速性两方面比较LSP2D模型和SP模型.Symbol Anode Cathode Separator $\sigma$/S·m–1 100 100 ${\varepsilon _{\rm s}}$ 0.49 0.59 ${\varepsilon _{\rm e}}$ 0.485 0.365 0.724 Brug 4.0 4.0 4.0 ${c_{{\rm{e,0}}}}$/mol·m–3 1000 1000 1000 ${c_{{\rm{s,0}}}}$/mol·m–3 916.65 48977.25 ${c_{{\rm{s,max}}}}$/mol·m–3 30555 51555 A /m2 $6.03 \!\times\! {10^{ - 4}}$ $5.31 \!\times\! {10^{ - 4}}$ ${D_{\rm{e}}}$/m2 ·s–1 $7.5 \!\times\! {10^{ - 10}}$ $7.5 \!\times\! {10^{ - 10}}$ $7.5 \!\times\! {10^{ - 10}}$ ${D_{\rm{s}}}$/m2 ·s–1 $3.9 \!\times\! {10^{ - 14}}$ $1.0 \!\times\! {10^{ - 14}}$ k /mol·(mol·m–3 )–1.5 $4.854 \!\times\! {10^{ - 6}}$ $2.252 \!\times\! {10^{ - 6}}$ ${R_{\rm{s}}}$/m $2 \!\times\! {10^{ - 6}}$ $2 \!\times\! {10^{ - 6}}$ x /m$8.8 \!\times\! {10^{ - 5}}$ $8.0 \!\times\! {10^{ - 5}}$ $8.0 \!\times\! {10^{ - 5}}$ ${R_{{\rm{SEI}}}}/\Omega$·m–2 0.01 I /A·m–2 20 $\alpha $ 0.5 0.5 F /C·mol96487 R /J·mol·K–1 8.314 T /K298.15
表2 锂离子电池参数表Table2. Parameters lists of Li-ion battery.图3 显示了1C和3C的放电倍率下在放电末期(电压下降到3 V以下)由LSP2D模型测得的液相Li+ 浓度${c_{\rm{e}}}$ 和P2D模型、SP模型测得的液相Li+ 浓度${c_{\rm{e}}}$ 的对比情况. 从图3 可以看出在放电倍率为1C的情况下, 两种模型的液相Li+ 浓度${c_{\rm{e}}}$ 误差都不大, 所以可以忽略. 但在放电率为3C的情况下, SP模型估算出的${c_{\rm{e}}}$ 有很大的误差(≤ 56.5%), 而LSP2D模型的误差较小(≤ 10%), 因为SP模型是直接忽略了${c_{\rm{e}}}$ 的变化.图 3 1C和3C放电率下, SP, LSP2D和P2D模型得到的放电末期液相Li+ 浓度${c_{\rm{e}}}$ 比较Figure3. Comparison of liquid phase Li+ concentration ${c_{\rm{e}}}$ obtained by SP, LSP2D and P2D model at 1C and 3C discharge rates.图4 显示的是P2D模型、LSP2D模型以及SP模型在放电率为1C和3C时的放电曲线. 根据图4 中的信息可以得到放电率为1C和3C时两种模型估算电池端电压的平均误差, 结果列于表3 中. 从表3 可以看出, 在放电率为1C时两种模型的精度都比较高, 而在放电率为3C时, LSP2D模型的估算精度较高,误差 ≤ 1.2%, SP模型的估算精度较低, 误差约为12%. 结合图3 可以发现, 在较高放电率的情况下, SP模型的误差很大, 所以在实际运用中价值不大, 而本文提出的模型在精度方面有很大的提升.图 4 三种模型在放电率为1C和3C时的放电曲线Figure4. Discharge curves of three models at 1C and 3C discharge rates.Model Average error at Average error at P2D 0 0 LSP2D 0.0056 0.014 SP 0.0052 0.142
表3 放电率为1C和3C时三种模型估算电池端电压的平均误差Table3. Average error of the battery terminal voltage is estimated by three models when the discharge rate is 1C and 3C.表4 记录了使用上述三种模型进行50次循环估计所需要的时间, 可知严格的P2D计算时间太长, SP模型的估计速度很快, 但是它的缺陷在前面已经提到, LSP2D模型相对于P2D模型计算时间减少了99.73%. 结合前面的模型精度讨论, 可以得出LSP2D模型在保证估计精度的同时, 很大程度上减少了计算量使估计时间大大降低, 对于将电化学模型用到实际当中具有非常重要的意义.Model Time for 50 cycles/s P2D 7860 LSP2D 21 SP 12
表4 比较三种模型估算速度Table4. Comparison of the estimated speeds of the three models.5.结 论 1)通过对电池的端电压方程进行分析和简化, 将原本高度耦合的包含了${c_{\rm{s}}},{c_{\rm{e}}}$ 和${\phi _{\rm{e}}}$ 三个参数的方程化简成耦合程度较低的包含${c_{\rm{s}}}\text{和}{c_{\rm{e}}}$ 两个参数的方程, 并用多项式方程近似表示沿着电极颗粒方向的Li+ 浓度来化简${c_{\rm{s}}}$ , 通过引入三个无量纲变量化简${c_{\rm{e}}}$ . 这样电池的端电压就可以通过几个多项式方程表示出来. 










 图 1 锂离子电池示意图
图 1 锂离子电池示意图



























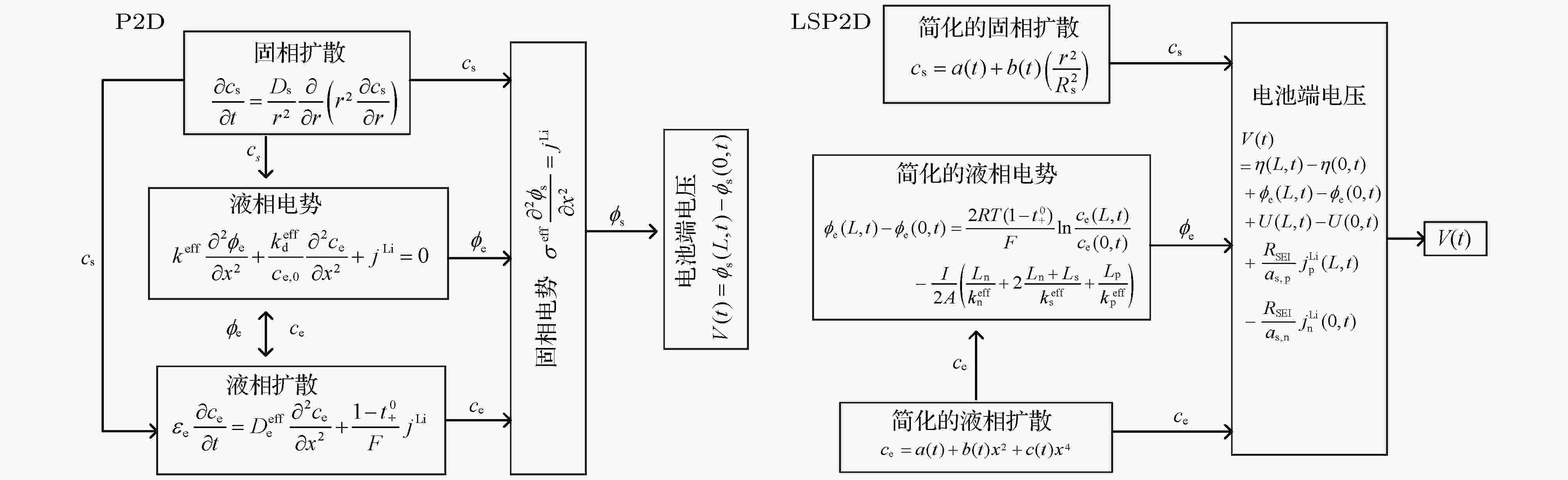 图 2 LSP2D模型简化示意图
图 2 LSP2D模型简化示意图













































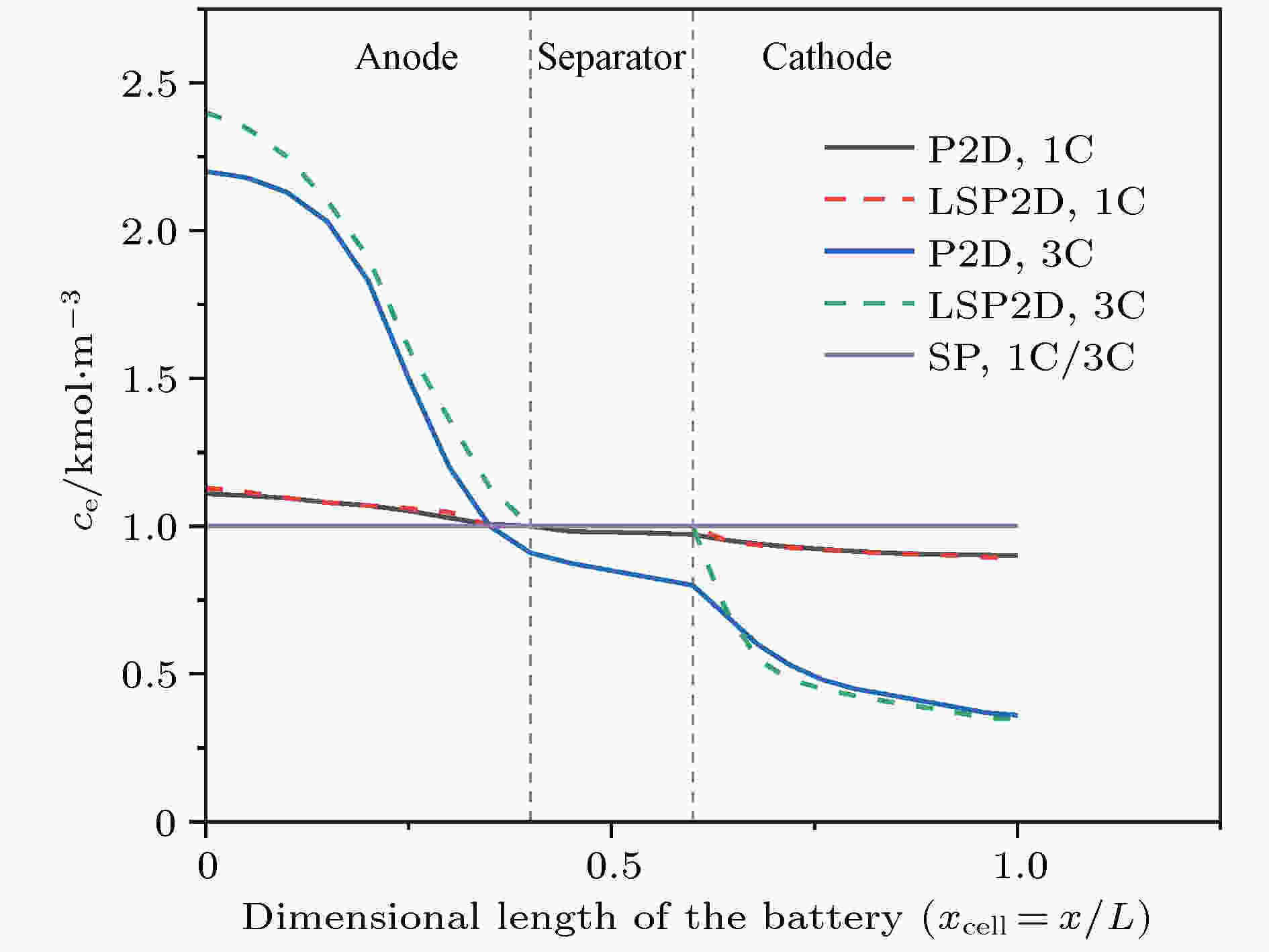 图 3 1C和3C放电率下, SP, LSP2D和P2D模型得到的放电末期液相Li+浓度
图 3 1C和3C放电率下, SP, LSP2D和P2D模型得到的放电末期液相Li+浓度

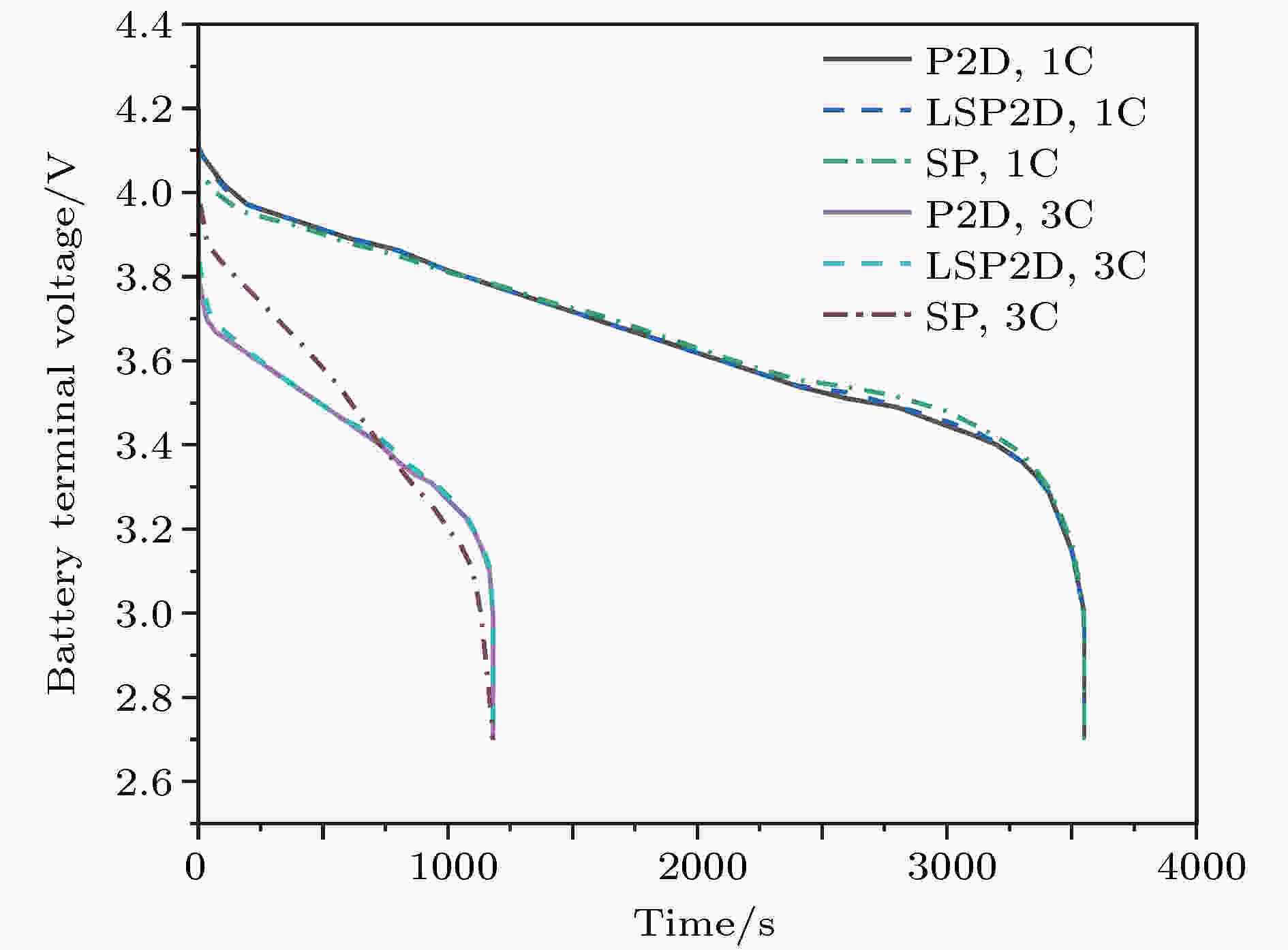 图 4 三种模型在放电率为1C和3C时的放电曲线
图 4 三种模型在放电率为1C和3C时的放电曲线




