摘要:中低纬地区经常发生的电离层闪烁, 严重影响卫星链路的无线电信号传播过程, 导致卫星通信导航信号质量下降, 甚至中断. 在电离层闪烁发生前的酝酿生成期, 通过向电离层闪烁“种子因素”的等离子体泡内释放电子密度增强类化学物质, 填充等离子体泡, 改变等离子体环境特性, 调控电离层动力学过程, 能够降低电离层等离子体不稳定性增长率, 进而抑制闪烁的发生. 本文开展了基于化学物质释放的电离层闪烁抑制理论及方法研究, 根据化学物质释放对电离层等离子体环境的影响, 定量计算控制因素改变对不稳定性增长率的贡献, 建立了基于电子密度增强类化学物质释放的电离层闪烁抑制物理模型, 仿真了等离子体泡的填充过程及等离子体不稳定性增长率的演化过程. 仿真结果表明该方法具有较好的闪烁抑制效果, 为我国中低纬地区卫星信号电离层闪烁抑制研究奠定了理论基础.
关键词: 电离层闪烁/
化学物质释放/
闪烁抑制

English Abstract

全文HTML

--> --> -->

随着人类的信息技术不断发展, 高技术信息系统性能发挥受空间环境的影响和制约越来越大. 近地空间电离层等离子体环境, 具有时空变化和多种尺度的电子密度不均匀结构, 会对穿越其中的无线电波产生显著影响, 从而直接影响和制约无线电信息系统^[1,2]. 当电波穿越电离层时, 电离层电子密度不均匀体会引起电波的聚焦和散焦效应, 从而导致无线电波信号的幅度、相位、到达角、极化状态等发生快速随机抖动, 这就是电离层闪烁. 电离层闪烁可以对几十MHz到10 GHz无线电频段的电子信息系统产生影响, 导致星地链路信号幅度、相位的随机起伏, 降低了卫星通信、卫星导航和天地基雷达目标监测等系统的性能. 严重空间天气事件期间, 高纬和低纬度地区发生的严重电离层闪烁, 甚至会导致卫星通信系统通信中断, 导致卫星导航系统接收机失锁, 导致天地基雷达系统测距误差甚至无法成像.
所有的电子信息系统都是在特定的空间环境下运行的. 空间环境的变化直接影响信息化系统的电波传播, 对各类电子信息系统性能产生不同的影响. 随着信息技术的发展, 电子信息系统精度和灵敏度越来越高, 受空间环境的影响和制约也越来越显著. 恶劣的空间环境将极大地影响电子信息系统的使用效能, 电离层闪烁将对电子信息系统产生最为严重的影响^[3-5], 图1是电离层闪烁对卫星导航和卫星通信系统影响的示意图.
图 1 电离层闪烁对卫星导航和通信的影响示意图
Figure1. The schematic diagram of the influence of ionospheric scintillation on satellite navigation and communication

以美国为首的发达国家很重视电离层闪烁对卫星通信系统影响的研究, 建立了完善的电离层闪烁监测系统, 有序推进了用于支撑通信卫星的地面电离层闪烁监测网系统, 以及用于通信/导航中断预报的C/NOFS卫星系统(communication/navigation outage forecasting system). 基于此, 开展了对电离层闪烁产生机理、闪烁地区形态的统计规律、闪烁对通信系统的影响效应及减缓技术等各方面的研究分析工作, 并且实现了电离层闪烁对各频段信息链路系统影响效应的现报和预报业务化服务. 除了上述电离层闪烁监测手段外, 美国等国也通过人工干预的手段, 开展了人工影响电离层闪烁的主动空间试验. 研究电离层闪烁机理、不稳定性触发等, 进一步对闪烁形成的机理进行了深化研究^[6,7].
1982年9月, 美国和巴西合作利用火箭开展物质释放实验, 试图激发不规则体和扩展F, 人工触发电离层闪烁效应. 开展了BIME系列试验(Brazilian Ionospheric Modification Experiment)^[8,9], 向电离层中释放中性气体, 试验地点位于巴西东部纳塔耳(Natal)海岸附近. 试验中都观测到强振幅闪烁及扩展F等现象, 这是首次通过主动的空间试验人工触发赤道F2层底部的电子密度扰动. 与此同时还在巴西海岸进行了“彩色泡计划”(Colored Bubbles), 该计划通过释放易电离的碱土金属, 在电离层局域产生电子密度的增强区.
1990年, 美国国家航空航天局(National Aeronsautics and Space Administration, NASA)在马歇尔群岛的Kwajalein(9.28°N, 167.73°E), 实施了两次空间释放试验^[10,11], 通过火箭向电离层释放六氟化硫(SF₆), 试图触发赤道底部的等离子体复合, 人工影响电离层闪烁, 两次试验都在人工扰动区域观测到了小尺度不规则体.
2013年, 美空军实验室牵头, 开展了金属氧化物空间云计划(The Metal Oxide Space Cloud Experiment, MOSC)^[12-17], 研究电离层闪烁控制和远距离通信能力增强技术. 随后2015年2月在白沙基地再次进行了人工电离层控制试验. MOSC试验通过向电离层特定区域释放电子密度增强类化学物质钐(Sm)改变了电离层等离子体局部电场分布及电子密度分布, 调控电离层动力学行为, 降低电离层等离子体不稳定性增长率, 进而抑制引起电离层闪烁的不规则体的产生, 图2^[13]为MOSC-2试验观测到得电离层闪烁抑制效果. 从实验效果看, 在试验当晚的电离层电子密度不规则体的强度明显弱于第二天夜晚同一时段, 但是不规则体强度减弱是否是由于释放试验引起的, 还需要开展更多的理论和试验研究, 对这一试验现象进一步确认.
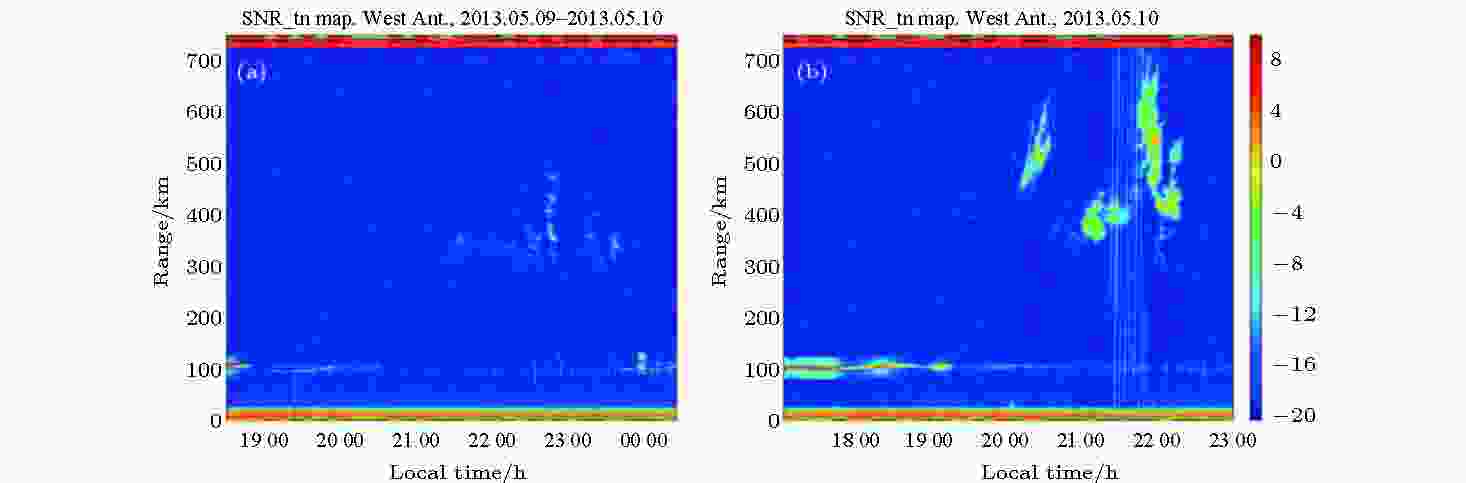图 2 (a) MOSC-2试验期间夜晚电离层电子密度分布图; (b) 试验后第二天夜晚电子密度分布图
Figure2. (a) Electron density distribution at night during the experiment; (b) electron density distribution at next night of the experiment

我国在电离层闪烁监测预报研究方面, 早在20世纪80年代, 中国电子科技集团公司第二十二研究所曾利用ETS-II卫星甚高频(VHF)信号对我国低纬电离层闪烁开展了相关研究; 90年代曾用C波段4 GHz卫星信号, 对电离层闪烁开展了观测研究. 研制了GPS闪烁接收机, 在低纬海口、广州、兰州、重庆等站和高纬南极长城站、中山站进行了闪烁观测, 使国内处于低谷的电离层闪烁观测研究得以重新开展, 并快速发展. 2006年以来, 又在北极建立了5个电离层闪烁观测站, 构成短基线测量. 目前, 我国已经建立了电离层闪烁监测与预报网, 能对外提供电离层闪烁及其影响程度的分布地图, 为各部门提供了必要的电离层天气保障.
在电离层化学物质释放研究方面, 中国科学院空间科学与应用技术研究中心黄文耿等^[18]研究了电离层水(H₂O)和SF₆释放条件下, 释放物在电离层中的扩散过程和化学反应过程; 数值模拟了不同种类中性气体释放, 产生的人工气辉辐射增强的幅度和持续时间^[19]. 武汉大学胡耀垓等研究了不同高度、不同释放质量条件下, H₂O和SF₆产生的电离层扰动效应^[20], 进而用射线追踪方法研究了化学物质释放产生的电离层扰动区对不同频率的短波信号传播过程的影响^[21,22]; 研究了电子密度增强类释放物钡(Ba)在电离层中的动力学过程, 分析了Ba原子的氧化和电离损耗机制, 探讨了Ba云释放早期的演化基本特征、Ba云形态、亮度以及电子密度分布等问题^[23]. 解放军理工大学汪四成等研究了SF₆和H₂O两种释放物的物理化学性质, 建立了化学物质释放二维动力学模型, 模拟了两种释放物的电离层扰动特性^[24]; 开展了化学物质释放激发中低纬电离层扩展F的数值模拟研究, 建立了人工激发中低纬扩展F的物理模型, 讨论了H₂O释放条件下, 激发电离层瑞利-泰勒不稳定性的可能性^[25]; 开展了电离层H₂释放的数值模拟研究, 分析了不同释放条件下的电离层扰动特性^[26]. 中国电子科技集团公司第二十二研究所开展了电离层中性气体释放、电子密度增强类物质Sm释放的机理和效应仿真研究^[27-30]. 中国科学技术大学刘宇等^[31,32]利用地面等离子体模拟装置, 在装置中释放SF₆气体, 探测到了电子密度涡状相干结构, 首次在地面模拟实验中观测到了化学物质释放产生的等离子体不稳定结构.
自从1946年观测到天鹅座64 MHz射电信号时发现其辐射强度的电离层闪烁以来, 人们利用卫星信标对电离层闪烁开展了大量的观测研究, 并基于电离层物理及传播机制和大量事件数据, 建立了预报模型. 但是, 模型只能提供系统规划设计参考, 预警和规避, 属于电离层闪烁的消极、被动应对策略. 面对严重空间天气事件期间缺乏电离层闪烁的积极、主动应对手段, 本文开展了通过在电离层中释放化学物质的人为干预方式, 短暂地影响电离层等离子体的组分、结构和物理过程, 从而影响电离层闪烁的研究.

2

-->

2.1.释放物扩散

化学物质释放的初始阶段, 在压力作用下, 释放物像铲雪机一样将周围的等离子体推开, 这一过程以超声速进行, 经历的时间很短, 一般只有几秒. 然后压力差骤减, 当其与背景压力可以相比拟时, 释放物和周围等离子体充分混合, 从而向空间扩散, 这一过程历经时间较长, 离子化学反应也主要发生在这一阶段.
扩散方程表达式为

$\frac{{\partial {n_i}}}{{\partial t}} = D\left[ {\frac{{{\partial ^2}{n_i}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{n_i}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{n_i}}}{{\partial {z^2}}}} \right],$

其中, ${n_i}\left( {x,y,z,t} \right)$为释放物数密度, 且满足${n_i}\left( {x,y,z,0} \right) = {N_0}\delta \left( {x,y,z} \right)$, ${N_0}$为释放分子总量.
将开始释放时的释放物看作一个点源, 在背景电离层和热层平面分层的假设下, 释放物的扩散过程可以用下式近似^[27]:

$\begin{split}{n_i}\left( {r,z,t} \right) =&\; \dfrac{{{N_0}}}{{{{\left( {4{\text{π}}{D_0}t} \right)}^{1.5}}}}\exp \left\{ {\! -\! \left( {z \!-\! {z_0}} \right)\left( {\dfrac{3}{{4{H_\alpha }}} \!+\! \dfrac{1}{{2{H_i}}}} \right)} \right. \\\begin{array}{*{20}{c}}\end{array} &-\! \alpha t\!-\! \dfrac{{{H_\alpha }^2{{\left\{ {1\! -\! \exp \left[ { - \left( {z \!-\! {z_0}} \right)/\left( {2{H_\alpha }} \right)} \right]} \right\}}^2}}}{{4{D_0}t}} \\\begin{array}{*{20}{c}}\end{array}&- \dfrac{{{r^2}\exp \left[ { - \left( {z - {z_0}} \right)/\left( {2{H_\alpha }} \right)} \right]}}{{4{D_0}t}}\\&\left. { -\! {{\left( {\dfrac{1}{{{H_\alpha }}}\! -\! \dfrac{1}{{{H_i}}}} \right)}^2}\dfrac{{{D_0}t\exp \left[ {\left( {z \!-\! {z_0}} \right)\!/\!\left( {2{H_\alpha }} \right)} \right]}}{4}} \right\}\end{split}$

其中, ${n_i}\left( {r,z,t} \right)$为释放物质密度, 它是时间t和空间的函数(r和z分别为离点源径向距离和电离层高度); ${z_0}$为释放点的高度;${N_0}$为释放的总分子数;${D_0}$为扩散系数;${H_\alpha } = kT/{m_a}g$为大气标高;${H_i} = $$kT/{m_i}g$为释放气体标高, 其中, $k$为波尔兹曼常数, $T$为中性气体温度, ${m_a}$,${m_i}$分别为大气平均分子量和释放气体的分子量, $g$为重力加速度; $\alpha t$为化学反应引起的损失项.
2 -->

2.2.释放物与电离层的化学反应

释放物包括电子密度耗空类释放物和电子密度增强类释放物, 释放物与电离层的化学反应过程极为复杂, 在此不做详细解释和说明, 仅给出本文采用的电子密度增强类释放物钐(Sm)与电离层的化学反应方程式^[27]:

${\rm{Sm}} + {\rm{O}}^{{\underrightarrow{\;k_{\rm{1}}\;}}} {\rm{Sm}}{{\rm{O}}^{\rm{ + }}}{\rm{ + }}{{\rm{e}}^ - }{\rm{ + }}\Delta E,$

其中, $\Delta E$是${\rm{SmO}}$的离解反应能量减去电离能量, ${k_{\rm{1}}}$化学反应系数. 这一化学反应过程为夜间在电离层高度通过化学物质释放产生等离子体云提供了可能, 打破了对电子密度增强类化学物质释放试验的光照条件限制.
如果Sm蒸气在阳光中释放, 除了与O的化学反应之外, 还将发生光致电离过程. 光致电离方程如下:

${\rm{Sm}} + hv \to {\rm{S}}{{\rm{m}}^{\rm{ + }}} + {{\rm{e}}^ - }. $

2 -->

2.3.等离子体扩散

电离层化学物质释放区域电子密度的改变, 破坏了原有的带电粒子的密度分布结构和动态平衡. 根据等离子体扩散理论, 假设等离子体只能沿磁力线运动, 可得到等离子体的输运方程如下^[27]:

$\begin{split} \frac{{\partial {n_p}}}{{\partial t}} = & \;{\sin ^2}I\left( {\frac{{\partial D}}{{\partial z}}\frac{{\partial {n_p}}}{{\partial z}} \!+ \!D\frac{{{\partial ^2}{n_p}}}{{\partial {z^2}}} \!+ \! \frac{{{n_p}}}{{{T_{\rm{p}}}}}\frac{{\partial D}}{{\partial z}}\frac{{\partial {T_{\rm{p}}}}}{{\partial z}}}\right. \\ &\left. {+ \frac{D}{{{T_{\rm{p}}}}}\frac{{\partial {n_p}}}{{\partial z}}\frac{{\partial {T_{\rm{p}}}}}{{\partial z}} \!-\! \frac{{D{n_p}}}{{T_{\rm{p}}^2}}\frac{{{\partial ^2}{T_{\rm{P}}}}}{{\partial {z^2}}} \!+\! \frac{{D{n_p}}}{{{T_{_{\rm{p}}}}}}\frac{{{\partial ^2}{T_{{\rm{p}}}}}}{{\partial {z^2}}}} \right) \\ \begin{array}{*{20}{c}}\end{array} &+ \sin I\cos I\left( {\frac{{\partial D}}{{\partial z}}\frac{{\partial {n_p}}}{{\partial x}} + D\frac{{{\partial ^2}{n_p}}}{{\partial x\partial z}}} \right) \\ &+ \sin I\sin \gamma \left( {\frac{{\partial D}}{{\partial z}}\frac{{\partial {n_p}}}{{\partial y}} + D\frac{{{\partial ^2}{n_p}}}{{\partial y\partial z}}} \right) \\ \begin{array}{*{20}{c}}\end{array}& + \!{\sin ^2}I\left( {\frac{{{n_p}}}{{{H_{\rm{p}}}}}\frac{{\partial D}}{{\partial z}} \!+\! \frac{D}{{{H_{\rm{p}}}}}\frac{{\partial {n_p}}}{{\partial z}}\! -\! \frac{{D{n_p}}}{{H_{_{\rm{p}}}^2}}\frac{{\partial {H_{\rm{p}}}}}{{\partial z}}} \right) \\&- {v_{\rm{D}}} \cdot \sin I\frac{{\partial {n_p}}}{{\partial z}} \\ \begin{array}{*{20}{c}}\end{array} &+ \sin I\cos I\left( {D\frac{{{\partial ^2}{n_p}}}{{\partial x\partial z}} + \frac{D}{{{T_{\rm{p}}}}}\frac{{\partial {n_p}}}{{\partial x}}\frac{{\partial {T_{\rm{p}}}}}{{\partial z}}} \right) \\ &+ D \cdot {\cos ^2}I\frac{{{\partial ^2}{n_p}}}{{\partial {x^2}}} + D \cdot \cos I \cdot \sin \gamma \frac{{{\partial ^2}{n_p}}}{{\partial y\partial x}} \\ \begin{array}{*{20}{c}}\end{array}& + \sin I\cos I\left( {\frac{D}{{{H_p}}}\frac{{\partial {n_p}}}{{\partial y}} - \frac{{D{n_p}}}{{H_{_{\rm{p}}}^2}}\frac{{\partial {H_{\rm{p}}}}}{{\partial x}}} \right) \\ &- {v_{\rm{D}}} \cdot \cos I\frac{{\partial {n_p}}}{{\partial x}} \\ \begin{array}{*{20}{c}}\end{array} &+ \sin \gamma \sin I\left( {D\frac{{{\partial ^2}{n_p}}}{{\partial z\partial y}} + \frac{D}{{{T_{\rm{p}}}}}\frac{{\partial {n_p}}}{{\partial y}}\frac{{\partial {T_p}}}{{\partial z}}} \right) \\ &+ D \cdot \sin \gamma \cos I\frac{{{\partial ^2}{n_p}}}{{\partial x\partial y}} + D \cdot {\sin ^2}\gamma \frac{{{\partial ^2}{n_p}}}{{\partial {y^2}}} \\ \begin{array}{*{20}{c}}\end{array} &+ \sin \gamma \sin I\left( {\frac{D}{{{H_{\rm{p}}}}}\frac{{\partial {n_p}}}{{\partial y}} - \frac{{D{n_p}}}{{H_{_{\rm{p}}}^2}}\frac{{\partial {H_{\rm{p}}}}}{{\partial y}}} \right)\\ &- {v_{\rm{D}}} \cdot \sin \gamma \frac{{\partial {n_p}}}{{\partial y}} + {P_{\rm{p}}}\ - {L_{\rm{p}}}, \end{split} $

其中, ${n_p}$是离子或电子密度; $P$和$L$分别代表带电粒子的产生率和复合率, $L = {L_0} + \displaystyle\sum\limits_{i = 1}^M {{K_1}_i{n_p}{n_i}} $,${L_0}$是${{\rm{O}}^ + }$与其他粒子反应和光解反应的损失率, 释放中性气体由M种中性分子组成, ${n_i}$为第$i$种中性气体与${{\rm{O}}^ + }$的化学反应速率; ${T_{\rm{p}}} = \left( {{T_{\rm{e}}} + {T_{\rm{i}}}} \right)/2$是等离子体温度; ${H_{\rm{p}}}$是等离子体标高, ${H_{\rm{p}}} = 2{T_{\rm{p}}}k/\left( {{m_{\rm{p}}}g} \right)$; $I$是磁倾角; $D$是有效双极扩散系数, $D = \left( {1 + {T_{\rm{e}}}/{T_{\rm{i}}}} \right)$${D_{\rm{i}}} $, ${D_{\rm{i}}}$是离子扩散系数; ${v_{\rm{D}}}$为外加漂移速度(风速).
等离子体在电离层中的运动, 除受到地磁场洛伦兹力的影响外, 还受电场力、等离子体密度梯度力和碰撞等影响, 因此假设等离子体只能沿磁力线运动, 给计算结果带来了误差. 在碰撞和电场力作用下, 等离子体可能出现跨越磁力线的运动, 致使等离子体云密度分布的仿真结果产生一定的失真. 由于在电离层F层高度, 磁场力远大于碰撞力和电场力, 因此误差在可接受范围内.

电离层闪烁的理论研究结果表明, 位于电离层F层底部附近的等离子体泡, 在瑞利-泰勒不稳定性作用下上升破碎, 形成大量多尺度电子密度不规则体, 电波信号穿越电子密度不规则体时, 波前发生了不同的相位改变, 最终在接收端产生了信号衰落, 发生了闪烁现象. 在电离层闪烁发生前的酝酿生成期, 通过向电离层闪烁“种子因素”的等离子体泡内释放电子密度增强类化学物质, 填充等离子体泡, 改变等离子体环境特性, 调控电离层动力学过程, 能够降低电离层等离子体不稳定性增长率, 进而抑制闪烁的发生. 本节模拟了在等离子体泡中释放电子密度增强类化学物质Sm对等离子体泡填充过程, 并研究了电离层不稳定性增长率随时间的演化过程.
2

-->

3.1.仿真模型建立

在电离层F层底部增加电子密度耗空类扰动结构, 模拟生成了电离层等离子体泡, 采用的扰动函数下:

$\begin{split}{n_p} =& \; {n_p} \times \left\{ {1 - \exp \left\{ { - \left[ {{{\left( {x - {x_0}} \right)}^2} + {{\left( {y - {y_0}} \right)}^2}} \right.} \right.} \right.\\& \left. {\left. {\left. { + a{{\left( {z - {z_0}} \right)}^2}} \right]/b} \right\}} \right\},\end{split}$

其中, ${n_p}$是离子或电子密度, $\left( {{x_0},{y_0},{z_0}} \right)$为扰动点位置, $a$为扰动形状调节因子, $b$为扰动范围调节因子.
根据释放物在电离层等离子体泡中的物理化学过程, 建立了电离层闪烁抑制物理模型, 模型算法设计流程如图3所示.
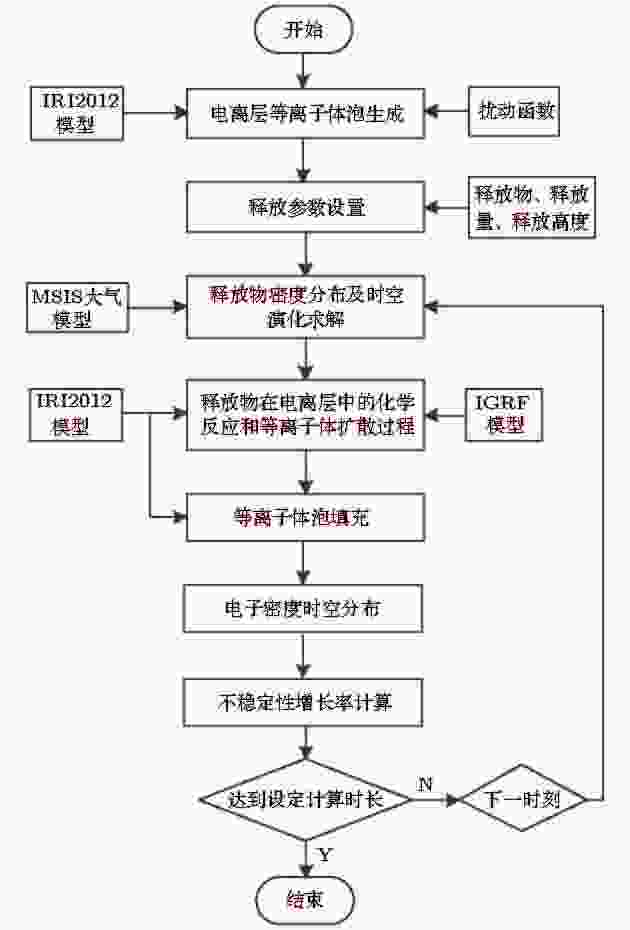图 3 电离层闪烁抑制仿真模型设计流程图
Figure3. The design flow chart of ionospheric scintillation suppression simulation model.

仿真模型设计流程按照以下5个步骤进行.
步骤1　电离层等离子体泡生成. 采用国际参考电离层模型IRI2012生成背景电离层, 采用扰动函数在背景电离层上生成椭球状电子密度空洞, 模拟电离层等离子体泡.
步骤2　根据电离层等离子体泡的尺度、高度和耗空深度等扰动参数, 设置试验参数, 包括试验参数包括释放物种类、释放量、释放高度等.
步骤3　采用微元叠加法, 求解释放物流场分布及时空演化过程, 获得释放物密度分布.
步骤4　依据释放物与电离层等离子的化学反应和等离子体扩散过程, 计算获得电子密度分布, 并计算等离子体不稳定性增长率, 评估抑制效果.
步骤5　化学反应剩余释放物继续扩散, 重复执行步骤3—4, 计算下一时刻的等离子体密度分布, 达到设定计算时长后结束计算, 得到等离子体泡填充演化过程.
2 -->

3.2.数值模拟

根据建立的电离层闪烁抑制物理模型, 模拟了在位于250 km高度的等离子体泡中释放5.6 kg Sm蒸气, 释放后0 s, 10 s, 50 s, 100 s, 200 s, 400 s, 600 s, 900 s, 1200 s电离层等离子体泡的填充过程, 以及电离层等离子体不稳定性增长率的演化过程, 仿真参数如表1所列.

参数	取值
时间	2016年9月25日24:00 LT
地点	三沙 (16.5 °N, 112.2 °E)
高度	250 km
释放量	5.6 kg
背景电离层	IRI2012
大气密度及中性气体温度	ATMOSNRLMSISE-00
化学反应系数	2.0 × 10–11 cm3/s[27]

表1仿真参数
Table1.Parameters for the simulation.

图4描述了在电离层250 km高度, 释放5.6 kg Sm蒸气后, 释放点电子密度剖面随高度的演化过程.
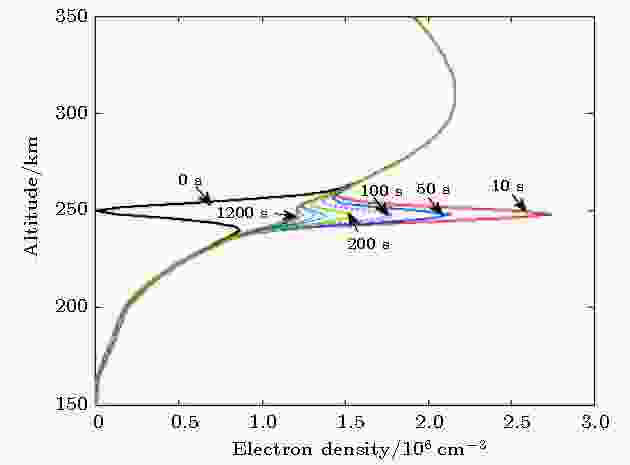图 4 在250 km高度释放5.6 kg Sm蒸气, 电子密度随时间的演化
Figure4. Electron density evolution after releasing 5.6 kg Sm at 250 km altitude.

从图4可以看出, 释放之前, 在250 km高度存在一个尺度约20 km的电离层耗空区, 最大耗空深度为100%, Sm蒸气释放之后快速形成了等离子体云, 释放后10 s等离子体云最大电子密度达2.7 × 10⁶/cm^–3, 释放后100 s等离子体云的密度约1.7 × 10⁶/cm^–3, 释放后1200 s等离子体云密度与背景电子密度相当, 电离层耗空区在垂直方向上基本填充完全.
图5模拟了在位于250 km高度的等离子体泡中释放5.6 kg Sm蒸气, 产生的等离子体云对等离子体泡的二维填充过程.
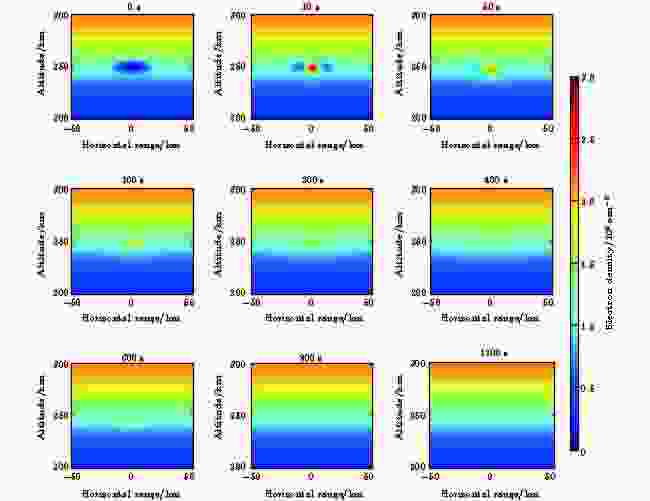图 5 在250 km高度释放5.6 kg Sm蒸气的电离层闪烁抑制效果
Figure5. The scintillation suppression effect of releasing 5.6 kg Sm at 250 km altitude

从图5可以看出, 释放前250 km高度存在一垂向尺度约20 km, 水平尺度约50 km的电离层耗空区, Sm蒸气释放后形成的等离子体云, 快速填充耗空区, 释放后10 s等离子体云尺度约10 km, 电子密度远高于背景等离子体; 释放后50 s等离子体云尺度快速扩大至30 km, 同时等离子体密度逐渐降低; 释放后100 s等离子基本上完成对耗空区的填充, 等离子体云密度高于背景等离子体; 释放后1200 s等离子云完全填充耗空区, 等离子体云密度与背景等离子体密度相当, 等离子体泡消失. 闪烁抑制效果的持续时间在1200 s以上, 闪烁抑制效果的空间尺度与等离子体泡的尺度、密度梯度以及释放量等参数有关, 等离子体泡尺度越大、耗空越深, 需要的释放量越大, 闪烁抑制效果范围越大, 同时闪烁抑制的代价越高.
图6模拟了在位于250 km高度的等离子体泡中释放5.6 kg Sm蒸气后, 电离层不稳定性增长率随时间的演化过程. 电离层等离子体不稳定性理论以及不稳定性增长率的计算方法如下:
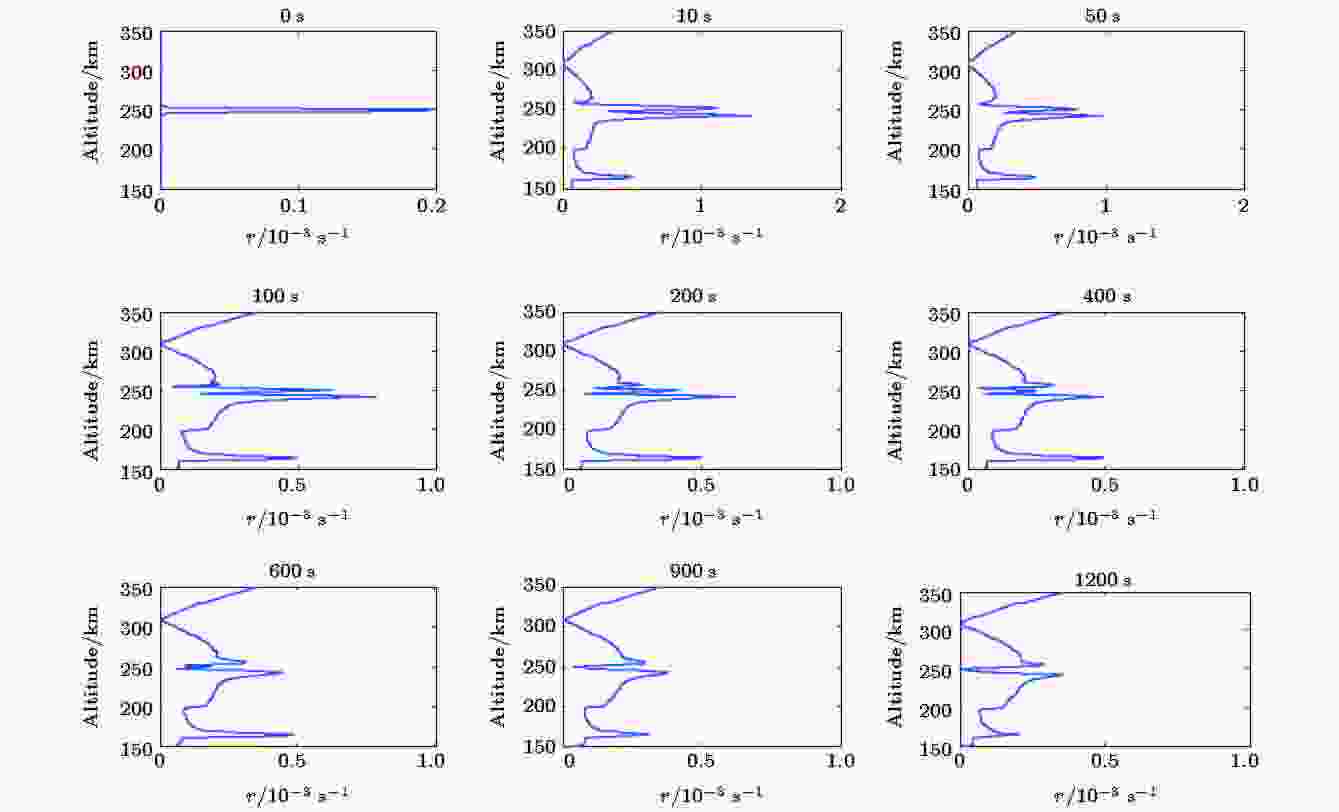图 6 在250 km高度释放5.6 kg Sm蒸气, 不稳定性增长率随时间的变化
Figure6. The evolution of instability growth rate after releasing 5.6 kg Sm at 250 km altitude.

$\gamma = - \dfrac{g}{{{\nu _{in}}}}\dfrac{1}{{{n_p}}}\dfrac{{\partial {n_p}}}{{\partial q}},$

其中, $g$为重力加速度, ${\nu _{in}}$为碰撞频率, ${n_p}$为中性大气密度, $q$为垂直于磁场向上的方向函数. 关于等离子不稳定的详细理论和方法请参考相关文献^[33,34].
从图6可以看出, 电离层不稳定性增长率最大值从释放前的0.2下降到释放后1200 s的约0.0004, 不稳定性增长率下降98%, 闪烁抑制效应明显, 并且在填充后的20 min内没有再次激发明显的不稳定现象. 对不稳定性增长率的模拟结果表明: 在等离子体泡中释放电子密度增强类化学物质, 能够对电离层闪烁触发的“种子”因素等离子体泡进行有效填充, 同时也降低了背景电离层不稳定性增长率, 并在短时间内没有触发新的不稳定性现象.

本文开展了基于化学物质释放的电离层闪烁抑制理论及方法研究, 建立了基于电子密度增强类化学物质释放的电离层闪烁抑制物理模型, 仿真了等离子体泡的填充过程及电离层等离子体不稳定性增长率的演化过程. 仿真结果表明, 在电离层闪烁触发的“种子”因素等离子体泡内释放电子密度增强类化学物质, 能够有效填充电子密度空洞, 从而有效降低电离层等离子体不稳定性增长率, 达到抑制电离层闪烁发生的目的.
但是需要指出的是, 本文仅考虑了电子密度梯度对等离子体不稳定性增长率的影响, 其他控制因素如电场、等离子体温度、风场等闪烁控制因素尚未考虑, 需要进一步考虑等离子体泡填充前后其他闪烁控制因素的改变对不稳定性增长率的影响. 另外, 与当地不稳定性增长率相比较, 通量积分不稳定性增长率在闪烁抑制效果评估上更具有代表性, 需要进一步考虑等离子体泡填充前后通量积分不稳定性增长率的变化.
我国广东、海南及南海地区, 均处在磁赤道异常区的峰值区域, 其闪烁出现率和严重程度较磁赤道和极区更为显著, 是全球范围内电离层闪烁出现最频繁、影响最严重的地区之一. 低纬南海地区的电离层强闪烁, 严重影响卫星链路的传播过程, 导致卫星通信质量下降甚至中断, 导致北斗、GPS等导航卫星接收机失锁, 导航定位误差增大, 甚至失效, 需要针对电离层强闪烁效应, 研究支撑发展具有特色的电波环境保障技术.
通过开展电离层闪烁抑制、减缓研究, 对于解决我国南海地区由于电离层闪烁引起的各类电子信息系统的工作性能故障, 具有至关重要的经济效益. 如在救援等特殊情况下, 可通过人工影响电离层闪烁系统有效解决南海地区卫星导航失锁和卫星通信中断问题, 具有很重要的应用价值. 电离层闪烁能够对多种航天系统的性能产生影响, 研究电离层等离子体中涉及的物理和化学过程, 为电离层闪烁模型的研究和电离层闪烁预报研究提供一定的数据支撑, 从而为天基/地基电子信息系统运行和应用提供服务保障.