摘要: 各类系统中的纠缠操控是量子信息科学的重要问题之一. 本文研究了热原子蒸气的级联四波混频过程中产生的纠缠增强及纠缠增强的相位敏感特性. 研究表明, 该级联四波混频过程第二级输出的探针光和共轭光的量子纠缠较第一级明显增强, 最大可达5 dB以上, 且随着强度因子的增大可实现完美纠缠. 文中还详细讨论了量子关联类型及纠缠大小与抽运光相位、非线性强度因子之间的变化关系, 结果显示, 由于纠缠增强及纠缠类型对抽运光相位的敏感性, 通过控制相位和强度因子可改变光场噪声特性从而实现对探针光和耦合光之间纠缠增强、纠缠度大小、纠缠类型的量子操控. 该理论研究对实验实现纠缠增强及双模压缩态压缩角、压缩度的光学参量操控具有重要的指导意义.
关键词: 相位敏感放大 /
四波混频 /
量子纠缠 /
量子操控 English Abstract Quantum manipulation of entanglement enhancement in cascaded four-wave-mixing process Yang Rong-Guo 1,2,4 ,Zhang Chao-Xia 1,2 ,Li Ni 1,2 ,Zhang Jing 1,2,4 ,Gao Jiang-Rui 1,2,3,4 1.College of Physics and Electronic Engineering, Shanxi University, Taiyuan 030006, China Fund Project: Project supported by the National Basic Research Program of China (Grant No. 2016YFA0301404), the National Natural Science Foundation of China (Grant Nos. 11504218, 11874248, 11874249), and the Program of State Key Laboratory of Quantum Optics and Quantum Optics Devices, China (Grant No. KF201007).Received Date: 11 October 2018Accepted Date: 22 February 2019Available Online: 01 May 2019Published Online: 05 May 2019Abstract: Entanglement manipulation in various systems is one of the important problems in quantum information science. In this paper, the phase sensitivity and entanglement enhancement of the cascade four-wave mixing of hot atomic steam are studied. The results show that the quantum entanglement of the probe light and the conjugate light output at the second level of the cascade four-wave mixing process is significantly stronger than that at the first level, and the maximum increment can reach more than 5 dB, and the perfect entanglement can be achieved by increasing the intensity factor. The relations of quantum correlation type and the size of the entanglement with the pump phase and the nonlinear intensity factor are also discussed in this work. The results show that because of the enhancement of entanglement and the sensitivity of entanglement type to pump phase, the light field noise characteristics can be changed by controlling the phase and intensity factors thus realize the enhancement of entanglement between the probe and coupling light and the quantum manipulation of entanglement extent and quantum entanglement type. The theoretical study is of important significance for guiding the experimental implementation of optical parameter manipulation of entanglement enhancement, compression angle and compression degree of two-mode compression state.Keywords: phase sensitive amplifier /four-wave-mixing process /quantum entanglement /entanglement manipulation 全文HTML --> --> --> 1.引 言 量子压缩、量子纠缠、量子测量及量子信息处理与不确定性原理密切相关[1 -3 ] . 量子压缩和量子纠缠的理论和实验研究是量子光学和量子信息科学的核心内容[4 ,5 ] . 可产生量子压缩和纠缠的系统有多种, 包括在腔内置入一块非线性晶体[6 ,7 ] , 热原子蒸气[8 ,9 ] 或光纤[10 ,11 ] 中的四波混频过程等. 大约在30年前人们首次在钠蒸气中发生四波混频过程并实验产生了量子压缩, 涉及热原子蒸气的不同机理也被相继提出并被实验证实[8 ,9 ] . 四波混频过程可分为相位敏感放大(有两个相干输入)和相位不敏感放大(有一个或没有相干输入). 相位敏感放大已在光纤放大器中有广泛的研究, 并且取得了显著的进展[10 -13 ] . 与具有相同强度因子的相位不敏感放大装置相比较, 相位敏感放大装置中产生的探针光与耦合光的强度差压缩在非常窄的抽运光相位变化范围内可以增强3 dB左右[13 ] . 2007年, McCormick等[13 ] 利用铷原子蒸气中的非简并四波混频过程在实验上产生了一对强量子关联光束. 四波混频系统有许多优点, 例如, 由于系统强的非线性而不需要光学腔, 没有了光学模式限制; 具有空间多模的特点; 产生的非经典光束能在空间上分离等. 这些优点使得四波混频系统在许多应用中备受欢迎, 包括量子信息过程、量子计量和量子成像[14 ] , 例如纠缠影像[15 ] 、Einstein-Podolsky-Rosen (EPR)纠缠的可调谐延时[16 ] 、非线性量子干涉仪[17 -19 ] 、高纯度窄带单光子[20 ] 、微悬臂梁位移的超敏感测量[21 ] 、量子影像多空间模正交压缩[22 ] 以及用于量子成像的局域多空间模的正交压缩[23 ] . 通过级联两个四波混频过程, 可以实现EPR纠缠态的可调谐延时[24 ] 、纠缠态的低噪声放大以及量子态之间的相互作用[25 ,26 ] . 此外, 四波混频过程在纠缠态产生、纠缠增强及量子操控等方面具有重要的应用价值. 2017年, Wang等[27 ] 提出了利用空间结构的抽运在Rb蒸气中通过四波混频过程产生多模量子纠缠态光场的方案. 同年, Xin等[28 ] 在Rb原子蒸气室中通过级联四波混频过程实验实现了纠缠增强. 本文理论上研究了在热原子蒸气的级联四波混频过程中产生的纠缠增强及纠缠增强的相位敏感特性, 并就其对抽运光相位和增益因子参数依赖性给出了更全面的分析. 结果表明, 通过两个热原子蒸气室组成相位敏感的级联四波混频过程可获得5 dB以上的纠缠增强(与单个四波混频过程相比), 利用纠缠增强的相位敏感特性, 通过精准控制相位及强度因子来改变光场噪声特性从而实现对探针光和耦合光之间纠缠增强、纠缠度大小、纠缠类型的量子操控. 该研究对实验实现双模压缩态压缩角、压缩度、纠缠增强等参量控制具有重要的指导意义. 实验上可以通过高灵敏度压电陶瓷对原子气室温度、原子数密度进行连续调节和精确控制, 因此该系统具有强的实验可行性.2.级联四波混频产生的量子纠缠增强 22.1.级联四波混频过程 2.1.级联四波混频过程 图1 是实现输出探针光和耦合光纠缠增强的级联四波混频系统. 如图1 所示, 探针场${\hat a_0}$ 和耦合场${\hat b_0}$ 是两个相干场, 与一束强的抽运光${\hat c_1}$ 同时并且对称地注入到第一个热原子蒸气室中(第一级四波混频). 通过发生第一个四波混频过程产生探针光${\hat a_1}$ 和耦合光${\hat b_1}$ , 然后将探针光${\hat a_1}$ 和耦合光(相位共轭光)${\hat b_1}$ 作为两个输入场与另一束强的抽运光${\hat c_2}$ 以相同的方式注入到第二个热原子蒸气室中(第二级四波混频), 而第二个四波混频过程产生了探针光${\hat a_2}$ 和耦合光${\hat b_2}$ . 把两个四波混频过程看作一个整体, 则整个系统只有两个输出光束, 分别是探针光${\hat a_2}$ 和耦合光${\hat b_2}$ . $\hat a$ , $\hat b$ 和$\hat c$ 分别代表探针场、耦合场和抽运场. 有两个相干输入场, 称为相位敏感放大器.图 1 相位敏感的级联四波混频系统Figure1. Cascaded four-wave mixing process in hot vapor.2.2.系统的哈密顿量和演化方程 -->2.2.系统的哈密顿量和演化方程 分别将探针光、耦合光和抽运光记为算符$\hat a$ , $\hat b$ 和$\hat c$ , 则对应于第一级和第二级四波混频过程的哈密顿量${\hat H_1}$ 和${\hat H_2}$ 的形式如下[26 ] :${\xi _1}$ 和${\xi _2}$ 分别是两个四波混频过程的相互作用强度, 取决于相互作用的时间长短并分别与输入抽运光${\hat c_1}$ 和${\hat c_2}$ 的强度成正比. 此外, 它们还与单光子失谐$\varDelta $ 和双光子失谐$\delta $ 有关. 抽运场${\hat c_1}$ 和${\hat c_2}$ 的相位分别记为${\phi _{{c_1}}}$ 和${\phi _{{c_2}}}$ . 这里, ${\theta _1}$ = $2{\phi _{{c_1}}}$ , ${\theta _2}$ = $2{\phi _{{c_2}}}$ . 由(1 )式可以得到第一个四波混频过程输出的两束光的时间演化方程如下:2 )式可以得到第二个四波混频过程输出的两束光的时间演化方程为${G_1} = {\cosh ^2}\left( {{\xi _1}t} \right)$ 和${G_2} = {\cosh ^2}\left( {{\xi _2}t} \right)$ 取决于四波混频过程的相互作用强度. ${G_1}$ 和${G_2}$ 分别对应第一级四波混频和第二级四波混频作用的强度因子. 如果探针端${\hat a_0}$ 注入相干场, 耦合端${\hat b_0}$ 注入真空场, 则${G_1}$ 和${G_2}$ 就是相位不敏感系统的强度因子[29 ] . 当探针和耦合端口同时注入相干场时, 输出场的噪声性质不仅由强度因子${G_1}$ 和${G_2}$ 决定, 而且与下面将要讨论的两个输入场的相位有关. 将算符写成平均值加起伏的形式, $\hat a = \alpha + {\text{δ}}a$ , $\hat b = \beta + {\text{δ}}b$ , 代入到(3 )—(6 )式中, 系统相应的量子起伏方程可以写成:2.3.量子纠缠的增强 -->2.3.量子纠缠的增强 2.2节分别给出了来自两个四波混频过程的探针光与耦合光的时间演化方程. 这里研究级联四波混频过程产生输出光束之间的纠缠特性. 场的正交振幅和正交相位定义如下:[30 ,31 ] ${\theta _1} \in \left[ {0,\;2{\text{π}}} \right]$ ,${\theta _2} \in \left[ {0,\;2{\text{π}}} \right]$ 时, 令${\theta _1} = {\theta _2} = 0,\;2{\text{π}}$ 或${\theta _1} = {\theta _2} = {\text{π}}$ 来分别研究Type-I类和Type-II类两种情况下, 强度因子${G_1}$ 和${G_2}$ 对输出探针光${\hat a_1}$ (${\hat a_2}$ )与耦合光${\hat b_1}$ (${\hat b_2}$ )两对纠缠的大小, 这里把两对纠缠分别表示成${S_{{a_1}{b_1}}}$ 和${S_{{a_2}{b_2}}}$ . 为了方便讨论, 令${G_1} = {G_2} = G$ , 纠缠随强度因子$G$ 的变化如图2 所示. 不论是Type-I类还是Type-II类情况, 两对输出光束的纠缠增强结果完全相同.图 2 量子纠缠随强度因子$G$ 的函数变化图, 其中红虚线为${S_{{a_1}{b_1}}}$ , 红实线为${S_{{a_2}{b_2}}}$ Figure2. Two pair of quantum entanglement as a function of intensity factor $G$ . Red dashed line corresponds to ${S_{{a_1}{b_1}}}$ and red solid line corresponds to ${S_{{a_2}{b_2}}}$ .图2 可以看出, 对相位敏感的级联四波混频系统输出的探针光与耦合光的纠缠能被极大地增强. 强度因子$G = 1.5$ 时, 第二级四波混频系统输出探针光与耦合光的最大纠缠度可以增加5 dB左右. 并且随着强度因子的增大纠缠值逐渐趋于0, 即在所取参数下输出探针光(${\hat a_2}$ )与耦合光(${\hat b_2}$ )几乎达到了完美纠缠. 同时可以看到, 选取特定的抽运光相位和强度因子, 可以使第二级四波混频过程产生的纠缠比第一级四波混频过程产生的纠缠增强的幅度达到最大.3.纠缠对抽运光相位的敏感性及纠缠操控分析 接下来分析级联系统中纠缠对抽运光相位的敏感性以及如何利用这种敏感性实现对纠缠的量子操控.${\theta _1}$ 和${\theta _2}$ 会同时影响探针光${\hat a_2}$ 与耦合光${\hat b_2}$ 之间的纠缠. 对于Type-I类情况的纠缠, 探针光${\hat a_2}$ 与耦合光${\hat b_2}$ 的纠缠${S_{{a_2}{b_2}}}$ 的等值线图如图3 所示. 当${\theta _1} \in [0,\;2{\text{π}}]$ , ${\theta _2} \in [0,\;2{\text{π}}]$ 时, ${S_{{a_2}{b_2}}}$ 的值小于2时即存在纠缠, 图中有颜色的区域为纠缠区域. 图中强度因子的取值分别为${G_1} = {G_2} = 1.5,\;2,\;2.5,\;3$ , 颜色越深的区域, 对应的纠缠越大. 最大纠缠区域出现在${\theta _1} = 0,\;2{\text{π}}$ 和${\theta _2} = 0,\;2{\text{π}}$ 处, 纠缠区域随着强度因子的增加逐渐变小, 因此, 相位和强度因子可以同时准确地控制纠缠的大小. 强度因子取特定值的情况下, 需要控制两个相位或者通过固定一个相位改变另一个相位来操控系统的纠缠. 接着令${\theta _1} = 0,\;2{\text{π}}$ 来探究Type-I类情况相位${\theta _2}$ 对探针光${\hat a_2}$ 与耦合光${\hat b_2}$ 纠缠态的影响. 纠缠随相位${\theta _2}$ 的变化如图4 所示.图 4 探针光${\hat a_2}$ 与耦合光${\hat b_2}$ 的纠缠随相位${\theta _2}$ 的变化Figure4. Entanglement of probe ${\hat a_2}$ conjugate ${\hat b_2}$ beams as a function of the phase ${\theta _2}$ for various values of the intensity gain.图 3 不同强度因子下第二级四波混频过程产生的两束光纠缠${S_{{a_2}{b_2}}}$ 的等值线图 (a) ${G_1} = {G_2} = 1.5$ ; (b) ${G_1} = {G_2} = 2$ ; (c) ${G_1} = {G_2} = 2.5$ ; (d) ${G_1} = {G_2} = 3$ Figure3. Contour plots for ${S_{{a_2}{b_2}}}$ with different intensity gains: (a) ${G_1} = {G_2} = 1.5$ ; (b) ${G_1} = {G_2} = 2$ ; (c) ${G_1} = {G_2} = 2.5$ ; (d) ${G_1} = {G_2} = 3$ .${S_{{a_2}{b_2}}}$ 值越小纠缠越大, 当${\theta _2} = 2{\text{π}}$ 时纠缠达到最大. 同样地, 继续研究Type-II类情况相位${\theta _1}$ 和${\theta _2}$ 对探针光${\hat a_2}$ 与耦合光${\hat b_2}$ 之间纠缠的影响. 探针光${\hat a_2}$ 与耦合光${\hat b_2}$ 的纠缠${S_{{a_2}{b_2}}}$ 等值线图如图5 所示.图 5 不同强度因子下第二级四波混频过程产生的两束光纠缠${S_{{a_2}{b_2}}}$ 的等值线图 (a) ${G_1} = {G_2} = 1.5$ ; (b) ${G_1} = {G_2} = 2$ ; (c) ${G_1} = {G_2} = 2.5$ ; (d) ${G_1} = {G_2} = 3$ Figure5. Contour plot for ${S_{{a_2}{b_2}}}$ with different intensity gains: (a) ${G_1} = {G_2} = 1.5$ ; (b) ${G_1} = {G_2} = 2$ ; (c) ${G_1} = {G_2} = 2.5$ ; (d) ${G_1} = {G_2} = 3$ .${\theta _1} \in [0,\;2{\text{π}}]$ , ${\theta _2} \in [0,\;2{\text{π}}]$ 时, 且${S_{{a_2}{b_2}}}$ 的值小于2时存在纠缠. 这里, 强度因子的取值分别为${G_1} = {G_2} = 1.5,\;2,\;2.5,\;3$ . 可以看到, 最大纠缠区域出现在${\theta _1} = {\text{π}}$ 和${\theta _2} = {\text{π}}$ 附近, 而且纠缠区域也会随强度因子的增加而明显变窄, 纠缠度对相位的改变更加敏感. 因此, 对于不同参数的物理系统都可以通过改变抽运光相位来操控Type-II类纠缠. 由图5 可知, 最大纠缠区域对应的相位取值在${\theta _1} = {\text{π}}$ 和${\theta _2} = {\text{π}}$ 附近, 因此, 对于Type-II类情况, 令${\theta _1} = {\text{π}}$ 来研究相位${\theta _2}$ 对输出探针光${\hat a_2}$ 与耦合光${\hat b_2}$ 之间纠缠的影响. 图6 为两束光的纠缠与相位${\theta _2}$ 的关系.图 6 探针光${\hat a_2}$ 与耦合光${\hat b_2}$ 的纠缠随相位${\theta _2}$ 的变化Figure6. Entanglement of probe ${\hat a_2}$ conjugate ${\hat b_2}$ beams as a function of the phase ${\theta _2}$ for various values of the intensity gain.图6 的结论与图5 的结论一致. 从图4 和图6 可以看出: 随着强度因子的增大, 纠缠区域越来越窄而最大纠缠逐渐增大, 且抽运光相位和四波混频过程的强度因子可以协同操控输出光的纠缠. $G = 1.5$ 时, 与第一级四波混频过程相比, 第二级四波混频过程产生的两束光的纠缠存在时对应的抽运光相位具有较宽的变化区域; 当${\theta _1} = {\theta _2} = {\text{π}}$ 时随着强度因子增大第二级四波混频输出场的纠缠也逐渐增大, 与图2 结论相符. 根据这一点, 如图7 所示, 令${G_1} = {G_2} = 1.5$ 来分析抽运光相位对两对探针光与耦合光纠缠的影响.图 7 相位${\theta _1}$ 对两对量子纠缠的影响 (a) ${\theta _2} = 0/2{\text{π}}$ , ${G_1} = {G_2} = 1.5$ ; (b) ${\theta _2} = {\text{π}}$ , ${G_1} = {G_2} = 1.5$ Figure7. Two pair of quantum entanglement versus phase ${\theta _1}$ : (a) ${\theta _2} \!= 0/2{\text{π}}$ , ${G_1} \!= {G_2}\! = 1.5$ ; (b) ${\theta _2} \!= {\text{π}}$ , ${G_1} \!= {G_2} \!= 1.5$ 图7 也可知, 对于Type-I类纠缠来说, 在${\theta _2} = 0,\;2{\text{π}}$ 的情况下, ${\theta _1} = 0,\;2{\text{π}}$ 时能获得最大纠缠; 对于Type-II类纠缠而言, 在${\theta _2} = {\text{π}}$ 的情况下, ${\theta _1} = {\text{π}}$ 时能获得最大纠缠. 与第一级四波混频过程相比, 第二级四波混频过程产生的两束光的纠缠存在时对应的抽运光相位具有较宽的变化区域, 也就是分别当${\theta _2} = 0,\;2{\text{π}}$ 和${\theta _2} = {\text{π}}$ 时, Type-I和Type-II情况下的探针光${\hat a_2}$ 与耦合光${\hat b_2}$ 的纠缠随着${\theta _1}$ 将实现全域纠缠. 由此可见, 对于不同参数的级联四波混频系统, 通过改变输入抽运的相位可以实现对输出场的纠缠类型、纠缠度大小、纠缠度增强的幅度、相位敏感区域选择、全域纠缠等量子操控.4.结 论 本文主要研究了级联四波混频系统纠缠特性与相对相位和强度因子的变化关系, 考虑实验上易于控制的实验参数(相位和增益因子), 理论上研究了对光场量子噪声特性的操控, 包括量子噪声的关联类型和量子噪声关联大小, 宏观上形成了对光场纠缠类型、纠缠大小的控制. 研究表明, 在选取合适的相位及强度因子时, 相位敏感的级联四波混频系统输出的探针光与耦合光的纠缠和单级系统产生的纠缠相比最大可提升5 dB. 同时详细讨论了抽运光相位对输出场的Type-I (正交振幅差与正交相位和)与Type-II (正交振幅和与正交相位差)两类纠缠的影响. 随着强度因子的增加, 纠缠变大, 而纠缠存在对应的相位区域逐渐变窄, 纠缠对相位更敏感. 纠缠对抽运光相位的敏感性研究是量子科学领域的重要研究方向[20 ] . 2018年, Shaked等[32 ] 利用级联的四波混频系统实验实现了宽带的参量零拍探测, 开创了基于级联系统的一种新的应用方向和方法. 






















 图 1 相位敏感的级联四波混频系统
图 1 相位敏感的级联四波混频系统




























































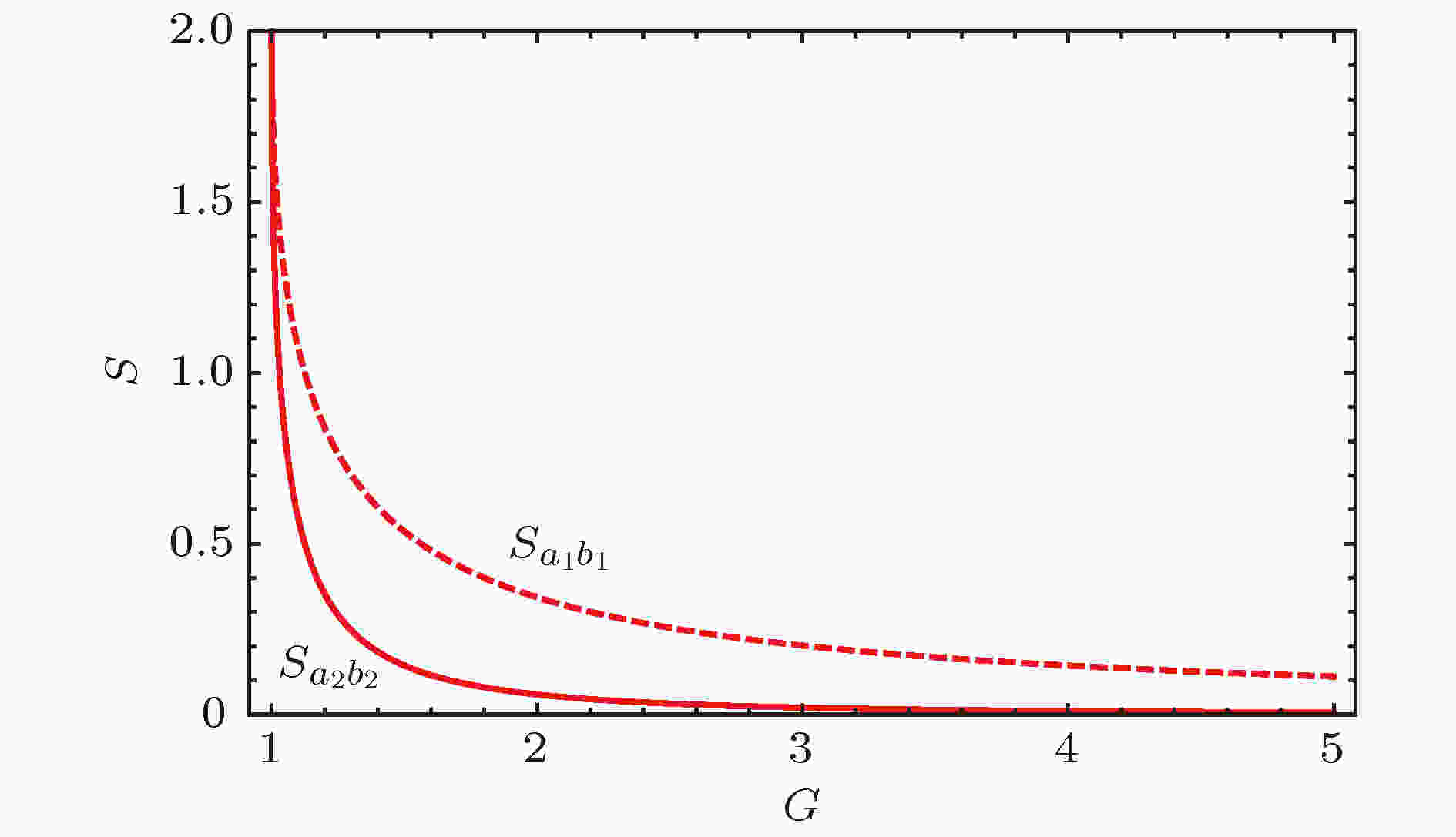 图 2 量子纠缠随强度因子
图 2 量子纠缠随强度因子
















































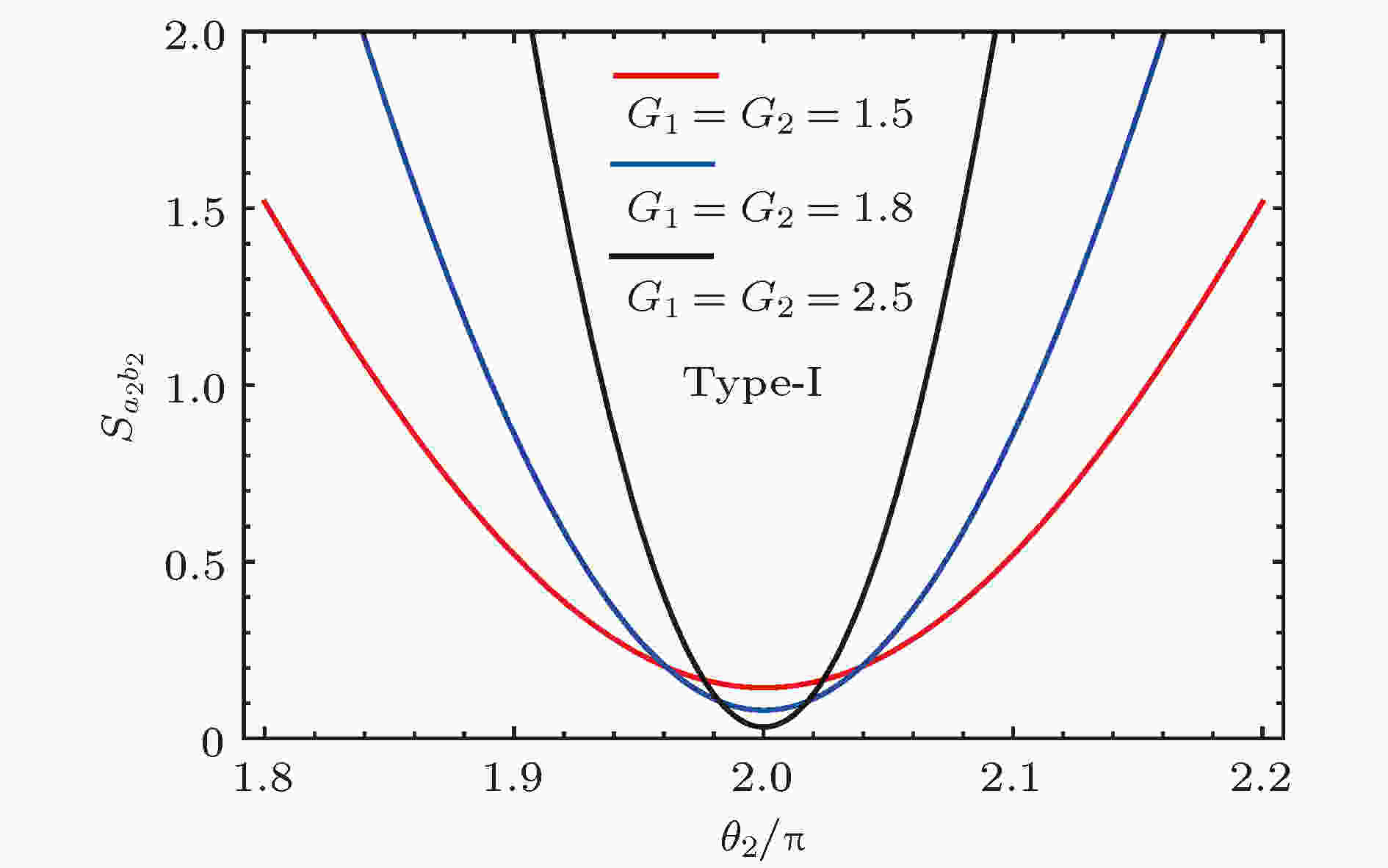 图 4 探针光
图 4 探针光





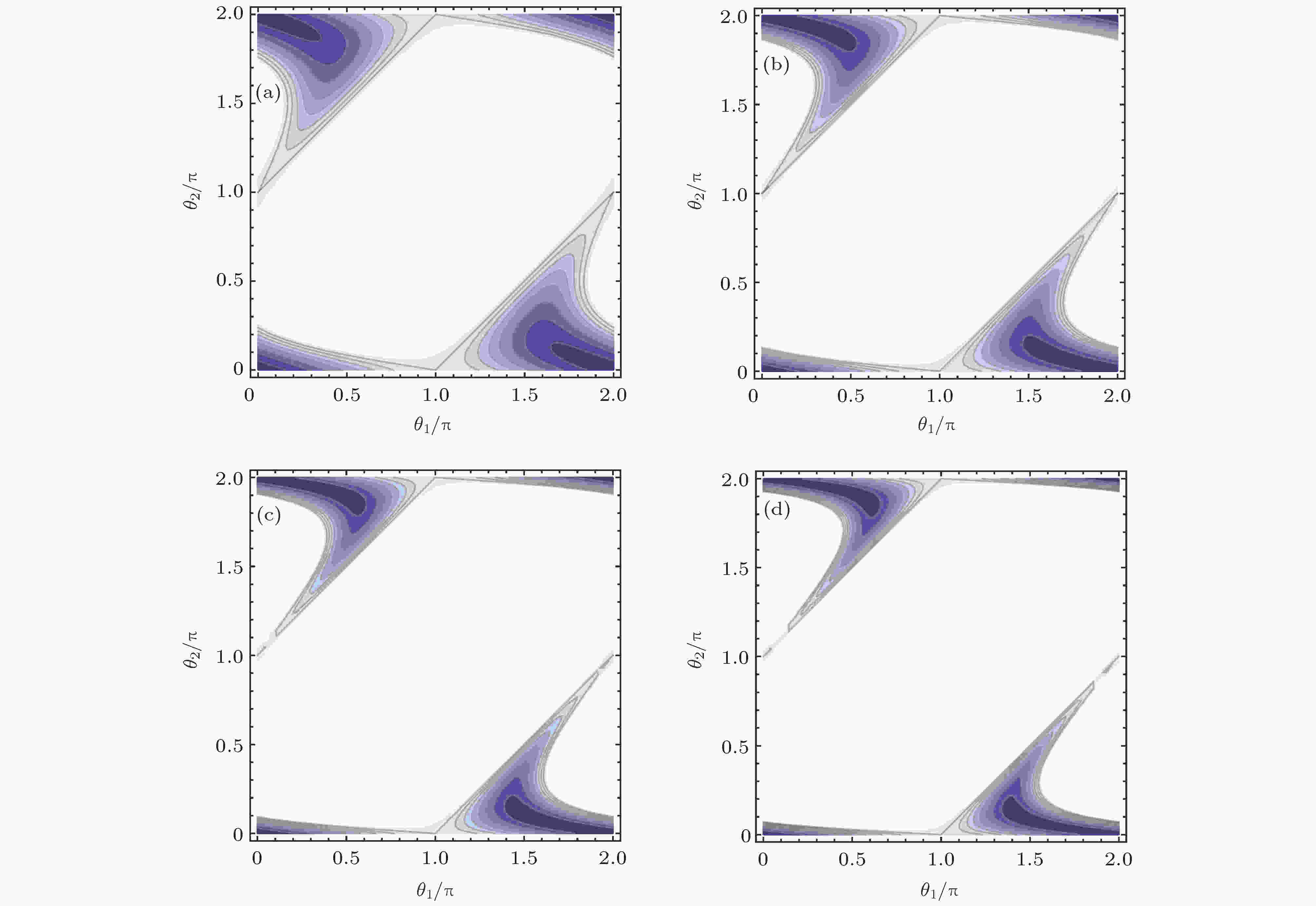 图 3 不同强度因子下第二级四波混频过程产生的两束光纠缠
图 3 不同强度因子下第二级四波混频过程产生的两束光纠缠
























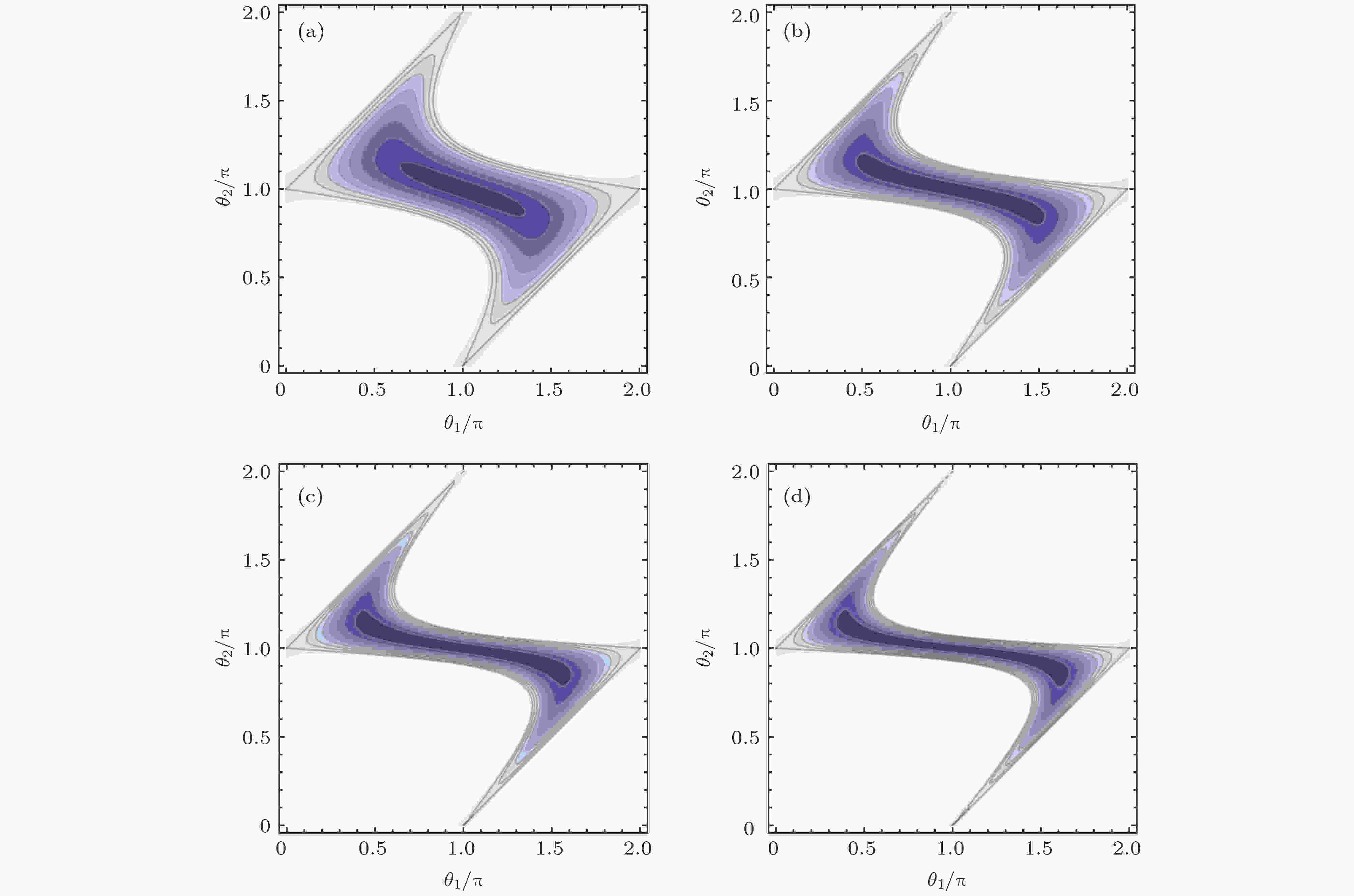 图 5 不同强度因子下第二级四波混频过程产生的两束光纠缠
图 5 不同强度因子下第二级四波混频过程产生的两束光纠缠
































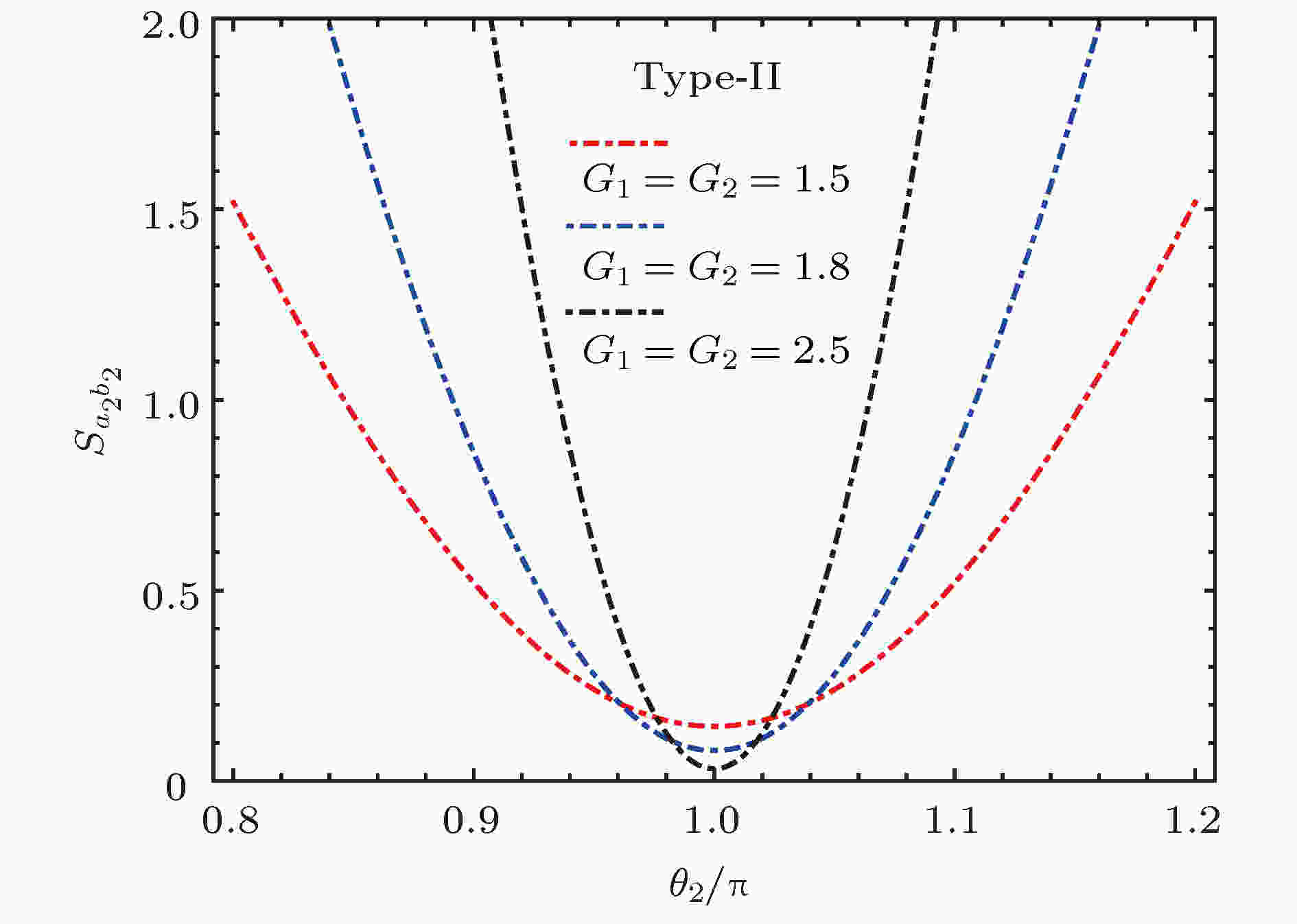 图 6 探针光
图 6 探针光








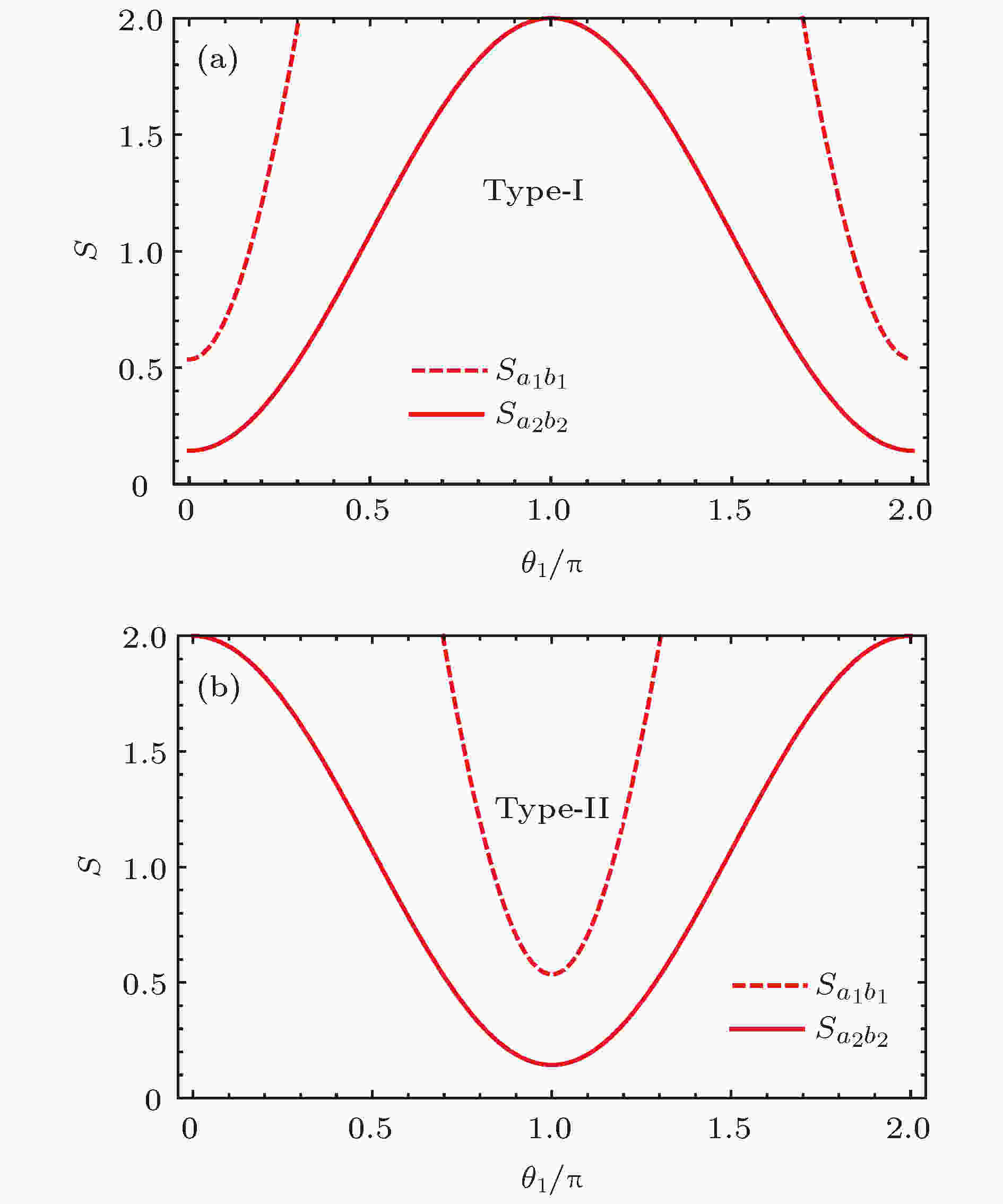 图 7 相位
图 7 相位
























