摘要:为提高Helmholtz型声子晶体低频隔声性能, 设计了一种Helmholtz腔与弹性振子的耦合结构, 通过声压场及固体振型对其带隙产生机理进行了详细分析, 建立了相应的弹簧-振子系统等效模型, 并采用理论计算和有限元计算两种方法研究了各结构参数对其带隙的影响情况. 研究表明, 该结构可等效为双自由度系统振动, 在低频范围内具有两个带隙; 在6 cm的尺寸下, 其第一带隙下限可低至24.5 Hz, 而同尺寸无弹性振子结构只能达到42.1 Hz, 带隙下限降低了40%, 较传统Helmholtz结构具有更为优良的低频隔声特性. 另外, 在框体尺寸一定的情况下, 降低结构间距、增大开口空气通道长度及振子质量、增大左侧腔体体积等方式, 是增大带隙宽度、提高低频隔声效果的主要手段.
关键词: Helmholtz共振/
低频带隙/
局域共振/
噪声控制

English Abstract

全文HTML

--> --> -->

Helmholtz共振腔是一种利用空气振动的声学结构, 该结构广泛应用于声学超表面^[1]、声透镜^[2]及具有负折射^[3]、超声聚焦^[4]等效应的声学超材料构建中. 近年来, 利用局域共振原理^[5]的Helmholtz型声子晶体成为声学超材料研究热点之一^[6-8], 该类型超材料的典型特点是具有带隙特性, 即在带隙频率范围内的弹性波会在结构中迅速衰减, 这为其在隔声降噪^[9-11]等方面的应用奠定了基础. 其中, Guan等^[12]通过螺旋设计增加了开口处空气柱长度, 将第一带隙范围降至217—492 Hz. 刘敏等^[13]设计的圆柱形开缝Helmholtz结构打开了100 Hz以下的低频带隙. 姜久龙等^[14]利用双开口的方式在晶格常数为10 cm的情况下将结构带隙降至87.1—138.2 Hz频率范围内. 随后, Jiang等^[15]又通过多腔耦合的方式设计了一种边长为5 cm的六角形Helmholtz型声子晶体, 该结构带隙下限低至62.1 Hz.
这些研究对于提高Helmholtz结构隔声效果具有重要意义, 但仍只有空气参与振动, 等效振子质量难以进一步提高, 若需进一步降低其带隙下限, 往往需要增大结构尺寸, 限制了其在工程上的应用. 2016年, Abbad和Ahmed ^[16]将Helmholtz腔的上下壁换为钝化薄膜, 并研究了其隔声量相对于传统结构变化情况. 2018年, Zhu等^[17]推导了穿孔板与薄膜耦合结构的吸声系数计算公式, 这种耦合结构同时利用了薄膜^[18-20]和固/气结构隔声特性, 取得了良好效果.
本文设计了一种带弹性振子的Helmholtz型声子晶体, 对其带隙机理进行了详细分析, 建立了等效模型, 在6 cm的腔体尺寸下, 将带隙下限降至24.5 Hz, 相比于传统单腔单开口Helmholtz型声子晶体, 带隙下限降低了40%, 实现了小尺寸控制大波长, 扩大了其在工程上的应用范围.

Helmholtz腔与弹性振子耦合结构横截面如图1所示, 其晶格常数为a, 腔体框架材料为钢, 外边长为l₁, 腔壁厚度为b, 在腔体右侧有“弓”字型的开口, 其空气通道总长度为l₂, 宽度为s, 腔体内部与左框体距离l₃处设置一宽度为b_s的弹性长杆, 并在上下两端用长h_r、宽b_r的硅橡胶连接至腔体框架上, 因本研究中选取橡胶厚度与一般薄膜相比较厚, 且预应力的施加一般会导致共振频率升高, 故不施加预应力. 在实际应用中, 可用外部框架将橡胶夹住长为l₁的橡胶板, 并在板上粘附金属质量片. 这样, Helmholtz腔就被弹性振子分为左右两个腔体. 另外, 为防止框架的振动模态对带隙形成机理研究造成干扰, 将其设定为固定约束状态.
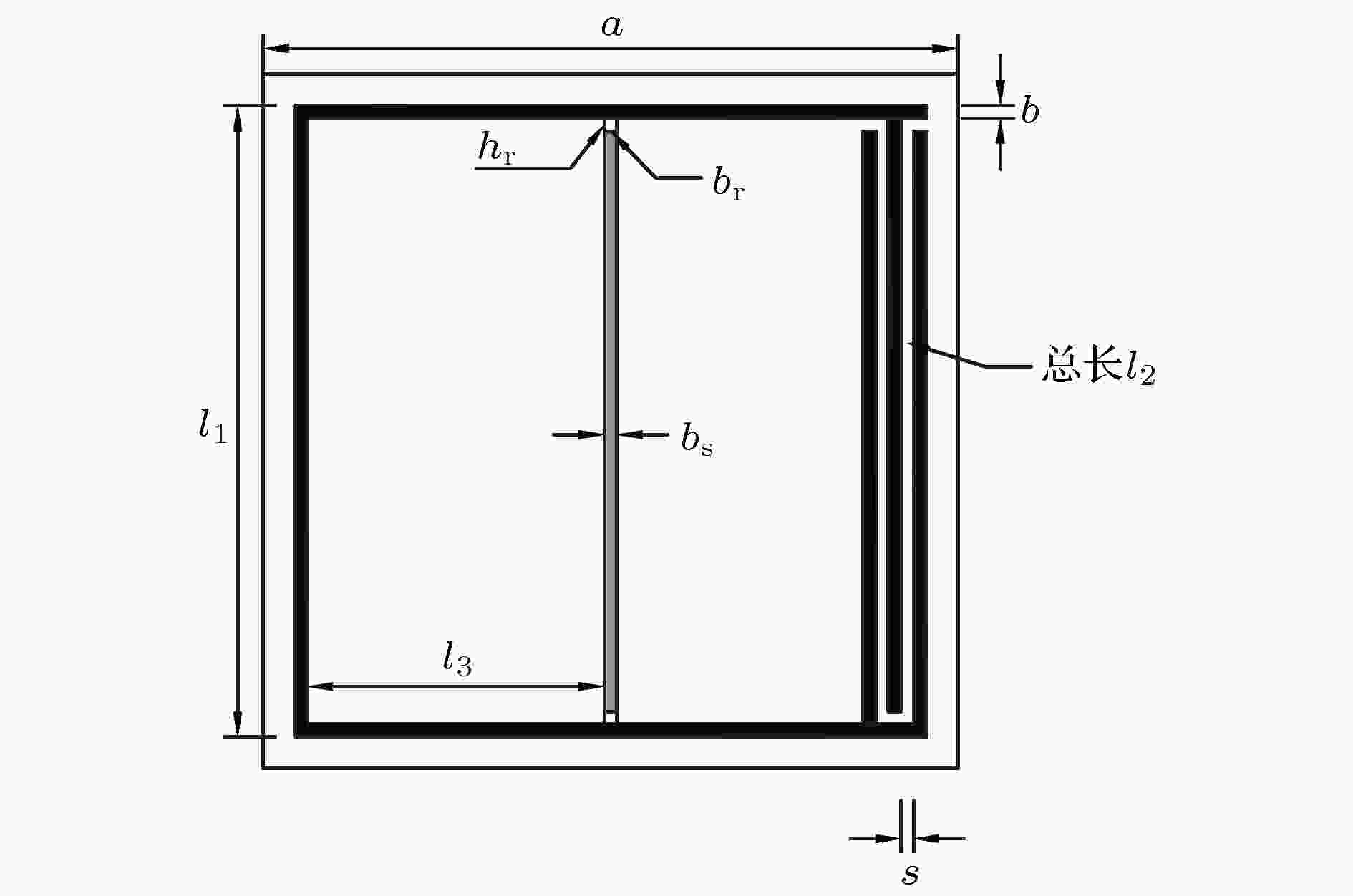图 1 Helmholtz腔与弹性振子耦合结构横截面
Figure1. Cross section of Helmholtz resonator coupled with elastic oscillator structure

将腔体外边长固定为l₁ = 60 mm, 腔壁厚度固定为b = 1 mm. 先利用理论计算方法对所选参数取值范围内所有可能组合进行遍历扫描(均以1 mm为间隔), 再利用有限元法进行验证和调整, 分别对Helmholtz腔与弹性振子耦合结构和其对应的传统Helmholtz腔结构进行求解, 其第一带隙下限最低时的参数组合及各参数取值范围如表1所列, 采用的材料参数列于表2, 得出其带隙结构如图2(a)所示.

名称	a/mm	l2/mm	l3/mm	br/mm	hr/mm	bs/mm	振子材料
Helmholtz腔与弹性振子耦合结构带隙下限最低参数	61 [61, 65]	50 [1, 1680]	40 [1, 56]	4 [1, 5]	9 [1, 9]	25 [1, 25]	钢
传统Helmholtz腔结构带隙下限最低参数	61 [61, 65]	848 [1, 1680]	—	—	—	—	—
初始结构参数	65	50	28.5	1	1	1	铝

表1各结构参数组合
Table1.Combination of various structural parameters

图 2 (a) Helmholtz腔与弹性振子耦合结构带隙图; (b) Helmholtz腔结构带隙图
Figure2. (a) Band diagram of the Helmholtz resonator coupled with elastic oscillator structure; (b) band diagram of the Helmholtz resonator structure

材料名称	硅橡胶	环氧树脂	碳	铝	钛	钢
密度/k·m–3	1300	1180	1750	2730	4540	7780
弹性模量/1010 Pa	1.175 × 10–5	0.435	23.01	7.76	11.70	21.06
剪切模量/1010 Pa	4 × 10–6	0.159	8.85	2.87	4.43	8.10

表2各材料参数
Table2.Material parameters

对于传统Helmholtz腔结构, 降低其第一带隙下限主要通过增大开口长度, 由于这样会使得腔体体积减小, 导致其第一带隙下限最低低至42.1 Hz(如图2(b)所示). 而对于Helmholtz腔与弹性振子耦合结构, 其第一、二带隙分别为24.5—47.7 Hz, 237.6—308.6 Hz (如图2(a)所示).
为探究Helmholtz腔与弹性振子耦合情况下的带隙机理, 设置初始结构参数如表1所列. 利用有限单元法得出其带隙结构如图3(a)所示, 从图中可以看出, 该结构在700 Hz以下存在两个带隙, 其中第一带隙为125.34—267.30 Hz, 第二带隙为355.13—397.22 Hz, 各带隙的起止点已在图中标出. 另外, 在179.17 Hz和254.69 Hz处出现了两条平直带.
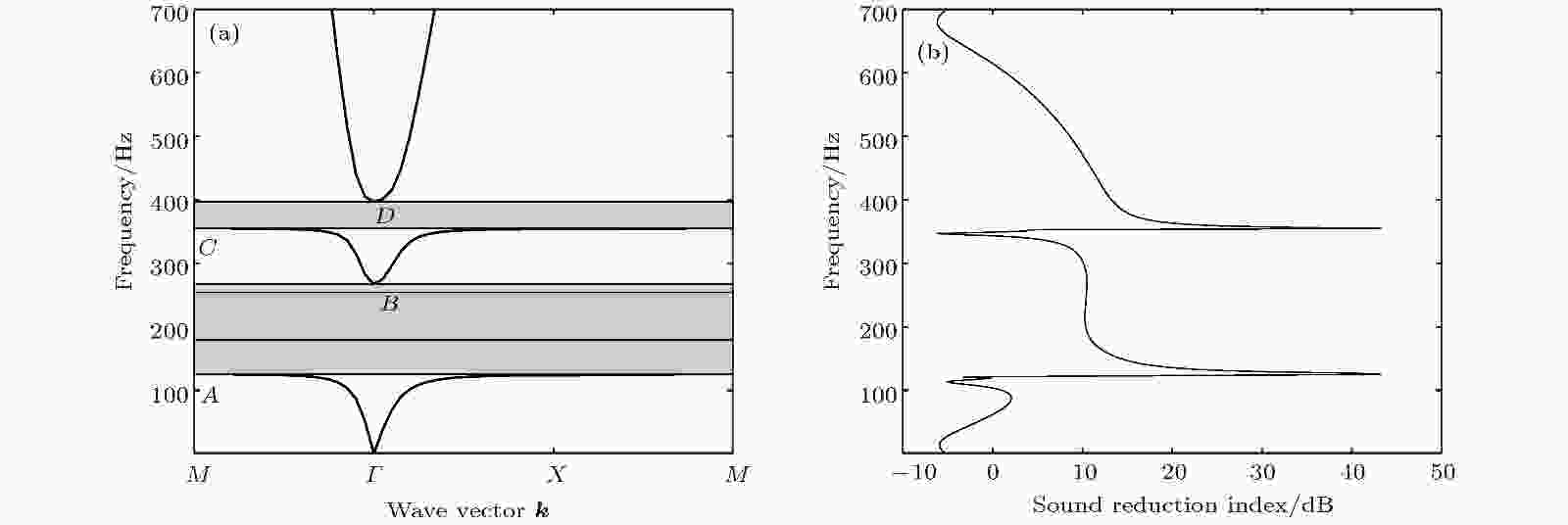图 3 (a) Helmholtz腔与弹性振子耦合结构带隙图; (b) Helmholtz腔与弹性振子耦合结构隔声曲线
Figure3. (a) Band diagram of the Helmholtz resonator coupled with elastic oscillator structure; (b) the transmission spectra of the Helmholtz resonator coupled with elastic oscillator structure

为研究该结构的隔声性能, 沿纵向串联3个元胞结构, 在结构的一端设置背景压力场, 并配置完美匹配层(PML), 利用声压模式的隔声量计算公式针对0—700 Hz范围内的声波进行隔声量计算:

$T = - 20\lg \frac{{|{P_{{\rm{out}}}}|}}{{|{P_{{\rm{in}}}}|}}, $

其中T代表隔声量, P_out代表出射声压, P_in代表入射声压, 其结果如图3(b)所示. 可以看出, 两个隔声峰均出现在带隙下限附近, 大小分别为43.2和43.3 dB, 而两个平直带对隔声曲线无明显影响.

Helmholtz腔与弹性振子耦合结构带隙上下限处的声压场如图4所示, 在A点(模态A), 左腔声压最大, 右腔次之, 而腔体外部声压为零. 表明此时振子与开口中空气做同向振动, 而外部空气未参与振动, 声波被局域在腔体内部, 无法向外传播, 由此形成带隙下限.
图 4 (a) A点, (b) B点, (c) C点, (d) D点的声场压力图
Figure4. Sound pressure distribution diagrams of point A (a), B (b), C (c), and D (d).

在B点(模态B), 左腔声压为负值, 右腔及腔体外部声压为正值且外部声压最大. 表明此时振子与开口中空气做同向振动, 且声波可以在腔体外部传播, 由此对应带隙上限.
C (模态C), D (模态D)两点处腔体外部声压分别与A, B两点处基本相同, 表明其带隙形成机理是一致的. 但C点处左腔声压为负值而右腔声压最大, 表明此处对应振动模态为振子与开口中空气做相向振动. D点处左右腔声压与B点处相比声压颠倒, 表明此处对应振动模态同样为振子与开口中空气做相向振动.
对于平直带处的振动模态, 通过声压场和弹性振子的振动模态相结合进行分析, 如图5所示. 为便于分析, 在声压场图中添加了等值线.
图 5 (a) 第一平直带弹性振子振型图; (b) 第二平直带弹性振子振型图; (c) 第一平直带声场压力图; (d) 第二平直带声场压力图
Figure5. The vibration mode of the elastic oscillatorat the first straight belt (a) and at the second straight belt (b); the sound pressure distribution diagrams of the first straight belt (c), and the second straight belt (d)

在两平直带处, 弹性振子的振动分别为绕中心转动和沿轴向振动, 虽然这种振动因流-固耦合作用会使得各腔内声场发生变化, 但因振动过程中左右腔体积均不变, 故各腔声场的变化分别是上下反对称的(如图5(c)和图5(d)所示), 其总的等效声压为零. 此时, 弹性振子的振动并不能激发开口处空气的振动, 从而无法将声压传导至腔外, 声波仍然被局域在腔内, 故对该结构的隔声性能没有影响. 这一点也从图3所示的隔声曲线上有所体现, 平直带对应的频率处, 隔声曲线没有特别的变化特征.
对于局域共振型声子晶体, 由于带隙上下限共振机理不同, 其等效模型一般通过弹簧-振子模型^[21,22]或声电类比模型^[14,15]对带隙上下限分别进行构建. 在本研究中, 选用弹簧-振子模型. 首先做如下假设:
1)对于开口处, 由于其体积相比内腔小得多, 且开口宽度较小, 假设开口内空气做同步运动且不计其受到的压缩, 即视为振子, 其等效质量由m₂表示;
2)对于左右腔及外部空气, 忽略其振动造成的惯性力, 即视为无质量弹簧, 其等效刚度分别由k₄, k₂, k₁表示;
3)对于弹性振子, 忽略其振动时的挠度变形, 将其视为刚性振子(在仿真时仍设定为弹性体), 并将两端橡胶质量通过集中参数法等效分布于振子和腔壁上, 其等效质量由m₁表示;
4)对于弹性振子两边的橡胶, 将其考虑为受剪切变形影响的横向振动无质量伯努利-欧拉梁, 忽略自身振型的影响, 在模型中用等效刚度为k₃的弹簧拟合其特性.
综上, 对该结构各带隙起止点建立等效模型如图6所示, 其中图6(a)对应带隙上限, 图6(b)对应带隙下限, 这两种等效模型的区别在于是否存在外部空气等效所得的弹簧k₁, 这种不同来源于对开口处空气的简化. 开口空气实际相当于一纵向振动弹性杆, 这与图4中其声压场逐渐变化相对应. 该结构更为精确的模型为“弹簧-质量块-弹簧-弹性杆-弹簧”. 但在k₁, k₂较小且开口长度适中的情况下, 可通过假设1)的处理, 仅考虑开口空气质心的振动位移, 此时在带隙上限处将弹性杆视为质量块即可. 但在带隙下限处, 外部空气声压始终为零, 即系统在振动过程中, 开口空气杆的外端始终静止, 无法体现弹簧k₁的作用, 但杆的质心仍在振动, 故可简化为图6(b)所示的等效模型.
图 6 (a) 模态B, D的等效模型; (b) 模态A, C的等效模型
Figure6. (a) The equivalent model of modal B and D; (b) the equivalent model of modal A and C

设该结构高度为1, 其等效质量和等效刚度的表达式分别为:

$\left\{ {\begin{aligned}& {{m_1} = {\rho _{\rm{s}}}{b_{\rm{s}}}({l_1} - 2b - 2{h_{\rm{r}}}) + {\rho _{\rm{r}}}{h_{\rm{r}}}{b_{\rm{r}}}}\\& {{m_2} = {\rho _{{\rm{air}}}}({l_2} + b)s},\end{aligned}} \right.$

$\left\{ {\begin{aligned}& {{k_1} = \frac{{{\rho _{{\rm{air}}}}{c^2}{s^2}}}{{{V_1}}}},\\& {{k_{2{\rm{left}}}} = \frac{{{\rho _{{\rm{air}}}}{c^2}s{l_1}}}{{{V_2}}}, \;{k_{2{\rm{right}}}} = \frac{{{\rho _{{\rm{air}}}}{c^2}{s^2}}}{{{V_2}}}},\\& k_{2{\rm{lef}}t}' = \frac{{{\rho _{{\rm{air}}}}{c^2}({l_1} - {h_{\rm{r}}}){l_1}}}{{{V_2}}}, \\& k_{2{\rm{right}}}' = \frac{{{\rho _{{\rm{air}}}}{c^2}({l_1} - {h_{\rm{r}}})s}}{{{V_2}}},\\& {{k_4} = \frac{{{\rho _{{\rm{air}}}}{c^2}({l_1} - {h_{\rm{r}}}){l_1}}}{{{V_4}}}},\end{aligned}} \right. $

其中$ {\rho _{\rm{s}}} $, $ {\rho _{\rm{r}}} $及$ {\rho _{\rm{air}}} $分别为弹性振子、橡胶及空气的密度; c为空气中声速; V₁, V₂及V₄分别为外部空气、右腔及左腔的体积. 需要说明的是, 在多自由度振动理论中, 将总的等效刚度定义为“k_ij是使系统仅在第j个坐标上产生单位位移而相应于第i个坐标上所需施加的力^[23]”, 而忽略自身质量的空气弹簧遵循帕斯卡定律, 则“所需施加的力”为第j个坐标上产生单位位移引起的压差对第i个坐标上空气与构件接触面积的积分. 对于右腔空气, 由于其分别与开口处空气及梁状振子接触, 会表现出四种不同的等效刚度, 分别为:
k_2left, 仅开口处空气产生单位位移时在弹性振子与右腔空气接触面上产生的力;
k_2right, 仅开口处空气产生单位位移时在开口处空气与右腔空气接触面上产生的力;
k′_2left, 仅弹性振子产生单位位移时在弹性振子与右腔空气接触面上产生的力;
k′_2right, 仅弹性振子产生单位位移时在开口处空气与右腔空气接触面上产生的力.
k₃可由传递矩阵法求得, 设弹性振子有一位移u, 根据橡胶短梁的传递矩阵和边界条件:

${{U}} = \left[ {\begin{array}{*{20}{c}}1&{{h_{\rm{r}}}}&{\dfrac{{{h_{\rm{r}}}^2}}{{2EI}}}&{\dfrac{{{h_{\rm{r}}}^3}}{{6EI}} - \dfrac{{{h_{\rm{r}}}}}{{G{b_{\rm{r}}}\kappa }}}\\0&1&{\dfrac{{{h_{\rm{r}}}}}{{EI}}}&{\dfrac{{{h_{\rm{r}}}^2}}{{2EI}}}\\0&0&1&{{h_{\rm{r}}}}\\0&0&0&1\end{array}} \right], $

$\begin{split}& {{{Z}}_{\rm{1}}} =[0\quad 0\quad {{M_1}}\quad Q]^{\rm{T}}\\& {{{Z}}_{\rm{2}}} = [u\quad 0\quad {{M_2}}\quad Q_2]^{\rm{T}}\end{split}, $

对于上下两橡胶短梁均有

$\left( { - \frac{{{h_{\rm{r}}}^3}}{{12EI}} - \frac{{{h_{\rm{r}}}}}{{G{b_{\rm{r}}}\kappa }}} \right){Q_2} = u, $

其中E, G分别为橡胶的弹性模量和剪切模量; I为截面惯性矩; $ \kappa $为截面系数, 取为0.833; M₁, Q₁, M₂, Q₂分别为与腔壁相连端及与振子相连端的弯矩和剪力. 由此可得出

${k_3} = 2{\left( {\frac{{{h_{\rm{r}}}^3}}{{12EI}} + \frac{{{h_{\rm{r}}}}}{{G{b_{\rm{r}}}\kappa }}} \right)^{ - 1}}.$

根据上述两种等效模型, 构建其刚度矩阵分别为:

${{{K}}_{{\rm{A, C}}}} = \left[ {\begin{array}{*{20}{c}}{k_{2{\rm{left}}}' + {k_3} + {k_4}}&{ - {k_{2{\rm{left}}}}}\\{ - k_{2{\rm{right}}}'}&{{k_{2{\rm{right}}}}}\end{array}} \right], $

${{{K}}_{{\rm{B, D}}}} = \left[ {\begin{array}{*{20}{c}}{k_{2{\rm{left}}}' + {k_3} + {k_4}}&{ - {k_{{\rm{2left}}}}}\\{ - k_{{\rm{2right}}}'}&{{k_{2{\rm{right}}}} + {k_1}}\end{array}} \right], $

其质量矩阵为

${{M}} = \left[ {\begin{array}{*{20}{c}}{{m_1}}&0\\0&{{m_2}}\end{array}} \right].$

根据多自由度振动理论, 由 (8)—(10)式即可分别计算出两阶固有频率, 对应于第一、二带隙的起止频率:

$\begin{split}& (2{\text{π}}f)^2 = \frac1{{2{m_1}{m_2}}} \Big[({K_{11}}{m_2} + {K_{22}}{m_1}) \pm \\& \sqrt{(K_{11}m_2 + K_{22} m_1)^2 - 4 m_1 m_2 (K_{11} K_{22} - K_{12}K_{21})} \Big], \end{split}$

式中K_ij代表刚度矩阵(8)和(9)式中各元素.
通过以上分析可以看出, 在Helmholtz腔中加入弹性振子之后, 系统由单自由度变为双自由度, 且其耦合效应改变了原有腔体的等效刚度. 另外, 该结构左腔中的空气和弹性振子局域共振单元一起, 形成了一个弹性壁, 但其对于外部空气来说仍为刚性壁, 故不能直接对外部空气起作用, 必须通过引起腔口空气振动而影响外部声压. 若去除左侧框架, 则等效模型中m₁, m₂应与双开口Helmholtz腔^[14]中类似, 用并联设置替代本文中的串联设置.

为分析各参数对带隙的影响, 进一步揭示其带隙形成实质, 采用有限单元法和等效模型两种方法计算了其带隙上下限频率随参数改变的变化情况, 结果如图7所示.
图 7 晶格常数a (a), 开口长度l₂ (b), 左腔体积V₂ (d), 右腔体积V₄ (e), 弹性振子密度$\rho_{\rm{s}}$ (f)对第一、二低频带隙的影响; (c) 橡胶长度h_r对各低频带隙的影响;
Figure7. The impact of different parameters a on first and second low frequency bandgap: (a) The lattice constant a; (b) the length of the cavity opening l₂; (d) the volume of the left cavity V₂; (e) the volume of the right cavity V₄; (c) the impact of the parameter h_r on each low frequency bandgap

图7(a)显示了晶格常数a与一、二带隙的关系. 可以发现, 晶格常数的改变对于带隙下限的影响可以忽略不计, 这与(4)式中不含外部空气的等效刚度一致. 而对于带隙上限, 单纯增大晶格常数而保持框体大小不变, 会直接导致k₁的减小, 从而使带隙上限向低频方向移动. 这说明对于该结构, 周期性排列间距越小越容易产生较宽的带隙.
图7(b)显示了开口处空气通道长度l₂与一、二带隙之间的关系, 可以看出, 随着空气通道长度的增加, 其带隙上下限都在下降, 其中第一带隙宽度略有增大, 而第二带隙宽度有较明显的减小. 另外需要指出的是, 当空气通道长度l₂较小时, 第二带隙等效模型与有限元分析结果差距较大, 这是因为在模态C, D处, 开口左右声压差值大, 导致开口附近空气受到的压缩程度更大, 更多的空气充当了振子的作用, 使得等效质量m₂增大, 而这种效应在开口长度较小时尤为明显. 此时, 应通过修正公式^[24]对m₂进行修正, 本研究中选取初始开口长度较长, 不影响其他讨论及最终结论, 故不再进行修正.
图7(c)显示了参数h_r与带隙宽度的关系, 在图中绘制了等效模型计算的两个带隙和有限元仿真的前6个带隙(若存在). 从图中可以看出, 由等效模型计算的带隙上下限变化较小, 这是因为铝密度与硅橡胶相差不大, h_r的增大只使m₂小幅变化, 而k₃由于与$k_{{\rm{2left}}}'$相差一个量级, 其变化对结果影响较小. 而有限元计算结果显示, 随着h_r的增大, 部分特征频率曲线或在原有带隙附近产生了宽度较小的新带隙, 或将原有带隙“分割”为两个带隙, 并影响了原带隙上下限. 此时, 视新带隙相对原带隙的位置, 有限元计算结果开始在理论计算结果上下波动.
这是由于随着h_r的增大, 弹性振子系统振动模态增多, 原有各阶固有频率下降, 在带隙上下限处, 对应的不再是原有的低阶振型, 如当h_r为1, 3, 7, 11 mm时, 第一带隙下限分别对应于弹性振子系统的第1, 2, 3, 5阶振型. 此时, 将质量和等效弹簧均集中于振子处的处理方法导致了误差的产生. 若要精确计算带隙上下限, 需要参考文献[25,26]等采用的腔口覆薄膜耦合振动计算方法并推广至含集中质量结构, 充分考虑强迫振动振型对固有频率的影响. 但综合图7(c)和图7(e)可以看出, 振型对于带隙的影响不如弹性振子等效质量的影响大, 且振型的影响规律性不强, 不利于带隙的优化, 本文不再进行精确计算.
图7(d)和图7(e) 表征的是随V₂, V₄增大时带隙的变化情况, 由于腔体被弹性振子分为两部分, 为使结构改变时保持k₂, k₄中的一项不变而另一项增大或减小, 在此没有对l₃进行变量分析, 而是采用在左腔或右腔中增加刚性填充物的方式进行参数控制. 从图中可以看出, 随着左侧腔体体积V₄的增大, 一、二带隙上下限均向低频方向移动, 而右侧腔体体积V₂的增大仅使第二带隙上下限下降, 对第一带隙的作用并不明显. 这说明在保证左侧腔体的一定体积的情况下, 降低右侧腔体的体积, 仍能获得良好的低频隔声性能, 有利于结构的小型化; 而在结构大小一定的情况下, 则应尽量增大参数l₃, 以使第一、二带隙均向低频方向移动. 就产生该现象的机理来看, 在第一带隙上下限处, 振子与腔口空气均做同向振动, 故削弱了右腔空气的作用; 而第二带隙上下限处振子与腔口空气做相向运动, 故与左右腔空气体积均有关.
图7(f)显示随着弹性振子密度$\rho_{\rm{s}}$的提高, 一、二带隙上下限都向低频方向移动, 但第一带隙宽度降低, 而第二带隙宽度增大. 在这里, 为改变其密度, 分别选用了环氧树脂、碳、铝、钛、钢等材料进行研究, 因其弹性模量基本处于同一量级, 故弹性模量的变化影响可以忽略. 综合图7(b)和图7(f)的结果, 可以看出, 振子质量与开口处空气质量对于带隙宽度的作用效果是相反的, 开口处空气质量对应于第一带隙, 而振子质量对应于第二带隙, 增大其中某质量会使其对应带隙宽度增大而另一带隙宽度减小.

本文设计了一种Helmholtz腔与弹性振子耦合结构, 利用多自由度振动理论建立了等效模型. 研究发现: 1)该结构可以突破传统Helmholtz腔结构带隙下限的极限值, 在6 cm的结构尺寸下达到24.5 Hz; 2) 弹性振子的加入将原结构单自由度系统振动变为双自由度系统的振动, 其前两个带隙可由等效模型计算得出, 且理论计算结果与有限元计算结果基本相符; 3)该结构可调参数大大增加, 通过降低结构间距、增大开口空气通道长度及振子质量、增大左侧腔体体积等方式, 可获得低频区域内较宽的带隙. 这些结论有利于Helmholtz腔结构与薄膜类结构耦合隔声理论的发展, 对于该类结构在低频隔声领域的应用有指导意义.