摘要: 脑神经网络在一定条件下可以自发出现行波、驻波、螺旋波, 这些有序时空斑图的出现往往与某种神经疾病有关, 但是其产生的机制尚未完全清楚, 如何定量描述这些时空斑图的性质仍需要探索, 为了解决这些问题, 本文采用Hindmarsh-Rose神经元模型研究了具有排斥耦合的二维双耦合层神经元网络从混沌初相位开始演化的动力学行为, 并用改进的集团熵来描述神经元网络的时空斑图. 数值模拟结果表明: 排斥耦合既可以促进有序斑图的形成, 也可以抑制有序斑图的形成. 适当选择排斥和兴奋性耦合强度, 排斥耦合可导致单螺旋波、多螺旋波、行波、螺旋波和靶波与其他态共存、行波与驻波共存等有序斑图出现, 螺旋波、行波出现概率分别达到0.4555和0.1667. 靶波与其他态共存和行波与驻波共存出现概率分别达到0.0389和0.1056, 我们提出的集团熵可以较好区分这些有序斑图和混沌态. 当排斥耦合强度足够大时, 网络一般处于混沌态. 当网络处于弱耦合状态时, 通过计算集团熵发现网络可以出现很大集团, 这些结果有助于理解在实验中观察到的现象, 从而能为神经疾病治疗提供帮助.
关键词: 螺旋波 /
驻波 /
Hindmarsh-Rose神经元 /
排斥耦合 English Abstract Entropy measurement of ordered patterns in neuronal network with repulsive coupling Huang Zhi-Jing Li Qian-Yun Bai Jing Tang Guo-Ning College of Physical Science and Technology, Guangxi Normal University, Guilin 541004, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11565005, 11847317).Received Date: 21 February 2019Accepted Date: 18 March 2019Available Online: 01 June 2019Published Online: 05 June 2019Abstract: Traveling waves, standing waves, and spiral waves occur spontaneously in the brain neural network in some brain states. The occurrence of these ordered spatiotemporal patterns is often related to some neurological diseases. However, the mechanisms behind the generation of the ordered pattern are not fully understood. How to quantitatively describe the nature of these spatiotemporal patterns still needs further exploring. In order to solve these problems, the Hindmarsh-Rose neuron model is used to study the dynamic behavior of the two-dimensional (2D) neuronal network with double-coupling layer, which is composed of nearest-neighbor excitatory coupling and long-range repulsive coupling layers and evolves from an initial state with a random phase distribution. An improved cluster entropy is proposed to describe the spatiotemporal pattern of the neuronal network. The numerical simulation results show that the repulsive coupling can either promote the formation of ordered patterns or suppress the formation of ordered patterns. When the repulsive coupling strength and excitatory coupling strength are appropriately selected, the chaotic network can spontaneously generate single spiral wave, multiple spiral wave, traveling wave, the coexistence of spiral wave and others wave state, the coexistence of target wave and others wave state, the coexistence of traveling wave and standing wave, etc. The probability with which spiral wave and traveling wave occur reach 0.4555 and 0.1667 respectively. The probability with which target wave and other states co-occur, and the probability with which the traveling wave and the standing wave co-occur, are 0.0389 and 0.1056, respectively. These ordered wave patterns and chaotic states can be distinguished by using the proposed cluster entropy. When the repulsive coupling strength is large enough, the neuronal network is generally in chaotic state. It is found by calculating cluster entropy that a large cluster can appear in the neuronal network when the excitatory coupling strength and repulsive coupling strength are both weak. These results can conduce to understanding the self-organization phenomena occurring in the experiments and also to treating various neurological diseases.Keywords: spiral wave /standing wave /Hindmarsh-Rose neuron /repulsive coupling 全文HTML --> --> --> 1.引 言 螺旋波广泛存在于自然界, 无论在物理系统、化学系统还是生物系统, 人们都观察到了螺旋波[1 -8 ] , 螺旋波产生机制已经在不同的系统中得到了广泛的探索. 研究发现: 药物可以在哺乳动物的大脑皮层中诱发螺旋波[7 ] , 癫痫发作可导致大脑皮层中出现螺旋波[9 ] , 噪声可以导致神经元网络中产生螺旋波[10 ] , 自突触可在规则神经元网络中诱发螺旋波[11 ] , 抑制性耦合可促使神经网络中产生螺旋波等有序斑图[12 ] . 在老化的心脏中, 螺旋波也可以自发地出现, 由于螺旋波是自维持波, 其频率高于窦房结的起搏频率, 因此当心脏组织中出现螺旋波时会导致心动过速, 而且螺旋波破碎成时空混沌将导致心颤, 危及生命, 所以螺旋波是引起人类心房颤动和心室颤动等复杂心律失常的原因之一[6 , 13 ] . 研究大脑和心脏系统中螺旋波产生机制及其动力学行为, 对了解大脑动力学斑图的形成以及临床治疗癫痫和心率失常等疾病具有非常重要的意义.[14 ] , 用吸引和排斥耦合(特殊的相移耦合)来研究神经网络的同步活动[15 ] , 发现抑制耦合和排斥耦合都可以促进神经元的同步[16 ,17 ] . 最近研究发现, 神经元之间和心肌细胞之间还可以通过电场耦合和膜纳米管道耦合[18 -20 ] , 而且膜纳米管道在许多疾病中扮演重要角色[21 ] , 这些发现为研究神经元的功能连接和解剖结构连接、神经元网络的斑图形成和同步、心脏心律失常机制提供了新的研究内容, 成为研究热点问题[22 ,23 ] .[24 ] , 所以最大熵被常用于揭示神经元网络和真实神经元网络实验中出现的集体行为[25 ,26 ] . 由于最大熵不能区分神经元网络和反应扩散系统中各种时空斑图, 因此不能用于比较模型的数据与实验结果的时空动力学, 而研究如何定量描述时空斑图以及揭示时空斑图自发在系统中出现的原因具有重要意义, 这些研究能为神经疾病和心脏病的治疗提供帮助.[27 ] 提出了一种将时空斑图分解成相干时空集团的方法, 发现用集团熵来描述时空斑图可以很好地区分螺旋波和时空混沌, 但是他们提出的集团熵不能很好地区分单螺旋波、多螺旋波等各种有序斑图, 需要改进. 本文采用Hindmarsh-Rose (HR)神经元模型[28 ] 研究长程排斥性耦合是否能在近邻兴奋性耦合混沌神经元网络中促进有序波产生. 我们发现, 适当选择两种耦合的耦合强度, 系统可以自发产生行波、单螺旋波、多螺旋波、靶波与其他态共存、行波与驻波共存等时空有序斑图, 通过改进集团分类, 使得集团熵可以较好地区分不同有序斑图和混沌态, 这些研究对了解大脑中螺旋波产生机制和对时空斑图的定量描述具有积极意义. 下面先介绍我们的模型和集团熵, 然后给出数值模拟结果, 最后给出结论.2.模型和集团熵 使用这样一个神经元网络: HR神经元均匀地分布在一个大小为$N \times N = 200 \times 200$ 的二维方形点阵上, 每一个神经元除了与近邻神经元有兴奋性耦合外, 还与随机选取的四个神经元之间存在长程排斥耦合, 这种由近邻兴奋性耦合和长程排斥性耦合组成的双耦合层神经元网络的动力学方程如下[28 ] :${x_{i,j}}$ , ${y_{i,j}}$ 和${z_{i,j}}$ 分别代表位于格点$\left( {i,j} \right)$ 上的神经元的膜电位、与内电流相关的恢复变量和与钙离子激活的钾离子电流相关的慢变调节电流, 下标$i,j = 1,2, \cdots,N$ ; a , b , c , d , r , s 和${\bar x}$ 为模型的参量; ${I_{{\rm{ext}}}}$ 为外部刺激; g 为近邻的兴奋性耦合强度. 方程(1 )最后一项为排斥耦合, 考虑到远距离耦合的神经元之间才容易出现大角度相移, 本文规定有排斥耦合的两个神经元之间的距离满足$\sqrt {{{\left( {i - ii'} \right)}^2} + {{\left( {j - jj'} \right)}^2}} > 20 = L$ , 式中$i',j' = 1,{\rm{ }}2,$ ${\rm{ }}3,{\rm{ }}4$ , $\left( {ii',jj'} \right)$ 是随机选取用于排斥耦合的神经元坐标, 因此称w 为长程排斥性耦合强度. 本文的HR神经元模型参量固定取为$a = 1.0$ , $b = 3.0$ , $c = 1.0$ , $d = 5.0$ , $r = 0.006$ , $s = 4.0$ , ${\bar x} = - 1.6$ , ${I_{{\rm{ext}}}} = 3.0$ , 根据文献[29 ]的结果可知, 在这些参量下, 单个HR神经元处于混沌态.$\Delta t = 0.01$ , 每次数值模拟时间长度为10000个时间单位, 考虑到在数值模拟中, L 取更大和更小的值得到相似的结果, 因此在下面的数值模拟中只将兴奋性耦合强度g 和排斥性耦合强度w 设为可变参量, 变化范围定为$0.1 \leqslant g \leqslant 2.0$ 和$0.{\rm{0}}1 \leqslant w \leqslant 0.{\rm{17}}$ .27 ]将网络状态斑图先转化为二维二进制图像, 然后将该图像分解成若干个集团, 再求集团熵, 具体做法如下.${x_{i,j}} \geqslant - 1.0$ 时, 该点二进制图像的像素值记为${X_{i,j}} = 1$ , 否则记为${X_{i,j}} = 0$ , 这样就将某时刻的网络状态斑图转化为该时刻的二进制图像.k 个, 则认为该集团大小为k . 如果两个集团的像素相同, 就把这两个集团归到大小为k 的集群${c_k}$ 中. 假设集群${c_k}$ 包含有${n_k}$ 个集团, 则认为该集群${c_k}$ 的体积为${V_k} = k{n_k}$ .${c_k}$ 在空间的相对覆盖率为${p_k} = {V_K}/{V_{{\rm{tot}}}}$ , 其中${V_{{\rm{tot}}}}$ 为网络中所有集群尺寸大小之和, 即${V_{{\rm{tot}}}} = {V_1} + {V_2} + {V_3} + \cdot \cdot \cdot + {V_K}$ . 这里${p_k}$ 相当于概率, 根据香农熵得到集团熵[27 ] 为:S 值较小时, 网络全局出现有序波态或大的集团; S 值适中时, 网络局部出现有序波态或出现各种尺寸的集团; S 值较大时, 网络处于混沌态或出现不同尺寸的小集团.27 ]为了得到单螺旋波态的熵值为0, 用方程(5 )计算熵时只考虑用像素为1的集群, 显然这种做法有不妥之处. 此外还存在如下不足之处: 因为没有考虑集群的时空关系, 导致虽同为螺旋波但由于波头位置不同, 得到的集群数量和大小就不一样. 例如, 假设网络中出现单个螺旋波占据整个空间, 当螺旋波波头位于介质中间时, 空间可划分为两个集群, 一个是像素为1的集群, 另一个是像素为0的集群. 但是当螺旋波波头位于介质边界时, 空间可划分为多个大小不同、像素为1和0的集群(因为螺旋波的波臂部分传播出边界, 形成不连续的几段波臂), 这时根据文献[27 ]的方法计算熵会得到不同结果. 为了避免这种情况的出现, 必须考虑集群的时空性质, 即在单螺旋波态下必须将不同大小、像素为1和0的集群合并为一个集群, 这样无论单螺旋波波头位于网络何处, 得到的熵值都为0. 为此我们对文献[27 ]中计算熵的方法以及集团的分类做如下改进: I) 在计算集团熵时, 同时考虑像素为1和像素为0的集群; II) 对于螺旋波、靶波、行波等有明显波峰波谷的波, 通过观察网络的演化来分辨出这些像素为1和0的集群是由哪个波(例如螺旋波、靶波、行波)产生, 然后将这些集群合并为一个与这个波对应的大集群; III)假设网络出现多个螺旋波、多个靶波以及螺旋波、靶波与其他态共存, 先将斑图转化成二进制图像, 然后分解成集群, 这个集群仅仅是将相同大小的集团合并后形成的集群, 在II的基础上对这些集群再进行合并时考虑如下情况: 如果出现多个大集群的集团相遇形成一个或者多个大集团(称为共融集团), 则通过观察波的传播来分辨这些共融集团的哪一部分属于哪一个大集群, 并将这些共融集团的像素按比率分拆后并入到相应的大集群中. 没有明显看出波的波峰和波谷(即集群的时空性质)的斑图, 在求出不同大小集群后不再进行合并. 通过这种改进, 集团熵可以很好区分不同时空斑图.3.数值模拟结果 首先给网络中的各神经元赋随机初值, 然后让神经元在无耦合($g = w = 0$ )情况下演化1000个时间单位, 将该网络演化后的状态作为有耦合情况下网络的初态, 显然该初态具有混沌的初相位分布, 即网络的初态为混沌态. 以下从这个初态出发研究排斥耦合是否会促进有序波的产生.图1 给出了几种典型有序波斑图, 斑图像点亮度与神经元${x_{i,j}}$ 变量的值成正比, 所有斑图都是从图1(a) 开始演化10000个时间单位后得到的结果. 在图1(a) 和图1(b) 所示斑图中看不出不同集群的时空性质(一个波的波峰和波谷), 所以在求出集群大小后不再合并, 在求图1(g) —图1(i) 斑图的熵时也作类似处理. 由于其他斑图出现螺旋波和靶波, 因此在根据集团大小得到集群后还要观察判断这些集群是由哪一个波产生, 并将由同一个波产生的集群合并成一个大的集群. 例如图1(d) 的斑图为两个螺旋波共存, 我们能明显看出有些集团是两个螺旋波的波臂相碰形成的, 这样的共融集团像素必须按比率分拆后合并到这两个螺旋波对应的大集群中, 类似处理其他多螺旋波斑图, 这样从图1(c) —图1(f) 分别得到一个、两个、三个、两个大集群. 对于图1(j) —图1(l) 只对属于螺旋波和靶波的集群做了合并, 其他集群没有做合并. 这样得到图1(a) —图1(l) 对应的集团熵分别为4.66, 2.642, 0, 0.7, 0.93, 0.34, 0.956, 0.992, 1.465, 1.451, 1.529, 1.854, 可见我们提出的集团熵可以有效区分不同斑图.图 1 不同耦合强度下的神经元${x_{i,j}}$ 变量斑图, 每一个图下方为相应斑图的熵值 (a) $w = 0,\;g = {\rm{0}}$ ; (b) $w = 0.{\rm{17}},\;g = {\rm{0}}.{\rm{3}}$ ; (c) $w = 0.05,\;g = 1.2$ ; (d) $w = 0.05,\;g = 1.1 $ ; (e) $w = 0.07,\;g = 1.3$ ; (f) $w = 0.0{\rm{9}},\;g = 1.{\rm{9}}$ ; (g) w = 0.05, $g = 1.0$ ; (h) $w = 0.01,\;g = 0.1$ ; (i) $w = 0,\;g = {\rm{0}}.{\rm{1}}$ ; (j) $w = 0.03,\;g = 1.0$ ; (k) $w = 0.07,\;g = 0.4$ ; (l) w = 0.05, $g = 0.4$ Figure1. Pattern of the variable ${x_{i,j}}$ for different values of coupling strength. Entropy of the corresponding pattern is given underneath each panel: (a) $w = 0,\;g = {\rm{0}}$ ; (b) $w = 0.{\rm{17}},\;g = {\rm{0}}.{\rm{3}}$ ; (c) $w = 0.05,\;g = 1.2$ ; (d) $w = 0.05,\;g = 1.1 $ ; (e) $w = 0.07,\;g = 1.3$ ; (f) $w = 0.0{\rm{9}},\;g = 1.{\rm{9}}$ ; (g) $w = 0.05,\;g = 1.0$ ; (h) $w = 0.01,\;g = 0.1$ ; (i) $w = 0,\;g = {\rm{0}}.{\rm{1}}$ ; (j) $w = 0.03,\;g = 1.0$ ; (k) w $ = 0.07,\;g = 0.4$ ; (l) $w = 0.05,\;g = 0.4$ .图1 可以看出: 1)网络可以自发地出现单螺旋波和多螺旋波. 网络从混沌初相位分布演化, 在适当的耦合强度下随机在网络边界附近产生一个或多个螺旋波波头, 这时网络就会出现单螺旋波或多螺旋波, 因为螺旋波的频率高于无规则波, 可以将无规则波驱赶出网络边界, 最后整个空间被一个或多个螺旋波占据. 出现单螺旋波时网络的熵值为0, 但是出现多螺旋波时网络的熵值不为0, 随着排斥耦合强度的增加, 螺旋波个数会增加, 相应的熵值也会增大(参见图1(c) —图1(e) ); 当排斥耦合强度足够大时, 网络中一般不会自发出现有序波, 网络的熵超过2.0 (参见图1(b) 的混沌斑图); 当单螺旋波未占据整个空间时网络的熵也比较大(参见图1(j) ). 由于网络演化了较长的时间, 波头才开始形成, 所以单螺旋波未占据整个空间, 随着网络演化时间的延长, 图1(j) 显示的单螺旋波会占据整个空间. 2)网络可以自发出现靶波. 靶波既可以是由螺旋波对产生(参见图1(f) 和图1(k) ), 也可以由单个振源产生(参见图1(l) ). 当网络在适当的耦合强度下随机在网络中产生线波时, 就会演化成螺旋波对, 最后形成靶波. 由于网络演化时间关系, 图1(k) 和图1(l) 中显示的靶波未占据整个空间, 处于靶波与混沌态的共存态. 随着网络演化时间的延长, 图1(k) 中显示的靶波会占据整个空间, 而图1(l) 显示的靶波会因为振源不稳定而消失, 之后网络自发出现螺旋波. 3)网络还会出现其他有序斑图, 图1(g) 显示的是振源在边界上, 产生向介质中间传播的内向行波. 如果除了在边界处出现振源外, 在中间也出现振源, 就会出现如图1(h) 和图1(i) 所示的斑图, 形成行波与驻波共存态.图1(g) 和图1(h) 显示的有序波有直观印象, 我们记录在网络演化过程中一行和一列格点上所有神经元的${x_{i,j}}$ 变量随时间变化, 得到不同耦合强度下的时空斑图如图2 所示. 图2(a) 和图2(b) 分别给出图1(g) 参数下$j = 100$ 这一行和$i = 100$ 这一列格点的时空斑图, 从这两个图可以看出, 图中出现向中间倾斜的粗线, 表明波从边界向中间传播, 我们把这种波称为内向行波.图 2 不同耦合强度下一行和一列格点的${x_{i,j}}$ 变量时空斑图 (a) $w = 0.05,\;g = 1.0$ ; (b) $w = 0.05,\;g = 1.0$ ; (c) w =$ 0.01,\;g = 0.1$ ; (d) $w = 0.01,\;g = 0.1$ Figure2. Spatiotemporal pattern of the variable ${x_{i,j}}$ of a row and a column of grid points for different values of coupling strength: (a) $w = 0.05,\;g = 1.0$ ; (b) $w = 0.05,\;g = 1.0$ ; (c) $w = 0.01,\;g = 0.1$ ; (d) $w = 0.01,\;g = 0.1$ .图2(c) 和图2(d) 分别给出图1(h) 参数下$j = 100$ 这一行和$i = {\rm{50}}$ 这一列格点的时空斑图, 从这两个图可以看出, 图中边界附近出现多条较长向左和向右倾斜的粗线, 中间也出现倾斜粗线, 但是倾斜粗线很短, 表明空间自发存在多个振源, 边界附近的振源明显产生了背离波源传播的行波, 中间振源产生的波出现传播有限距离即相遇, 所以粗线接近水平线, 看起来像驻波, 因此把图1(h) 所示的斑图称为行波与驻波共存斑图, 从图2(c) 和图2(d) 还可以看出, 图中出现形状相近的几条粗线, 这是因为特定斑图重复出现, 这些结果说明图1(h) 是有序斑图, 只是斑图形状不够规则, 图1(i) 参数下的网络也有类似行为. 行波和驻波也在脑网络中已经被发现[30 ,31 ] , 我们的结果可以解释这些有序波产生的机制.图3(a) —图3(f) 分别给出了图1(c) 、图1(d) 、图1(e) 、图1(g) 、图1(h) 和图1(l) 所对应的参数下网络的集团熵随时间的变化. 从图3 中可以看出, 初态斑图的熵值很大, 网络演化初期集团熵急剧减少, 这是因为网络出现越来越大的集团的缘故. 网络经过500个时间单位的演化后, 大部分参数下集团熵变化趋向平稳变化, 变化规律相近, 单螺旋波态的熵值最后等于0 (参见图3(a) ), 多螺旋波态趋于稳定值(参见图3(b) 和图3(c) ). 通过观察网络演化过程, 发现在图3(b) 和图3(c) 参数下, 网络演化约2000个时间单位出现螺旋波波头, 且出现在熵值首次达到极小值附近, 这时斑图的熵值约为1.5. 这表明, 要使网络自发地出现螺旋波, 网络中一般要出现一定大小的集团, 并且排斥耦合要足够大. 从图3 还可以看出: 网络经过500个时间单位的演化后, 图3(e) 所示网络集团熵变化规律与其他网络集团熵变化有较大不同, 由于排斥耦合强度很小, 兴奋性耦合强度也小, 网络在演化初期反复出现集团熵接近0的情况, 说明网络中反复出现很大的集团, 这个结果与Schneidman等[32 ] 的实验结果一致, Schneidman等发现: 在脊椎动物的视网膜中, 在记录10多个神经元的电活动中, 虽然神经元对之间相关是微弱的, 但是整体出现强的集体行为.图 3 不同耦合强度下网络的集团熵随时间变化 (a) $w = 0.05,\;g = 1.2$ ; (b) $w = 0.05,\;g = 1.1$ ; (c) $w = 0.07,\;g = 1.3$ ; (d) $w = 0.05,\;g = 1.0$ ; (e) $w = 0.01,\;g = 0.1$ ; (f) $w = 0.05,\;g = 0.4$ .Figure3. Time evolution of the cluster entropy of the network for different values of coupling strength: (a) $w = 0.05,\;g = 1.2$ ; (b) $w = 0.05,\;g = 1.1$ ; (c) $w = 0.07,\;g = 1.3$ ; (d) $w = 0.05,\;g = 1.0$ ; (e) $w = 0.01,\;g = 0.1$ ; (f) $w = 0.05,\;g = 0.4$ .图4 和图5 分别给出了在g -w 参量平面上的相图以及熵分布的直方图, 它们是网络从图1(a) 所示的初态演化10000个时间单位后得到的结果. 从图4 和图5 可以看出: 1)当$w = 0.01$ 时, 网络仍可以出现有序结构, 但是不会出现螺旋波, 其集团熵对于不同g 参数有所不同, 集团熵在[0.556, 1.18]范围内变化, 因此我们得出: 尽管斑图形状不是很规则, 但是网络状态斑图是有序斑图; 2)当w = 0.03—0.05时, 适当选择g 和w 参量的值, 网络可出现单螺旋波和多螺旋波以及螺旋波与其他态共存态, 集团熵在[0, 2.116]范围内波动, 出现大的熵值是因为在g 很小情况下出现混沌斑图; 3)当w =0.07—0.13时, 网络很容易出现多螺旋波, 多螺旋波斑图的集团熵依赖波头数量的不同而不同, 网络的集团熵在[0.294, 2.669]范围内变化, 由于在g 很小情况下出现混沌斑图, 所以在这个排斥耦合强度区间同样存在熵值很大的斑图; 4) 当w = 0.15—0.17时, 网络一般为混沌态, 此参数下网络的集团熵范围为[1.200, 3.113].图 4 在g -w 参量平面上的相图 Figure4. Phase diagram in the g -w parameter plane.图 5 在g -w 参量平面上的熵分布Figure5. Entropy distribution in the g -w parameter plane.图4 可以得到, 在180组参量中有3, 38, 14, 27组参数分别出现单螺旋波、多螺旋波、单螺旋波与其他态共存、多螺旋波与其他态共存, 单螺旋波、多螺旋波出现的比率分别为1.67%和21.1%, 单螺旋波与其他态共存和多螺旋波与其他态共存出现的比率分别为7.78%和15%, 螺旋波出现总比率为45.55%, 表明排斥耦合有促进螺旋波形成的作用. 有7组参数出现靶波与其他态共存, 靶波与其他态共存出现的比率达到3.89%. 有30, 19组参数分别出现内向行波和行波与驻波共存态, 它们出现的比率分别达到16.67%和10.56%. 有42组参数出现混沌态, 混沌态出现的比率为23.33%, 但是当排斥耦合足够强时, 网络出现混沌态的比率达到95%. 可见在长程排斥耦合下, 螺旋波出现概率最大, 混沌态次之, 单个螺旋波出现概率最小. 综上所述, 排斥耦合强度在一定范围内取值, 有利于网络中产生螺旋波、靶波、行波等有序结构.图4 所示的各种现象都可以观察到, 甚至观察到单个靶波, 而且不同排斥耦合强度下有序波产生的规律相同, 只是在不同初态下螺旋波、靶波和靶波与其他共存态、内向行波、行波与驻波共存态、混沌态出现的比率有所不同, 4个不同的初态下, 螺旋波出现比率分别为43.0%, 40.0%, 47.0%和45.55%, 其出现比率范围为[40.0%, 47.0%]; 靶波和靶波与其他共存态出现比率分别为3.0%, 3.0%, 3.0%, 3.89%, 出现比率基本在3%附近; 内向行波出现比率分别为24.0%, 24.0%, 20.0%, 16.67%, 出现比率范围为[16.67%, 24%]; 行波与驻波共存态出现的比率分别为4.0%, 6.0%, 4.0%, 10.56%, 出现比率范围为[10.56%, 6.0%]; 混沌态出现的比率分别为26.0%, 27.0%, 26.0%, 23.33%, 出现比率范围为[23.33%, 27.0%]. 同样得到单螺旋波出现比率是很小的. 上述结果表明, 同一参数、不同初态可得到不同网络斑图, 这是由于这些有序斑图是随机产生的.[7 ] , 为了模拟在大脑皮层中观察到的现象, 了解其背后的物理机理, 选图1(c) 所示的单螺旋波态为初态, 先将$w = 0.05$ 改为$w =$ $ - 0.15$ , 即将排斥性耦合转变为兴奋性耦合, 然后让网络演化10000个时间单位, 在这个过程中图1(c) 中的单螺旋波破碎成混沌态, 紧接着将$w = - 0.15$ 变化为$w = 0.05$ 后继续演化10000个时间单位, 网络最后出现多螺旋波, 螺旋波破碎又重现的过程如图6 所示.图 6 在$g = 1.2$ 和不同耦合强度w 下不同时刻的${x_{i,j}}$ 变量斑图 (a) $w = - 0.15$ , $t = 0$ ; (b) $w = - 0.15$ , $t = 1000$ ; (c) $w = - 0.15$ , $t = 2000$ ; (d) $w = - 0.15$ , $t = 4000$ ; (e) $w = - 0.15$ , $t = 6000$ ; (f) $w = - 0.15$ , $t = 8000$ ; (g) $w = - 0.15$ , $t = 10000$ ; (h) $w = 0.05$ , $t = 12000$ ; (i) $w = 0.05$ , $t = 14000$ ; (j) $w = 0.05$ , $t = 16000$ ; (k) $w = 0.05$ , $t = 18000$ ; (l) $w = 0.05$ , $t = 20000$ .Figure6. Pattern of the ${x_{i,j}}$ variable at different time moments for g = 1.2 and different values of coupling strength w : (a) $w = - 0.15$ , $t = 0$ ; (b) $w = - 0.15$ , $t = 1000$ ; (c) $w = - 0.15$ , $t = 2000$ ; (d) $w = - 0.15$ , $t = 4000$ ; (e) $w = - 0.15$ , $t = 6000$ ; (f) w = –0.15, $t = 8000$ ; (g) $w = - 0.15$ , $t = 10000$ ; (h) $w = 0.05$ , $t = 12000$ ; (i) $w = 0.05$ , $t = 14000$ ; (j) $w = 0.05$ , $t = 16000$ ; (k) $w = 0.05$ , $t = 18000$ ; (l) $w = 0.05$ , $t = 20000$ .图1(e) 所示的多螺旋波态为初态, 先将$w = 0.07$ 改为$w = - 0.17$ , 然后让网络演化8000个时间单位, 在这个过程中多螺旋波破碎成混沌态, 紧接着将$w = - 0.17$ 改为$w = 0.07$ 继续演化12000个时间单位, 网络又出现多螺旋波, 只是螺旋波波头数量由原来的3个变成了2个, 这些结果表明, 大脑皮层的中螺旋波寿命短和频繁出现可能与排斥耦合的变化有关.4.结 论 采用HR神经元模型研究了排斥耦合在神经元网络自发出现有序波中所起的作用, 发现排斥耦合有两方面的作用. 一方面的作用是排斥耦合导致有序波的产生. 当排斥耦合强度在一定范围取值时, 排斥耦合可以导致网络中产生单螺旋波、多螺旋波、靶波、内向行波、行波与驻波共存态等有序波. 螺旋波、靶波、内向行波和行波与驻波共存态出现的概率分别达到0.4555, 0.0389, 0.1667和0.1056. 排斥耦合有促进网络自发产生螺旋波的作用, 但是单螺旋波(或者大螺旋波)出现概率很小. 另一方面的作用是排斥耦合抑制网络出现有序结构, 因为当排斥耦合强度足够大时, 网络几乎处于混沌态. 当长程排斥耦合转变成长程兴奋性耦合时, 会导致有序结构被破坏, 而长程兴奋性耦合转变成长程排斥耦合时, 网络又可自发出现有序结构. 











































 图 1 不同耦合强度下的神经元
图 1 不同耦合强度下的神经元




























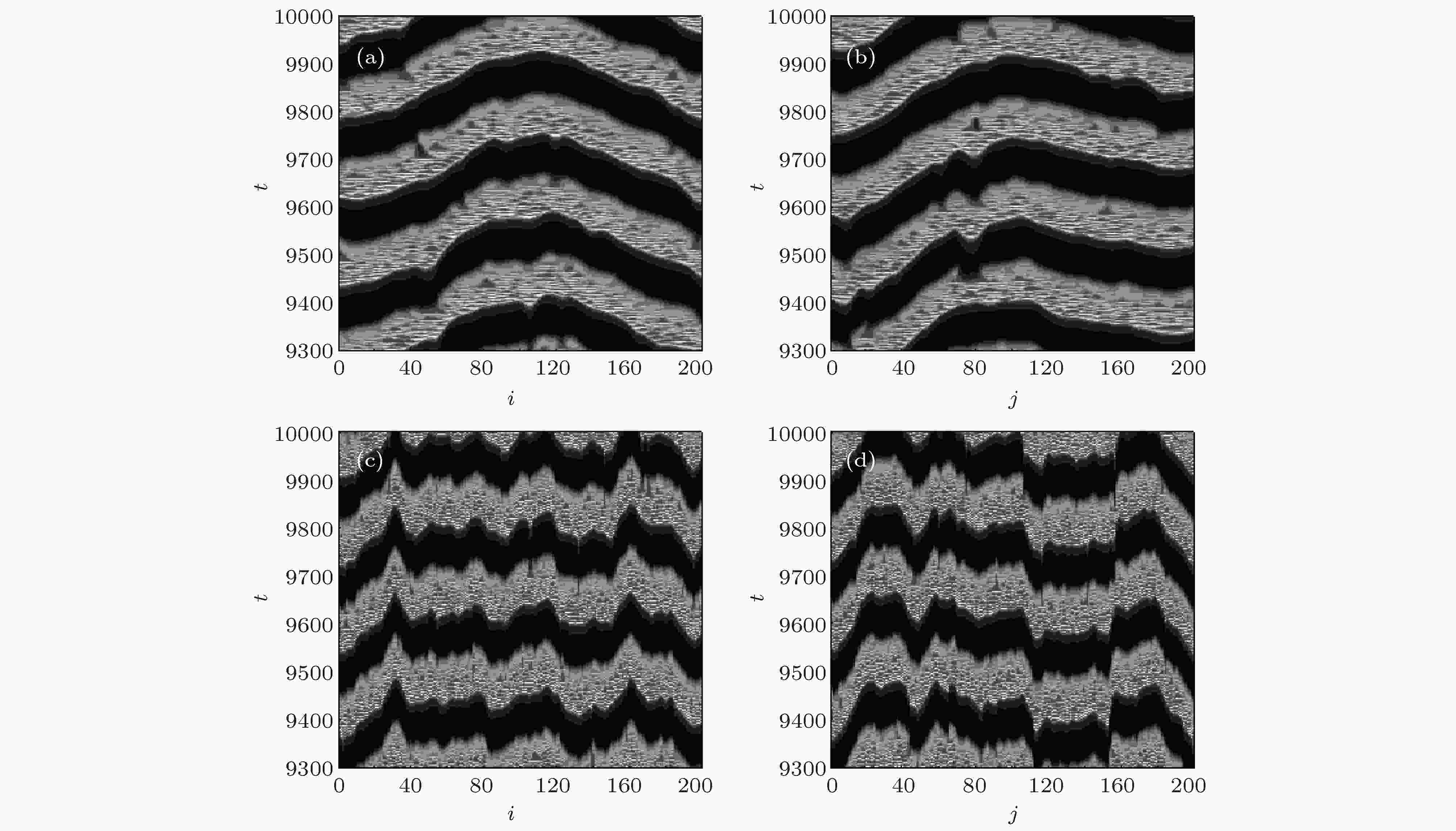 图 2 不同耦合强度下一行和一列格点的
图 2 不同耦合强度下一行和一列格点的

















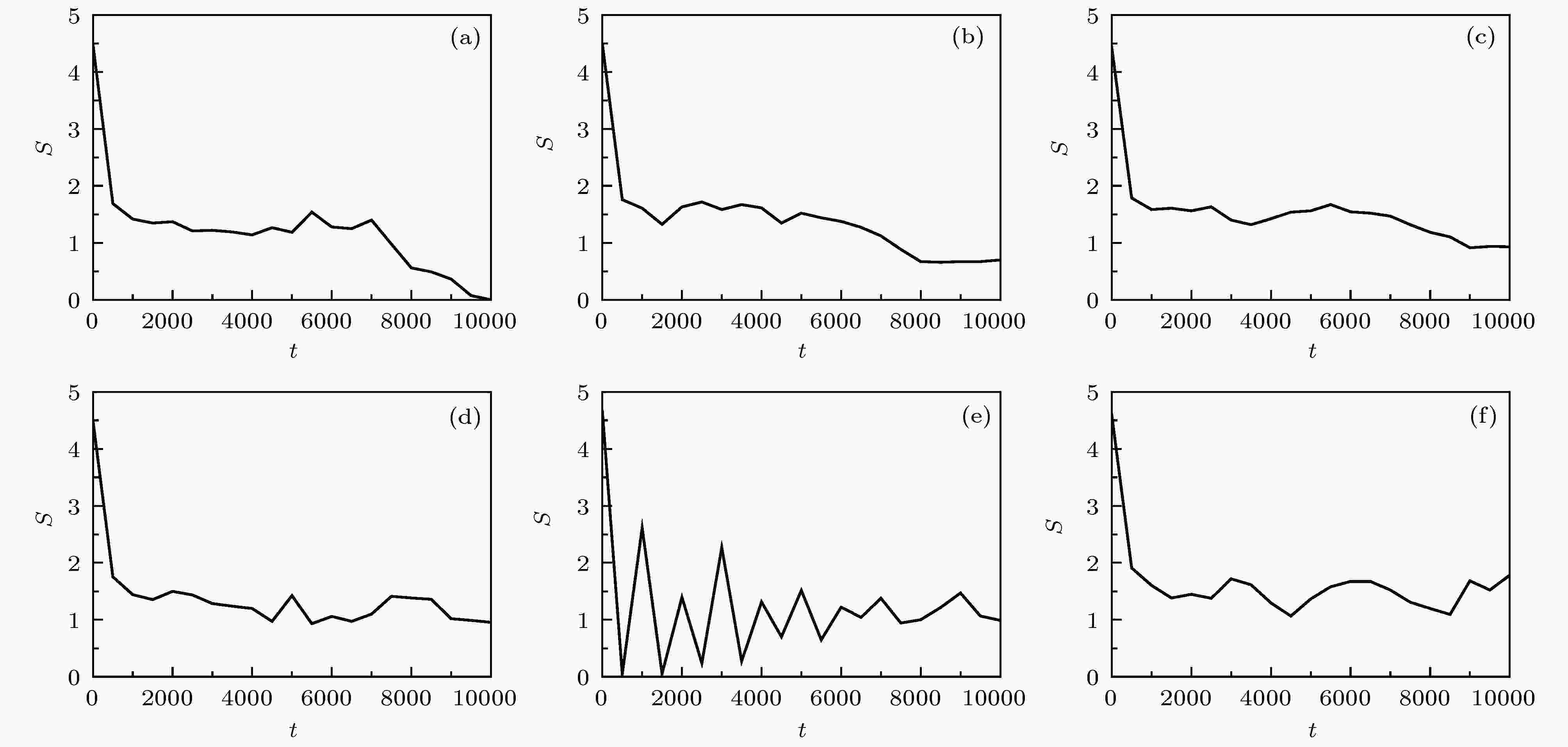 图 3 不同耦合强度下网络的集团熵随时间变化 (a)
图 3 不同耦合强度下网络的集团熵随时间变化 (a) 












 图 4 在g -w参量平面上的相图
图 4 在g -w参量平面上的相图 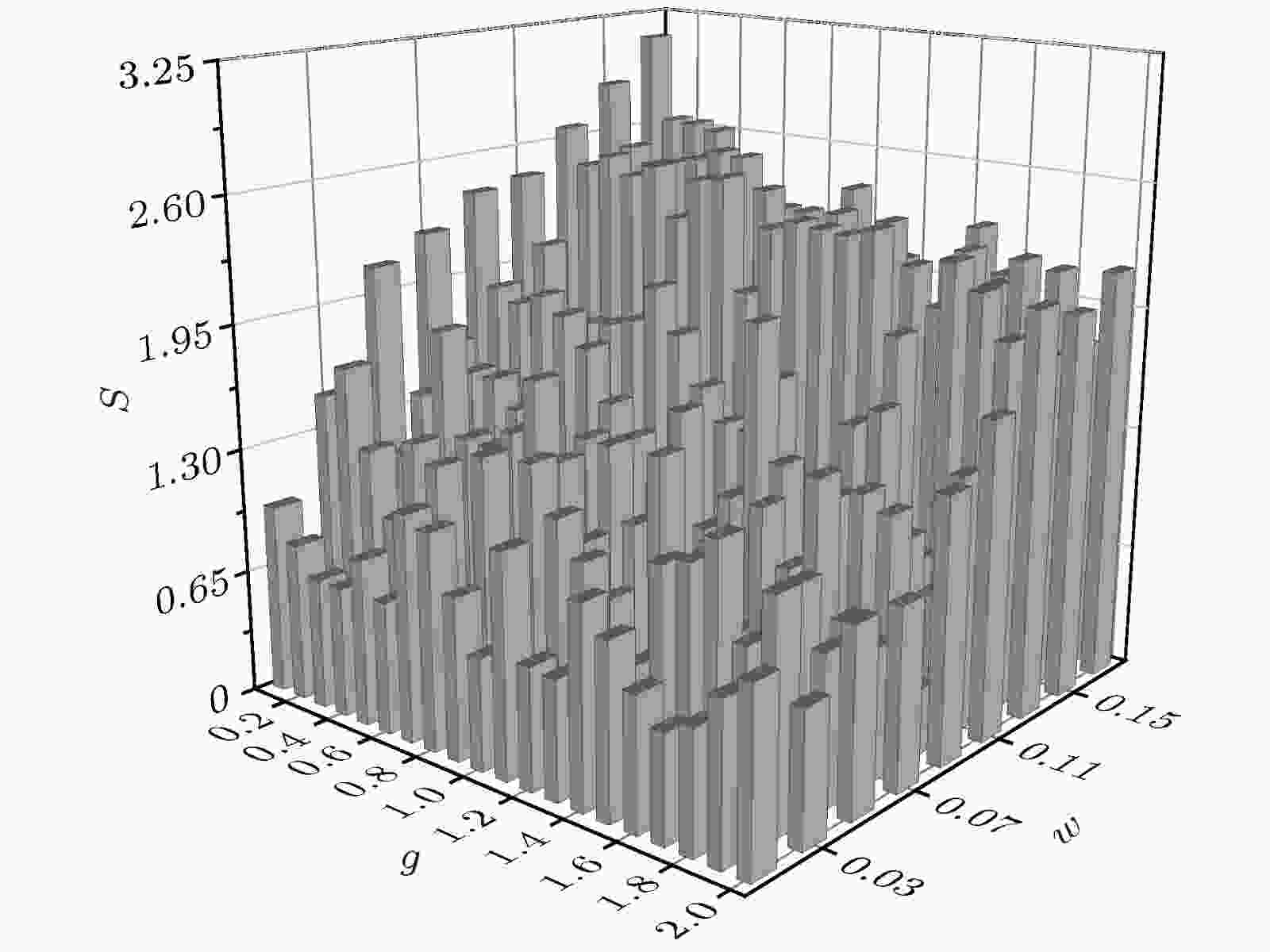 图 5 在g -w参量平面上的熵分布
图 5 在g -w参量平面上的熵分布






 图 6 在
图 6 在









































































































































































