<script type="text/javascript" src="https://cdn.bootcss.com/mathjax/2.7.2-beta.0/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script> <script type='text/x-mathjax-config'>MathJax.Hub.Config({tex2jax: {inlineMath: [['$','$'], ['\\(','\\)']]},"HTML-CSS": {linebreaks: { automatic: true},scale: 100}});</script> 摘要:知识图谱是人工智能研究的新热点, 用于解决智能检索、自动回答等应用问题. 概念图谱是微软发布的大型知识图谱, 本文以概念图谱为研究对象构建了概念图谱网络, 并对其特性进行了分析. 为解决概念图谱海量数据带来的计算困难, 提出一种适合概念图谱的最大子网构建方法和一种网络近似平均路径的计算方法; 对不同度值给出了不同的聚类系数求解方法, 并通过Map/Reduce模式进行提速. 结果表明: 概念图谱网络具有无标度和极端小世界网络的特征; 平均路径长度随网络规模增加而减小并趋于4这一定值, 网络的“菱形”结构能很好地解释这一现象; 概念图谱网络是异构的, 相邻节点的度负相关; k-shell分解表明子概念占核心层节点的99.5%, 在概念图谱中起重要的连接作用; 子概念的缺失对概念图谱的完整性影响最大、概念其次、实例最小; 82%的实例节点度为1, 40%的概念节点度为1, 实例比概念更不易因一词多义而引起理解歧义.
关键词: 微软概念图/
复杂网络/
子网抽取/
近似平均路径

English Abstract

全文HTML

--> --> -->

复杂网络理论兴起于20世纪90年代, 是对复杂系统的一种抽象和描述方式. 复杂网络由节点和边组成, 节点表示元素, 边表示元素之间的互相作用. 复杂网络普遍存在于现实世界, 如生物分子网、互联网、交通网、电力网等.
知识图谱由Google公司于2012年提出后, 就在搜索引擎与人工智能领域备受关注. 知识图谱旨在通过语义知识的结构化储备实现智能检索、自动问答等应用, 相关研究主要围绕着知识图谱的知识提取、知识融合以及知识推理等进行. 知识图谱描述知识之间的语义关联, 同样可以网络化. 网络化的知识图谱是否符合复杂网络模型？知识间的关系是否可以通过复杂网络理论进行分析？目前尚没有明确的结论. 微软概念图谱(Microsoft concept graph)是微软研究院于2016年发布的一个知识图谱, 其形式为概念(concept)、实例(instance)和关系(relation)的三元组, 描述实例与概念之间的IsA关系, 用于实现实例的概念化推理^[1]. 例如三元组(sport, basketball, 6423)表示basketball与sport之间存在IsA关系, 即basketball是一种sport. 其中basketball (篮球)是实例, sport (运动)是概念, 6423是从微软bing搜索日志中抽取到的basketball和sport之间的IsA关系的次数, 以下称为共现次数. 概念和实例是对事物的描述, 概念较抽象, 通常描述事物的类别, 例如fruit (水果); 实例描述较为具体, 一般为具体事物的名称或标识, 例如orange (橙子). 概念图谱正是通过这些由用户搜索记录提取到的实例、概念以及它们之间的IsA关系反映人们对实物的认知和理解.
本文以微软概念图谱为研究对象, 构建描述概念与实例之间概念化关系的概念图谱网络, 进而研究概念词与实例词之间的关联关系. 选取该研究对象的优势在于: 1)图谱数据来源于bing搜索日志中数以亿计的用户搜索记录, 反映了用户对事物的真实看法; 2)图谱中的共现次数反映了IsA关系的可信度, 可据此调整网络规模; 3)微软概念图谱只有IsA一种关系, 在构造网络时不需要对关系进行区分, 简化了网络模型的构建.
首先采用NetworkX工具计算相关统计特征^[2], 但由于概念图谱网络的节点数量巨大, 导致计算时间过长, 因此本文提出一种适用于概念图谱的子网提取算法, 用来获取最大连通子网, 在时间和空间效率上都有显著提高, 并对最大子网的复杂网络特征进行了分析. 在计算网络的最短平均路径长度时, 本文提出了一种计算概念图谱网络近似平均最短路径的方法, 并对算法准确性进行了验证. 对于聚类系数的计算, 本文根据节点度值给出了不同的聚类系数求解方法, 并采用Map/Reduce模式进行了计算提速.

复杂网络理论起步于Erdos和Renyi的随机图论(ER图), 而后随着Watts和Strogatz^[3]提出的小世界网络、Barabási和Albert^[4]提出的无标度网络逐渐兴起, 复杂网络理论为复杂系统的特征分析提供了重要的理论依据, 已被广泛应用于社会网络分析^[5]、城市建设用地布局^[6]、国际贸易交流分析^[7]、交通运输分析^[8]等. 其中交通运输领域的应用又包括公路交通^[9]、轨道交通^[10]、铁路^[11]、航运^[12]、航空^[13]等. 通过求解网络特征, 如网络节点的度分布、平均路径长度、聚集特性以及介数中心性等, 分析复杂系统中各因子之间的关系和整体稳定性^[14]. 以上文献中复杂网络系统的节点以交通站点、城市、国家等为主, 边以交通线路、城市区域间道路、国家关系等为主, 系统中节点和边的数量较少, 且多为连通网络, 因此分析其统计特性时资源消耗不大.
在研究如万维网^[15,16]、电话呼叫网^[17,18]这类超大规模网络时, 由于很难得到描述整个网络结构的全部信息, 通常的方法是先分析局部实际数据的特性, 根据这些特性建立实际网络的数学模型, 再由数学模型推算整个网络的相关特性. Albert等^[16]先从万维网抓取了部分实际数据, 得到其局部结构, 据此分析出节点的度分布符合幂律分布, 并根据拟合结果对局部网络进行扩展得到较大规模的拓扑结构; 据此分析万维网的拓扑结构和连接特性, 得到网络半径与节点数量之间的函数关系; 最后, 将万维网节点实际数量代入该函数推测出万维网的网络直径. Aiello等^[17,18]也通过类似的方法对电话呼叫网进行了拓扑建模和演化研究. 目前较快的串行最短路径算法的时间复杂度也只能降低到O(n^2.376)^[19], n为网络节点的数量.
随着时间的发展, 万维网的节点数量早已超过数十亿数量级, 边的数量更是不计其数; 电话呼叫网络根据已存在的电话线路之间的关系进行建立, 包括约47000000个节点, 80000000条边. 对于规模如此巨大的网络直接计算其直径(节点间最短路径的平均值)和聚类系数几乎是不可行的. 这可能是相关文献均未给出具体的网络聚类系数值, 对于网络直径也只给出由网络模型计算得到的推测值的原因^[15,17,18].
因此有****开展了网络精简、评估方法改进、网络结构优化等研究. 网络精简通过阈值网络^[20]、最小生成树^[21]、差分网络^[22]等方法减小网络的规模. 孙延风和王朝勇^[23]采用互信息表示金融网络中节点间的关系, 并用阈值网络和最小生成树对网络进行精简, 最后验证了网络模型的有效性.
评估方法改进包括基于度中心性的评估方法^[24]、k-shell分解^[25]和基于PageRank的评估方法^[26]等. Ruan等^[27]将约束系数引入节点核心性的度量, 提出了一种综合节点邻居节点的k-shell值和邻居节点间拓扑结构的核心性度量方法, 该方法能更准确地评估节点的传播能力. 孔江涛等^[28]利用复杂网络动力学模型描述复杂网络中节点间的相互影响活动, 建立了基于偏离均值与偏离均值的方差的两级节点重要性评估标准, 并通过扰动测试和破坏测试验证了标准的有效性.
网络结构优化主要以实际应用为目的, 如韩定定等^[29]结合时变特征和网络客流分布, 对航空网进行优化, 提出了一种快速推算航线网络最优拓扑及相应航班频率分布的方法. Niu和Pan^[30]通过自组织优化机制对运输网络进行优化, 证明了无标度网络在gradient-driven运输模式下可以有效地通过自组织优化机制提高运输能力. Jiang等^[31]以中国航空运输网(CNTA)为例研究多层网络融合过程的本质, 通过一系列拓扑属性刻画多层网络的融合过程, 发现CNTA在融合过程中发生了明显的结构转换, 为中国航空运输系统的网络结构优化和管理提供了启示.
而知识图谱作为智能化的语义知识储备, 其规模也会随着时间而不断积累扩大, 节点数量往往突破千万数量级, 对这类大规模网络的特征计算也必然十分复杂与耗时. NetworkX是一款用Python语言开发的复杂网络构建与分析软件工具包, 是复杂网络建模与分析的有力工具^[2]. 由于知识图谱的规模巨大, 使用NetworkX仅是构建出整个网络便需要消耗近40 GB的内存. 万维网可以通过网络中的路由设备找到通往各个网站节点需要跳转的次数, 即平均最短路径长度, 而知识图谱与万维网不同, 知识间的拓扑距离无法如此计算. 为了解决大规模复杂网络分析的问题, 有****设计了近似算法以计算复杂网络的平均距离. Rattigan等^[19]通过引入网络结构索引(network structure index, NSI)计算节点间路径, 从而降低计算网络平均路径长度这样的基于节点间路径应用的搜索复杂度. NSI由各个节点的标记和根据节点标记估算节点对间距离的函数构成. 唐晋韬等^[32]提出了基于区域中心点距离(centers distance of zone, CDZ)的复杂网络最短路径计算的近似方法, 根据网络特征将网络分成多个区域, 每个区域都设置一个中心点, 将两节点之间的距离转换为节点到中心点以及中心点间的距离之和, 实现近似计算. 受CDZ思想的启发本文提出了一种根据节点所在网络层与中心节点的距离及不同网络层之间的距离计算概念图谱网络近似平均最短路径的方法.

2

-->

3.1.概念图谱网络构建

微软官方提供的概念图谱的数据文件是一个纯文本文件, 构成该文件的元数据是描述实例与概念之间IsA关系的三元组. 通过对该数据文件的遍历发现, 有些词既作为概念(Concept)出现, 也作为实例(Instance)出现, 本文将这部分词称为子概念词(subConcept). 为了构建描述实例与概念之间的实例关系的复杂网络, 将概念、子概念和实例作为网络的节点, 在存在IsA关系的两个节点之间添加一无向条边, 表示它们之间的实例关联, 从而构建出如图1所示的描述概念、子概念、实例之间的实例关联的概念图谱网络.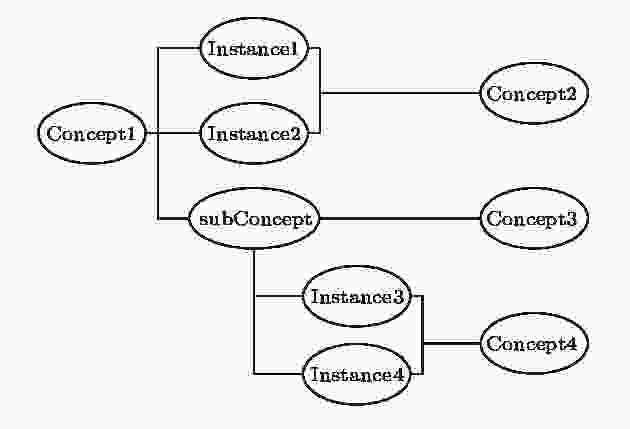
图 1 概念图谱网络示意图
Figure1. Network of concept graph.

建立的概念图谱网络是一种无向非加权网, 具有如下特征: 1)网络规模巨大, 包括16936670个节点和33354328条边, 因此建立非加权网络以减少计算复杂度, 便于特征分析; 2)只描述概念和实例间的IsA关联及关联间的跳转层次, 忽略关系的方向; 3)共现次数描述节点间关系的可信度, 旨在通过阈值设置得到不同较小规模的概念图谱网络以进行深入的比较分析.
表1列出了在整体概念图谱网络中, 概念词、实例词以及子概念词的度值分布. 在概念图谱网络中, 概念节点的度表示有多少个实例或子概念与该概念存在IsA关系. 实例节点的度表示该实例与多少个概念或子概念具有IsA关系. 首先, 因为概念图谱的基本数据是由概念、实例和它们之间的IsA关联构成的三元组, 因此, 每个概念至少与一个实例相关, 一个实例也至少与一个概念相关, 因此所构建的概念图谱网络中不应有孤立节点, 即不存在度为0的节点, 这与表1的统计数据一致. 其次, 由于子概念既可以处在概念的位置, 也可以处在实例的位置, 所以子概念的度都应大于等于2. 但由表1可知概念图谱网络中有18个子概念节点的度为1. 为探究该现象, 在概念图谱的数据文件中对度为1的子概念节点进行了检索和分析, 发现存在类似于(small business issuer, company, 4)和(company, small business issuer, 1)这样的两个节点互为对方的概念与实例的情况. 同时, 因为这两个节点都未出现在其他三元组中, 所以它们的度都为1. 这些度为1的子概念节点也揭示了所构建的概念图谱网络并非一个连通网络. 因此, 为了真实描述其网络特性, 必须抽取该网络的最大连通子网, 并将其作为后续研究对象分析概念图谱网络的复杂网络特性.

k	Concept			k	Instance			k	SubConcept
	Quantity	Proportion			Quantity	Proportion			Quantity	Proportion
1	2061496	0.464809		1	9610146	0.831317		1	18	1.91208 × 10–5
2	1165725	0.262838		2	1014355	0.087746		2	140735	0.149498132
3	538652	0.121451		3	312310	0.027016		3	186330	0.197932191
4	252438	0.056918		4	156703	0.013555		4	125273	0.133073361
5	130975	0.029531		5	96100	0.008313		5	78365	0.083244546
6	74760	0.016856		6	64809	0.005606		6	52113	0.055357915
7	46336	0.010447		7	46409	0.004015		7	37615	0.039957169
8	31509	0.007104		8	34801	0.00301		8	29314	0.031139292
9	22506	0.005074		9	27177	0.002351		9	23419	0.024877229
10	16510	0.003723		10	21928	0.001897		10	19484	0.020697208
11	12921	0.002913		11	18095	0.001565		11	16465	0.017490224
12	10012	0.002257		12	14935	0.001292		12	14188	0.015071443
13	8188	0.001846		13	12688	0.001098		13	12491	0.013268776
$\vdots$	$\vdots$	$\vdots$		$\vdots$	$\vdots$	$\vdots$		$\vdots$	$\vdots$	$\vdots$
32773	1	2.25 × 10–7		6716	1	8.65 × 10–8		364276	1	1.06227 × 10–6
Total	4435143	1		Total	11560144	1		Total	941383	1

表1概念图谱网络的节点度分布
Table1.Degree distribution of the concept graph network.

2 -->

3.2.子网抽取算法

由于概念图谱网络不是连通网络, 无法计算节点间的平均距离, 所以需要计算出概念图谱网络的最大连通子网. 我们按照广度优先思想, 实现了基于广度优先的子网提取算法(SubNet Extraction based on Breadth-first, SNEBF).
算法1 基于广度优先的子网提取算法(SNEBF)
输入: 概念图谱数据文件Graph
输出: 最大连通子网节点集合MaxSubNet
1)从Graph中抽取一个三元组, 该三元组包含的两个节点的度之和最大, 将该三元组中的概念和实例作为两个初始节点, 构成初始节点集合InitialSet, 并将这两个节点加入MaxSubNet.
2)对InitialSet中的每一个节点node
　{a. 遍历Graph中的三元组(概念(con), 实例(ins), 关系(rel))信息, 如果其con或ins等于node, 则将该三元组中相应的ins或con加入节点node的邻居节点集合NeighborSet.
　b. 判断NeighborSet中是否还有未加入MaxSubNet的节点, 如果有, 将这些节点加入MaxSubNet, 将NeighborSet集合与MaxSubNet的差集并入InitialSet.}.
3)返回MaxSubNet.
类似于广度优先的按层扫描, 对于InitialSet中的每一节点node算法1总是找出其全部相邻节点并据此对最大子网进行扩展, 对找出的相邻节点重复相同的操作. 但在实际运行时, 由于网络中的节点之间关系复杂, 不同节点的邻居节点集合可能相互包含了许多相同的节点. 如在图2所示的概念图谱网络中, Concept1的邻居节点集合包括4个节点: Instance2, Instance3, Instance4和Instance5. Concept2也有4个邻居节点: Instance1, Instance2, Instance3和Instance4. 其中Instance2, Instance3和Instance4是Concept1的邻居节点也是Concept2的邻居节点.
图 2 导致节点的邻居节点集合冗余的网络结构
Figure2. Network structure leading to the overlap of neighbor node sets.

这些相同的节点在处理Concept1的邻居节点和Concept2的邻居节点时会被重复进行递归检索处理. 这不但会增加大量的冗余存储空间而且需要多次重复检索图谱数据. 同时由于算法中循环嵌套了循环, 所以在进行遍历时十分耗时. 因此我们引入集合运算, 从而得到基于集合运算的子网抽取算法(SubNet Extraction based on Set Operation, SNESO).
算法2 基于集合运算的子网抽取算法(SNESO)
输入: 概念图谱数据文件Graph
输出: 最大连通子网节点集合MaxSubNet
1)从Graph中抽取一条包含度值最大节点的三元组信息, 将该三元组中的概念和实例作为中心节点构成最大连通子网的中心层SubNet_i (此时i = 1), 并将其加入MaxSubNet.
2)寻找SubNet_i集合的邻居节点, 即遍历Graph中的(con, ins, rel)信息, 判断其con或ins是否属于SubNet_i集合, 若存在, 则表示对应的ins或con是集合SubNet_i的邻居节点, 将这些节点加入SubNet_i的邻居节点集合NeighborsSet_i.
3)判断NeighborsSet_i中是否还有新的未在MaxSubNet中的节点, 如果有, 则将NeighborsSet_i并入MaxSubNet, 将SubNet_i替换为NeighborsSet_i与MaxSubNet的差集, i = i+1. 然后跳转至步骤2; 若无, 则继续步骤4.
4)返回MaxSubNet.
算法1和算法2的关键操作是对Graph三元组信息的遍历. 由中心层出发, 每扫描一次Graph, 算法1获得一个节点的邻接节点, 算法2获得一层节点的全部邻接节点, 因此算法2能显著减少对Graph的扫描次数. 由于度值大的节点在最大连通子网的概率较高, 为了保证可以找到最大子网, 我们从度值最大的节点以及与最大节点相连的度值较大的节点开始进行搜索. 在实际运行中, 运算时间和空间复杂度确实有所降低, 具体的复杂度分析见3.3节.
先由算法2得到最大连通子网的节点集合MaxSubNet; 再根据MaxSubNet从概念图谱数据文件Graph中提取出最大子网的边的集合, 其中的每条边依然采用Graph中的三元组形式并存储在文本文件GraphLink中; 最后由MaxSubNet和GraphLink生成如图3所示结构的最大连通子网. 其中, 中心层(Central Layer)由两个节点构成, 这两个节点是各三元组对应的节点对中度值和最大的节点对; 第二层(Layer-2)为中心层各节点的邻居节点的集合; 第三层(Layer-3)为第二层的各节点的邻居节点的集合. 以此类推, 直到网络的最外层(Outermost Layer).
图 3 最大连通子网的分层逻辑结构
Figure3. Hierarchical logical structure of the largest connected subnet.

2 -->

3.3.算法复杂度分析

根据算法1我们实现了函数GetNeighbor(Node, Graph), 该函数遍历Graph中的边(三元组)信息, 判断Node是否为当前边的端点. 由于一条边有两个端点, 完成一条边的扫描需要两次判断操作. 将1个端点的判断操作定义为1次基本操作, Graph的边数为n, 则GetNeighbor(Node, Graph)的时间复杂度为2n. 由算法1可知, 每当最大连通子网中有一个新的节点, 就要调用一次GetNeighbor(Node, Graph). 设最大连通子网的节点数为m, 则算法1的时间复杂度为m × 2n. 由后面3.4节的实际计算结果可知, m近似为n/2, 所以算法1的时间复杂度为O(n²).
算法2在算法1的基础上引入了集合运算, 两者的区别在于: 算法1每遍历一次Graph可以找出一个节点的邻居节点; 算法2每遍历一次Graph可以找出一层节点的全部邻居节点, 只要将函数GetNeighbor的参数由Node改为NodeSet即可. 该函数遍历Graph中的边信息, 判断边端点是否在集合NodeSet中. 由于GetNeighbor(Node, Graph)的时间复杂度为2n, 由3.4节的实验可知GetNeighbor(NodeSet, Graph)的平均运算时间约为算法1中GetNeighbor(Node, Graph)运行时间的1.6倍, 所以GetNeighbor(NodeSet, Graph)的时间复杂度为1.6 × 2n = 3.2n. 由算法2可知, 对最大子网的每一子网层需调用一次GetNeighbor(NodeSet, Graph), 设构建最大连通子网过程中, 子网层数为nl, 则运行GetNeighbor(NodeSet, Graph)的次数为nl次, 所以算法2的时间复杂度为nl × 3.2n. 通过3.4节的最大子网抽取实验发现, nl的实际值为12, 由于nl远小于n(33377320), 所以算法2的时间复杂度近似为O(n).
2 -->

3.4.最大子网抽取实验与对比

分别采用NetwrokX和算法1(SNEBF)、算法2(SNESO)对所构建的概念图谱网络进行了最大连通子网的抽取实验, 具体的实验环境为64位Win7系统, 16 GB内存, Anacodna集成Python开发环境, 其时间复杂度和实际运算时间见表2.

Algorithm	Parameters			Time complexity	Time cost
NetworkX	—	—		—	15 d以上
SNEBF	m = 15 114 834	n = 33 377 320		m × 2n = 15 114 834 × 2n	约5.22 a
SNESO	nl = 12	n = 33 377 320		nl × 3.2n = 19.2 × 2n	3.49 min (实际运算3.80 min)

表2最大子网提取算法时间复杂度对比表
Table2.Time complexity of the subset extraction algorithms.

其中采用NetworkX以及SNEBF求解最大子网时程序并未运行出结果, 在实际运行时间为15 d时终止了这两个程序, 由此可以得出NetworkX构建最大子网时间大于15 d的结论. 实验过程中SNEBF中的GetNeighbor (Node, Graph)运算时间约为10.9 s, SNESO中的GetNeighbor (NodeSet, Graph)的平均运算时间为17.6 s, 约为GetNeighbor (Node, Graph)的1.6倍. 因为SNEBF的时间复杂度为(m × 2n), 而2n, 即GetNeighbor(Node, Graph)的平均运行时间为10.9 s, 所以可以推算出SNEBF的运行时间约为m × 2n = 15114834 × 10.9 s = 5.22 a. 由GetNeighbor(NodeSet, Graph)的平均计算时间和nl = 12, 得到SNESO的运行时间为3.49 min, 而该算法的实际运行时间为3.80 min. 所以, SNESO时间复杂度最小, 计算速度最快, 运算时间在可接受范围内, 远小于SNEBF的运行时间.
使用NetworkX抽取最大子网, 首先通过其内部函数connected_component_subgraphs(Graph)求解所有子网^[33], 再从中找到节点数量最多的子网, 即为最大连通子网. connected_component_subgraphs(Graph)的输入是一个无向NetworkX图G, 输出是G的所有连通子网的列表. 该函数是一个由两行代码构成的for循环:
for c in connected_components(G):
　　yield G.subgraph(c).copy()
其中connected_components(G)返回各个连通子网的全部节点c的列表, G.subgraph(c).copy()将节点列表c转换成图G的一个连通子图. 以下是connected_components(G)的定义:
①seen={};
② for v in G: /*对G中的每个节点v*/
　③ if v not in seen: /*如果没有遍历过节点v*/
　　④ c = sp_length(G, v); /*计算点v到所有可以连通节点的距离字典c*/
　　⑤ yield list(c); /*将获得的c转换为列表返回*/
　　⑥ seen.update(c);/*更新seen的值以确保不会寻找重复节点*/
　⑦ end if
⑧ end for;
NetworkX求解最大子网的关键操作是sp_length(G, v)函数, 具体的时间复杂度分析在第4节中采用事后统计法给出.
表3列出了NetworkX与算法2运行时的实际内存消耗. 实验中NetworkX抽取概念图谱最大连通子网至少需要40 GB内存. 采用SNESO求解最大子网时, 占用内存的变量为SubNet_i, NeighborsSet, MaxSubNet, 数值与最大子网的节点数、子网某层的节点数相关, 实际占用内存为5.23 GB.

Algorithm	Parameters	Space complexity	Memory cost
NetworkX	—	—	40 GB
ESNSO	SubNeti, NeighborsSet, MaxSubNet	31724479	5.23 GB

表3算法空间复杂度和实际内存消耗对比表
Table3.Space complexity of the algorithms.

由算法2根据概念图谱的数据文件生成的最大子网包含15114834个节点和32274081条边, 分别占整个概念图谱网络节点和边的89.24%和96.69%. 可知该子网覆盖了概念图谱网络绝大部分的节点与边, 其网络特性可以较好地反映出整个网络的特征, 后续对概念图谱复杂网络特性的分析都基于此最大连通子网.

复杂网络的统计特征主要包括度分布、k-shell核心性、平均路径、聚类系数和度相关性等.
1) 度分布p(k): 度分布可以用来表征网络最基本的拓扑特性. 图4是最大连通子网的节点累积度分布, 节点度呈幂律分布, 符合无标度网络特性.
图 4 概念图谱最大连通子网累积度分布
Figure4. Cumulative degree distribution of the largest connected subnet.

表4统计了三类节点中度值为1—13的节点数量与比例: 82%的实例节点度值为1, 即82%的实例只与一个概念相关. 度值为1的节点, 实例占85.5%, 概念占14.5%. 由此判断在自然语言处理过程中使用实例词比使用概念词更不易因一词多义而引起文本描述的歧义. 82%的概念度值在1—3之间, 表明绝多数概念只有1—3个含义. 在度值相同的节点中, 子概念的比例随度值的增大而增加, 表明子概念通常作为连接多个节点的核心节点.

k	Concept			Instance			SubConcept			Total
	Quantity	Percentage		Quantity	Percentage		Quantity	Percentage		Quantity
1	1468308	40.3		8636049	82.0		0	0.0		10104357
2	1014641	27.9		968156	9.2		138875	14.8		2121672
3	503109	13.8		309716	2.9		185665	19.8		998490
4	242308	6.7		156248	1.5		125045	13.3		523601
5	127833	3.5		96027	0.9		78311	8.3		302171
6	73429	2.0		64778	0.6		52090	5.6		190297
7	45834	1.3		46398	0.4		37604	4.0		129836
8	31237	0.9		34799	0.3		29301	3.1		95337
9	22401	0.6		27173	0.3		23417	2.5		72991
10	16439	0.5		21925	0.2		19488	2.1		57852
11	12880	0.4		18095	0.2		16464	1.8		47439
12	9981	0.3		14934	0.1		14187	1.5		39102
13	8169	0.2		12688	0.1		12503	1.3		33360
$\vdots$	$\vdots$	$\vdots$		$\vdots$	$\vdots$		$\vdots$	$\vdots$		$\vdots$
Total	3639631	···		10536663	···		938540	···		15114838

表4概念图谱最大子网度分布分析
Table4.Degree distribution analysis of the largest connected subnet.

2) k-shell核心性: 思想是处于网络核心位置的节点, 即使度很小, 对网络的影响力也可以很大. k-shell分解把网络由边缘至中心划分成若干层, 能够有效识别网络核心.
概念图谱最大子网经k-shell分解为185层, 图5是各层节点的度分布及平均度值, 可见节点度越大其k-shell分层越高, 越靠近中心层, 说明大度值节点位于靠近概念图谱网络中心的位置, 而不是边缘位置. 如图5所示, 度高于10000的节点大都划分到了核心层, 只有极少数k-shell值很低. 我们发现这些节点的多数邻居节点的度很低. 如划分到13-shell层的节点“common search term”和“connected tool”的度高达102033和31963, 但这两个节点的邻居节点中度为1的分别多达101892个和31942个.
图 5 节点度与k-shell分解中心性关系
Figure5. Relationship between degree and k-shell.

核心层(185-shell)包括786个节点, 其中子概念782个, 概念和实例各2个. 核心层节点间有119162条边, 构成了一个稠密图, 网络密度0.386, 远高于最大子网的2.825 × 10^–7. 表5是核心层中度值最高的20个节点及其度值.

node	k		node	k
factor	364343		Event	113364
feature	204130		company	110609
issue	202331		program	93963
product	174283		technique	92341
item	159164		application	90644
area	144595		organization	90605
topic	137781		Name	87637
service	137398		Case	85863
activity	124670		method	84157
information	114500		project	82122

表5核心层中度值最高的20个节点
Table5.Top 20 nodes with the highest degree in core.

虽然子概念只占最大子网节点的6.2%, 却占核心层的99.5%. 说明子概念在概念图谱中起着重要的连接作用. 其根源在于子概念既可以作为比其描述能力抽象的词的实例, 也可以作为比其描述具体的词的概念, 如topic作为概念时包括cultural, political, physica等实例, 这些实例都可以说是某一种具体的topic (话题), 都与topic具有IsA关系. 作为实例时, topic又是多个概念的实例, 如concept, document, information等.
3) 平均路径: 网络的平均路径avg(l)是所有节点对之间距离的平均值, 它描述了网络中节点间的分离程度. 目前最快的串行最短路径算法只能将计算的时间复杂度降到O(n^2.376)^[19]. 概念图谱网络的节点数为15114834, 要精确计算平均最短路径, 需要计算114229095866361个节点对之间的最短路径, 计算量巨大; 同时计算过程中每条路径上需要存储多个节点信息, 存储消耗也很大.
首先尝试用NetworkX计算最大子网的avg(l), 运行了30 d没有输出结果. 为了探究其时间复杂度, 需要对较小规模的概念图谱网络进行计算. 为此将共现次数作为阈值限制边的数量从而形成不同较小规模的网络, 如表6所列. 其中t为阈值, n为节点数, e为边数.

t	n	e		t	n	e		t	n	e		t	n	e
10	415491	936536		60	27654	66704		150	9492	19845		600	1788	2637
20	119367	303323		70	23089	54533		200	6850	13315		700	1453	2059
30	66272	169774		80	19567	45510		300	4336	7566		800	1076	1487
40	45410	114629		90	17042	38921		400	3013	4920		900	922	1222
50	34467	85085		100	15086	33983		500	2318	3577		1000	770	994

表6部分阈值网络及节点数
Table6.Threshold networks and the number of nodes.

图6展示了NetworkX计算表6中各网络平均路径的实际运算时间time(s)与网络规模(节点数n), 经过拟合可知存在函数关系: time(n) = 5.121 × 10^–7 × n^2.236. 当t = 10时, NetworkX实际运行了1868428.416 s, 约22 d. 将最大子网节点数代入该函数可知NetworkX需要计算184 a, 这也是计算30 d没有输出结果的原因.
图 6 NetworkX计算平均路径所需时间
Figure6. Time cost of NetworkX for avg(l).

随后, 尝试用唐晋韬等^[32]提出的CDZ方法进行计算. 该方法首先根据局部中心性寻找区域中心点并据此对网络进行区域划分; 之后用区域中心点的距离表示区域间节点的路径长度, 此时节点间路径近似等于区域中心点的路径与区域内路径的和. 其时间复杂函数为O(nlogn + e + d³), n是节点数, e是边数, d是中心点数量^[32]. 相对于随机网络, CDZ更适合具有无标度特征的复杂网络. CDZ计算无标度网络Cora平均路径的时间为20余秒. Cora的n = 30751, e = 134450, 按照文献所述方法计算得到的d为46, 因此时间复杂度函数值为369792. 对于概念图谱最大子网而言, n = 15114834, e = 32274081, d = 130109, 因此时间复杂度函数值为2202531075674600, 是Cora的5956132434倍. 按照CDZ计算Cora平均路径用时为20 s计算, CDZ计算概念图谱的最大子网平均路径需要3777 a.
为此我们提出了一种概念图谱网络最短路径长度的近似计算方法, 该算法区别于CDZ的是用网络层代替区域, 且忽略同层内节点的具体距离. 根据图3所示的最大连通子网的层次结构, 用层与层之间的距离近似代替点与点之间的距离, 计算网络的近似平均最短路径长度:

${\rm{AppAvg}}\left( l \right) = \frac{{{\rm{minavg}}\left( l \right) + {\rm{maxavg}}\left( l \right)}}{2}, $

其中AppAvg(l)表示网络的近似平均最短路径长度, minavg(l)表示可能存在的近似平均最短路径长度的最小值, maxavg(l)表示可能存在的近似平均路径长度的最大值.

${\rm{minavg}}\left( l \right) = \frac{{\mathop \sum \nolimits_{i = 1}^n \mathop \sum \nolimits_{j = i + 1}^n ({l_{{\rm{min}}\_ij}})}}{{n \times \left( {n - 1} \right)/2}}, $

${\rm{maxavg}}\left( l \right) = \frac{{\mathop \sum \nolimits_{i = 1}^n \mathop \sum \nolimits_{j = i + 1}^n ({l_{{\rm{max}}\_ij}})}}{{n \times \left( {n - 1} \right)/2}}, $

其中l_{min_ij}表示节点i到节点j可能的最小路径长度, l_{max_ij}表示节点i到节点j可能的最大路径长度.
由于网络的层级关系, 节点i到节点j之间必定存在一条路径为(节点i, 中心节点, 节点j), 此路径为可能存在的最大的近似路径, 其距离公式为

$\min \left( {{l_{ij}}} \right) \leqslant {l} = {l_{i{\rm{Center}}}} + {l_{{\rm{Center}}j}}, $

其中l_iCenter和l_Centerj分别表示节点i到中心节点(Center)的距离和Center到节点j的路径长度. 根据对称性, 节点i到节点j与节点j到节点i的路径长度相同.

${l_{{\rm{Center}}i}} = {l_{i{\rm{Center}}}} = {\rm{floor}}\left( i \right) - 1 + 1 = {\rm{floor}}\left( i \right), $

其中floor(i)表示节点i所在的层数. 由于中心层包括两个节点, 所以在计算时统一为节点所在的层数减去1再加1. 减1表示节点所在层数到中心层的路径长度, 加1表示中心层两个节点之间的路径长度.
表7为经过算法2的运行结果后统计的网络层数及各层包含的节点数量. 根据(4), (5)式以及表7计算得到子网中各节点之间的最大距离的和为770350922065817, 代入(3)式maxavg(l) = 6.74.

Layer	Quantity		Layer	Quantity		Layer	Quantity		Layer	Quantity
1	2		4	4639826		7	11921		10	73
2	553406		5	639119		8	1609		11	16
3	9202185		6	66347		9	327		12	3

表7子网结构与节点数量
Table7.Subnet structure and quantity of nodes.

假设每层节点到其他各层节点的最短距离为层数相减的绝对值, 此时, 节点对之间的路径长度最短, 有

${l_{{\rm{min}}\_ij}} = \left| {{\rm{floor}}\left( i \right) - {\rm{floor}}\left( j \right){\rm{}}} \right| \leqslant \min \left( {{l_{ij}}} \right).$

根据(6)式及表7中的数据可以求得子网节点间最小距离的和为125617583016439, 将其代入(2)式可知最小近似平均最短路径长度minavg(l)为1.10. 所以子网的实际平均最短路径长度处于(1.10, 6.74)的开区间内, 根据(1)式可计算得到网络的近似平均最短路径长度为3.92, 表明知识图谱网络中的实体平均经过3.92个实体就可以到达任意实体的位置, 概念图谱网络具有小世界的特性. 相对于逐条匹配而言, 以基于网状拓扑结构进行的知识搜索更为迅速.
图7是由NetworkX和本文方法计算的不同规模网络的实际平均路径RealAvg(l)和近似平均路径AppAvg(l), n为节点数量. AppAvg(l)与RealAvg(l)变化趋势相同, 且随网络规模增加而减小, 并稳定在一个4左右的定值. 我们计算了各规模网络平均路径的真实值与近似值比值的平均值, 有RealAvg(l) ≈ 1.1 × AppAvg(l).
图 7 平均路径精确值、近似值与节点数的关系
Figure7. Relationships of RealAvg(l) and AppAvg(l) to n.

根据随机网络平均最短路径长度的估算公式计算相同规模随机网络的平均最短路径为L_random ～ ln(N)/ln(k) = 11.38, 其中N是最大子网的节点数, k = 4.274是节点的平均度值, 根据互联网平均最短路径长度^[16]公式, 可以计算得$\left\langle i \right\rangle$～0.35 + 2.06 × lgN = 15.14, 可知概念图谱网络的节点间的联系比同等规模的随机网络和万维网节点间的联系更紧密. 此外, 不同于互联网平均最短路径随网络规模的增大而增大, 概念图谱网络的平均路径随网络规模的增大反而减小, 并最终趋近于一个4左右的定值. 这一现象可能与概念图谱的结构有关, 为解释此现象, 对由算法2计算各阈值网络最大子网时得到的网络层次结构进行了统计. 表8是各阈值网络由中心层扩展时形成的层次结构及各层包含的节点数.

Layer	t = 10	t = 20	t = 30	t = 50	t = 100	t = 200	t = 300	t = 500	t = 1000
1	2	2	2	2	2	2	2	2	2
2	26993	10212	6226	3409	1534	748	456	258	88
3	223659	65471	34244	16456	6445	2437	1305	558	103
4	131967	36095	21646	12077	5712	2829	1722	832	205
5	28219	6590	3563	2037	1116	656	661	438	108
6	3745	821	505	418	206	129	157	187	128
7	766	143	74	55	62	41	30	29	89
8	98	25	12	11	7	4	3	13	29
9	27	6	—	2	2	3	—	1	13
10	12	2	—	—	—	1	—	—	5
11	3	—	—	—	—	—	—	—	—

表8不同阈值网络的层次结构及各层的节点数
Table8.Layer structure and node number in each layer.

从表8可以看出, 这些阈值网络与概念图谱最大子网在结构上十分相似, 都形成了类似“菱形”结构: 大量节点集中在中间靠前的网络层, 少量节点处于两端的“边缘”层. 随着网络规模的增加, 大量的节点更是集中在了前4层, 表明大部分节点间经由中心层节点经过不超过4步就可到达彼此, 可以一定程度地解释概念图谱网络平均最短路径随着网络规模增加而趋近于4左右这个定值的原因. 概念图谱反映的是知识间的联系, 可以将其看作人拥有的知识. 通常一个人掌握的知识越多, 其由一个知识推理或搜索到另外一个知识的速度也就越快.
4) 聚类系数: 聚类系数C是所有节点聚类系数的平均值, 描述网络中节点的聚集情况, 即网络紧密性.
对于度为1的节点, 计算其聚类系数没有实际意义, 为此在计算网络的聚类系数前首先要剔除度值为1的节点. 在剔除度为1的节点后, 最大子网还有5010477个节点. 由于我们只有记录最大子网边信息的三元组的文本文件GraphLink, 如果对每个节点直接计算其聚类系数, 首先需要遍历最大子网边集合GraphLink得到该节点的邻居节点集合, 为此需调用3.3节中的GetNeighbor(Node, Graph)函数, 并将参数Graph替换为GraphLink; 之后再次遍历GraphLink得到邻居节点集合中存在的边的数量, 为此需再次调用GetNeighbor(Node, Graph), 此处也应将Graph替换为GraphLink. 参照3.4节中时间复杂度的分析, 可知计算一个节点聚类系数的时间复杂度为以上两个函数的时间复杂度之和, 即2n + 3.2n = 5.2n, 此处的n为GraphLink包含的边数(32274033). 由于需要计算聚类系数的节点数量为5010477, 约为边数的1/6, 所以计算网络的聚类系数的时间复杂度为5.2n × n × 1/6 ≈ 0.867n², 时间复杂度仍较高, 所以我们采用分段式计算方法.
Node_ki表示度值为k_i的节点的集合. 根据度分布可知, 度值越小, 对应的节点数量越大, 设定阈值θ = 100.
对于度值大于θ的节点的集合Node_ki(ki = θ+1, θ+2, ···, k_max, 其中k_max表示节点的最大度值): 先根据最大连通子网的边集合GraphLink寻找到每个节点Node_j∈Node_ki的邻居节点的集合Neighbor_j^ki然后遍历GraphLink中的每一条边, 对Node_ki中的每个Node_j, 判断该边的两个端点是否都属于Neighbor_j^ki, 若是, 则表示该边是连接Node_j的两个邻居节点的边. 度值为k_i的各个节点的邻居节点间的边数构成边数集合Edge_ki, 其存储形式为k-value形式, 如Edge_ki = {{Node₁:edge₁}, {Node₂:edge₂}, ···, {Node_j:edge_j}}, 其中edge_j为节点Node_j的邻居节点间的边数. 节点Node_j的聚类系数计算公式如下:

${C_{{\rm{Node}}}}_j = \frac{{{\rm{Edg}}{{\rm{e}}_{ki}}\left( {{\rm{Nod}}{{\rm{e}}_j}} \right)}}{{{k_i}\left( {{k_i} - 1} \right)}}, $

其中Edge_ki(Node_j)表示Edge_ki中与Node_j对应的edge_j.
对于度值小于等于θ的节点集合Node_ki(ki = 1, 2, ···, θ): 首先同上得到与度值k_i对应的Node_ki及Neighbor_j^ki(j = 1, 2, ···, length(Node_ki)), 其中length(Node_ki)表示Node_ki中节点的数量; 然后根据(Node_ki∪Neighbor_j^ki, j = 1, 2, ···, length(Node_ki))从GraphLink中筛选与这些节点相关的边, 组成部分边集合PartOfGraph_ki; 再对PartOfGraph_ki中的每一条边, 对Node_ki的每个Node_j, 判断边的两个端点是否属于Neighbor_j^ki, 若是, 则表示该边是连接Node_j的两个邻居节点间的边. 得到度值k_i对应的Node_ki中各个节点Node_j的邻居节点间的边数构成集合Edge_ki, 然后根据(7)式计算该集合中每个节点的聚类系数.
由于度值越小, 节点数量越多, 聚类系数就越难计算. 在实验中, 度值在2—10范围内的节点数占所有可计算聚类系数节点的89.66%, 所以我们在度值小于阈值时引入Map/Reduce模式, 将大型计算任务分解为多个小计算量任务, 然后同时进行计算. 对于度值相同的节点统一计算其聚类系数, 在计算时分别计算分子, 分母只需要计算一次(分母是相同的). 并且, 此种计算模式在分析度-平均聚类系数时也十分方便.
最大连通子网中聚类系数不为0的节点为1837431个, 占12.16%, 由全部节点聚类系数计算得到的网络聚类系数为0.0468; 剔除度值为1的节点后计算得到的网络聚类系数为0.1410. 为了判断网络的小世界特性, 计算了相同规模(节点数量和平均度相同)的随机网络的聚类系数C_random～ k/N = 2.83 × 10^–7, 其中N = 15114834为节点数, k = 4.274是网络的平均度值^[3]. 显然概念图谱网络的聚类系数远大于C_random, 可知概念图谱网络中节点聚群现象比较明显. 图8是度值与平均聚类系数的关系, 可知低度值节点的聚类系数较大, 高度值节点的聚类系数普遍较小.
图 8 度值对应的平均聚类系数分布
Figure8. Average clustering coefficient distribution corresponding to degree.

5) 度相关性: 度相关性描述的是节点之间根据度值作为相互之间连接的选择偏好性, 如度值为k的节点的邻点平均度k_nn(k)随k增加, 表示度大的节点偏好连接其他度大的节点, 则网络是正相关的; 反之, 如果k_nn(k)随k而减小, 表示度大的节点偏好连接度小的节点, 则网络是负相关的.
表9列出了部分度值和该度值对应的所有节点的邻点平均度, 可知值最低的5个度其所有节点的邻点平均度非常大, 而值最高的5个度其所有节点的邻点平均度相对而言却非常小.

k	Nk	knn(k)		k	Nk	knn(k)
1	10104357	31235.02		159164	1(item)	122.577
2	2121672	13384.27		174283	1(product)	98.812
3	998490	10435.94		202331	1(issue)	91.266
4	523601	10231.12		204130	1(feature)	85.926
5	302171	10388.98		364343	1(factor)	56.088
$\vdots$	$\vdots$	$\vdots$		$\vdots$	$\vdots$	$\vdots$

表9部分度的节点数与该度值的所有节点的邻点平均度
Table9.Part of N_k and k_nn(k).

将度值k和与度为k的所有节点的邻点平均度k_nn的关系绘制成图9, 可以看出, k_nn随着k的增大而减小, 呈现负相关性, 表明概念图谱网中与高度值节点相连接的节点的度值偏低, 与低度值节点相连接的节点的度值偏高.
图 9 度-邻点平均度相关性分析
Figure9. Analysis of degree and average degree of neighbor nodes.

Newman^[34]还给出了一种通过网络节点度的Pearson相关系数r来判断网络相关性的量化方法, 具体公式如下:

$r = \frac{{{M^{ - 1}}\mathop \sum \nolimits_i {j_i}{k_i} - {{\left[ {{M^{ - 1}}\mathop \sum \nolimits_i \frac{1}{2}\left( {{j_i} + {k_i}} \right)} \right]}^2}}}{{{M^{ - 1}}\mathop \sum \nolimits_i \frac{1}{2}\left( {j_i^2 + k_i^2} \right) - {{\left[ {{M^{ - 1}}\mathop \sum \nolimits_i \frac{1}{2}\left( {{j_i} + {k_i}} \right)} \right]}^2}}}, $

其中M表示网络的边数, j_i和k_i分别是第i条边$(i=1,2,\cdots,M)$的两个端点的度值, r (–1 $\leqslant $r $\leqslant $ 1)表示网络相关性. 经计算可知概念图谱最大连通子网的相关性为–0.067, 网络是负相关的, 与度值的邻点平均度分析结论相同. 同时, 网络的负相关性也保证了低度值节点可以与高度值节点相连, 由于高度值节点可以连接到很多其他节点, 所以在应用中可以实现推理过程.
6) 知识丢失对概念图谱完整性的影响: 用节点删除模拟知识丢失, 通过随机删除和定向删除(度值由高到低)分别测试了不同阈值下较小规模概念图谱网络的完整性. 图10(a)是阈值为500的实验结果, x轴是节点删除比, y轴是最大子网节点比例S, 能够一定程度上描述概念图谱的完整性. 随机删除对S影响很小, 删除80%以上的节点时S才接近0; 定向删除对S影响显著, 仅减少0.5%左右的节点时S就减少到了0. 定向删除下S的下降规律与computer network十分相似, 快于同是无尺度网的BA网和科学合作网^[35].
图 10 知识丢失对概念图谱完整性的影响
Figure10. Size of the giant component when nodes are removed.

还测试了概念、实例、子概念丢失对概念图谱完整性的影响, 图10(b)是随机删除1—140个三类节点时S的变化, 可见子概念的丢失对图谱完整性影响最大, 其次是概念, 最后是实例. 为了分析以上现象, 由度分布计算了各类节点的度期望值: 概念节点的度期望为2.911, 实例为1.899, 子概念为36.214. 也就是说随机删除1个概念同时丢失约3条边(知识之间的联系); 随机删除1个实例同时丢失不到2条边, 随机删除1个子概念, 平均会减少约36条边, 因此子概念的丢失对网络完整性影响最大.
概念图谱来源于数亿用户的搜索记录, 是反映人类对事物认知的知识库. 尽管每个人拥有的知识只是其中的一部分, 但却有类似的结构特征. 即最具体的实例对于掌握知识而言重要性最低, 而抽象的概念或子概念更重要. 现实世界中, 若忘记了某个实例, 比如忘记了3是prime number (素数), 只要掌握了prime number的概念, 就可以推断出3是prime number. 但如果忘记的是概念或者子概念, 如prime number, 由3推理出prime number或其他素数就非常困难.

本文运用复杂网络理论对由微软概念图谱所构建的概念图谱网络进行了分析. 由于概念图谱网络中包含多个子网结构, 提出了一种适合概念图谱的最大子网抽取算法, 实验表明对于节点数量庞大的概念图谱网络, 该算法在时间和空间上都优于NetworkX. 在进行节点度分布分析时不但发现最大连通子网具有无标度特性, 还发现子概念在概念图谱中扮演着连接其他节点的角色. 82%的实例节点只与一个概念存在IsA关联, 向我们揭示了实例词在文本分析中通常不会因为一词多义的原因导致理解上的歧义. 为解决网络规模巨大导致的计算困难, 提出了一种近似网络平均距离的计算方法, 对比NetworkX和CDZ具有明显优势. 分析表明概念图谱网络具有小世界特性, 平均路径随网络规模增加而减小并趋于定值4; 概念图谱网络的“菱形”结构揭示了平均路径趋于定值4的根源; 平均路径随网络规模增加而减小这一现象与人类认知和推理能力随知识增加而提升这一现象一致. 网络聚类系数较大, 网络中节点的群聚现象较为明显. 根据度相关性的分析, 可知网络中与高度值节点相连接的节点的度值偏低, 与低度值节点相连接的节点的度值偏高, 度-平均度呈现负相关, 有利于实现概念图谱中的知识推理; 概念图谱完整性对知识的随机缺失不敏感且子概念对概念图谱完整性的影响明显高于概念和实例.
考虑到概念图谱的海量数据, 以上对全网特性的分析都没有考虑关系的方向和关系的紧密程度(边的长度), 在以后的工作中可以将关系的方向和边长引入概念图谱网络模型的构建中, 在此基础上利用局部拓扑特性进行概念图谱的自动补全研究.