摘要:高聚物粘结炸药(PBX)的热力学性质是用于炸药结构响应、安全性评估、数值模拟分析等的重要参数. 由于PBX结构的多尺度特性, 完全采取实验方法精细表征这些参数存在巨大的挑战. 本文运用第一性原理和分子动力学计算的方法, 系统研究了三氨基三硝基苯(TATB)基高聚物粘结炸药的热力学参数和界面热传导性质. 利用散射失配模型研究了TATB与聚偏二氟乙烯(PVDF)界面的热传导过程, 发现热导率随温度升高而上升, 并且在高温情况下接近于定值. 基于分子动力学获得的TATB热导率并结合界面热导率, 分析了PBX炸药的热导与颗粒尺寸的关系, 当颗粒尺寸大于100 nm时, 界面热阻对于PBX热导率的影响有限.
关键词: 三氨基三硝基苯/
第一性原理计算/
分子动力学/
热力学参数

English Abstract

全文HTML

--> --> -->

高聚物粘结炸药(PBX)是一类在武器行业有着重要应用的颗粒复合含能材料, 具有机械感度低、加工性能良好、力学性能优异等特点, 在现代高性能战斗部系统中得到广泛应用^[1,2]. 在PBX炸药中, 以三氨基三硝基苯(TATB)为基的PBX在武器中有着广泛的应用前景. TATB的机械感度和热感度相比于其他含能材料有着明显的优势, 而且其熔点高, 耐热性能好, 具有非线性光学性质^[3-5], 是唯一通过美国能源部钝感高能炸药11项安全鉴定的高能炸药. 美国已率先将TATB基PBX用于核战斗部, 从而显著提高了核战斗部的安全性. 在武器服役的过程中, 外界复杂的力-热环境, 不仅要求PBX部件具有良好的结构完整性, 还要具备较强的环境适应性, 因此对PBX的力学性能提出了设计要求^[6]. 另一方面, 在复杂的热-力环境作用下, 热传导及由于热作用引起的内应力都可能导致PBX产生内部损伤, 严重的可能导致结构破坏. 但是由于PBX炸药是一类高聚物混合材料, 主要由高能单质炸药、高聚物黏结剂和相关添加剂组成, 在界面包覆处不可避免地存在缺陷, 这些缺陷的存在不仅使界面成为制约PBX热传导的重要因素, 而且这些PBX内部缺陷在受外部刺激时易产生热点, 还会带来严重的安全性问题^[7,8]. 因此对高聚物粘结炸药的热力学性质, 尤其是炸药界面热传导的理论研究, 对于炸药感度的理解和PBX的设计都有着重要意义.
国内外仅有少数研究团队开展了含能材料热力学性质的理论计算研究, 且多集中于单质含能材料. Gee等^[9]和Bedrov等^[10]分别开发了针对TATB分子动力学(MD)计算的力场参数; Stevens等^[11]和Rykounov^[12]研究了TATB的状态方程; Kroonblawd和Sewell^[13,14]利用分子动力学方法系统研究了TATB的各向异性热导; Fan等^[15]采用德拜声子理论方法研究了TATB热导与压力和温度的关系; 蒋文灿等^[16]、Wu等^[17]和Liu等^[18]也基于第一性原理方法研究了TATB的声子振动模式. 目前, 单质TATB的状态方程、热容、热膨胀、热导率等性质目前已较为完善, 但是关于PBX等复合含能材料的热导率、界面热阻的研究则鲜有报道. Long和Chen^[19]利用分子动力学方法最早研究了奥克托今(HMX)基PBX的界面热导率. 该方法基于线性响应理论和德拜声子理论, 认为声子在界面处的散射率等同于弹性波的散射率, 以此得到了HMX和氟聚物(F2312, F2313), TATB等界面处波的散射率. 界面热导在低频区正比于振动频率的平方, 在高频区因分子振动模的耦合而变得无规律. Long和Chen^[20]采用第一性原理方法, 通过计算TATB和石墨的声子谱, 得到TATB和石墨界面的声子折射率和界面热导率, 并界定出五个主导TATB/石墨界面热导率的入射声子模. 总体来看, 目前针对含能材料的热力学性质的理论计算研究已有初步进展, 开展了部分含能材料的声子谱研究, 这对于今后从晶格动力学角度开展热导率计算有着很好的助益.
含能材料的热力学理论计算主要有第一性原理和分子动力学计算两种途径. 但是, 受制于含能材料结构的复杂性, 目前用于炸药分子的力场参数的可靠性尚未得到有效检验. 第一性原理计算是目前能准确针对复杂体系含能材料进行声子研究的有效方法, 但需要注意的是该方法仍在计算能力方面存在着一定的制约. 本文对于TATB和PVDF的声子色散问题将采用第一性原理计算方法进行. 而在热传导问题上, 分子动力学方法通过牛顿力学方程描述体系中原子的相互作用, 相较于第一性原理的计算更为简单和直观, 且计算的结果与实验符合较好. 本文用分子动力学方法进行在TATB热导率的计算. 第一性原理和分子动力学方法可以从微观尺度上解释其结构与性能之间的关系. 这不仅有助于含能材料的配方设计, 还可缩短研制周期并提高研制过程中的安全性.
本文的研究基于晶格动力学理论^[21], 结合第一性原理计算和分子动力学方法系统探讨了TATB基PBX炸药的热力学性质. 首先采用冻声子法计算得到TATB和PVDF的声子色散曲线和热容等热力学性质; 根据散射错配模型, 详细讨论了TATB与高聚物界面的声子透射率和界面热导随温度的变化情况; 最后, 结合平衡分子动力学获得的热导率数据, 对TATB基PBX炸药的热导率做了简要分析. 研究结果为PBX混合炸药的热力学参数研究方法的构建, 以及对理解PBX中热传导的本质可以提供理论上的解释.

2

-->

2.1.第一性原理计算模型

第一性原理计算的TATB和PVDF结构见图1. 其中TATB(C₆H₆N₆O₆)晶体属三斜晶系, 单胞中包含两个TATB分子, 共48个原子. TATB分子的构型与石墨层状结构类似. PVDF是一种高分子聚合物材料, 目前实验已发现α, β, γ, δ四种晶相的九种构型形式^[22,23], 其中β相单胞中有两条全反式分子链, 分子链中相邻的CH₂和CF₂具有相同朝向. 目前针对β相的研究最为广泛, 为便于结果比较, 在此我们选取β相构型为代表构型, 进行本文的声子谱计算和界面热导率研究. 针对上述两种晶体, 构建了2 × 2 × 2的TATB超胞和3 × 3 × 3的PVDF超胞分别用于声子谱的计算.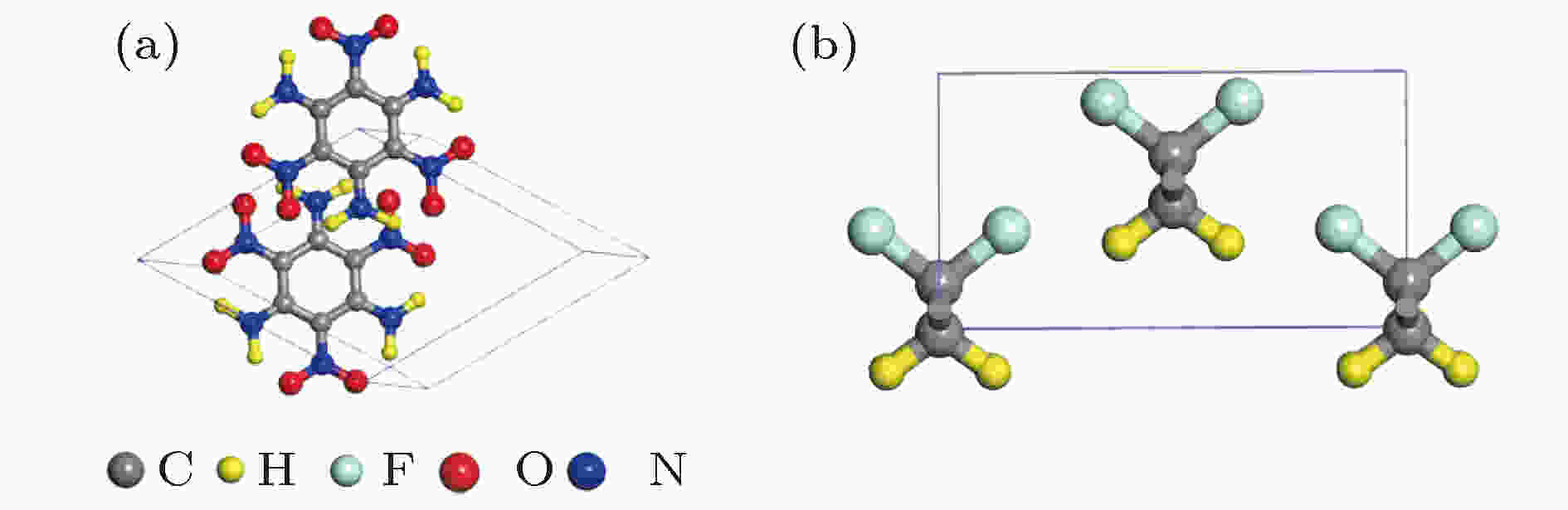
图 1 TATB和PVDF晶体结构图
Figure1. The crystal structure of TATB (a), and PVDF (b).

TATB和PVDF的声子谱由冻声子法^[24]计算得到, 结构优化和力的计算利用VASP^[25]软件进行. 计算中, 我们选取投影缀加平面波(PAW)赝势^[26,27]结合Perdew-Burke-Ernzerhof (PBE)交换关联泛函^[28,29]的方法. 其平面波截断能为550 eV, 能量的收敛标准为10^–6 eV, 结构优化过程中力的收敛标准为10^–4 eV/?, K点的设置为4 × 4 × 4. 二阶力常数和声子谱的处理均通过phonopy^[30]软件进行.
2 -->

2.2.简谐晶格动力学

声子是晶格振动的简正模式的量子化描述, 在晶格的动力学行为和热力学性质中起着重要的作用, 晶体中的声子色散曲线可以依据简谐晶格动力学理论^[31,32]计算. 晶格动力学理论认为, 原子能够在格点附近发生振动. 对于包含N个原子的晶体体系, 其势能函数可以在平衡位置附近展开成泰勒级数的形式:

$\begin{split}\varPhi =\, & {\varPhi _0} + \mathop \sum \nolimits_{l\kappa } \mathop \sum \nolimits_\alpha {{\rm{\varPhi }}_\alpha }\left( {l\kappa } \right){u_\alpha }\left( {l\kappa } \right) \\ &+ \frac{1}{2}\mathop \sum \nolimits_{l{l'}\kappa \kappa '} \mathop \sum \nolimits_{\alpha \beta } {\varPhi _{\alpha \beta }}\left( {l\kappa {\rm{,}}l'\kappa '} \right){u_\alpha }\left( {l\kappa } \right){u_\beta }\left( {l'\kappa '} \right) \\ & +\frac{1}{{3!}}\mathop \sum \nolimits_{l{l'}l''\kappa \kappa '\kappa''} \mathop \sum \nolimits_{\alpha \beta \gamma } {\varPhi _{\alpha \beta \gamma }}\left( {l\kappa ,l'\kappa ',l''\kappa ''} \right) \\ & \times {u_\alpha }\left( {l\kappa } \right){u_\beta }\left( {l'\kappa '} \right){u_\gamma }\left( {l''\kappa ''} \right) + \cdots ,\end{split}$

式中α, β, γ是笛卡尔坐标的三个方向; ${\varPhi _0}$, ${\varPhi _\alpha }\left( {l\kappa } \right)$, ${\varPhi _{\alpha \beta }}\left( {l\kappa ,{l'}\kappa '} \right)$, ${\varPhi _{\alpha \beta \gamma }}\left( {l\kappa ,{l'}\kappa ',{l''}\kappa ''} \right), \cdots $分别对应0阶、一阶、二阶、三阶等力常数. 对于固定体积的晶体体系, 我们对体系内的原子施加一个微小的位移, 原子的振动问题可由二阶项的简谐近似得以解决. 通过构建体系的动力学矩阵${D}\left( {q} \right)$:

${D}_{\kappa \kappa '}^{\alpha \beta }\left( {q} \right) = \mathop \sum \nolimits_{l'} \frac{{{\varPhi _{\alpha \beta }}\left( {0\kappa {\rm{,}}l'\kappa '} \right)}}{{\sqrt {{m_\kappa }{m_{\kappa '}}} }}{{\rm{e}}^{{\rm{i}}{q}\cdot\left[ {{r}\left( {l'\kappa '} \right) - {r}\left( {0\kappa } \right)} \right]}}.$

在动力学矩阵做对角化处理后, 即可得到简谐近似中原子的振动频率.

$\begin{split} &{D}\left( {q} \right){{e}_{{q}j}} = \omega _{{q}j}^2{{e}_{{q}j}}\; \; {\text{或}}\\ &\mathop \sum \nolimits_{\beta \kappa '} {D}_{\kappa \kappa '}^{\alpha \beta }\left( {q} \right)e_{{q}j}^{\beta \kappa '} = \omega _{{q}j}^2e_{{q}j}^{\alpha \kappa }.\end{split}$

2 -->

2.3.界面热传导模型

虽然基于傅里叶定律的传热理论宏观上可以使用, 但界面的研究多涉及微观的原子或分子尺度, 此时界面声子的散射影响加大, 必须从微观角度重新考虑界面传热问题. 首先定义界面处的净热流密度和界面热阻^[33], 其计算公式分别为

${q_{{\rm{net}}}} = {q_{1 \to 2}} - {q_{2 \to 1}},$

${r_{{\rm{int}}}} = {\Delta}T / {q_{{\rm{net}}.}}$

在单位时间、单位面积内物体1通过界面传输到物体2的能量为

$\begin{split}{q_{1 \to 2}}\left( {{T_1}} \right) =\, &\frac{1}{2}\mathop \sum \nolimits_j \mathop \smallint \nolimits_{\theta = 0}^{{\text{π}} / 2} \mathop \smallint \nolimits_{\omega = 0}^{{\omega _d}} {N_1}\left( {\omega ,{T_1},j} \right) \\ &\hbar \omega {c_{1,j}}{a_{1 \to 2}}\left( {\theta ,j,\omega } \right)\sin \left( \theta \right)\cos \left( \theta \right){\rm{d}}\omega {\rm{d}}\theta ,\end{split}$

式中, j为声子模, N₁为物体1的声子密度, ω为声子频率, θ为声子入射角, $\hbar $为约化普朗克常数, ω_d为声子截断频率, ${c_{1,j}}$为物体1中声子模为j的声速, ${a_{1 \to 2}}\left( {\theta ,j,\omega } \right)$为声子透射率. 通过(6)式可以发现, 界面声子透射率${a_{1 \to 2}}\left( {\theta ,j,\omega } \right)$是界面热输运的关键参数. 根据Swartz和Pohl提出的散射失配模型(DMM)^[33], 我们认为所有声子在入射到界面处时发生随机散射, 并且与入射声子的初始状态无关. 声子通过界面的概率与该声子对应的态密度成正比, 且与入射角θ无关. 声子透射率${\alpha _{1 \to 2}}\left( \omega \right)$的计算公式有

${\alpha _{1 \to 2}}\left( \omega \right) = \dfrac{{\displaystyle\sum\nolimits_j {c_{2,j}}{N_{2,j}}\left( {\omega ,T} \right)}}{{\displaystyle\sum\nolimits_{i,j} {c_{i,j}}{N_{i,j}}\left( {\omega ,T} \right){\rm{}}}}{\rm{}},$

${\varGamma _{1,j}} = \mathop \int \nolimits_0^{{\text{π}}/2} {\alpha _{1 \to 2}}\left( \omega \right){\rm{cos}}\theta {\rm{sin}}\theta {\rm{d}}\theta .$

结合(6)式得到界面热导率

$h = \frac{{{\rm{d}}q}}{{{\rm{d}}T}} = \frac{1}{2}\mathop \sum \nolimits_j {c_{1,j}}{\varGamma _{1,j}}\mathop \int \nolimits_0^{{\omega _{\rm{d}}}} \hbar \omega \frac{{{\rm{d}}{N_{1,j}}\left( {\omega ,T} \right)}}{{{\rm{d}}T}}{\rm{d}}\omega .$

目前, DMM模型已在界面热导率的计算上广泛应用, 计算结果也较接近于实验值. 不过需要指出的是DMM模型预测的数值是界面热阻的下限, 其真实数值会根据界面的粗糙程度有不同程度的偏高.
2 -->

2.4.平衡态分子动力学

平衡态分子动力学(EMD)计算热导率的工作, 主要是基于格林-久保公式进行^[34]. 格林-久保公式建立了非平衡过程的输运系数与平衡态中相应物理量的涨落之间的联系. 输运系数等于自相关函数对于时间的积分. 因此热导率的计算公式^[35,36]为

${\kappa _{\mu v}}\left( t \right) = \frac{1}{{{k_{\rm{B}}}{T^2}V}}\mathop \smallint \nolimits_0^t \left\langle {{J_\mu }\left( 0 \right){J_v}\left( {t'} \right)} \right\rangle {\rm{d}}t',$

式中, ${k_{\rm{B}}}$表示玻尔兹曼常数, T和V表示体系温度和体积, ${J_\mu }$表示在μ方向上的热流, t' 表示关联时间.
本文的计算使用由Gee等^[9]提出的TATB全原子力场进行分子动力学计算. 上述力场已在研究中广为应用^[37,38], 其模拟结果与实验匹配较好. 力场详细参数见文献[9]. 我们构建了3 × 4 × 5 的超胞用于分子动力学模拟. 平衡态分子动力学的计算主要利用LAMMPS(large-scale atomic molecular massively parallel simulator)模拟程序包^[39]. 在分子动力学的计算中, 计算时间步长设定为0.5 fs, 力的收敛标准为10^–6 kcal/mol·?. 首先利用分子力学对建立的模型进行构型优化, 确保体系能量最小化. 随后在300 K温度及大气压条件下进行等压等温(NPT)分子动力学模拟, 使体系得到充分的弛豫, 模拟时长为100 ps. 最后使体系在微正则(NVE)系综下继续模拟, 总时长为1000 ps, 关联时长为100 ps.

2

-->

3.1.声子谱计算

声子色散关系是固体的一个重要物理量, 可以反映出晶格振动模式与动量、能量的关系. 声子色散关系中, Γ点处的晶格振动与材料的红外和Raman特性有关. 基于冻声子法, 我们得到了TATB, PVDF的声子色散关系和声子振动模式结果(见图2(a)和图2(b)以及图3(a)和图(b)). TATB晶体的单胞有48个原子, 共有144个振动模式, 其中包含3个声学支和141个光学支.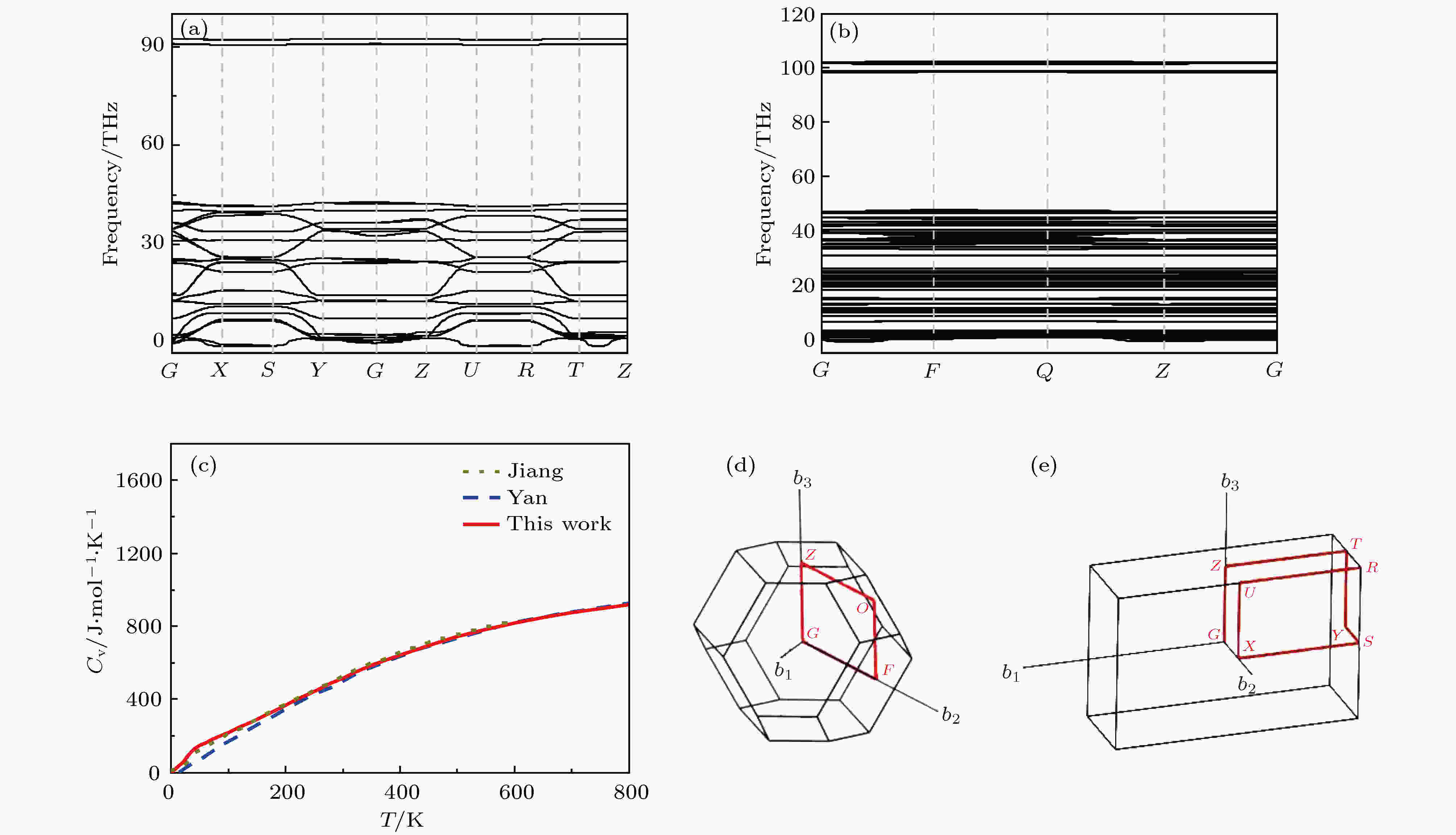
图 2 (a), (b) TATB和PVDF声子色散曲线; (c) TATB晶格热容随温度的变化; (d), (e) TATB和PVDF第一布里渊区高对称点积分路径
Figure2. The phonon dispersion relation of TATB (a), and PVDF (b); (c) the heat capacity of TATB as a function of temperature; the Brillouin zone and high symmetry points of TATB (d), and PVDF (e).

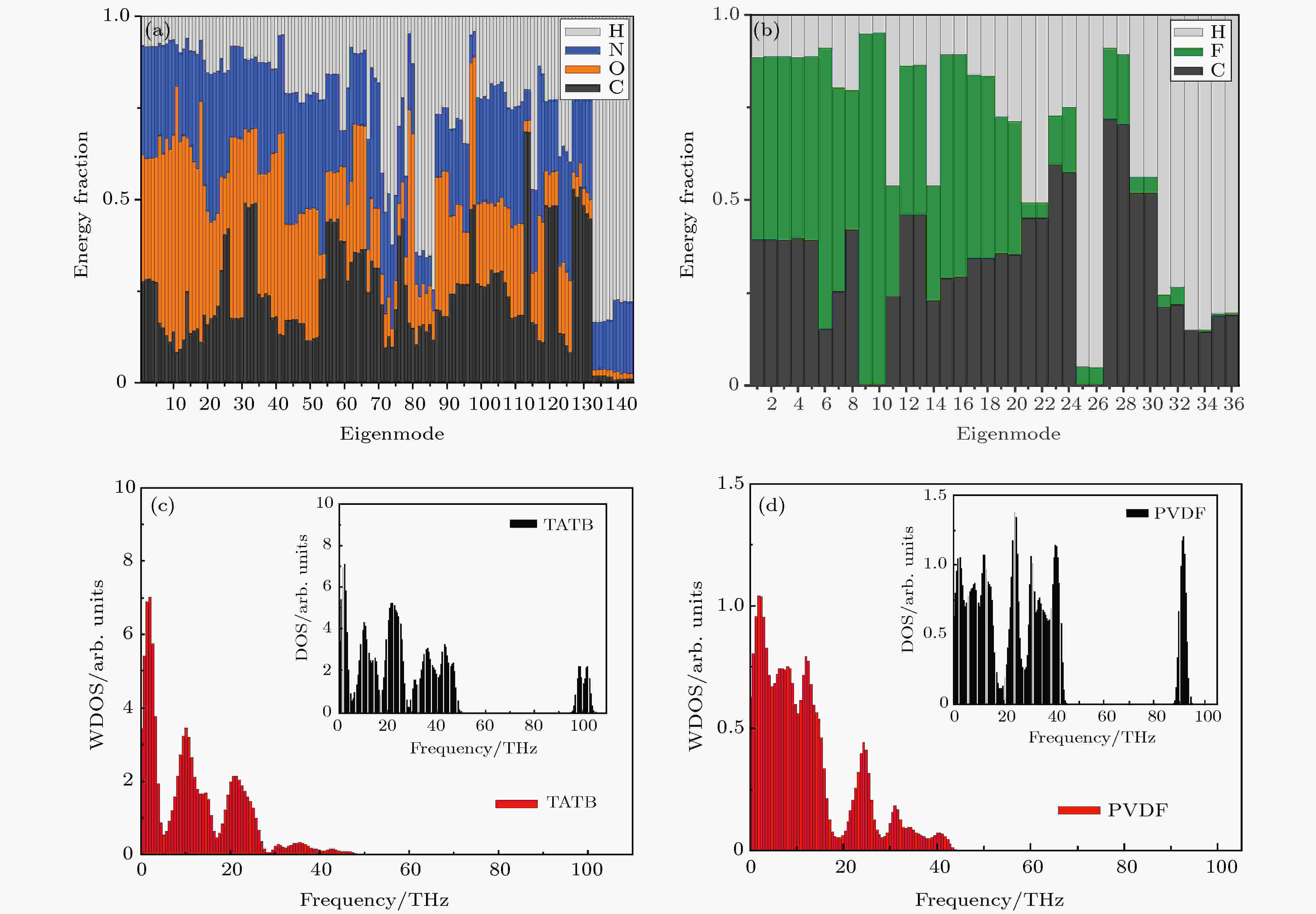图 3 (a), (b) TATB和PVDF的Γ点声子模分析; (c), (d) TATB和PVDF的加权声子态密度和声子态密度(小图)
Figure3. Decomposition of the gamma-point eigenmodes of TATB (a), and PVDF (b); the weighted phonon density of states of TATB (c), and PVDF (d).

对比表1和图2(c)中理论计算结果和实验数据, 本文采用广义梯度近似(GGA)交换关联泛函的计算结果与其他研究组采用不同交换关联泛函的计算结果符合较好. 交换关联泛函及考虑范德瓦耳斯修正等因素对计算结果的影响不大. 在高频区, 尤其是大于3000 cm^–1时, GGA的结果会略小于Jiang(局域梯度近似(LDA))的计算结果, 更接近于实验值. TATB晶格比热的计算数值与其他计算结果相符. 其中在温度293 K时计算的比热(498.3 J/mol·K)与实验值(495.7 J/mol·K)^[41]的误差为0.52%. 结合图3和表1分析TATB的晶格振动情况, 可以发现在低频区( < 300 cm^–1)尤其是频率低于100 cm^–1的区域, TATB晶体中硝基(–NO₂)的振动是主要的振动模式. 随着振动频率提高, 在300—1600 cm^–1区间, 苯环的振动贡献有着明显的提升, 同时硝基(–NO₂)和氨基(–NH₂)的振动也有着一定程度的贡献. 在高频区(> 3000 cm^–1), TATB晶格振动的贡献绝大部分来自于氨基(-NH₂)的振动. 伴随着晶格的振动, 固体内的传热问题随之而生. 在此, 我们基于振动模式的结果, 简要分析材料热导率这一表征传热能力的重要的物理参数. 热导率是声子弛豫时间、声子群速度和声子比热的函数. 声子群速度和声子比热可由简谐晶格动力学获得, 而声子弛豫时间的获得, 则需要通过非简谐晶格动力学方法求得三阶等高阶力常数. TATB等复杂材料的高阶力常数计算仍较为困难, 目前仍暂未获得. 我们在此仅对TATB和PVDF的声子比热进行分析, 以初步探究TATB和PVDF的导热情况. 晶格动力学中晶格热容与声子态密度$g\left( \omega \right)$有关, 公式如下:

声子模	本文工作			蒋文灿等[16]		Liu等[18]/cm–1	Exp.[40]/cm–1	不可约表示
	波数/cm–1	偏差/%		波数/cm–1	偏差/%
Q27	283	–4.30		288	–2.70	292	296	E′
Q30	284	–4.32		289	–2.69	295	297	E′
Q32	330	–0.45		331	–0.30	312	332	E″
Q33	331	–1.01		332	–0.59	318	334	E″
Q36	352	–4.53		359	–2.71	370	369	E′
Q38	354	–4.55		362	–2.42	371	371	E′
Q42	380	–2.72		382	–2.30	391	391	${\rm{A}}_2'$
Q44	431	–3.19		440	–1.12	436	445	E′
Q46	432	–3.88		441	–1.78	438	449	E′
Q50	507	–3.27		518	–1.14	520	524	E′
Q64	699	–0.72		680	–3.41	704	704	E′
Q65	700	–0.72		696	–1.27	708	705	E′
Q88	869	–0.28		846	–2.87	870	871	E′
Q89	872	–0.39		851	–2.74	874	875	E′
Q91	1027	–0.06		996	–3.11	1026	1028	E′
Q94	1029	–0.23		1001	–2.91	1032	1031	E′
Q105	1217	0.14		1154	–5.02	1215	1215	E′
Q107	1221	0.19		1162	–4.67	1219	1219	E′
Q109	1308	–0.34		1244	–5.18	1320	1312	E′
Q111	1313	–0.35		1250	–5.16	1327	1318	E′
Q119	1442	–0.33		1407	–2.76	1446	1447	E′
Q127	1551	–0.93		1542	–1.53	1575	1566	${\rm{A}}_1'$
Q129	1560	–2.07		1548	–2.82	1586	1593	E′
Q130	1564	–2.33		1549	–3.25	1596	1601	E′
Q134	3281	2.39		3325	3.78	3313	3204	E′
Q138	3298	2.66		3351	4.29	3334	3213	${\rm{A}}_1'$
Q142	3399	2.91		3439	4.12	3436	3303	E′

表1TATB部分Raman活性模计算数值与文献结果的比较
Table1.Comparison of the Raman modes of TATB crystal obtained in the present and previous calculations with experimental results.

${C_{\rm{V}}} = \mathop \int_0^{{\omega _{\rm{d}}}} {k_{\rm{B}}}{\left( {\frac{{\hbar \omega }}{{{k_{\rm{B}}}T}}} \right)^2}\frac{{{\rm{exp}}\left( {\dfrac{{\hbar \omega }}{{{k_{\rm{B}}}T}}} \right)}}{{{{\left[ {{\rm{exp}}\left( {\dfrac{{\hbar \omega }}{{{k_{\rm{B}}}T}}} \right) - 1} \right]}^2}}}g\left( \omega \right){\rm{d}}\omega .$

定义声子的加权态密度为

$WDOS = {\left( {\frac{{\hbar \omega }}{{{k_{\rm{B}}}T}}} \right)^2}\frac{{{\rm{exp}}\left( {\dfrac{{\hbar \omega }}{{{k_{\rm{B}}}T}}} \right)}}{{{{\left[ {{\rm{exp}}\left( {\dfrac{{\hbar \omega }}{{{k_{\rm{B}}}T}}} \right) - 1} \right]}^2}}}g\left( \omega \right).$

根据图3(c)和图3(d), 我们分析了TATB和PVDF在300 K温度时的声子加权态密度情况. 可以看到, 尽管TATB和PVDF在分别在100 THz和90 THz附近有着较大的态密度, 但是经过权重分析后, 二者的高频声子比例明显减少, 低频声子在导热中占据着主导贡献.
另外需要注意到的是, 我们的计算结果中TATB在部分高对称点附近存在着一定的虚频, 该现象在蒋文灿等^[16]和Wu等^[17]的结果同样也有出现. 虚频的产生, 有计算中未考虑非简谐效应和温度效应的原因, 冻声子计算超胞的结构较小等. 本文计算中, TATB的2 × 2 × 2超胞有384个原子. 受制于结构的复杂性, 目前计算资源无法高效针对更大超胞做出计算. 与已有实验和理论数据对比, 本文的声子谱计算结果具有可靠性, 可用于后续的界面声子散射研究.
2 -->

3.2.界面热导

界面热导率的计算结果如图4所示. 从图4(a)可以看出, 界面热导随温度的升高而相应提高, 并在高温时趋于平稳. 在低温区间, 界面两侧的晶格中只有少部分声子模式被激发, 随着温度的升高, 更多的声子模式随之被激发, 进而参与界面处的传热, 当温度接近或达到德拜温度时, 被激发的声子模式数量接近饱和, 声子模对界面热导的贡献不再增加. 进一步分析, 根据声子透射率公式(7)式, 可以发现界面的热传导主要发生在界面两侧振动频率重叠的地方, 且与重叠程度大小有关. 图4(b)展示了声子透射率和累积界面热导率随频率的变化关系, TATB-PVDF界面的热传导集中在声子频率小于45 THz的范围内. 其中在0—5 THz区间, 累积界面热导率已经达到总热导率的50%, 随后的声子贡献程度逐渐下降, 在大于45 THz的高频区间, 声子对界面热传导几乎无贡献. 界面热导在声子态密度重叠程度最大处达到最大值. 另外, 声子从TATB侧到PVDF侧的透射率, 明显大于反向的情况. 从图4(b)中可以看出, 声子透射率在2, 10和20 THz附近出现了拐点, 这与图3(c)TATB的加权声子态密度的变化趋势基本一致. DMM模型认为, 界面的声子透射率与入射声子的声子模、声子群速度和入射角无关, 声子通过界面的概率与该声子对应的态密度成正比, 因此我们并没有分析各声子模对声子透射率的影响. TATB声子主导着TATB-PVDF界面的声子透射, 也进一步主导着界面的热传导.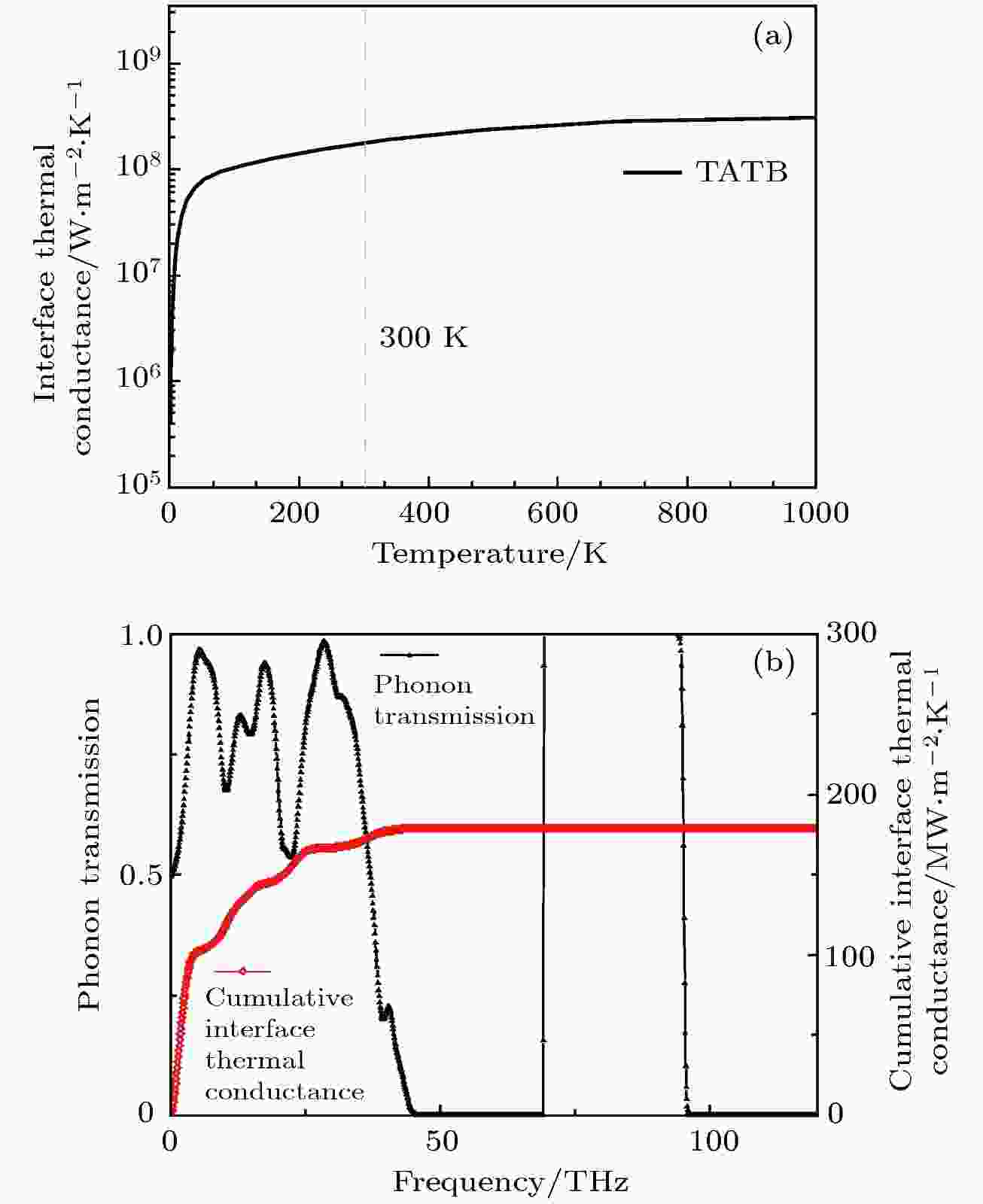
图 4 (a) TATB-PVDF界面热导率随温度变化情况; (b) TATB-PVDF界面声子透射率(黑)和累积热导率(红)
Figure4. (a) The interface thermal conductance of TATB-PVDF as a function of temperature; (b) phonon transmission of TATB-PVDF interface as a function of frequency.

以上的研究表明, PBX炸药各组分的声子谱计算, 可以作为指导炸药配方设计的一种手段. 通过计算各组分声子谱, 我们可以根据振动频率匹配程度, 初步筛选出界面热阻小的配方. 另外, 以上研究也预示着通过高分子功能化、接枝手段, 改变界面两侧振动频率的情况, 可以获得更高界面热导率的配方. 目前在实验方面, 我们尚无有效测量手段获知炸药界面的热导数据, 而且PBX炸药界面的理论研究也不多见, 我们较完整地研究了PBX炸药的界面热传导问题.
2 -->

3.3.热导率

我们通过EMD方法获得TATB的热导率为0.58 W/mK, 结果见图5(a), 计算细节参考2.4节. EMD的交换关联时长为100 ps, 本文TATB的计算共重复10组, 并对最后的热导率结果做平均. 可以看到交换关联时间在25 ps逐渐收敛. 由于TATB的低热导率, 其声子平均自由程也仅有0.54 nm, 远小于硅、锗等中高热导率材料的自由程. 因此, 我们用于EMD模拟的参数, 包括模型尺寸和交换关联时间均较合理. 其300 K热导率计算结果也与实验值0.54 W/mK^[42]符合较好. 此外我们选取PVDF的热导率实验值0.13 W/mK, 和3.2节中获得的界面热导率进行PBX热导率计算.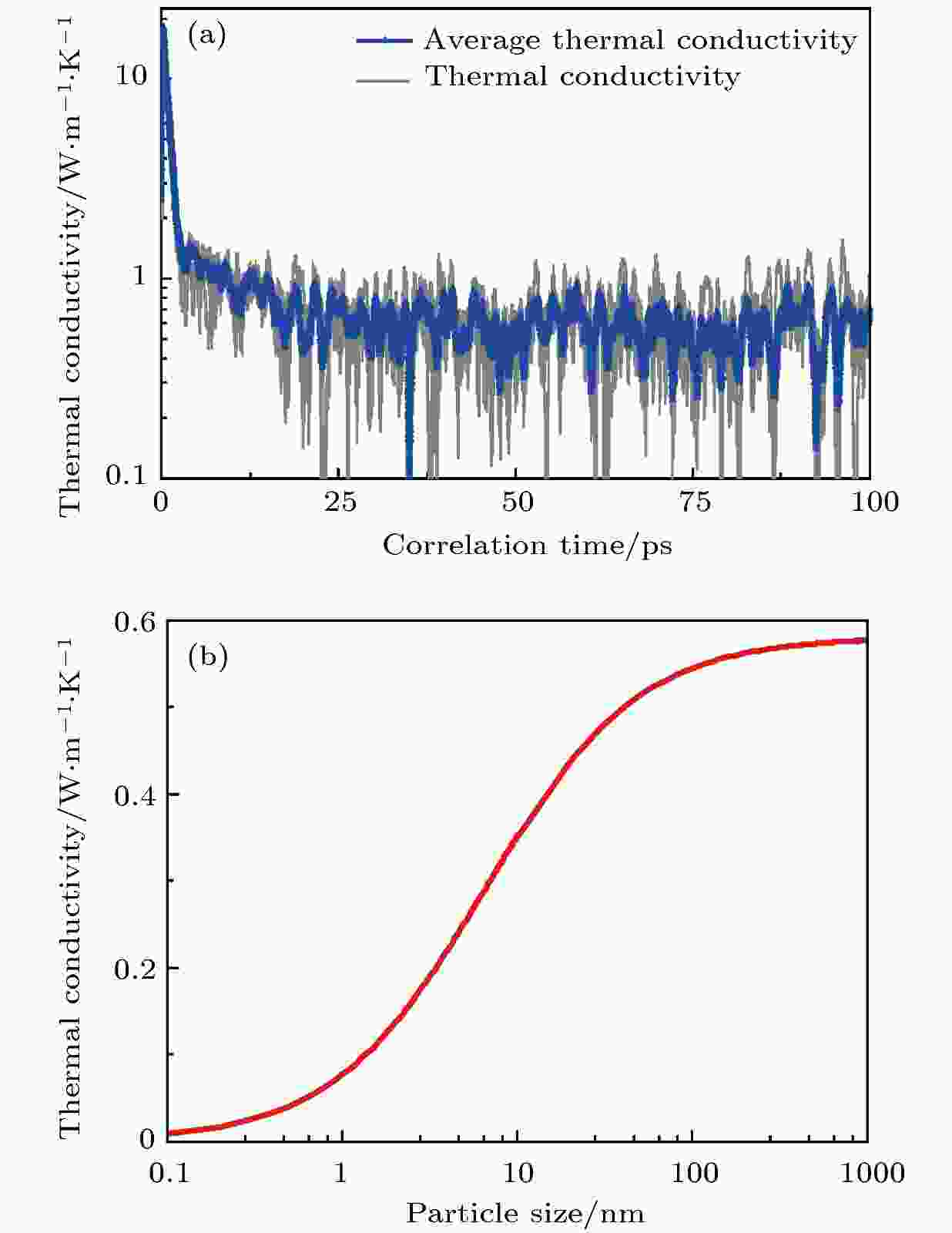
图 5 (a) EMD方法计算TATB热导率结果; (b) TATB基PBX炸药热导率随颗粒尺寸的变化
Figure5. (a) EMD calculation of TATB thermal conductivity; (b) thermal conductivity of TATB-based PBXs as a function of particle size.

对于复合材料的热导率, 通常我们考虑采用串并联的基本模型预测热导. 结合3.2节中DMM模型所获得的界面热导率, 我们基于串联模型计算得到了TATB-PVDF高聚物粘结炸药的热导率. 该体系的热导率由三部分贡献组成, 分别是主炸药TATB、黏结剂PVDF和TATB-PVDF界面的热导率. 当我们从某一方向对尺寸为L的炸药体系施加一个热流q, 则该体系的温度变化${\Delta}T$可由式(13)得到:

$\begin{split}& {\Delta}T = {\Delta}{T_{\rm{c}}} + {\Delta}{T_{\rm{a}}} + {\Delta}T,\\& {\Delta}{T_{\rm{c}}} = \frac{q}{{{\kappa _{\rm{c}}}}}\frac{{Ld}}{{d + \delta d}},\;\;{\Delta}{T_{\rm{a}}} = \frac{q}{{{\kappa _{\rm{a}}}}}\frac{{L\delta d}}{{d + \delta d}},\\& \Delta {T_{\rm{I}}} = \frac{q}{{{\kappa _{\rm{I}}}}}\frac{{2L}}{{d + \delta d}},\end{split}$

式中, ${\Delta}{T_{\rm{c}}},\Delta {T_{\rm{a}}},\Delta {T_{\rm{I}}}$分别为主炸药、黏结剂和界面的温度差; ${k_{\rm{c}}},{\rm{}}{k_{\rm{a}}},{k_{\rm{I}}}$为对应三者的热导率; d表示主炸药的粒径尺寸; $\delta d$为包覆厚度.
PBX炸药的热导由(14)式得出,

$\kappa = - \frac{q}{{\nabla T}} = \frac{q}{{\Delta T/L}}.$

将(13)式代入(14)式, 并认为包覆的厚度$\delta d$极小可忽略不计, 最终化简得到PBX的热导率

$\kappa = \frac{1}{{\left( {1/{\kappa _{\rm{c}}}} \right) + \left( {1/{\kappa _{\rm{I}}}2d} \right)}} = \frac{{{\kappa _{\rm{I}}}{\kappa _{\rm{c}}}d}}{{{\kappa _{\rm{I}}}d + 2{\kappa _{\rm{c}}}}}.$

图5展示了TATB-PVDF高聚物粘结炸药的热导率随颗粒尺寸的变化情况. 当颗粒尺寸大于100 nm时, 界面热阻对于PBX热导率的影响有限. 此外, 由于TATB的平均声子自由程仅为5 ?左右, 界面层的厚度远大于声子自由程, 因此TATB-PVDF界面的热传导将不会受到声子弹道输运的限制, 界面热传导满足宏观的傅里叶扩散理论. 考虑到PBX的实际结构, 其粘结剂包覆的炸药颗粒是一个诸多炸药晶体的集合体, 颗粒间的接触热阻、以及颗粒尺寸也都会影响PBX的热导. 目前暂无有效实验数据进行比较, 本研究采用的的串联传热模型, 虽预测的是复合材料热导率的下限, 但是考虑到PBX炸药中主成分的质量分数超过90%且该部分热导率明显高于粘结剂组分的事实, 该模型仍然适用. 在分析颗粒尺寸对热导率影响的问题上, 串联模型则可以给出不受界面热阻影响的颗粒临界最小尺寸, 对PBX设计有着指导意义. 复合含能材料有效热导率模型研究, 以及利用分子动力学方法模拟真实结构PBX热导的工作将在接下来的工作中开展.

本文基于晶格动力学, 结合第一性原理和分子动力学方法, 系统研究了TATB基高聚物黏结炸药的声子色散关系、界面透射系数和热导率.
1)计算了TATB和PVDF的声子色散关系, 计算结果与实验符合较好. TATB在低频区主要以硝基(-NO₂)的振动为主, 中频区苯环的振动贡献有着明显的提升, 而在高频区TATB晶格振动的贡献绝大部分来自于氨基(-NH₂)的振动. 低频声子在导热中有着明显的主导贡献.
2)利用DMM模型和声子色散关系, 研究了TATB与PVDF界面的热传导. 热导率随温度升高而上升, 并且在高温情况下接近不变. 通过提高界面两侧的振动频率的重合程度, 可以改善界面热导. DMM模型仅考虑了界面二声子的弹性散射情况, 多声子的非弹性散射修正的界面热传导将在接下来的研究进行.
3)基于串联模型, 分析了界面热导率和颗粒尺寸对PBX热导率的关系. 当颗粒尺寸大于100 nm时, 界面热阻对于PBX热导率的影响有限. 现实情况中, 由于PBX炸药中主炸药颗粒并非以单晶状态存在, 其粘结剂包覆的炸药颗粒是一个诸多炸药小颗粒的集合体, 颗粒间的接触热阻、以及颗粒尺寸都会影响PBX的热导.
鉴于炸药分子的复杂结构, PBX的大规模第一性原理计算目前仍难以实现. 目前计算结果的准确程度仍有提高的空间. 本文构建了PBX炸药界面热导的研究方法, 对炸药配方研究、PBX设计有着指导作用.