摘要: 自驱动粒子系统由可以从环境获取能量并转化为主动运动的粒子组成, 与经典的被动粒子系统有显著的区别. 对于这样的主动系统, 是否存在经典的物态方程这一问题引起了广泛的关注. 最近的研究以谐振子势场中的主动系统为模型, 研究了物态方程的适定性. 与之不同, 本文探讨了封闭空间的主动粒子系统, 在墙壁与粒子间存在双电层相互作用下, 系统物态方程存在的条件及具体形式. 结果表明, 壁面压强与主动粒子的形状有关, 当有墙壁施加力矩于主动粒子时, 在力矩作用下粒子趋向转向平行于壁面的平衡态, 而壁面-粒子相互作用强度增加使平行取向的趋势增强, 从而使系统压强降低. 此时压强和壁面的关联意味着主动系统没有通用的物态方程. 同时讨论了在壁面-粒子相互作用强度极小或极大的情况下压强的形式, 通过定义有效温度, 给出了主动系统与理想气体类似的物态方程. 此外研究发现, 对于不同粒子, 其形状偏离转动对称性的程度是影响主动粒子压强的关键因素. 该结果对当前主动系统热力学性质的研究提供了一定的参考, 并为更复杂的相互作用势下研究主动系统的热力学性质提供了基础.
关键词: 主动物质 /
物态方程 /
双电层相互作用 /
压强 English Abstract Pressure of active system under the electric double layer interaction Jin Kang Jing Guang-Yin School of Physics, Northwest University, Xi'an 710127, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11774287) and the Natural Science Foundation of Shaanxi Province, China (Grant No. 2018JM1017).Received Date: 27 March 2019Accepted Date: 21 June 2019Available Online: 01 September 2019Published Online: 05 September 2019Abstract: Self-driven particle systems consist of particles that can extract energy from the environment and transform into active motion, and thus are significantly different from the classical passive particle systems. For such an active system, the question of whether there is a classical equation of state (EOS) has caused spreading concern. Recent studies analyzed the validity of the EOS of an active system under the harmonic potential (Solon et. al, 2015 Nature Physics , 11 673). In contrast, this paper explores the conditions for and the specific forms of the EOS of an active system under electric double-layer interaction between the wall and the particles. The results show that the wall pressure is related to the shape of the active particles. When a wall exerts a moment on the active particles, the particles orientation turns to the equilibrium state parallel to the wall surface under the action of the moment, and the increase of the wall-particle interaction strength enhances the parallel-orientation trend, which reduces the system pressure. The association of pressure and wall means that the active system does not have a general equation of state. In the case where the wall-particle interaction intensity is extremely small or extremely large, by defining the effective temperature, the active system has an equation of state similar to that of the ideal gas. In addition, it is found that the extent of the shape of particles deviating from the rotational symmetry is a key factor affecting the pressure of active particles. The research results provide a reference for the study of the current active system equilibrium properties, and provide a basis for studying the thermodynamic properties of active systems under more complex interaction potentials.Keywords: active matter /equation of state /electric double layer interaction /pressure 全文HTML --> --> --> 1.引 言 主动物质系统由活性粒子组成, 每个粒子可以把周围环境的化学能、生物能转化为推动自身运动所需的能量. 不同于经典的被动粒子系统, 主动系统中粒子的运动不再是来自环境的随机力所驱使. 例如, 通过合成手段制备的Janus粒子[1 ] , 可以在化学催化反应下产生主动运动, 以及振动表面的极化圆盘, 将振动转化为主动运动动能[2 ] . 在生物物理领域, 已知存在着大量的主动系统样本, 包括细菌运动[3 ] 、细胞内部肌动微丝[4 ] 、细胞分裂的微观运动[5 ] 、蛋白马达[6 ] 、以及大尺度鱼群[7 ] 、鸟群[8 ] 等系统. 在这些系统中如何理解个体自主性和集群运动一直是主动系统研究的热点.[9 ] . 而对于上述这些主动系统, 人们对很多经典热力学中的概念提出了新的问题, 即如何定义系统的温度T 、内能E 及相应的统计描述等等. Loi等[10 ] 首先提出借助平衡态涨落-耗散理论定义自驱动系统有效温度的方法, 借助该方法, 研究者分析了不同主动系统中有效温度与主动力[11 ] 、主动粒子集群运动[12 ] 等效应的关系. 相对于温度, 压强的定义更为有趣, 在热力学中通常可以引入三种方式定义压强. 一种是通过系统的自由能对体积的改变量获得, 即热力学压强$ P_{\rm th} = -\partial F/\partial V $ . 另一种定义是粒子数密度为ρ 的系统里作用在容器壁上的应力可表示为$ {P_{\rm m}} = \int \rho ( r)\nabla V{\rm d} r $ , 其中V 为粒子-器壁相互作用势能. 第三种是从三维系统中的应力张量定义的流体动力学压强$ P_{\rm hyd} = -T_r(\bar{\bar{\sigma}})/3 $ . Solon等[13 ] 沿用了第二种压强定义, 刻画了谐振子势场中的主动系统压强随主动粒子运动的关系, 并首先将系统压强根据成因分为热运动压强、粒子相互作用压强及粒子运动关联压强, 进而指出不同类型压强对系统中的相分离效应的影响. Takatori等[14 ] 首先定义了主动系统中的游泳压强$ \varPi = nk_{\rm s}T_{\rm eff} $ , 提出了此压强可通过测量主动扩散系数$ D_{\rm swim} $ 并借助关系$ \varPi = n\xi D_{\rm swim} $ 获得, 同时定义了主动系统的有效玻尔兹曼系数$ k_{\rm s} $ 和有效温度$ T_{\rm eff} $ . 而相应的有效系数概念也被用于刻画其他尺度上的人工活性系统及微生物系统[15 ] . Takatori等[16 ] 构造了声学谐振势阱中的主动粒子系统, 在实验上直接测量了游泳压强的大小 . 在活性胶体系统中, Ginot等[17 ] 间接测量了系统的游泳压强.[18 ] 指出, 在器壁附近粒子与器壁相互作用满足动量守恒条件下, 流体动力学压强与单位面积上应力等价. Liu等[19 ] 观察到细菌具有群体感应(quorum-sensing), 从而建立了一种动态作用下种群态密度分布关系; Baskaran和Marchetti[20 ] 考虑了棒状粒子扩散各向异性, 给出了主动系统里修正的Smoluchowski方程; Solon等[21 ] 基于这些主动粒子相互作用机制, 解析地分析压强后发现其大小与边界-系统相互作用有关, 预测了对应的主动系统不存在通用的物态方程; Junot等[22 ] 设计了一个巧妙的实验, 通过盘状自驱动粒子推动一条柔性链, 对链进行受力分析得到体系压强, 结果表明系统的压强与边界形状相关, 第一次从实验角度表明主动系统不存在一般含义上的物态方程.[21 ] 的工作中, 引入了一种特殊谐振作用势, 建立了压强对自驱动粒子与器壁动量交换细节依赖性, 指出系统不存在物态方程. 据我们所知, 除了这种特殊的粒子-壁相互作用势外, 目前尚未有其他形式的作用力下主动系统的压强物态方程. 然而在溶液体系中, 粒子表面经常会带有电荷, 吸附到壁面上后, 使周围带异种电荷粒子被暂时束缚, 从而形成一个异种电荷浓度不断衰减的双电荷层, 而溶液中其他粒子靠近壁面就会受到双电荷层的作用力[23 ] . 本文在经典胶体的DLVO作用力框架下, 主要考虑胶体系统存在壁面-粒子双电层排斥势能条件下, 器壁上压强对粒子的长径比、几何形状、以及粒子主动运动的依赖关系. 与已有关于主动系统压强研究工作[13 ] 不同的是, 我们研究了双电层势能下不同形状主动粒子, 包括球形、椭圆、矩形及与真实细菌“细胞加鞭毛”类似的双矩形的粒子主动压强大小和形状对称性的关系. 结果发现, 主动系统粒子形状对称性会明显影响主动压强的大小, 而在经典的被动粒子系统中, 例如真实气体, 不同形状分子(偏心因子)在标准条件下造成的压强差异较小[24 ] . 这点充分表明了主动系统稳态物态方程与经典热力学系统物态方程的本质差异性. 就我们所知, 这一点在以往的报道中还没有涉及.2.主动系统模型 考虑标准的主动运动粒子模型, 假设粒子的自驱动速度为v [25 ,26 ] 已经被用来描述主动胶体[27 ,28 ] 、菌群[29 ] 等系统的集群运动. 基于不同主动粒子主动运动依赖的机制不同, 为明确, 表1 给出部分已有的研究报道中, 不同主动系统粒子运动参数的取值.粒子类型 尺寸/μm 主动速度/μm·s–1 平动扩散率D t 2 ·s–1 转动扩散率D r / rad2 ·s–1 翻转率α/ s–1 被动布朗粒子[27 ] 1.00 (直径) 0 0.2 0.17 0 主动布朗粒子[30 ] 1.00 (直径) 3.3 1.9 1.10 0 运动-翻转粒子[31 ] 2.00 (长), 0.25 (直径) 20.0 100.0 3.30 10
表1 不同类型主动系统粒子运动参数取值说明Table1. Description of particle motion parameters of different types of active systems.L 的微型棒, 如图1 所示. 运动速度为$ { v} = v(\cos \theta, \sin\theta) $ , θ 为粒子的取向角. 粒子单位长度受到来自墙壁的双电层相互作用力为$ \kappa Z {\rm e}^{-\kappa D} $ , 其中Z 是相互作用常数[23 ] . $ \kappa^{-1} $ 是德拜长度, D 是双电层作用力作用距离.图 1 主动系统粒子示意图, 粒子质心距离壁面水平距离为x , 粒子长度为2L , 取向角为θ Figure1. Schematic diagram of the active particle, the horizonal distance between the wall and the centroid of the particle is x , the length of the particle is 2L and the orienting angle is θ .y 方向上的边界满足周期性边界条件, 整个系统可以近似为一个准一维系统, 壁面-粒子相互作用力仅存在于水平方向. 对于一个质心位置水平分量为x , 取向角为θ 的粒子, 所受的作用力f 和力矩M (参看附录A )分别为:$ V(x) $ 是x 位置的壁面-粒子势能, $\rho(x) = $ $ \int_0^{2{\text{π}}} p(x, \theta){\rm d}\theta $ , 其中$ p(x, \theta) $ 是粒子概率分布函数的稳态表达式, 粒子的概率分布函数$ P({ r}, \theta, t) $ 满足福克-普朗克方程[9 ,21 ] v $ \mu_{\rm t} $ 和$ D_{\rm t} $ 分别是粒子的平动迁移率和扩散率, 相应地, $ \mu_{\rm r} $ 和$ D_{\rm r} $ 是转动迁移率与扩散率, 而α 是粒子运动翻转率.$ p(x, \theta) $ 进行投影积分[21 ] , 并选取边界条件: $ x = 0, \; \rho = \rho_0, \; x\rightarrow\infty, \; \rho = 0 $ , 可算出压强为3.主动系统压强研究 23.1.压强随壁面-粒子相互作用强度变化研究 3.1.压强随壁面-粒子相互作用强度变化研究 由(5 )式给出的主动系统压强表达式, 为判断是否存在系统的物态方程提供了依据. 首先考虑无力矩作用的主动粒子系统(例如球形粒子,$ M(x,\theta) = 0 $ ), 系统压强可以写为$ T_{\rm effe} = \dfrac{\mu^2}{2\mu_{\rm t} (D_{\rm r}+\alpha) k}+\dfrac{D_{\rm t}}{k\mu_{\rm t}} $ , 其中k 是玻尔兹曼常数, 压强表达式可写为$ P = \rho_0 k T_{\rm effe} $ , 形式和被动的理想气体系统物态方程一致. 因此可以判断: 1)在墙壁对粒子施加的力矩为零的情况下, 主动系统的压强与墙壁-粒子相互作用失耦; 2)系统存在与分子几何形状无关, 而与主动系统粒子输运参量相关的物态方程.$ \alpha = 0, D_{\rm t} = 0 $ ), 研究系统压强与墙壁-粒子间双电层相互作用系数Z 的变化关系. 从(5 )式可以解出压强为(参照附录B )$ \lambda = \dfrac{\mu_{\rm r} Z L^3 \kappa^2}{3 D_{\rm r}} $ . 定义约化相互作用强度$ Z_{\rm r} = Z/Z_{\rm c} $ , $ Z_{\rm c} = 3D_{\rm r}/(L^3 \kappa^2 \mu_{\rm r}) $ . 根据(6 )式, 可得出$ Z_{\rm r}\rightarrow 0 $ ), $ P = \dfrac{\rho_0 v^2}{2\mu_{\rm t} D_{\rm r}} $ . 当$ Z_{\rm r} $ 稍微增大, 将表达式(7 )式做展开至一阶, 可得$ \dfrac{2\mu_{\rm t} D_{\rm r}}{\rho_0 v^2}P = 1-\dfrac{Z_{\rm r}}{2} $ . 即随着$ Z_{\rm r} $ 的增大, 系统压强降低. 图2 给出了$ \dfrac{2\mu_{\rm t} D_{\rm r}}{\rho_0 v^2}P $ 随约化相互作用强度$ Z_{\rm r} $ 的变化曲线. 相互作用增强, 粒子受到更大的来自墙壁的转动力矩 ((2 )式), 转动速度增加, 更快地达到$ \theta = \text {π}/2 $ 的平衡位置(见附录A ). 根据(1 )式, 在$ \theta = \text {π}/2 $ 时, 作用力最小, 因此压强下降. 需要说明的是, 解析结果(6 )式是在弱相互作用近似下微扰展开解得的. 因此, 对于强相互作用, (7 )式并不能正确描述系统压强. 可以推断, 在强相互作用极限下, 粒子有很大的分布几率处于$ \theta = \text {π}/2 $ . 回到(5 )式, 可以得到系统的物态方程图 2 等效压强随约化相互作用强度Z r 的变化Figure2. Effective pressure as the function of reduced interaction intensity.3.2.压强与主动粒子长度关系 -->3.2.压强与主动粒子长度关系 图3 给出了$ \dfrac{2\mu_{\rm t} D_{\rm r}}{\rho_0 v^2}P $ 随约化粒子长度的变化曲线, 其中粒子约化长度定义为$ L_{\rm r} = L/L_{\rm c} $ , $ L_{\rm c} = (3D_{\rm r}/Z\kappa^2\mu_{\rm r})^{1/3} $ . 可以看出, 在$ L_{\rm r}\rightarrow 0 $ 的极限条件下, $ P = \rho_0 v^2/(2\mu_{\rm t} D_{\rm r}) $ , 与无力矩作用下的球形粒子压强一致. 随着$ L_{\rm r} $ 的增大, 墙壁压强起初缓慢减小, 之后下降斜率增大. 容易判断, 在θ 不变的情况下, $ L_{\rm r} $ 增加, 分子与墙壁的相互作用力会增加. 但同时, 粒子受到的转动力矩也会增加, 意味着粒子会加速达到平衡位置($ \theta = \text {π} /2 $ ), 从而减少与墙壁的作用力. 因此, 压强缓慢减少正是这两种效应的综合结果. 当$ L_{\rm r} $ 继续增加, 粒子的角加速度增大. 从曲线变化趋势上可以看出, 增加长度带来的加速趋近平衡位置对压强的减小超过长度增加带来的作用力范围增大对压强的影响. 综合以上的分析可以看到, 压强的减小是由于壁面-粒子相互作用力导致微棒粒子轴向平行于壁面而造成的.图 3 等效压强随主动粒子约化长度L r 的变化Figure3. Effective pressure as the function of reduced length of active particle.3.3.压强与主动粒子形状的关系 -->3.3.压强与主动粒子形状的关系 粒子的形状会影响壁面-粒子间力矩的大小[32 ] . 在主动系统中, 主动粒子的形状可以由制备过程所决定[33 ] , 而对于自然界存在的主动粒子系统, 其单元具有自己的特征形状, 例如螺旋菌“细胞加鞭毛”类似两个宽度不同的矩形相接的形状. 椭圆型粒子的布朗运动的实验研究已有相关的报道[34 ] . Solon等对椭圆形主动粒子系统粒子运动与压强的关系进行了理论探讨. 由于主动系统的丰富性, 对更多不同形状的主动粒子所受力矩和系统压强关系进行探讨是一个有趣的研究命题. 接下来讨论矩形粒子、类似螺旋菌的双矩形粒子几何形状与所受力矩及系统压强的关系, 同时引入椭圆粒子模型为参照, 对三种粒子形状和压强的关系进行比较.l , w , 双矩形粒子两个矩形长宽分别为$ l_1, w_1, l_2, w_2 $ (见图4(a) 标注图例, 其中$ l_1,\; w_1 $ 是下端矩形的长和宽, $ l_2,\; w_2 $ 是上端矩形的长和宽). 为方便运算, 矩形面积及其他参量定义为: $lw = 2, $ $ l_1 w_1 = l_2 w_2 = 1,\; l_1 = 1 $ . 设两类粒子的结构常数$ s_1,\; s_2 $ 分别为$ \dfrac{l}{w} $ 及$ \dfrac{l_2}{w_1} $ . 粒子的取向角为θ , 矩形和双矩形粒子所受力矩分别为图 4 力矩和压强随三种粒子结构常数的变化Figure4. The variations of the torques and the pressures as a function of structure constants of the three kinds of particle.$ A = \text {π} a b = 2 $ , 其中a , b 分别是椭圆的长短轴. 由于椭圆与矩形形状上的相似性, 椭圆粒子的结构常数同取为$ s_1 = a/b $ , 并以同样的$ s_1 $ 值比较两类粒子系统的力矩和压强. 可算得壁面-椭圆粒子间的力矩为$ M_3 = \dfrac{1}{2{\text{π}}}\Big( {{s_1} - \dfrac{1}{{{s_1}}}} \Big)\kappa Z\sin(2\theta) $ . 基于矩形粒子和椭圆形粒子形状上的类似, 可以比较同样的结构常数对应的力矩和压强. 而对于双矩形形状的粒子, 可以知道$ s_2 = 1 $ 对应的形状等同于$ s_1 = 2 $ 的矩形粒子形状. 因此以$ s_1 = 2 $ 及$ s_2 = 1 $ 为初始的结构常数值, 将三种粒子的力矩(压强)呈现在图4(a) (图4(b) ). 在图4(a) 中, 可以看到相同面积的椭圆形和矩形粒子结构常数相同时, 相应的力矩差异很小. 与矩形粒子不同, 双矩形粒子所受力矩随结构常数增加呈非线性增加 (图4(a) ). 由图可知, $ s_2/s_1 = 3/6 $ , $ M_2/M_1 \!=\! 1.47 $ , $ s_2/s_1 \!=\! 3.5/7 $ , $ M_2/M_1 \!= $ 1.62. 在图4(b) 展示了相应的压强变化. 三种粒子压强表达式同(6 )式, $ \lambda $ 的值为$[{\mu_{\rm r} \kappa^2 Z}/({2\text {π} D_{\rm r}})]\left( s - (1/s) \right) $ (椭圆形状的粒子), $[{\mu_{\rm r} \kappa^2 Z}/({6 D_{\rm r}})]\left( {s - (1/s)} \right) $ (矩形粒子), $[{{\left( { - 2 + 3{s_2}^2 + 6{s_2}^3 + 5{s_2}^4} \right){\mu _{\rm r}}{\kappa ^2}Z}}]/({{48{D_{\rm r}}{s_2}^2}}) $ (双矩形形状的粒子). 可以看出, 随着结构常数的增加, 系统的压强下降, 与力矩随着结构参数增加相对应. 比较而言, 双矩形粒子力矩及压强随结构常数变化更明显. 可以想象, 越大的$ s_2 $ , 表明双矩形里下端矩形长度越长(见图4(a) 里标注图例), 体系的质心就会向后方矩形偏移. 正是这样的结构对称性的改变, 使得壁面-粒子相互作用力矩增大, 进而加速向平衡位置的运动, 减小压强.$ \mu_{\rm r} $ 升高也会降低系统的压强. 图5 展示了不同粒子转动迁移率, 压强随粒子密度的变化曲线. 可以看到, 对同样的粒子密度, 压强随转动迁移率的升高而降低. 同时, 图中曲线表明, 压强随着粒子数密度的增加线性增加. 然而已有研究[20 ,21 ] 指出在存在粒子间相互作用的情况下, 压强随数密度的变化会呈现出非线性特性. 并且粒子数密度对粒子间相互作用的影响也是实验中样本准备需要考虑的因素[34 ] . 因此, 在存在双电层壁面-粒子相互作用的主动系统里, 考虑粒子间相互作用, 建立起系统压强求解的解析或者数值方法, 并研究压强特性及物态方程存在的条件, 是一个很有意义的、也是我们下一步准备探讨的课题.图 5 对于不同的转动迁移率, 压强随粒子数密度的变化Figure5. The variations of pressures as a function of particle number density for different rotational mobilities.4.结 论 总结本文, 可以得到以下主要结论: 在墙壁与主动粒子间存在双电层相互作用时, 墙壁对粒子施加力矩会引起壁面压强降低, 原因在于外力矩会导致粒子旋转到与墙壁平行的平衡位置. 零力矩作用下, 主动系统存在与理想气体类似的物态方程. 我们得出了主动布朗流体中双电层相互作用强度及微棒粒子长度与压强的关系, 可以看到相互作用强度和棒的长度的增大都会降低主动系统的压强; 而在弱相互作用和强相互作用极限下, 主动系统的压强仅与粒子参量相关; 与墙壁-粒子相互作用无关. 主动粒子的形状也会影响主动系统的压强. 研究结果表明, 粒子相对于质心的旋转对称性的破坏, 会增强粒子所受到的转动力矩, 从而降低压强.附录A: 微棒粒子所受力、力矩及转动平衡位置 由图A1 , 微棒上的长度元dl , 距离棒中心长度l , 受到作用力为$ {\rm d}f = \kappa Z \mathrm{exp}[-\kappa (x+l\cos\theta)]{\rm d}l $ , 积分可得到总受力为$ f = 2 Z \mathrm{exp}[-\kappa x]\sec\theta\sinh(L\kappa\cos\theta) $ ((1) 式). 容易验证$ \theta = \text {π}/2 $ 时f 取极小值. 双电层静电作用力$ f(x) = \kappa Z {\rm e}^{-\kappa x}$ 做展开保留至一阶得$ f(x)\doteq \kappa Z(1-\kappa x) $ . 相对于图A1 坐标原点, 棒上长度元dl 所受力矩$ {\rm d}M(x, \theta) = \kappa Z[1-$ $\kappa(x+l\cos\theta)]{\rm d}l\sin\theta $ , 积分得到$ M = \dfrac{1}{3}\kappa Z L^3\sin 2\theta $ ((2) 式). 对于不为零的初始角度($ \theta\neq 0 $ ), 在初始非零的(2 )式力矩作用下, 棒的运动为永不停止的周期运动. 但是, 如果考虑一个转动的阻尼, 与转动角速度成正比, 运动方程可以写为α 是阻尼系数, J 是棒的转动惯量, 取约化时间$ t_{\rm r} = \dfrac{3Jt}{Z\kappa^2 L^3} $ , 约化阻尼系数$ \alpha_{\rm r} = \alpha/J $ , 运动方程简化为图A1 ), 平衡位置均为$ \theta = 0.5\text {π}$ .图 A1 对于不同的初始角坐标, 粒子取向角随时间的演化, 约化阻尼系数α r = 0.5FigureA1. For different initial angular coordinates, the evolutions of orienting angles. Reduced damping coefficient α r = 0.5.附录B: 主动布朗流体压强解析结果 考虑主动布朗流体(α = 0), 为方便计算, 假设粒子平动扩散系数$ D_{\rm t} = 0 $ . 在(5 )式中力矩对压强的贡献可写为$ \lambda = \mu_{\rm r} Z L^3 \kappa^2/(3D_{\rm r}) $ . 首先将概率分布$ p(x, \theta) $ 以λ 展开为32 ](17)式—(24)式), 可解得B3 )式, 可得到6 )式. 










 图 1 主动系统粒子示意图, 粒子质心距离壁面水平距离为x, 粒子长度为2L, 取向角为θ
图 1 主动系统粒子示意图, 粒子质心距离壁面水平距离为x, 粒子长度为2L, 取向角为θ







































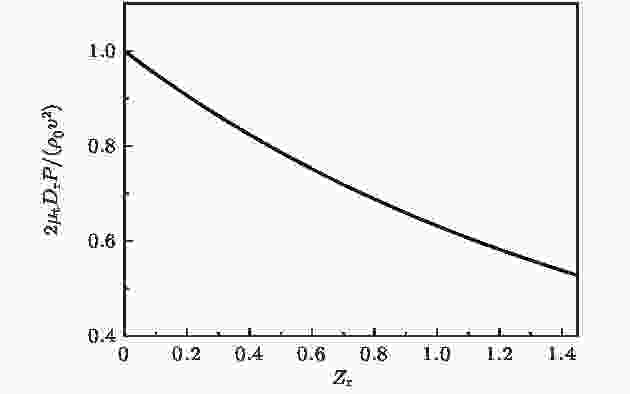 图 2 等效压强随约化相互作用强度Zr的变化
图 2 等效压强随约化相互作用强度Zr的变化














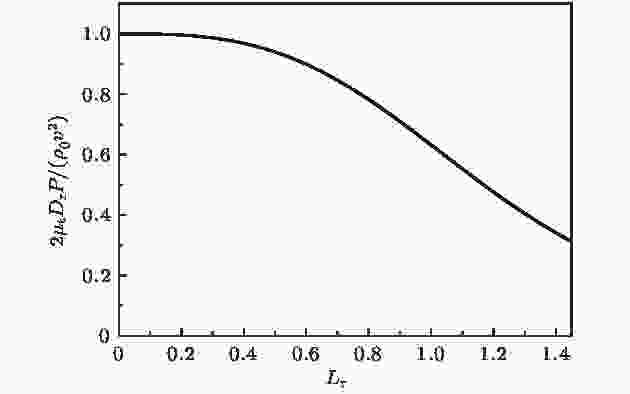 图 3 等效压强随主动粒子约化长度Lr的变化
图 3 等效压强随主动粒子约化长度Lr的变化







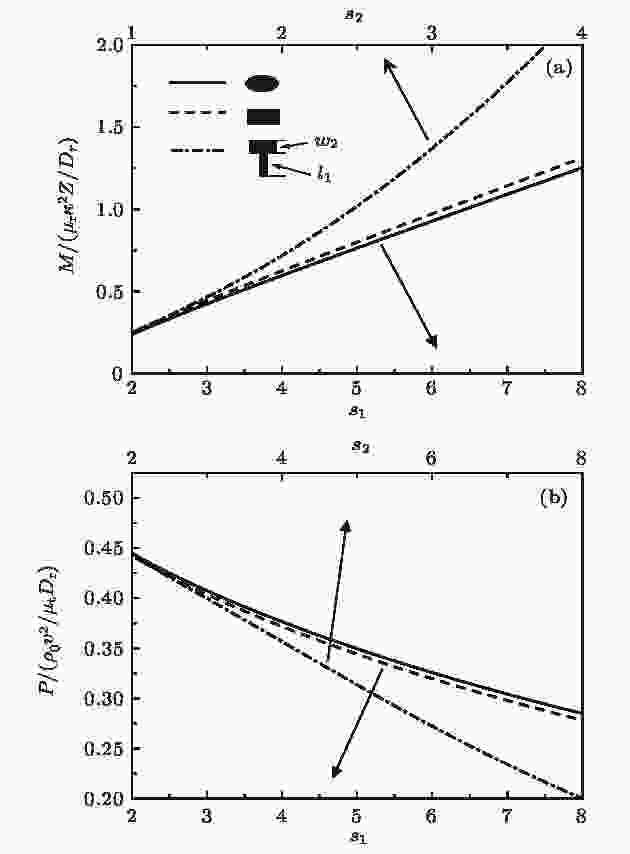 图 4 力矩和压强随三种粒子结构常数的变化
图 4 力矩和压强随三种粒子结构常数的变化





















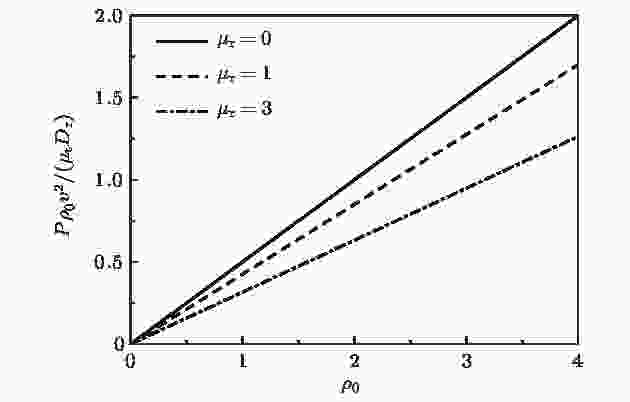 图 5 对于不同的转动迁移率, 压强随粒子数密度的变化
图 5 对于不同的转动迁移率, 压强随粒子数密度的变化











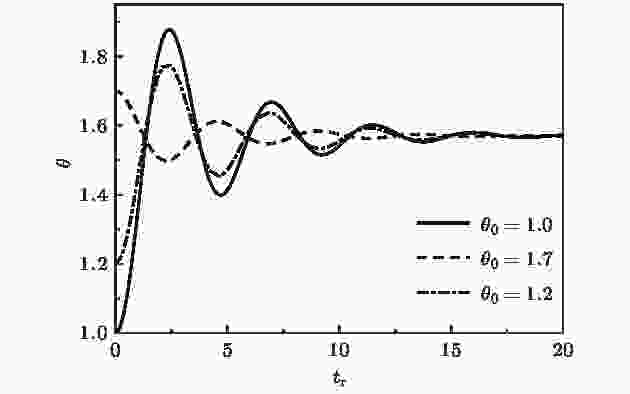 图 A1 对于不同的初始角坐标, 粒子取向角随时间的演化, 约化阻尼系数αr = 0.5
图 A1 对于不同的初始角坐标, 粒子取向角随时间的演化, 约化阻尼系数αr = 0.5


