摘要:柱-孔汇聚结构(PHC)附近高功率脉冲电流的损失是脉冲功率技术领域的研究热点, 是研制下一代大型脉冲功率装置的技术瓶颈. 本文建立了单孔柱-孔汇聚结构的3维仿真模型, 采用粒子(PIC)仿真算法, 分别在阴极发射电子以及阴极等离子体等情况下, 计算了单孔柱-孔汇聚结构的电流传输特性, 首次在仿真过程中考虑了阴极负离子的运动对单孔PHC阴阳极间隙闭合的影响. 仿真结果表明阴极等离子体导致了阴阳极间距明显地缩短, 从而引起电流损失. 同时获得了阴极等离子体平均扩展速度为3.76 cm/μs. 更为重要的是, 当阴极等离子体中含有负离子时, 单孔柱-孔汇聚结构电流损失的现象更为显著. 同时获得了负离子平均漂移速度约为10 cm/μs. 仿真结果显示阴极负离子在PHC阴阳极间隙闭合过程中, 同样发挥了显著的作用, 是阴阳极间隙闭合的重要因素之一. 研究结果有助于深入理解高功率PHC电流损失的物理机理, 也可为高功率PHC的设计提供重要理论基础.
关键词: 磁绝缘/
柱-孔汇聚结构/
负离子/
等离子体

English Abstract

全文HTML

--> --> -->

多层真空磁绝缘传输线(magnetically iInsulated transmission lines, MITLs)是大型脉冲功率驱动源的重要部件, 可传输和汇聚高功率脉冲. 位于MITLs末端的柱-孔汇聚结构(post-hole convolute, PHC)可将多路高功率脉冲合并为一路. 合并后的高功率脉冲再经一段圆盘传输线被馈送至负载. PHC不仅广泛应用于大型脉冲功率源^[1-3], 甚至在下一代大型脉冲功率驱动源的概念设计中仍得以应用^[4,5].
然而在高电压(MV量级)大电流(10 MA量级)运行条件下, PHC附近存在大量的电流损失. 当Z装置的堆栈电流达到22 MA时, PHC附近损失电流的峰值达到4 MA, 损失比例达到18%^[6,7]. “聚龙一号”装置能够输出前沿75—600 ns, 电流峰值值5—10 MA的脉冲电流. 该装置PHC附近同样发现了大约330—743 kA的电流损失^[3].
MITLs以及PHC电极表面等离子体复杂的运动特性(空间粒子密度、粒子种类、漂移速度)是理解其宏观参数(电压、电流、阻抗)变化特性的关键. 等离子体鞘层的边界可视为“虚电极”, 阴极等离子体和阳极离子的鞘层边界的运动会缩短阴阳极间隙的距离, 从而降低间隙等效阻抗, 严重时甚至导致间隙阻抗崩溃. 因此通过对等离子体运动进行仿真研究获得其运动特性, 有助于PHC的设计和性能评估. 通常采用3维粒子(PIC)仿真运算方法以研究PHC的电极表面等离子体动力学特性^[8-19]. 当阴极仅发射电子时, MITLs能够有效地传输高功率脉冲^[9-18]. 然而, 阴极发射等离子体时, MITLs的工作特性便发生显著的改变. 阴极等离子体会逐渐靠近阳极而缩短阴阳极间隙, 最终使得阴阳极闭合, 导致电流损失. 拥有复杂拓扑结构电磁场的PHC更是电流损失的重灾区^[9-13].
现有的仿真计算中, 阴极等离子体成分通常为电子、离子和中性气体^[9-13], 认为阴极等离子体因其内部压力而产生的扩展运动是导致间隙减小或闭合的重要因素. 仿真研究并未涵括阴极等离子体含有负离子的情况, 未能深入细致地研究其运动特性以及对PHC电流损失的影响. 然而实验表明阴极附近同样能生成负离子^[20-22], 且由于具有质量大、负极性等特点, 负离子更容易到达阳极. 本文构建了一个含有负离子的阴极等离子体发射模式, 并比较了几种发射模式对PHC电流传输特性的影响, 初步探索了PHC附近空间等离子体的运动特性.

2

-->

2.1.几何模型

图1展示的是用于仿真计算的单孔PHC几何模型结构示意图. 单孔PHC连接着负载和三板传输线, 负责将三板传输线传输的高功率脉冲汇聚传输至负载. 仿真计算时, 主要关注传输线平直部分, 而传输线弧形过渡段仅用以馈入脉冲功率信号, 不是本文研究的重点. 该模型的几何结构与在“强光一号”加速器上实验的单孔PHC完全一致.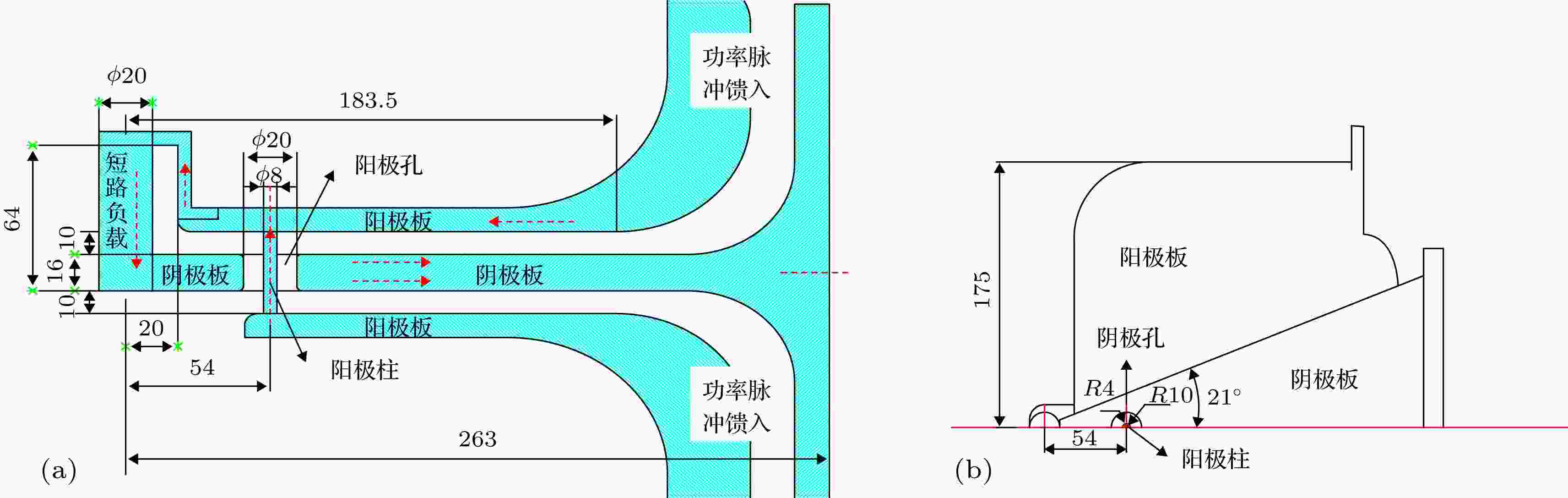
图 1 仿真模型的结构示意图　(a) 单孔PHC及三板传输线剖面图(单位: mm); (b) 单孔PHC及三板传输线俯视图(单位: mm)
Figure1. The configuration of the simulated model:　(a) The cutaway drawing of the single-hole PHC and the tri-plated transmission line (units: mm); (b) the vertical drawing of the single-hole PHC and the tri-plated transmission line (units: mm).

三板传输线阴极的几何形状为三角形平板阴极, 底宽为200 mm, 长度为263 mm, 张角约为42°, 厚度为16 mm. PHC附近宽度最短约为18 mm. 阳极分为上、下阳极板, 宽度皆为350 mm, 上阳极板长为250 mm, 下阳极板长为150 mm. 三板传输线阴阳极间距为10 mm. 图1中, 阳极柱直径约为8 mm. 阳极柱穿过阴极孔, 将上、下阳极板连接起来. 图中阴极孔直径为20 mm. 负载和阴极孔的中心距离为54 mm. 短路负载是一个直径为20 mm的铜杆.
2 -->

2.2.仿真设置

为了较理想地引入电压信号, 在图1中单孔PHC的右方引入同轴馈电结构. 在馈电结构区域设置恰当的介电常数, 确保驱动源阻抗总是等于馈电结构的特征阻抗. 仿真过程中为贴近实际实验效果, 馈电结构区域的等效特性阻抗设为0.75 Ω, 等效“强光一号”加速器输出阻抗. 负载设置为一个电阻介质构成的圆柱体, 圆柱体两端连接到阴极和阳极连接板, 设置介质电阻率使得负载等效电阻为0.3 Ω.
仿真采用常用的Vsim专业PIC仿真软件. 为了保证计算的精确度和稳定性, 时间步长需满足电子回旋频率和时间步长的乘积小于2的条件^[8]. 基于服务器有限的计算能力, 为确保模型能有效地开展运算, 经多次验算, 设定时间步长为1.3 ps (总时长为130 ns), 网格宽度为1 mm (网格数量为10⁸), 宏粒子权重为7 × 10⁹.
仿真计算主要关注柱-孔结构附近等离子体的演化特性, 因此设置粒子发射区域时有所侧重: 1)电子发射区域为阴极平直段所有表面; 2)阴极等离子体发射区域为阴极孔及其附近平面区域. 电极发射粒子种类主要有电子、离子(H⁺)以及负离子(H^–)^[20,21]. 此三类粒子是MITL电极等离子体发射模型^[8]中较为重要的成分.
通常的阴极等离子包含了电子、中性气体和离子, 很少讨论其中有负离子时的情况. 本文对阴极负离子的运动过程和作用进行探索性研究. 仿真过程忽略中性气体的运动和电离以及粒子之间的碰撞等复杂物理过程, 重点关注含有负离子的等离子体充满PHC阴阳极间隙对PHC电流传输效率的影响. 阴极发射电子的电场阈值为240 kV/cm, 其发射模型遵循理想的SCL模型. 考虑到电极表面中性气体的脱附率0.003—0.25 mL/ns ^[8], 本文假设中性气体的注入率为0.01 mL/ns, 且全部均匀电离, 意味着在临近电极表面的第一个网格中等离子体的注入率为10¹³ cm^–2/ns. 依据实验结果^[20,21], 负离子的发射模型发射电流密度遵循

${j_ - } = 0.001{J^3},$

其中J为阴极面电流密度(单位为kA/cm); j_–为阴极负离子的电流密度(单位为A/cm²). 在仿真过程中保持等离子体引起的流向阴极的离子流与电子发射的电子流以及阴极负离子运动引起的电流之和相当, 以确保电荷守恒.
仿真计算时, 采用的前行电压波形是一个梯形脉冲, 如图2所示, 以此模拟加速器输出电压波形. 电压幅值为1 MV, 信号前/后沿皆为30 ns, 电压脉宽为100 ns, 接近加速器输出电压波形参数. 另外, 图1中单孔PHC的左边是开放结构, 阴阳极间隙中的电子及其他带电粒子会漂移出单孔PHC. 因此为避免极端情况出现, 在开放区域设置了“完美匹配层边界”, 认为所有到达边界的带电微粒都被吸收, 不再影响单孔PHC内部空间的电磁场.
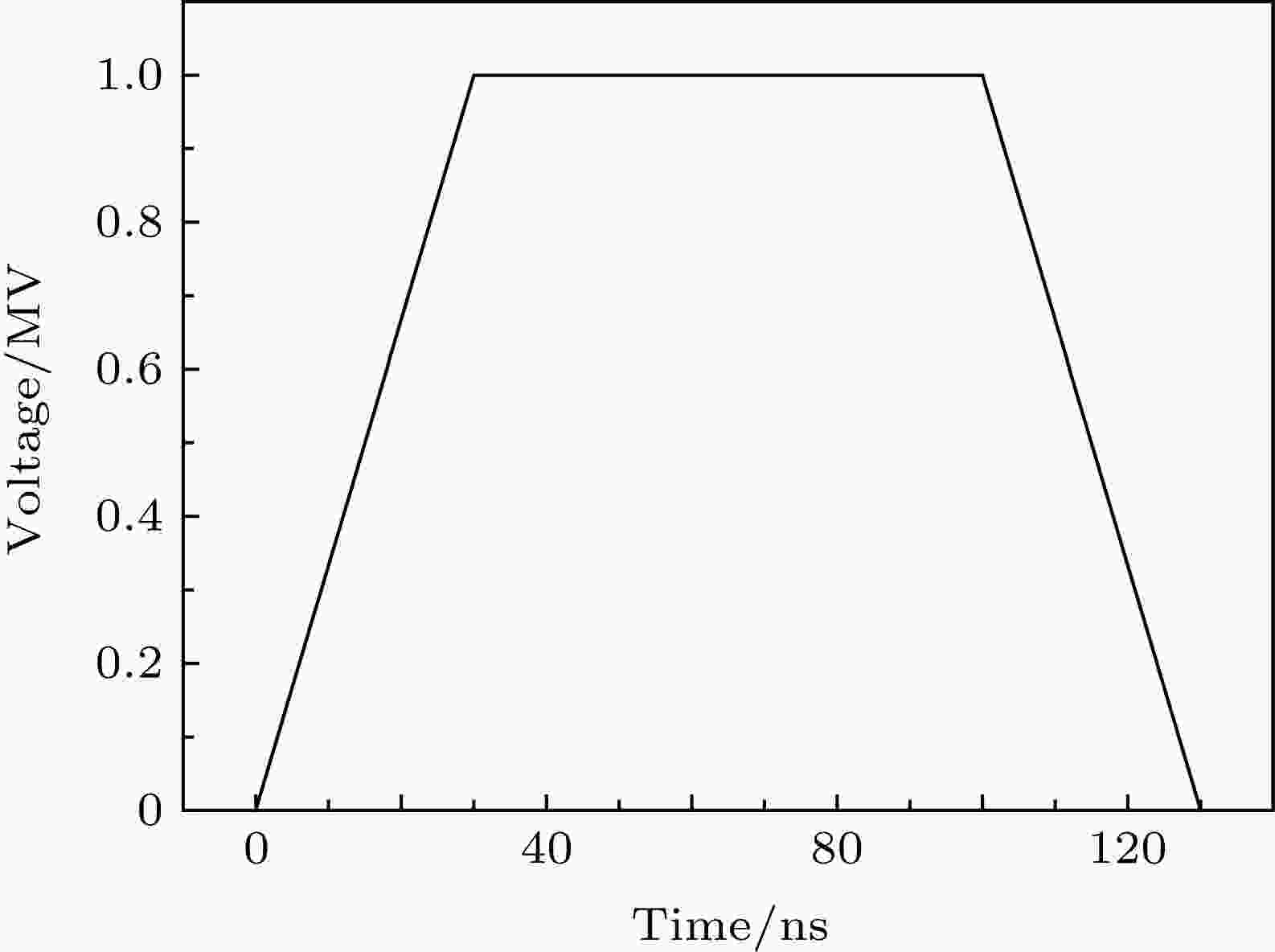图 2 仿真计算时馈入的理想电压信号
Figure2. The forward voltage waveform used in simulation.

2

-->

3.1.阴极发射电子

图3展示了单孔PHC上/下游阳极电流的波形, 其中损失电流为上/下游电流的差值. 可以看到, 上游电流和下游电流几乎完全重合, 仅在电流起始附近有少许差别, 其最大值约为23 kA. 损失电流仅在电流起始附近较为明显, 是因为在电子发射初期, 单孔PHC以及三板传输线还未建立磁绝缘状态, 因此有部分电子直接到达阳极. 这种损失的电子流, 称为电流的前沿损失. 磁绝缘初始时刻空间电子的行为特性已有大量的研究资料^[1,8-16], 本文不再详细分析.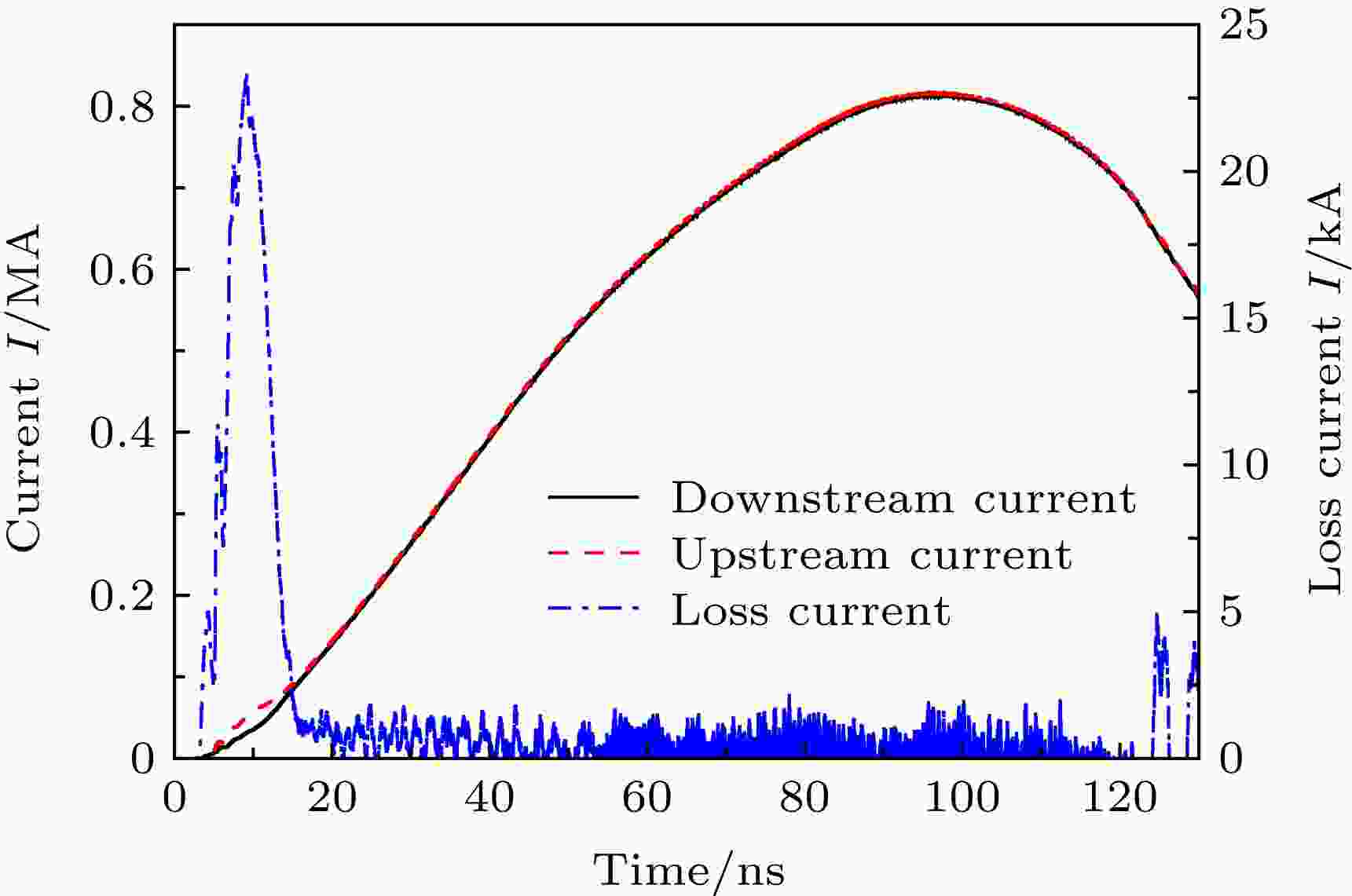
图 3 阴极发射电子时, 单孔PHC的上/下游电流
Figure3. The upstream and the downstream currents of the single-hole PHC while the cathode emitted only electrons

仿真结果表明当传导电流大于百千安时, 本文设计的单孔PHC及其传输线结构已能形成良好的磁绝缘状态. 因此在“强光一号”加速器(约1 MV, 1.5 MA)上实验时, 该结构能够达到磁绝缘状态.
因此, 当阴极仅发射电子时, 单孔PHC结构能够有效传输电流并不存在显著电流损失. 这表明电子并非导致PHC电流损失的主要因素.
2 -->

3.2.阴极发射等离子体

当阴极发射等离子体, 即电子和离子(H⁺)时, 单孔PHC的传输特性发生明显的变化. 图4展示了单孔PHC上/下游电流及损失电流. 图4和图3相比, 传导电流幅值略有增加. 损失电流波形则完全不同. 图4中损失电流在20 ns附近有明显的峰值. 此时, 电极表面附近电场强度超过240 kV/cm. 因此可以认为该峰值属于电子流前沿损失. 然后, 损失电流幅值稍下降继而缓慢增加, 直至100 ns其幅值再度上升到10 kA左右. 虽然电流峰值处损失程度仅达到1%左右, 但与2.1的仿真结果相比, 电流损失现象是明显的.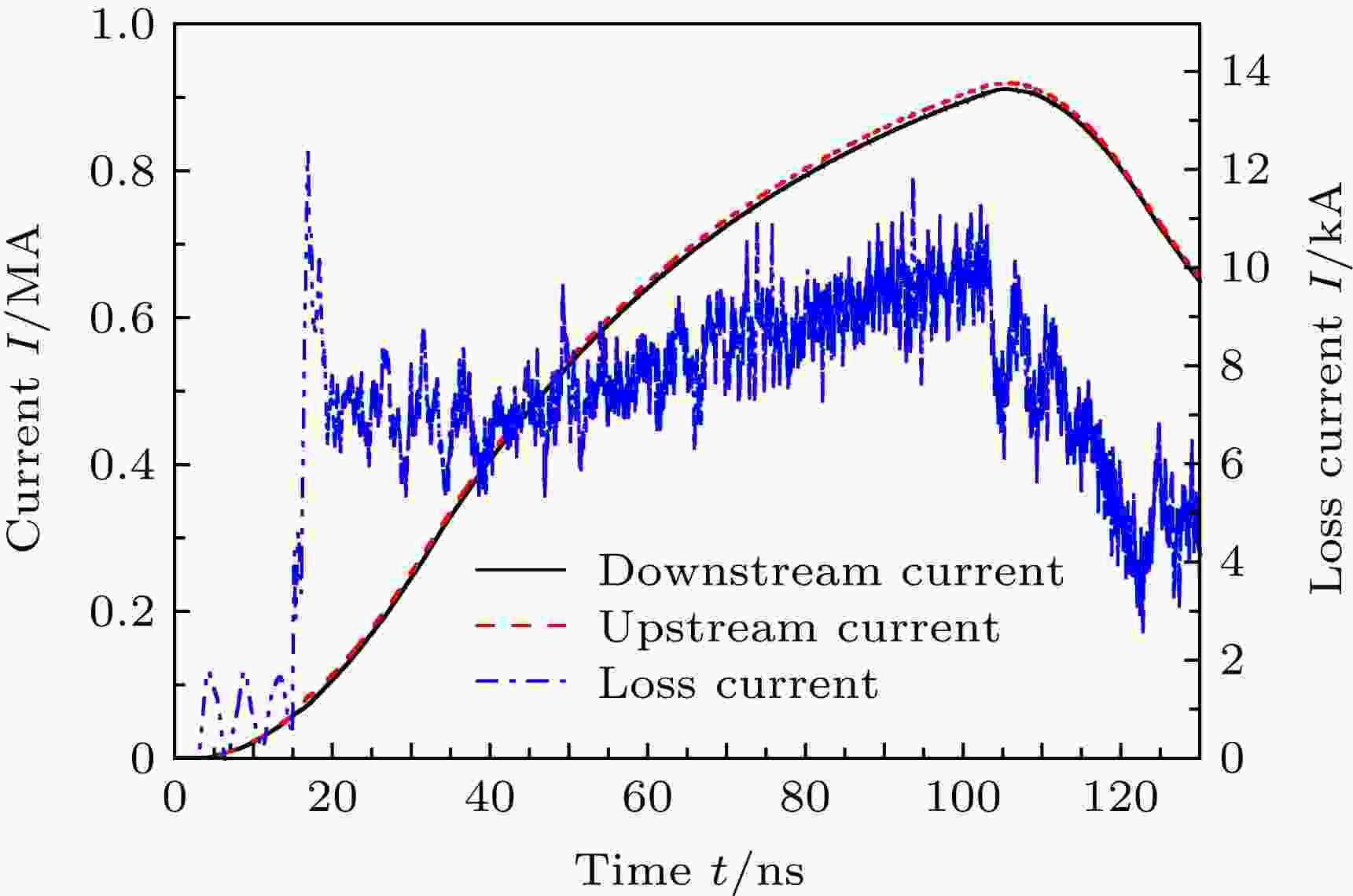
图 4 阴极发射等离子体时, 单孔PHC的上/下游电流
Figure4. The upstream and the downstream currents of the single-hole PHC while the cathode emitted electrons and ions.

图5展示了不同时刻, 阴极等离子体在阴阳极空间的分布. 图5(a)中, 蓝色箭头表示功率传输方向. 功率脉冲由下方进入PHC, 经汇聚后继续传播至负载. 在大约15 ns左右, 阴极开始发射电子, 此时也开始出现质子. 随后电子很快弥漫整个阴阳极空间, 而质子由于电场力的作用被束缚在阴极孔附近. 随着时间推进, 质子开始慢慢向阳极运动, 且质子明显地聚集在红色箭头所指的区域, 而该区域相比其他区域磁场强度相对较高. 最后和电子一样, 质子也逐渐填充满整个间隙, 从而导致阴阳极间隙闭合, 引起电流损失. 由于本文介绍模型自身的结构特点, 有部分电子和质子在电磁力作用下漂移出PHC附近区域. 在分析过程中, 认为这部分粒子的损失并不对PHC间隙闭合有明显影响.
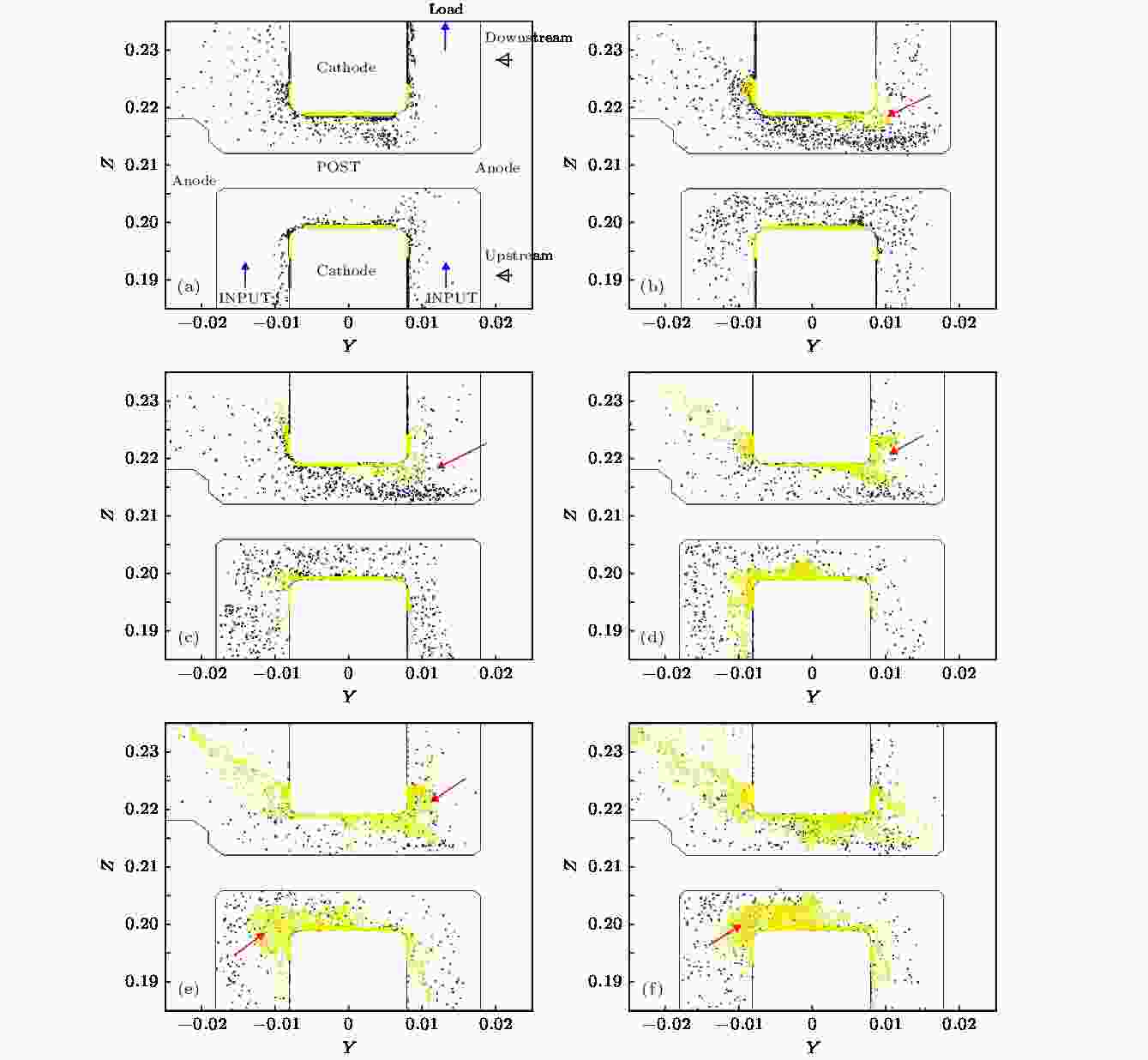图 5 柱-孔附近等离子体随时间运动分布的二维图, 紫色代表电子, 黄色代表质子(横坐标和纵坐标单位: m)　(a) t = 15.8535 ns; (b) t = 23.7802 ns; (c) t = 31.7069 ns; (d) t = 55.4871 ns; (e) t = 71.3401 ns; (f) t = 103.0475 ns
Figure5. Particles distribution near the convolute of the plasmas motion, the purple is electrons, the yellow is ions (unit of the Y/Z-axis: m): (a) t = 15.8535 ns; (b) t = 23.7802 ns; (c) t = 31.7069 ns; (d) t = 55.4871 ns; (e) t = 71.3401 ns; (f) t = 103.0475 ns.

仿真结果显示等离子体密度最大约10¹³ cm^–3, 这可能与电极表面气体脱附率的选择以及电子发射模型的细节设置有关. 如图5所示, 随着时间的推进, 等离子体逐渐漂移至阳极柱. 从阴极孔边沿到阳极柱表面的径向线段上(如图5(b)蓝色线段所示), 等离子体密度分布如图6所示, 横坐标表示空间位置由阳极柱中轴线起, 沿径向至阴极孔边缘并继续延长1 cm左右. 图6中虚线分别标示出阳极柱和阴极孔边缘所在的位置. 等离子体密度分布特点为峰值在阴极孔边沿, 往阳极柱方向迅速减小. 在阴极表面(> 10 mm)则聚集着相对较多的等离子体.
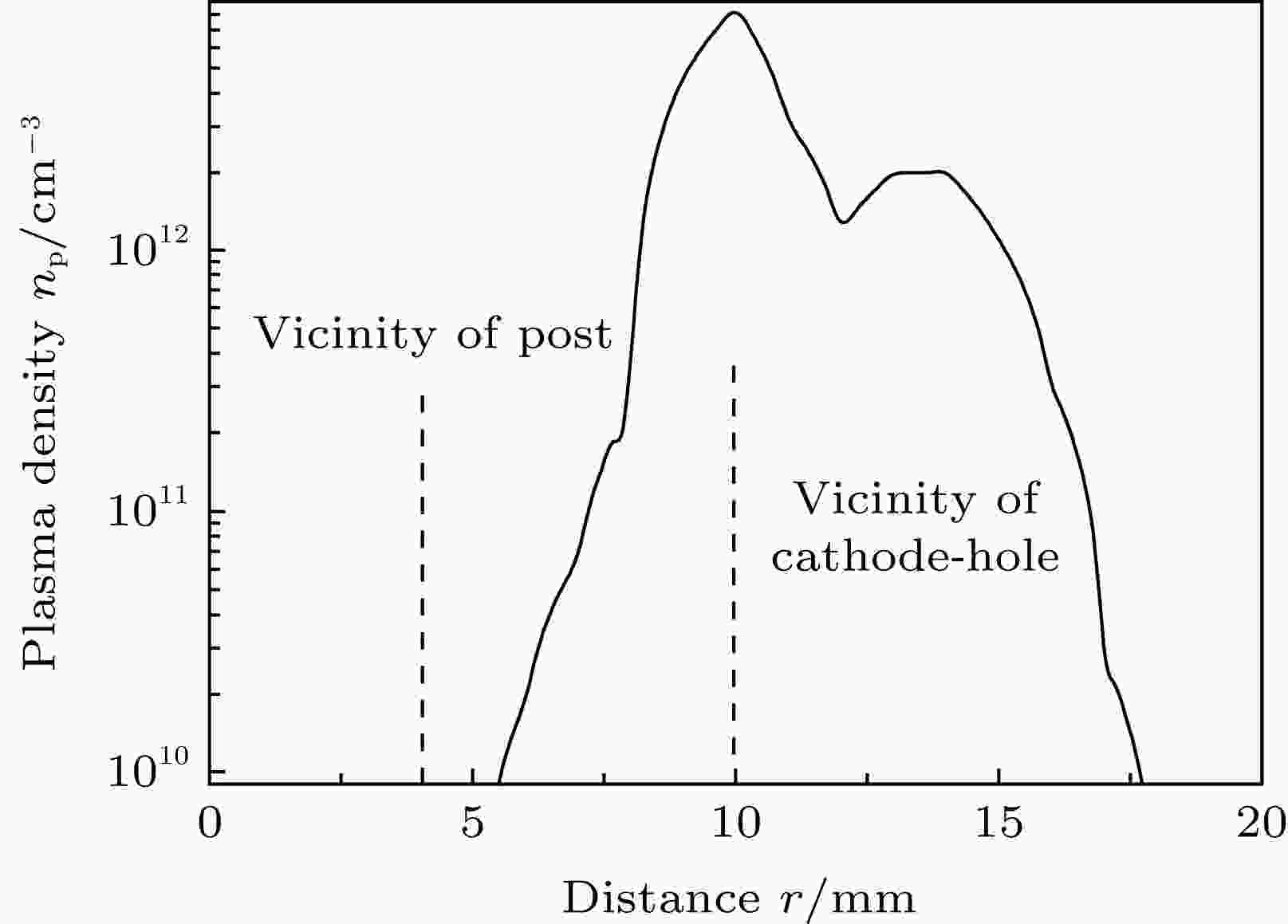图 6 20 ns时刻, 阴极等离子体的密度分布
Figure6. Density distribution of the cathode plasma when time is 20 ns.

选择等离子体密度分布曲线峰值的10%等效为等离子体前沿. 通过寻找不同时刻等离子体前沿的位置可以获得等离子体扩展速度. 图7展示了等离子体前沿的位置随时间变化的情况. 黑色曲线表示实际仿真结果, 红色曲线则是对仿真数据平滑后的结果.
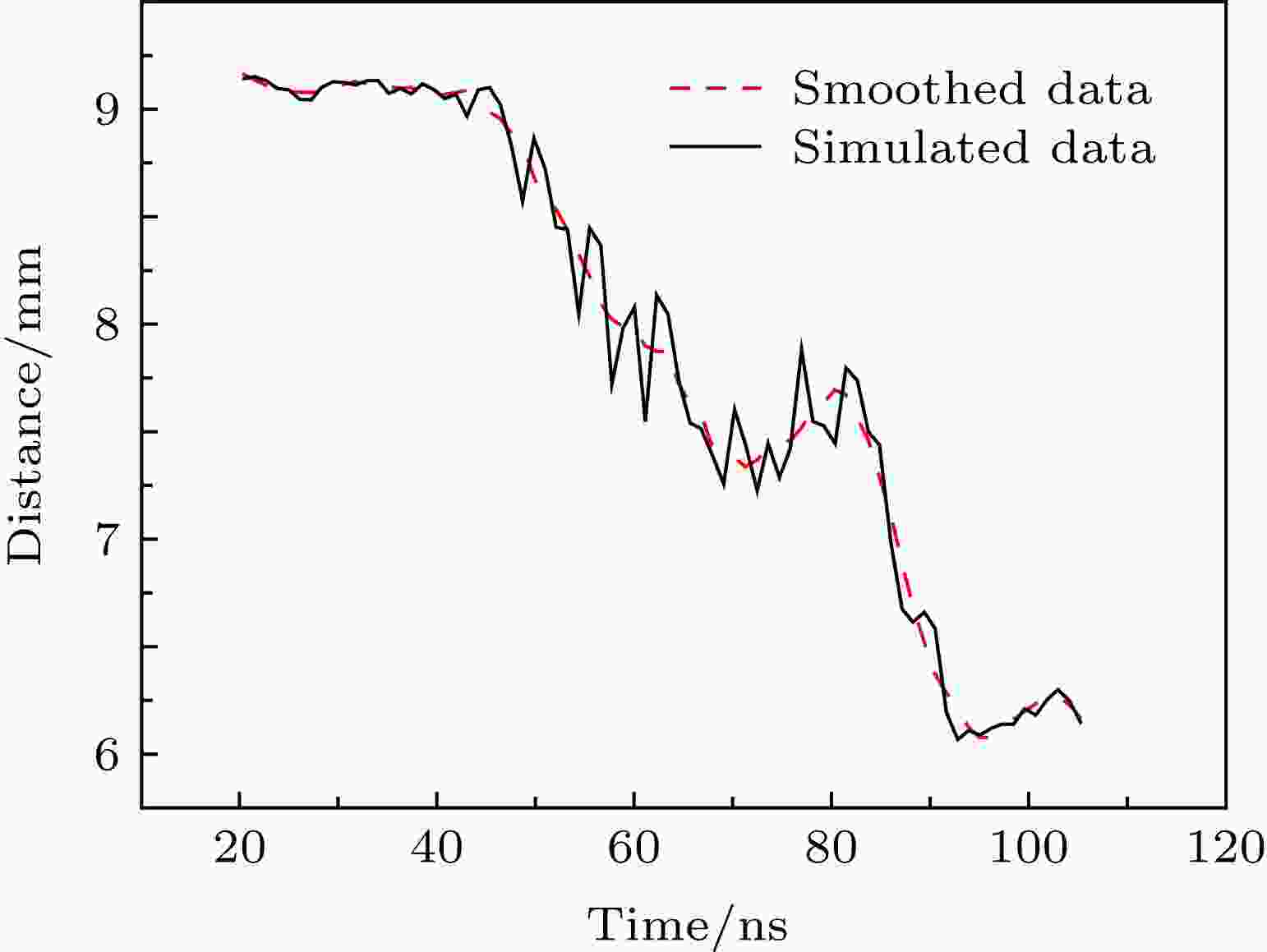图 7 等离子体密度前沿位置随时间变化曲线
Figure7. Motion curve of the front of the plasma density.

由图7可以看出, 在初始阶段(< 40 ns), 等离子体基本被束缚在阴极孔附近, 随后开始向阳极柱移动. 受PHC附近复杂电磁场以及等离子体自身不稳定性的影响, 等离子体的移动过程并不是单调变化的. 在70—80 ns时, 等离子体前沿的移动似乎停滞. 随后, 等离子体继续往阳极柱移动, 但是并未完全到达阳极柱. 整个过程可以获得等离子体平均扩展速度约为3.76 cm/μs. 如果仅考虑图7中等离子体前沿实际移动的过程, 那么等离子体扩展平均速度为5.96 cm/μs.
从仿真结果可以看出, 在整个仿真过程中阴极等离子体明显缩短了阴阳极间距, 然而并未完全导致阴阳极间隙完全导通. 因此单孔PHC仍能较好地传输脉冲电流. 当设置阳极柱发射离子(H⁺), 单孔PHC的电流损失略有增加. 分析其主要原因可能是等离子体密度总体偏低, 导致单孔PHC的阴阳极间隙闭合效果并不明显.
2 -->

3.3.阴极发射含负离子的等离子体

阴极表面发射负离子(H^–)的现象已被多个实验验证^[20,21]. 在阴阳极分别发射等离子体的基础上, 进一步研究了阴极负离子在PHC电流损失过程中对阴阳极间隙闭合的影响. 图8展示了阴极等离子体含有负离子时, 单孔PHC上/下游的电流波形. 图8与图4相比, 上/下游电流在峰值附近的差别更为明显, 电流损失达到20 kA, 损失比约为2.2 %.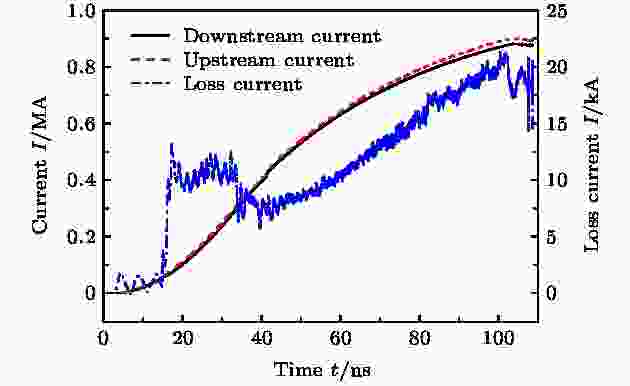
图 8 阴极等离子体含负离子时, 单孔PHC的上/下游电流
Figure8. The upstream and the downstream currents of the single-hole PHC while the cathode emitted electrons, ions, and negative ions.

图9展示了在单孔PHC的阴阳极间隙间, 等离子体的空间位置随时间的变化, 其中紫色为电子, 黄色为离子, 绿色为负离子. 相比离子, 阴极负离子的运动明显更剧烈, 除了往阳极漂移, 部分阴极负离子在电磁场作用下漂移至负载区. 往阳极柱漂移的阴极负离子移动很快, 大约在34 ns左右已有少量阴极负离子到达阳极柱表面. 这意味着, 阴极负离子会导致间隙更快闭合.
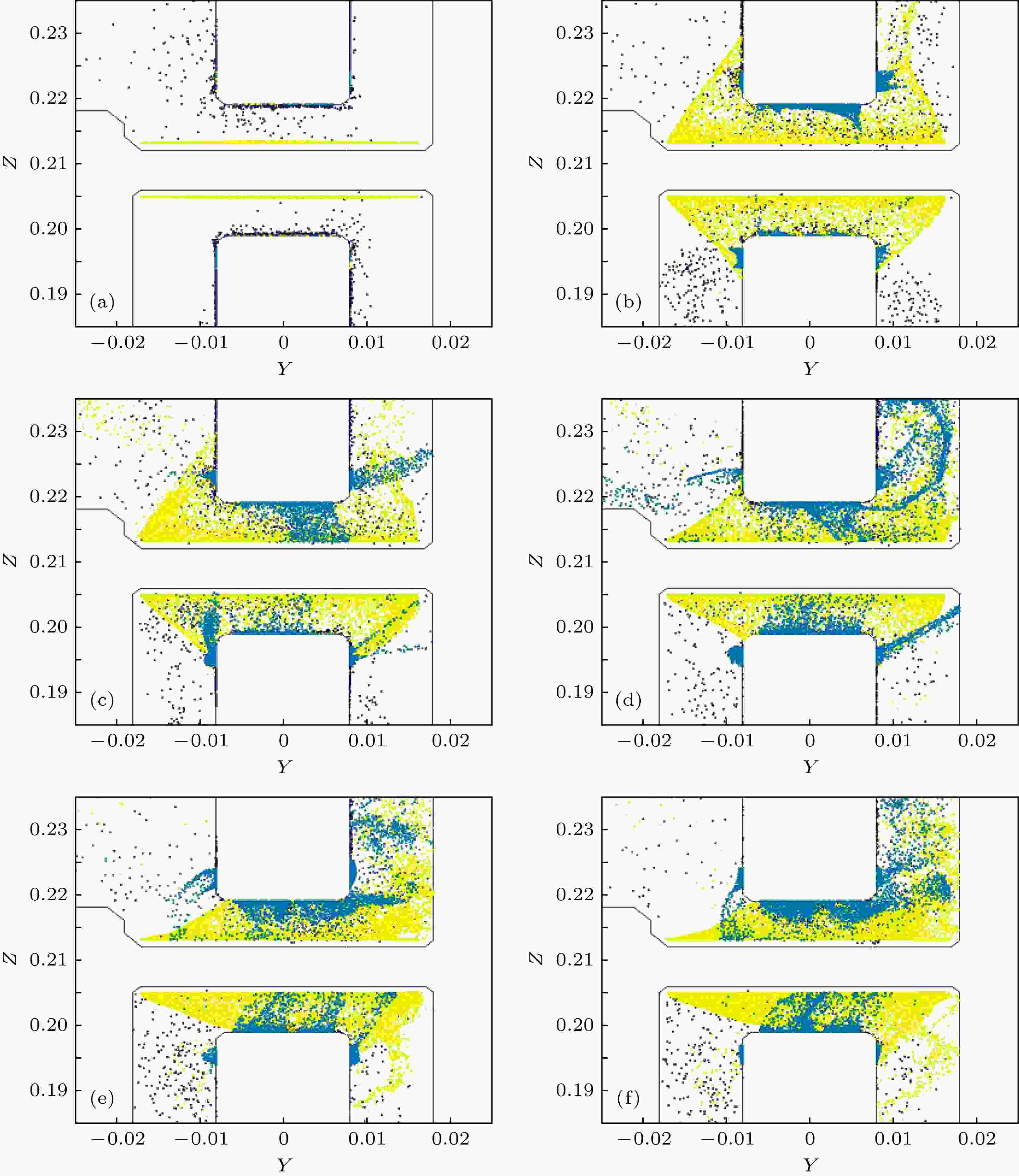图 9 柱-孔附近等离子体随时间运动分布的二维图(横坐标和纵坐标单位: m)　(a) t = 15.4005 ns; (b) t = 21.7419 ns; (c) t = 34.4247 ns; (d) t = 59.7902 ns; (e) t = 97.8381 ns; (f) t = 108.6064 ns
Figure9. Particles distribution near the convolute of the plasmas motion (unit of the Y/Z-axis: m): (a) t = 15.4005 ns; (b) t = 21.7419 ns; (c) t = 34.4247 ns; (d) t = 59.7902 ns; (e) t = 97.8381 ns; (f) t = 108.6064 ns.

阴极负离子的密度分布规律与图6相近, 其密度最大值仅为10⁹ cm^–3. 依据同样的方法, 可以得到阴极负离子前沿随时间变化的曲线. 图10与图7相比, 负离子从产生时刻起, 就在电磁场作用下往阳极柱漂移. 在30—40 ns区间, 负离子的漂移略有停滞. 然后在50 ns左右, 负离子到达阳极柱表面. 分析整个移动过程, 可获得负离子平均漂移速度约为10 cm/μs.
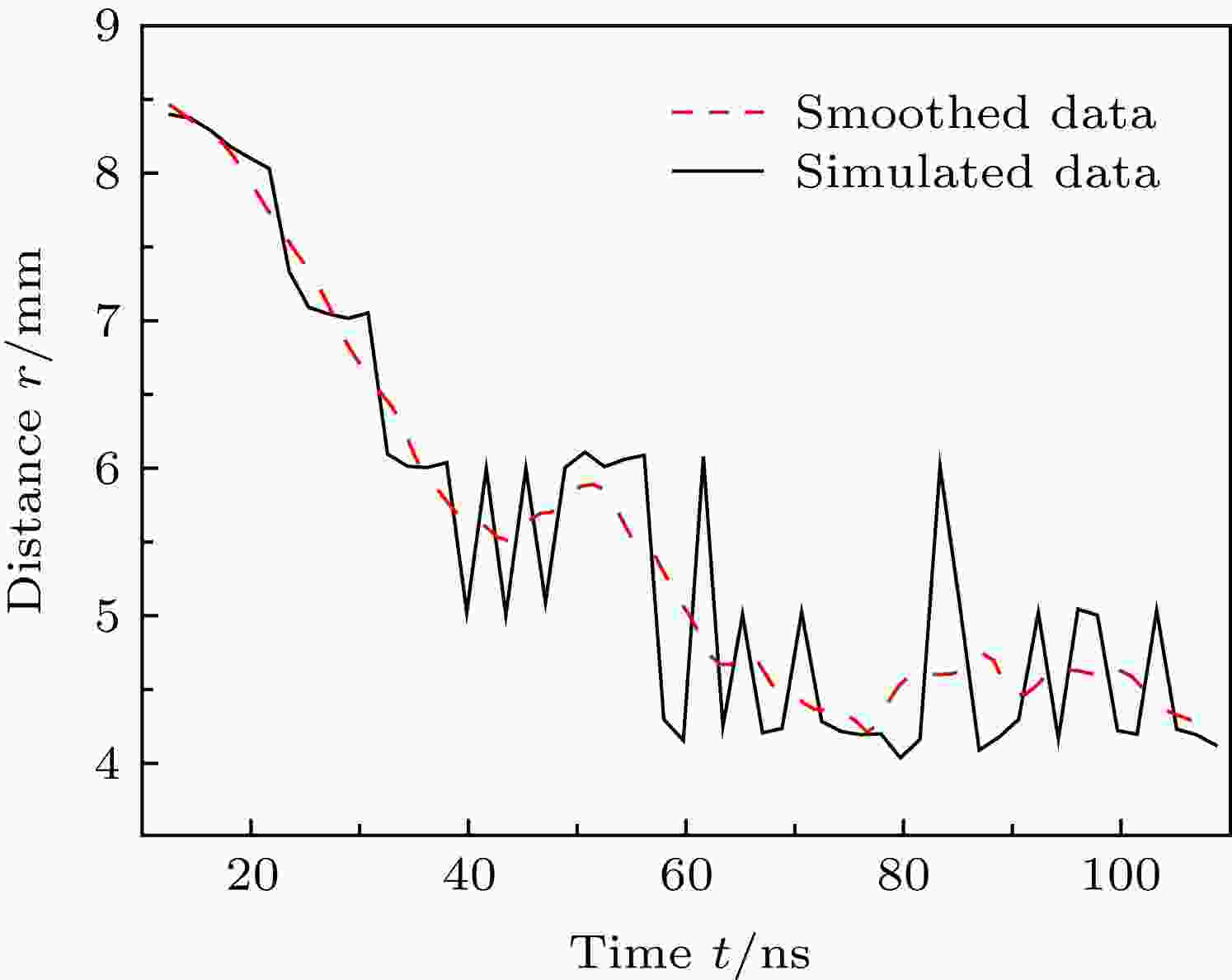图 10 负离子密度前沿位置随时间变化曲线
Figure10. Motion curve of the front of the negative density.

仿真结果表明, 阴极负离子的存在增强了单孔PHC阴阳极间隙闭合效果, 损失电流明显增加. 阴极负离子的移动速度大于阴极等离子体扩展速度, 因此能使阴阳极间隙更早闭合. 阴极负离子发射模型选择确定了负离子的密度. 阴极负离子在密度较低的前提下, 依然导致了明显的电流损失. 本文仿真结论与文献[22]关于负离子在磁绝缘二极管电流损失的仿真研究结论基本一致, 认为负氢离子可以使阴阳极间隙闭合, 导致电流损失.
2 -->

3.4.仿真结果与实验结果的比较分析

同时在“强光一号”加速器上开展了一系列单孔PHC电流传输实验研究, 获得了单孔PHC上/下游电流波形以及损失电流. 通过对单孔PHC上/下游电流波形的分析, 获得了单孔PHC阴阳极间隙闭合的平均速率. (2)式用于估算阴阳极间隙闭合的平均速率.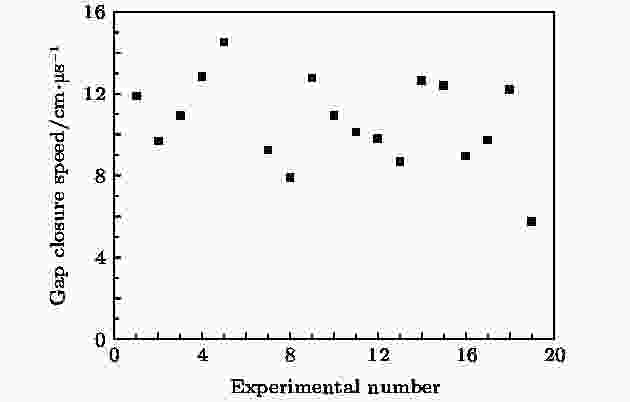

${v_{\rm{g}}} = \frac{l}{{{t_2} - {t_1}}},$

其中l为阴阳极间隙距离; t₂为间隙完全闭合时刻, 定义为上/下游电流波形出现明显差别的时刻; t₁为间隙开始闭合时刻, 定义为电流幅值为峰值10%的时刻. 实验中, 可以调整阴极孔和阳极柱的直径. 图11展示了根据(2)式估算得到的全部单孔PHC的阴阳极间隙闭合平均速率, 为5.74—14.52 cm/μs.
图 11 阴阳极间隙闭合速率
Figure11. Experimental data of the gap closure speed.

经比较分析, 发现通过实验数据估算得到的阴阳极间隙闭合速率的数值范围涵盖了3.3节中阴极负离子前沿平均漂移速度值, 但是大于 3.2节中阴极等离子体前沿平均漂移速度值. 结果间接证明阴极负离子的运动对高功率单孔PHC的电流损失有明显的影响.
关于PHC附近等离子体的仿真^[9-13]研究中, 阴极等离子体的扩散速度始终采用大约3 cm/μs的经典扩散速度. 理论上对于间隙为1 cm的MITLs (含有PHC), 前沿约为100 ns的脉冲电流的主峰能够无损失或很少损失地传输至负载, 电流损失现象应当出现在电流后延部分. 然而实验结果却与理论仿真结果不同, 电流损失现象常常出现在电流峰值之前^[6,7]. 这暗示必定有另外的机制使得阴极等离子体扩展更快, 阴阳极间隙闭合时刻更早. 通过分析等离子体可能的组成成分^[20,21], 认为负氢离子是该机制最有力的竞争者. 本文以及文献[22]的仿真结果, 证明了负氢离子能够脱离磁场约束到达阳极, 从而导致明显的电流损失. 本文的仿真结果, 结合实验结果相互佐证, 显示负氢离子的漂移速度明显大于经典的阴极等离子体扩散速度3 cm/μs, 进一步证明负氢离子的存在能够更快地导致阴阳极间隙闭合.

本文介绍了单孔PHC电流传输特性的仿真实验研究, 描述单孔PHC仿真几何模型及其仿真设置, 比较了阴极发射电子、等离子体以及阴极发射含负离子等离子体等三种工作模式.
当阴极仅发射电子时, 单孔PHC能够高效地传输脉冲电流. 虽然电子弥漫整个阴阳极空间, 但是并不能导致间隙有效闭合. 当阴极发射等离子体时, 仿真结果发现较明显的电流损失. 等离子体的运动缩短了阴阳极间隙的有效长度, 其平均扩展速度约为3.76 cm/μs. 仿真结果与现有磁绝缘理论、仿真研究和实验结果一致.
当阴极发射含负氢离子的等离子体时, 此时等离子体的成分主要有电子、离子和负氢离子. 仿真结果发现单孔PHC的电流损失进一步增大. 阴极负离子的平均移动速度约为10 cm/μs, 能够更快使间隙闭合. 通过仿真计算获得的氢负离子运动速度与实验估算的间隙闭合速度接近. 基于负离子的发射模型采用实验经验公式, 负离子的密度偏低, 仅为10⁹ cm^–3. 对仿真结果的分析认为阴极负离子在PHC电流损失现象中发挥了重要作用, 是导致PHC电流损失的主要机制之一. 结果同时暗示等离子体内部微粒的运动复杂, 并不是完全作为一个整体而运动. 复杂电磁场可能导致等离子体内部微粒局部分离为多个小部分. 每个小部分主要聚集了电荷极性相同的微粒, 并在电磁场的作用下做复杂的运动.
文中因为等离子体发射模型设置等原因, 电子-等离子体密度最大值仅为10¹³ cm^–3, 远小于常用的密度值^[8-10]. 虽然在低密度条件下, 仍能发现明显的电流损失, 且能定性分析等离子体的运动特性, 但是以此解释高密度条件下, 单孔PHC电流传输及等离子体的运动特性, 则有一定的局限性. 仿真计算中, 还未仔细考虑粒子输运过程中粒子碰撞、中性气体电离等复杂物理机理, 仿真结果偏理想化. 另外, 馈入前行电压波形并非实验波形, 也会对仿真结果带来偏差. 因此未来的仿真研究工作, 主要是调整馈入电压信号, 采用实际的实验电压波形, 并合理调节等离子体发射模型参数, 逐渐加入粒子输运过程中粒子输运的物理机理, 以期获得等离子体密度在10¹⁵—10¹⁷ cm^–3时, 单孔PHC电流传输及等离子体的运动特性.