摘要:太赫兹时域光谱技术在安检、无损检测、生物医学等领域有广泛的应用, 而其在雷达目标特性领域的应用一直存在诸多争议. 针对目前太赫兹时域光谱雷达散射截面定量测量的难题, 本文基于太赫兹时域光谱技术搭建了太赫兹时域光谱目标散射测量系统, 利用该系统测量了金属球、金属圆盘、金属圆柱等典型定标体在0.2—1.6 THz频段内的极窄时域脉冲回波, 数据处理后得到了各定标体的雷达散射截面, 与理论数据对比验证了系统测量结果的精度. 在此基础上, 测量了太赫兹频段电大尺寸复杂目标的雷达散射截面, 并将表面积分方程法与多层快速多极子算法相结合对目标的雷达散射截面进行了数值计算, 测量值与理论值达到了较好的一致性. 研究结果为太赫兹时域光谱技术在太赫兹目标特性领域的应用奠定了基础.
关键词: 太赫兹/
时域光谱/
雷达散射截面

English Abstract

全文HTML

--> --> -->

太赫兹波(频率0.3—10 THz, 波长1—30 μm)是位于微波与红外之间的一段特殊电磁波段, 长期以来, 由于缺乏有效的太赫兹波发射和探测装置而一直处于未开发状态, 从而形成了电磁波研究中的“空隙”, 近年来, 随着技术的发展, 这一波段已经在医疗卫生、航天航空、基础科研等领域有了广泛的应用. 太赫兹在目标特性领域的主要优势有: 相对于激光, 太赫兹波的穿透力更强, 能够穿透烟雾、沙尘等, 可用于复杂环境; 相对于微波, 带宽更大, 带来更高的目标分辨率, 高分辨图像能够获得目标更丰富的特征信息, 更好地获取目标的精细结构和微动特征; 在反隐身方面有极大的应用潜力^[1,2].
目前, 美、欧等国已建立了多个微波倍频太赫兹波目标特性实验室. 其中比较典型的是美国马萨诸塞大学罗威尔分校(University of Massachusetts Lowell)所属的亚毫米波技术实验室(Submillimeter-Wave Technology Laboratory, STL), 研究人员已经建立了多套连续太赫兹波实验系统(例如: 0.24, 0.35, 0.52, 0.585, 1.56 THz等频段)^[3,4], 并对这些频率的雷达散射截面(radar cross section, RCS)等目标特性进行了深入研究. 国外基于时域光谱技术的太赫兹频段目标特性研究同样起步较早, 2000年, 美国俄克拉荷马州立大学的研究人员利用其搭建的太赫兹时域光谱雷达系统对3 mm直径氧化铝圆柱体的散射进行了研究, 在0.2—1.4 THz范围内, RCS的测量结果与PO理论解具有非常好的一致性^[5]. 2010年, 丹麦科技大学基于时域光谱测量系统获得了1.1 THz等频点处的1︰150缩比F-16飞机模型的360°全方位向RCS结果, 并对缩比模型进行了成像^[6]. 2012年, 德国太赫兹中心的研究人员通过光纤耦合太赫兹时域光谱系统测量了200 GHz等频点处金属球、圆柱等定标体RCS, 与理论解比较测量值达到了较小的误差, 并测量了1︰250缩比旋风飞机模型的180°方位向RCS^[7].
近来, 国内国防科技大学对太赫兹目标特性进行了相关的研究^[8]; 中国工程物理研究院于2011年采用自主研制的太赫兹器件构建了国内首个0.14 THz高分辨率逆合成孔径雷达成像实验系统^[9], 2013年又完成了670 GHz全固态成像雷达^[10].
当前国内的研究成果多基于太赫兹低频段连续波系统, 而对基于太赫兹时域光谱技术的RCS测量一直缺少准确的定量研究, 时域光谱技术目前能够覆盖非常大的频率范围(2 THz以上), 在如此宽的频域范围内要对目标的RCS进行准确的测量具有非常大的难度. 本文基于太赫兹时域光谱技术, 搭建了时域光谱散射测量系统, 具备0.1—1.6 THz目标RCS测量及成像能力. 在系统性能测试的基础上^[11], 测量了几种典型定标体的RCS, 与理论结果误差在3 dB以内, 验证了系统的测量能力. 然后测量了几种复杂目标的RCS, 并将表面积分方程法与多层快速多极子算法相结合对目标的雷达散射截面进行了数值计算, 经测量与仿真结果对比, 0.2—1.6 THz范围内误差均在3 dB以内. 本文的工作解决了时域光谱宽频段(0.2—1.6 THz)RCS定量测量的难题, 对后续目标RCS测量等夯实了基础; 测量结果与理论仿真结果具有非常好的一致性, 验证了测量与数值计算方法的准确性.

基于太赫兹时域光谱技术建设了一套太赫兹时域光谱目标散射测量系统, 该紧缩场系统可以实现远场测试环境, 系统后向散射角为6.5°, 具有目标准后向散射信号的测量能力, 测量系统如图1所示. 太赫兹波由光电导天线产生后经紧缩场系统扩束准直后入射到目标处, 目标散射的太赫兹波经收集紧缩场光路进入接收天线, 接收天线采集到的数据由锁相放大器处理最终得到原始时域回波数据. 有机玻璃密闭罩将整个太赫兹波传输光路密封在湿度可控的环境中. 测量时, 系统湿度控制在3%以下, 以最大限度地减少太赫兹波传输中的空气损耗. 系统搭建完成后, 我们对系统的各项性能进行了测试, 其中对目标区太赫兹波强度的测量结果如图2所示, 图中显示了在垂直于入射波方向的二维平面上的太赫兹波强度分布, 呈明显的高斯分布, 由此可确定静区的范围.
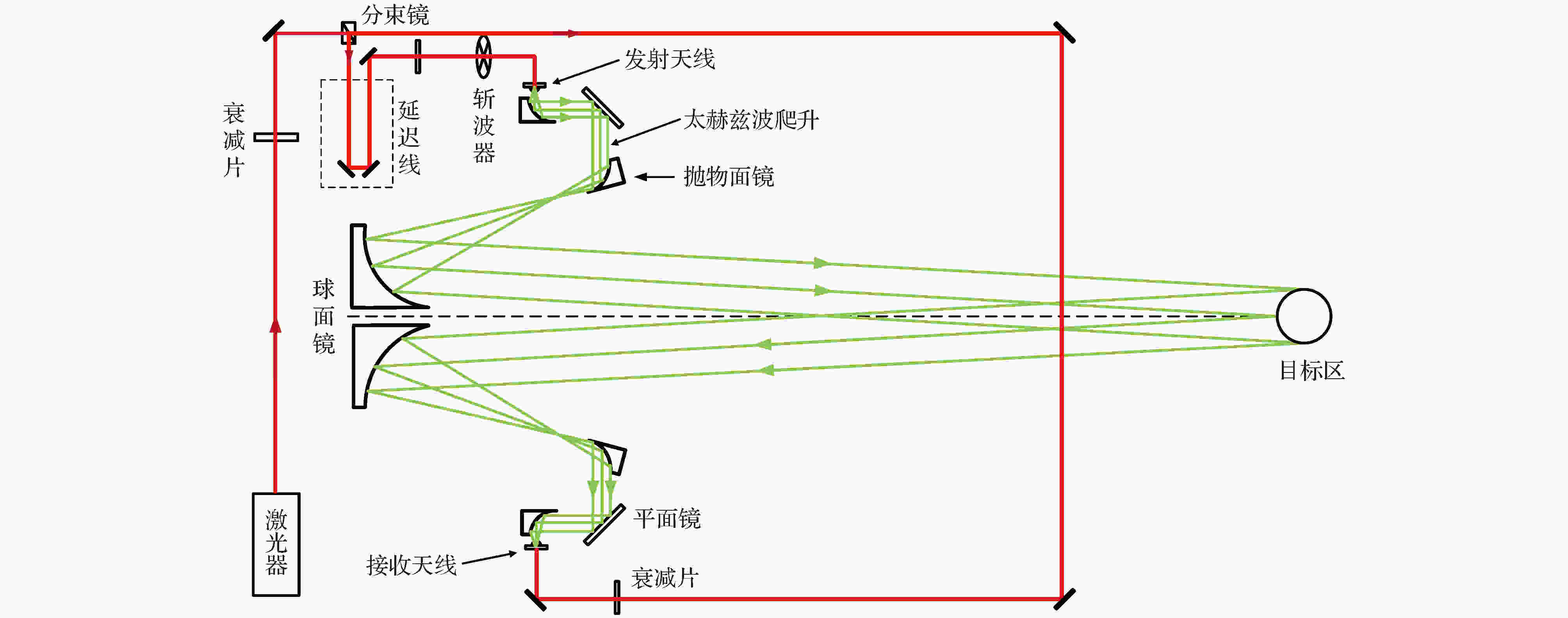图 1 太赫兹时域光谱散射测量系统光路图
Figure1. Scattering measurement system of terahertz time domain.

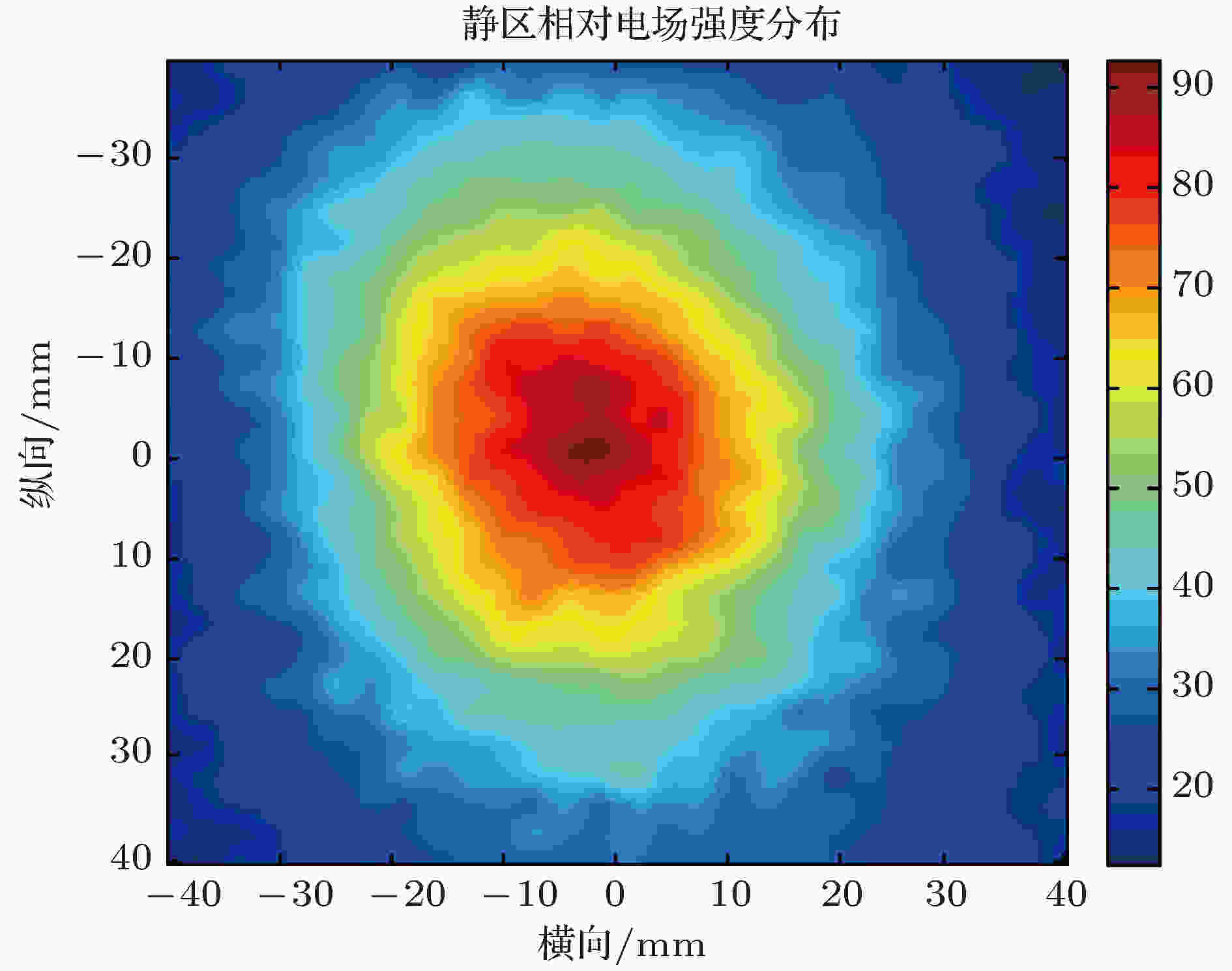图 2 目标区太赫兹波场强分布图(单位: μV)
Figure2. Distribution of the field intensity (unit: μV).

上述区域场强峰值变化较大, 场强均匀区域较小, 对于直径超出该区域的的金属球仍然可测得其准确的RCS. 原因如下: 测试所用的金属球直径在厘米量级, 电尺寸超过20, 处于光学区, 此时金属球的散射中爬行波可忽略, 主要为镜面反射, 而金属球镜面反射区域小于场强均匀区域, 保证了测量结果的准确.

2

-->

3.1.定标体

采用相对定标法测量目标的RCS, 公式如下:

${\sigma _{{\rm{obj}}}}(f) = {\sigma _{{\rm{cal}}}}(f)\frac{{{P_{{\rm{obj}}}}(f)}}{{{P_{{\rm{cal}}}}(f)}},$

式中, ${\sigma _{{\rm{cal}}}}(f)$为定标体在频率f处的理论RCS, ${P_{{\rm{obj}}}}(f)$和${P_{{\rm{cal}}}}(f)$分别为目标和定标体时域回波测量值经傅里叶变换后在频点f处的回波功率值. 实际计算时, 由于时域光谱系统的频谱分辨率较低, 本文测试时将信号频谱分辨率统一处理为10 GHz, 为消除个别频点数据的偶然性, (1)式中频点f处的功率由以该频点为中心频率、带宽40 GHz范围内的功率的平均值得到.
金属球、圆盘、圆柱的RCS理论精确解分别由(2), (5)及(6)式得出^[12].

$\sigma = {\lambda ^2}/\pi {\left| {\sum\limits_{n = 1}^\infty {{{( - 1)}^n}} (n + 0.5)\left( {{b_n} - {a_n}} \right)} \right|^2} ,$

${a_n} = \frac{{{j_n}(ka)}}{{h_n^{(1)}(ka)}} ,$

${b_n} = \frac{{ka{j_{n - 1}}(ka) - n{j_n}(ka)}}{{kah_{n - 1}^{(1)}(ka) - nh_n^{(1)}(ka)}} ,$

其中$k = \dfrac{{2\text{π}}}{\lambda }$, 为波数, a为导电球半径; λ为雷达工作波长.
$h_n^{(1)}(x) = {j_n}(x) + {\rm i}{y_n}(x)$为第一类球汉克尔函数; ${j_n}(x)$为第一类球贝塞尔函数; ${y_n}(x)$为第二类球贝塞尔函数.

$\sigma = \frac{{4{\pi^3}{r^2}{{\cos }^2}\varphi {{\sin }^2}(2kr\sin \varphi )}}{{{{(2\lambda kr\sin \varphi )}^2}}},$

式中r是圆盘半径, φ是入射角.

$\sigma = \frac{{ka{l^2}{{\cos }^2}\varphi {{\sin }^2}(kl\sin \varphi )}}{{{{(kl\sin \varphi )}^2}}},$

式中a, l分别是圆柱地面半径及柱高, φ是入射角.
此外, 为实现导体目标太赫兹频段散射特性的数值仿真, 本文采用表面积分方程法(surface integral equation method, SIE)结合阻抗边界条件(impedance boundary condition, IBC)建模技术进行分析^[13].
在太赫兹频段导体目标的电导率不再趋于无限大, 而是随频率变化. 导体目标可以认为是有耗介质, 表面波阻抗增加. 此时导体目标边界上满足阻抗边界条件, 其表面电场与磁场的关系为:

${\hat{ n}} \times \left( {{\hat{ n}} \times { E}} \right) = - {\eta _0}{\eta _{\rm{s}}}\left( {{\hat{ n}} \times { H}} \right) = - {\left. { E} \right|_{\tan }},$

${\hat{ n}} \times \left( {{\hat{ n}} \times { H}} \right) = \frac{1}{{{\eta _0}{\eta _{\rm{s}}}}}\left( {{\hat{ n}} \times { E}} \right) = - {\left. { H} \right|_{\tan }},$

其中${\eta _0}$表示自由空间波阻抗, ${\eta _0}$为相对表面阻抗, ${\hat{ n}}$为导体表面单位外法向矢量.
根据等效原理${ J} = {\hat{ n}} \times { H}$, ${ M} = { E} \times {\hat{ n}}$, 推导出表面电流和磁流的关系:

${ J} = \frac{1}{{{\eta _0}{\eta _{\rm{s}}}}}{\hat{ n}} \times { M} \;\;{ M} = - {\eta _0}{\eta _{\rm{s}}}{\hat{ n}} \times { J},$

从而建立表面积分方程进行求解.
在太赫兹频段采用数值法进行电磁建模时往往面临电大尺寸问题, 本文采用多层快速多极子算法(multilevel fast multipole algorithm, MLFMA)对矩阵方程加速计算^[14,15]. MLFMA利用几何分组, 将子散射体(基函数)之间的耦合关系分为近区和远区关系. 近区组内子散射体的耦合通过严格的矩量法(moment of method, MoM)直接计算; 远区组内的子散射体耦合关系则利用加法定理将格林函数在谱域内进行展开:

$\frac{{{{\rm e}}^{{\rm i}k{{r}_{ji}}}}}{{{r}_{ji}}}=\frac{{\rm i}k}{4{\text{π}}}\int{{{{\rm d}}^{2}}\hat{k}{{{\rm e}}^{{\rm i}\hat{k}\cdot ({{r}_{jm}}-{{r}_{i{m}'}})}}{{\alpha }_{m{m}'}}({{{\hat{r}}}_{m{m}'}}\centerdot \hat{k})},$

其中i和j为场源基函数编号, m和m'为场源分组编号, k为自由空间波数, $ {{\alpha }_{m{m}'}}({{\hat{r}}_{m{m}'}}\centerdot \hat{k})$为转移因子. 最后通过聚合-转移-配置过程来实现. MLFMA将传统MoM的计算量和存储量从$O\left( {{N^2}} \right)$量级减少为$O\left( {N\log N} \right)$量级, 其中N为数值计算未知量数. MLFMA采用迭代算法求解矩阵方程, 应用了广义最小残差方法(generalized minimal residual, GMRES)并结合预条件技术加速收敛. GMRES每次迭代只需进行一次矩阵矢量相乘运算, 具有较稳健的收敛性能; 预条件则利用MLFMA的附近组阻抗矩阵元素构造预条件矩阵, 能够显著提高迭代求解的计算效率.
经此数值方法计算得到的定标体RCS与经典解具有非常好的一致性, 验证了数值方法的准确性.
测量过程中, 以直径35 mm的金属球作为定标体, 测量直径50 mm的金属球、直径20.9 mm的金属圆盘以及底面直径20 mm柱高20 mm的金属圆柱, 直径50 mm的金属球RCS测量结果及理论值如图3所示, 直径20.9 mm的金属圆盘测量结果如图4所示, 底面直径20 mm柱高20 mm的金属圆柱测量结果如图5所示. 目标由金属铝制作, 表面粗糙度均小于0.3 μm.
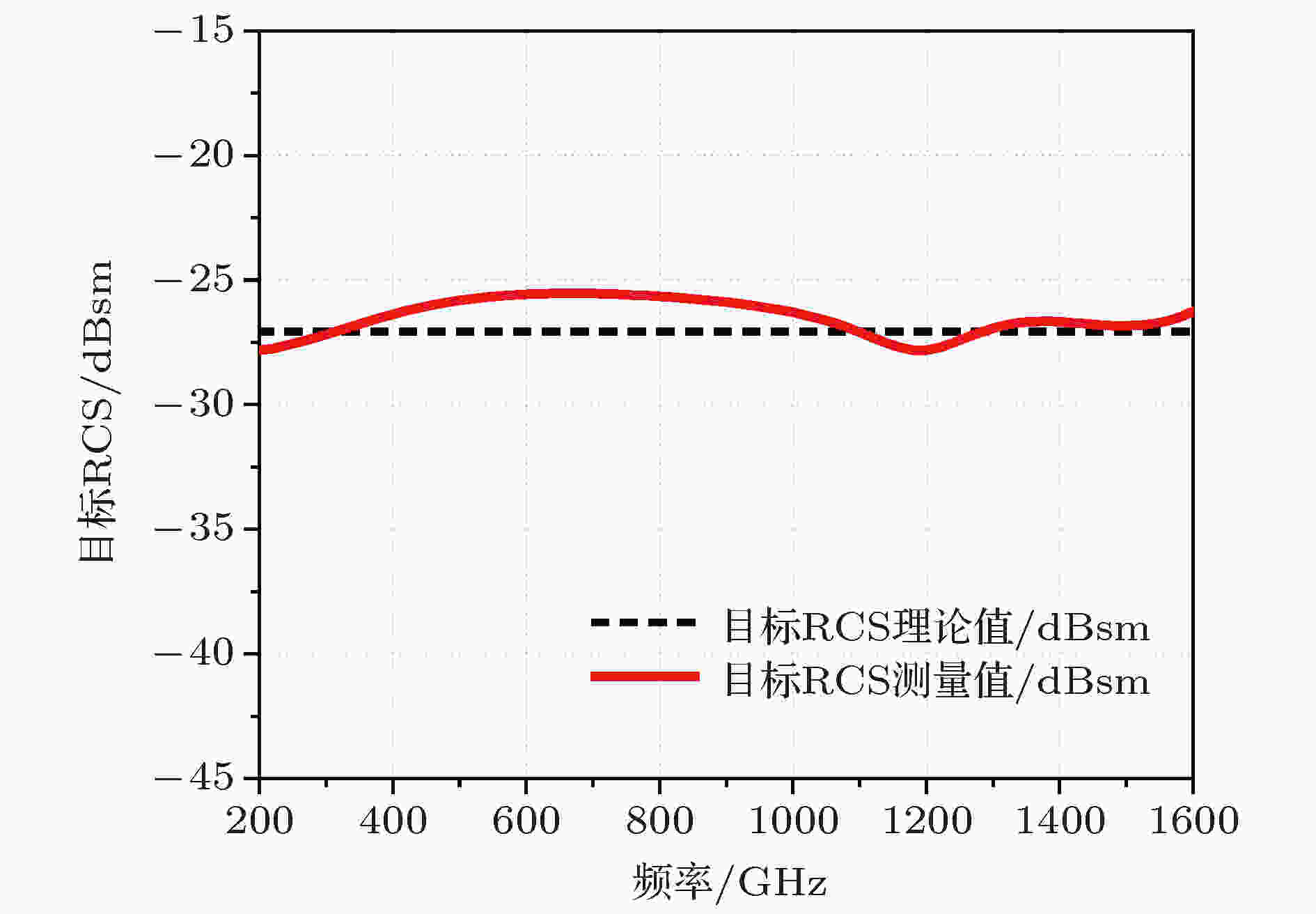图 3 直径50 mm金属球RCS
Figure3. RCS of the sphere with the diameter of 50 mm.

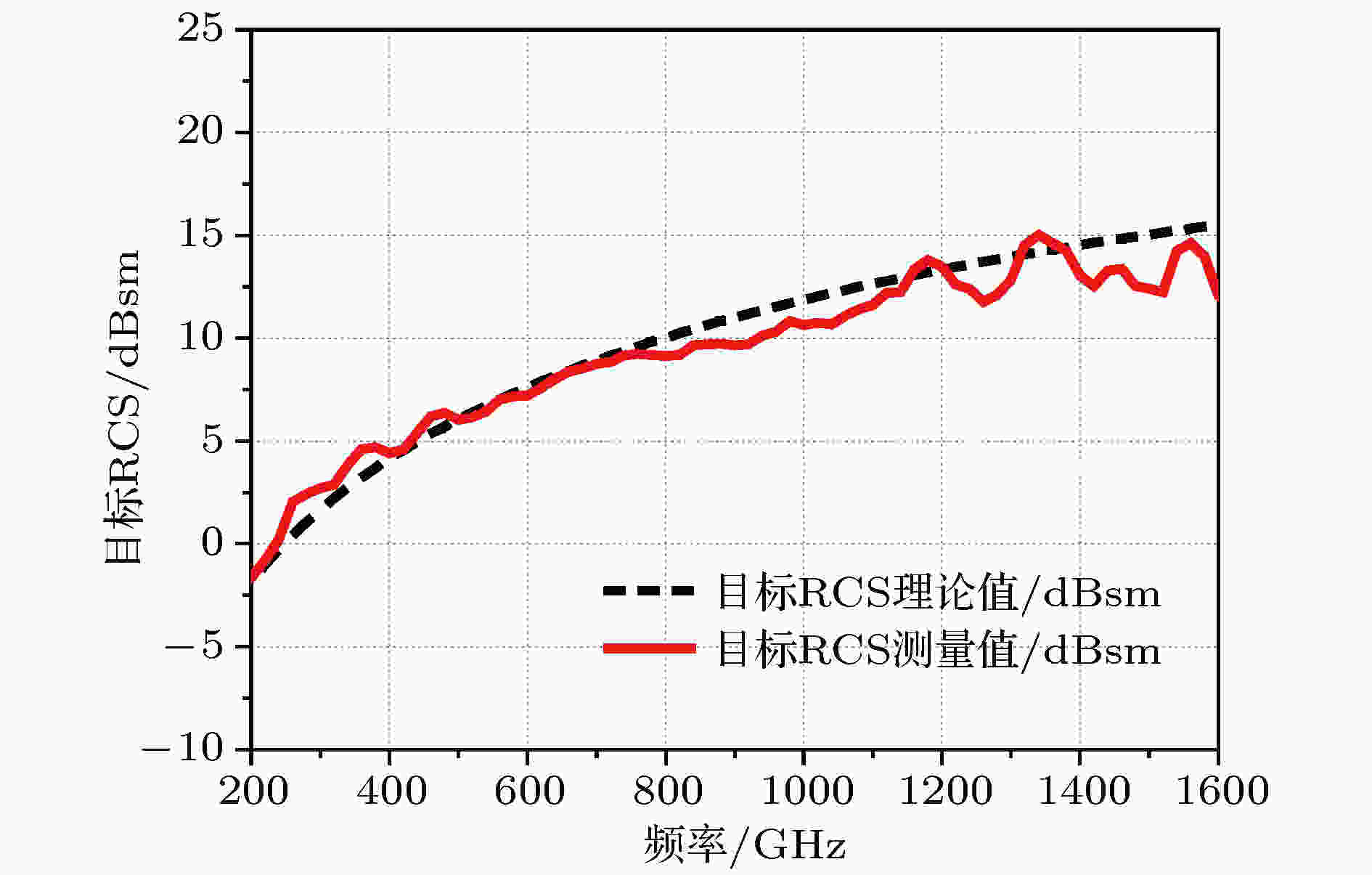图 4 直径20.9 mm金属圆盘RCS
Figure4. RCS of the disk with thediameterof 20.9 mm.

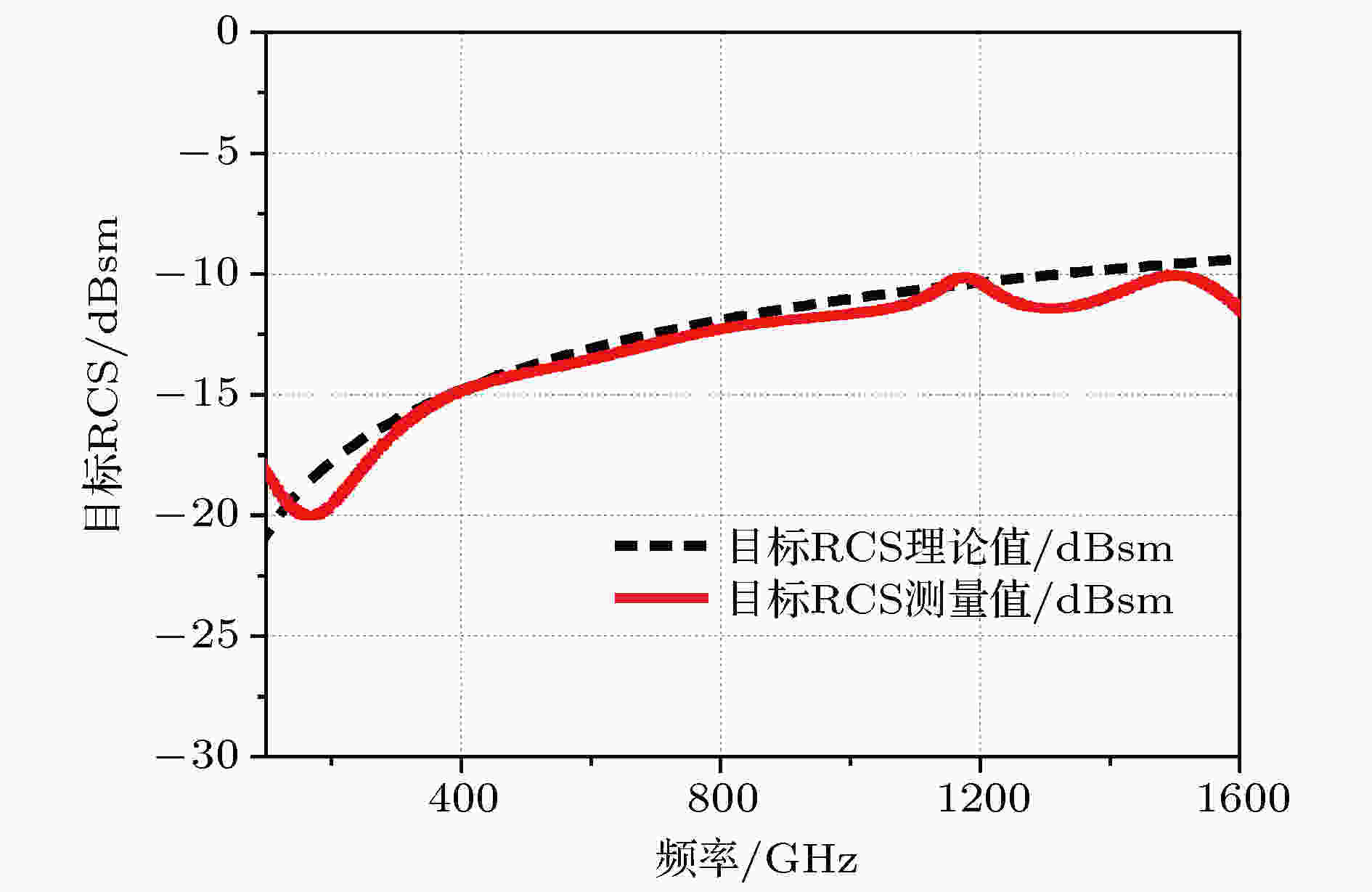图 5 金属圆柱RCS定标结果
Figure5. RCS of the cylinder with the diameter of 20 mm and height of 20 mm.

2 -->

3.2.复杂目标

在0.2—1.6 THz范围内定标体的RCS测量误差小于3 dB, 由此验证了系统及测量技术的有效性. 为进一步测量复杂目标的RCS, 我们制作了带有细微结构的边长30 mm的正方形复杂样件, 目标材质为金属铝, 表面粗糙度均小于0.3 μm, 如图6和图7所示. 测量时, 由于系统的双站角为6.5°, 因此目标姿态为垂直放置, 入射角3.25 °. 对目标建模计算时, 由于目标加工有一定随机性, 会造成模型与实物有一定的误差. 在建模时也对实物几何尺寸进行了多次测量, 尽量减小目标的加工带来的误差. 计算时部分频点处材料的复介电常数如表1所列, 其余频点处的数值由拟合得到.
图 6 贯穿孔结构平板实物
Figure6. Photos of the plate with through-holes.

图 7 螺钉结构平板实物
Figure7. RCS of the plate with screws.

频率/GHz	300	500	700	1000	2000
介电常数实部	–138064.3	–133443.8	–128980.3	–122568.8	–103475.4
介电常数虚部	372225.1	354601.0	337760.7	313903.6	245394.5

表1不同频点处复介电常数
Table1.Complex permittivity in different frequency.

普通定标体在太赫兹频段的散射中心相对单一, 主要为镜面散射中心. 而凹腔等结构的多次复杂散射是实际情况中普遍存在的, 因此对此类目标的测量就更具现实意义.
由于时域光谱系统时域(空域)的超高分辨力, 我们能够得到目标细微结构的回波, 如图8所示. 与一维距离像相对应, 目标的各处散射中心对应的回波在时域信号中清晰可辨, 并可根据回波峰值的位置精确计算出目标不同散射面的几何结构数据. 两类复杂目标的RCS理论计算及测量结果如图9及图10所示. 复杂目标的RCS测量结果显示0.2—1.6 THz范围内测量与理论值误差在3 dB以内, 表明系统对复杂目标的RCS测试精度同样在3 dB误差内.
图 8 螺钉结构平板时域回波
Figure8. Time domain echo of the plate with screws.

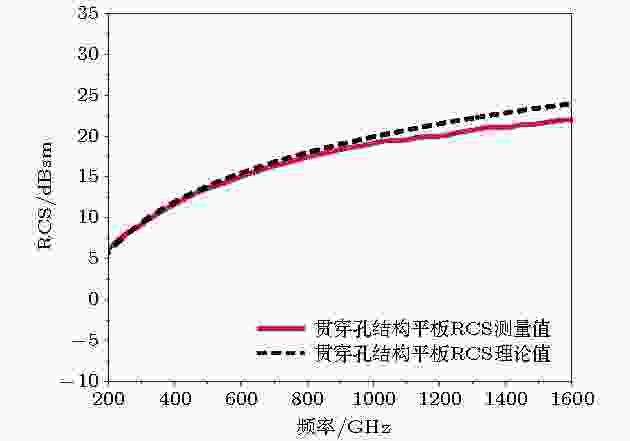图 9 贯穿孔结构平板RCS测量值与理论值
Figure9. RCS of the plate with through-holes.

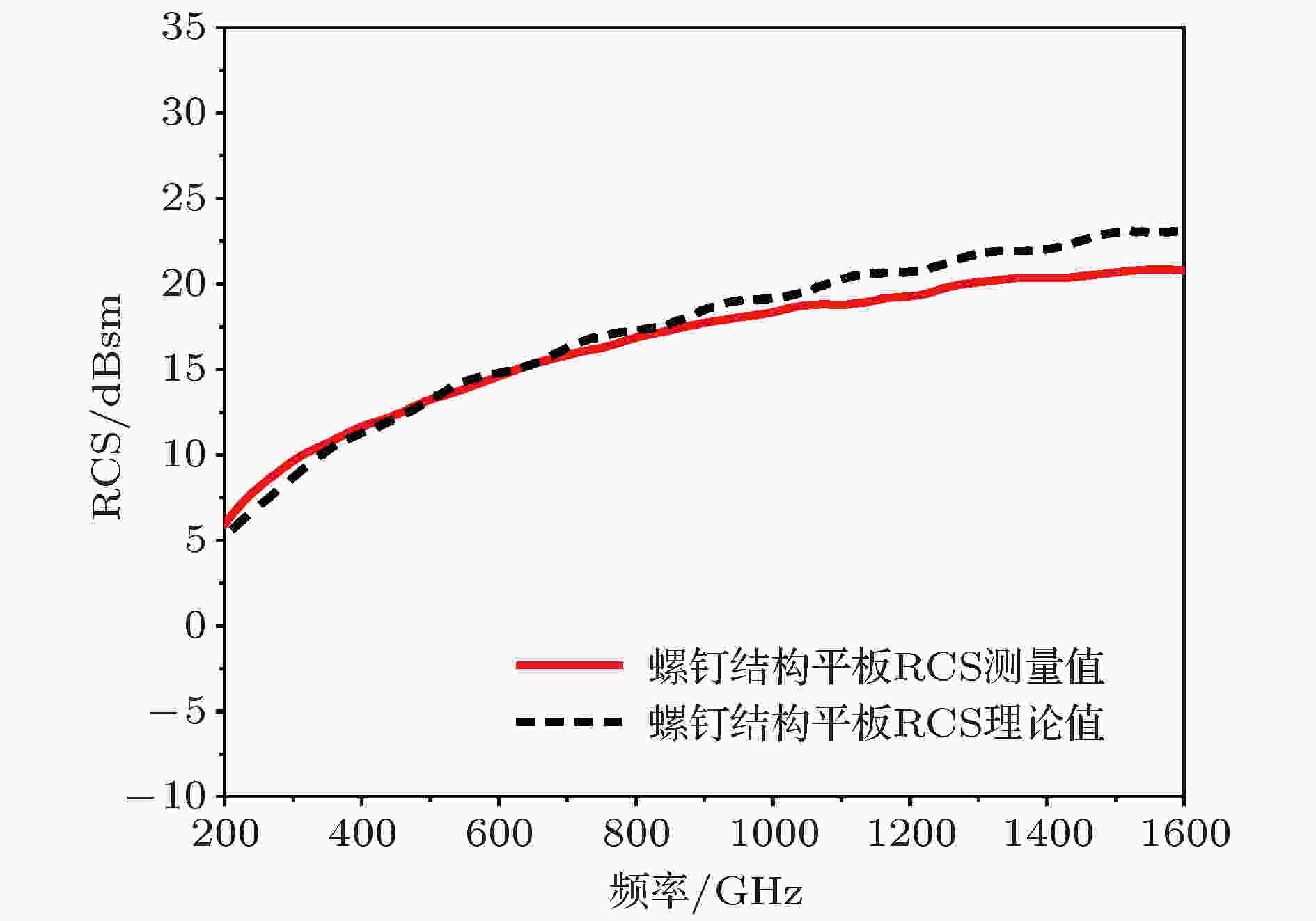图 10 螺钉结构平板RCS测量值与理论值
Figure10. RCS of the plate with screws.

太赫兹波长在亚毫米量级, 而太赫兹时域光谱系统可以通过控制延迟线的扫描精度, 从而在时域回波上获得非常高的分辨率, 达到微米量级, 因此能够识别目标的极细微结构. 本文测试的带有细微结构的复杂目标代表了军事目标表面的螺钉(铆钉)、小孔等结构, 这正是太赫兹时域光谱技术在目标特性领域的重要应用. 在对系统进行了充分的优化调试后, 系统的动态范围、线性度、底噪、频率稳定性等均达到测试要求, 降低了系统本身带来的测试误差. 在放置目标时采用激光定位从而保证了定位误差最小化. 充分降低这些误差才能保证最终的测量误差达到最小. 与微波、毫米波导体目标建模不同的是太赫兹频段导体目标的电导率不再趋于无限大, 而是随频率变化. 导体目标可认为是有耗介质. 本文基于时域光谱系统对几种典型定标体及复杂目标在0.2—1.6 THz的RCS进行了测量, 并采用表面积分方程法进行建模仿真, 多层快速多极子算法加速计算得到了目标太赫兹频段RCS的理论数值结果, 测量结果与理论结果误差在3 dB以内. 3 dB的误差来源主要有: 一是目标的定位误差, 由于太赫兹波的指向性非常好, 导致目标回波对目标姿态极为敏感; 二是静区的波束均匀性, 当前对静区波束的精确整形存在较大困难, 导致静区波束幅度起伏较大, 增加了测量误差.
当前时域光谱系统存在的难题在于, 对1.6 THz以上的频段存在测量不准的问题, 主要原因是受限于当前太赫兹收发天线的功率, 在高频区动态范围不足. 另外, 对于时域光谱系统, 其不同频率的太赫兹波波束宽度不同, 频率越高, 波束宽度越小, 且时域光谱系统的太赫兹波束为高斯线型, RCS测量可用波束范围很小, 如何将高斯波束整型成为更大的测量可用波束是今后的研究重点之一.