摘要:灵敏度高、可重复性好的固态表面增强拉曼散射基板可作为生物医学、环境科学、化学化工、纳米科技等领域的生化感测器, 具有十分重要的实际应用价值. 传统的表面增强拉曼散射基于金属颗粒提供的局域表面等离谐振这一物理机制, 但其组装不易且模式损耗大. 本文基于周期性金属亚波长结构, 构建增强拉曼散射信号的“热点”, 同时保证测量信号的可重复性. 从表面光子能带结构出发, 提出了区别于局域表面等离谐振的其他三种增强机制: 表面等离子极化激元带边增强机制、间隙等离子极化激元增强机制以及二者相耦合增强机制. 采用一定的工艺, 提高金属表面平整度, 抑制表面等离子极化激元的传播损耗, 从而提高表面增强拉曼散射的增强因子. 理论结合实验, 且二者一致性好. 研究结果有望将表面增强拉曼散射光谱技术进一步向实用化方向推进.
关键词: 表面增强拉曼散射/
表面等离子极化激元/
亚波长结构/
近场光学

English Abstract

全文HTML

--> --> -->

具有指纹性识别能力的拉曼散射光谱在生物、医学与化学等领域有着长期而广泛的实际应用. 拉曼散射信号属于微弱光信号, 一般情况下, 因信号强度过低而难以被检测到, 1974年由Fleischmann等^[1]实验发现的表面增强拉曼散射 (surface-enhanced Raman scattering, SERS)现象, 克服了拉曼散射的弱信号特征, 使拉曼散射光谱适用于微量样品的测定, 大大促进了拉曼散射的实际应用进程. 其增强机制主要分为化学增强和物理增强, 化学增强倍数通常较小, 大部分的SERS现象由物理机制主导. 局域表面等离谐振(localized surface plasmon resonances, LSPRs)因提供了大的电磁场增强, 成为目前SERS的主要物理增强机制. 两个金属粒子表面的LSPRs之间可发生强烈近场耦合, 在间隙处产生更强的场强, 这种两金属粒子组成的结构对也被称为二聚体结构^[2-4]. 二聚体的近场耦合强度具有偏振依赖性, 即入射光偏振方向平行于二聚体轴向时, 间隙处的场强大于二者相互垂直时的场强^[2]. 通过调节金属粒子间距, 构建具备强电场分布的“热点”, 能够探测到单个分子的拉曼散射信号^[5-8]. 将“热点”在空间上进行周期性排布, 可使测量的SERS信号具有均一性, 这类具有可重复性的SERS基板更为实际应用所需^[9-13].
物理上, LSPRs是表面等离子极化激元(surface plasmon polaritons, SPPs)的一种非传播、准静态形式. “表面等离子极化激元亚波长光学(surface plasmon polaritons subwavelength optics)”是基于SPPs发展起来的一门新兴学科, 在可见光波段主要是研究纳米尺度的光学现象, 通过SPPs可获得亚波长的光场限域, 具有克服电磁波衍射极限以及对器件小型化与集成化的实现能力. 尽管LSPRs与SPPs性能独特、应用广泛, 但因其谐振特征所带来的损耗始终会伴随产生, 为此光场限域形成的场增强能力与损耗二者成为矛盾统一体. 为提高器件性能, 可引入耦合效应等新颖物理机制, 通过结构优化设计, 构建低损耗模式, 改善场的空间分布, 在减少模式体积的同时, 将场向低损耗材料所处位置转移, 并采取先进的微纳加工与新材料制备工艺, 进一步降低模式传播损耗和材料损耗. 本文拟以简单的金属单界面亚波长结构为研究对象, 避免LSPRs的高损耗特征, 克服SPPs的传播损耗, 吸取超构材料^[14]与超构表面^[15]领域在亚波长结构设计与器件研制方面的成果与经验, 探索亚波长结构中新颖的物理增强机制, 以研制拉曼散射信号强、可重复性好的固态SERS基板.

考虑一维金属Ag光栅结构, 如图1(a), 结构参数分别为周期P, 深度D, 以及宽度W, 设占空比γ = W/P. SERS增强因子EF = |E_ex/E₀|²$\times$|E_scat/E₀|^2[16], 其中E₀, E_ex与E_scat分别表示入射光、结构对入射光的弹性散射光、拉曼活性材料非弹性散射光的电场强度. 图1(b)为深度D = 30 nm, 入射波长λ = 532 nm, TM偏振光垂直入射时, 计算出的SERS增强因子随周期P和占空比γ的变化情况, 图中区域1与区域2对应于两种不同的增强机制.
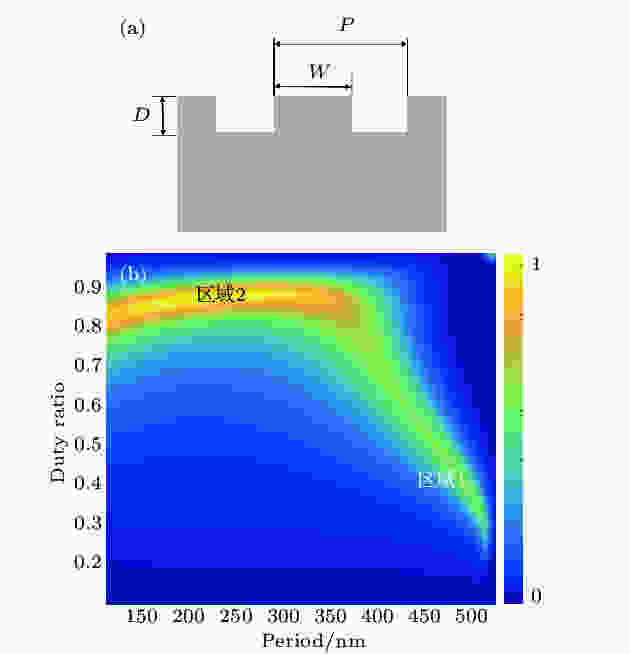图 1 (a)一维金属亚波长结构示意图; (b) D = 30 nm时, SERS增强因子随周期P和占空比γ的变化
Figure1. (a) The cross-sectional sketch of the one-dimensional gratings; (b) the calculated enhancement factor as a function of the period and duty ratio.

2

-->

2.1.SPP带边增强机制

区域1的局部最优结构参数是周期P = 475 nm, 宽度W = 273 nm. SPP带隙大小随深度D和占空比γ改变, 而带隙中心位置由周期P决定. 对γ = W/P = 273 nm/475 nm = 0.575, 通过反射率计算描绘的周期P = 445, 475, 505, 525 nm所对应的SPP能带结构如图2(a)所示. 可以看出, 随着周期变大, SPP带边位置会发生红移, 当周期P = 475 nm时, 上带边位置处在532 nm波长, 当周期P = 505 nm时, 532 nm位置处为带隙位置, 而当周期P = 525 nm时, 下带边位置处在532 nm波长. 在532 nm波长处, 随周期变化的垂直(0°)反射率计算结果如图2(b)所示, 反射率曲线中的两个谷, 分别对应着SPP的上带边和下带边. 反射率越低, 暗示着远场光能量向SPPs近场模式的转化越多, 因此场增强与反射率随周期变化的规律正好相反. 图2(c)是计算的532 nm波长的电场分布图, SPP上带边对应的电场强度最强, SPP带隙位置则最弱, 与SPP带边增强机制一致, 这是因为SPP群速度v_g = dω/dk在带边位置最小, 根据电场强度大小反比于群速度大小的原理^[17], 获得最大场增强, 而在带隙位置不存在SPP模式. 在SPP上带边位置, SERS增强因子达到峰值, 理论计算值达到6 × 10⁶, 如图2(b)所示.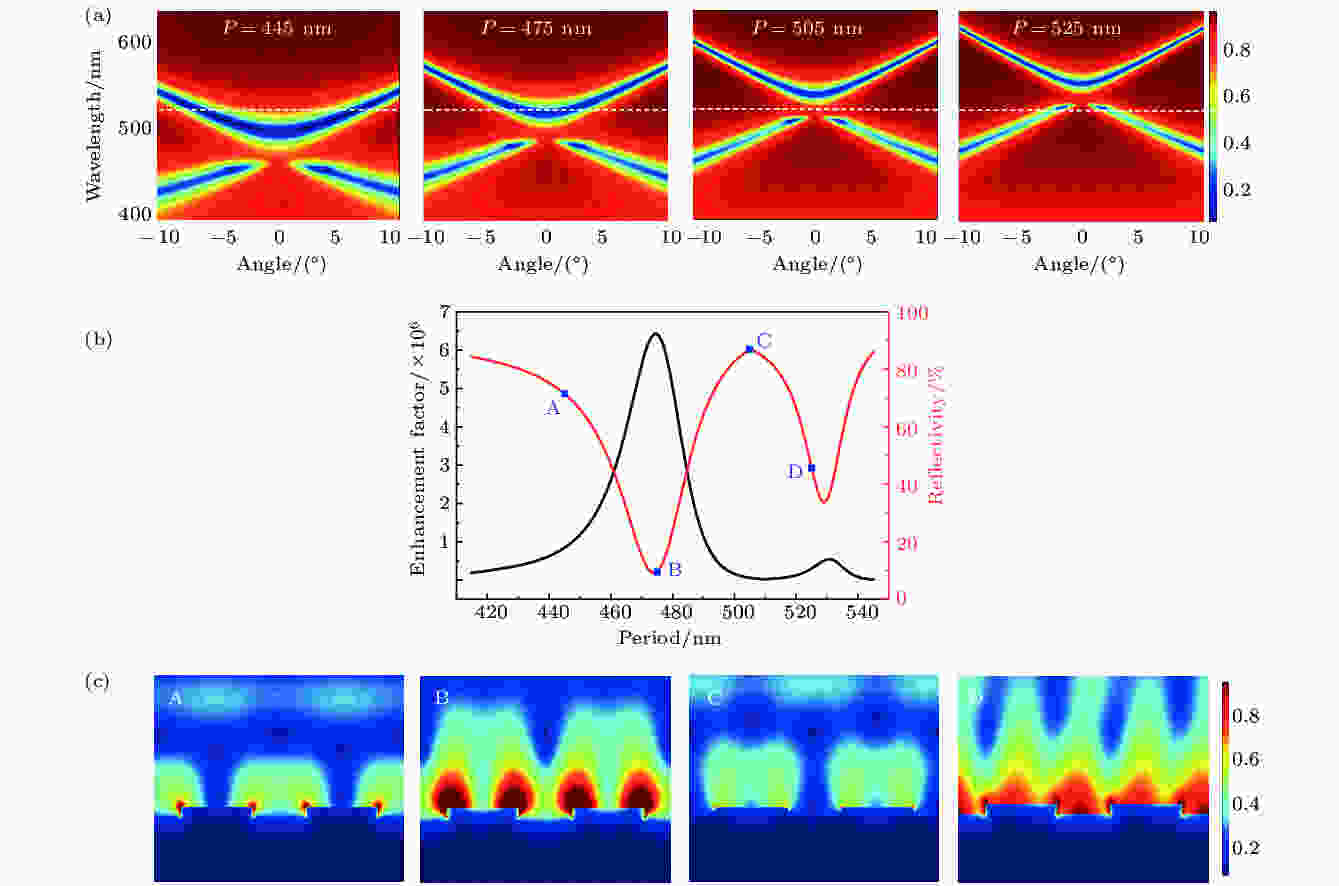
图 2 (a)计算的不同周期的SPP能带结构图, 其中白色虚线表示λ = 532 nm位置; (b)计算的不同周期结构在532 nm的反射率以及SERS增强因子; (c)对应(b)中四个不同周期值的电场分布图
Figure2. (a) The calculated bandgap structures for various periods but the same depth and duty ratio; (b) the calculated enhancement factor and reflectivity as a function of the period; (c) the calculated electric field distribution of structures with different periods corresponding to the positions A, B, C, and D in (b).

2 -->

2.2.GPP增强机制

从图1(b)来看, 区域2所对应的SERS增强因子比区域1的更大. 最优结构参数为周期P = 200 nm, 占空比γ = 0.9, 即槽非常窄, 此时槽宽约为20 nm, 这种情况下结构可以被归类为金属-介质-金属(metal-insulator-metal, MIM)结构^[18]. MIM结构支持间隙等离子极化激元(gap plasmon polaritons, GPPs)模式的传播. 图3(a)是计算的这一结构的能带结构图, 为一条水平线, 对应于群速度v_g = 0, 亦代表着场增强效应, 且GPP模式随着深度增加发生红移. 取周期P = 200 nm, 改变深度D和槽的宽度W_g = P –W, 可以计算出SERS增强因子随着深度D和槽的宽度W_g的变化关系, 如图3(b)所示. 图3(b)中出现若干个增强区域, 固定宽度为20 nm, 在每个区域内取一增强因子最大时对应的深度, 依次分别为35, 160以及290 nm, 计算的电场分布如图3(c), 可以看到, 这些不同的区域对应着槽中间GPP模式的不同阶次, 其中最低阶模式的场增强最显著. 图3(d)是周期P = 200 nm, 槽的宽度W_g = 20 nm时, 计算的SERS增强因子随着深度D变化的曲线, 最大增强因子达到2 × 10⁷.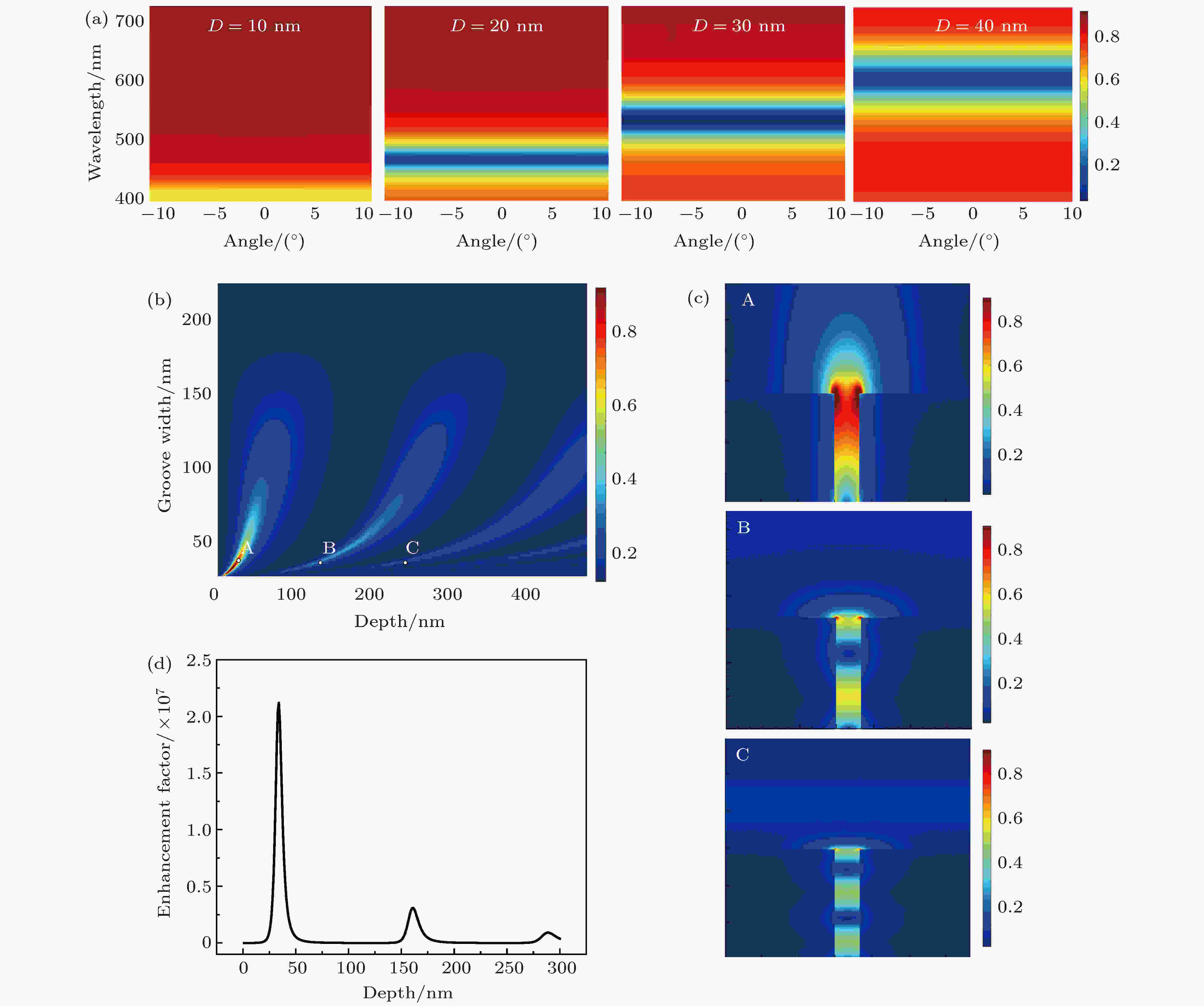
图 3 (a)计算的不同深度的GPP能带结构图; (b)周期P = 200 nm时, 计算的SERS增强因子随深度以及槽的宽度的变化图; (c)图(b)中三个位置处的电场分布图; (d)周期P = 200 nm, 槽的宽度W_g = 20 nm时, 计算的不同深度的SERS增强因子
Figure3. (a) The calculated bandgap structures for different depths but the same period and width; (b) the calculated enhancement factor as a function of depth and groove width, in which the period is set as 200 nm; (c) the electric field distribution of structures with different depths and widths, corresponding to the positions A, B, and C in (b); (d) the calculated enhancement factor as a function of the depth.

2 -->

2.3.SPP和GPP耦合增强机制

基于上述两种不同模式的SERS增强机制, 与亚波长结构的结构参数紧密相关, 理论上可以通过相应的结构参数来独立调节这两个模式. 可以推知, 当这两种模式靠得很近时, 将会发生模式耦合效应, 一般来讲, 耦合后的模式其场增强效果会更佳.
为此, 我们设计加工了图4(a)的双槽结构, 也就是在一个周期内加工两个不同的槽, 其中窄槽提供GPP模式, 周期和占空比调节SPP的带边位置. 令两个槽的深度D一致, 两个槽中间的金属部分宽度和窄槽的宽度一致. 对于周期P、两个槽的宽度分别为W₁和W₂, 则占空比γ = 1－(W₁ + W₂)/P. 我们取周期P = 475 nm, W₁ = 182 nm, W₂ = 20 nm, 占空比γ = 273 nm/475 nm = 0.575. 改变槽的深度D, 则窄槽提供的GPP模式随之移动, 而因周期和占空比不变, SPP带边位置基本不发生移动. 图4(b)是不同深度D对应的能带结构图, 当深度D = 30 nm时, SPP带边和GPP模式在532 nm波长处发生耦合谐振现象. 图4(c)是计算的不同深度的SERS增强因子, 可以看出, 在深度D = 30 nm时, 两个模式发生耦合, SERS增强因子达到峰值. 图4(d)是不同深度下的电场分布图, 分别对应于图4(c)中的A, B和C点位置, 深度分别为10, 30和55 nm. 可以看出在深度为30 nm时, 模式耦合效应令电场显著增强.
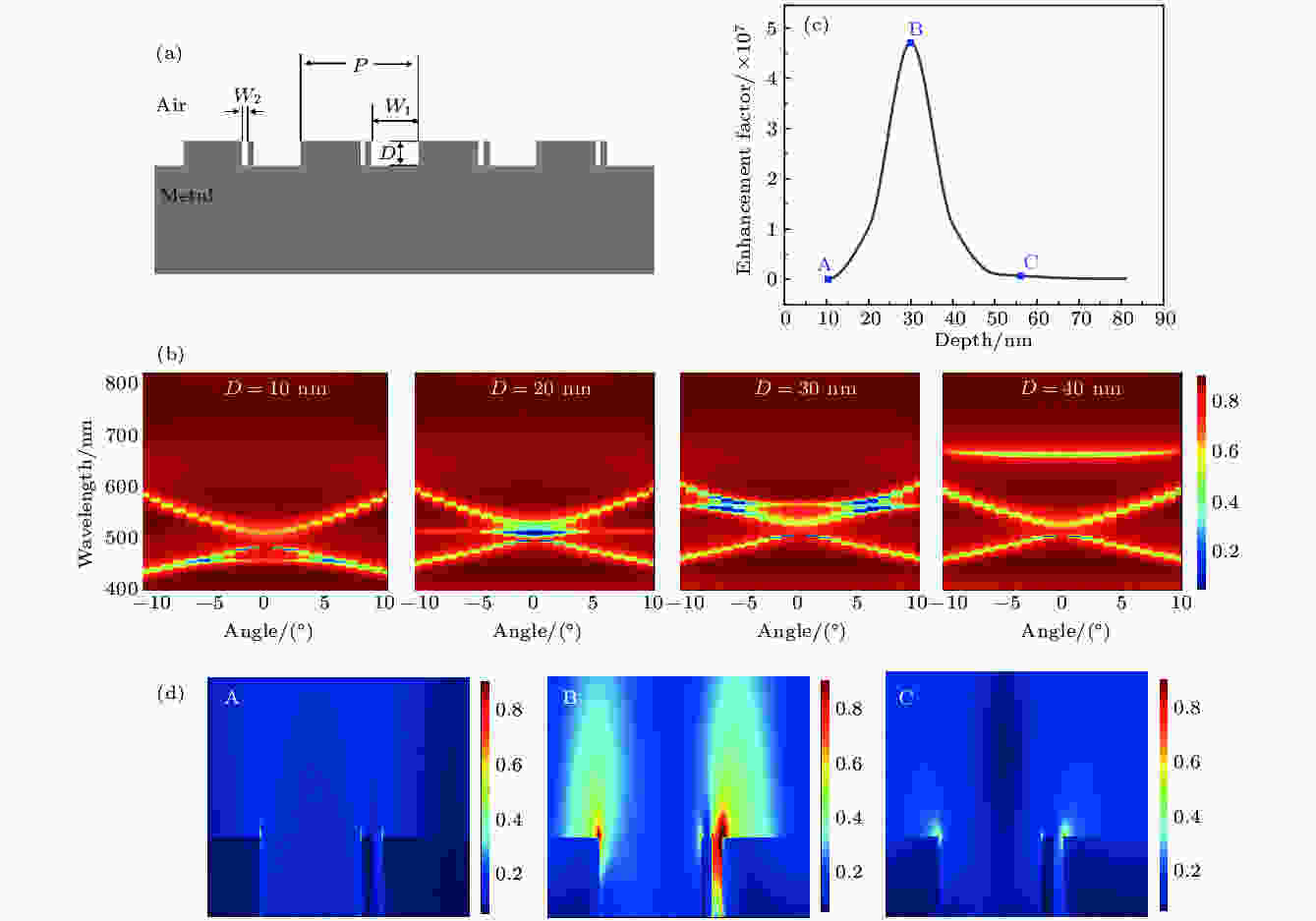图 4 (a)双槽结构示意图; (b)计算的不同深度的双槽结构的能带结构图; (c)计算的不同深度的SERS增强因子; (d)计算的不同深度下的电场分布图, 对应于(c)中的A, B和C点的参数
Figure4. (a) The cross-sectional sketch of the structure with double grooves; (b) the calculated bandgap structures for different depths with P = 475 nm, W₁ = 182 nm and W₂ = 20 nm; (c) the calculated enhancement factor as a function of the depth; (d) the calculated electric field distribution of different depth corresponding to the positions A, B, and C in (c).

下面, 我们以SPP带边增强机制为例, 给出实验验证.

实验上, 采用离子束溅射镀膜的方法制备金属Ag膜, 电压为7 keV、电流为300 mA时, Ag膜的生长速率大约是6.2 nm/min. 使用FEI公司的Helios 600i聚焦离子束(focused ion beam, FIB)刻蚀方法加工出Ag膜上的亚波长结构, 电压30 kV, 电流7.7 pA, Ga⁺束刻蚀.
考虑到SPPs是一种传播波模, 会受到镀膜表面金属颗粒的非定向散射, 这一部分散射增大了传播损耗, 最终弱化SERS性能. 为此我们利用撕膜工艺, 降低表面的散射损耗, 实验上对比了直接镀膜及经撕膜工艺后的器件性能差别, 撕膜的工艺流程如图5(a)所示. 首先在Si片上加工出所需结构的反结构, 在其上镀200 nm左右的Ag膜, 再利用电镀的方式, 在Ag膜上面镀约1 mm厚度的Cu箔, 然后将Cu箔从Si片上整体剥离下来, 剥离后的Cu箔承载着Ag膜, 并且带有亚波长结构的Ag表面裸露在外, 供实验测试. 图5(b)和图5(c)分别是在镀膜样品上直接加工以及通过撕膜的方法获得的Ag光栅的扫描电子显微成像(scanning electron microscopy, SEM)图, 可以看出镀膜样品有非常明显的颗粒, 而撕膜的样品表面则要光滑很多. 借助原子力显微成像 (atomic force microscopy, AFM), 对镀膜样品和撕膜样品的表面平整度测试的结果表明, 在2 μm × 2 μm的面积范围内, 镀膜样品粗糙度的均方根是2.72 nm, 而撕膜样品的只有0.980 nm. 图5(d)给出了撕膜样品与镀膜样品的SPP传播情况对比, 在633 nm波长时, 撕膜样品上的SPP传播距离(20 μm)大约是镀膜样品的(10.95 μm)两倍, 这说明经撕膜工艺的Ag表面的SPP传播损耗确实要小, 改进和优化工艺有望提升器件性能.
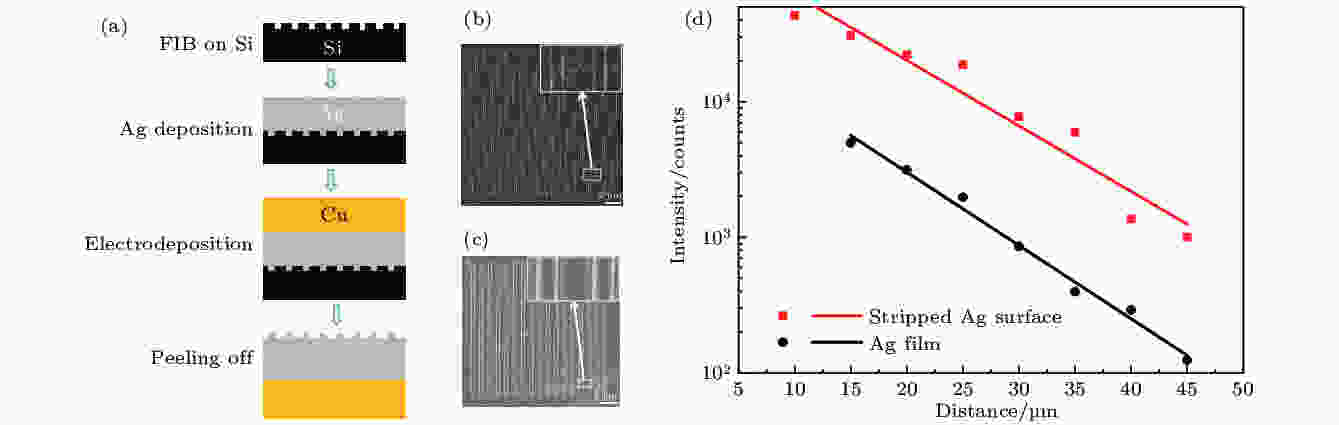图 5 (a)撕膜的工艺流程; (b)镀Ag膜样品表面直接加工光栅的SEM图; (c)通过撕膜方法获得光栅的SEM图; (d)镀膜和撕膜Ag表面的SPP传播测量结果
Figure5. (a) Schematic diagram of the template stripping process; (b) the SEM images of gratings on coated Ag film; (c) the SEM images of stripped Ag gratings; (d) the propagation measurements of 633 nm laser on conventional Ag film and stripped Ag surface.

实验上, 能带结构测量系统由光学显微镜和光谱仪组合而成. 用科勒照明方式把白光经由100×物镜聚焦在样品上, 样品表面的反射光也经过同一物镜收集, 使用凸透镜将物镜的后焦面移送到光谱仪, 经光栅分光后在CCD中成像, 获得能带结构图, 光路中加入偏振片, 可得到不同偏振模式的能带结构图. 对应于图2(a)中理论计算的SPP能带结构, 图6是实验测量结果, 其差别主要来自于实验上有限的分辨率所致.
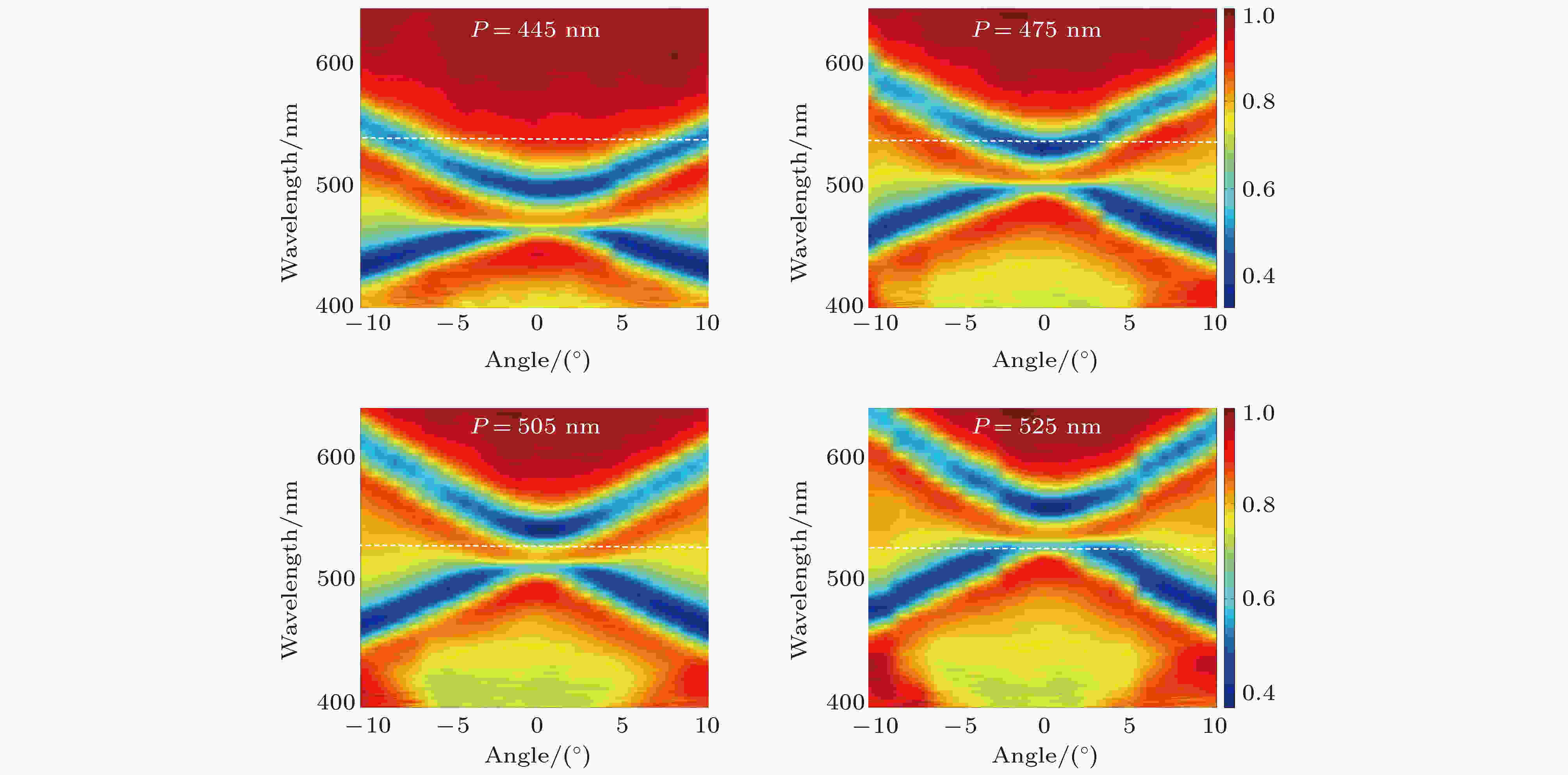图 6 不同周期的SPP能带结构测量结果, 与图2(a)中的计算结果相对应
Figure6. Experimental bandgap structures corresponding to those in Fig. 2 (a).

为了表征亚波长结构的拉曼散射效应, 我们选用4-甲基苯硫酚(4-aminothiophenol, 4-ATP)分子作为拉曼活性材料, 4-ATP分子可在Ag表面形成单分子层. 首先在乙醇中配置一瓶浓度为1 × 10^–4 M (1 M = 1 mol/L)的4-ATP溶液, 将Ag样品放入浸泡6 h, 取出来后用乙醇和去离子水反复冲洗若干次, 再用氮气将表面残留的液体吹去, 之后立即对样品进行实验测量. 采用显微共聚焦拉曼散射测量系统(Horiba Scientific, LabRAM HR Raman spectrometer), 532 nm连续光进行激发测量, 实验上的SERS增强因子由下式获得: EF = (I_SERS/N_Surf)/(I_Rs/N_Vol)^[19], I_SERS和I_Rs分别是吸附于Ag表面的4-ATP单分子层的拉曼散射信号和作为对比的4-ATP粉末的拉曼散射信号, 前者属于金属亚波长结构增强后的拉曼散射信号, 后者是没有被增强的标准拉曼散射信号, N_Surf和N_Vol分别是收集到增强信号的4-ATP分子数目和收集到的标准信号的分子数目.
4-ATP分子在Ag基板上的拉曼散射光谱如图7(a)所示, 4-ATP的标准拉曼散射信号的两个主要峰分别位于1092 cm^–1和1177 cm^–1, 而当4-ATP单分子层吸附到Ag上之后, 这两个峰位会发生位移, 变为1076 cm^–1和1145 cm^–1. 实验上采用1145 cm^–1这个峰位来作为SERS增强因子的定标峰位. 撕膜样品的拉曼散射信号强度要远大于镀膜样品的拉曼散射信号强度, 大约是40倍的关系, 图7(b)是通过撕膜工艺所得样品, 在不同周期结构所测得的SERS增强因子, 在周期为475 nm时, 获得了4 × 10⁵的增强因子. 我们进一步测量不同空间位置的拉曼散射信号, 以检验样品的可重复性, 使用50 × 物镜, 扫描面积15 μm × 15 μm, 225个数据点, 测得拉曼散射信号的相对标准方差(relative standard deviation, RSD)约为10.9%, 如图7(c)所示.
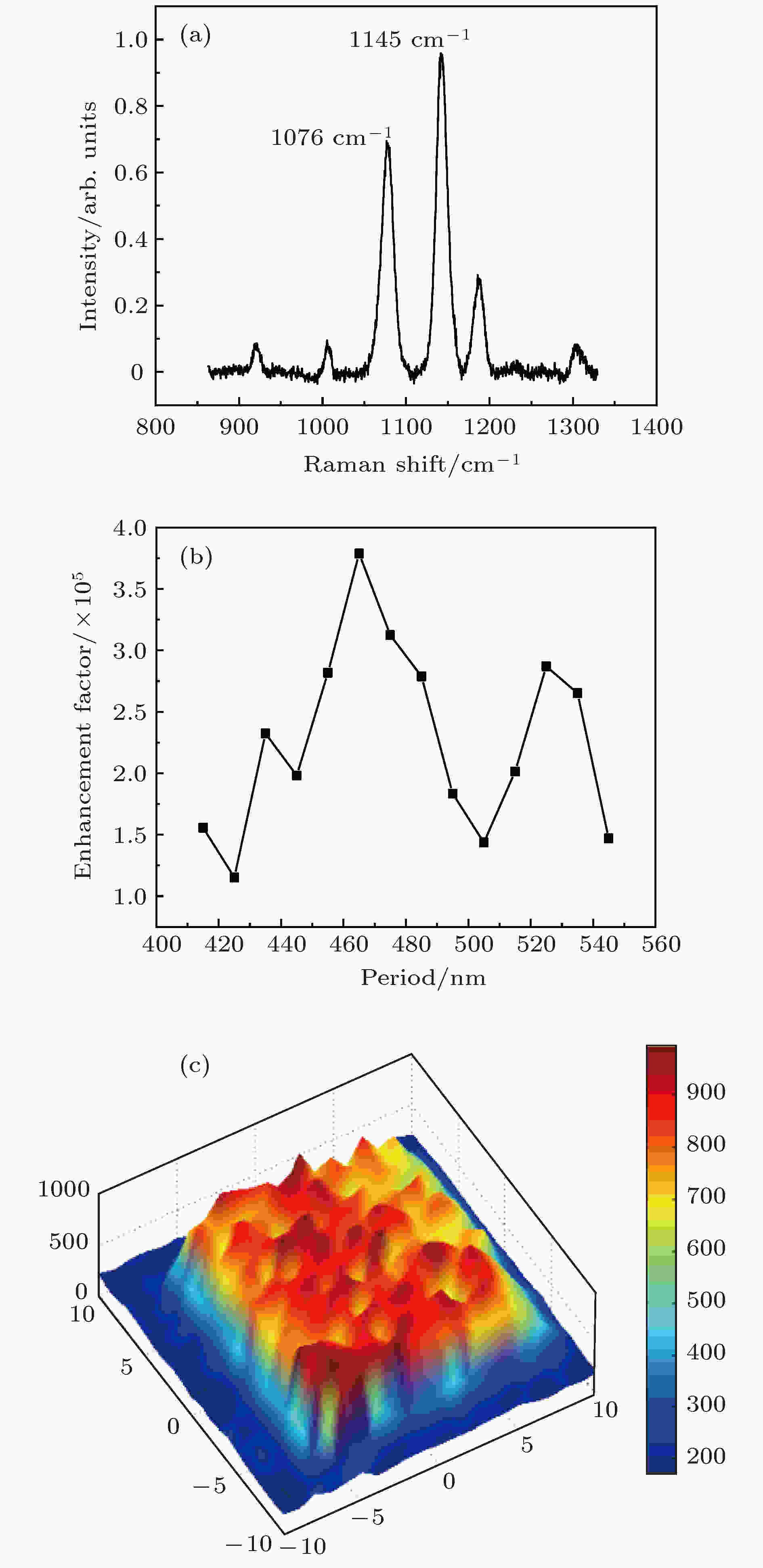图 7 (a) 4-ATP分子在Ag基板上的拉曼散射光谱; (b)测量的不同周期结构的SERS增强因子; (c)拉曼散射的空间扫描测量结果图
Figure7. (a) The Raman spectrum of 4-ATP molecules on Ag substrate; (b) the experimental enhancement factor as a function of the period; (c) SERS mapping image at 1145 cm^–1

针对表面增强拉曼散射这一实用性强的研究领域, 本文着重研究了金属亚波长结构充当表面增强拉曼散射基板的可能性, 理论上提出了几种新颖的物理增强机制, 即SPP带边增强机制、GPP增强机制以及SPP和GPP耦合增强机制, 并对SPP带边增强机制进行了实验验证. 这几种物理机制可以通过结构参数优化, 提供非常大的增强因子, 可针对不同激光源, 通过调节结构参数来匹配其工作波长实现增强效果. 考虑到传播损耗带来的负面影响, 利用撕膜工艺降低损耗, 显著提高了信号增强因子. 周期性亚波长结构的制备工艺简单, 可重复性好, 符合表面增强拉曼散射领域的实际应用需求, 必将贡献于未来的生化感测器.