全文HTML
--> --> -->近年来, 以表面等离激元(surface plasmons, SPs)[5—9]、超构材料(metamaterials)[10—15]为代表的亚波长人工微结构材料吸引了人们的广泛关注. 这些微结构材料虽各具特色, 但都具有如下共同特点: 可通过一些特殊设计的微结构单元及其排列方式实现对电磁波的有效调控, 如对电磁波/光波的亚波长束缚, 选择性增强吸收等. 亚波长人工微结构材料的出现同时为电磁波减反增透提供了新的思路. 这些微结构减反体系不但可以按照需求在任意波段进行设计, 而且通常都具有亚波长的性质, 因此可以很好地满足先进光电系统对器件小型化、集成化的要求. 本文简要介绍基于此类亚波长人工微结构材料的电磁波减反增透的若干典型工作及相关进展. 具体内容安排如下: 第2节主要回顾简单层状介质减反膜及梯度渐变介质减反膜等传统减反方法, 简单介绍了这些方法的基本工作原理及各自的优缺点; 第3节主要介绍基于表面等离激元的电磁波减反增透方法, 包括局域表面等离激元抑制光反射增强光耦合, 以及传播表面等离激元、局域共振模式诱导高透隧穿; 第4节主要介绍基于超构材料的电磁波减反增透研究进展, 包括ABA三明治型超构材料“透明金属”, 人工微结构超表面红外、太赫兹减反膜等相关内容.
2
2.1.简单层状介质膜减反方法
各向同性均匀介质减反方法的基本原理是薄膜干涉. 假设一束光由光疏介质1如空气(折射率为n1)向光密介质3 (折射率为n3)入射, 在两介质层之间引入一层减反膜2 (折射率为n2). 如图1所示, 这三层介质形成了两个界面: 界面①即介质1与减反膜2形成的界面; 界面②即减反膜2与介质3形成的界面. 如果将减反膜设定合适的折射率和厚度, 可以使在界面①处反射的光与界面②处反射的光振幅相同、相位相差180°, 从而形成完美干涉相消的效果, 以降低反射. 为了使得干涉相消的效果达到最佳, 各层折射率之间需要满足条件
图 1 单层减反膜原理示意图Figure1. Schematic of a single thin film anti-reflection coating
针对可供选择的材料种类有限这一约束条件, 除了寻找具有特定折射率的材料外, 人们还通过将具有不同折射率的材料进行混合从而获得具有合适折射率的材料[16,62]. 如图2(a)所示, Walheim等[62]就将聚苯乙烯(polystyrene, PS)和聚甲基丙烯酸甲酯(polymethylmethacylate, PMMA)混合制备出折射率可调谐的多纳米孔结构, 如图2(b)所示, 通过调节PS和PMMA的参比成分可以将混合多孔结构的等效折射率在1.0—1.5之间自由调节, 并且在400—1000 nm波段范围内有效地降低了玻璃界面的反射并增强了透射(见图2(c)). 这种方法可以实现可见光波段较好的减反效果, 并且减反波段可以实现一定范围内的调控, 但是由于等效折射率调控能力有限且减反效果无法精确控制, 这两个缺点一定程度上限制了有机物混合材料减反应用的发展.
图 2 (a)两种不同配比下的有机聚合物混合的多纳米孔结构的原子力显微镜图; (b)等效折射率关于聚合物参比成分的函数曲线; (c)将不同配比的两种减反层覆盖于显微镜镜片两侧后, 镜片的透射率关于波长的曲线[62]Figure2. (a) Atomic force microscope images of two porous PMMA films, after spin-casting of a PS- PMMA-THF mixture onto silicon oxide surfaces; (b) variation of the refractive index as a function of polymer composition; (c) light transmission versus wavelength of microscope glass slides that were covered on both sides with AR layer[62].
2
2.2.梯度渐变介质减反方法
光在传播的过程中之所以会产生反射, 是由于遇到了阻抗不匹配的突变界面, 如果当光波在传播的过程中不再遇到突变界面, 而是在一个折射率梯度变化的介质中传播, 则反射会被大大降低. 1879年, Rayleigh[63]首次提出了梯度介质减反膜, 并通过数学手段验证了其可靠性. 但是由于当时微纳加工技术条件有限, 无法制备出相应的样品, 理论工作未能得以及时证实, 也因此没有得到人们的重视. 直至1960年, Jacobsson[64]首次制备出了具有梯度折射率的光学减反膜. 1967年, Bernhard[65]进一步发现飞蛾的眼睛表面具有尖锥状凸起的阵列结构, 这样的锥状阵列功能上等效于具有渐变折射率的薄膜, 其可以大幅降低眼睛表面的反射. 自此梯度渐变折射率型减反结构被人们广泛研究[20—61]. 1973年, Clapham等[60]在玻璃片的表面利用光刻胶仿照飞蛾眼角膜中的突起结构, 在可见光波段实现了宽带的减反效果. Sai等[37]受仿生学的启示通过在硅片表面进行加工处理, 将硅的表面刻蚀成纳米量级的金字塔结构(图3(a)), 该金字塔结构在紫外-可见-近红外波段观察到了明显的宽带减反效果. Huang等[53]利用类似的原理结合现代化的制备工艺在不同的频段实现了超宽波段的有效减反. 其主要实现方法为通过在硅晶圆片上生长非周期性的纳米针阵列, 并且不同尺寸的纳米针阵列可以在不同的波段实现减反, 如图3(b)所示, 高度在百纳米量级的硅纳米针阵列可以在紫外-可见-近红外波段实现很好的减反效果, 而高度在10 μm量级的硅纳米针(siliconnanotip, SiNTs)阵列在远红外波段也可以观察到明显的减反效果.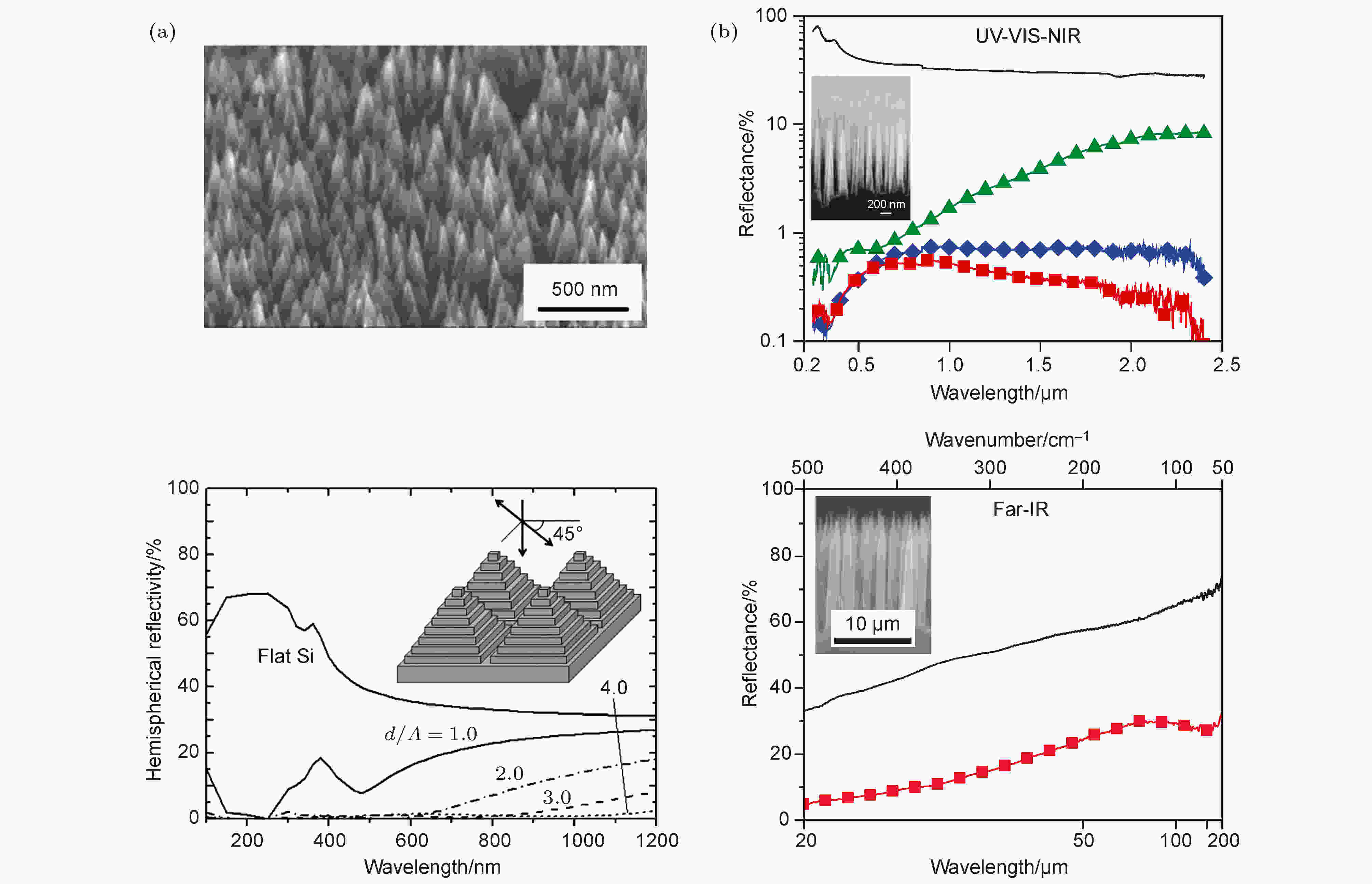
图 3 (a)上图为利用快速原子束刻蚀过的硅表面的扫描显微镜图, 下图为不同周期的二维硅金字塔结构反射率的模拟计算结果[37]; (b)上图为表面平整的硅晶圆 (黑色实线)与高度L = 1.6 μm (绿色标记), 5.5 μm (蓝色标记)和16 μm (红色标记)的SiNTs在紫外-可见-近红外波段反射率的对比, 其中左侧插图为高度L = 1.6 μm SiNTs的SEM侧视图, 下图为表面平整的硅晶圆 (黑色实线)与高度L = 16 μm (红色标记)的SiNTs在远红外波段反射率的对比, 其中左上方插图为高度L = 16 μm SiNTs的SEM侧视图[53]Figure3. (a) Top panel is the scanning microscope photographs of the Si surface after FAB etching, bottom panel is the calculated spectral reflectivity of two-dimensional Si pyramid gratings with different periodicities[37]; (b) top panel is comparison of the reflectance as a function of wavelength for a planar Si wafer (solid line, black) and SiNTs (symbols) for L = 1.6 μm (green), 5.5 μm (blue) and 16 μm (red) at UV, VIS and NIR wavelengths, inset in top panel shows the cross-sectional SEM image of the L = 1.6 μm SiNTs; bottom panel is comparison of specular reflectance as a function of wavelength for a planar silicon wafer (solid line, black) and SiNTs with L = 16 μm (red) in the far-infrared regions, inset in bottom panel shows the cross-sectional SEM image of the L = 16 μm SiNTs[53].
此外, 关于梯度渐变介质减反研究中值得指出的是, 1983年Southwell[66]理论研究分析比较了线性、三次方和五次方的梯度折射率的渐变形式, 并得出了五次方形式渐变的梯度介质具有较好的减反效果的结论, 结果如图4(a)所示. 2007年, Xi等[67]通过多层的SiO2和TiO2的纳米棒堆栈结构(见图4(b)), 通过改变SiO2和TiO2的纳米棒生长时沉积的入射角度, 使得倾斜的SiO2纳米棒结构的折射率可以在1.05—1.46之间变化, 而倾斜的TiO2纳米棒结构则可以在1.3—2.7之间变化, 通过选取五层在1.05—2.70之间变化的纳米棒结构, 构造出了折射率近似为五次方形式渐变的多层膜体系, 多层膜的各层具体信息见图4(b)下的表格. 实验上将这种减反结构应用于AlN(氮化铝)衬底, 结果显示反射率降到了1%以下, 如图4(c)所示, 从而验证了Southwell的五次方[66]渐变行为理论.
图 4 (a)折射率随入射深度以线性、三次方、五次方形式渐变的曲线的对比[66]; (b)由三层TiO2纳米棒结构和两层SiO2纳米棒层构成的折射率成五次方形式渐变的多层膜的SEM截面图与结构示意图, 下面的表格中为五层膜体系中各层膜的详细信息; (c)正入射条件下的梯度折射率减反膜的反射谱, 其中实线为理论计算值, 虚线为实验测量值[67]Figure4. (a) Linear-, cubicandquintic-index profiles that have index matching with air[66]; (b) cross-sectional SEM image of graded-index coating with a modified-quintic-index profile, the graded-indexcoating consists of three TiO2 nanorod layers and two SiO2 nanorod layers; (c) wavelength dependence of theoretical (solid line) and measured (dashed line) reflectivity of graded-index coating at normal incidence[67].
梯度渐变介质膜与简单层状介质膜相比, 在减反效果和适用工作波段的范围上都有了很大的提升, 但是由于其减反结构尺寸通常体积较为庞大, 且制备工艺复杂、加工成本高, 所以这类方法也难以满足日益苛刻的器件小型化、集成化的发展需求.
2
3.1.局域表面等离激元减反方法
金属纳米颗粒由于具有局域表面等离激元性质, 可将电磁波束缚在一个很小的空间范围内, 将金属纳米颗粒与半导体、氧化物等高反射介质相结合, 可以有效改变体系的光散射性质, 减少入射光的反射, 提高光的利用效率. 1995年, Stenzel等[69]报道了在透明导电膜氧化锡铟(ITO)与铜酞菁有机太阳能薄膜之间掺入一层金属纳米颗粒团簇可以有效地提升该薄膜电池性能的相关工作. 以铜纳米颗粒团簇为例, 光电转化效率提升了近3倍, 研究表明, 性能提升的主要原因是金属纳米颗粒团簇局域表面等离激元的激发增强了入射光与器件的耦合. 紧接着, Stuart和Hall[70,71]研究发现金属纳米颗粒对绝缘硅(silicon-on-insulator, SOI)薄膜探测器也有增强效果, 结构如图5(a)所示. 他们系统地研究了不同种类和尺寸的金属纳米颗粒(如金、银和铜)对器件性能的影响(见图5(b)), 实验结果显示与无金属纳米颗粒绝缘硅薄膜探测器相比光电转化效率最高可提升了近20倍. 这些研究成果激发了大批科学家对相关领域的研究热情, 很快人们就将类似的想法推广到了单晶硅[72]、多晶硅[73,74]、量子阱[75]、砷化镓太阳能电池[76]等体系.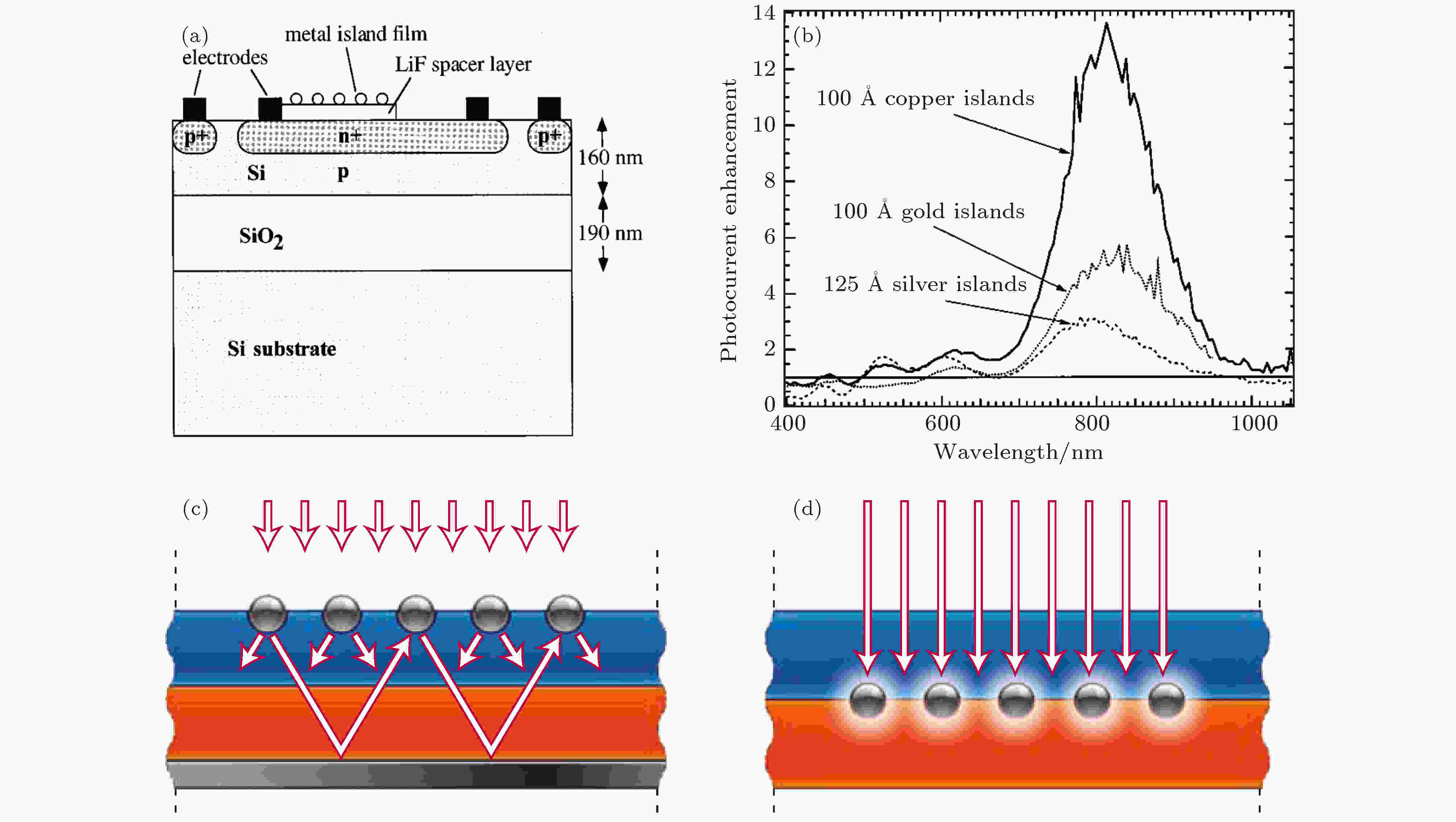
图 5 (a) 金属纳米颗粒增强绝缘硅薄膜探测器的结构示意图; (b)不同金属纳米颗粒光电流增强系数的实验测量值, 增强系数定义为存在/不存在金属纳米颗粒的探测器的光电流之比[70]; (c)金属纳米颗粒制备生长于器件的表面, 光通过多重和高角度散射被诱捕进入了下层的硅材料中; (d)嵌埋半导体材料中的金属纳米颗粒引起的局域表面等离激元与半导体材料进行近场耦合, 从而增强了材料的光吸收[77]Figure5. (a) SOI photodetector with metal island film; (b) measured enhancements due to the presence of the metal island layer, enhancement is defined as the ratio of the photocurrent of the device with the islands to that without the islands[70]; (c) light trapping by scattering from metal nanoparticles at the surface of the solar cell, light is preferentially scattered and trapped into the semiconductor thin film by multiple and high-angle scattering, causing an increase in the effective optical path length in the cell; (d) light trapping by the excitation of localized surface plasmons in metal nanoparticles embedded in the semiconductor, the excited particles’ near-field causes the enhancement of light absorption in the semiconductor[77].
在半导体光伏器件中利用金属纳米颗粒抑制光反射增强光耦合从技术手段上大致可以分为两类[77]: 1)金属纳米颗粒制备生长于器件的表面, 通过激发表面等离激元来增大散射截面以增强入射光与器件的耦合[78—90], 提高光吸收(见图5(c)); 2)将纳米金属颗粒嵌入半导体材料内部[91,92], 利用纳米金属颗粒激发的局域表面等离激元增强材料与金属颗粒的近场耦合作用, 以此来提高光吸收利用效率(见图5(d)). 这里需要指出的是, 虽然利用金属纳米颗粒确实有效地减小了器件对入射光的反射损失, 起到了减反增吸收的作用, 但是对器件(特别是薄膜器件)性能的增强[93—99], 即光电转换效率的巨大提升, 起到关键作用的还是等离激元金属纳米颗粒对入射电磁波的超强耦合束缚能力及亚波长局域场的增强效应.
局域表面等离激元共振波长虽然可以通过颗粒的形状和大小进行调节, 但主要还是由材料的本征物理性质决定. 通常情况下, 共振波长的调控范围也仅限于紫外到近红外波段, 当入射波长的进一步变长, 金属纳米颗粒对电磁波的束缚能力将大大减弱, 因此基于局域表面等离激元的减反增透结构仅能在有限波长范围内工作.
2
3.2.传播表面等离激元电磁波减反增透方法
与局域表面等离激元相比, 传播表面等离激元对电磁波的减反增透无论是工作机制还是应用场景都大不相同. 我们知道, 金属一般都是良导体, 其良好的导电性与金属内存在的大量自由电子有关. 当电磁波入射到导体表面, 电磁波与金属内的自由电子相互作用, 激发导体表层上的电荷有序流动, 该感生电流向空间反射电磁波. 导体中自由电子密度越高, 电导率越大, 反射系数越接近于1. 因此, 如果能够让高导电不透光的金属材料变得透明, 这样的工作不管是科学层面还是应用角度都很有意义.1998年, Ebbesen等[5]报道了在具有周期性亚波长孔阵列的金属薄膜(厚度200 nm)下观察到异常光学透射(extraordinary optical transmission, EOT)现象(其透射谱如图6(a)), 该金属薄膜的厚度远大于光的趋肤深度, 但实验结果显示其透射率比传统孔径理论的预测值大一到两个数量级, 并且如图6(b)所示金属薄膜的透射峰值与孔阵列的几何结构有关[6]. 如此异常的光学透射现象与金属表面所激发的表面等离激元有着密不可分的联系[5—7,100—106]. 我们知道, 对于由平板金属薄膜/介质组成的界面, 如金属/空气界面, 由于动量失配(表面等离激元波矢大于入射光的波矢, kssp > k0), 光从空气中入射到金属表面无法直接耦合激发表面等离激元. 但该金属薄膜由于周期性的亚波长孔阵列的存在引入了布拉格散射机制, 补偿了失配的光波矢, 因此如下动量匹配条件得以满足:
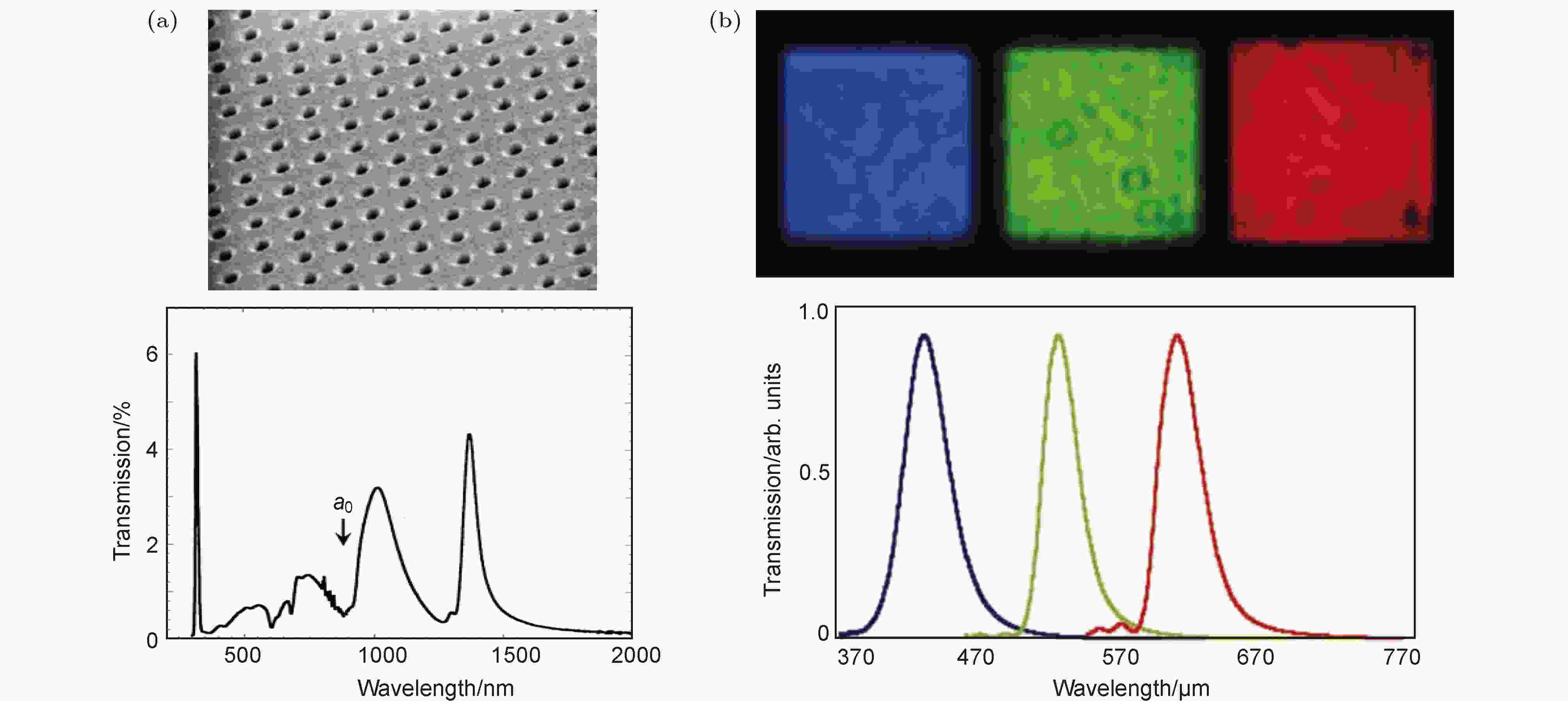图 6 (a) 上图为周期性亚波长金属薄膜的扫描电子显微镜图, 下图是厚度为200 nm的银薄膜的正入射条件下的零阶透射谱(周期为900 nm, 孔直径为150 nm)[5]; (b)上图为周期性亚波长金属薄膜的正入射透射照片, 下图为三种不同几何结构孔阵列的透射谱, 其中蓝线、绿线和红线所对应的周期分别为300, 450和550 nm, 孔的直径分别为155, 180和255 nm, 而它们的透射峰值分别为436, 538和627 nm[6]Figure6. (a) Top panel is sample picture of an optically thick metal films perforated with a periodic array of subwavelength apertures, bottom panel is zero-order transmission of 200 nm thick Ag film (periodicity of air holes 900 nm; hole diameter 150 nm) at normal incidence[5]; (b) top panel is normal incidence transmission images for subwavelength holes, bottom panel is normal incidence transmission spectra for three square arrays of subwavelength holes. For the blue, green and red arrays, the periods were 300, 450 and 550 nm, respectively, the hole diameters were 155, 180 and 225 nm and the peak transmission wavelengths 436, 538 and 627 nm[6].
随后, 科学家们在具有不同类型孔隙结构的金属薄膜上也观察到了EOT现象, 不过这些孔隙所支持的局域共振模式相比全局布拉格散射而言, 起到了更为重要的作用. 1999年, Porto等[110]通过数值实验的方法研究了具有一维周期性亚波长窄而深狭缝的金属光栅结构的共振透射现象, 发现诱导光共振透射存在两种物理机制, 除了激发耦合表面等离激元增强透射以外, 光也可以通过耦合狭缝中所支持的波导共振模式增强穿透. 翌年, Went等[111]采用金属/介质(空气)周期性堆叠的方法制备了深窄狭缝的金属光栅结构, 并在微波波段观察到了系列共振透射峰, 该系列透射峰的产生机理是由于上述两种机制共同作用的结果, 电磁波入射到样品表面激发表面等离激元, 再与狭缝法布里-珀罗(Fabry-Pérot, FP)波导模式耦合共振形成高透射. 数年后, Ruan等[112]运用数值模拟结合理论分析展示了该波导共振模式辅助下的高透射现象与结构的周期性质无关, 从而揭示了该现象的局域共振本质. Lee等[104]采用了随机排布的矩形孔和长方形狭缝阵列结构在实验上观察到了太赫兹波段由局域共振诱导的共振透射现象.
增强透射现象也可以由激发微结构所支持的特殊“形状共振”模式所产生. 2003年, Wen等[101]在实验上观察到具有分形孔隙结构的金属圆盘在红外波段具有多带高透射的现象, 而这一现象主要归因于这些孔隙所能支持的自相似多重形状共振. 这样的局域共振所展现出的深亚波长特性和多带响应使得它们在人工亚原子设计中具有优势, 而且可以应用于不同的频段[102]. 类似的高透射现象也可以由其他类型的孔隙结构所实现.
上述各类增强透射物理机制新颖, 让我们对该类现象有了全新的认识. 但是由于这些现象本质上都与“共振”有关, 因此通常会表现出带宽窄、偏振选择、入射角度敏感等特征, 并且在实际应用中可能会带来不便. 2010年, Huang等[105]研究发现一维周期性亚波长窄而深狭缝的金属光栅结构, 如图7(a)所示. 当TM波以大角度斜入射到该结构表面时, 会呈现超宽带高透射现象. 2011年, Alù等[113]指出这种斜入射超宽带透射现象的物理根源是这样特殊条件体系的等效阻抗与空气阻抗适配, 即满足阻抗匹配条件, 是一种非共振式的高透射现象, 这个超宽透射的斜入射角被类比为等离激元布鲁斯特角(plasmonic Brewster angle). 上述理论预言很快得到了证实. 2012年, Fan等[100]和Ak?zbek等[103]各自报道其实验上分别在太赫兹(如图7(b)所示)和微波波段(如图7(c)所示)观察到了上述斜入射超宽带透射现象.
图 7 (a) 左图为斜入射条件下导电光栅的光透射的示意图, 其中
Figure7. (a) Left panel is light transmission through conducting gratings, oblique incidence under the flat transmission condition,
2013年, Fan等[114]再次提出该超宽带透射效应可以用于抑制太阳能电池表面的反射, 与上述工作不同的是, 他们在电池表面设计了二维金属立方体阵列结构(见图8(a)), 计算结果显示对于超宽波段的近红外(800—2000 nm)入射光, 在大角度入射的条件下可有效降低反射增强透射, 且与偏振无关, 结果如图8(b)所示. 通过数值模拟技术分别计算了透射峰1020 nm和1600 nm处的电磁场分布, 如图8(c)所示, 当入射光以0o角(正入射)时, 电场分布呈现驻波形态, 表明在该条件下引起高透射的主要原因是FP共振; 当入射角为68°时, 体系同样具有很高的透射, 但从透射峰处的场强分布图(见图8(d))看并没有表现出很明显的共振特性, 而且此时金属狭缝内的电场强度要比FP共振条件下的电场强度小得多, 也就是说, 该阵列结构不但可以有效地降低体系的反射, 而且还能够抑制金属结构在整个吸收内所占的权重, 从而提升太阳能电池的有效吸收率.
图 8 (a) 氧化硅衬底上生长金属立方体阵列的结构示意图; (b) 在入射角分别为0°和68°时, 计算得到的透射谱, 其中几何结构为dx = dy = 320 nm, wx = wy = 80 nm, h = 320 nm, ns = 1.47; (c), (d) 金属立方体与氧化硅衬底结构中心位置的电场(|E|2)分布的截面图(c)入射角为0°, 此时入射波长为1020 nm, (d) 入射角为68°, 此时入射波长为1600 nm时[114]Figure8. (a) Schematic of metallic cuboids on a glass substrate; (b) calculated transmission spectra under incidence of 0° and 68°, dx = dy = 320 nm, wx = wy = 80 nm, h =320 nm, and ns = 1.47; (c), (d) the cross-sectional distribution of electric fields (|E|2) at the center of the cuboids (y = 120 nm): (c) θ = 0° at λ = 1020 nm; (d) θ = 68° at λ = 1600 nm[114].
自然界中材料的介电常数和磁导率取值范围有限[14], 这一条件极大地束缚了人们对于电磁波调控的能力. 为了解决这一难题, 科学家们试图通过设计人工微结构来填补自然界材料介电常数和磁导率在取值范围内的空白. 1996年, Pendry等[10]提出通过亚波长的金属网格结构实现低频段的电共振响应, 从而构造出了一种介电常数较小的人工材料. 1999年, Pendry等[11]又提出通过亚波长的金属双开口环结构实现高频段的磁共振响应, 从而构造了在某一频率拥有负磁导率的人工材料. 2000年, Smith等[12]通过将两种结构相结合的方式, 构造出了同时拥有负介电常数和负磁导率的材料, 并且提出了微波波段的负折射的实验设计. 2001年, Smith等[13]将以上的电磁共振结构相结合进行周期性的排列, 首次在实验上实现了微波波段的负折射现象.
近年来, 人们相继发现和提出了与超构材料有关的众多奇异电磁波调控现象和有趣的应用, 如负折射[12,13,115—124]、超棱镜[125—129]、电磁隐身[130—134]、偏振调控[135—138]及增强电磁波吸收[139—152]等. 本节简要回顾基于人工超构材料的电磁波减反增透相关研究工作.
在第 3节中我们讨论到材料的高导电性和高透光性通常是一对矛盾体. 让高导电不透光的金属材料保持高导电性同时具有高透光性十分重要. 针对这一科学问题, 早在2005年, Zhou等[153]报道了一个基于超构材料理念的解决方案. 与利用表面等离激元诱导高透隧穿、FP共振穿透等方法不同的是, Zhou等的方法无需在不透明的金属材料开凿小孔、沟槽等微结构, 而只是在一块平整金属薄膜(ε2 < 0)的两侧贴附具有特定光学性质的超表面结构(ε1 > 0)组成ABA三明治型结构体系就可以实现高透光性, 如图9(a)所示. 通过严的格理论分析揭示, 该体系完美透射需满足如下条件:
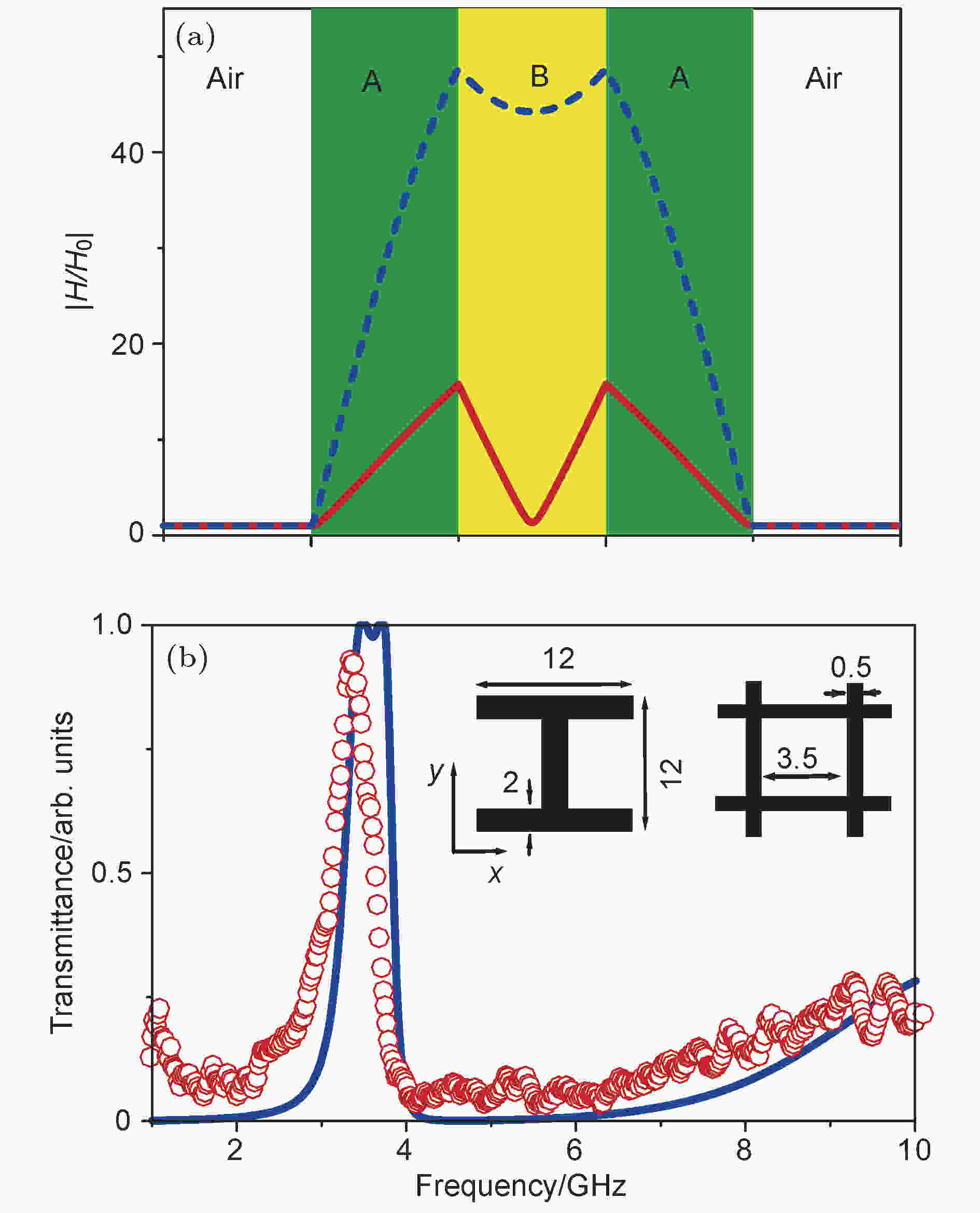图 9 (a) 通过有效媒质理论计算出来的高透射频段的ABA结构内的磁场分布图; (b) 实验测量 (圆圈)与计算得到(实线)的实际ABA结构样品的透射谱, 插图为遵循超构材料的基本精神构造的等效A, B材料的结构示意图, 其中金属网格和“工”字型分别代表在微波波段具有负介电常数ε的B材料与正介电常数ε的材料[153]Figure9. (a) Normalized magnetic field distribution inside the ABA structure at the high transmission frequency obtained by effective medium level calculation; (b) measured (circles) and calculated (lines) transmission spectra of a practical ABA sample, following the spirit of metamaterials, the subwavelength metallic mesh structures and H-shaped resonators (inset) are adopted to realize respectively the desired B layer with negative ε and A layers with positive ε at the working frequencies[153].
2008年, Thoman等[159]利用化学沉积方法在单晶硅衬底表面生长一层金属薄膜层, 原子力显微镜图片(见图10(a)上图)显示该金属薄膜没有成膜而是呈现纳米(平均直径约20—30 nm)团簇岛状结构. 图10(a)下图测试结果显示, 该体系在0.2—2.2 THz宽波段范围内反射率降至1%以下, 该结果优于利用体金属薄膜减反的最好结果(约5%). 究其物理本质, 基于等效媒质理论, 发现该纳米团簇岛状结构薄膜与体材料相比不但电导率的实部可调, 而且其虚部可做到近乎为零(在该太赫兹频率范围, 空气(nair = 1.0)与硅(nSi = 3.42)的折射率都为实数, 而且近似为常数), 因此该金属岛状结构薄膜能够使得整个体系更好地满足阻抗匹配条件, 从而达到更优的减反效果. 不过, 该方法的缺点是微结构大小难以精确控制, 薄膜的品质和重复性难以保证. 2013年, Ding等[160]利用光刻微加工技术在单晶硅衬底上制备一层深亚波长超薄铬金属光栅(周期10 μm, 厚度20 nm, 占空比0.35), 并发现该结构对超宽带太赫兹波(0.06—3.00 THz)的反射同样可以起到有效的抑制作用(如图10(b)所示). 不过, 因狭缝型光栅结构本身是各向异性的, 因此减反增透对入射光的偏振也有选择性. 针对这一问题, 翌年, Ding等[161](见图10(c))再次提出并实验证明了采用深亚波长正方形金属网格结构超表面可实现与偏振无关的超宽带太赫兹波的减反.
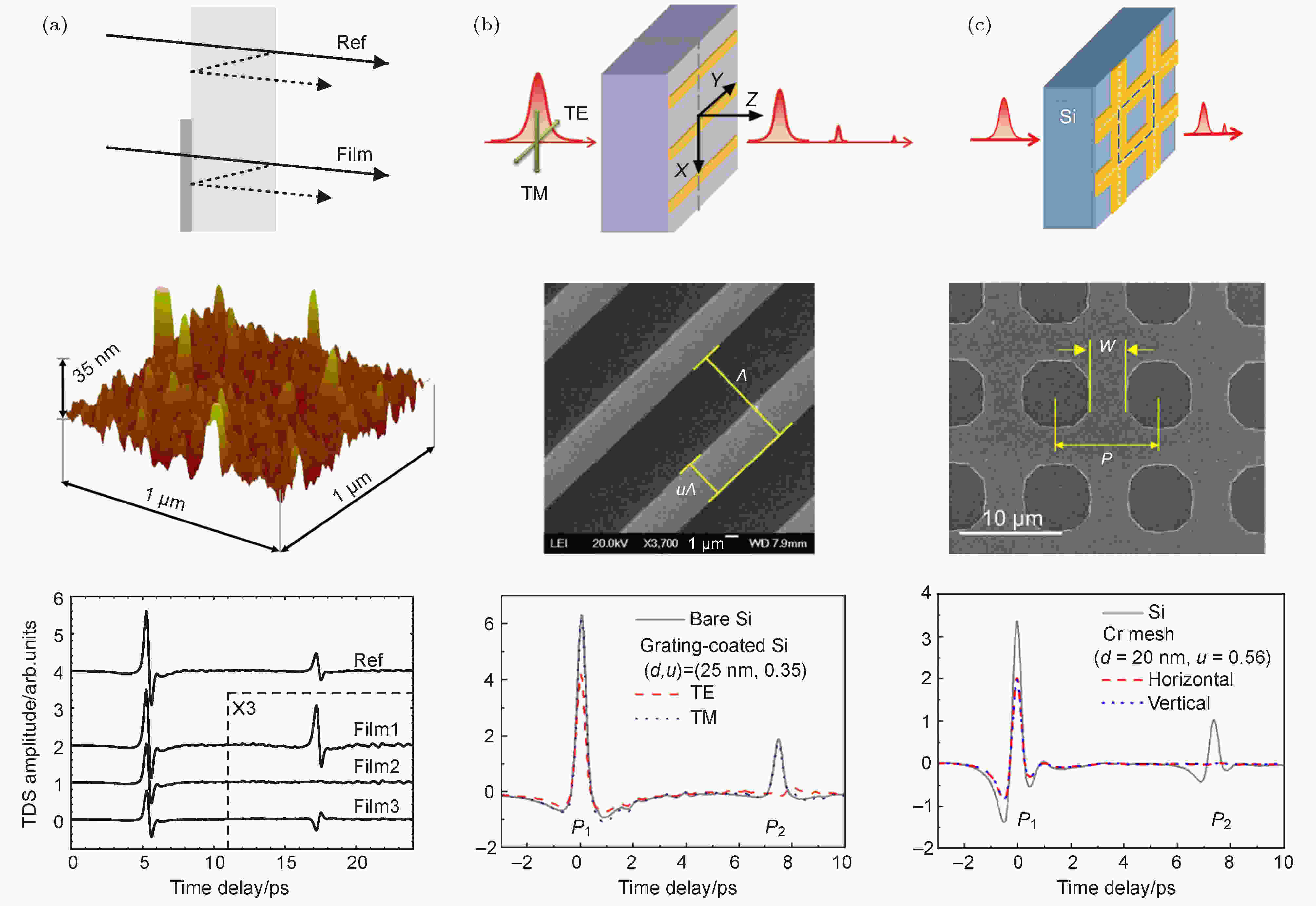图 10 (a) 上图为太赫兹脉冲通过存在/不存在减反层硅衬底的示意图, 与实验测试一致; 中图为化学沉积方法生长的金薄膜; 下图为太赫兹时域光谱仪测得的透射信号[159]; (b)上图为太赫兹测试实验示意图; 中图为铬金属光栅的扫描电子显微镜图; 下图为正入射条件下的太赫兹时域光谱仪测得的透射谱[160]; (c) 上图为太赫兹测试实验示意图; 中图为铬金属正方形网格结构的扫描电子显微镜图; 下图为正入射条件下的太赫兹时域光谱仪测得的透射谱[161]Figure10. (a) Top panel is illustration of Terahertz-pulse propagation through the uncoated and coated silicon substrate, as measured in our experiment, middle panel is AFM images of a chemically deposited gold film, bottom panel is Terahertz time-domain spectrometer (TDS) transmission signals[159]; (b) top panel is schematic diagram of the THz measurement, middle panel is SEM picture of a Cr grating on Si, bottom panel is THz TDS transmission signals under normal incidence[160]; (c) top panel is a schematic of the THz measurement, middle panel is SEM picture of a Cr mesh on Si, bottom panel is THz TDS transmission signals under normal incidence[161]
Thoman等和Ding等提出的方法虽然可以非常有效地降低宽频段的太赫兹入射波的反射, 但是同时金属减反结构对电磁波也会有很强的吸收并引起损耗, 因此体系的透射率并不是很高. 2009年, Zhang等[162]将超构材料结构与传统双层膜减反方法相结合不但可以有效地抑制反射(如图11(a)所示), 而且也实现了宽波段太赫兹波的增强透射的效果, 实验与数值模拟结果显示在0.56—1.56 THz波段范围内透射率高达90%, 见图11(b). 该方法的缺点是对于多层膜减反技术而言, 每层材料的介电常数通常都有特定的要求, 因此受制于材料本身的物理光学性质.
图 11 (a) 人工复合介质结构的示意图; (b)存在减反层的石英盘的透射谱[162]Figure11. (a) Basic structure of the artificial dielectric; (b) transmission of the complete ARC quartz plate[162].
2010年, Chen等[163,164]报道了基于超构材料干涉相消(相长)实现太赫兹波减反(增透)的原创性工作. 如图12(a)所示, 超构材料减反膜由上到下共分为三层, 即金属微结构层/介质层/金属微结构层. 顶层是金开口谐振环阵列结构(split-ring resonators, SRR), 底层为金网格(mesh)结构, 中间层为通过旋涂及加热固化方法制备的厚度约为13 μm的聚压胺介质层(dielectric spacer). 将该超构材料减反膜制备在砷化镓(介电常数εGaAs = 12.7)衬底之上, 可以降低电磁波从空气入射到砷化镓界面的反射. 图12(a)展示的是该样品透反射谱曲线, 结果显示在入射波频率为1.2 THz处反射率低至0.32%, 而透射率高达90%. 与无超构材料减反膜体系相比观测到高达约30%的透(反)射率变化(相同条件下砷化镓衬底透、反射率分别为32%和68%). 理论分析表明, 顶层金属开口谐振环阵列结构和底层金属网格结构可等效为阻抗可调谐且厚度近零的界面, 这些等效界面(空气/介质层之间的等效界面和介质层/衬底之间的等效界面)对于反射波和透射波的振幅和相位具有很强调控能力. 整个超构材料减反系统类似于一个非对称的FP谐振腔, 当一束电磁波入射到该体系后, 将发生多次反射和折射, 最终反射(透射)谱是所有反射(透射)光线干涉叠加的结果. 这一点与传统金属/介质/金属型超构材料通常利用磁共振的工作机理完全不同.
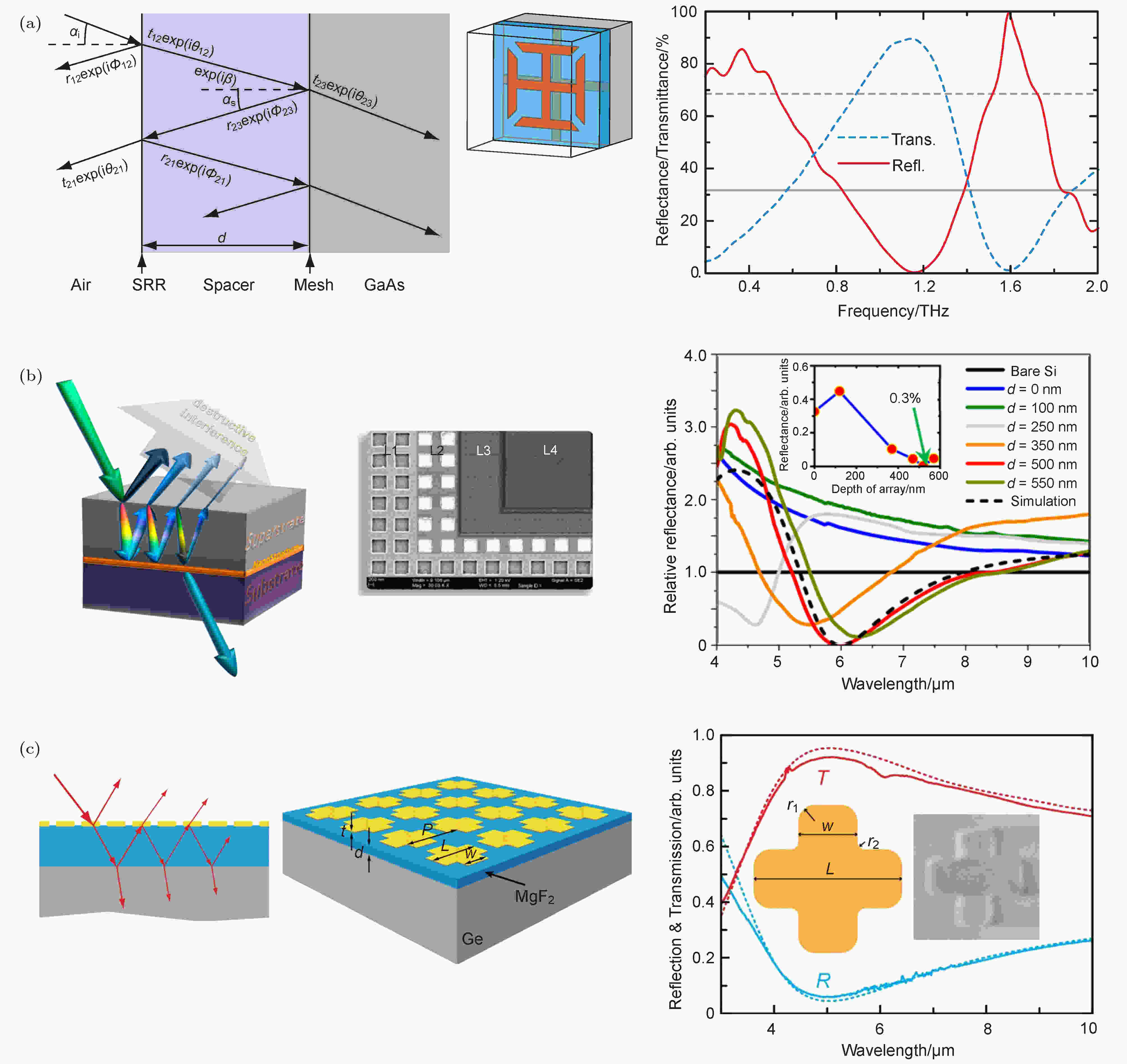图 12 (a) 左图为超材料减反层中干涉模型以及相关变量, 中图为超材料减反层的结构示意图, 右图为正入射条件下实验测得的反射谱与透射谱[163]; (b) 左图为覆盖介质层下埋入金属纳米结构的减反机理示意图, 中图为方块天线结构的SEM图, 展示了四层结构, 分别为L1刻蚀有图案的衬底、L2嵌入式纳米金属天线结构、L3覆盖介质层为100 nm的多晶硅、L4覆盖介质层为500 nm的多晶硅, 右图为实验测得的反射谱[170]; (c) 左图为超表面减反结构中的多重反射的示意图, 中图为锗衬底上的超表面减反结构示意图, 右图为金十字架共振体的数值模拟计算 (虚线)和实验测量 (实线)的透射谱 (T)与反射谱 (R), 其中内置图单元结构的SEM图[171]Figure12. (a) Left panel is illustration of interference model of the metamaterial antireflection coating and associated variables, middle panel is schematic design of the metamaterial antireflection coating, right panel is experimentally measured reflectance and transmittance under normal incidence.[163] (b) Left panel is schematic of antireflection mechanism, middle panel is SEM images for square nanoantennas. SEM images demonstrate the following four layers: L1, patterned substrate; L2, embedded nanoantennas; L3, covered amorphous silicon layer (100 nm); and L4, covered amorphous silicon (500 nm). Right panel is measured reflectance for square nanoantennas[170]. (c) Left panel is schematic of multireflection within the metasurface antireflection structure, middle panel: is schematic of the metasurface antireflection coating on a germanium substrate, right panel is experimentally measured and nume-rically simulated metasurface antireflection performance, the optical reflectance (R) and transmittance (T) spectra at normal inci-dence are plotted as solid curves for experiments and dotted curves for simulations. Insets: SEM images of the unit cells[171].
Chen等的工作开拓了人们利用超构材料设计减反增透膜的思路, 特别是超构材料的光学性质主要取决于人工微结构单元对电磁波的响应, 其工作波段可根据需求调节, 通过精确的设计可在不同的频段实现对电磁波/光波减反增透[165—169]. 其中特别值得介绍的是, 2013年Kabiri等[170]提出了介质覆盖层(superstrate)加超构表面(原文称金属纳米天线)的复合减反结构. 体系之所以可以有效地降低反射, 是因为多重反射光之间干涉相消的存在, 如图12(b)所示, 图中光线颜色表示光的相位变化, 而粗细则表示光的强度的变化. 光在空气/介质覆盖层界面和介质覆盖层/超构表面界面之间发生多次反射, 在每一轮光程中, 光的相位与强度改变与电磁波在介质覆盖层的传播过程和埋在介质层与衬底之间的金属纳米天线的相互作用密切相关. 当电磁波与埋在中间的金属纳米天线超构表面结构相互作用时, 将在特定频率产生共振(共振频率由组成超构表面微结构的几何性质与金属材料以及衬底材料所共同决定的), 并引起电磁波的振幅和相位发生强烈变化(其原理与Chen等[163,164]提出等效界面类似). 为了满足干涉相消条件以降低反射, 可通过纳米天线微结构的选取和排布方式来进行有效调节. 该工作系统地研究了各种不同形状的纳米金属结构按照不同排布方式埋入介质覆盖层与衬底材料之间体系的透反射行为. 具体细节感兴趣的读者可参与参考文献[170].
微结构超构表面嵌埋在介质覆盖层和高反射的材料之间, 利用多光束干涉的方法可以实现减反增透的效果, 将超构表面置于介质层之上, 通过精巧地设计同样也可以基于干涉的原理起到降低反射增强透射的作用. 2014年, Zhang等[171]首次报道了这样一个超构表面中红外减反膜. 如图12(c)所示, 顶层设计为厚度60 nm的金十字架形共振体阵列, 在顶层与高反射锗(nGe = 4)衬底之间生长了一层厚度为520 nm的氟化镁(
无论是Chen等早期提出的多层超构材料减反膜, 还是上述后续各类基于单层超构表面的减反体系都有一个相同的缺点, 即工作波长范围较窄. 其主要原因是这些工作只针对单一波长进行优化设计使其满足干涉相消/相长条件, 因而只获得窄带宽的减反增透效果. 2017年, Huang等[172]提出了新型双层超构表面减反膜. 与之前的设计不同的是, 该减反方法没有在目标减反材料表面上制备减反结构而是先对其进行刻蚀, 利用刻蚀出来的上下表面的空间错位来形成两个等效界面的. 如图13(a)所示, 首先利用先进的微纳加工工艺(紫外光刻技术或者电子束曝光技术)在硅衬底上制作十字架图案, 再利用反应离子刻蚀(RIE)方法在硅衬底表面刻蚀形成突起的十字枕结构, 接着采用高定向电子束(e-beam)沉积方法在十字枕的上表面和错位形成的十字孔结构的下表面上蒸镀一层30 nm的金膜, 且保证凸起十字枕结构的侧壁上没有金薄膜. 由此金属十字架阵列结构构成上超构表面, 十字孔阵列结构为下超构表面, 而十字枕与空气间隙共同组成等效中间介质层. 通过调节十字架的几何参数与十字枕的刻蚀深度可以有效调控上下两个表面反射/折射光的相位与强度. 而且有趣的是, 通过优化设计可使两个不同的波长同时满足相干条件, 实现双波长减反增透. 进一步经过精确调控可使双波段交叉重叠在宽波段范围内做到降低反射增强透射. 为了证明这个想法, 他们分别在中红外和太赫兹波段设计和制备了样品. 图13(b)和图13(c)分别展示的是中红外和太赫兹波段的样品数值模拟仿真与实验测量的透、反射谱曲线. 由图13(b)可知, 太赫兹结果显示在0.719—0.952 THz频率范围内透射率大于87%, 反射率低于3%. 在0.9 THz附近, 透射率达到最大值, 峰值高达92%. 红外结果显示透射率大约85%, 反射率低于5%可覆盖从5.34—6.83 μm宽波段范围(见图13(c)). 除了空间错位的双层超表面可以实现宽带的减反以外, Zhao等[173]在2018年提出随机排布的超表面结构在微波波段也实现了宽带减反. 该结构由两种不同的结构单元在同一平面内进行随机排布而构成, 其中这两个结构单元反射的电磁波振幅相近相位相差180°从而形成了干涉相消的效果, 起到了减反的作用.
图 13 (a) 上图为双层超表面减反层的十字枕结构单元示意图, 每个单元由顶层的金的十字架共振体、底层的金十字槽和硅的十字枕三部分构成, 下图为十字枕结构单元SEM假色(false-colored)图(比例尺: 50 μm); (b) 中红外波段双层超表面结构的透射和反射谱的模拟计算值与实验测量值; (c) 太赫兹波段具有不同十字长度L的双层超表面结构对应的透射谱和反射谱的实验测量值(右侧); (b), (c)图中由小点构成的线是裸硅片的透射谱和反射谱[172]Figure13. (a) Top panel is unit cell schematic of the bilayer metasurface structure consisting of top gold cross resonator, bottom gold cross-slot, and silicon cross-pillar, bottom panel is false-colored SEM image of the unit cell (scale bar: 50 μm); (b) bilayer antireflection metasurface at mid-infrared wavelengths, measured reflection and transmission spectra; (c) bilayer antireflection metasurface at THz wavelengths, reflection and transmission measured in experiments for three different values of cross-length L; (b) and (c) dotted lines are reflection and transmission for a bare silicon surface[172].
