摘要:利用第一性原理计算研究了氟化物钙钛矿NaFeF₃的基态电子态和磁构型, 并模拟分析了衬底应力和阴离子置换对材料基本物性的影响. 计算结果表明, NaFeF₃块材的G-AFM磁基态十分稳定, 不会受到衬底应力调控以及F位氧掺杂的影响. 当低浓度掺杂(~8.3%)时, 氧离子倾向于替换FeF₂面内的F, 形成非对称的Fe-O-Fe链, 导致产生局域极化. 此外, 不对等的Fe—O键还会在氧离子两侧的Fe上形成电荷序, 进而产生非零净磁矩. 值得注意的是, 该局域极化和亚铁磁性均源于不等位氧掺杂, 因此有可能通过外电场调控实现极化翻转并同时改变净磁矩的方向实现电控磁. 更高浓度的氧掺杂会使得Fe的化合价整体升高, Fe离子上的局部电荷序和净磁矩随之消失. 该研究结果有望促进氟化物的理论和实验研究, 并为多铁性材料的设计研发提供新的材料.
关键词: 第一性原理计算/
氟化物/
钙钛矿/
氧掺杂

English Abstract

全文HTML

--> --> -->

过渡金属氧化物钙钛矿材料ABO₃具有特殊的氧八面体构型, 加之B位过渡元素丰富的物理特性, 使得该类材料在电学、磁学以及结构方面表现出异常丰富的物理性质, 如巨(庞)磁电阻效应、超导电性、多铁电性^[1—4]等. 上述这些特殊性质都是由材料内部的多种自由度相互耦合与竞争导致的. 该类材料的这种强关联特性使其成为了凝聚态物理和强关联电子体系的理想研究平台.
与氧化物钙钛矿材料ABO₃相类似, 氟化物钙钛矿材料ABF₃也具有众多特殊性质, 针对此类材料的研究自20世纪60年代以来未曾停止过. 例如在钙钛矿型KBF₃系列材料中, KCrF₃拥有与锰氧化物相类似的巨磁电阻效应^[5]; KCuF₃是自旋1/2海森伯反铁磁体, 其奈尔温度接近室温(280 K)^[6]; KFeF₃中电荷有序导致存在多铁电性^[7]. 即便如此, 与氧化物钙钛矿材料相比, 氟化物钙钛矿材料的研究还是相对滞后, 相关报道并不多见^[8,9]. 近年来, 随着NaBF₃系列材料在光催化活性和电化学性质方面的深入研究, 该类氟化物作为环保类功能材料以及电极材料获得了一定的关注^[10—13].
目前, 关于NaFeF₃材料电学、磁学及结构信息的详尽报道仍然较少. 与立方相KFeF₃相比, 由于A位Na离子半径较小, 材料中氟八面体必将随之发生畸变, 相关实验推断其结构对称性属于Pnma空间群. 基于目前人们对于钙钛矿结构的了解, 结合在材料物性分析领域广泛应用的第一性原理计算方法, 本文针对钙钛矿结构NaFeF₃的电磁学性质展开系统研究, 分析应力以及阴离子替换对材料电子结构的影响, 希望能够为后续实验提供参考.

2

-->

2.1.理论模型

本文计算采用NaFeF₃正交相钙钛矿结构, 该结构属于Pnma空间群. 其中FeF₆八面体彼此间共角相连构成三维框架, Na离子位于FeF₆八面体围成的空间中心. 每个结构单胞中包含4个分子式, 其具体结构如图1所示. 相关实验报道的晶格结构参数为a = 5.48 ?, b = 5.66 ?, c = 7.88 ?^[14].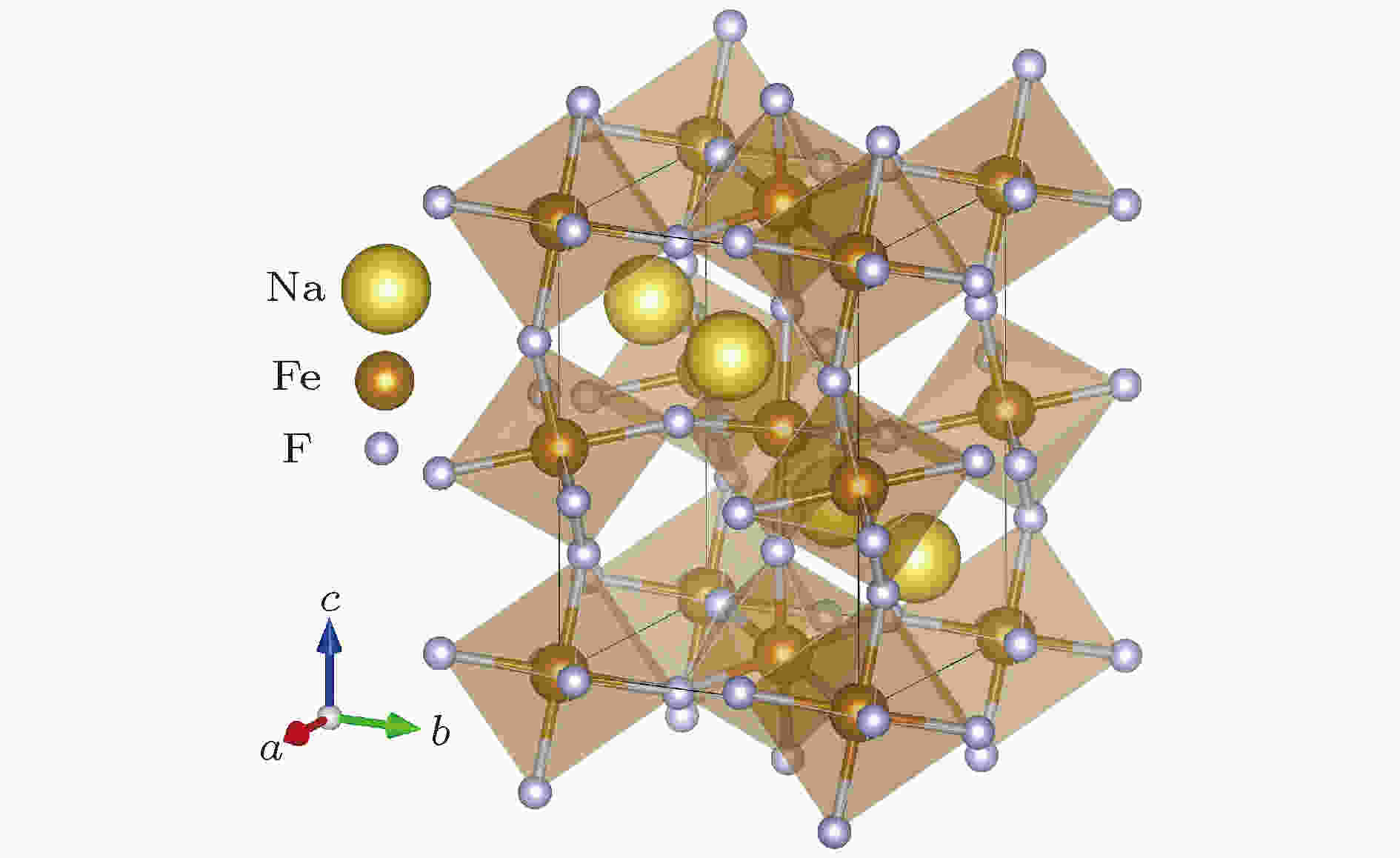
图 1 钙钛矿型氟化物NaFeF₃的结构示意图　浅褐色的是由氟离子构成的FeF₆八面体, 其中心为B位Fe离子, 近邻八面体之间通过共角F离子相连, A位Na离子位于FeF₆八面体围成的三维框架中
Figure1. Schematic diagramof perovskite fluoride NaFeF₃. The light brown structures are corner-sharing FeF₆ octahedra. The center of octahedra are B-site iron ions, which are shown in dark brown. The yellow Na ions are located in the framework surrounded by the FeF₆ octahedra

2 -->

2.2.计算方法

文中计算采用基于密度泛函理论(DFT)的第一性原理计算软件(Vienna ab initio simulation package, VASP)完成^[15,16]. 具体计算采用广义梯度近似(GGA)^[17]的Perdew-Burke-Ernzerhof for solids (PBEsol)函数对电子与电子之间的交换关联作用进行处理^[18]. 体系中Na, Fe, F原子外层价电子组态分别为2p⁶3s¹, 3d⁶4s², 2s²2p⁵. 在布里渊区内以Gamma点为中心采用Monkorst-Park法^[19]取5 × 5 × 3的K点网格进行积分求和, 平面波截断能设为500 eV. 晶体结构几何优化迭代的能量收敛判据为1 × 10^–5 eV, 原子力收敛判据为0.01 eV/?. 考虑到Fe元素3d电子的强关联特性, 计算中采用Hubbard模型加入on-site库仑排斥能U进行拟合修正. 根据文献[20]及实际验算, 当Fe的3d轨道上的有效修正U取4 eV时, 优化后的结构参数以及磁性基态与实验吻合较好, 文中后续计算均以该U值进行.

2

-->

3.1.结构性质

NaFeF₃块材全局优化后的结构对称性属于Pnma空间群, 优化所得晶格参数a = 5.47 ?, b = 5.67 ?和c = 7.78 ?, 与实验报道值5.48 ?, 5.66 ?, 7.88 ?均吻合较好. 优化后结构沿[110]和[001]方向Fe—F—Fe键角分别为145.5°和143.0°. 可见相对于立方相KFeF₃而言, NaFeF₃中Na离子半径减小导致结构产生显著的GdFeO₃型畸变. 该畸变主要表现为FeF₆八面体的扭转, 用Glazer标记法可表述为a^–a^–c⁺模式, 具体又分为a^–a^–c⁰和a⁰a⁰c⁺两种模式, 即沿着赝立方的[100]和[010]方向FeF₆八面体反相等幅转动, 而在[001]方向则为同相转动. 此外, Fe—F键长也出现分化, 表明FeF₆八面体在扭转的同时还发生了Jahn-Teller畸变. 理论计算与相关实验数据详见表1. 从表1中不难看出, 本文理论计算结果与实验报道值较为吻合, 进一步验证了相关计算参数的合理性.

	a/?	b/?	c/?	Space group	Fe-F				∠Fe—F—Fe
					ab plane		c axis		ab plane	c axis
GGA + U	5.47	5.67	7.78	Pnma	2.096	2.029	2.052		145.5	143.0
Expt.[14]	5.48	5.66	7.88	Pnma	2.084	2.052	2.072		144.6	143.9

表1NaFeF₃晶格优化后的结构参数与相应实验报道值
Table1.Optimized structural parameters of NaFeF₃ and the corresponding experimental values.

2 -->

3.2.磁性及电学性质

为了研究NaFeF₃的电磁学性质, 首先对材料的磁基态进行了计算. 计算中考虑了四种可能的磁序: 1) 铁磁性(FM), 即ab面内及面间自旋取向均为平行排列; 2) A型反铁磁(A-AFM), 即ab面内自旋平行排列, 面间呈反平行排列; 3) C型反铁磁(C-AFM), 即ab面内反铁磁排列, 面间最近邻自旋间平行排列; 4) G型反铁磁(G-AFM), 即ab面内和面间最近邻自旋间均反平行排列. 通过比较不同磁序间优化后的最终体系能量, 发现NaFeF₃的磁性基态为G-AFM, 该结果与实验报道一致^[14]. 此外, 计算结果显示每个Fe²⁺离子上的平均磁矩为3.8μ_B, 与Fe²⁺的3d⁶的高自旋态S = 2相一致.
我们注意到已有文献报道NaMF₃ (M = Mn, Co, Ni)为弱铁磁, 即在G型反铁磁的基础上, 自旋略有倾斜从而导致产生微小的非零磁矩^[21—23]. 但目前NaFeF₃相关实验报道较少, 材料的精细磁结构性还有待中子散射等实验的进一步验证. 考虑到复杂磁性计算需要构建较大的结构体系, 涉及原子数目众多, 对计算资源和时间都有极高要求, 实际计算不具有可操作性. 而目前材料磁基态又与现有实验报道基本吻合, 因此除了磁性基态对比验算外, 后续计算分析均是在G-AFM磁序下进行的.
图2是NaFeF₃块材的分波态密度图, 不难看出, 材料能隙为3.0 eV, 经过杂化泛函(HSE)验算, 块材带隙为3.14 eV, 进一步确认了计算中所用参数的合理性和结果的可信度. 费米面附近电子态主要来自Fe和F的贡献, Na的态密度分布主要局域在相对较深层能级. 具体而言, 在价带顶和导带底处态密度主要源于Fe的3d轨道贡献. 此外在–2.4—1.7 eV的能量范围内, Fe的3d和F的2p轨道存在较强的杂化, 而Na的2p轨道则分布于–3 eV以下能量区域. 考虑到Fe—F键中阴阳离子较大的电负性差异, 不难理解FeF₆八面体中Fe—F离子键作用较强, –2 eV及以下深能级Fe 3d和F 2p轨道杂化较强, 而费米面处材料的电学性质主要由Fe离子3d轨道决定. 此外, 费米面附近相对独立且展宽较窄的态密度分布可以近似看作是FeF₆的分子轨道.
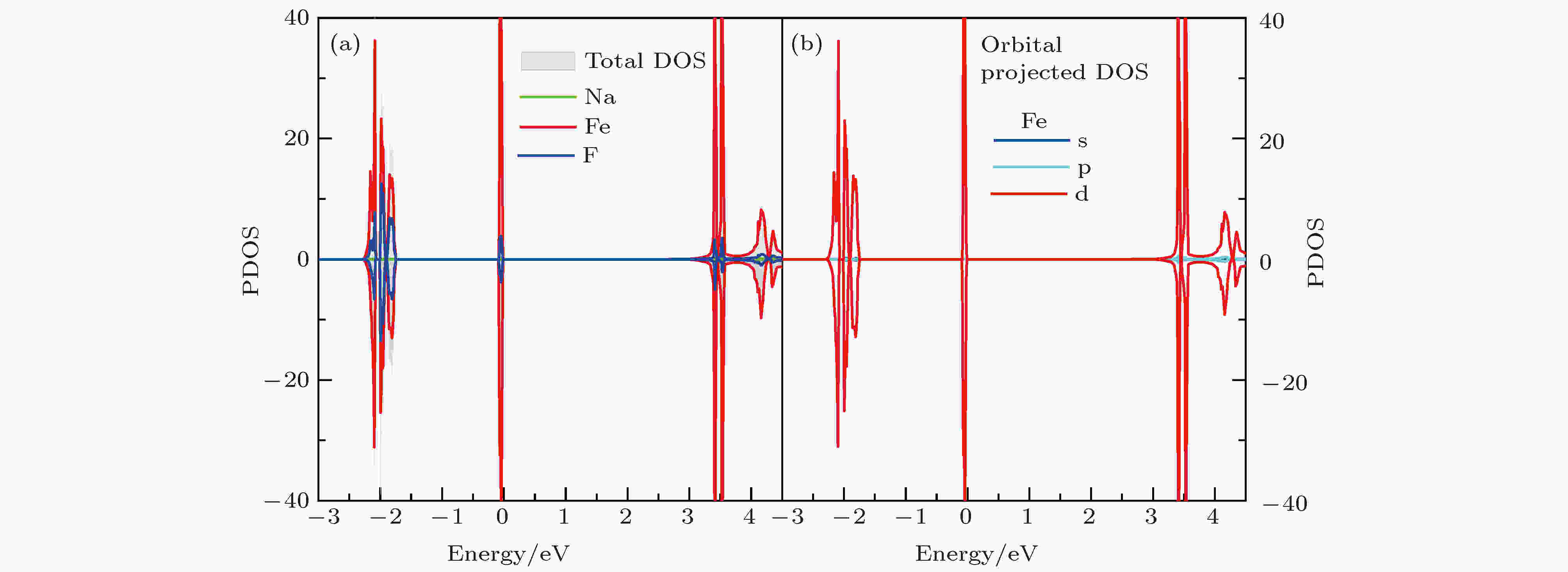图 2 　(a) NaFeF₃块材的原子分波态密度图; (b) 块材中Fe²⁺离子的3d轨道分波态密度
Figure2. (a) The projected DOS of bulk NaFeF₃; (b) the 3d orbital-projected DOS of Fe²⁺ ion.

值得一提的是NaFeF₃的能隙宽度与TiO₂的相近, 相应的吸收波长主要位于400 nm附近的紫外波段. 类似于TiO₂的能带调制, 想要提高材料的光电转化效率, 最直接的方法之一就是通过元素掺杂置换. 后续我们会对材料进行硫族阴离子置换, 研究其对材料能带以及能隙的影响.
2 -->

3.3.应力对磁性和电学性质的影响

由于强关联电子体系中晶格和自旋、轨道、电子之间存在较强的耦合作用, 衬底应力对材料结构、磁性和电学性质有着非常丰富的调制作用, 例如在衬底作用下材料会表现出块材母相中不具备的磁序或铁电性等. NaFeF₃由于GdFeO₃形畸变以及Jahn-Teller效应导致晶格常数a, b不再相等, 通过施加双轴应力, 是否会诱导出新的不同于块材的磁性? 为此, 我们对材料进行了一系列双轴应力下的磁性模拟计算. 结果如图3所示, 在具有现实可行性的 ± 5%应力范围内, G-AFM始终是能量最低的磁基态, NaFeF₃并未出现任何新的磁序, 母相G-AFM十分稳定. Fe²⁺离子上的磁矩也始终保持在3.8μ_B左右, 并未随应力改变出现明显变化. 此外, 材料的晶格结构对称性也并未出现改变.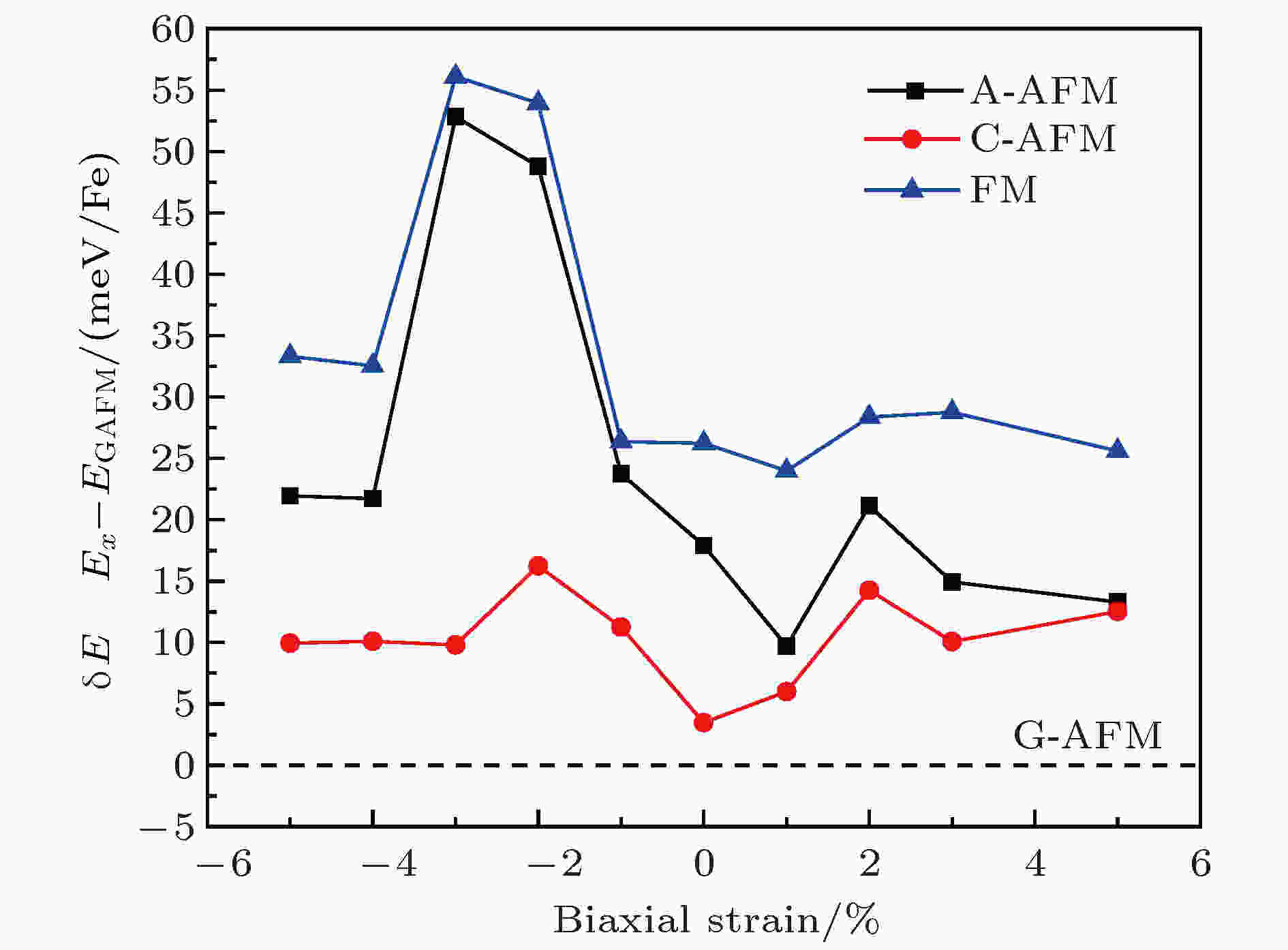
图 3 面内双轴应力对NaFeF₃块材中A-AFM, C-AFM, FM磁序以及G-AFM磁序之间相互能量差的影响, 以G-AFM能量作为参考值, 如虚线所示
Figure3. The biaxial strain dependent energy differences between A-AFM, C-AFM, G-AFM and FM states. The energy of G-AFM ground state is denoted by dash line for reference.

该G-AFM磁基态的成因可能源于Fe²⁺离子的3d⁶高自旋电子构型, e_g轨道电子通过F^－离子的2p轨道与近邻Fe²⁺离子形成反铁磁超交换作用. 上述计算结果表明该超交换作用较强, 在应力可调控范围内, NaFeF₃的结构及磁性较为鲁棒, 并未受到明显影响.
通过分析对比施加应力后材料的态密度和能带结构, 我们发现在 ±5%的面内双轴应力作用下, 材料能隙产生了一定的变化. 如图4所示, 在–5%的收缩应力作用下, NaFeF₃的能隙约为2.6 eV, 而随着应力逐渐从压缩向拉伸转变, 材料能隙呈现出单调递减的变化趋势, 在 +5%的拉伸应力下能隙减小至不足2.4 eV. 从图4(a)—(e)不难看出, 材料导带底随应力增大而逐渐下移, 从而导致了能隙的减小. 除此之外, 能带基本结构并未发生显著改变, 价带顶与导带底均处于Gamma点, 表明在双轴应力作用下材料为直接带隙半导体.
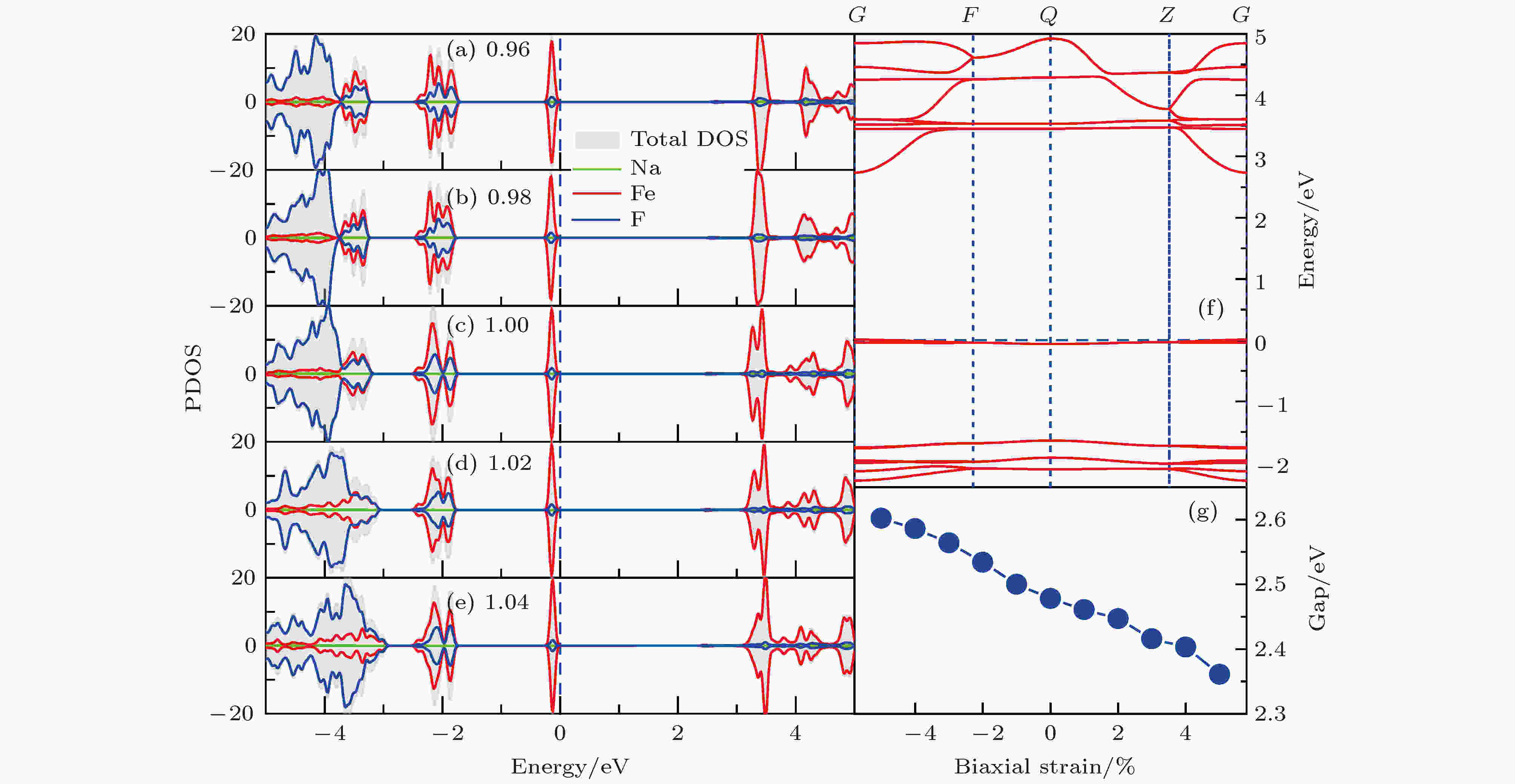图 4 　(a)?(e) 面内双轴应力作用下NaFeF₃块材的态密度分布; (f) NaFeF₃块材能带结构图; (g) NaFeF₃块材带隙随应力的变化
Figure4. (a)–(e) The pDOS of NaFeF₃ with different biaxial strain; (f) the representative band structure of NaFeF₃ with –5% in-plane strain; (g) the biaxial strain dependent band gap diagram.

2 -->

3.4.氧元素置换对材料性质的影响

在钙钛矿化合物的磁性研究中, 离子置换掺杂是一种常用的磁性调控手段^[24,25]. 考虑到Fe的多价态性, Fe³⁺价态化合物在自然界中相对较多稳定存在, 加之O^2－离子半径约为137 pm与F^－离子半径132 pm十分接近, 理论上O替换F具有一定的现实可操作性. 因此, 我们针对O置换F展开了系统研究.
首先, 对晶胞中12个F位中的一个进行O离子置换研究, 相应的阴离子掺杂浓度约为8.3%. 先从能量角度找出最优替换F位, 并对替换后的材料磁性进行验算. 由于F八面体结构的特殊性, 我们分别对八面体顶点以及FeF₂面内的F位进行了置换分析. 计算结果表明, 面内置换后体系能量要比顶点F位上O离子置换低14 meV, 说明O离子更倾向于占据FeF₂面内的F位. 而无论是顶点还是面内F位的O离子置换, 材料G-AFM磁基态始终比亚稳态磁序低100 meV以上, 说明8.3%浓度氧离子掺杂对于材料的磁结构未产生显著影响, G-AFM磁基态非常稳定.
浓度为8.3%的阴离子置换后材料的态密度分布如图5所示. 材料的能带发生了明显变化, 由于氧离子的掺杂导致导带底明显下移, 能隙锐减至0.3 eV左右. 费米面附近电子态主要源于与O较近的Fe离子的贡献, Fe的3d和阴离子2p轨道杂化依然较为明显. F位的O离子置换导致个别Fe离子价态升高, 原本占据态的3d轨道穿过费米面变成导带底. 此外, 阴离子置换改变了八面体中Fe离子周围的配位场, 使得不同Fe位上的电子态分布也发生了显著变化, 原本对称分布的自旋反平行的3d电子态, 出现了相对位移, 如图5所示. 值得注意的是, 上述态密度分布变化导致材料价带顶出现了高自旋极化率的电子态, 即所谓双极化反铁磁半导体, 该类材料在自旋器件设计及自旋电子学研究领域具有巨大的应用价值和研究意义^[26].
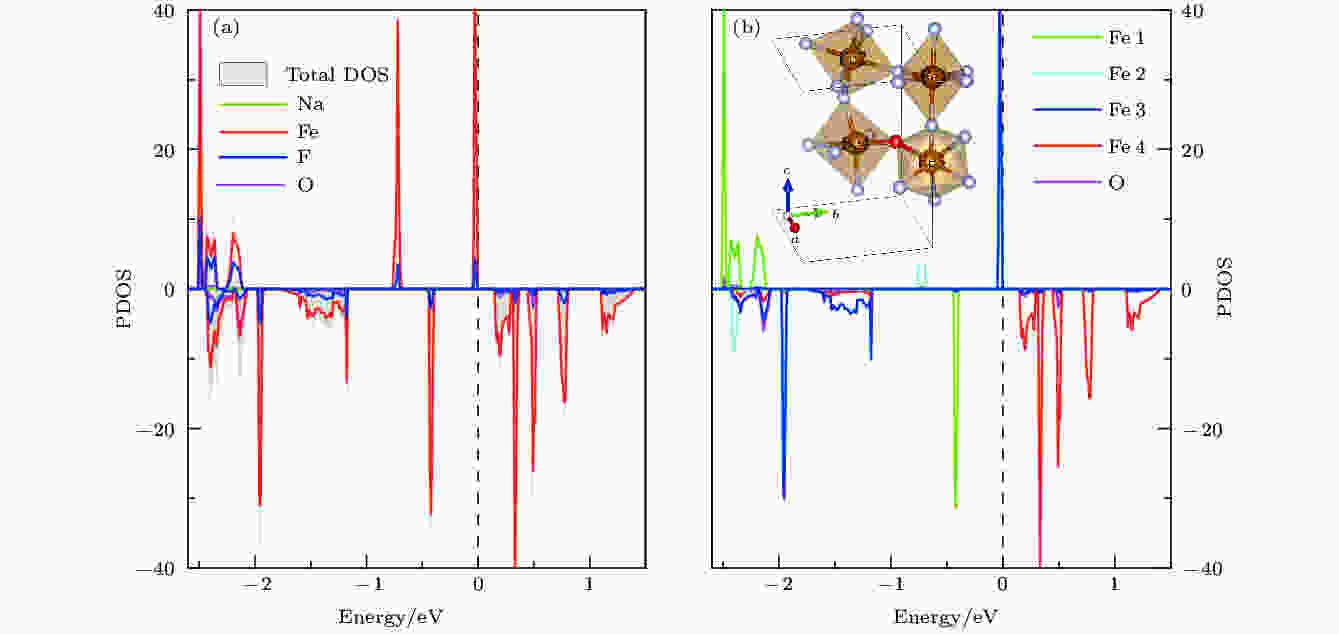图 5 　(a) 低浓度氧掺杂时, 费米面附近NaFeF_3－xO_x (x = 0.25)的原子分波态密度图; (b) 原胞中不同B位Fe离子的分波态密度, 其中插图为氧离子掺杂后的结构示意图, 为了清晰直观地表述, 图中仅给出Fe-F(O)八面体结构
Figure5. (a) The pDOS of NaFeF_3－x O_x (x = 0.25) near Fermi level; (b) the PDOS of different B-site iron ions, which are specified in the inset, Na atoms are omitted for clarify.

由于O离子的不对称掺杂导致八面体中Fe—F和Fe—O键长明显分化, 材料结构由Pnma对称性空间群变为P1空间群. 8.3%浓度的O掺杂导致材料沿[001]方向出现FeF₂/FeF_1.5O_0.5/FeF₂面交替堆叠, 而在FeF_1.5O_0.5面内形成Fe-O-Fe-F-Fe-O-Fe的一维链. 在掺杂面内与O相对接近的Fe进一步被氧化成Fe³⁺离子, 而Fe-O-Fe链上另一端的Fe以及近邻FeF₂层内Fe的价态均未受影响, 从而呈现出Fe的电荷有序性分布. 这一点从计算获得的Fe离子磁矩上也有所体现: 除与掺杂O成键较强的Fe离子上磁矩显著增大至4.3μ_B外, 该磁矩大小与氧化后的Fe³⁺离子的3d⁵高自旋构型相符, 其余Fe离子的磁矩仍维持在3.7μ_B—3.8μ_B之间. 由于材料G型反铁磁磁序没有改变, 而晶胞中单个Fe离子的价态和磁矩发生了变化, 因此材料呈现出亚铁磁性, 并产生0.6μ_B/u.c.的净磁矩.
此外, 氧离子掺杂导致结构对称性降低. 优化后的结构中, Fe-O-Fe-F-Fe链上的Fe—O键作用强弱差异导致Fe—O键长明显分化, 两者键长差别大于0.1 ?, 形成局部偶极矩. 通过Berry phase方法计算所得的极化强度约为15 μC/cm², 该数值与点电荷模型估算获得的极化强度13 μC/cm²相近. 随着FeF₂面内方向上电场的调控, Fe-O-Fe链中氧离子将在高对称位置的附近随外场偏移, 从而影响到链两端Fe离子的价态. 由于G-AFM的近邻磁性离子自旋反平行排列的特点, 势必会导致每个原胞内的净磁矩出现反转, 实现电场对材料磁性的调节. 当然实际材料制备过程中, O离子的分布未必如理论模型中这般均匀, 因此实际材料中可能会产生局部极化区域, 宏观上表现出弛豫形多铁现象.
接下来, 我们将掺杂浓度进一步提高. 计算发现NaFeF₂O材料中, 面内F位上的O离子置换导致体系能量相对于顶点和部分面内顶点F位替换后的体系能量分别低530 meV和12 meV, 说明33%的高浓度掺杂情况下, O离子依然倾向于替换FeF₂面内的F位, 并与近邻Fe离子形成zigzag形Fe-O-Fe链, 优化后的晶格结构对称性属于Pmc21空间群, 通过群论分析不难发现, 该对称群仍属于极化点群. 由于结构中离子位置的非中心对称性, 材料依然可以呈现出一定的铁电极化强度. 但是由于氧掺杂浓度的显著增多, 材料中Fe均被氧化为 +3价, 平均磁矩均为4.3μ_B, 在G-AFM磁基态下净磁矩为零.
NaFeF₂O的电荷密度分布如图6所示. 与氧掺杂浓度为8.3%时能隙的急剧减小不同, 此时材料的能隙与未参杂块材能隙相似, 约为2.7 eV, 处于理想的可见光吸收区. 费米面以下直至–2 eV能量范围内态密度分布主要源自Fe, F和O的电子态, 该区域存在着较强的3d和2p轨道杂化. 磁性能量对比计算表明, NaFeF₂O的磁基态依然是G型反铁磁序, 该反铁磁序与Fe离子外层3d⁵电子组态密切相关. 与G-AFM的NaMnF₃中Mn离子的近邻磁交换作用相类似^[23], 近邻Fe离子半占据的3d轨道通过中间阴离子2p轨道实现反铁磁超交换. 考虑到O^2－离子与F^－离子半径相近, 阴离子置换并未严重影响到材料八面体构型, 不同方向上近邻磁性离子的自旋仍然保持反平行排列, 因此G-AFM磁序没有受到高浓度阴离子置换的影响. 此外, 费米面以下能带的显著展宽与弱氧化性元素置换有助于材料电子态退局域化的趋势相符. 我们还分别尝试验算了SrTiO₃和LaAlO₃衬底应力对材料磁性的影响, 结果表明NaFeF₂O的磁性仍然没有出现明显改变, 可见NaFeF₃材料的G-AFM磁序不仅不会受到应力作用的影响, 对于阴离子掺杂也并不敏感, 甚至上述两种因素共同作用也无法改变材料的反铁磁基态特性.
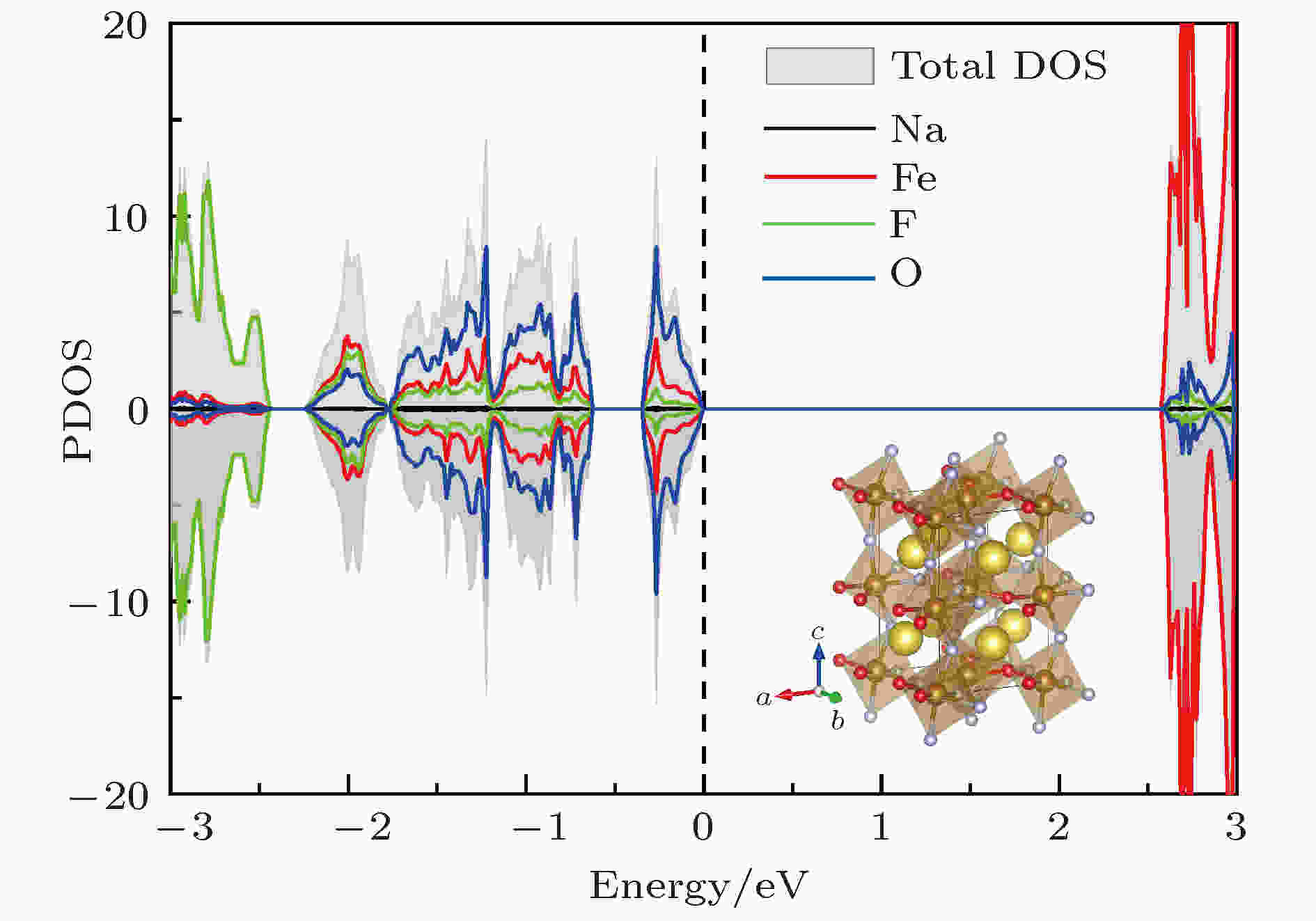图 6 高浓度氧掺杂后, NaFeF₂O的总态密度和原子分波态密度图, 其中插图为相应的结构示意图
Figure6. The total DOS and pDOS of NaFeF₂O near Fermi level; the structure is illustrated by the inset.

至此, 我们系统地研究了钙钛矿型氟化物NaFeF₃的磁电以及结构性质, 并通过衬底应力和阴离子掺杂置换的手段, 尝试对其进行了改性调控. 计算表明, NaFeF₃的G型反铁磁基态非常稳定, ±5%以内的衬底应力以及氧掺杂调控均无法改变该磁序. 但是阴离子掺杂却可以有效改变材料的能带分布及其能隙大小. 当8.3%低浓度氧掺杂时, 掺杂面内会出现Fe²⁺/Fe³⁺的电荷序, 从而产生净磁矩, 同时伴随着氧离子非对称偏移导致的局域偶极矩. 该偶极矩会受到外电场调控产生极化翻转, 进而影响到Fe离子的电荷序, 最终改变净磁矩的取向. 当掺杂浓度提升至NaFeF₂O时, 材料内Fe离子电荷序消失, 净磁矩也随之消失. 此时材料能隙处于2.7 eV附近, 处于理想的可见光吸收波段, 在光伏材料设计和光催化应用领域具有较大的研究价值. 上述研究结果有助于促进NaFeF₃以及与之相类似的钙钛矿型氟化物材料的物性研究, 同时也为氟化物材料的改性和多功能应用材料的设计研发提供参考.