摘要:针对低频噪声的隔离问题, 设计了一种基于压电材料的可调控薄膜声学超材料, 该材料由压电质量块嵌入弹性薄膜制成. 建立了材料的有限元分析模型, 并且计算了材料的各阶特征频率与20—1200 Hz频段的传输损失曲线, 并通过实验验证了有限元计算的真实性. 计算结果表明: 此声学超材料在20—1200 Hz频段内隔声性能良好, 存在两个50 dB以上的隔声峰与一个可调式的隔声峰. 通过分析简单结构的首阶共振模态并构建其等效模型, 从理论上探究了结构参数对薄膜声学超材料隔声性能的影响, 并通过有限元计算验证了其等效模型的正确性; 综合分析材料的特征频率与传输损失曲线, 进一步讨论了结构的隔声机理, 分析结果表明, 在特征频率处, 薄膜的“拍动”会导致声波在其后的传播过程中干涉相消, 实现声波的衰减; 通过Fano共振理论, 探究了各共振点处传输损失曲线特征不同的原因; 压电质量块与外接电路组成LC振荡电路, 在电路的共振频率处, 压电材料的振动可以吸收声波的能量从而造成一个隔声峰, 同时可以改变外接电路的参数来调整电路的共振频率, 从而实现对隔声性能的调控. 最后, 探究了压电质量块偏心量对材料性能的影响, 并通过有限元计算验证了材料隔声性能的可调性. 研究结果为可调式薄膜声学超材料的设计提供了理论参考.
关键词: 压电材料/
薄膜声学超材料/
有限元法

English Abstract

全文HTML

--> --> -->

随着科技的进步, 各类装备不断向着高速、轻质、重型方面发展, 随之而来的噪声污染也日益严重, 影响到了人们日常生活和装备的性能^[1]. 尤其对于1000 Hz以下的低频噪声, 由于其波长较长, 难以在传播中衰减, 同时由于质量定律^[2]的限制, 传统的材料难以对其进行有效地隔离.
近年来, 有许多****对低频噪声的隔离问题进行了研究. 2000年, Liu等^[3]提出了局域共振机制, 基于这一机制的声学超材料可以实现“小尺寸控制大波长”的功能. 张思文和吴九汇^[4]以及张帅等^[5]进一步讨论了其低频带隙特性. 同时, 声学超材料也在其他方面有广泛的应用. 赵甜甜等^[6]借助声子晶体原理对超声塑料焊接工具的横向振动进行了抑制. 王莎和林书玉^[7]基于二维声子晶体原理对大尺寸夹心换能器进行了优化设计. 张振方等^[8]研究了内插扩张室声子晶体管路带隙特性. 杜春阳等^[9]对X形超阻尼局域共振声子晶体梁弯曲振动带隙特性进行了研究.
薄膜型声学超材料由于轻质、性能好等原因, 在低频噪声隔离方面有着广阔的应用前景. 2008年, Yang等^[10]首先提出了“薄膜声学超材料”的概念. 2012年, Mei等^[11]设计的“声学暗材料”, 由于薄膜结构中软硬介质的相互作用所导致的局域共振与声波振动的耦合, 产生了一种“拍动”^[12]的振动模式, 实现了在一些频率上对声波的完全吸收. Chen等^[13]对薄膜附加质量块结构进行了解析建模. Langfeldt等^[14]优化了薄膜声学超材料传输损失的计算方法, 大大减少了计算量. 还有许多****设计了诸多性能良好的薄膜声学超材料^[15—19].
但是目前大部分的薄膜声学超材料, 结构设计一旦固定, 其性能便难以修改, 满足不了实际应用的需求. 为了实现材料性能的可调性, 压电分流阻尼技术被运用到了声学超材料的结构设计之中. 压电分流阻尼技术是一种起源于20世纪的振动控制技术, 其原理是通过压电片与外接分流电路互相作用产生阻尼衰减效果^[20]. Chen等^[21]通过在梁上附加压电片, 实现了一维梁结构带隙的可调性. Zhang等^[22]则在铝板上附加了压电片, 并实现了其隔声性能的可调性. 董亚科等^[23]在外接电路中加入负电容, 拓宽了压电局域共振带隙的频带. 廖涛等^[24]对二维压电声子晶体板带隙可调性进行了研究. 孙炜海等^[25]对含磁电弹夹层的压电/压磁声子晶体带隙特性进行了研究.
本文设计了一种附加压电质量块的薄膜声学超材料, 使用有限元法计算了材料的特征频率与20—1200 Hz频段内材料的传输损失曲线, 并通过实验验证了有限元计算的可靠性, 发现这种材料在此频段内隔声性能优良, 并具有一个可调隔声峰.

通过以往的研究^[26]可知, 在声学超材料中加入偏心质量单元, 并进行合理的参数设置, 可以显著提升材料的性能. 故此, 在这里提出一种附加偏心质量块的薄膜声学超材料, 如图1所示, 该材料由压电质量块嵌入紧张弹性膜, 并固定在金属外框上构成, 压电材料的上下表面接有电极, 与外部电路连接. 其中A为压电材料, 其长为b = 8 mm, 宽为a = 5 mm, 厚度为e = 2 mm; B为方形膜, 其边长为c = 20 mm厚度为f = 0.2 mm; C为正方形边框, 其外边长为d = 25 mm, 厚度为f = 0.2 mm, m = 2 mm, n = 7.5 mm分别为压电质量块距离边框上边界与左边界的距离. 压电质量块材料为PZT-5H, 方形膜材料为硅橡胶, 金属外框材料为钢. 表1和表2为所涉及到的材料参数, 其中压电材料参数来源于文献[27], 其中$s_{11}^{\rm{E}}$为弹性柔顺系数, $\varepsilon _{33}^{\rm{T}}$为垂直膜面方向的自由介电常数, d₃₁为压电应变常数.
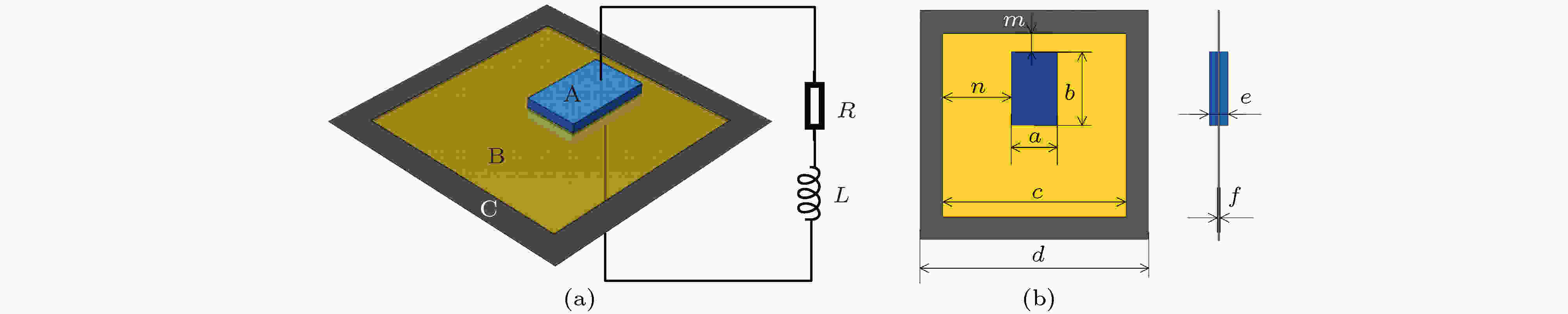图 1 材料结构　(a)结构示意图; (b)结构参数
Figure1. Material structure: (a) Structural sketch; (b) structure parameter.

ρ/kg·m–3	$s_{11}^{\rm{E}}/{{\rm{m}}^3} \cdot {{\rm{N}}^{ - 1}}$	d31/C·m–2	$\varepsilon _{33}^{\rm{T}}/{\rm{F}} \cdot {{\rm{m}}^{ - 1}}$
7500	1.65 × 10–11	–2.74 × 10–10	3.01 × 10–8

表1压电材料参数
Table1.Piezoelectric material parameters.

Material	ρ/kg·m–3	E/1010 Pa	Possion rate
Silastic	1300	1.175 × 10–5	0.469
Steel	7780	21.06	0.3

表2材料参数
Table2.Material parameters.

在材料中, 由于金属框厚度较小而且受到的激励垂直于版面, 在计算中可将其看作薄板发生横向振动, 振动方程为

${D_0}\left( {\frac{{{\partial ^4}w}}{{\partial {x^4}}} + 2\frac{{{\partial ^4}w}}{{\partial {x^2}\partial {y^2}}} + \frac{{{\partial ^4}w}}{{\partial {y^4}}}} \right) + \rho h\frac{{{\partial ^2}w}}{{\partial {t^2}}} = p\left( {x,y,t} \right),$

其中, w为板的横向位移, ${D_0}$为金属板的抗弯刚度, $\rho $为板的密度, h为板厚度; $p\left( {x,y,t} \right)$为薄板受到的横向激励, x, y和t分别为位置坐标和时间.
材料中膜的振动方程为

${\nabla ^{\rm{2}}}\eta = \frac{1}{{{c^2}}}\frac{{{\partial ^2}\eta }}{{\partial {t^2}}},$

其中$c = \sqrt {\dfrac{T}{\sigma }} $, T为薄膜张力, σ为薄膜面密度; ${\nabla ^2} = \dfrac{{{\partial ^2}}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}}}{{\partial {y^2}}}$为二维直角坐标拉普拉斯算符.
对于压电材料^[28]来说, 其压电本构方程, 动力学方程和准静态电荷方程分别为:

$\left\{ \begin{aligned}& {T_{1j}} = c_{1jk1}^E{u_{k,1}} + {e_{11j}}{\varphi _{,1}},\\& {D_i} = {e_{1k1}}{u_{k,1}} + \varepsilon _{11}^S{\varphi _{,1,}}\\& {T_{1j,1}} = \rho {{\ddot u}_i},\\& {D_{1,1}} = 0,\end{aligned} \right.$

其中${T_{ij}},{u_j},\varphi ,{D_i}$分别为应力、位移、电势和电位移; $\rho ,c_{ijkl}^{\rm{E}},{e_{ijk}},\varepsilon _{ij}^{\rm{s}}$分别为材料密度、弹性常数、压电常数和介电常数, 下标i, j, k, l别取1, 2, 3.
得到压电晶体中的振动方程为

${\bar c_{1jk1}}{u_{k,11}} - \rho {\ddot u_i} = 0.$

本文通过Comsol有限元计算软件计算结构的传输损失曲线与特征频率, 将结构四周的边界条件设置为固定, 将压电片上边界设置为悬浮电位, 与电路模块耦合, 将压电片下边界设置为接地. 在有限元计算中, 设置D型压电方程作为压电片的本构方程, D型压电方程为

$\left\{ \begin{aligned}& {S_1} = s_{11}^E{T_1} + {d_{31}}{E_3}\\& {D_3} = {d_{31}}{T_1} + \varepsilon _{33}^T{E_3}\end{aligned} \right.,$

其中: T₁, S₁分别为压电片垂直于膜面方向的应力与应变; D₃, E₃分别为压电材料上下表面的电场密度与电势.
外界电路结构如图1(a)所示, 其中R为电阻, L为电感, 二者串联. 在计算结构传输损失曲线时, 构建如图2所示腔体结构. 整个腔体长为400 mm, 材料设置为空气, 空气中的声速为p₀ = 343 m/s, 空气密度为c₀ = 1.25 kg/m³. 在腔体结构的左侧边界垂直入射平面波激励, 并在结构的右侧边界上拾取响应, 计算两者的差值得到结构的传输损失(transmission loss, TL), 其单位为分贝.

$TL = 10{\rm{log}}\left( {\frac{{{W_{{\rm{in}}}}}}{{{W_{{\rm{out}}}}}}} \right),$

其中W_in与W_out分别为入射声能与出射声能, 即为

$\left\{ \begin{aligned}& {W_{{\rm{in}}}} = \int_{{\rm{S}}1} {\frac{{p_{{\rm{inc}}}^{\rm{2}}}}{{2{\rho _0}{c_0}}}{\rm{d}}S} \\ & {W_{{\rm{out}}}} = \int_{{\rm{S}}2} {\frac{{p_{{\rm{tr}}}^{\rm{2}}}}{{2{\rho _0}{c_0}}}{\rm{d}}S}\end{aligned} \right.,$

S1与S2分别为图2腔体结构的左侧边界与右侧边界.
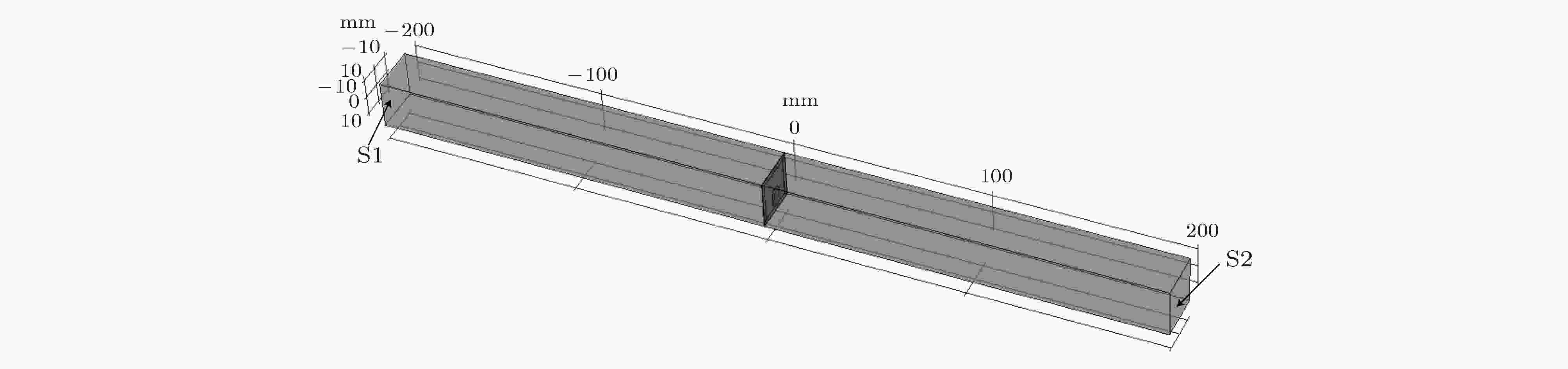图 2 腔体结构
Figure2. Cavity structure.

在设置串联电阻R = 0 Ω, 串联电感L = 200 H的情况下, 使用上节所述方法计算结构的特征频率与传输损失曲线. 表3所示为结构前14阶特征频率与其模态, 图3为20—1000 Hz频率范围的传输损失曲线.

阶数	频率/Hz	模态图	阶数	频率/Hz	模态图
1	111.77		8	689.74
2	135.84		9	793.01
3	147.67		10	835.10
4	185.63		11	842.97
5	201.65		12	945.92
6	231.21		13	981.43
7	458.62		14	1148.40

表3模态图
Table3.Modal diagram.

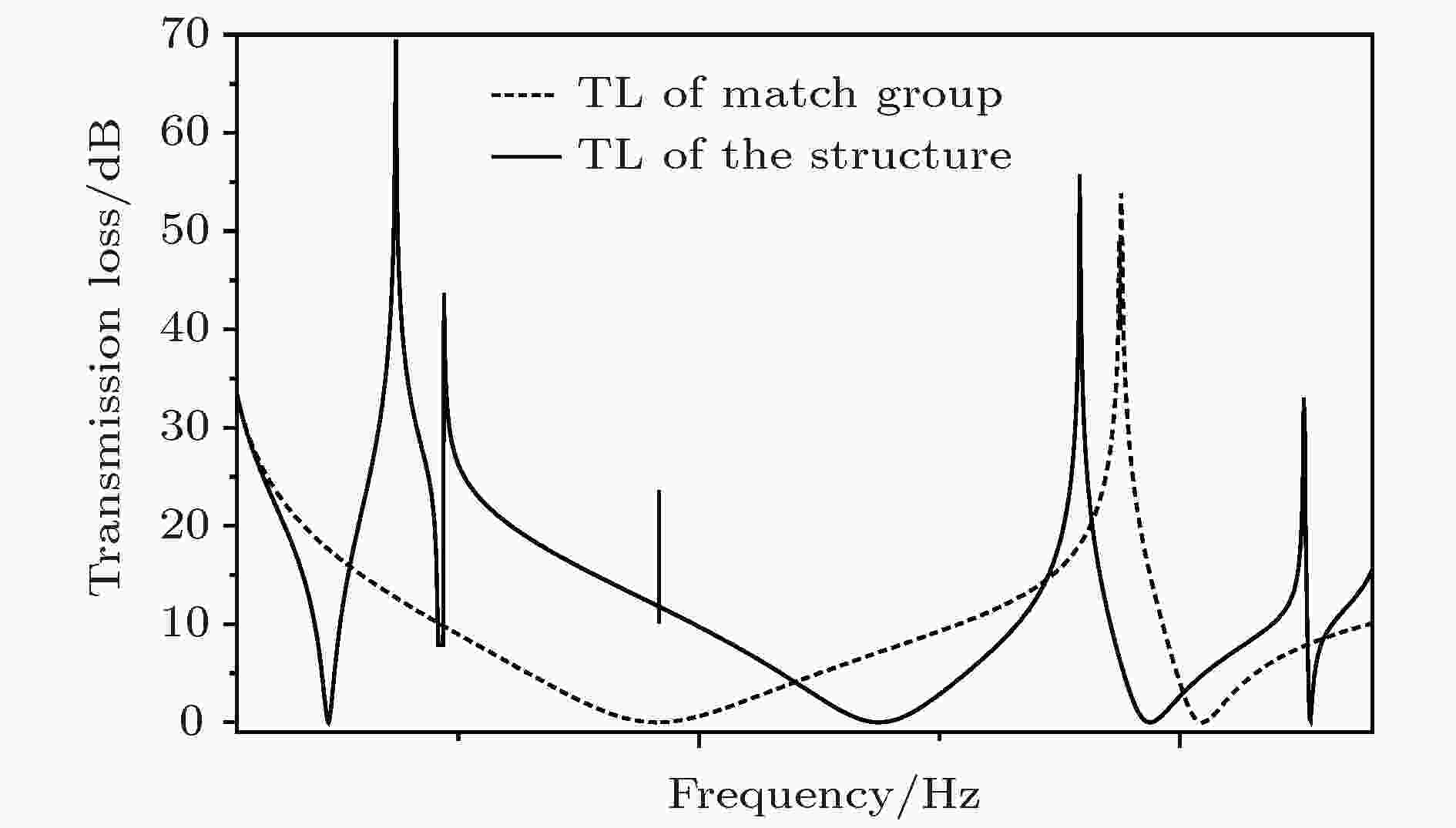图 3 传输损失曲线
Figure3. Transmission loss curve.

通过分析模态图可知, 包含质量块振动的模态都集中于500 Hz以下, 500 Hz以上则展现了丰富的薄膜振动的模态. 材料的传输损失曲线如图3实线所示. 作为对照组, 计算了未嵌入压电质量块材料的传输损失曲线, 如图3虚线所示.
材料在200—1200 Hz频率范围内具有较为良好的隔声性能. 虽然在嵌入压电质量块后, 传输损失在100 Hz附近出现衰减, 但总体上来看, 材料的隔声性能有了较大提升, 并在458 Hz处出现压电隔声峰.
结构的共振点都已在图3中表示处, 尤其值得注意的是在216, 1251 Hz频率处出现非对称的共振峰, 即为传输损失的“突变”. 在第4节中, 将结合特征频率与振动模式图, 进一步讨论结构的隔声机理.
观察传输损失曲线可以发现, 一些特征频率处并未出现共振点, 这是由于在计算传输损失曲线时, 仅仅考虑了平面波垂直膜面入射的情况, 而一些模态难以与此方向上的行波发生耦合^[29]作用, 故此不出现共振点. 此外, 大量的工程实践也证明, 并不是所有的共振模态都可以被激起.

为了验证有限元计算的可靠性, 这里使用AWA6290T型吸声测量系统测试了声学超材料结构的隔声性能, 由于此测量系统的阻抗管呈圆柱形, 故设计圆形结构如图4所示.
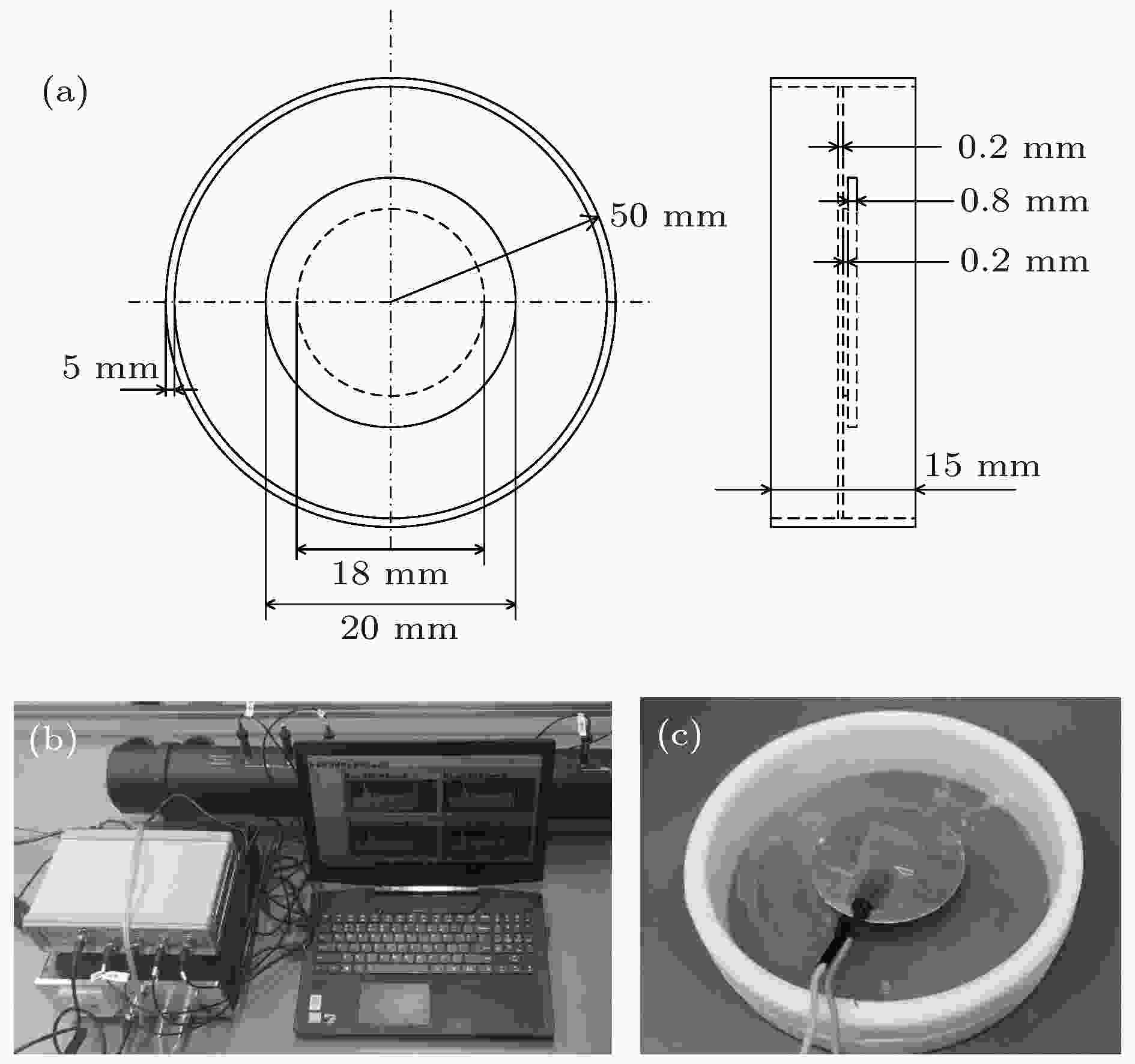图 4 实验示意图　(a)样件结构; (b)实验装置; (c)样件实物图
Figure4. Experimental schematic diagram: (a) Sample structure; (b) experimental facility; (c) physical samples.

图4中环形外框材质为类 丙烯腈-丁二烯-苯乙烯(ABS)白色SLA( stereo lithography apparatus)树脂, 其密度为1.13 g/cm², 杨氏模量为2600 MPa, 泊松比为0.37, 薄膜材质为硅橡胶, 张力为1.5 MPa, 所贴压电材料为镀银电极PZT-5H压电陶瓷附加铜质基板. 压电陶瓷与硅橡胶间使用氰基丙烯酸酯粘合剂连接. 压电片外部串联0—1 H可调电感与10 Ω电阻. 由于在电路中所需电感值较大, 这里使用Antoniou’s电路来模拟大电感 (参见图5). 由于采样精度有限, 通过调节电感可以更方便地监测到压电隔声峰的存在.
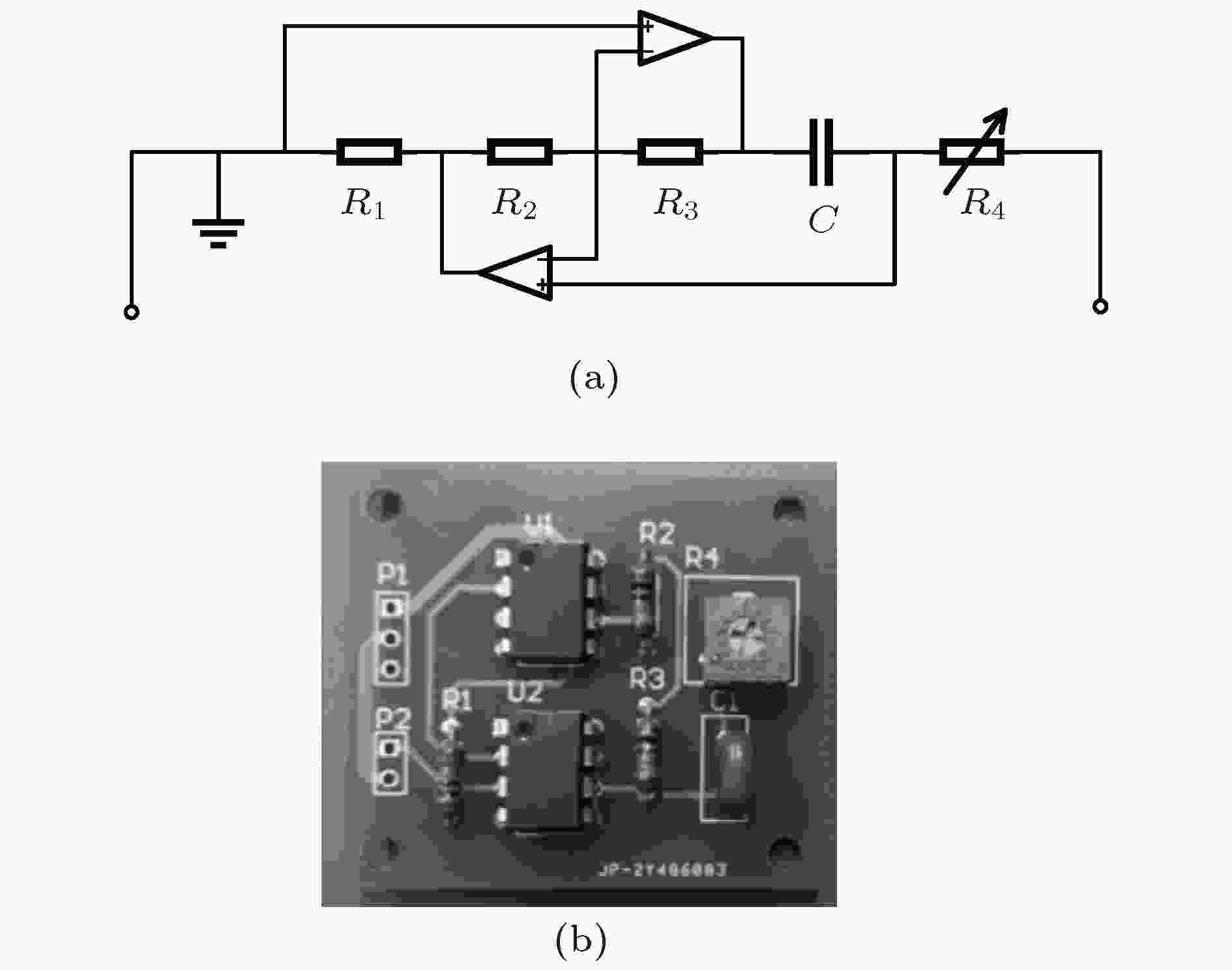图 5 大电感　(a)电路图; (b)实物图
Figure5. Large inductance: (a) Circuit diagram; (b) physical diagram.

分别使用实验方法与有限元计算方法得到结构的传输损失曲线, 如图6所示. 实验数据由500次采样求均值得到.
图 6 传输损失曲线
Figure6. Transmission loss curve.

可以看出, 实验虽然存在一些误差, 但两支曲线基本吻合, 验证了有限计算的真实性. 在实验中, 通过调节电感, 可以在630 Hz检测到尖锐隔声峰, 与有限元计算得到的583 Hz压电隔声峰相印证, 验证了压电隔声峰的真实性.

2

-->

5.1.等效模型

一般来说, 薄膜声学超材料的首阶特征频率对其低频隔声性能有极大的影响, 更高的首阶特征频率, 往往意味着更好的低频隔声性能. 虽然本文所设计的结构性能较好, 但是由于其结构形状较为不规则, 难以进行分析. 为进一步揭示薄膜附质量块结构的隔声机理, 这里对实验中的结构进行了解析建模, 最后构建了“弹簧-振子”等效模型来估算其首阶特征频率. 同理, 由于此简单与前文所设计的结构相似, 有理由相信二者隔声机理相同.
由于首阶特征频率不涉及压电材料. 可以将结构简化为如图7所示, 其中小圆部分为薄膜, 材质为硅橡胶, 其余部分为附加质量块, 薄膜张力为44 N/m, 边缘固定. 其结构尺寸如图7所示.
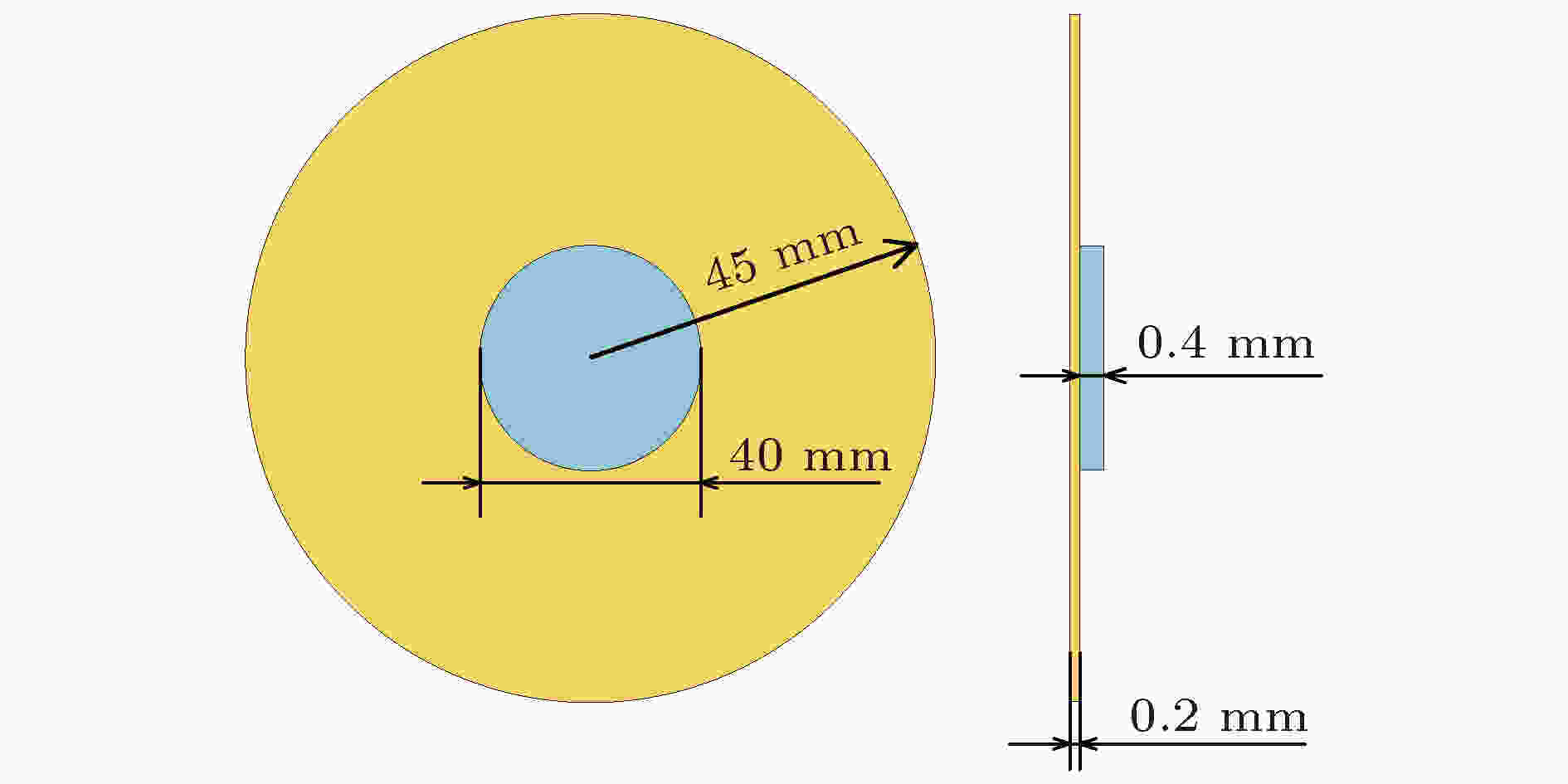图 7 简化结构示意图
Figure7. Simplified structure sketch.

设一不附加质量块的薄膜, 其振动方程为

${\nabla ^2}\xi = \frac{1}{{{\varphi ^2}}}\frac{{{\partial ^2}\xi }}{{\partial {t^2}}},$

其中$\xi $为薄膜的纵向位移; ${\nabla ^{\rm{2}}} = \dfrac{{{\partial ^2}}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}}}{{\partial {y^2}}}$为二维坐标拉普拉斯算符; $\varphi = \sqrt {\dfrac{T}{\sigma }} $, 其中, T为膜表面张力, σ为膜的面密度.
已知首阶共振模态为圆对称情形, 故可将振动方程的解写为径向距离γ与时间t的函数:

$\xi \left( {\gamma ,t} \right) = A{{\rm{J}}_0}\left( {\kappa \gamma } \right){{\rm{e}}^{{\rm{j}}\omega t}},$

其中${{\rm{J}}_0}$为零阶贝塞尔函数, $\kappa = \dfrac{\omega }{\varphi }$.
设圆膜的半径为R, 则边界条件为${\xi _{\left( {\gamma = R} \right)}} = 0$. 代入解中可得, ${{\rm{J}}_0}\left( {\kappa R} \right) = 0$.
在MATLAB调用Besselj函数, 可以画出贝塞尔函数在[0, 1]区间上的图线, 如图8所示.
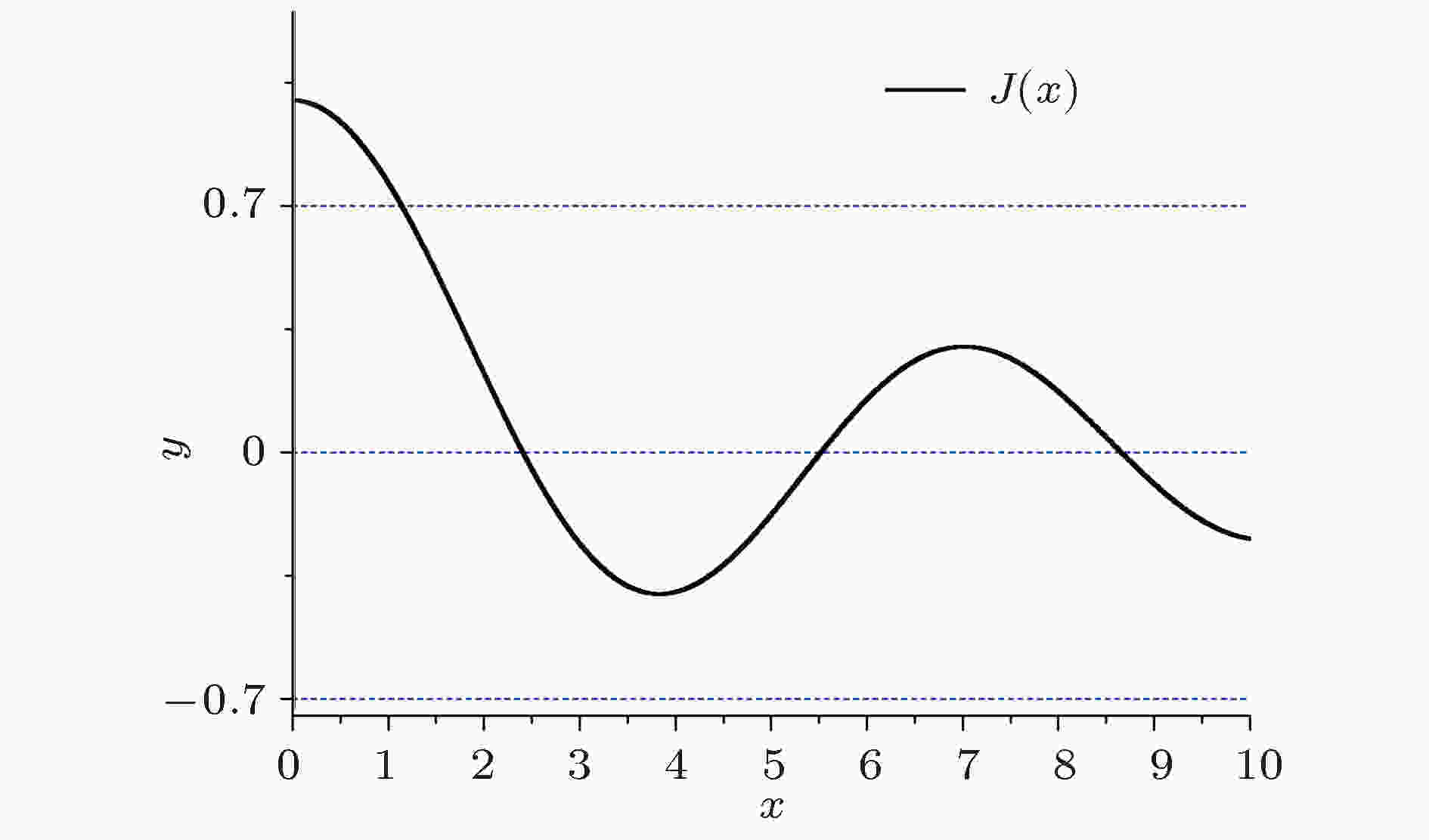图 8 贝塞尔函数曲线
Figure8. Bessel function curve.

通过最小二乘法搜索得到J₀(μ) = 0的解, 精确到三位小数得到μ = 2.405. 根据$\kappa R = \mu $, 可得首阶特征频率f为

$f = \frac{\mu }{{2{\text{π}}R}}\sqrt {\frac{T}{\sigma }} .$

在圆膜上取微元, 其径向距离为(r, r + dr), 其动能为dE:

${\rm{d}}E = \frac{1}{2}\left( {2{\text{π}}\sigma r{\rm{d}}r} \right){\left( {\frac{{{\rm{d}}\xi }}{{{\rm{d}}t}}} \right)^2}.$

将运动方程代入(11)式并取其实部可得此模态下的平均动能为

$\bar E = \frac{1}{4}{\text{π}}{A^2}{\rm{J}}_1^2(\mu ){\omega ^2}{R^2}\sigma ,$

其中J₁为一阶贝塞尔函数.
若将此薄膜的振动等效为“弹簧—振子”结构, 设振子的位移为薄膜中心的位移. 可以得到振子速度v的值为

$v = {\left( {\frac{{\partial \xi }}{{\partial t}}} \right)_{(r = 0)}} = - A\omega \sin (\omega t - \phi ).$

设M为系统等效质量, 则系统在一个周期内的平均动能为

${\bar E_{{\rm{sys}}}} = \frac{1}{T}\int_0^T {\frac{1}{2}} M{v^2}{\rm{d}}t = \frac{1}{4}M{\omega ^2}{A^2}.$

令${\bar E_{{\rm{sys}}}} = \bar E$, 即可得到

$M = m{\rm{J}}_1^2(\mu ),$

其中m为薄膜的质量, 从而得到如图9(a)所示“弹簧—振子”系统, 其中K为等效弹簧的质量. 此系统的特征频率${f_{{\rm{sys}}}} = \dfrac{1}{{2{\text{π}}}}\sqrt {\dfrac{K}{M}} $, 令${f_{{\rm{sys}}}} = f$, 可得

$K = {\omega ^2}m{{\rm{J}}_1}(\mu ).$

现考虑在原膜中心附加质量块的情况, 其等效模型如图9(b)所示, 即在原先质量M之上在附加质量M_add. 在附加质量块之后, 可知系统的等效弹性模量也会发生变化, 但可以近似地认为K₁ = K.
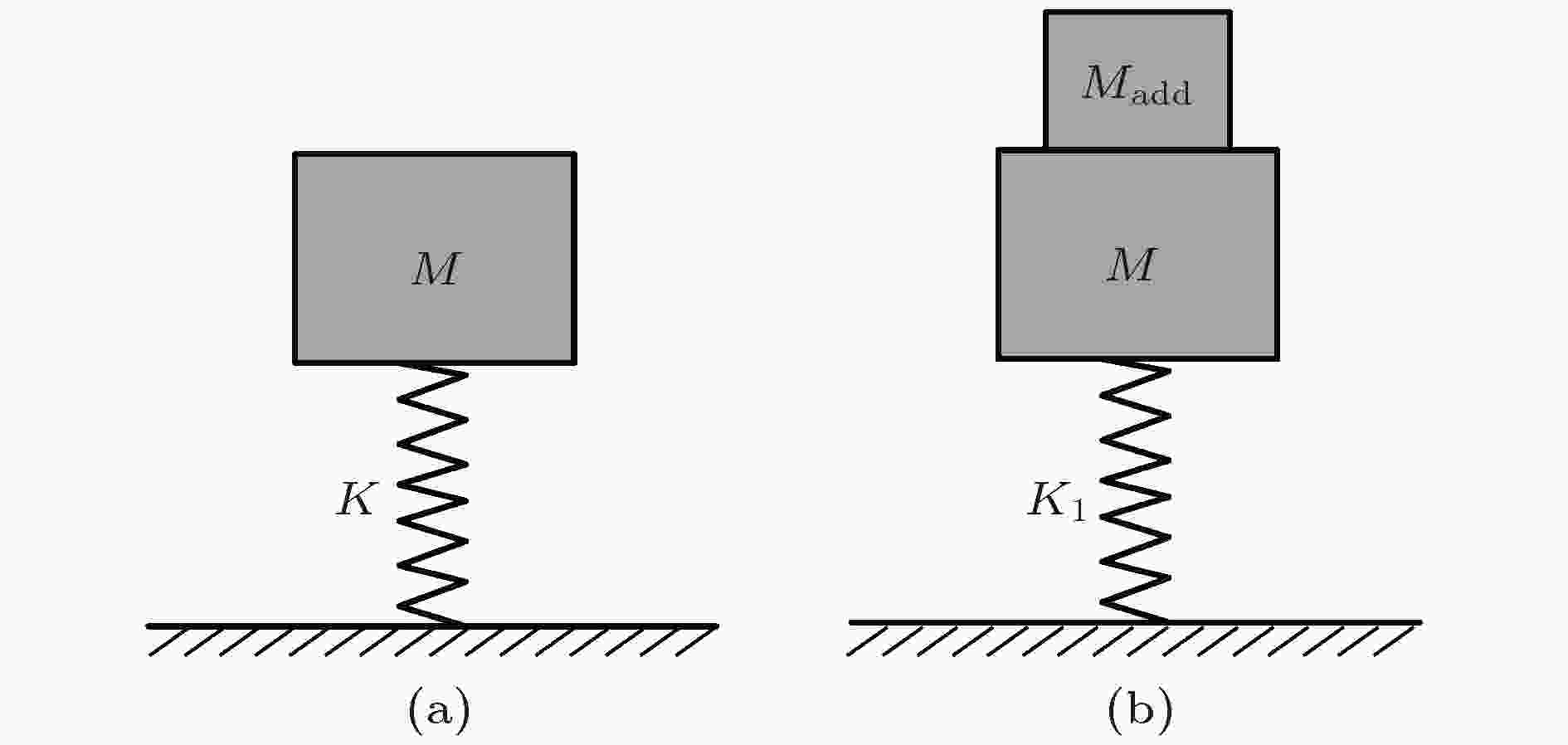图 9 等效模型示意图
Figure9. Schematic diagram of equivalent model.

故此, 简化结构的首阶特征频率为

${f_1} = \frac{1}{{2{\text{π}}}}\sqrt {\frac{K}{{M + {M_{{\rm{add}}}}}}} .$

分别使用有限元法与等效模型方法, 计算了简化模型的首阶特征频率, 取附加质量块的密度为1000—5000 kg/m², 结果如图10所示, 两种方法可以基本吻合, 但是仍存在一定误差, 这是由于简化模型所附加的质量块底面积较大, 对薄膜的等效弹性模量产生了影响.
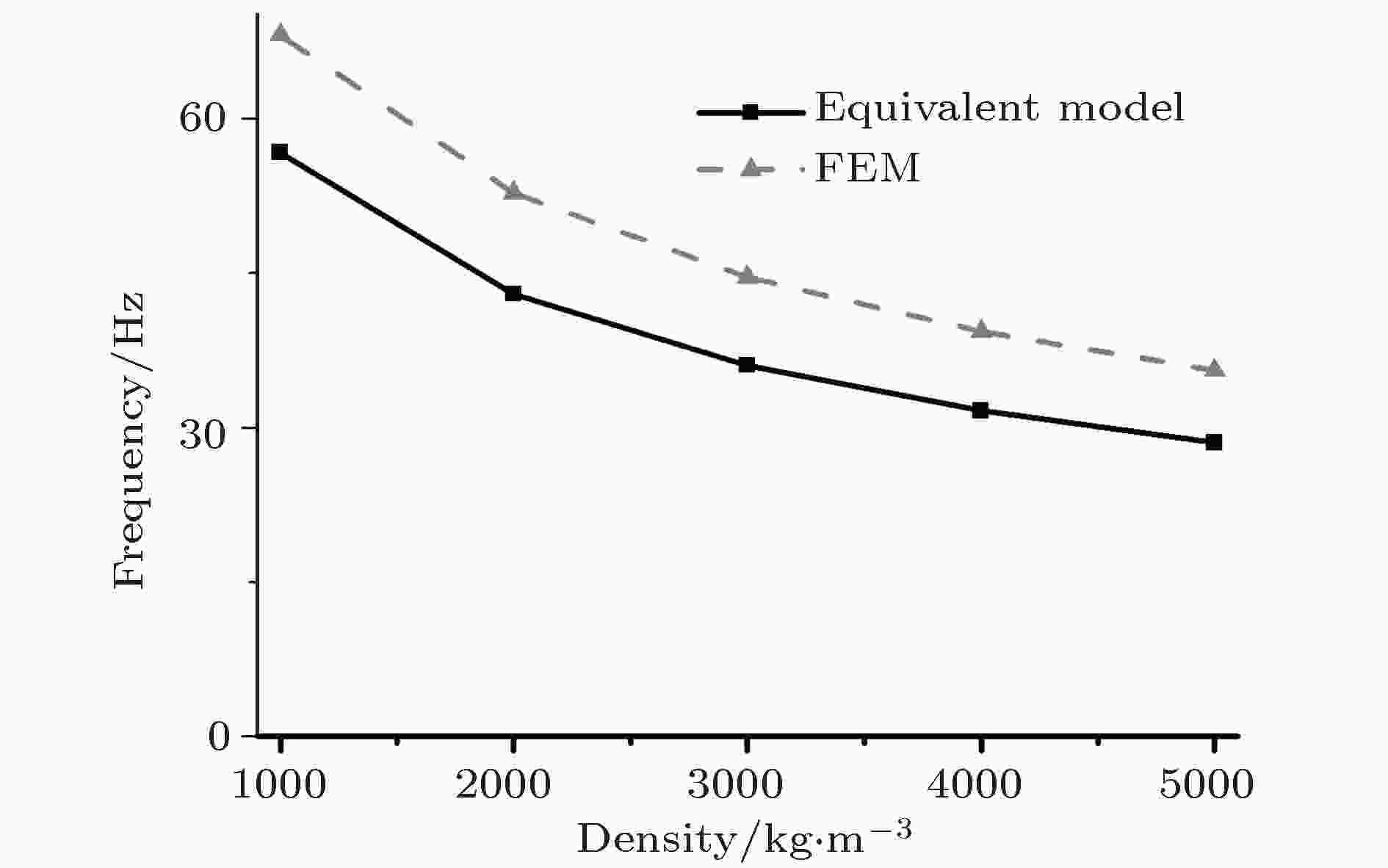图 10 首阶特征频率
Figure10. First natural frequency.

2 -->

5.2.模态分析

为了进一步研究结构的隔声机理, 这里计算了各隔声峰、隔声谷和传输损失“突变”处的振动模式图.
根据如图11所示的消声原理, 首先对隔声峰出现的机理进行分析. 图12(a)所示为结构在185 Hz处隔声峰处的振动模式图, 此处的传输损失高达69.5 dB. 当材料受到此频率声波激励时, 压电质量块与薄膜反向振动, 呈现出“拍动”模式, 由于二者振幅相等, 相位相反, 使得在远场处, 薄膜振动产生的声波与压电片振动产生的声波干涉相消, 从而使得入射声波得到极大的衰减. 同时材料本身也发生了极大的形变, 将声波的能量局域在材料之中.
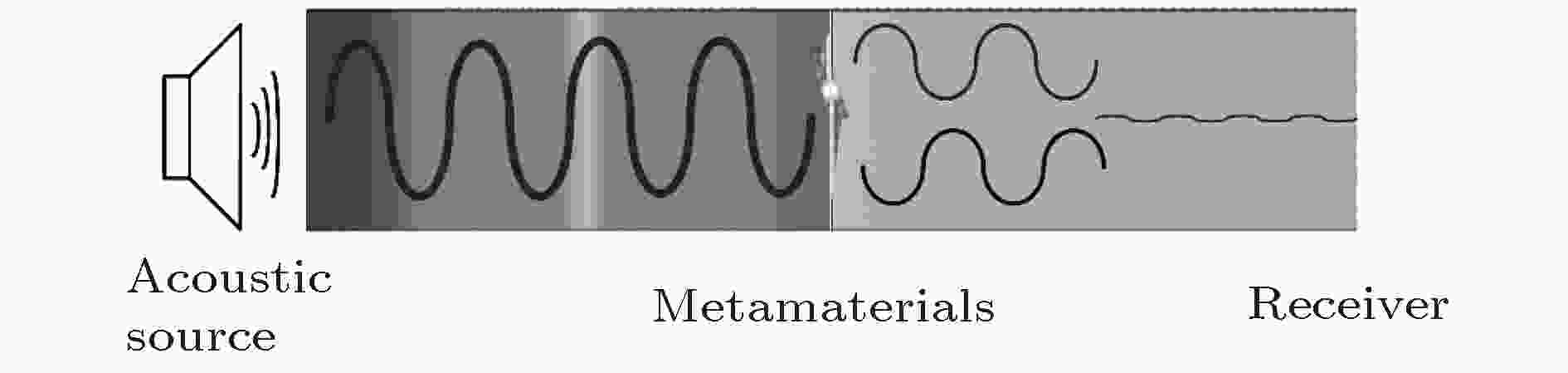图 11 消声原理图
Figure11. Anechoic schematic diagram.

这一振动模式未体现在共振模态中, 之所以出现这样的现象, 一是由于在计算传输损失时考虑了空气阻尼, 二是由于声波入射的方向垂直与膜面, 致使多个平行于膜面的模态难以展现. 但这种振动模式仍可以看作是多个共振模态的叠加.
位于485.62 Hz的压电隔声峰的带宽只有0.59 Hz, 这一频率下的传输损失为23.65 dB, 相较于其左右1 Hz频率范围内, 此处传输损失上升了12 dB, 其振动模式图如图12(b)所示. 从图中可以看出, 此模态下压电质量块横向压缩形变, 行波的能量被压电片所吸收.
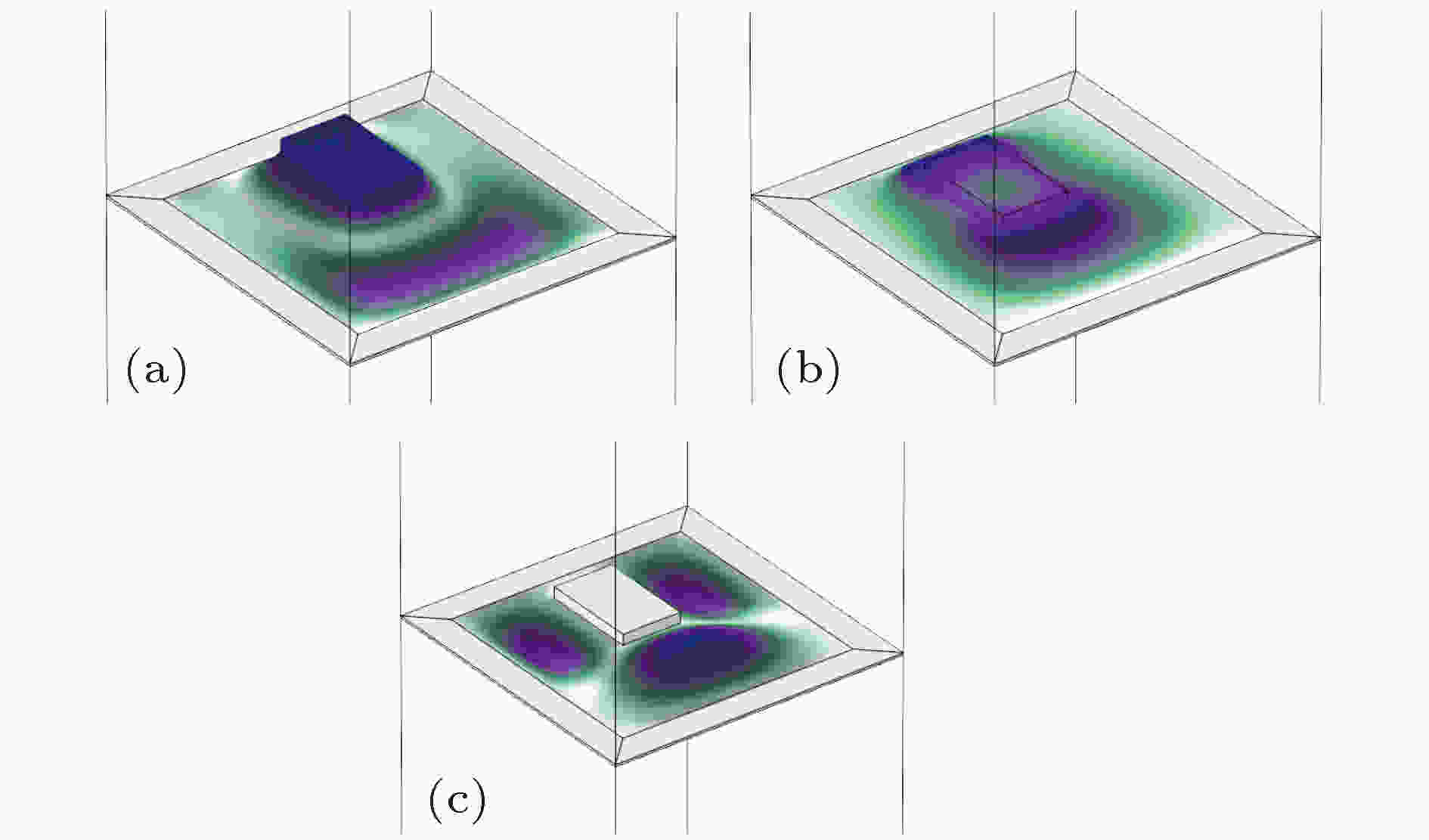图 12 隔声峰处的振动模式图　(a) 185 Hz; (b) 485.6 Hz; (c) 896 Hz
Figure12. Vibration mode diagram at sound insulation peak: (a) 185 Hz; (b) 485.6 Hz; (c) 969 Hz.

在材料中, 压电片可看作电容(电容值可通过Comsol有限元软件可求得)连接外接电路中的电感与电阻, 共同组成了LC振荡电路. 由D型压电方程可知, 当压电片受到一定频率声波激励时, 其上下表面的电荷密度发生同频率的改变. 当压电片两端电荷密度变化频率接近LC振荡电路的共振频率时, 电路就会发生强烈的振荡, 声波的能量被转化为电能并消耗. 这一隔声峰的存在, 是本结构的重要特性.
图12(c)为896 Hz隔声峰处结构的振动模式图, 对应于第13阶特征频率, 此振动模式表现为薄膜分两部分发生“振幅相等, 相位相反”的振动, 形成“拍动”模式, 这一隔声峰形成机理与185 Hz隔声峰类似.
图13(a)所示为结构在115 Hz隔声谷处的振动模式图, 对应于首阶特征频率, 图13(b)为对照组在457 Hz隔声谷处的振动模式图. 从以往的研究可知, 结构的首阶特征频率会对其低频隔声性能产生极大的影响. 在附加质量块的结构中, 115 Hz隔声谷处的传输损失几乎下降至0, 此时材料发生强烈的横向共振, 声波的大部分能量得以透过薄膜. 未附加质量块的薄膜结构出现隔声谷的机理与之类似, 但是由于未附加质量块薄膜的等效质量更小, 根据公式$f = \dfrac{1}{{2{\text{π}}}}\sqrt {\dfrac{K}{M}} $, 其首阶特征频率会更高, 根据有限元计算可知, 其首阶特征频率为456 Hz, 因此, 未附加质量块薄膜在低频范围内隔声量衰减得更慢. 但也由于未附加压电材料, 其隔声性能较为平庸.
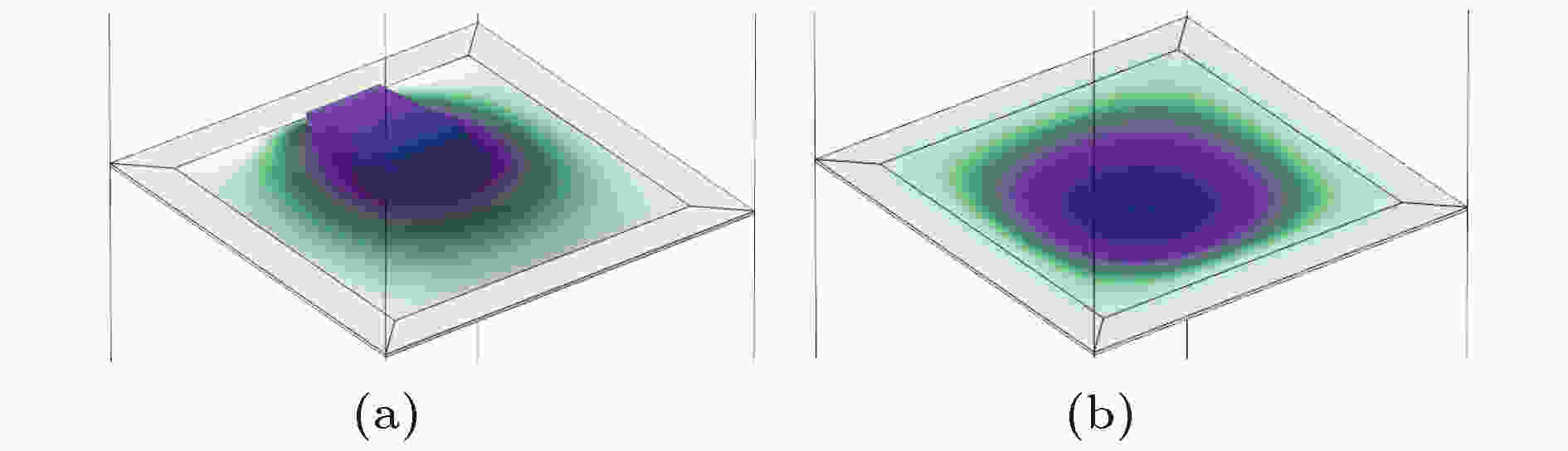图 13 隔声谷处的振动模式图　(a) 115 Hz; (b) 457Hz
Figure13. Vibration mode diagram at sound insulation peak: (a) 115 Hz; (b) 457Hz.

图14(a)所示为687 Hz隔声谷处结构的振动模式图, 对应于第8阶特征频率, 可以看出, 其与图13(b)的振动模式类似, 隔声谷产生机理也类似, 但由于压电片的存在, 膜的振动面积较小, 使其频率更升高. 图14(b)所示为969 Hz隔声谷处结构的振动模式图, 可以看出, 其振动模式与896 Hz隔声峰处的振动模式及其类似, 表现为压电片长边侧两边与短边一侧的振动, 但是在896 Hz隔声峰处, 此两部分的振幅与膜的振动面积大致相等, 故此在远场处其波动可以相互抵消, 但是在969 Hz隔声谷处, 长边两侧振动的振幅与膜的振动面积要远大于其短边侧的振幅, 使其在远场处其波动难以干涉相消, 故此在传输损失曲线上表现为隔声谷. 与之机理类似的还有处于1129—1136 Hz频率范围内的突变, 图14(c)为1129 Hz处的振动模式图, 图14(d)为1136 Hz处的振动模式图, 在1129 Hz处结构表现高达33 dB的传输损失, 紧接着在1136 Hz急剧下降, 造成这样突变的原因也是由于膜上不同部位振动的细微差别导致, 当不同振动相位相反的两部分的振动面积与振幅大致相等时, 则表现为传输损失上升, 反之, 则表现为传输损失的下降.
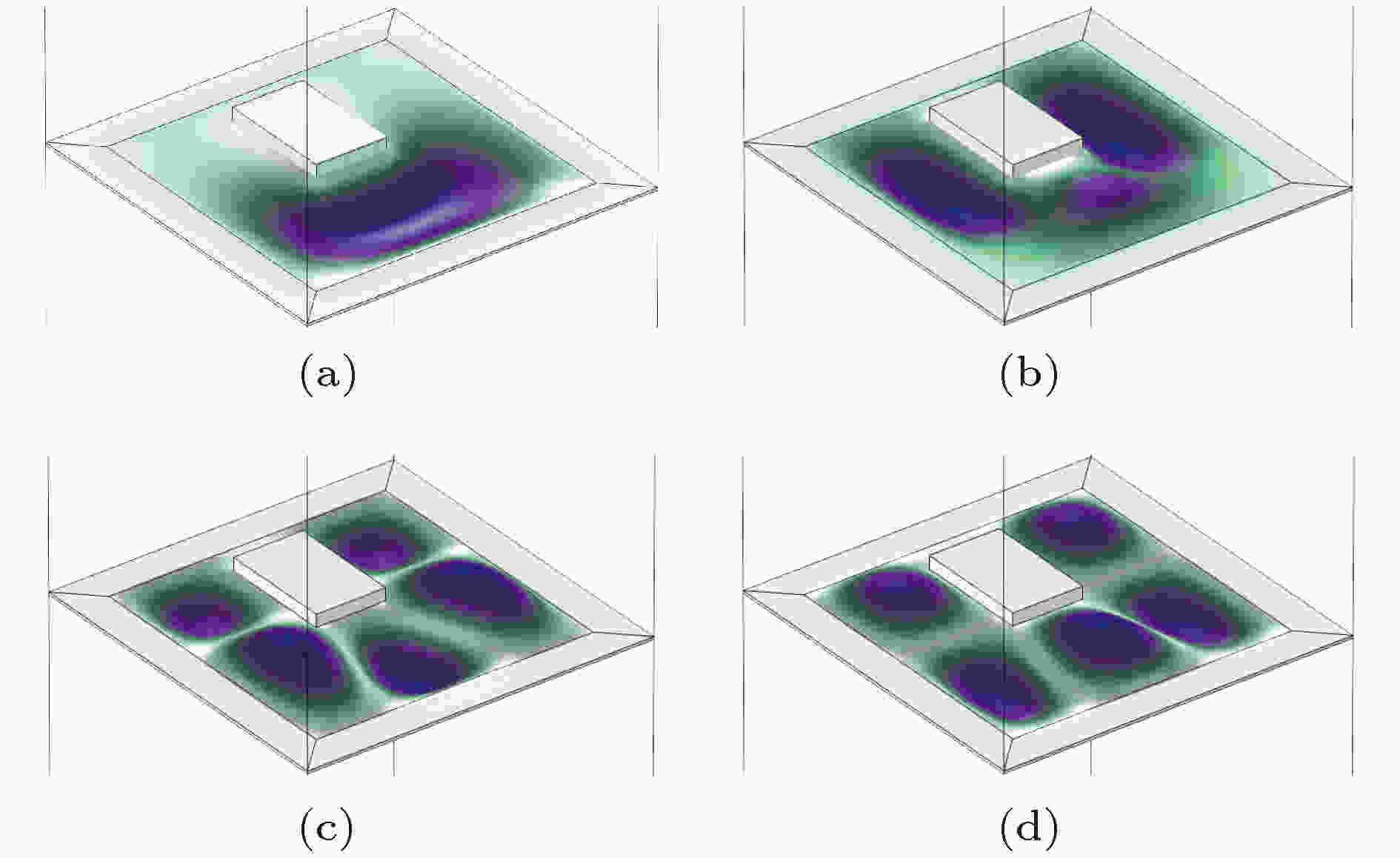图 14 隔声谷与传输损失突变处的振动模式图　(a) 687 Hz; (b) 969 Hz; (c) 1129 Hz; (d) 1136 Hz
Figure14. Vibration mode diagram at TL peak and TL sudden change: (a) 687 Hz; (b) 969 Hz; (c) 1129 Hz; (d) 1136 Hz

在229—235 Hz附近也出现了一次突变, 其中229 Hz的振动模式图如图15(a)所示, 235 Hz的振动模式如图15(b)所示. 从传输损失曲线中可以看出在229 Hz时, 结构传输损失迅速衰减, 但在235 Hz时急剧升高. 从图中可以看到, 两者的振动模式图极其类似, 都表现为压电片以平行于短边的线为转轴的转动振动, 但是也可以明显看出, 在235 Hz时, 结构的转轴更加靠近压电片的中轴线, 这意味着, 在235 Hz时, 结构的振动更加接近于“拍动”的模式, 而在228 Hz时, 压电片两端的振幅不同, 使得在远场处二者难以相互抵消, 传输损失下降.
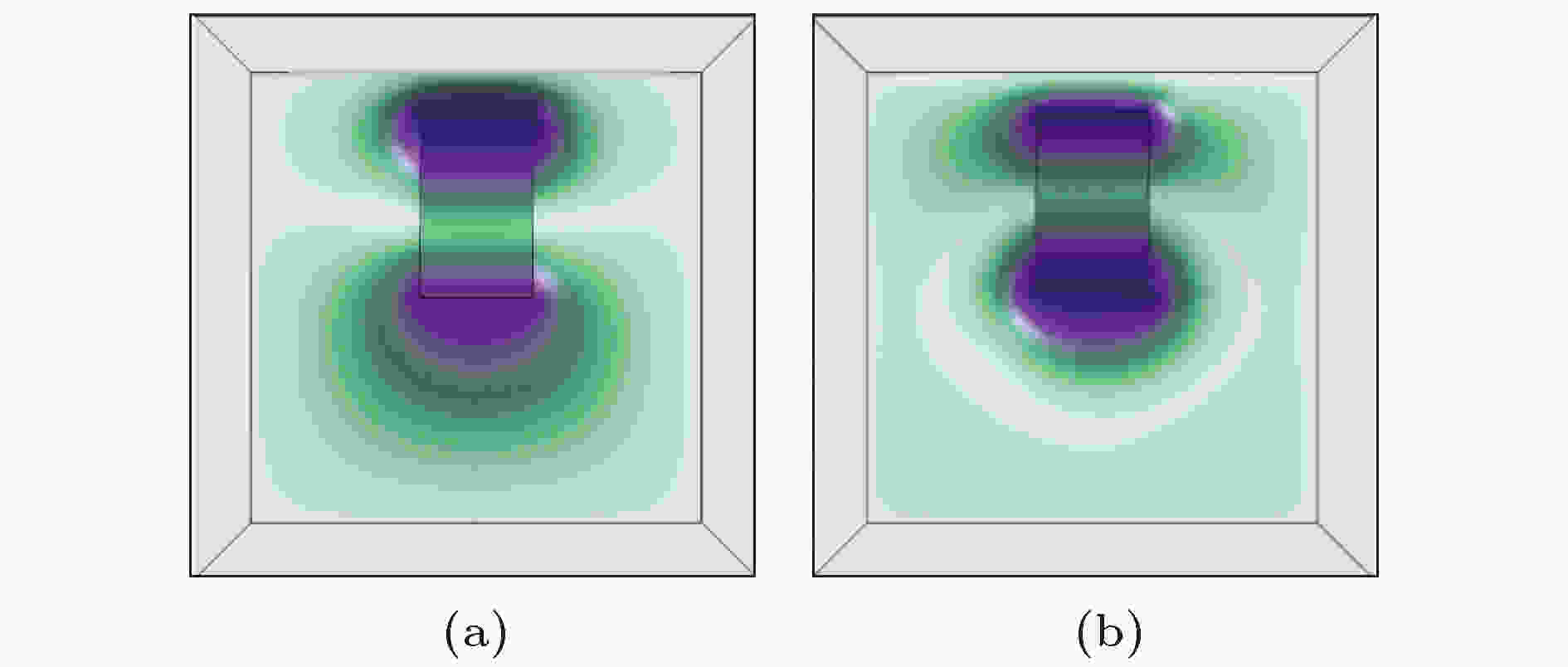图 15 传输损失突变处的振动模式图　(a) 229 Hz; (b) 235 Hz
Figure15. Vibration mode diagram at TL sudden change: (a) 229 Hz; (b) 235 Hz.

2 -->

5.3.Fano共振对结构隔声性能的影响

综合分析特征频率与传输损失曲线可以发现, 结构在各特征频率处的传输损失表现出不同的特征, 例如出现“隔声峰”、“隔声谷”, 以及“突变”等. 5.2节已经从模态分析的角度讨论了其产生机理, 这里从Fano共振的角度, 解释在不同特征频率处传输损失曲线表现出不同特征的原因.
根据共振机理不同, 共振可以分为Lorentz共振与Fano共振. 其中Lorentz共振只涉及一种模态, 在频谱中呈现对称的谱线形状, 如前文所述的“隔声峰”、“隔声谷”等一类情况. 当涉及多种模态的耦合, 则会出现Fano共振, 即在频谱中表现出非对称的谱线形状, 例如前文所述的“突变”.
Fano resonance(FR)概念起源于量子物理领域, 于1961年被Ugo Fano提出^[30], 并得到了Fano谐振的公式:

$I(\omega ) = \frac{{{{\left( {q + \varepsilon } \right)}^2}}}{{1 + {\varepsilon ^2}}},$

其中$I(\omega )$为频率响应; q为Fano参数(Fano parameter), 其定义为两种互相干涉模态的强度比值, 影响着Fano共振频谱的非对称性; ε为归一化的调谐频率. 图16所示为Fano参数不同时, 特征频率附近的频率响应曲线. 从图中观察可得, 当q = 0时, 在特征频率附近的频率响应呈现Lorentz共振模式, 这时由于q = 0时, 两种模态有一种的强度为0, 故此不存在干涉的情况; 当q = ± 1时, 此时两种模态的能量最为接近, 频率响应呈现标准的Fano共振的非对称特性. 同理, 当q值逐渐趋向于无穷时, 频率响应又会变为Lorentz共振模式.
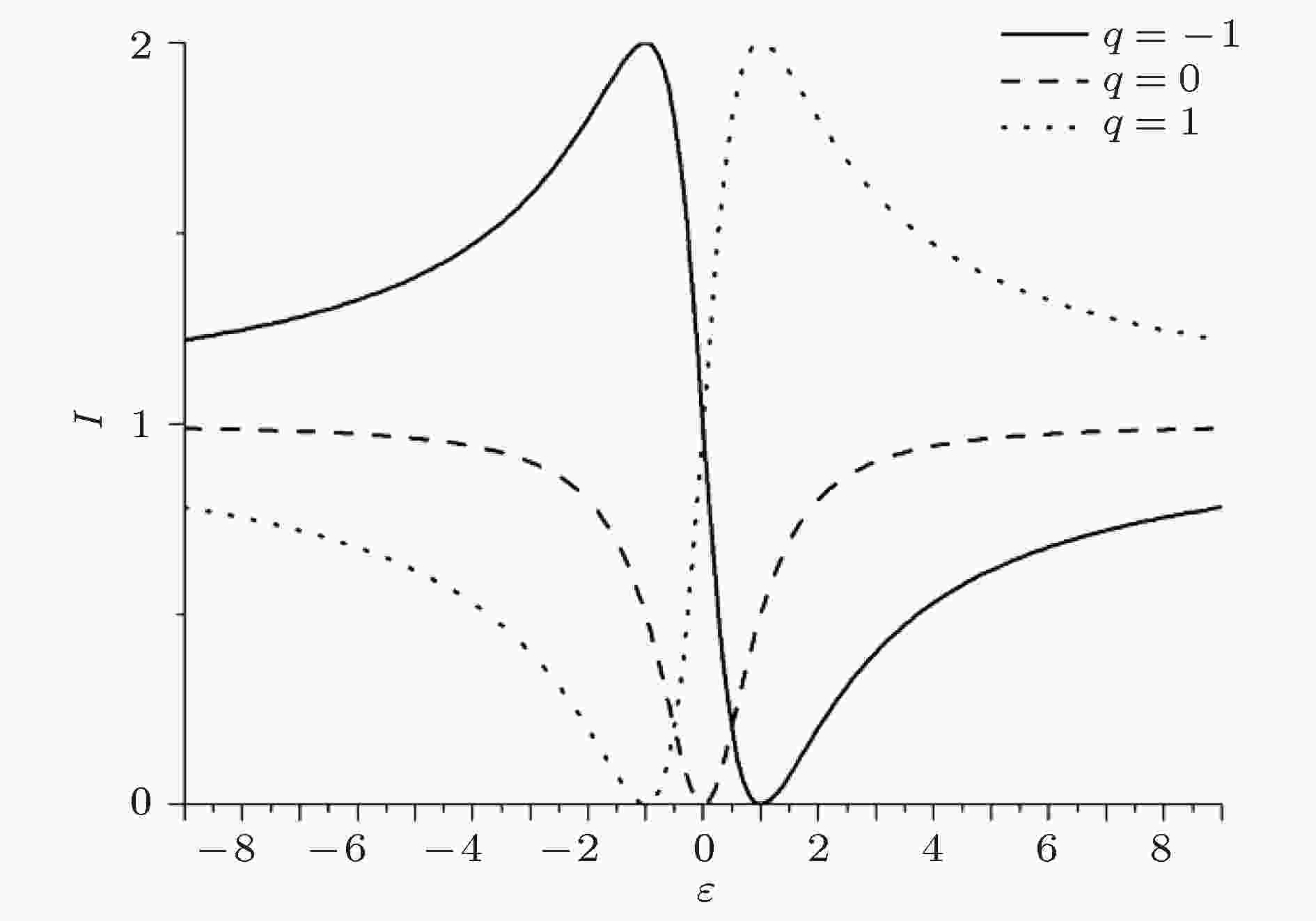图 16 Fano共振
Figure16. Fano resonance.

后来Fano共振的概念拓展到光学领域^[31], 广泛应用于光子晶体^[32]等方面的研究中, 被用于描述两个模态耦合的情况下, 材料对入射波的响应情况. 由于两个模态的相位响应不同, 当二者互相影响时, 其谱线并不是简单的强度叠加, 当两种模态存在相位差时, 会出现干涉相消的情况, 在谱线中表现为谷值, 或者当两种振动模态的相位响应随入射波频率变化的速率差别较大时, 则会出现类似于上文所述的隔声量“突变”的情况.
在对薄膜声学超材料的研究过程中发现, 当薄膜受到较高频率声波激励时, 薄膜的振动往往被“分割”开来, 例如第10阶模态、第14阶模态, 薄膜的各个部分表现为相互独立的振动, 这种独立的振动可以看作分立的模态, 在薄膜后的传播过程中, 各分立模态发生干涉作用.
类比于光学领域, 由于各振动模态的Fano参数不同, 相位响应也不同, 导致在不同特征频率处展现出不同的共振模式. 例如在各隔声峰与隔声谷处表现为Lorentz共振模式, 在216, 1251 Hz表现为非对称的Fano共振模式, 同时896 Hz隔声峰与969 Hz隔声谷也可以看作Fano参数适中的Fano共振.

2

-->

6.1.压电片偏心量对材料性能的影响

图17所示为压电片偏心量m不同时, 20—1200 Hz频段内结构的传输损失曲线. 从图中可知, 压电片的偏心量对结构的低频隔声性能影响较小, 但是对结构的高频隔声性能影响较大, 并且, 无论m值如何变化, 在458 Hz处, 结构的隔声量都会有约12 dB的上升.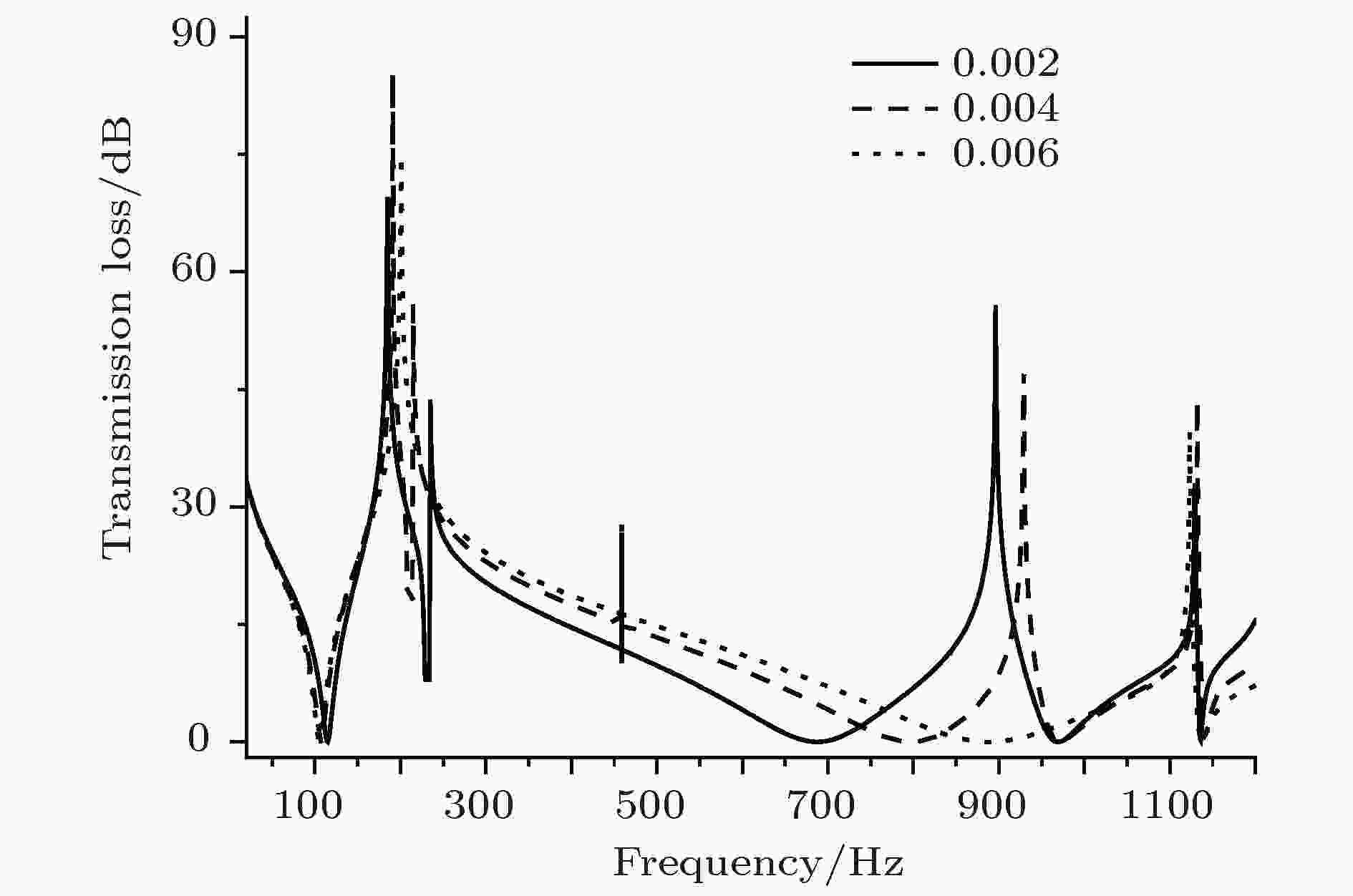
图 17 传输损失曲线m = 0.001, 0.004, 0.006 m
Figure17. TL curve m = 0.001, 0.004, 0.006 m.

之所以传输损失曲线出现这样的变化, 是由于低频特征频率对m值较敏感, 高频特征频率对m值较为不敏感. 图18所示为m = 0.001, 0.004, 0.006 m时材料的各阶特征频率.
图 18 特征频率
Figure18. Eigen frequencies.

如图17所示, 压电片的偏心量对300 Hz以下的特征频率影响甚小, 这是因为300 Hz以下的共振模态表现为“弹簧-振子”模式, 由于膜的面积较大, 压电片的偏心量对“弹簧-振子”系统的等效刚度影响不大. 例如图19所示为m值不同时第五阶特征频率的模态图, 其振动表现为压电片带动周围一部分膜进行振动, 压电片的位置对其影响较小.
图 19 第五阶共振模态　(a) m = 0.002 m; (b) m = 0.004 m; (c) m = 0.006 m
Figure19. Fifth order vibration: (a) m = 0.002 m; (b) m = 0.004 m; (c) m = 0.006 m.

但是嵌入压电片的位置对500 Hz以上的特征频率影响较大. 从前文的分析可知, 500 Hz以上的共振模态表现为薄膜的振动, 嵌入薄膜的压电片则会在一定程度上 “分割”薄膜, 改变薄膜振动的位置与面积, 从而影响材料的特征频率.
从图18中也可以看到, m值改变对结构的第七阶特征频率影响很小. 这是由于第7阶特征频率是由压电片外接的LC电路所决定的, 与压电片的位置无关, 使得无论m值如何变化, 在458 Hz附近总会出现隔声峰.
2 -->

6.2.电路参数对隔声量的影响

对于一般的薄膜声学超材料而言, 一旦其结构固定, 其性能便也同时固定. 但是本材料中加入了压电材料, 可以通过改变外接电路的系数来调节材料的性能, 使其能够更好地满足需求. 图20(a)和图20(b)分别为外接电阻为1, 10, 100, 1000 Ω时与外接电感为200, 201, 202, 203 H时结构的隔声量.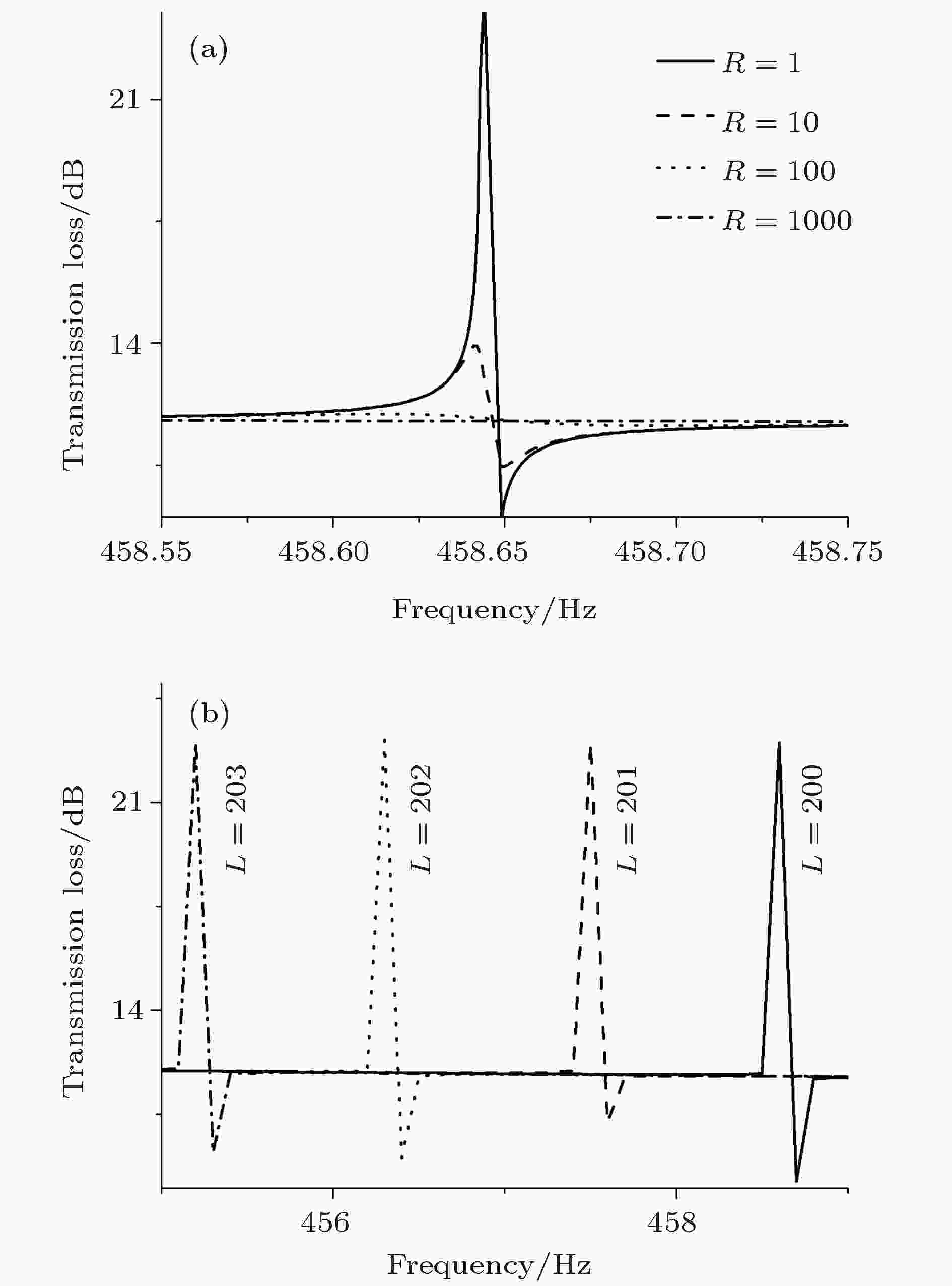
图 20 电路参数不同时隔声量的变化 (a)不同电阻; (b)不同电感
Figure20. TL with different circuit parameters: (a) Different resistors; (b) different inductances.

从图20(a)中可以看出, 随着电阻的增大, 隔声峰的峰值逐渐减小(此时设定L = 200 H), 而隔声峰的位置不发生改变. 峰值减小的原因主要是电阻的增大使电磁振荡作用减弱. 从图20(b)中可以看出, 随着电感增大(此时R = 1 Ω), 隔声峰逐渐向低频移动. 这是由于LC振荡电路的谐振频率f_r为

${f_{\rm{r}}} = \frac{1}{{2{\text{π}}}}\sqrt {\frac{1}{{LC}}} ,$

随着电感值的增大, 谐振频率f_r逐渐变小.

本文设计了一种基于压电材料的薄膜声学超材料, 得到结论如下:
1)使用有限元方法计算了结构的特征频率与20—1200 Hz频段的隔声量, 发现材料此频率范围内隔声性能良好, 存在两个50 dB以上的隔声峰和一个可调隔声峰, 并在实验中验证了有限元计算的真实性;
2)建立了简化结构首阶共振模态等效模型, 并且使用有限元法验证了其合理性; 综合分析材料的传输损失曲线与共振模态, 讨论了材料的隔声机理, 并通过Fano共振理论解释了传输损失“突变”出现的机理;
3)探究了压电片偏心量对结构性能的影响, 通过调整电路参数, 实现了材料性能的可调性.