摘要:采用第一性原理, 研究了不同浓度的氮掺杂石墨烯还原氧分子的机理. 结果表明, 掺杂氮原子以后, 氧分子的吸附能增大, 获得的电荷增多, O—O键长变长, 说明氮掺杂石墨烯增强了对氧分子的还原能力. 进一步分析发现, 氧分子吸附之后, 氮原子和氧分子均从碳原子上获得电荷, 氮原子同时也向氧分子转移电荷, 从而使氧分子与基底的相互作用增强. 另外, 通过对比不同浓度的氮原子掺杂, 发现3.13 at%的氮原子掺杂比例对氧分子的还原性能最好.
关键词: 锂-空电池/
氮掺杂石墨烯/
氧分子吸附/
氧还原机理/
第一性原理

English Abstract

全文HTML

--> --> -->

随着社会工业化进程的不断发展, 大量消耗化石能源造成的环境污染严重影响了人们的日常生活与身体健康. 因此, 研究人员将目光转向了更高效清洁的能量储存及转换装置, 如超级电容器、燃料电池、锂离子电池等^[1,2]. 可再充锂离子电池被认为是一种简单、高效的储能系统, 尤其是高能量密度的锂-空电池. 锂-空电池的阴极活性物质来自周围的氧气, 因此又称锂-氧电池, 其理论能量密度达到3500 W·h/kg, 使得锂-空电池有希望作为纯电动汽车或混合动力汽车的储能装置^[3-6].
锂-空电池是以金属锂和空气中的氧分子作为活性物质的新型电池装置, 主要结构包括正极多孔碳材料、负极金属锂以及隔开正负极材料的电解质层^[7,8]. Abraham和Jiang^[9]在1996年首次报道了有机电解质锂-空电池. 2006年, Ogasawara等^[10]证明了有机电解质锂-空电池的良好循环性. 实验证明, 有机电解质锂-空电池在放电过程正极的氧分子被还原, 与锂离子反应生成过氧化锂等产物, 放电产物堆积在空气电极上, 阻碍氧气传输, 影响电池的整体性能^[11-13]. 所以理想的正极材料首先应该是多孔结构, 便于为氧分子提供足够多的扩散通道和储存放电产物, 其次应该具有较高的电解质湿润性以满足充放电期间离子输运的要求^[14-16], 更为重要的是要有极好的催化能力以加速阴极的氧还原反应和氧化反应^[17-21].
石墨烯是由碳原子构成的蜂窝状单原子层晶体结构, 既有很好的电子迁移率、高的比表面积和热化学稳定性^[22,23], 又有理想的三相电化学区域, 其独特的结构又能提供氧分子的扩散渠道, 非常适合做锂-空电池的正极材料^[18,24-28]. Li等^[24]用石墨烯纳米片作为有机电解质锂-空电池的正极, 结果显示在电流密度为75 $ {\rm mA\cdot g_{carbon}^{-1}}$的情况下放电容量达到8705.9 $ {\rm mA\cdot h\cdot g_{carbon}^{-1}}$, 远高于商业碳材料的放电容量(BP 2000: 1909.1 ${\rm mA\cdot h\cdot g_{carbon}^{-1}} $; Vulcan XC-72: 1053.8 ${\rm mA\cdot h\cdot g_{carbon}^{-1}} $), 其原因是石墨烯边缘的活性位对氧还原反应有极好的催化活性, 说明石墨烯纳米片是一种有效的锂-空电池催化剂. Xiao等^[18]利用分层多孔石墨烯构造的空气电极显示出高达15000 ${\rm mA\cdot h\cdot g_{carbon}^{-1}} $的放电容量, 这是由于分层多孔石墨烯独特的形貌有利于氧分子的快速扩散和放电产物的分离, 因此, 石墨烯被认为是最有希望的非水锂-空电池的正极材料.
研究证明一定量的非金属元素掺杂碳材料能引入缺陷和官能团, 从而提高其电化学性能. Shao等^[29]通过将石墨烯暴露在氮等离子体中获得氮掺杂石墨烯, 发现氮掺杂石墨烯比本征石墨烯对氧气的还原具有更高的电催化活性. Li等^[30]研究了氮掺杂的碳纳米管, 发现掺氮后碳纳米管的放电容量增加了1.5倍. Li等^[31]2012年首次提出氮掺杂的石墨烯片用于锂-空电池的阴极材料, 结果显示在电流密度分别为75, 150和300 ${\rm mA\cdot h\cdot g_{carbon}^{-1}} $的情况下, 放电容量分别达到了11660, 6640和3960 ${\rm mA\cdot h\cdot g_{carbon}^{-1}} $, 远远高于纯石墨烯片作为电极材料的放电容量. Higgins等^[32]研究表明20 wt%的氮掺杂石墨烯作为电极材料, 放电容量可以达到11746 $ {\rm mA\cdot h\cdot g_{carbon}^{-1}} $, 高于纯ketjen black (KB)电极42%. Zhao等^[33]实验上合成了一种新型的三维多孔氮掺杂石墨烯气凝胶材料, 具有优异的倍率性能(3.2 ${\rm A\cdot h\cdot g_{carbon}^{-1}} $时具有5978 $ {\rm mA\cdot h\cdot g_{carbon}^{-1}} $的容量)和长期的循环稳定性(1 ${\rm A\cdot h\cdot g_{carbon}^{-1}} $下可循环54周). Yan等^[34]研究表明氮掺杂石墨烯能使氧分子的解离势垒从未掺杂的2.39 eV降低到1.20 eV, 有效降低了氧分子的解离势垒.
虽然已经有大量工作研究了氮掺杂石墨烯作为锂-空电池正极材料的性能, 但是到目前为止, 氮掺杂石墨烯提高氧气还原的机理还不清楚, 不同浓度的氮原子掺杂对氧分子还原的影响还没有报道. 本文基于第一性原理方法, 应用VASP (Vienna ab-initio simulation package)软件包计算了三种不同浓度的氮掺杂石墨烯对氧分子的吸附, 通过对比不同氮掺杂浓度下石墨烯对氧分子的吸附能, 氧分子的键长、电荷布居以及体系的电子结构来分析氮原子掺杂及不同氮浓度掺杂对氧分子还原反应的影响.

本文所有计算都是基于密度泛函理论的第一性原理软件包VASP^[35,36]完成, 选用投影缀加平面波方法^[37,38]描述离子实与价电子的相互作用. 描述电子与电子相互作用的交换关联函数采用广义梯度近似^[39]下的Perdew-Burke-Ernzerh^[40]泛函形式. 计算氧分子吸附时考虑了范德瓦耳斯修正^[41]. 平面波基组展开的截断能设为520 eV. 石墨烯结构由4 × 4 × 1的超胞构成, 包含32个碳原子. 为消除周期性结构中Z方向相邻石墨烯层之间的相互作用, 选取真空层为20 ?. 布里渊区积分采用Monkhorst-Pack型网格^[42], K点取值为3 × 3 × 1. 弛豫计算时总能量的收敛标准为10^–4 eV, 每个原子上力的收敛标准为–0.02 eV/?. 整个计算过程中均考虑了自旋极化. 石墨烯及氮掺杂石墨烯用N_xG表示, x取0, 1, 2和3分别对应本征石墨烯G、一氮掺杂石墨烯N₁G、二氮掺杂石墨烯N₂G和三氮掺杂石墨烯N₃G.

2

-->

3.1.N_xG (x = 0, 1, 2, 3)的结构与稳定性

首先, 采用上述计算方法与测试参数对本征石墨烯进行优化, 得到本征石墨烯的稳定构型, 其几何结构与电子性质如图1所示. 如图1(a)所示, 本征石墨烯为碳原子构成的二维蜂窝状六角晶格结构, 其中C—C键长为1.425 ?, 晶格矢量为9.873 ?, 与文献[43]报道的结果相一致. 从图1(b)可以明显看出, 在对称点K处存在狄拉克锥, 带隙为零. 态密度在费米能级附近也为零, 表现出零带隙半导体(半金属)性质. 电子性质与实验文献[44, 45]符合得很好, 说明本文的计算理论水平和参数设置是可靠的.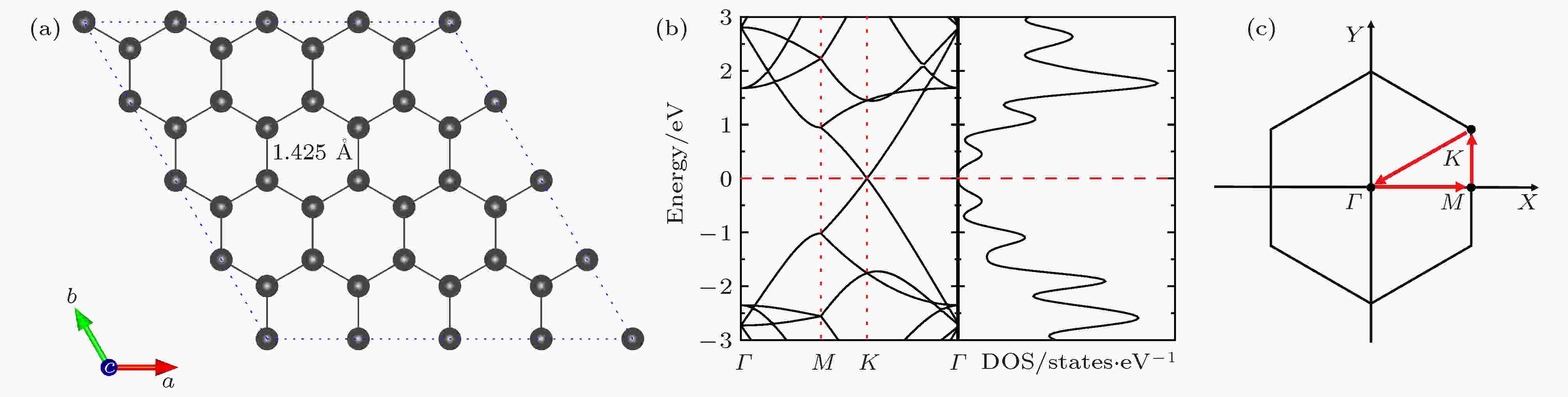
图 1 本征石墨烯的几何结构与电子性质　(a)结构图; (b)能带和态密度图; (c)布里渊区高对称点的示意图
Figure1. Optimized structure and electronic properties of graphene: (a) Optimized structure; (b) the energy band and density of states (DOS); (c) the irreducible Brillouin zone. The irreducible k-point path ΓMKΓ corresponds to the graphene.

为了理解不同氮掺杂浓度对氧分子还原的影响, 首先优化了N_xG (x = 1, 2, 3)的稳定结构, 如图2所示. 对于一氮掺杂(x = 1), 由于本征石墨烯的对称性, 每一个碳原子都是等价的, 因此N₁G只有一种构型, 如图2(a)所示. 对于二氮掺杂(x = 2), 按照两个氮原子之间的距离由小到大, 设计7种掺杂构型并进行弛豫(见补充材料的图S1 (online)), 然后选取能量最低的一种结构作为吸附氧分子的基底材料. 图2(b)为N₂G的最低能量结构, N-N距离为5.700 ?, 与文献[43]报道的掺杂构型相一致. 图2(c)中两个氮原子位于碳六元环的对角位置, N-N距离为2.870 ?, 能量仅比图2(b)高出0.016 eV. 对于三氮掺杂(x = 3), 考虑了尽可能多的掺杂构型(见补充材料的图S2 (online)), 最终发现N₃G的最佳构型是三个氮原子位于两个相邻六元环的对角位置, N-N距离为2.870 ?, 如图2(d)所示. 另外, 从图S1和图S2还可以看出N-N距离最近的构型能量最高, 说明氮原子是分散掺杂在石墨烯当中. 值得注意的是, N_xG (x = 1, 2, 3)的结构没有凸起或凹陷, 即氮掺杂并没有改变石墨烯的二维平面结构.
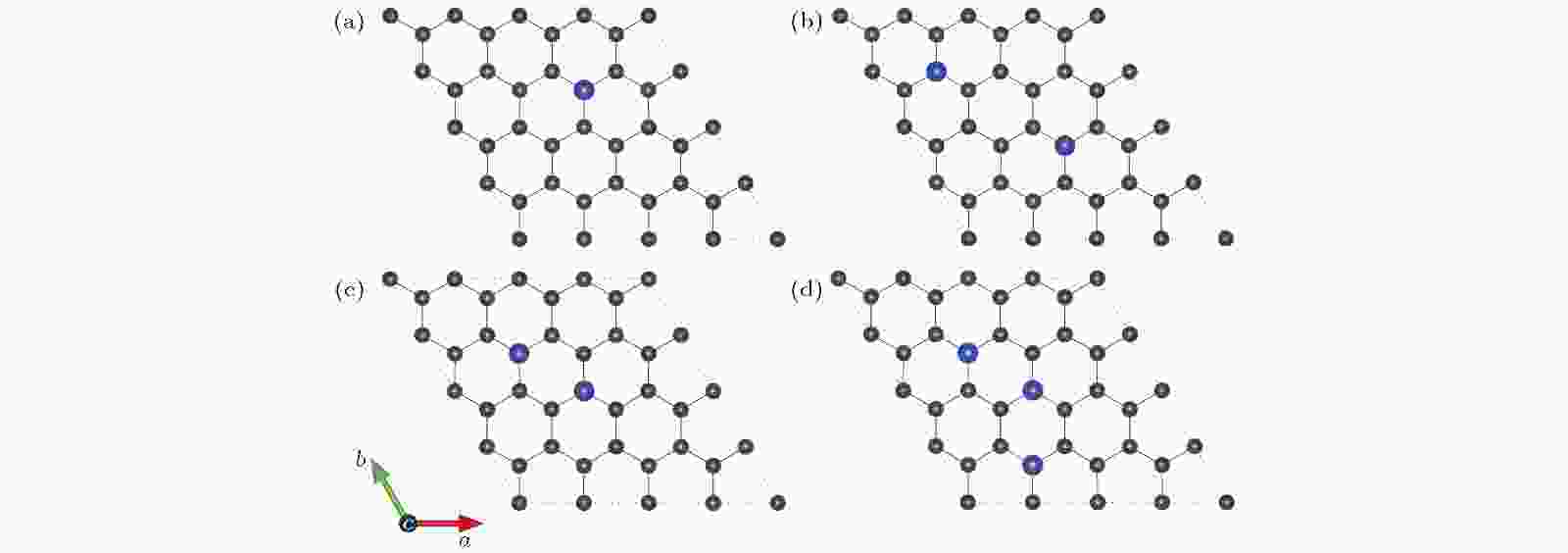图 2 N_xG (x = 1, 2, 3)的最稳定构型(碳原子和氮原子分别用灰色和蓝色小球表示)　(a) N₁G (x = 1); (b) N₂G-1 (x = 2); (c) N₂G-2 (x = 2, 亚稳态构型); (d) N₃G (x = 3)
Figure2. Optimal structures of N_xG (x = 1, 2, 3): (a) N₁G (x = 1); (b) N₂G-1 (x = 2); (c) N₂G-2 (x = 2, metastable state); (d) N₃G (x = 3). The C atom and N atom are represented by grey and blue sphere, respectively.

2 -->

3.2.氧分子的吸附性质

3 -->

3.2.1.N_xG-O₂的结构与稳定性

接下来, 研究氧分子在N_xG (x = 0, 1, 2, 3)基底上的吸附性质. 对于每一种基底, 分别考虑了氧分子位于N_xG六元环中心正上方(空位, 用字母H表示)、C—C键/N—C键的正上方(桥位, 用字母B表示)和碳/氮原子的正上方(顶位, 用字母T表示)三种吸附位. 每一种吸附位, 又分别考虑了氧分子与基底的平行、倾斜和垂直三种吸附方式. 这样, 对于每一种基底材料, 我们最少考虑了九种不同的氧分子吸附结构作为初始结构进行弛豫. 最后比较弛豫后的总能量, 确定氧分子在N_xG (x = 0, 1, 2, 3)基底上的最稳定吸附构型, 如图3所示. 为了定量地描述氧分子在基底上的吸附强度, 定义吸附能公式如下: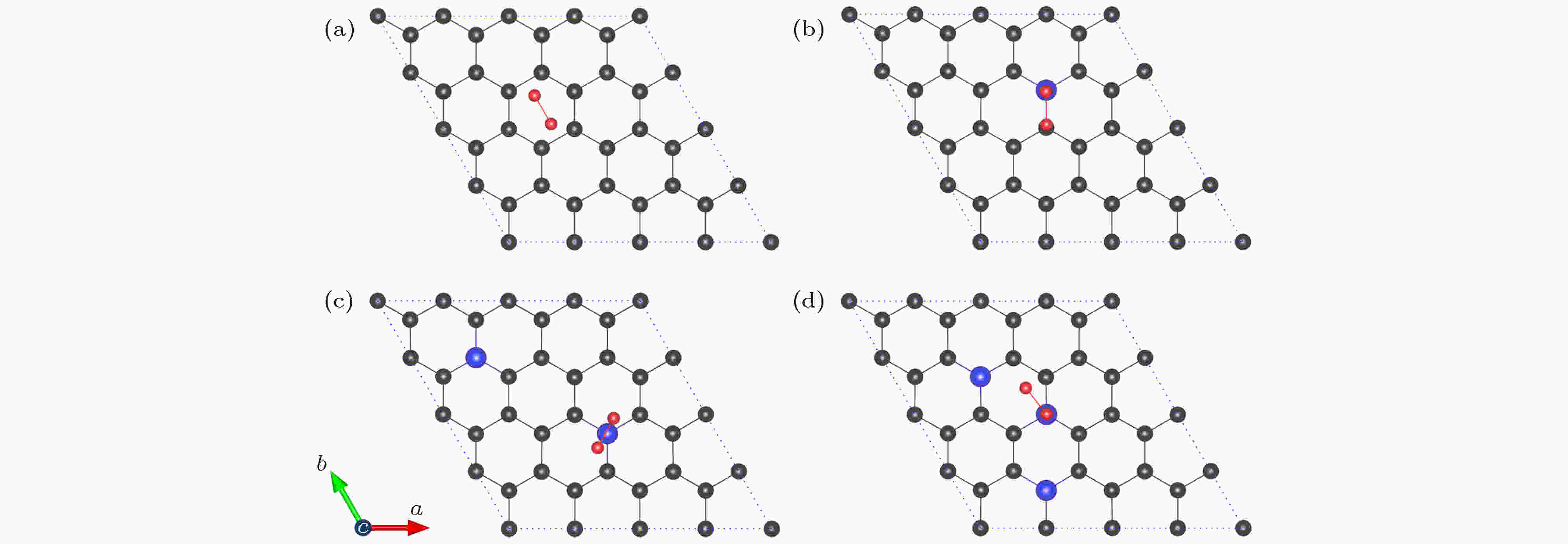
图 3 N_xG (x = 0, 1, 2, 3) 吸附氧分子的最稳定构型(碳原子、氮原子和氧原子分别用灰色、蓝色和红色小球表示)　(a) G-O₂; (b) N₁G-O₂; (c) N₂G-O₂; (d) N₃G-O₂
Figure3. Optimal structures of N_xG (x = 0, 1, 2, 3): (a) G-O₂; (b) N₁G-O₂; (c) N₂G-O₂; (d) N₃G-O₂. The C atom, N atom, and O atom are represented by grey, blue, and red spheres, respectively.

${E_{{\rm{ad}}}} = {E_{{{\rm{N}}_x}{\rm{G}}}} + {E_{{{\rm{O}}_2}}} - {E_{{{\rm{N}}_x}{\rm{G}} + {{\rm{O}}_2}}}\;\;(x=0,1,2,3),$

其中${E_{{{\rm{N}}_x}{\rm{G}}}}$和${E_{{{\rm{N}}_x}{\rm{G}} + {{\rm{O}}_2}}}$分别表示吸附氧分子前后基底的能量, ${E_{{{\rm{O}}_2}}}$是自由氧分子的基态能量. 按照定义, 吸附能越大氧分子吸附越稳定. 计算得到不同基底下氧分子的吸附能列于表1. 另外, 氧分子键长、各元素的Bader电荷^[46]与氮掺杂浓度同样列于表1当中.

NxG-O2/at%	Ead/eV	dO—O/?	$Q_{{\rm O}_2} $/e	QN/e	N含量
O2	—	1.233	—	—	—
G-O2	0.13	1.242	–0.04	—	—
N1G-O2	0.31	1.261	–0.22	–1.24	3.13
N2G-O2	0.33	1.259	–0.25	–2.39	6.25
N3G-O2	0.28	1.258	–0.21	–3.72	9.38

表1N_xG (x = 0, 1, 2, 3) 吸附氧分子的相关性质
Table1.Adsorption properties of O₂ molecule on the N_xG (x = 0, 1, 2, 3).

从图3(a)可以看出, 对于本征石墨烯, 氧分子的最稳定吸附构型是氧分子平行吸附在本征石墨烯的H位, 两个氧原子分别靠近六元环两个相对的C—C键, 与文献[34]中报道的两个氧原子分别靠近两个对角的碳原子不同. 因此, 我们采用相同的计算方法与参数优化了文献[34]中的吸附构型, 发现其能量仅比我们当前优化的构型能量高0.001 eV, 说明两个结构是等能异构体结构, 具体详见补充材料的图S3(a)和图S3(b)所示(online). 图S3所示为所有的本征石墨烯吸附氧分子(G-O₂)的异构体结构及相对能量, 可以看出G-O₂亚稳态的能量差别非常小, 说明各种吸附构型都会发生. 其原因是石墨烯的大$ {\text{π}}$键分布均匀, 对不同的氧分子吸附没有明显变化. 如表1所列, 氧分子的吸附能为0.13 eV, 与已有的理论计算值0.11 eV^[43]非常接近. 氧分子距离石墨烯的平均距离(即两个氧原子在Z方向距离本征石墨烯的平均值)是3.026 ?. O—O键长为1.242 ?, 比自由氧分子键长(1.233 ?)增加约0.01 ?, 氧分子获得少量电荷(–0.04 e, 1 e = 1.6 × 10^–19 C), 说明氧分子吸附在本征石墨烯上, O—O之间的结合有所减弱, 氧分子在一定程度上得到还原.
对于一氮掺杂基底N₁G, 氧分子的最稳定吸附构型如图3(b)所示. 氧分子吸附在N₁G表面, O—O键平行于N—C键并位于N—C键的上方(B位), 位于氮上方的氧原子比位于碳上方的氧原子大约高出N₁G基底0.050 ?. 文献[34]报道氧分子在N₁G上的吸附构型为一个氧原子位于相邻N的C原子上方, 另一个氧原子位于C₅N环的上方. 我们也对此吸附构型进行了测试计算, 结果发现此吸附构型比我们当前报道的吸附构型总能量高出0.015 eV, 详见补充材料的图S4(e)所示(online). 图S4所示为所有的一氮掺杂石墨烯吸附氧分子(N₁G-O₂)的异构体结构及相对能量. 可以看出这些N₁G-O₂异构体的能量同样差别很小, 说明氧分子可以随机吸附在氮原子周围. 由表1可以看出, N₁G-O₂的吸附能为0.31 eV, 氧分子距离基底之间的平均距离为2.896 ?, 氧分子获得较多电荷(–0.22 e), O—O键长为1.261 ?. 相对氧分子吸附在本征石墨烯上, 氧分子吸附能变大, 距离基底变近, 氧分子所得电荷增加, O—O键长进一步变长, 说明氧分子与基底之间的相互作用增强了, O—O之间的结合进一步减弱, 氮原子掺杂提高了氧分子的还原反应. 同时, 掺杂的氮原子从周围的碳原子获得–1.24 e的电荷, 氧原子和氮原子同时得到电荷, 碳原子失去电荷. 由于库仑相互作用, N—O之间表现出一定的排斥性, C—O之间表现出一定的吸引性, 这也是位于氮原子上方的氧原子比位于碳原子上方的氧原子相对基底的距离高的原因.
对于二氮掺杂基底N₂G, 氧分子的最稳定吸附构型见图3(c). 氧分子平行吸附在N₂G表面, 氧分子中心位于一个氮原子的正上方(T位). 此时, 氧分子距离基底之间的平均距离约为2.923 ?, 稍高于氧分子吸附在N₁G表面时的情况(2.896 ?), O—O键长为1.259 ?, 稍短于氧分子吸附在N₁G表面时的键长(1.261 ?), 吸附能变化不大. 分析可知掺杂的两个N原子N—N间距太远(5.700 ?), 距离较远的N原子对氧分子吸附几乎不起作用, 所以N₂G-O₂类似于N₁G-O₂的性质. 氧分子获得的电荷量为–0.25 e, 比吸附在N₁G表面的电荷量多–0.03 e, 说明N₂G比N₁G对氧分子的还原略有增强. 另外, 对于N₂G的亚稳态结构(图2(c)), 也计算了氧分子吸附的各种情况, 详见补充材料的图S6所示(online). 由图S5和图S6可知, 对于同样结构的基底材料, 氧分子吸附的异构体能量相差很小, 有的几乎是等能异构体, 说明氧分子的这些吸附构型都有可能发生. 另外, 二氮掺杂石墨烯的亚稳态吸附氧分子N₂G-O₂-2的最低能量结构比基态吸附氧分子N₂G-O₂的最低能量结构总能量高0.07 eV, 氧分子的吸附能小0.05 eV.
对于三氮掺杂基底N₃G, 氧分子吸附(N₃G-O₂)的异构体结构及相对能量详见补充材料的图S7所示(online), 可以看出, 氧分子吸附的异构体能量同样相差不大, 说明氧分子的这些吸附构型也都有可能发生. 氧分子的最稳定吸附构型如图3(d)所示, 一个氧原子位于一个氮原子的正上方, 另一个氧原子则位于C₅N环的上方, 前者比后者高出基底约0.07 ?. 此时, 氧分子距离基底的平均距离为2.903 ?, O—O键长为1.258 ?, 氧分子的吸附能为0.28 eV. 相对于N₁G-O₂和N₂G-O₂, O—O键长和O—O吸附能均略微减小, 但比G-O₂大. 此时, 氧分子从基底获得的电荷为–0.21 e, 相对于N₁G-O₂和N₂G-O₂少, 但仍然比G-O₂获得的电荷多. 这说明三氮掺杂石墨烯对氧分子的还原相对于本征石墨烯显著增强, 但相对于一氮掺杂和二氮掺杂石墨烯并没有增强.
由以上分析可知, 本征石墨烯掺杂氮原子以后, 氧分子的吸附能显著增加, O—O键长明显增长, 氧分子获得的电荷量也显著增多, 说明氧分子的反${\text{π}} $键轨道被电荷填充, O—O之间的结合变弱, 进而说明掺杂氮原子可以提高石墨烯对氧分子还原的催化性能. 另外, 随着氮掺杂浓度的提高, N_xG (x = 1, 2, 3)基底对氧分子的吸附能、O—O键长和电荷转移影响不明显. 为了进一步讨论这个问题, 我们又分别计算了不同大小的石墨烯超胞掺杂氮原子吸附氧分子的情况, 详见3.3节讨论部分.
3 -->

3.2.2.N_xG-O₂的电荷分析

一般来说, 氧分子被还原的程度取决于有多少电荷转移到氧分子, 即氧分子获得电荷越多, 氧分子被还原的程度越强. 为了进一步理解氮掺杂石墨烯对氧分子还原的机理, 以N₁G-O₂为例, 计算氧分子获得的电荷量与N-O距离(氮原子到O—O键中心的距离定义为N-O距离)之间的关系, 并绘制在图4中. 由图4明显可见, 氧分子获得的电荷量与N-O距离呈现出一定的线性关系, 即氧分子距离氮原子越近, 其获得的电荷量越多, 氧分子被还原的程度越强, 充分说明氮掺杂石墨烯能提高氧分子的还原反应. 同时, 为了对比, 也给出了本征石墨烯吸附氧分子的情况, 氧分子获得电荷量与不同C-O距离(此处的碳与上面的氮处于同一原子位置)的关系同样绘制在图4中. 由图4可知氧分子吸附在石墨烯上获得的电荷量随着C-O距离的增大而减小, 获得电荷量小于吸附在氮掺杂石墨烯上获得的电荷量. 总之, 氧分子不仅从碳原子得到电荷, 也从氮原子得到电荷.
图 4 G-O₂和N₁G-O₂中氧分子获得的电荷与C/N-O距离之间的关系
Figure4. Charges of O₂ molecule vs. the C-O distance in the G-O₂ system (red line) and the N-O distance in the N₁G-O₂ system (blue line).

为了更直观地观察氧分子与N_xG (x = 0, 1, 2, 3)基底之间的电荷转移, 分别计算了N_xG-O₂ (x = 0, 1, 2, 3)体系的差分电荷密度, 如图5所示, 黄色区域表示获得电荷, 蓝色区域表示失去电荷. 差分电荷密度计算公式定义为
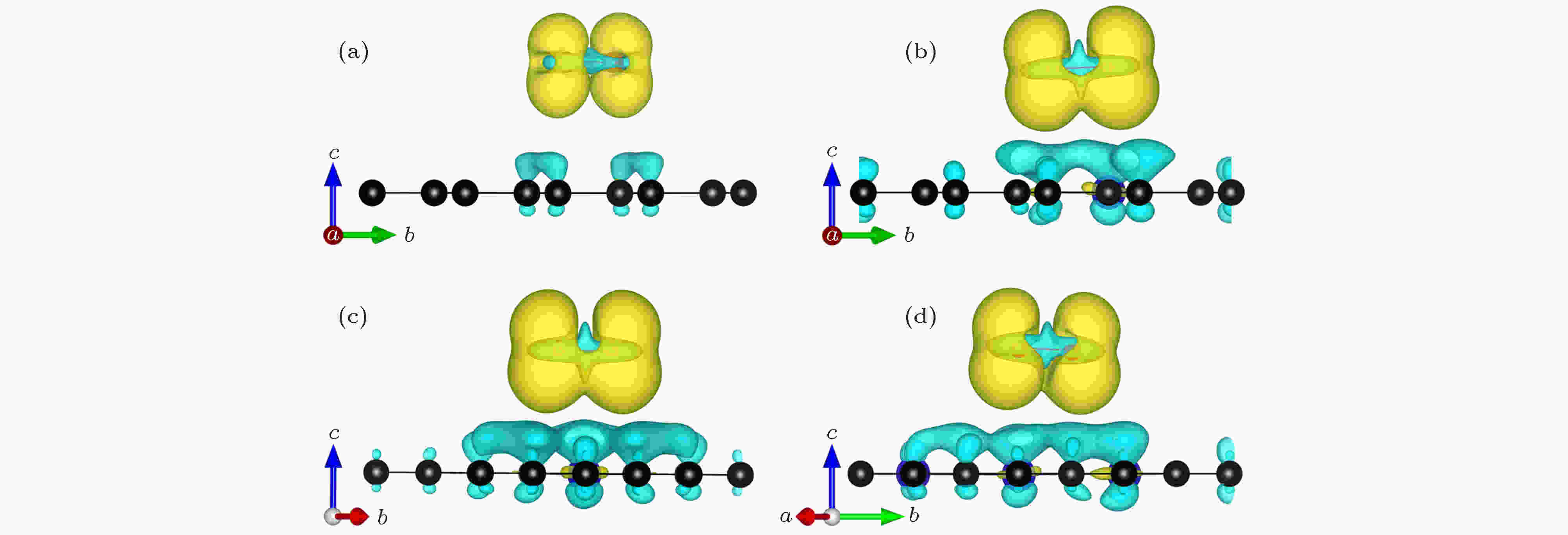图 5 N_xG-O₂ (x = 0, 1, 2, 3) 差分电荷密度图(黄色代表电荷聚集, 蓝色代表电荷失去; 电荷等势面是6 × 10^–4 e/?³) (a) G-O₂; (b) N₁G-O₂; (c) N₂G-O₂; (d) N₃G-O₂
Figure5. Charge density difference of N_xG-O₂ (x = 0, 1, 2, 3): (a) G-O₂; (b) N₁G-O₂; (c) N₂G-O₂; (d) N₃G-O₂. The gain of electrons is indicated in yellow and the loss of electrons is indicated in blue. The isosurface value is 6 × 10^–4 e/?³.

$\Delta \rho = {\rho _{{{\rm{N}}_x}{\rm{G}} + {{\rm{O}}_{\rm{2}}}}} - {\rho _{{{\rm{N}}_x}{\rm{G}}}} - {\rho _{{{\rm{O}}_{\rm{2}}}}}\left( {x = 0,\;1,\;2,\;3} \right), $

其中${\rho _{{{\rm{N}}_x}{\rm{G}}}}$和${\rho _{{{\rm{N}}_x}{\rm{G}} + {{\rm{O}}_{\rm{2}}}}}$分别表示吸附氧分子前后体系的电荷密度; ${\rho _{{{\rm{O}}_{\rm{2}}}}}$为氧分子的电荷密度. 从图5可以清晰地看到氧分子获得电荷, N_xG (x = 0, 1, 2, 3)基底失去电荷. 氧分子获得的电荷主要是碳原子的贡献, 并且原来局域在两个氧原子中间的电荷开始向两个氧原子方向聚集, 这意味着O—O之间的结合减弱, 与氧分子吸附之后键长变长是一致的. 另一方面, 氧分子吸附在氮掺杂石墨烯上获得的电荷明显多于吸附在本征石墨烯上获得的电荷, 再次证明氮掺杂石墨烯能提高氧分子的还原反应. 另外, 还看到氮原子上有少量电荷聚集, 说明电荷从碳原子转移到了氮原子, 这与前面的Bader电荷分析是一致的.
3 -->

3.2.3.N_xG-O₂的电子性质分析

为了更深入地理解氮掺杂石墨烯还原氧分子的机理, 分别画出了氧分子吸附在本征石墨烯及氮掺杂石墨烯表面的能带结构图和分态密度图, 如图6和图7所示. 由图6(a)所示, 本征石墨烯吸附氧分子以后, 狄拉克锥上移, 穿过费米能级, 体系呈现出金属性质, 说明本征石墨烯吸附氧分子以后失去电子, 使部分价带变成导带, 氧分子吸附相当于p-type掺杂效果. 由Bader电荷分析可知, 这部分失去的电子转移给了氧分子, 使氧分子得到还原. 结合图7(a)所示的分态密度, 还可以看出氧分子发生了自旋极化, 自旋向上的态占据在–1.969 eV附近, 自旋向下的态占据在0.230 eV附近的空轨道.
图 6 N_xG-O₂能带结构图　(a) G-O₂; (b) N₁G-O₂; (c) N₂G-O₂; (d) N₃G-O₂
Figure6. Band structures of N_xG-O₂: (a) G-O₂; (b) N₁G-O₂; (c) N₂G-O₂; (d) N₃G-O₂.

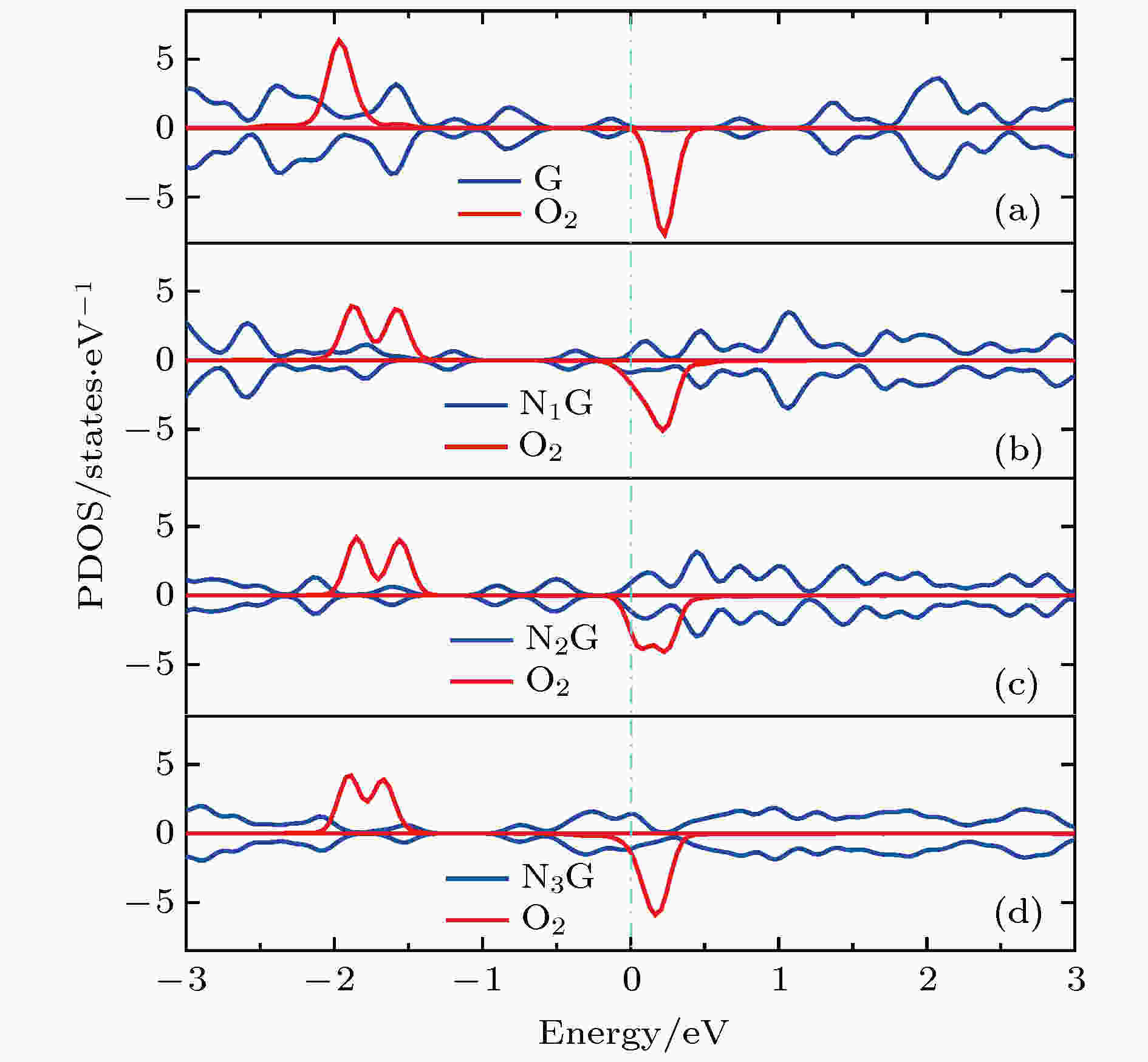图 7 分态密度图　(a) G-O₂; (b) N₁G-O₂; (c) N₂G-O₂; (d) N₃G-O₂
Figure7. Projected density of states (PDOS): (a) G-O₂; (b) N₁G-O₂; (c) N₂G-O₂; (d) N₃G-O₂.

从图6(b)可知, 一氮掺杂石墨烯吸附氧分子以后, N₁G狄拉克锥下移, 穿过费米能级, 体系仍呈现金属性质, 说明相对于本征石墨烯而言, 氮原子掺杂使得石墨烯部分导带被电子填充变成价带, 氮原子掺杂相当于n-type掺杂效果. 另外, 氮原子掺杂使得狄拉克锥点打开0.2 eV, 与文献[43]报道相一致. 进一步观察发现氧分子吸附在氮掺杂的石墨烯上发生能级劈裂. 图7(b)所示的分态密度显示氧分子从基底获得电荷量增加, 使部分导带被填充变成价带, 这与Bader电荷分析的结果是一致的. 相比G-O₂而言, N₁G-O₂的O₂态密度在费米能级附近与基底N₁G的交叠增大, 说明氧分子与N₁G的相互作用增强, 导致被还原程度增加. 氧分子自旋向上的能级分别在–1.589 eV和–1.884 eV附近, 自旋向下的能级出现在0.216 eV附近, 相对于吸附在本征石墨烯表面, 自旋向上的能级上移, 而自旋向下的能级下移, 能级位置降低了约0.014 eV.
对比图6(b)—(d)可知, 随着氮含量的增加, 体系中的总电子数增加, 多出的电子填充基底的导带使其变成价带, 狄拉克锥点进一步下降. 氧分子能级位置随着氮含量的增加并没有明显变化. 图7(b)—(d)显示基底N_xG (x = 1, 2, 3)的狄拉克锥点随着氮浓度的增加而左移(下移). 氧分子自旋向上和自旋向下的能级位置没有明显变化. 电子结构分析与前面的氧分子吸附性质是一致的.
2 -->

3.3.讨　论

由前面的分析可知, 氧分子在N_xG (x = 0, 1, 2, 3)基底上吸附的异构体能量差别很小(详见补充材料的图S3—图S7 (online)), 说明氧分子是随机吸附在N_xG (x = 0, 1, 2, 3)基底上. 为了理解不同吸附异构体对氧分子还原的影响, 计算了N_xG-O₂ (x = 0, 1, 2, 3)所有异构体的氧分子获得电荷及氧分子键长, 见图8. 可以看出氮原子掺杂石墨烯明显增多了氧分子获得的电荷量, 增加了氧分子的键长, 提高了对氧分子的还原. 但是, 随着氮掺杂浓度的提高, 氧分子获得的电荷量及氧分子键长并没有明显的变化, 结论与前面分析一致.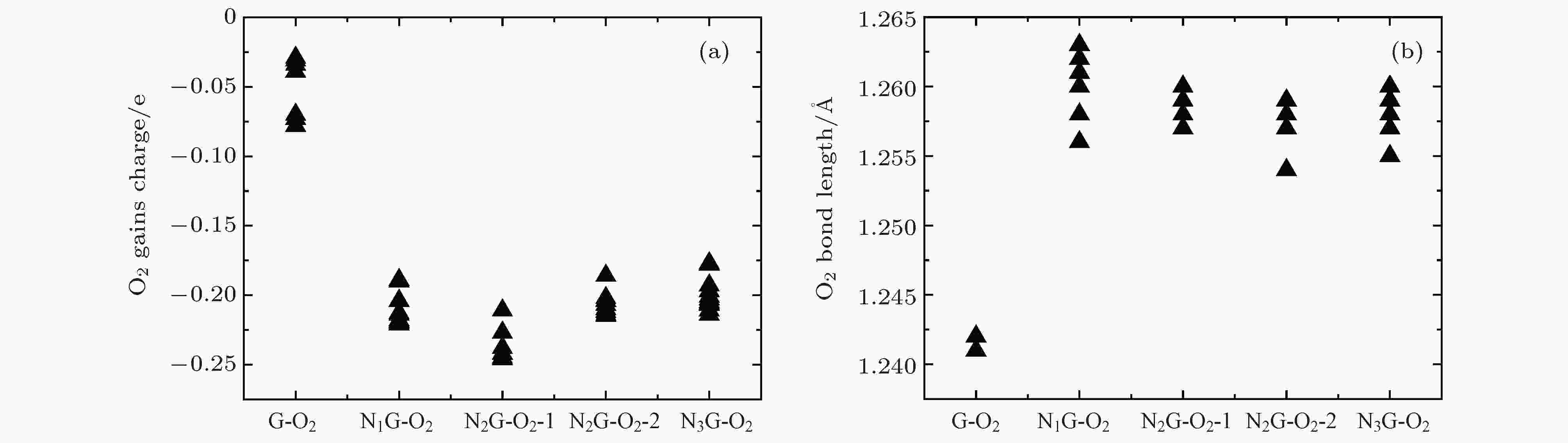
图 8 N_xG-O₂(x = 0, 1, 2, 3)不同异构体的氧分子获得电荷 (a)及键长(b)统计
Figure8. Charges (a) and O—O distances (b) of isomers of N_xG-O₂ (x = 0, 1, 2, 3).

由以上分析得知, 氮原子掺杂石墨烯大大提高了对氧分子的还原, 但是对氧分子的还原能力随着我们考虑的三种氮掺杂浓度(一氮掺杂3.13 at%, 二氮掺杂6.25 at%, 三氮掺杂9.38 at%)的增加并不明显. 为此, 我们进一步考虑了三种不同大小的超胞作为基底, 即氮原子分别掺杂3 × 3 × 1, 4 × 4 × 1, 5 × 5 × 1的石墨烯超胞, 相应的氮掺杂浓度分别为5.56 at%, 3.13 at%, 2.00 at%. 三种超胞吸附氧分子的稳定结构如图9所示, 对氧分子的相关吸附性质列于表2. 由表2可以看出掺杂浓度为3.13 at%时的吸附能最大, O—O键长最长, 氧分子离基底的距离最小, 氧分子与氮原子分别获得的电荷最多, 说明3.13 at%的氮原子掺杂比例比较合适, 浓度过大或过小都达不到最好的效果. 另外, 为了说明不同氧分子覆盖度对氧分子吸附能的影响, 同样计算了氧分子分别吸附在3 × 3 × 1, 4 × 4 × 1和5 × 5 × 1的石墨烯超胞上, 发现吸附能分别是0.10, 0.13和0.11 eV, 此结果并不影响我们对最佳氮掺杂浓度的判断.
图 9 GN 吸附氧分子的最稳定构型(碳原子、氮原子和氧原子分别用灰色、蓝色和红色小球表示)　(a) 3 × 3 × 1 GN-O₂; (b) 4 × 4 × 1 GN-O₂; (c) 5 × 5 × 1 GN-O₂
Figure9. Optimal structures of GN-O₂: (a) 3 × 3 × 1 GN-O₂; (b) 4 × 4 × 1 GN-O₂; (c) 5 × 5 × 1 GN-O₂. The C atom, N atom, and O atom are represented by grey, blue, and red spheres, respectively.

NG-O2	Ead/eV	dO—O/?	$ d_{{\rm O}_2\text{-}{\rm NG}}$/?	$ Q_{{\rm O}_2}$/e	QN/e	$d_{{\rm O}_2\text{-}{\rm N}} $/?	N含量/at%
3 × 3 × 1	0.27	1.257	2.937	–0.19	–1.23	3.011	5.56
4 × 4 × 1	0.31	1.261	2.896	–0.22	–1.24	2.969	3.13
5 × 5 × 1	0.20	1.254	2.977	–0.20	–1.14	3.056	2.00

表2不同N掺杂石墨烯基底吸附氧分子的相关性质
Table2.Adsorption properties of O₂ molecule on the 3 × 3 × 1 GN-O₂, 4 × 4 × 1 GN-O₂, and 5 × 5 × 1 GN-O₂.

通过第一性原理计算, 系统研究了本征石墨烯G、一氮掺杂石墨烯N₁G (掺杂比例为3.13 at%)、二氮掺杂石墨烯N₂G (掺杂比例为6.25 at%)、三氮掺杂石墨烯N₃G (掺杂比例为9.38 at%)对氧分子还原反应的影响. 结果表明N_xG (x = 0, 1, 2, 3)均能使氧分子还原, 氮原子掺杂更有利于氧分子还原. Bader电荷分析发现碳原子失去电荷, 氮原子从周围的碳原子得到电荷, 氧分子同时从碳原子和氮原子得到电荷, 这与碳、氮、氧的电负性大小相一致. 掺杂氮原子以后, 氧分子的吸附能增大, 氧分子与基底之间的相互作用增强, 氧分子获得的电荷量增加, O—O键长变长. 但是, 在我们考虑的三种掺杂比例下, 计算结果表明对氧分子的还原并没有随氮掺杂浓度的提高而明显增强. 进一步用不同大小的石墨烯超胞计算氧分子的吸附性质, 发现3.13 at%的氮原子掺杂比例比较合适, 对氧分子的还原最好. 希望本工作对实验研究人员合成氮掺杂石墨烯材料起到一定的参考作用.