摘要: 在铽镓石榴石(TGG)晶体中掺杂Pr
3+ 离子能够有效提升材料的磁光性能, 但目前缺乏系统的理论计算阐明此问题. 本文根据量子理论, 分析了掺杂Pr
3+ 离子的影响机理并进行了定量计算. 根据微扰理论解算久期方程, 得到自旋-轨道耦合、晶场、有效场及离子之间的超交换作用下, Tb
3+ , Pr
3+ 离子的能级位移及波函数; 进一步解算出Tb
3+ , Pr
3+ 离子自基态4f至5d的跃迁电偶极矩、各能级上的分布概率及平均磁矩; 获得了Pr:TGG晶体的维尔德常数和磁化率, 以及维尔德常数与Pr
3+ 离子掺杂量之间的关系. 研究结果表明: 由于Pr
3+ 离子引起的法拉第旋转角较Tb
3+ 离子大, 同时Tb
3+ 离子和Pr
3+ 离子之间强烈的超交换作用引起了能级的进一步分裂, 导致Pr:TGG晶体维尔德常数明显提升; 掺杂Pr
3+ 离子后, 晶体内部有效磁矩增高, 磁化率增大, 且温度依赖性降低; 维尔德常数数与Pr
3+ 离子掺杂量成分段线性关系, 当晶体内部的Tb
3+ 离子和Pr
3+ 离子含量相等时, 达到最大值. 本文的计算结果与已有的实验数据符合较好.
关键词: 法拉第旋转 /
量子理论 /
维尔德常数 /
磁化率 English Abstract Quantum calculation of the influence of trivalent praseodymium ions doping on the magneto-optical properties of terbium gallium garnet crystal Cai Wei 1,2 ,Xu You-An 1 ,Yang Zhi-Yong 1 1.Armament Launch Theory and Technology Key Discipline Laboratory of China, Rocket Force University of Engineering, Xi′an 710025, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 61505254).Received Date: 19 April 2019Accepted Date: 14 May 2019Available Online: 01 July 2019Published Online: 05 July 2019Abstract: Compared with those materials with superior magneto-optical properties, such as YIG, Ce:YIG and Ba3 Tb(PO4 )3 , pure terbium gallium garnet (TGG) crystal has comparative low Verdet constant and cannot meet the requirements of some high-power devices. Doping Pr3+ ions in TGG crystal can remarkably enhance its magneto-optical properties and expand its application scope, but there are still lack of systematic theoretical calculations to clarify this phenomenon. Based on the quantum theory, this paper presents the influence of doping Pr3+ ions on the magneto-optical performance and the corresponding quantitative calculation results. Firstly, taking various effects on Tb3+ ions and Pr3+ ions in the crystal into consideration, the Hamiltonian is modeled and discussed in detail. The secular equations are solved by applying the perturbation method, and then the energy level shifts and wave functions of the Tb3+ ions and Pr3+ ions are worked out, where the spin-orbit coupling, crystal field, effective field and super-exchange interaction between the two types of ions are considered. Furthermore, the transition dipole moments of Tb3+ ions and Pr3+ ions from the 4f ground state to higher level 5d, together with the distribution probability at each energy level and the average magnetic moment, are resolved. Finally, the Verdet constants and magnetic susceptibilities of pure TGG crystal and Pr:TGG crystal are calculated and compared with each other. Moreover, the relationship between the Verdet constant of Pr:TGG crystal and the Pr3+ -doping amount is derived. The results show that the Faraday rotation angle caused by Pr3+ ions is larger than that of Tb3+ ions, meanwhile, the strong super-exchange between Tb3+ ions and Pr3+ ions causes further splitting of the 4f energy level, resulting in a significant increasement of the Verdet constant of the Pr:TGG crystal, which reaches 313.4 rad/m·T, 191.2 rad/m·T and 60.4 rad/m·T at the wavelengths of 532 nm, 632.8 nm and 1064 nm, respectively. In addition, doping Pr3+ ions inside the crystal improves the internal effective magnetic moment, which can reach 9.92 μB at 10 K. At the same time, the magnetic susceptibility increases, while the temperature interdependency decreases. The linear relationship between the reciprocal of magnetic susceptibility and temperature reduces from 4.41/K to 3.92/K. The Verdet constant of the Pr:TGG crystal is linear with the amount of Pr3+ ions doping. When the contents of Tb3+ ions and Pr3+ ions inside the crystal are equal, the maximum value is reached, which is about 2913.4 rad/m·T. The calculation results in this paper are in good agreement with the existing experimental data. Keywords: Faraday rotation /quantum theory /Verdet constant /magnetic susceptibility 全文HTML --> --> --> 1.引 言 1845年, Faraday发现了在外磁场作用下, 入射光经过某种特定材料后偏振面会发生偏转的磁光效应. 这种具有磁光效应的特定材料称为磁光材料, 并被用于磁光调制器、光纤电流传感器及光信息处理等各领域[1 —4 ] . 其中铽镓石榴石(Tb3 Ga5 O12 /TGG)晶体因具有导热系数高、物理化学性质稳定及尺寸扩展性好等优点[5 —7 ] , 应用最为广泛.8 ]获得了TGG晶体并对衍射数据进行了指标化; 文献[9 ]利用微提拉法使晶体直径达到了10 mm; 文献[10 ]对TGG晶体进行了较为完善的磁光性能测试; 文献[11 ]对TGG晶体缺陷进行了研究; 文献[12 ,13 ]研究了TGG晶体的偏心生长及挥发机理; 文献[14 ]采用自制的JGD-800型自动提拉炉生长了大尺寸的TGG晶体.3 Tb(PO4 )3 等磁光材料相比, 纯TGG晶体维尔德常数较低, 不能满足高功率法拉第隔离器、旋转器及磁性开关等部分器件的要求. 为了解决这一问题, 文献[15 ,16 ]从工艺层面生长了性能良好的Pr:TGG晶体. 但关于Pr3+ 离子掺杂对TGG晶体磁光性能影响的内在机理, 目前尚未见到详细的理论计算.3+ , Pr3+ 两种稀土离子之间强烈的超交换作用, 最终定量求解出纯TGG晶体和Pr:TGG晶体的维尔德常数及磁化率.2.Tb3+ , Pr3+ 能级及波函数计算 22.1.晶场及自旋-轨道耦合作用 2.1.晶场及自旋-轨道耦合作用 Tb3+ , Pr3+ 离子在晶体中受诸多作用的影响, 总哈密顿量为${\hat H_0}$ 为库仑相互作用, ${\hat H_{{\rm{LS}}}}$ 为自旋-轨道耦合, ${\hat H_{\rm{C}}}$ 为晶体场作用, ${\hat H_{\rm{i}}}$ 为有效场对离子的作用, ${\hat H_{\rm{S}}}$ 为磁相互作用(可忽略不计).m 为电子质量, $\hbar $ 为约普朗克常数, $\displaystyle\frac{{{z^*}{e^2}}}{{4{\text{π}}{\varepsilon _0}r}}$ 为电子所处的周期性势场, $\xi $ 为自旋-轨道耦合系数, L S ${B_{k,q}} = \displaystyle\frac{{4{\text{π}} }}{{2k + 1}}$ $ \displaystyle\sum\limits_j {\displaystyle\frac{{{q_j}}}{{{R^{k + 1}}}}} {{\rm{Y}}_{k,q}}({\theta _j},{\varphi _j})\left\langle {{r^k}} \right\rangle $ 为晶场参数, Tb3+ , Pr3+ 离子位于坐标原点, $({R_j},{\theta _j},{\varphi _j})$ 为第j 个近邻配位子的球坐标向量, ${q_j}$ 为第j 个近邻电子的电荷, $\left\langle {{r^k}} \right\rangle $ 为径向积分, ${{\rm{Y}}_{k,q}}({\theta _j},{\varphi _j})$ 为球谐函数.3+ 离子的周围局部环境具有D 2 点群对称性, 掺杂的Pr3+ 离子将占据Tb3+ 离子的格位, 因此具有相同的晶场结构. 对于4f电子, 球谐函数积分不为零时, k ≤ 6且为偶数, 晶场可简化为k ≤ 4, 晶场为3+ , Pr3+ 离子占据了6个不等价十二面体的中心位置, 考虑附近占据a , d 位的Ga 3+ 离子及O2- 离子的影响, 由点电荷模型解出的晶场参数列于表1 .能级 ${B_{2,0}}$ ${B_{2,2}}$ ${B_{4,0}}$ ${B_{4,2}}$ ${B_{4,4}}$ ${B_{6,0}}$ ${B_{6,2}}$ ${B_{6,4}}$ ${B_{6,6}}$ Tb3+ 4f –129.9 271.2 –2558.8 296.2 1121.6 682.3 –157.2 1048 –4.7 5d –3063 1180 –139845 72999 5412 Pr3+ 4f –334 144 –2630 252 1126 932 –207 1622 –199 5d –4162 2150 –128877 79630 8425
表1 作用于Tb3+ , Pr3+ 离子的晶场参数(cm–1 )Table1. Crystal field parameters acting on Tb3+ and Pr3+ ions (cm–1 ).3+ , Pr3+ 离子的第一激发组态7 F5 , 3 H5 而言, 在H 0 作用下分别劈裂为7 F5 →1983 cm–1 , 3 H5 →2152 cm–1 , 而在${\hat H_{\rm{C}}}{\rm{ + }}{\hat H_{{\rm{LS}}}}$ 作用下仅为几百个cm–1 , 因此可将${\hat H_{\rm{C}}}{\rm{ + }}{\hat H_{{\rm{LS}}}}$ 作为微扰量, 通过下列久期方程得到Tb3+ , Pr3+ 离子的晶场能级及波函数${\psi _{i1}}$ , ${\psi _{j1}}$ 为未微扰的本征波函数; ${E_{a1}}$ 为自旋-轨道耦合和晶场引起的基态能级位移; ${E_{b1}}$ 为激发态能级位移. 非Karmers离子Tb3+ , Pr3+ 的总角动量分别为J = 6, 4, 在晶场效应的影响下, 简并基态7 F6 和3 H4 分裂成13, 9个单态. 由于能级越高, 经有效场进一步作用后能级之间的混合及电子存在概率越小, 对磁光旋转的贡献可忽略不计. 为方便计算, 此处只取8组最低的晶场能级, 得到相同J 不同ms (自旋磁量子数)波函数的多种线性组合. 考虑4f及5d多重态的耦合, 分别以4f基准态7 F6 , 3 H4 为能级零点, 计算得到的能级位移如表2 .1 2 3 4 5 6 7 8 Tb3+ Ea 1 41.6 49.7 84.9 89.2 267.5 272 303.2 310.5 Eb 1 –863.2 –336.4 –56.3 784.6 1446.7 1996.2 Pr3+ Ea 1 –7.4 –8.9 55 452.8 512.4 549.9 567.1 722.4 Eb 1 –1767.6 –542.9 1115.9 1198.2 2349.5
表2 晶场及自旋轨道作用下的能级位移(cm–1 )Table2. Energy level shift under the action of crystal field and spin orbit (cm–1 ).2.2.有效场作用 -->2.2.有效场作用 Pr:TGG晶体中近邻电子之间存在着较强的相互作用, 产生了一个与磁化强度成正比的附加磁场${{{H}}_{\rm{\nu }}} = \nu {{M}} = \nu \chi {{{H}}_{\rm{e}}}$ , 实际作用于电子的有效场可看成是外磁场和附加磁场的叠加, 即$\chi {\rm{ = }}C/(T - {T_p})$ 满足Currie-Weiss定律. 由Kramers定理可知, 由 (6 ) 式得到的晶场能级至少二重简并, 在有效场的影响下, 4f基态能级将产生Zeeman分裂, 由于激发态能级较高, 有效场对5d的作用可忽略不计. 考虑附加磁场${H_\nu }$ 只作用于自旋, 则有效场的哈密顿量为${\hat H_{\rm{i}}} \ll {\hat H_{\rm{C}}}{\rm{ + }}{\hat H_{{\rm{LS}}}}$ , 可将其看成自旋-轨道耦合及晶场的微扰量, 在一级近似下, 有效场引起的基态能级位移为${\psi _{a1}}$ ,为晶场及自旋-耦合作用后的基态波函数. 室温下${k_{\rm{B}}}T \approx 200\;{\rm{c}}{{\rm{m}}^{ - 1}}$ , 其中${k_{\rm{B}}} =1.3807 \times $ $ {10^{ - 23}}\;{\rm{J}}/{\rm{K}}$ 为玻尔兹曼常数. 因此表2 中Tb3+ 离子的第1—4个基态能级、Pr3+ 离子的第1—3个基态能级上都有一定概率的电子分布, 由 (9 ) 式计算得到的基态能级分裂列于表3 .1 2 3 4 Tb3+ (± 2.342$\mp\; 0.9516 \nu \chi $) (± 0.463$\mp\; 0.1422 \nu \chi $) (± 0.897$\mp\; 0.3641 \nu \chi $) (± 1.499$\mp \;0.6561 \nu \chi $) Pr3+ (± 1.641$\mp \;0.8244 \nu \chi $) (± 0.423$\mp\; 0.0893 \nu \chi $) (± 3.302$\mp\; 0.1176 \nu \chi $)
表3 有效场作用下的能级分裂(cm–1 )Table3. Energy level splitting under the action of effective field (cm–1 ).2.3.稀土离子之间的超交换作用 -->2.3.稀土离子之间的超交换作用 TGG晶体中掺杂Pr3+ 离子后, Tb3+ 、Pr3+ 离子之间的轨道和自旋角动量之间会产生强烈的超交换作用, 外壳电子轨道-自旋相关项的哈密顿量可表示为i , j 分别与Tb3+ , Pr3+ 离子相关; ${m_i}$ ,${m_j}$ 代表基态轨道, ${m_i}^\prime $ ,${m_j}^\prime $ 代表激发态轨道; ${{J}}({m_i}^\prime,{m_j}^\prime,{m_i}, $ ${m_j}) = \left\langle {{m_i}^\prime,{m_j}^\prime } \right|{{J}}(i,j)\left| {{m_i},{m_j}} \right\rangle $ 表示混合轨道角动量; ${{{S}}_i}$ ,${{{S}}_j}$ 表示两个离子的自旋角动量. 根据简并微扰理论求解下列久期方程得到超交换作用引起的能级位移及波函数${\psi _{i3}}$ , ${\psi _{j3}}$ 分别为晶场、自旋-轨道耦合及有效场作用后的本征波函数;${E_{a3}}$ ,${E_{b2}}$ 分别为Tb3+ , Pr3+ 离子之间的超交换作用引起的基态及激发态能级位移, 列于表4 .1 2 3 4 5 6 7 8 Tb3+ Ea 3 –201.3 –152.3 –96.4 –3.2 82.4 141 168.3 210 Eb 2 –499.1 –112.7 78.8 236.7 774.1 1135.8 Pr3+ Ea 3 –262.1 –194.3 –32.4 56.9 61.5 176.5 211.7 387.9 Eb 2 –844.1 –10.3 743.5 882.4 1178.3
表4 超交换作用下的能级位移(cm–1 )Table4. Energy level shift under the action of super-exchange interaction (cm–1 ).${E_a}{\rm{ = }}{E_{a1}}{\rm{ + }}{E_{a2}}{\rm{ + }}{E_{a3}}$ ; Tb3+ , Pr3+ 离子5d激发态与4f基态之间的能级间距分别为38462, 63580 cm–1[17 ,18 ] , 因此激发态的最终能级为${E_b}{\rm{(T}}{{\rm{b}}^{3 + }}{\rm{) = }}{E_{b1}}{\rm{ + }}{E_{b2}}{\rm{ + 38462 c}}{{\rm{m}}^{ - 1}}$ , ${E_b}{\rm{(P}}{{\rm{r}}^{3 + }}) =$ ${E_{b1}}+{E_{b2}}+ {\rm{ 63580 c}}{{\rm{m}}^{ - 1}}$ .3.维尔德常数及磁化率 23.1.法拉第旋转 3.1.法拉第旋转 单位长度上的法拉第旋转(FR)可表示为${\theta _{\rm{F}}}{\rm{ = }}{\theta _{\rm{p}}} + {\theta _{\rm{d}}}$ [19 ] , 其中${\theta _{\rm{p}}}$ 为Tb3+ , Pr3+ 离子4f→5d电偶极子跃迁引起的顺磁性FR, ${\theta _{\rm{d}}}$ 为磁偶极子跃迁引起的抗磁性FR. 对于Tb3+ 离子, 晶场为非单态, 抗磁性FR可忽略不计, ${\theta _{\rm{F}}} \cong {\theta _{\rm{p}}}$ ; 但对于晶场为单态的Pr3+ 离子, 抗磁性FR与顺磁性FR同等重要, 将引起较Tb3+ 离子大的法拉第旋转角. 顺磁性及抗磁性FR的量子表示式分别为[20 ,21 ]: $\omega _{\rm{p}}^2 = \displaystyle\frac{{4{\text{π}}N{e^2}}}{m}$ , ${L_n} = {\left[ {\left( {{n^2} + 2} \right)/3} \right]^2}$ 为Lorentz-Lorenz修正项, N 为单位体积内的离子数, n 为平均折射率; e , m 为电子电荷及质量;$\omega $ 为入射光频率, ${\omega _{ab}}$ 为激发态与基态之间的频率;${\varGamma _{ab}}$ 为线宽, k ${f_{ab}}^ \pm = \displaystyle\frac{{m{\omega _{ab}}}}{{\hbar {e^2}}}{\left| {{P_{ab}}^ \pm } \right|^2}$ (± 分别表示右旋和左旋)为电子从基态跃迁到激发态的概率.${P_{ab}}^ \pm $ 为左右旋跃迁偶极矩; ψa , ψb 分别为晶场、轨道耦合、有效场及超交换作用后的基态和激发态波函数. 根据表2 —表4 的能级位移及 (6 )和(11 ) 式求得的波函数, 可算出左右圆偏振光激发下, Tb3+ 离子和Pr3+ 离子全部的48, 30个跃迁矩阵元.${\beta _a}$ 为电子处于基态能级a 的概率, 根据Zeeman定律, 可表示为3.2.维尔德常数 -->3.2.维尔德常数 磁光材料的维尔德常数可表示为V 及与掺杂的Pr3+ 离子浓度之间的关系, 将Pr:TGG表示为Tbx y z 12 (x + y ≈ 3, z ≈ 5). 由于Pr:TGG晶体的维尔德常数主要取决于外层电子4f→5d的跃迁[22 ] , 则Pr:TGG的维尔德常数可看成是Tb3+ 离子与Pr3+ 离子的贡献之和.x ≥ y 时, 只有等量的Tb3+ 离子与Pr3+ 离子发生超交换, 因此维尔德常数表示为y < x 时, 相当于在纯PrGG晶体中掺杂Tb3+ 离子, 维尔德常数表示为V 1 (Tb3+ ), V 1 (Pr3+ )表示发生超交换后的维尔德常数, V 2 (Tb3+ ), V 2 (Pr3+ )表示没有超交换下的维尔德常数.T =298 K, 外磁场H e =0.1 T, 取波长变化范围为400—1500 nm, 分别计算纯TGG(x = 3, y = 0, z = 5)及5%Pr:TGG(x = 2.926, y = 0.073, z = 5.03)在不同波长下的维尔德常数, 如表5 .波长λ /nm 457.9 532 632.8 830 1064 1300 TGG V c 290.1 179.4 122.2 51.9 31.8 18.5 V e 305.7 190 134.4 61 40.2 20 5%Pr:TGG V c 421.8 312.5 190.2 108.8 59.7 45.9 V e 437 324.5 200.1 121.4 68.7 49.2 注: V c 为本文维尔德常数的计算值, V e 为实验值[16 ,23 ,24 ] .
表5 不同波长下的维尔德常数V (${\rm{rad/m}} \cdot {\rm{T}}$ )Table5. Verdet constant at different wavelengths (${\rm{rad/m}} \cdot {\rm{T}}$ ).λ =532nm、632.8nm、1064nm, 计算Pr:TGG晶体在不同Pr3+ 离子含量(y )下的维尔德常数, 列于表6 .λ /nmy 0 0.073 1 1.5 2 2.927 3 532 179.4 312.5 2002.1 2913.4 2021.4 367.9 237.7 632.8 122.2 190.2 1099.8 1588.6 1112.9 231 161.5 1064 31.8 59.7 432.1 632.3 438 77.8 49.4
表6 不同Pr3+ 离子含量(y )下的维尔德常数V (${\rm{rad/m}} \cdot {\rm{T}}$ )Table6. Verdet constant under different Pr3+ ions content (${\rm{rad/m}} \cdot {\rm{T}}$ ).3.3.磁化率 -->3.3.磁化率 磁化率与磁化强度之间的关系为N 为单位体积内的离子数, $\bar m$ 为单个4f离子的平均磁矩, 通过计算电子分布概率得到3+ 离子与Pr3+ 离子的贡献之和,${\chi _1}({\rm{T}}{{\rm{b}}^{{\rm{3 + }}}})$ , ${\chi _1}({\rm{P}}{{\rm{r}}^{{\rm{3 + }}}})$ 表示发生超交换后的磁化率; ${\chi _2}({\rm{T}}{{\rm{b}}^{{\rm{3 + }}}})$ , ${\chi _2}({\rm{P}}{{\rm{r}}^{{\rm{3 + }}}})$ 表示没有超交换下的磁化率.λ =1064 nm, 取温度变化范围为10—300 K, 分别计算纯TGG及5%Pr:TGG在不同温度下磁化率的倒数1/χ , 如表7 .温度T /K 10 100 150 200 250 300 TGG 1/χ c 80.3 458.4 688.3 942.8 1167.8 1399.5 1/χ e 72.2 469.3 659.2 908.9 1128.7 1349.6 5%Pr:TGG 1/χ c 64.3 441.2 637.7 852.4 1029.3 1210.5 1/χ e 56.4 419 599.2 803.7 987.1 1163.2 注: 1/χ c 为本文计算值, 1/χ e 为实验值[16 ,25 ] .
表7 不同温度下磁化率的倒数1/χTable7. Inverse magnetic susceptibility at different temperatures.3.4.结果分析 -->3.4.结果分析 分析掺杂Pr3+ 离子对TGG晶体的维尔德常数及磁化率影响情况, 分别如图1 和图2 所示.图 1 维尔德常数的波长特性Figure1. Wavelength characteristics of the Verdet constant.图 2 磁化率的温度特性Figure2. Temperature characteristics of the magnetic susceptibility.图1 和图2 中红色曲线为纯TGG晶体, 蓝色曲线为5%Pr:TGG, 虚线代表本文计算值, 实线代表实验数据. 由图可见, 计算值与实验数据基本符合, 说明本文的计算方法是可行的. 但本文忽略了哈密顿微扰的高级修正项、磁偶极子之间的相互作用及电场引起的Stark位移等微观参数, 导致计算结果与实验数据之间存在一定的偏差.图1 可见, 掺杂Pr3+ 离子后, 晶体的维尔德常数有了明显提升, 在波长532, 632.8, 1064 nm处分别为313.4, 191.2, 60.4 rad/m·T. 这是由于: 1) Pr3+ 离子的跃迁矩阵元较Tb3+ 离子大, 且Pr3+ 离子还包含抗磁性FR部分, 引起了较大的法拉第旋转角; 2)掺杂Pr3+ 离子后, Tb3+ 离子与Pr3+ 离子之间产生了强烈的超交换作用, 导致了能级的进一步分裂.图2 可见, 与纯TGG晶体相同, Pr:TGG的磁化率倒数与温度成线性关系, 满足Currie-Weiss定律, 具有顺磁特性. 但Pr:TGG磁化率较大, 对温度的依赖性较小, 这是由于Tb3+ 离子与Pr3+ 离子的外层电子之间存在自旋-轨道角动量耦合, 晶体内部磁矩增大, 在10 K处有效磁矩达到了9.92 μB , 由 (17 ) 式可见, 磁化率随磁矩的增大而增大.3+ 离子含量(y )之间的关系, 如图3 所示.图 3 维尔德常数随Pr3+ 离子含量(y )的变化情况Figure3. The variation of Verdet constant with Pr3+ ions content (y ).图3 中颜色不同的曲线分别表示不同的波长值, 实线为实验数据的拟合曲线[16 ] , 虚线为本文计算值. 由图可见, Tb3+ 离子与Pr3+ 离子之间强烈的超交换作用是维尔德常数增大的主要原因; 维尔德常数与Pr3+ 离子含量成分段线性关系, 发生超交换的离子数越多, 晶体的维尔德常数越高; 当y = x = 1.5即晶体中Tb3+ 离子与Pr3+ 离子的含量相等时, 达到最大值2913.4 ${\rm{rad/m}} \cdot {\rm{T}}$ .4.结 论 由于Pr3+ 离子引起的法拉第旋转角较大, 且Tb3+ 离子与Pr3+ 离子之间会产生强烈的超交换作用, 因此在纯TGG晶体中掺杂Pr3+ 离子后, 维尔德常数得到明显提升, 在波长532, 632.8, 1064 nm处分别达到了313.4, 191.2, 60.4 rad/m·T. 同时Tb3+ 离子与Pr3+ 离子自旋-轨道角动量之间的耦合提高了晶体内部的有效磁矩, 磁化增大, 磁化率倒数与温度之间的线性关系由4.41/K降低至3.92/K. Pr:TGG晶体的维尔德常数与Pr3+ 离子含量(y )成分段线性关系, 当晶体中Tb3+ 离子与Pr3+ 离子的含量相等时, 达到最大值2913.4 rad/m·T. 本文的计算思路可为新型磁光材料的研究提供一定的理论借鉴. 


































































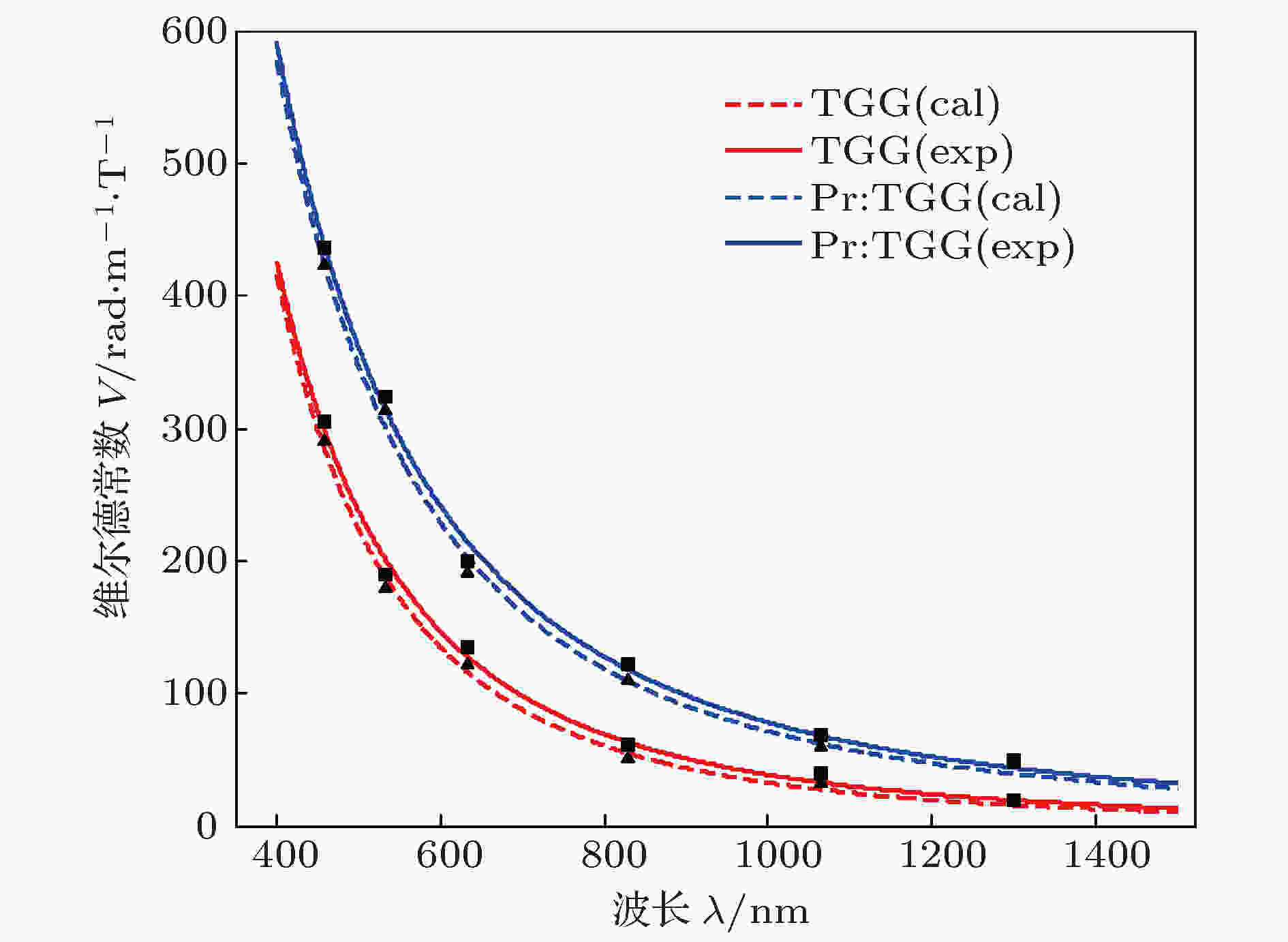 图 1 维尔德常数的波长特性
图 1 维尔德常数的波长特性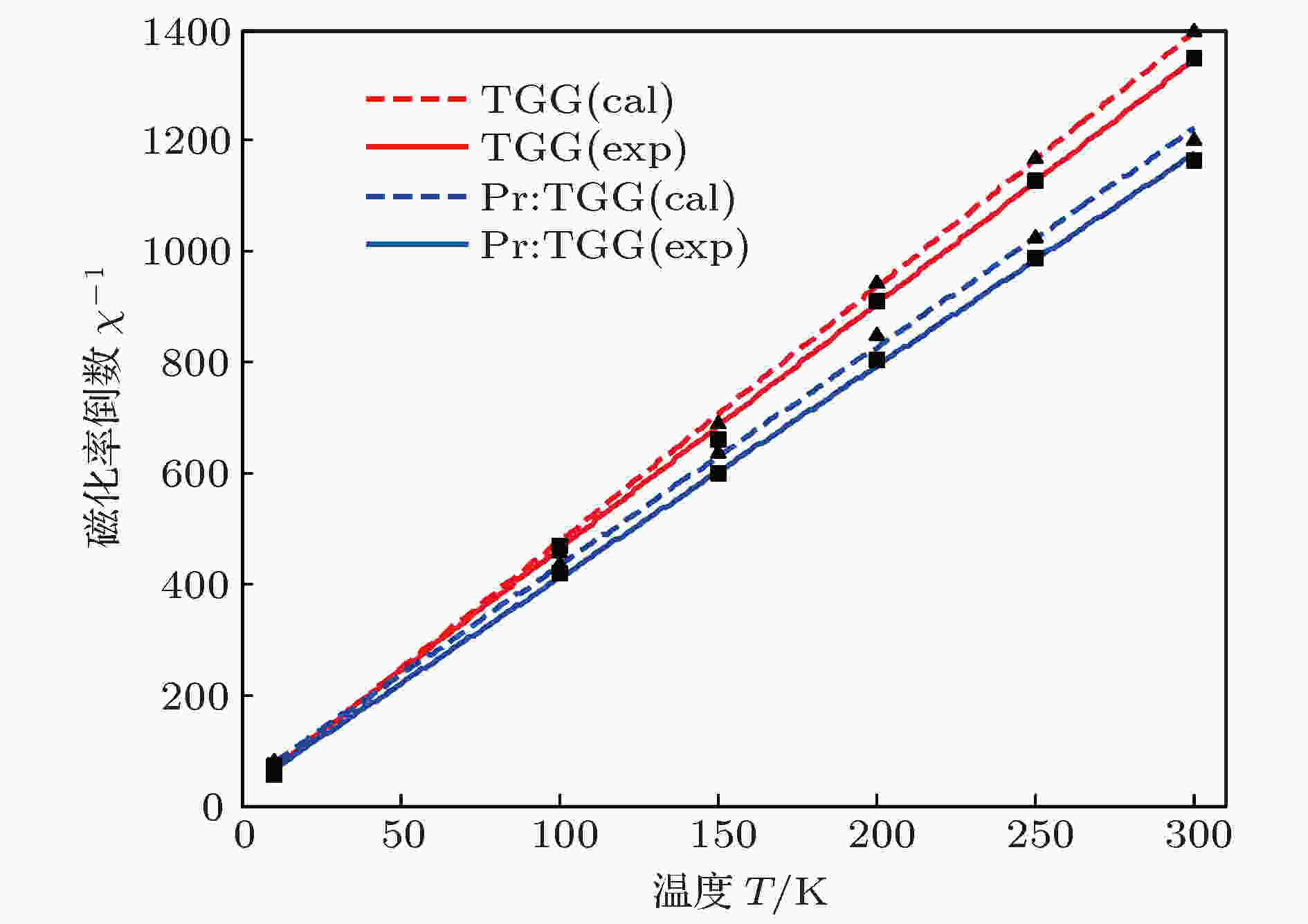 图 2 磁化率的温度特性
图 2 磁化率的温度特性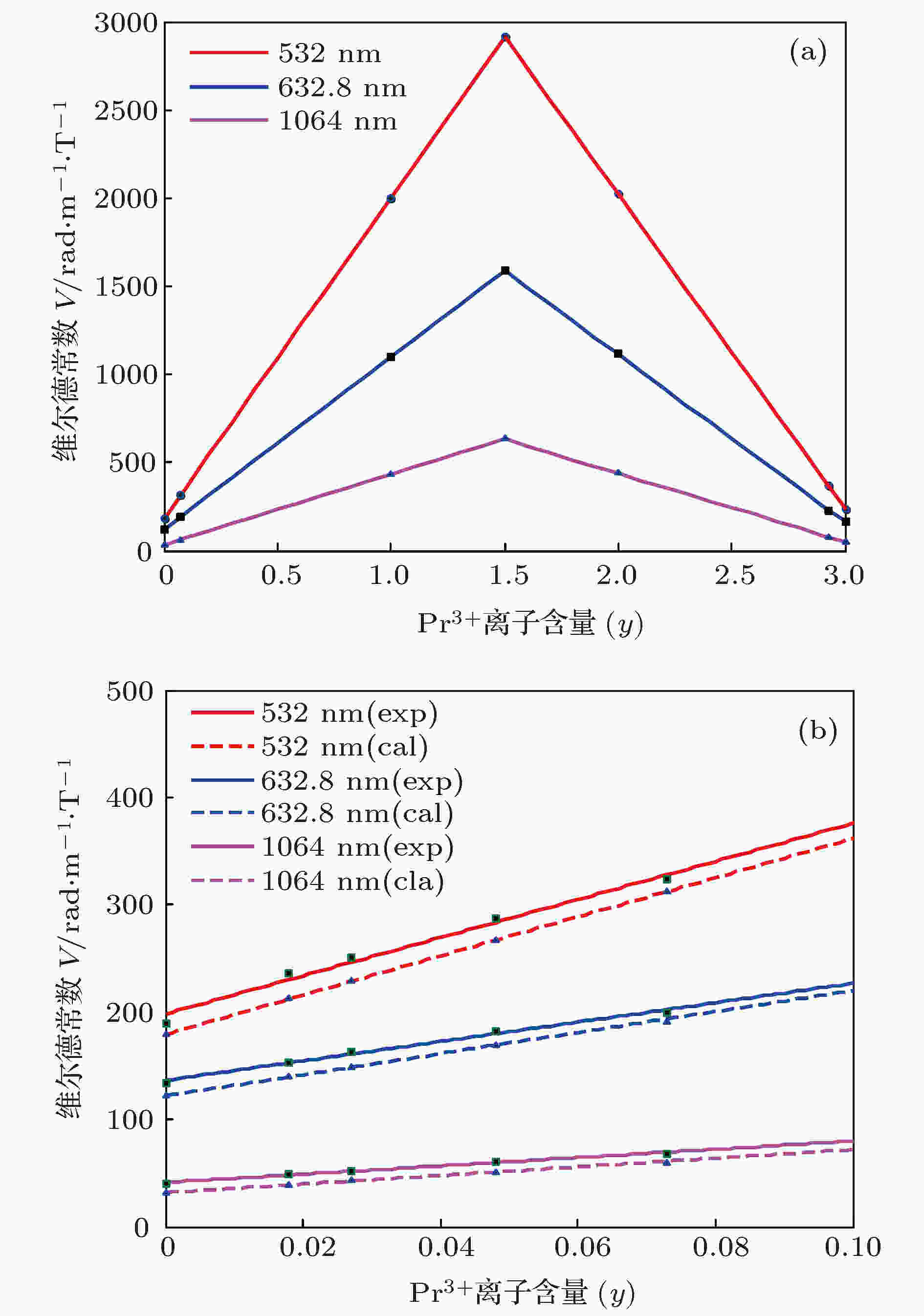 图 3 维尔德常数随Pr3+离子含量(y)的变化情况
图 3 维尔德常数随Pr3+离子含量(y)的变化情况
