摘要:充液管道低频声的有效吸收和消减一直是一个颇具挑战性的难题. 受声学超材料理论启发, 本文设计了一种沿管道轴向方向等距布置小体积声学短管的充液周期管道系统. 该管道系统可以诱发声波传播超宽低频带隙的产生, 使得声波在带隙频率范围内传播将被显著衰减, 乃至无法透射, 近乎被完全吸收, 称为暗声学超材料型充液管道. 进一步, 揭示了暗声学超材料型充液管道中声传播带隙的产生机理、参数影响规律, 研究了该波导管对低频噪声的降噪特性, 初步探讨了工程实际可实现的暗声学超材料型充液管道的结构实现形式. 研究成果有望为管道低频噪声控制提供一条新的技术途径.
关键词: 暗声学超材料/
充液管道/
噪声控制/
声波带隙

English Abstract

全文HTML

--> --> -->

低频振动和噪声在生产生活中普遍存在, 它既影响装备产品性能的发挥, 又造成噪声污染, 影响人的身心健康^[1]. 一直以来, 低频噪声的消减问题始终是一个颇具挑战性的难题, 特别是充液管道中的低频噪声传播控制问题^[2,3]. 不少****致力于充液管道的低频噪声降噪研究.
管内介质作为一种极佳的声学载体, 低频声波极易在管内传播, 具有传播距离远、衰减小、控制难度大等特点^[4]. 因此, 在噪声传播途径对其进行控制研究变得十分必要. 常见的管道噪声传播控制措施主要有: 在管道中布置弹性接头^[5]和波纹管等元件^[6,7]、安装消声弯头^[8,9]、在阀后安装节流板孔^[10]、优化设计以减少管路急弯头和支管等二次噪声源^[11]、有源消声技术^[12]、安装管道消声器^[13], 其中, 在充液管道中安装管路消声器可以有效降低系统流噪声, 是目前应用最广泛、效果最显著的一种方法. 尽管如此, 现有的噪声传播控制措施在低频降噪上仍存在不少问题: 譬如有源控制技术虽可以对低频噪声进行较好的控制, 但其只能针对若干频线噪声进行处理, 且控制复杂度高、可靠性不足^[14]; 安装消声器受其外形尺寸和结构限制, 消声效果或是低频消声频带过窄(如共振腔式消声器虽然消声频率较低, 但其消声频带过窄^[15,16]), 或是消声频率过高(如扩张式消声器虽然中高频段消声效果良好, 但低频消声能力不足^[17,18]), 仍难以满足管道系统噪声的低频宽带控制要求.
近年来, 凝聚态物理领域声子晶体概念的提出引起了减振降噪研究者的极大兴趣^[19,20]. 声子晶体一般指一类人工结构单元经周期有序排列构成的具有弹性波带隙、定向传播、负折射与声聚焦、声吸收等特性的材料/结构, 它是凝聚态物理领域中晶体概念在弹性波意义下的延伸^[21—24]. 利用声子晶体的弹性波带隙特性可以人为操控弹性波在介质或结构中的传播, 实现工程结构的减振降噪设计. 无独有偶, 一些****基于新兴的声学超材料理论^[1,15,25], 同样获得了弹性波传播的带隙现象, 并开展了声学超材料的低频宽带吸隔声研究, 可以说, 声学超材料的提出进一步丰富和促进了声子晶体的减振降噪应用探索. Lu等^[24]研究认为当局域共振型声子晶体的散射体(子结构单元)处于亚波长尺度时, 声子晶体可视为声学超材料. 声学超材料和局域共振声子晶体带隙机理突破了布拉格散射机理的限制, 可以实现“小尺寸控制大波长”, 从而打破低频噪声控制技术瓶颈^[24—26]. Mei等^[27]设计出了一种声学超材料, 使得声波在低频区域几乎能够被百分之百地吸收, 而其散射体结构尺寸比声波长度小几个数量级, 实现了毫米级结构厚度对大波长低频声波的有效控制. 类比光学黑暗现象, 这种声学超材料在低频段对于声波是“黑暗的”, 因此, 他们将其称之为暗声学超材料.
受声学超材料理论启发, 本文设计了一种沿管道轴向方向等距布置小体积声学短管的充液周期管道结构, 该周期管道可以诱发声波传播超宽低频带隙的产生, 使得声波在带隙频率范围内传播将被显著衰减, 乃至无法透射, 近乎被完全吸收, 称为暗声学超材料型充液管道(简称暗声学超材料管). 进一步, 揭示了声学超材料管中超宽低频带隙的产生机理、参数影响规律, 研究了该声学超材料管的低频噪声传播特性.

本文所构建的暗声学超材料管如图1所示, 它由充有气体和液体的末端封闭的声学短管沿充液管道轴向等间距布置构成. 短管上半部分为气体腔, 下半部分为液体腔. 液体腔内液体与管内液体为同一介质且相连通. 不失一般性, 选取充液管和声学短管为均质圆管道, 其半径分别为r_p和r_m, 面积分别为S_p和S_m; 声学短管安装间距, 即一个基本管道单元长度为l_p; 声学短管的充气腔和充液腔长度分别为l_g和l_f, 体积分别为V_cg和V_cf.
图 1 暗声学超材料管结构示意图
Figure1. Sketch map of the 1D dark metamaterial pipe.

在无能量损耗、静态、连续、均匀的理想介质假设下, 管内声学介质的波动方程可由下式给出^[4]:

${\nabla ^2}p - \frac{1}{{c_{}^2}}\frac{{{\partial ^2}p}}{{\partial {t^2}}} = 0, $

式中p和c分别表示流体介质的静态声压和声速, 则其体积模量κ为ρc². 该式可进一步写成时谐解的形式,

$\frac{{{\partial ^2}p}}{{\partial {x^2}}} + k_{}^2p = 0.$

为了简化公式, 式中exp(–jωt)一项已经被省略, 其中, ω和k分别为角频率和波数, k可由ω/c计算得到. 则声压p和流体体积速度Q的时谐解可分别表示为:

$p = {A_{\rm t}}{{\rm e}^{{\rm j}kx}} + {A_{\rm r}}{{\rm e}^{ - {\rm j}kx}},$

$Q = \frac{{{S_{\rm p}}}}{{\rho c}}\left( {{A_{\rm t}}{{\rm e}^{{\rm j}kx}} - {A_{\rm r}}{{\rm e}^{ - {\rm j}kx}}} \right),$

式中A_t和A_r分别代表入射波和反射波波幅系数, 声波波速v源自声压p与声波波速v的关系式^[6]: $v = - \rho _0^{ - 1}\int {\partial p/} \partial x{\rm{d}}t$. 从而, 在一段长为l_p的均质波导管两端的声学状态矢量有如下的矩阵关系式(以图1所示的在第n–1和n单元间的管道段为例):

$\begin{split}&\left\{ {\begin{array}{*{20}{c}} {{{{p}}_{n - 1,R}}} \\ {{{{Q}}_{n - 1,R}}} \end{array}} \right\} \\= &\left[ {\begin{array}{*{20}{c}}{\cos \dfrac{{\omega {l_{\rm p}}}}{c}}&{{\rm j}\dfrac{{\rho c}}{{{S_{\rm p}}}}\sin \dfrac{{\omega {l_{\rm p}}}}{c}} \\ {{\rm j}\dfrac{{{S_{\rm p}}}}{{\rho c}}\sin \dfrac{{\omega {l_{\rm p}}}}{c}}&{\cos \dfrac{{\omega {l_{\rm p}}}}{c}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{{p}}_{nL}}} \\ {{{{Q}}_{nL}}} \end{array}} \right\},\end{split}$

字符n表示与第n个周期单元有关的变量. 当在均质管道中安装图1所示的声学短管时, 则声学短管两边管道的声学状态传递矩阵方程式有如下关系式^[28]:

$\left\{ {\begin{array}{*{20}{c}} {{{{p}}_L}} \\ {{{{Q}}_L}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} 1&0 \\ {{Z_{\rm H}}^{ - 1}}&1 \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{{p}}_R}} \\ {{{{Q}}_R}} \end{array}} \right\},$

式中Z_H为声学短管的阻抗. 综合 (5)和 (6) 式, 可得到安装声学短管的周期管段两端的声学状态传递关系:

$\begin{split}&\left\{ {\begin{array}{*{20}{c}} {{{{p}}_{n - 1,L}}} \\ {{{{Q}}_{n - 1,L}}} \end{array}} \right\} \\= &\left[\!\!\!{\begin{array}{*{20}{c}} {\cos \dfrac{{\omega {l_{\rm p}}}}{c}+ {\rm j}\dfrac{{\rho c}}{{{Z_{\rm H}}{S_{\rm p}}}}\sin \dfrac{{\omega {l_{\rm p}}}}{c}}&{{\rm j}\dfrac{{\rho c}}{{{S_{\rm p}}}}\sin \dfrac{{\omega {l_{\rm p}}}}{c}} \\ {\dfrac{1}{{{Z_{\rm H}}}}\cos \dfrac{{\omega {l_{\rm p}}}}{c}+{\rm j}\dfrac{{{S_{\rm p}}}}{{\rho c}}\sin \dfrac{{\omega {l_{\rm p}}}}{c}}&{\cos \dfrac{{\omega {l_{\rm p}}}}{c}} \end{array}}\!\!\! \right]\left\{\!\!\!\!{\begin{array}{*{20}{c}} {{{{p}}_{nL}}} \\ {{{{Q}}_{nL}}} \end{array}} \!\!\!\!\right\}.\end{split}$

事实上, 图1中的声学短管在考虑气液混合腔的情况下, 可视为亥姆霍兹共振器. 通过声电类比, 其值可由Z_H = jωL_H + (jωC_H)^–1计算得到, 其中L_H = ρ_fl_fe/S_m和C_H = V_cg/κ_g分别为声抗和声容, κ_g为流体的体积模量^[15]; 声学短管液柱修正长度^[17], l_fe=l_f+0.55l_f, 下标f和g分别标示液体和气体所对应的物理参数; 声学短管的共振频率f_H可由式$f_{\rm{H}}=(2 {\text{π}})^{-1}\left(L_{\rm{H}} C_{\rm{H}}\right)^{-1 / 2}$进行计算. 这样的一个物理模型当所考虑的频率范围比较低时是足够精确的, 因为此时的声波波长比声学短管的尺寸大得多. 进一步, 在(7)式中引入声学状态矢量Γ ={p, Q}′, 那么式子可以简化为

${{{\varGamma}} _{n - 1}} = {{{T}}_{\rm c}} \cdot {{{\varGamma}} _n},$

式中T_c为单个周期单元管道两端声学状态矢量的传递矩阵. 此外, 由于暗声学超材料管的周期性, 周期单元左右两端状态矢量还应满足Bloch周期边界条件^[20]:

${{{\varGamma}} _{n - 1}} = {{\rm{e}}^{{\rm j}\mu {l_{\rm p}}}} \cdot {{{\varGamma}} _n}.$

综合 (8) 式和 (9) 式, 得到

$\left| {{{{T}}_{\rm c}} - {{\rm{e}}^{{\rm j}\mu {l_{\rm p}}}}{{I}}} \right| = 0.$

将μ视为频率的函数, 求解 (10) 式在不同频率下μ的值, 便可得到暗声学超材料管的声波色散关系曲线函数, 即声波能带结构图, 其中μ的虚部表征波幅系数从单元一侧到另一侧的衰减程度, 即所谓的衰减常数, 实部则为相位常数. 倘若在一定频率范围内, μ的虚部为均零, 即μ为纯实数时, 则声波可在管内无衰减传播, 该频率范围称为通带. 倘若衰减常数在所计算的一些频率段不为零, 则声波在管内传播将被衰减, 此时的频率段则称为带隙.
对于由N个安装声学短管的周期管道单元组成的有限长暗声学超材料管, 声波在管中传播的声学状态矢量传递关系为

${{{\varGamma}} _{\rm{i}}} = {{T}}_{\rm{c}}^N \cdot {{{\varGamma}} _{\rm{o}}},$

式中下标i和o分别标示暗声学超材料管声波入口和出口的声学状态矢量. 当有限长暗声学超材料管两端的管口几何尺寸一样且满足声波辐射口条件时, 可获得声波透射系数t_p关于μ的显式表达式^[4]:

${t_{\rm{p}}} = \left| {\frac{{2\sin \left( {\mu {l_{\rm{p}}}} \right)\left( {\tau _{\rm{p}}^2 - 1} \right)\tau _{\rm{p}}^N}}{{{{\left( {1 - {\tau _{\rm{p}}}{{\rm{e}}^{ - {\rm{j}}\mu {l_{\rm{p}}}}}} \right)}^2} - \tau _{\rm{p}}^{2N}{{\left( {{\tau _{\rm{p}}} - {{\rm{e}}^{ - {\rm{j}}\mu {l_{\rm{p}}}}}} \right)}^2}}}} \right|,$

式中τ_p = exp(±jkl_p); 则吸声系数a_p为^[27]

${a_{\rm{p}}} = 1 - {t_{\rm{p}}}^2 - {r_{\rm{p}}}^2,$

其中反射系数r_p = A_r/A_t. 相应地, 声学传递损失可以表示为

$TL = 10\lg (t_{\rm{p}}^{ - 1}).$

基于 (10)—(14) 式便可对无限周期和有限周期的暗声学超材料管的声波传播特性进行计算和研究.

声波在线性系统的声能耗散功率正比于响应函数随时间变化率的平方, 即正比于频率的平方. 生活中常见的普通材料基本上都是线性材料, 这使得低频声的衰减十分有限, 难以实现强衰减. 低频声的有效吸收和消减一直是一个颇具挑战性的难题. 近年来, 声学超材料理论在减振降噪领域的应用和探索, 虽然在低频段消声取得了丰硕成果, 但随着研究的深入, 不少****都遇到了这样的技术瓶颈: “低频、宽带、强衰减”与“轻质小巧”, 难以兼得. 本文所提出的周期管路结构, 恰可以利用较小的体积尺寸获得充液管道系统噪声的低频、宽带、强衰减消声效果. 下面以具体算例展示该管道结构的消声特性.
图2所示为暗声学超材料管的声波能带结构图和声传递损失: 图2(a)和图2(b)分别为μ的实部和虚部, 即相位常数和衰减系数; 图2(c)为有限长暗声学超材料管的声传递损失, 周期单元个数为4个. 计算中管道半径r_p和声学短管半径r_m分别取为0.05 m和0.04 m; 晶格常数, 即周期管道元胞长度l_p为0.96 m; 声学短管的充气腔和充液腔长度l_g和l_f分别为0.025 m和0.1 m. 图中实线和虚线分别对应传递矩阵法和COMSOL有限元仿真软件计算的结果. 两种不同计算结果高度吻合, 这有力地验证了本文所开发的传递矩阵法的正确性.
图 2 暗声学超材料管的声波能带结构图和声传递损失
Figure2. Acoustic bang structure and sound transmission loss of the dark acoustic metamaterial-type pipe.

从图2(a)和图2(b)可以看出, 在22.9—465.0 Hz和781.2—1049.0 Hz这两个频率范围内, 声波波矢μ的虚部均不为零. 由于μ的虚部表征声波波幅系数从周期单元一侧到另一侧的衰减程度, 因此可以预测, 这两个频率范围内的声波在管内的传播将受到衰减, 相应地, 这两个频率段即为暗声学超材料管的声波带隙. 图2(c)的声传递损失曲线验证了图2(a)和图2(b)的预测结果. 从图2(c)中可知, 在22.9—465.0 Hz和781.2—1049.0 Hz这两个带隙范围内, 声波在管内传播均有不同程度的衰减. 特别在第一个带隙内, 声传递损失在15 dB以上的频率带宽度可达444 Hz, 声传递损失在30 dB以上的频率带宽度可达380 Hz以上, 声传播开始发生衰减的频率低达22.9 Hz. 同时, 在该频率段内还存在一个衰减声压级超过320 dB的衰减峰值, 这个峰值位置位于34.5 Hz处. 由$f_{\rm{H}}=(2 {\text{π}})^{-1}\left(L_{\rm{H}} C_{\rm{H}}\right)$计算得到气/液混合腔声学短管的共振频率亦为34.5 Hz, 可见衰减峰值与气/液混合腔声学短管的共振频率一致. 如此大的衰减声压级对相应频率的透射波而言, 基本无法通过管内介质向管端传播, 如图3的声波透射系数与吸声系数所示. 从图3中可以看出, 该周期管路在第一带隙频率范围内对入射声波的吸收高达99%, 显示出相当强的消声吸声效果, 从而使该超材料管声传播末端的声接收器几乎接收不到声信号. 图4的声压等值面和声压分布图进一步显示了管内声压的分布情况, 其中声压激励信号在管道左端施加. 很明显, 声能量基本集中在上游管道的一个周期单元内, 在声波传播方向的下游管道, 声压微乎其微, 基本为零, 可见在这些频率点上声波几乎不可能从管内透射而往前传播. 类比光学“黑暗”现象, 可以称该频率区域为声学“黑暗”区域. 这样的声学“黑暗”区域正好迎合了管道的低频噪声控制需要. 探讨声学“黑暗”区域的形成机理和参数影响规律, 可以指导带隙的低频、宽带优化, 最终实现管道低频噪声传播抑制和消减.
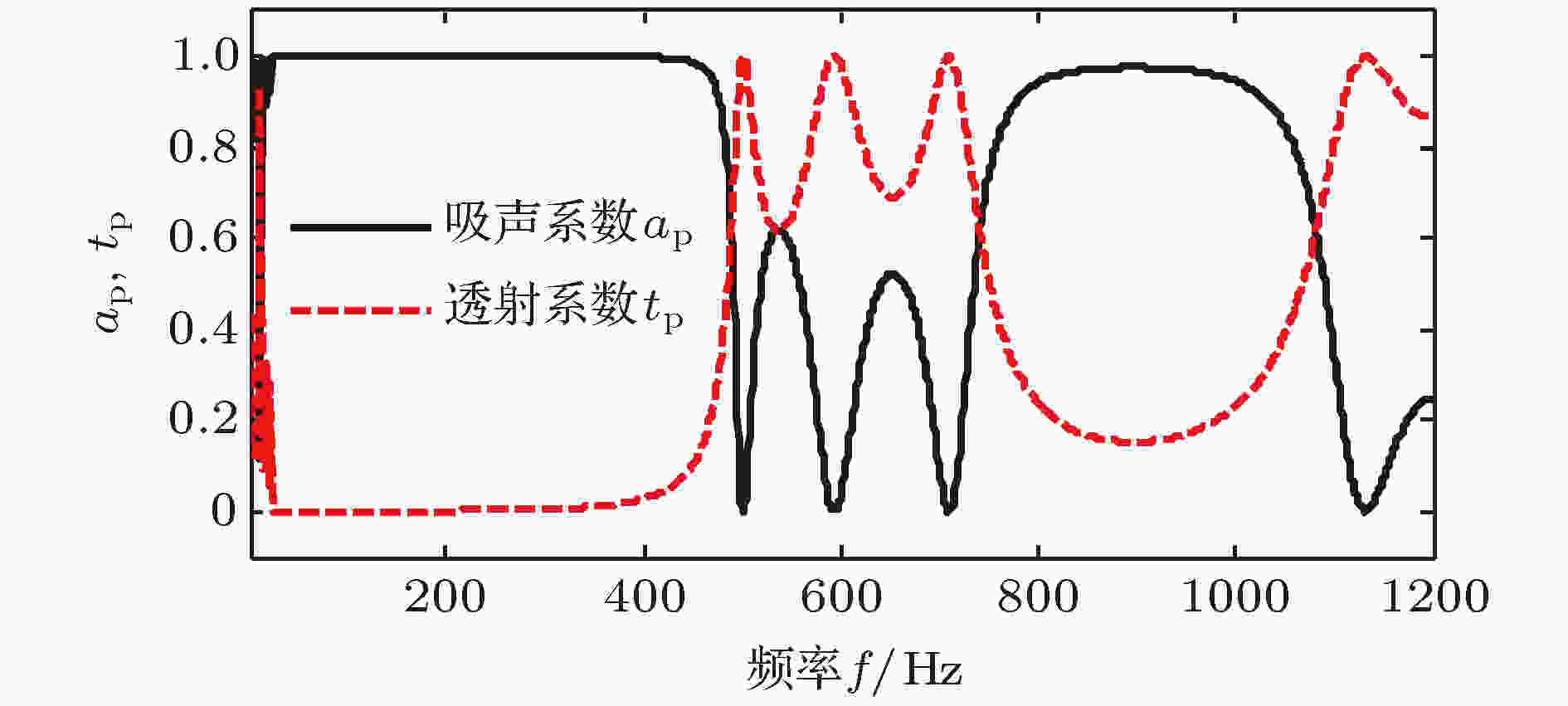图 3 暗声学超材料管的声波透射系数与吸声系数
Figure3. The transmission and absorption coefficients of acoustic waves in the dark acoustic metamaterial-type pipe.

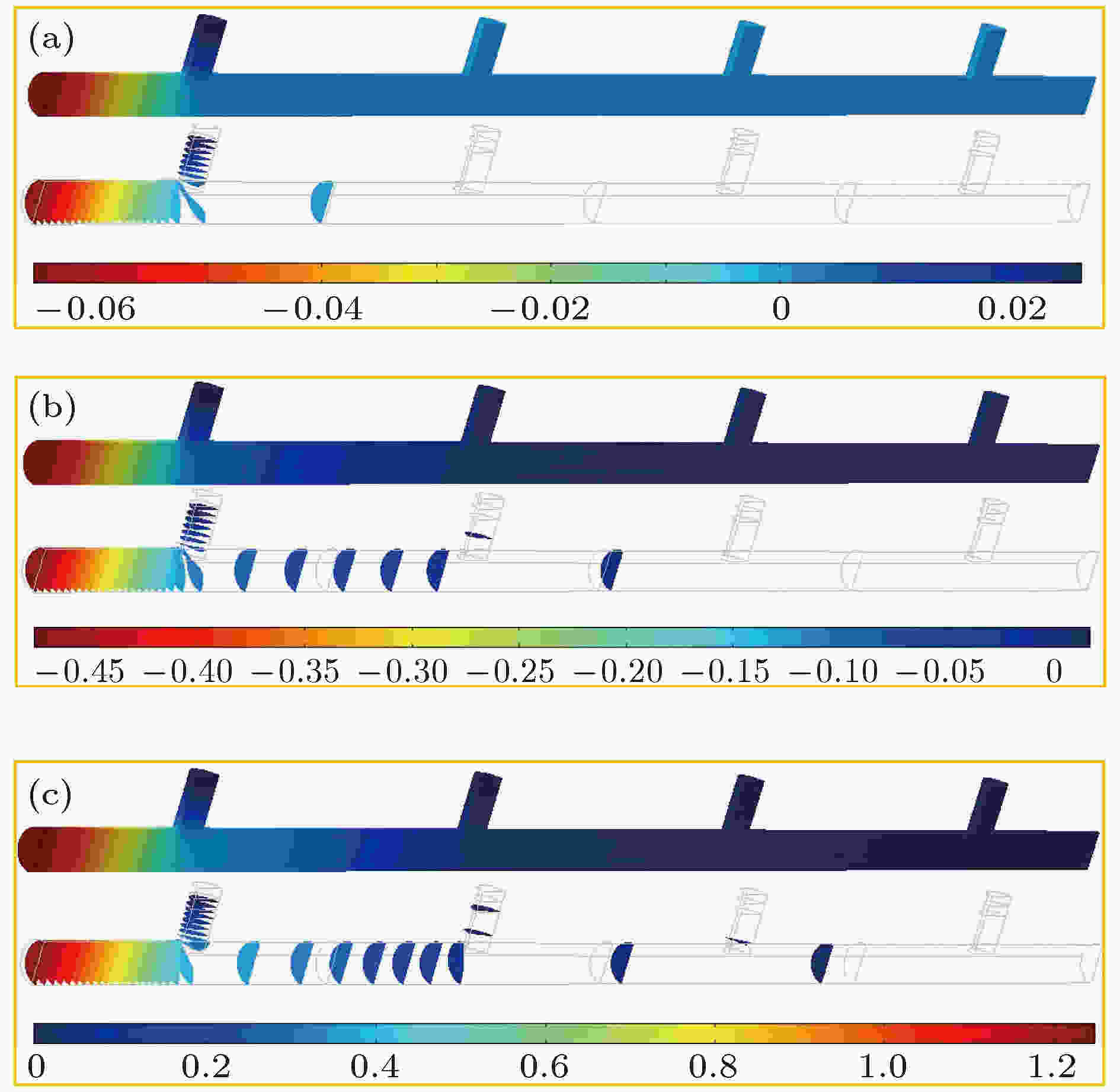图 4 带隙内若干频率处的管内声压分布图和等值面　(a) 34.5 Hz; (b) 95.5 Hz;(c) 305.5 Hz
Figure4. Acoustic pressure distributions and isosurfaces inside the dark metamaterial pipe, for several frequencies which located within the band gaps: (a) 34.5 Hz; (b) 95.5 Hz; (c) 305.5 Hz.

为对比暗声学超材料管的消声效果, 下面将声学短管的气液混合腔取代为液腔, 计算同样激励条件和边界条件下, 有限长周期管道的声传递损失, 如图5所示. 当声学短管为单纯的充液腔时, 它便构成了1/4波长管, 属于旁支消声器, 其共振频率f_p为(2n－1)c/4(l_g+l_f), n为自然数, 表示第n个共振模态. 在上述参数条件下, 该声学短管的第一个共振频率为3000 Hz, 这远大于气液混合腔情况下的34.5 Hz. 不过, 在图5中所关注频率范围出现了一个消声带隙, 该带隙其中一个带边频率约位于f_nB = nc/(2l_p)处(781.2 Hz, n =1), 最大衰减声压级不超过1.6 dB, 带宽也相对较窄. 事实上, 该带隙属于布拉格带隙, 其形成机理下文再进行阐述. 可见, 当声学短管为单纯的充液腔时, 虽然其在所关注频率范围也出现了消声带隙, 但在这样的小体积条件下该消声带隙的消声效果相当微弱. 相比而言, 图2所示的消声带隙不仅衰减声压级大, 而且频率低、带隙宽, 可谓是不折不扣的超宽低频强衰减带隙.
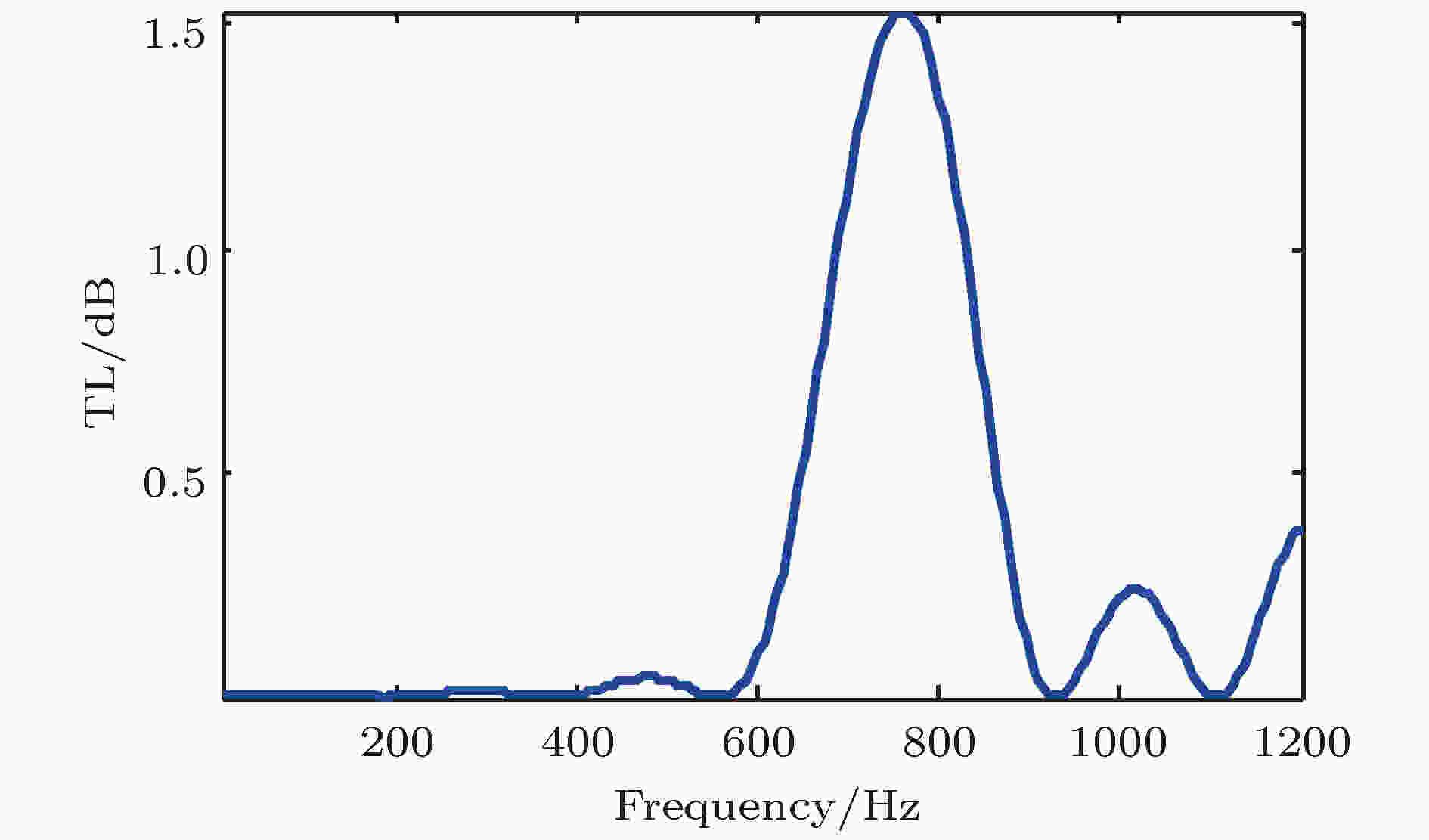图 5 充液声学短管周期管道的声传递损失
Figure5. The sound transmission loss for a fluid-filled pipe system with short acoustic pipes attached periodically.

下面探讨暗声学超材料管的消声带隙的形成机理. 在图2(a)和图2(b)所示的能带结构图中, 有两个声波带隙, 即22.9—465 Hz和781.2—1049 Hz, 其中第一个带隙的衰减因子在整个带隙频率范围内均比较大. 该带隙衰减因子在0.15以上的宽度可达440 Hz, 最大衰减系数位于声学短管的共振频率34.5 Hz处, 如图2(b)所示, 在该处出现了一个尖峰, 其峰值约为9.9. 事实上, 这个带隙可称为共振带隙, 它是声学短管的声波谐振与充液管内长波声波相互耦合共振诱导引起的声能耗散作用产生的. 作为极佳的声传播载体的管内介质, 在管道等间距引入低频大阻抗的气液混合腔声学短管后, 系统声阻抗发生变化, 使得原本的声传播模态被改变, 在充液管与声学短管间的介质内形成声学共振模态, 从而阻碍声波向下游管道传播. 定义管道引入声学短管带来的阻抗失配系数为Z_p/(2Z_H), 其中Z_p等于jρc/S_p. 阻抗失配系数随频率变化曲线如图6所示. 显然, 在声学短管的共振频率34.5 Hz处, 系统阻抗变化剧烈, 声阻抗急剧变化, 出现共振峰、反共振峰, 由此带来声学共振模态的骤变.
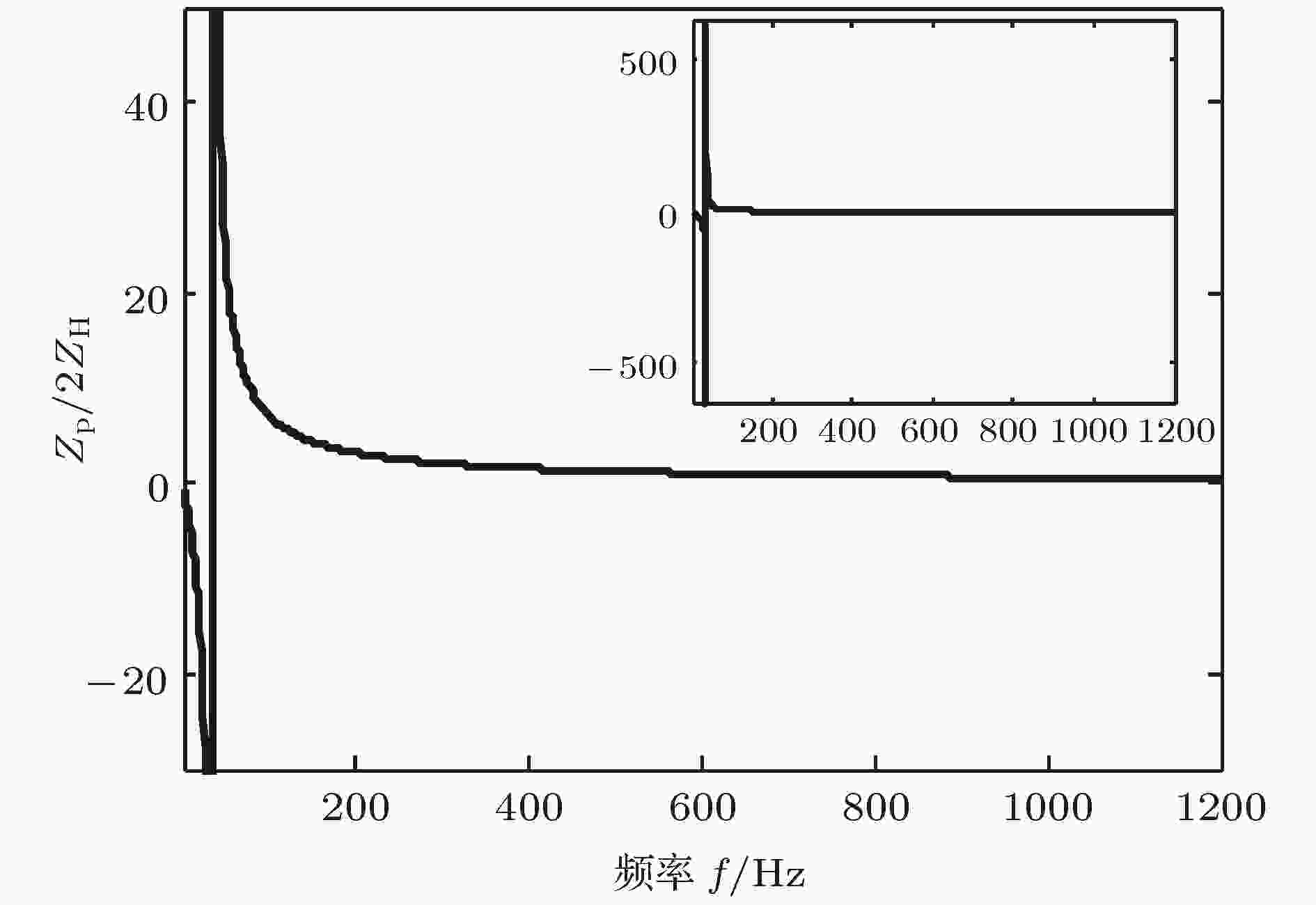图 6 气液混合腔声学短管的归一化阻抗
Figure6. The normalized acoustic impedance for the short pipe equipped with a gas-fluid hybrid chamber.

由于暗声学超材料管为空间周期结构, 故可以取其中一个周期元胞计算和分析其在不同频率点处的声学模态, 计算结果如图7所示. 图7(a)—(c)是共振频率以下频率范围若干频率点的声学模态, 而图7(d)—(f)是在共振频率之上若干频率点处的声学模态. 其中, 图7(a)和图7(f)的频率位于上下带边频率处. 从图7(a)和图7(f)可以看出, 在带边频率处, 声压以声学短管为中心在整个管道元胞呈对称分布模态. 在共振频率以下的带边声学模态, 其声压峰值位于声学短管内, 声压在整个管道元胞均有分布, 此时声波波长远大于声学短管几何尺寸. 在共振频率以上的带边声学模态, 其声压峰值位于主管道两端, 同样声波波长远大于声学短管几何尺寸. 从这两种带边声学模态可以知道, 声能尚不能在暗声学超材料管中形成有效衰减. 而在共振带隙频率范围内的声学模态, 譬如图7(b)和图7(c)的声学模态(处于带隙内且位于共振频率以下), 其声压在声学短管与声学短管一侧的主管道内形成剧烈的不对称共振模式, 声能在主管道一侧或声学短管内聚集, 这种模态将导致声能在管内共振耗散, 从而阻止声波向下游管道传播. 当频率越过共振峰后, 虽然声学共振模态发生了转变, 声压从声学短管一侧聚集转变成另一侧聚集, 如图7(d)和图7(e)所示. 但这种共振模态同样吸收了大部分声能, 抑制了声波传播. 可见, 共振带隙频率范围内的声能耗散的确是声学短管内的声波谐振与充液主管道内的声波长波相互耦合共振诱导作用引起的.
图 7 单个周期元胞在若干频率点处的声学模态
Figure7. Acoustic modes of the periodic pipe cell at several frequency points.

声学短管空间阵列的引入, 不仅与充液主管道内声波形成共振, 而且在声波传播的波导管内形成了波传播不连续结构, 并诱发反射波、透射波. 每两个声学短管间的反射波、透射波与入射波在一定频段内满足相消干涉条件而发生相消干涉, 且同一频率的声波相消干涉作用在不断重复的周期元胞内得到强化, 相消干涉效果得到增强, 从而诱发了图2中的第二个带隙的产生, 即781.2—1049 Hz. 该带隙称之位Bragg带隙, 其带边频率满足Bragg条件, 即f_nB = nc/2l_p, n表示第n条带隙. 在上述参数下, 当n = 1时, f_nB刚好为781.2 Hz, 位于第二个带隙的下带边. 可以预见, 当声学短管安装间距, 即晶格常数变长时, Bragg带隙将会向低频移动, 为实现低频Bragg带隙需要较大的安装间距才能实现.
图8所示为晶格常数变长时暗声学超材料管的声传递损失变化情况. 观察图中的第二条带隙, 可见随着l_p的增加, 其明显向低频移动. 但l_p的增加不仅影响了第二条带隙, 即Bragg带隙, 也影响了第一条带隙, 即共振带隙. 更贴切地说, l_p增加虽没有改变共振带隙的消声峰位置和带隙下带边频率, 但是使共振带隙上带边往低频移动, 从而缩减了第一带隙宽度. 究其变化原因, 也许可以从图7所示的单个周期元胞在第一带隙带边频率处的声学模态得到解答. 共振带隙下带边频率处的声学模态, 其声能主要集中在声学短管的气体腔, 能量从气体腔到液体腔及向两端的主管道液体逐渐减弱, 可见该模态频率起决定性作用的是声学短管的气体腔状态. 相反, 在共振带隙上带边频率处, 管道周期元胞声能则主要分布在主管道液体内, 声学短管内液体腔的能量相对薄弱, 特别是气体腔内, 声能微乎其微, 故而此声学模态频率主要取决于主管道的运动模态, 该模态与管内液体长度密切相关. 因此, 调节晶格常数l_p, 不仅仅是改变了Bragg带隙的位置, 还调节了共振带隙的上限位置, 即上带边频率, 如图9所示. 不过, 随着晶格常数的增长, 共振带隙上带边和Bragg带隙下带边的下降趋势变缓, 并且共振带隙上带边比Bragg带隙下带边的下降趋势要缓慢得多.
图 8 不同晶格常数下暗声学超材料管的声传递损失
Figure8. The sound transmission losses of the dark metamaterial pipe, for different lattice constants.

图 9 共振带隙上带边和Bragg带隙下带边随晶格常数的变化
Figure9. The curves for the upper edge of resonance gap and the lower edge of Bragg gap, as functions of the increased lattice constant.

如上述分析, 共振带隙下带边频率主要取决于声学短管的气体腔状态, 上带边频率与主管道管内液体长度密切相关. 调节晶格常数l_p, 仅仅改变了Bragg带隙位置和共振带隙的上限位置, 但未能有效改变共振带隙下带边频率. 我们通过改变声学短管的气体腔大小, 研究暗声学超材料管的消声特性变化情况. 不失一般性, 增长声学短管气体腔的长度l_g, 保持其他参数与初始参数一致, 计算暗声学超材料管的声传递损失函数曲线, 如图10所示. 由图可见, 声学短管气体腔的增大, 能使共振带隙的消声峰和下带边进一步向低频移动, 且保持上带边不动, 故而共振带隙能向低频域得到一定的展宽. 其实, 声学短管气液混合腔的情况下相当于亥姆霍兹共振器. 当频率足够低时, 其物理模型可视为弹簧质量振子系统或LC振荡电路. 通过声电类比, 可以知道声学短管的气体腔相当于LC振荡电路的电容, 即所谓的声容, 其值C_H可由V_cg/κ_g计算获得. 可见, 声学短管气体腔体积增大(声学短管气体腔长度增长)可使声容增大. 而声学短管的共振频率$f_{\rm{H}}=(2 {\text{π}})^{-1}\left(L_{\rm{H}} C_{\rm{H}}\right)^{-1 / 2}$与声容大小成反比, 所以随着l_g的加长, 共振频率f_H将有所降低, 从而使图中的消声峰和第一带隙下带边向低频进一步移动, 展宽第一带隙宽度和抑噪下限.
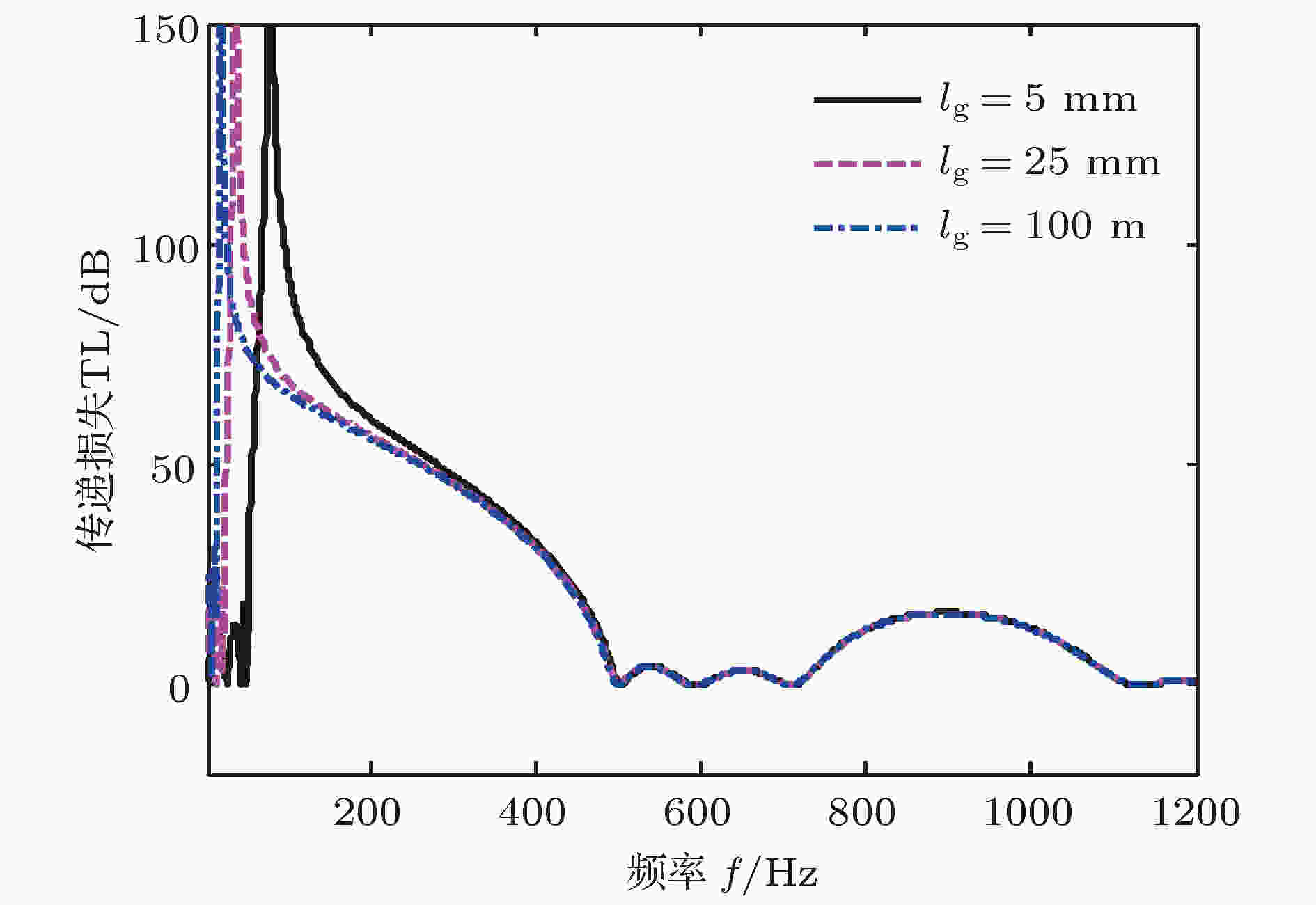图 10 不同充气腔长度下暗声学超材料管的声传递损失
Figure10. The sound transmission losses of the dark metamaterial pipe, for different lengths of gas-filled section of the attached short pipe.

同理, 声学短管的液体腔可视为LC振荡电路的电感, 即声抗, 其值L_H等于ρ_fl_fe/S_m. 因此, 声学短管液体腔体积的增大(此处为l_f加长)可使共振频率f_H降低, 如图11所示. 但因为此处的共振峰值已经很低了, 因此l_f的加长对f_H影响不是很大. 体现在图11中则是消声峰向低频移动效果不明显, 共振带隙下带边变化甚微, 但其上带边和第二带隙即Bragg带隙上带边频率变化明显, 而且消声带内消声量也有较大的改变. 第一带隙的变化特点可以回顾共振带隙的形成机理: 它主要由各个“局域共振单元(声学短管)”在一定频率的声波/弹性波激励下产生谐振并与基体弹性波长波行波相互作用导致的. 共振峰以上带隙频率范围的消声机理正是声学短管与主管道内的声波形成剧烈的声学谐振模态并进而引发管内声能耗散消声的. l_f加长将使两声学短管间的主管道内声波半波长谐振频率降低, 从而导致图中共振带隙的上带边随着l_f的增长向共振峰收拢; 反之, 当l_f变短将使共振带隙上带边向高频移动, 拓宽带宽. 类比弹簧质量振子, 声学短管液体腔具有一定的“质量”, 它相当于弹簧质量振子的质量块, 能抗拒由于声压脉动而引起的运动速度的变化. 当声学短管液柱变短时, 管内液体与声学短管气体腔声压发生“振动”的剧烈程度增加, 并使声能损耗能力增强, 消声带内消声量增大.
图 11 不同充液腔长度下暗声学超材料管的声传递损失
Figure11. The sound transmission losses of the dark metamaterial pipe, for different lengths of the fluid-filled section of the attached short pipe.

为更加贴合工程实际应用, 下面考虑在声学短管的液体腔和气体腔之间加一层橡胶隔膜, 研究加装橡胶隔膜对暗声学超材料管消声特性的影响情况, 如图12所示. 加装橡胶隔膜的声学短管示意图如图12右边插图所示. 计算中, 橡胶隔膜的杨氏模量、密度和泊松比分别取为400 MPa, 1200 kg/m³和0.3. 图中实线、点划线和虚线分别对应无隔膜、隔膜厚度t_r为3 mm和5 mm三种情况. 从图中可以看出, 在声学短管的液体腔和气体腔之间加装橡胶隔膜后, 暗声学超材料管的共振带隙和Bragg带隙的上带边均会略微向低频偏移, 但偏移微乎其微. 这是因为橡胶本身是一种与水中声波和空气声波阻抗匹配性良好的材料, 加之隔膜厚度较薄, 声波穿透性良好, 因此影响也较小. 我们认为该变化量可以忽略不计. 可以说, 加装橡胶隔膜后, 暗声学超材料管仍然保持了其良好的低频消声特性, 这也意味着本文所构建的暗声学超材料管结构在工程实际中实现的可能性.
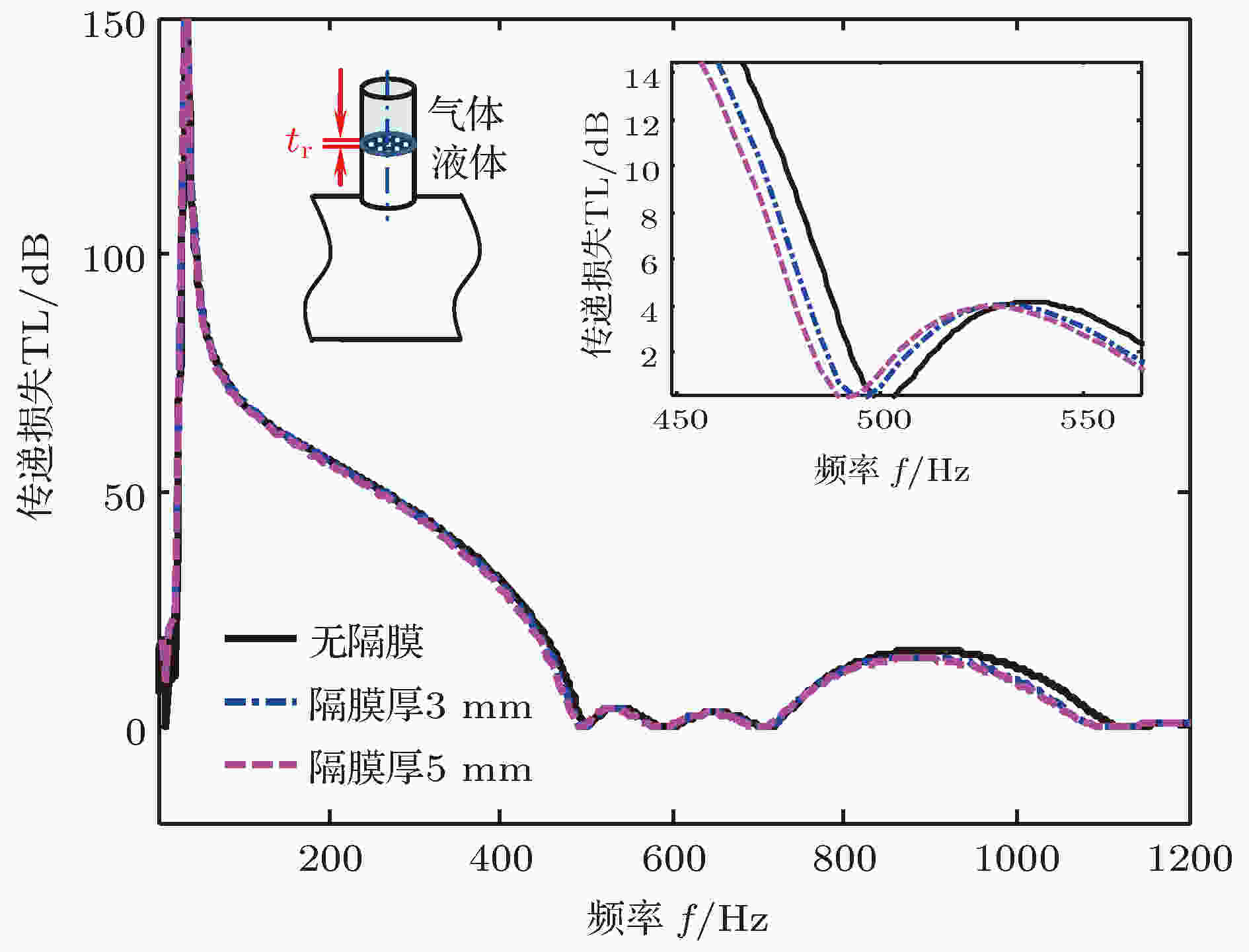图 12 声学短管液腔和气腔加橡胶隔膜条件下暗声学超材料管的声传递损失
Figure12. The sound transmission losses of the dark metamaterial pipe under the condition when a rubber membrane is installed to separate the liquid and gap inside the attached short pipe.

提出了一种具有超宽低频声波带隙的充液周期管道结构. 它由充有气体和液体的末端封闭的声学短管沿充液管道轴向等间距布置构成. 短管上半部分为气体腔, 下半部分为液体腔, 液体腔内液体与管内液体为同一介质且相连通. 带隙内对声波具有很强的衰减作用, 使得该管道末端的声接收器, 几乎接收不到声信号, 相当于声学“黑暗”, 因此称该充液周期管道为暗声学超材料型充液管道, 简称暗声学超材料管.
暗声学超材料管的消声带隙形成机理可以归结为声学短管内的声波谐振与充液管内长波声波相互耦合共振引起的声能耗散作用所产生. 因为在管道等间距引入低频大阻抗的气液混合腔声学短管后, 系统声阻抗发生空间周期变化, 这使得均质管中原本的声传播模态被改变. 在每两个声学短管间的管内液体介质中形成剧烈的声学共振模态. 这种空间周期剧烈共振模态耗散大部分声能, 从而抑制了声波在管内的传播. 同时, 该暗声学超材料管在频率稍高一些的频域还存在Bragg带隙, 这主要是因为声学短管空间阵列的引入, 除了在充液主管道内声波形成共振外, 还在管内形成了波传播的不连续结构, 并诱发反射波、透射波. 每两个声学短管间的反射波、透射波与入射波在一定频段内满足相消干涉条件而发生相消干涉, 且同一频率的声波其相消干涉作用在不断重复的周期元胞内得到强化, 相消干涉效果得到增强, 从而诱发了Bragg带隙的产生. Bragg带隙会随着晶格常数的增加, 向低频移动, 并影响共振带隙的下带边频率, 缩减第一带隙宽度. 调节晶格常数可以改变Bragg带隙位置和共振带隙的上限位置; 调节声学短管气体腔体积, 譬如增大气体腔, 能使共振带隙的消声峰和下带边进一步向低频移动, 且保持上带边不动, 从而使共振带隙向低频域展宽; 调节声学短管液体腔, 譬如增大液体腔可使共振频率降低, 从而影响消声峰位置. 不过, 增大液体腔降低共振频率的同时, 共振带隙上带边也会向低频移动, 而且移动幅度远比其下带边的变动值大得多, 这反而使共振带隙宽度减小, 带隙内噪声衰减程度减弱. 在声学短管的液体腔和气体腔之间加一层橡胶隔膜, 会使暗声学超材料管的共振带隙和Bragg带隙的上带边均会略微向低频偏移, 但影响较小. 也即加装橡胶隔膜后暗声学超材料管仍保持其低频消声特性. 加橡胶隔膜使气液腔在工程实际更容易构建.
总之, 本文所探讨的暗声学超材料管的低频消声特性、带隙形成机理和参数影响规律, 可以指导带隙的低频、宽带优化, 为管道低频噪声控制提供一条新的技术途径.