摘要:形状记忆合金在工程应用中的难点主要来自于系统在温度和外载荷作用下产生的复杂全局动力学行为. 本文以形状记忆合金薄板动力系统为研究对象, 分析在温度和激励振幅两个控制参数作用下系统的全局动力学. 通过全局分岔图, 可以观测到系统会发生复杂的激变现象, 然后利用复合胞坐标系方法, 获取系统的吸引子、吸引域、鞍和域边界等信息, 展现系统的全局演变过程. 研究发现, 系统随着振幅和温度变化会呈现复杂的全局结构, 并发生一系列的边界激变、合并激变现象, 同时多次发生分形-Wada, Wada-Wada, Wada-分形等域边界突变. 通过对指定区域细化, 可以清晰地显示域边界的分形特征. 研究结果对于如何通过调控温度与外载荷强度, 使形状记忆合金薄板在系统中发挥最佳性能具有理论指导意义.
关键词: 形状记忆合金/
全局动力学/
激变/
分形域边界

English Abstract

全文HTML

--> --> -->

形状记忆合金(shape memory alloy, SMA)表现出的独特力学性能来源于马氏体相变及其逆变化, 相变的驱动力可以由温度变化和机械载荷提供, 温度诱发的相变引起形状记忆效应, 外加应力诱导的相变产生超弹性. 利用这两个性质, SMA被制成各种参数可控的智能元件, 在机翼结构的变形、精密机械系统的高速驱动及机器人仿生等方面得到广泛应用^[1—5]. 目前关于SMA元件的力学性能研究主要集中在温度和载荷变化下SMA梁、振子及支架系统的平衡点稳定性、分岔行为及混沌现象等非线性动力学特征方面^[6—10], 对于SMA薄板系统的全局动力学研究较少, 相较于局部分析, 全局分析能够揭示更多的动力学信息^[11], 有利于从力学理论角度突破SMA薄板系统在机械驱动和振动控制等领域的局限性.
激变^[12,13]作为混沌系统中较为常见的全局分岔现象, 主要刻画了混沌吸引子和混沌鞍的不连续变化. 常见的激变包括边界激变、内部激变和合并激变. 边界激变是指混沌吸引子与吸引域边界上的不稳定周期轨道碰撞, 导致吸引子的突然消失. 内部激变是混沌吸引子与其所在吸引域内的不稳定周期轨道发生碰撞引起的. 合并激变是指两个及以上的吸引子同时与吸引域边界上的不稳定周期轨道发生碰撞, 合并形成新的吸引子. 尽管通过分岔图可以观测到激变现象, 但具体类型并不清楚, 需进一步绘制全局图进行判断. 近年来, 不少系统的激变现象均有所研究, 例如分数阶和单边碰撞系统^[14—17].
当系统中存在多个吸引子时, 吸引域边界可以是光滑的, 也可以呈现出“你中有我, 我中有你”的分形结构. 如果吸引子的个数为三个及以上, 且边界上任一点的任意小领域, 覆盖三个及以上吸引域, 则称此域边界具有Wada特性. 随着系统参数变化, 域边界结构会突然发生改变, 称为域边界突变, 包括光滑-Wada域边界突变、分形-Wada域边界突变和Wada-Wada域边界突变等. 域边界突变作为混沌动力学的一个研究重点, 对于确定系统的整体结构具有重要的物理意义, 在非光滑系统和准周期强迫系统^[18,19]中都有所研究, 但分形性使得动力系统的力学行为很难预测, 随着胞映射技术的发展, 域边界突变和激变现象的研究得到了突破. 其中经典的广义胞映射、图胞映射、插值胞映射等方法均可获得系统的全局信息^[20—22], 但在刻画域边界时有一定的局限性. 复合胞坐标系方法通过对连续相空间的多级分割构造一个复合胞空间, 基于点映射的原理, 不仅可以获取动力系统的吸引子、吸引域和鞍等信息, 还能细化任意小区域, 在全局图中优化对域边界的刻画.
本文以SMA薄板动力系统为研究对象, 温度和外部激励的振幅为分岔参数, 在全局分岔图的基础上, 通过复合胞坐标系方法进一步分析系统在演变过程中出现的激变类型和域边界突变现象, 并通过对指定区域的细化, 展示域边界的分形特征. 研究结果在工程领域中对控制系统的动态响应有重要意义.

在SMA薄板中, 相对于奥氏体, 马氏体更具延展性, 当外加应力低于马氏体的屈服强度时, SMA薄板可表现出超弹性. 马氏体的转变与温度相关, 低温相称为马氏体, 高温相称为奥氏体, 降温时SMA薄板发生马氏体相变, 呈现形状记忆效应. 定义T_M为马氏体相变临界温度, 该温度之下, 马氏体稳定; T_A为奥氏体相变临界温度, 该温度之上, 奥氏体稳定, a, b, c均为材料常数, 满足:

${T_{\rm{A}}} = {T_{\rm{M}}} + \frac{{{b^2}}}{{4ac}}.$

根据Falk ^[23]的研究, SMA薄板的本构模型可以由一个五次多项式表示, 该模型给出了应变(ε)-应力(σ)的关系:

$\sigma = a(T - {T_{\rm{M}}})\varepsilon - b{\varepsilon ^3} + c{\varepsilon ^5}.$

Savi等^[10,24]给出了很多关于SMA弹簧振子的数学模型, 文献[25]在此基础上演变出SMA薄板横向振动的非线性动力学模型. 本文考虑密度ρ, 厚度h, 长宽分别为l₁, l₂的SMA薄板, 在环境黏性阻尼e下, 受到横向简谐激振力F₀ = FsinΩt作用, 如图1所示.
图 1 SMA薄板的横向振动
Figure1. Transverse vibration of SMA thin plate.

薄板的横向位移为w (x, y, t), 单位长度上的内力矩分别为U_x(x, y, t), U_y(x, y, t), U_xy(x, y, t), 其横向振动方程为^[25]

$\frac{{{\partial ^2}{U_x}}}{{\partial {x^2}}} + 2\frac{{{\partial ^2}{U_{xy}}}}{{\partial x\partial y}} + \frac{{{\partial ^2}{U_y}}}{{\partial {y^2}}} + {F_0} - e\dot w - \rho h\frac{{{\partial ^2}w}}{{\partial {t^2}}} = 0.$

薄板面内的3个应力分别为σ_x, σ_y, τ_xy, 内力矩为^[25]

$\begin{array}{l}{U_x} = \displaystyle\int_{{{ - h} / 2}}^{{h / 2}} {{\sigma _x}z{\rm{d}}z},\; {U_y} = \displaystyle\int_{{{ - h} / 2}}^{{h / 2}} {{\sigma _y}z{\rm{d}}z},\\{U_{xy}} = \displaystyle\int_{{{ - h} / 2}}^{{h / 2}} {{\tau _{xy}}z{\rm{d}}z} .\end{array}$

在满足四周简支边界条件下取位移模式^[25]:

$w(x,y,t) = W(t)\sin \frac{{{\text{π}}x}}{{{l_1}}}\sin \frac{{{\text{π}}y}}{{{l_2}}}.$

通过Galerkin原理和应变-应力本构关系, 并对系统参数量纲归一化, 得到SMA薄板的横向振动非线性动力学方程^[25]:

$\ddot W + \xi \dot W + \alpha (\theta - 1)W - \beta {W^3} + \gamma {W^5} = g{\rm{sin}}\varOmega t.$

方程(6)可化为以下形式的一阶微分方程组:

$\left\{ \begin{array}{l} \dot x = y, \\ \dot y = - \xi y - \alpha (\theta - 1)x + \beta {x^3} - \gamma {x^5} + g{\rm sin}\varOmega t, \\ \end{array} \right.$

其中α, ξ, β, γ均为正常数; θ, g分别是无量纲化的温度和简谐激振力振幅. 参数选取同文献[24]所示, ξ = 0.2, α = 1, β = 1300, γ = 470000, Ω = 1. 接下来基于复合胞坐标系方法, 分析温度θ和激励振幅g两个参数变化时, SMA薄板系统的全局动力学特性变化过程.

当温度θ = 0.7, 此时SMA薄板位于马氏体临界温度下, 含有两个稳定的马氏体相. 选取不同的初值点(–0.0553, –0.09), (–0.031, 0.045), (0.083, –0.032), (0.047, 0.059)构造Poincare映射, 保留稳态映射点, 得到对应的多值分岔图, 如图2所示. 随着幅值g值的变化, 系统呈现明显的多吸引子共存特征, 并伴随有丰富的激变和域边界突变等现象.
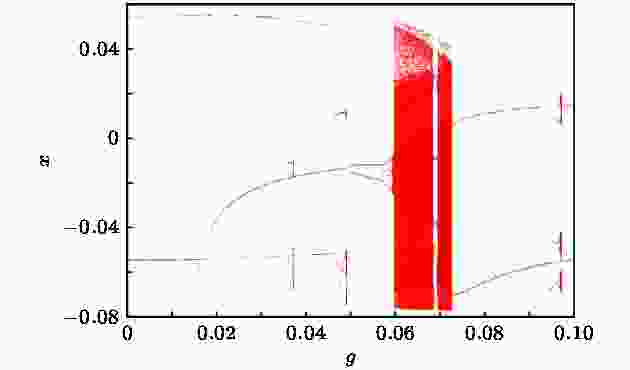图 2 系统(7)随振幅g变化的多值分岔图
Figure2. Multivalued bifurcation diagram of the system (7) with the variation of amplitude g.

在区域D = {(x, y)|–0.1 ≤ x ≤ 0.1, –0.12 ≤ y ≤ 0.12}上, 均匀划分1000 × 1200个胞, 利用复合胞坐标系方法获取系统的吸引子、吸引域和边界鞍等全局信息, 阐述g在0.0460到0.0727的范围内激变现象出现的机理. 为更直观理解全局图, 对以下图形做以下说明: 用△表示吸引子A, 不同颜色代表不同的吸引子; 吸引域用B表示, 不同吸引域颜色不同; S表示边界鞍; IS表示吸引域内部鞍; 下标表示吸引子、吸引域和内部鞍的个数, 例如A₁, A₂表示系统两个吸引子共存, B₁, B₂为其对应的吸引域.
2

-->

3.1.边界激变

当g从0.0471增大到0.0472时, 发生两次逆的边界激变, 如图3所示. A₅和A₆表示周期为2的吸引子, A₅与嵌在吸引域B₁, B₅边界的鞍S碰撞, A₆和嵌入吸引域B₂, B₆边界的鞍S碰撞, 使得A₅, A₆和部分边界鞍S突然消失, 成为内部周期鞍IS₁, IS₂, 同时吸引域B₅, B₆消失, 吸引域B₁, B₂变大.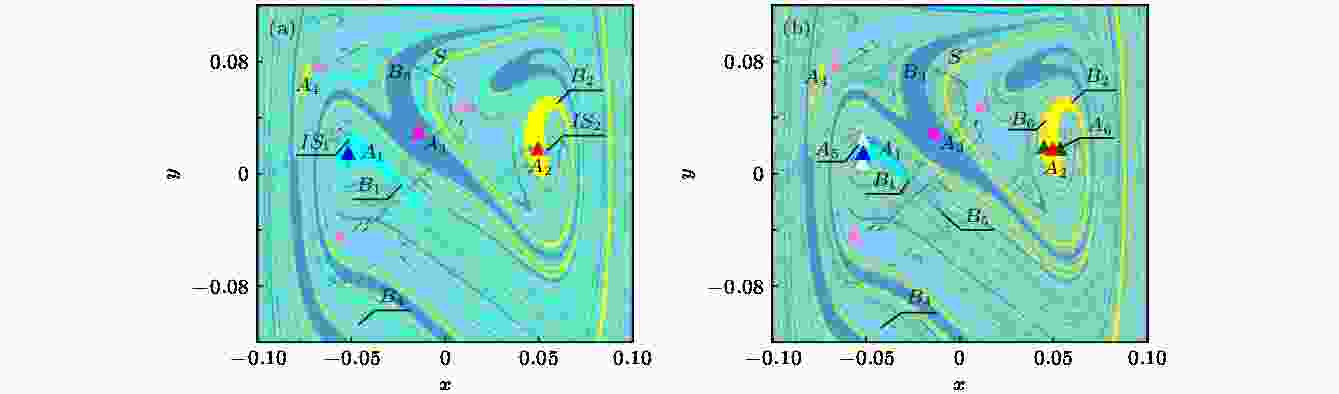
图 3 系统(7)的全局图　(a) g = 0.0471; (b) g = 0.0472
Figure3. Global diagram of the system (7): (a) g = 0.0471; (b) g = 0.0472.

当g从0.0482变化到0.0483时, 系统再次发生两次边界激变, 两个周期1吸引子A₁和A₂与边界上的鞍S发生碰撞, 变为吸引域B₅, B₆的内部鞍IS₅, IS₆, 同时吸引域B₁和B₂消失, 如图4所示.
图 4 系统(7)的全局图　(a) g = 0.0482; (b) g = 0.0483
Figure4. Global diagram of the system (7): (a) g = 0.0482; (b) g = 0.0483.

当g从0.0491增大到0.0492时, 混沌吸引子A₂与吸引域边界上的混沌鞍S发生碰撞, 发生边界激变, 变成新的更大的边界混沌鞍, 吸引域B₂随之消失, 状态空间中为四个周期吸引子和混沌边界鞍共存, 如图5所示.
图 5 系统(7)的全局图　(a) g = 0.0491; (b) g = 0.0492
Figure5. Global diagram of the system (7): (a) g = 0.0491; (b) g = 0.0492.

3 -->

3.2.合并激变

当g从0.0490变化到0.0491时, 混沌吸引子A₂和A₄不断接近吸引域边界上的混沌鞍S, 发生合并激变, 成为新的混沌吸引子A₂, 与此同时吸引域B₂, B₄合并为新的吸引域B₂, 如图6所示.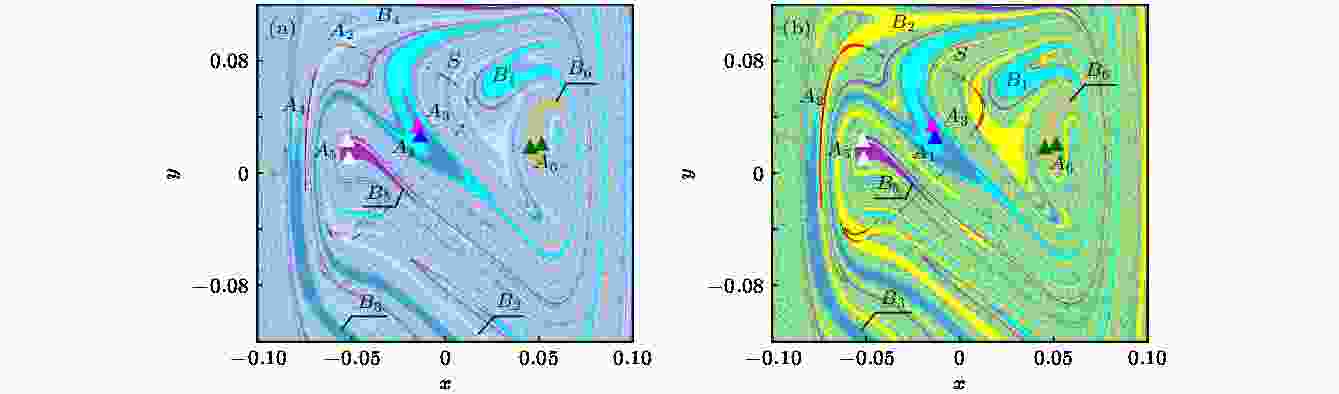
图 6 系统(7)的全局图　(a) g = 0.0490; (b) g = 0.0491
Figure6. Global diagram of the system (7): (a) g = 0.0490; (b) g = 0.0491.

当g从0.0596变化到0.0597时, 混沌吸引子A₁, A₂与边界上的混沌鞍S碰撞, 发生合并激变, 变为新的混沌吸引子A₁, 如图7(a)和图7(b)所示. 当g从0.0726增大到0.0727时, 发生逆合并激变, 混沌吸引子A₁消失, 出现两个新的周期1吸引子A₁, A₂及混沌边界鞍S, 如图7(c)和图7(d)所示.
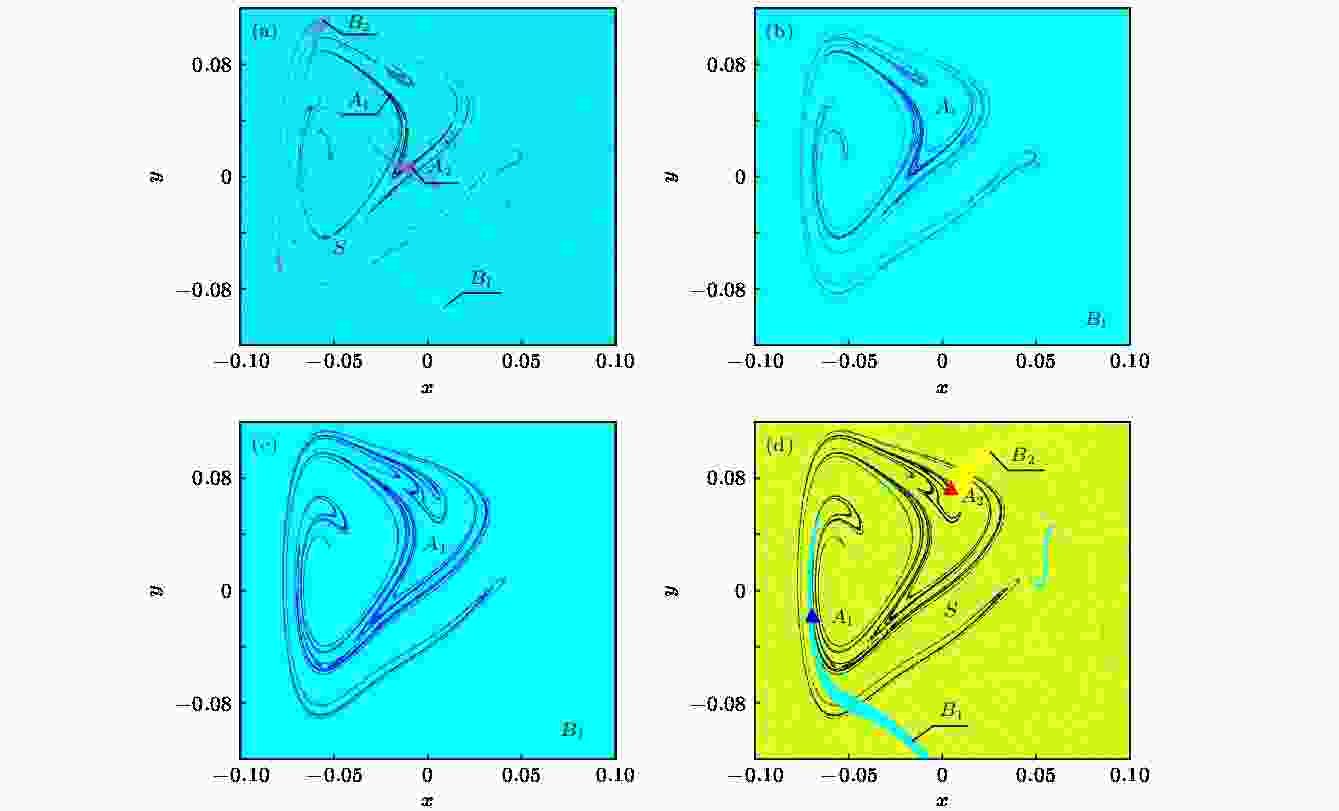图 7 系统(7)的全局图　(a) g = 0.0596; (b) g = 0.0597; (c) g = 0.0726; (d) g = 0.0727
Figure7. Global diagram of the system (7): (a) g = 0.0596; (b) g = 0.0597; (c) g = 0.0726; (d) g = 0.0727.

2 -->

3.3.域边界突变

当g = 0.0460时, 系统存在三个周期1吸引子A₁, A₂, A₃和嵌在吸引域B₁, B₂, B₃边界上的混沌鞍S, 此时的域边界呈现出Wada特性. 当g增大到0.0461时, 系统新出现一个周期3吸引子A₄, 此时的域边界由4个吸引域构成, 仍具有Wada特性, 系统发生Wada-Wada域边界突变, 如图8所示.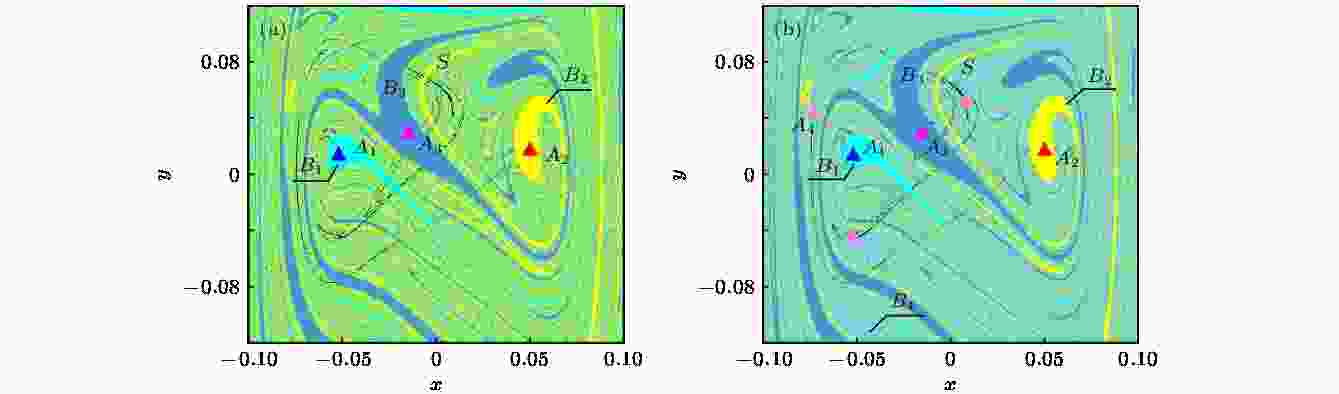
图 8 系统(7)的全局图　(a) g = 0.0460; (b) g = 0.0461
Figure8. Global diagram of the system (7): (a) g = 0.0460; (b) g = 0.0461.

当g从0.0478增大到0.0479时, 吸引子的个数从6个变为7个, 为判断吸引子变化过程, 对区域v ={(x, y)|–0.075 ≤ x ≤ –0.055, 0.068 ≤ y ≤ 0.092}进行细化. 可以发现, 原周期3吸引子A₄消失, 并在其附近出现两个新的周期3吸引子A₄和A₇, 如图9(c)和图9(d). 原吸引域B₄分裂为新吸引域B₄和B₇, 且参数变化前后域边界均呈现Wada特性, 域边界结构更加复杂, 系统再次发生Wada-Wada域边界突变.
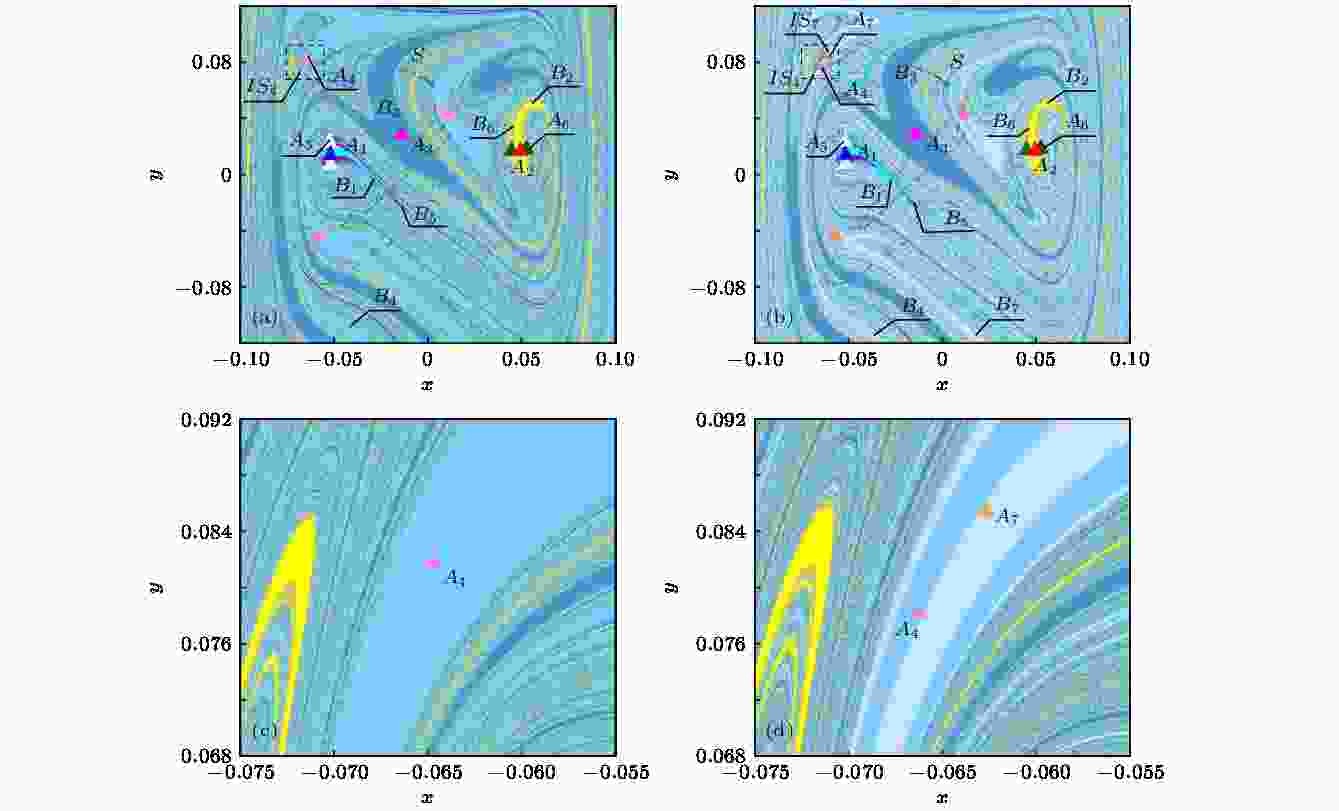图 9 系统(7)的全局图　(a) g = 0.0478; (b) g = 0.0479; (c), (d) 分别对应于(a), (b)图的区域细化
Figure9. Global diagram of the system (7): (a) g = 0.0478; (b) g = 0.0479; (c), (d) the region refinement of panels (a) and (b).

当g = 0.0533时, 状态空间中有4个周期1吸引子共存, 此时域边界仍具有Wada特性. 当g增大到0.0534时, 周期吸引子A₃和A₄消失, 状态空间中仅剩2个周期1吸引子A₁, A₂, 此时域边界的Wada特性消失, 只呈现分形特性, 系统发生Wada-分形域边界突变, 如图10所示.
图 10 系统(7)的全局图　(a) g = 0.0533; (b) g = 0.0534
Figure10. Global diagram of the system (7): (a) g = 0.0533; (b) g = 0.0534.

温度作为SMA薄板的一个可控参数, 利用温度改变SMA薄板的力学特性在工程领域中有重要运用. 取g为0.06, 分析温度θ变化对系统的影响, 选取不同的初值点(–0.0553, –0.09), (–0.031, 0.045), (0.083, –0.032), (0.047, 0.059)构造Poincare映射, 得到对应的分岔图, 如图11所示. 可以发现, 随温度θ的变化, 系统中吸引子个数、类型及大小会发生改变, 并出现激变现象. 为从全局角度分析温度变化对系统激变的影响, 本节基于复合胞坐标系方法, 将区域D = {(x, y)| –0.1 ≤ x ≤ 0.1, –0.12 ≤ y ≤ 0.12}, 均匀划分为1000 × 1200个胞, 获得系统的吸引子、吸引域、鞍和域边界等全局特性.
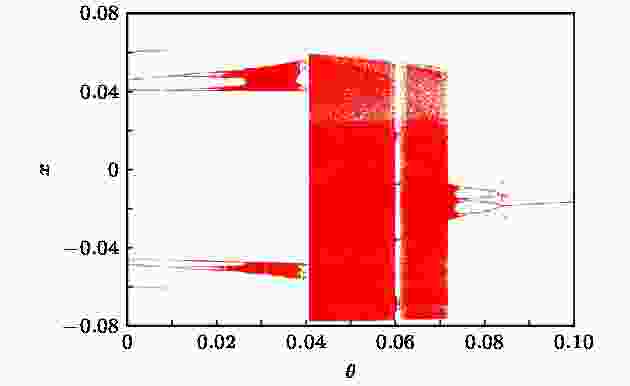图 11 系统(7)随温度θ变化的多值分岔图
Figure11. Multivalued bifurcation diagram of the system (7) with the variation of temperature θ.

2

-->

4.1.边界激变

当θ = 0.8379时, 状态空间中两个周期1吸引子A₁和A₂共存, S为嵌入在分形域边界上的混沌鞍, IS₁, IS₂是吸引域B₁, B₂内部的混沌鞍. 当θ增大为0.8380时, 系统出现两个新的吸引子A₃和A₄, 内部鞍IS₁, IS₂消失, 系统发生两次逆边界激变, 如图12所示.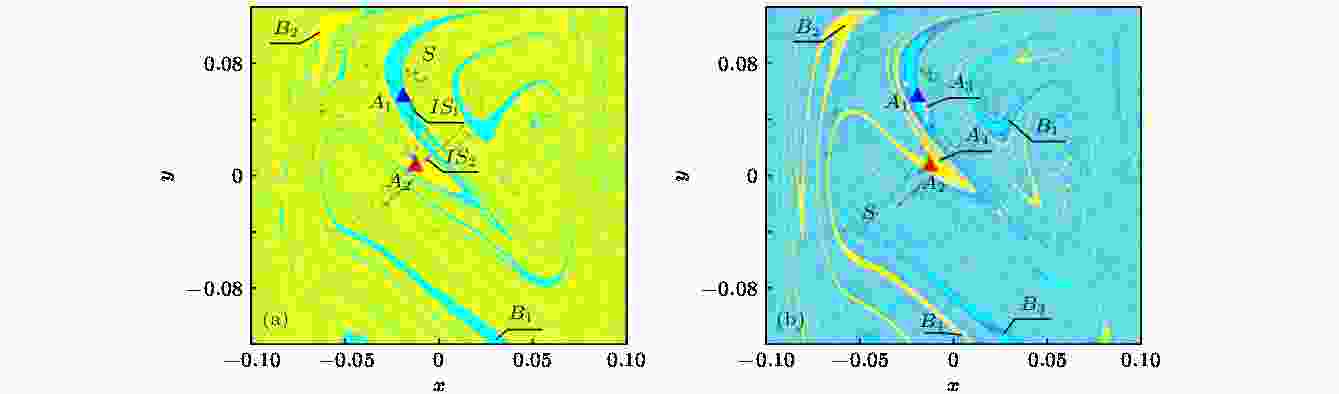
图 12 系统(7)的全局图　(a) θ = 0.8379; (b) θ = 0.8380
Figure12. Global diagram of the system (7): (a) θ = 0.8379; (b) θ = 0.08380.

2 -->

4.2.合并激变

当θ从0.4088变化到0.4089时, 周期2吸引子A₁和A₂同时与域边界上的混沌鞍S发生碰撞, 合并为一个新的混沌吸引子A₁, 吸引域B₁和B₂合并成为新吸引域B₁, 系统发生合并激变, 如图13(a)和图13(b)所示. 当θ从0.7182增大到0.7183时, 混沌吸引子A₁消失, 出现两个新的混沌吸引子A₁和A₂, 以及嵌在域边界上的混沌鞍S, 系统发生逆的合并激变, 如图13(c)和图13(d)所示.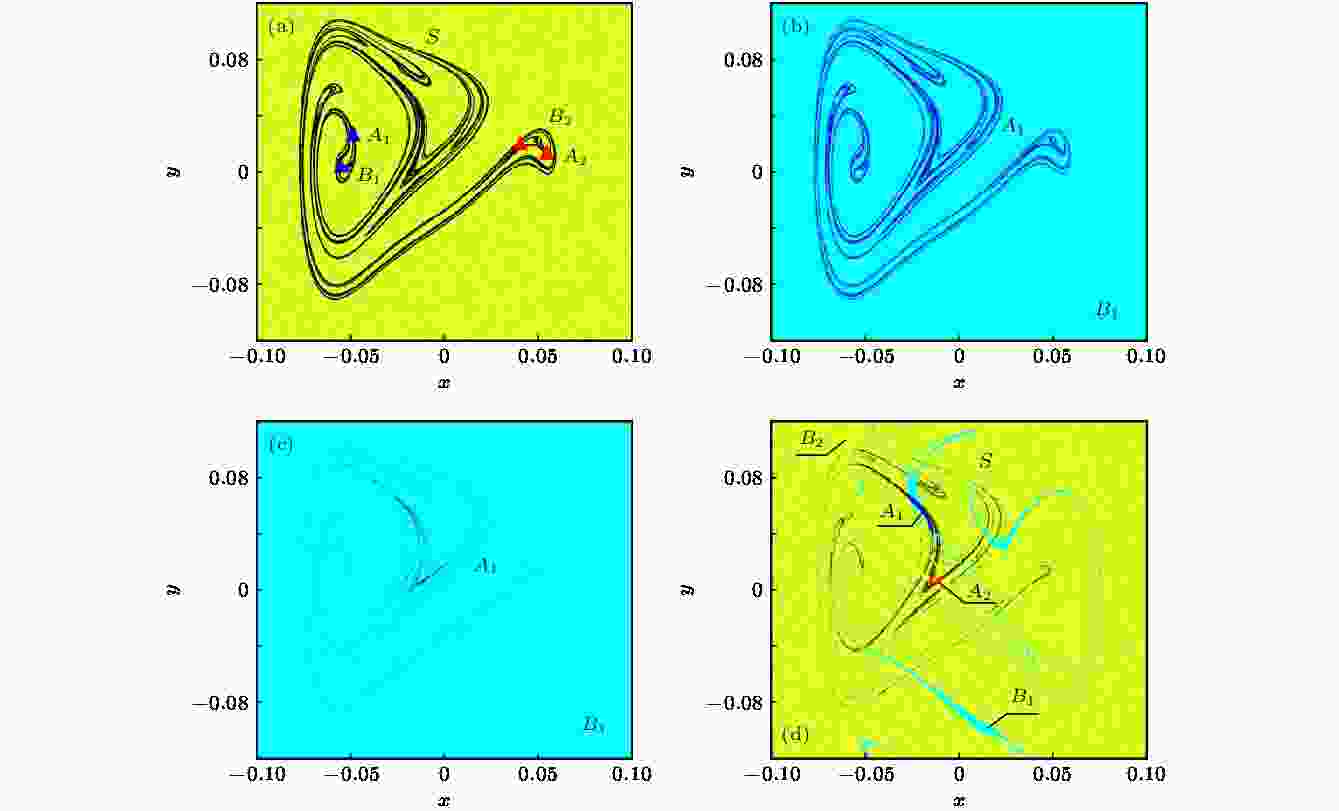
图 13 系统(7)的全局图　(a) θ = 0.4088; (b) θ = 0.4089; (c) θ = 0.7182; (d) θ = 0.7183
Figure13. Global diagram of the system (7): (a) θ = 0.4088; (b) θ = 0.4089; (c) θ = 0.7182; (d) θ = 0.7183.

2 -->

4.3.域边界突变

当g = 0.0950时, 状态空间中两个周期2吸引子A₁, A₂, 和两个周期1吸引子A₃, A₄共存, 吸引域边界呈现Wada特性. 当g增大为0.0951时, 两个周期1吸引子A₃和A₄消失, 吸引域边界变为由B₁和B₂构成的分形边界, 系统发生Wada-分形域边界突变, 如图14所示.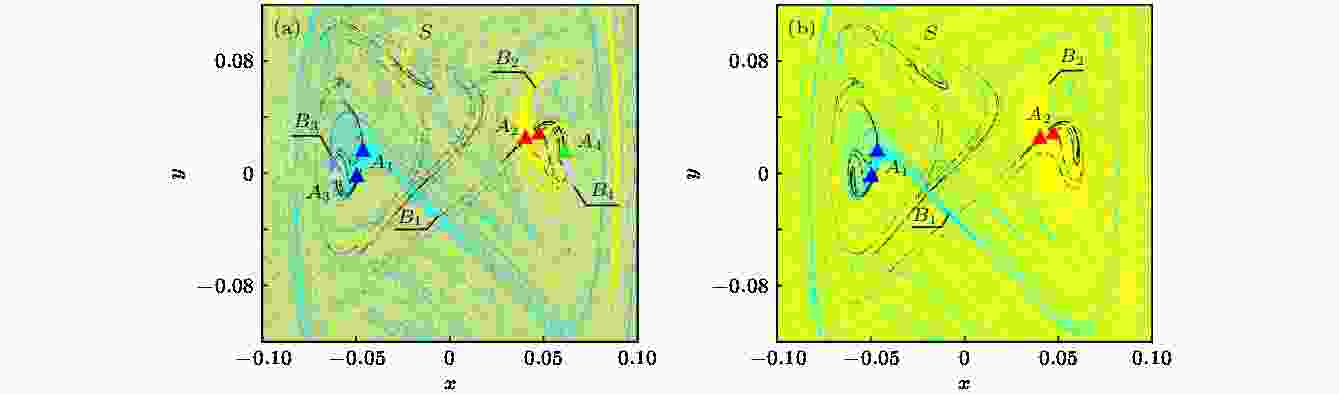
图 14 系统(7)的全局图　(a) θ = 0.0950; (b) θ = 0.0951
Figure14. Global diagram of the system (7): (a) θ = 0.0950; (b) θ = 0.0951.

考虑实际工程中温度和应力对于SMA的力学特性的影响, 本文选取SMA薄板为研究对象, 以温度θ和激振力振幅g作为分岔参数, 采用复合胞坐标系方法分析其全局分岔特性, 探究在参数的连续变化下, 系统激变现象及域边界突变的演化过程.
在一定的参数变化范围内, 系统呈现丰富的激变现象, 如周期或混沌吸引子与域边界上的周期鞍或混沌鞍发生碰撞的边界激变, 周期吸引子或混沌吸引子同时与边界上的混沌鞍发生碰撞的合并激变等. 当多吸引子共存时, 域边界会呈现分形结构, 并随着参数的变化, 发生Wada-Wada, Wada-分形和分形-Wada等域边界突变现象. 本文的研究结果对于通过控制温度和激励强度等参数, 调控SMA薄板系统的动态响应, 优化机械设备的变形及振动控制等问题上提供有效的分析手段.