摘要:在杂化密度泛函水平上, 利用响应函数方法, 计算了一类四苯基乙烯衍生物的双光子吸收性质. 考虑了四苯基乙烯上给电子基团的位置和数目对双光子吸收性质的影响. 并且, 根据实验者采用的分子, 通过增加分子的平面性和共轭长度, 以及增强给体强度, 理论设计了三种分子结构, 并计算了它们的双光子吸收性质. 结果表明, 给体位置和数目对双光子吸收性质有重要影响. 位于分子末端的给体取代基能有效提高双光子吸收强度. 随着给体数目的增加, 双光子吸收波长发生红移. 在四苯基乙烯的不同侧位上添加给体取代基对双光子吸收性质的影响有明显差异. 与实验者采用的分子相比, 理论设计的分子结构双光子吸收截面均明显增大. 当三苯胺基代替四苯基乙烯基之后, 双光子吸收峰发生较大红移, 双光子吸收截面明显增大.
关键词: 四苯基乙烯/
双光子吸收/
给体位置/
给体数目

English Abstract

全文HTML

--> --> -->

近年来, 许多同时具有双光子吸收(two-photon absorption, TPA)和聚集诱导发光(aggregation-induced emission, AIE)特性的化合物被合成, 并且已经应用于双光子荧光显微成像、上转换激射和光动力学治疗等领域^[1-10]. Kim等^[2]首先报道了一种具有TPA和AIE特性的染料分子^[1], 并成功地用于双光子荧光细胞成像. 对于此类分子材料, 不仅要求具有强的TPA, 还要求在高浓度下能够克服荧光猝灭现象^[1]. 一方面, 为了增强TPA, 在分子设计中经常引入给电子基团(donor, D)或吸电子基团(acceptor, A). 已有的研究表明, 增强分子内电荷转移可以提高TPA强度^[11,12]. 另一方面, 为了产生足够强度的荧光, 基于分子内旋转受限机制^[13,14], 具有特殊螺旋桨结构的四苯基乙烯(tetraphenylethylene, TPE)和三苯胺基团经常出现在TPA和AIE材料中^[3-8]. 它们不仅具有良好的电子给予能力, 而且其结构在聚集状态下可以有效避免紧密堆积和荧光猝灭现象. Hu等^[3]和Zhang等^[4]发现, 一类由TPE构成的材料显示出优异的TPA和AIE特性. Jiang等^[5]和Wang等^[6]合成了一系列含有三苯胺基团的多枝分子, 这些分子均有较强的TPA, 同时也具有AIE特性. 尽管目前实验者已经合成了许多具有AIE特性的TPA材料, 但据我们所知, 相关的理论研究还非常少^[1,15,16]. 在我们以前的工作中, 理论研究了一组TPE衍生物的TPA性质, 分析了二聚化和异构对TPA性质的影响, 并且理论设计了一系列具有强TPA性质的TPE衍生物分子^[15].
对于含有TPE基团的TPA和AIE材料, 实验者通常在TPE上添加给电子基团以增强TPA强度, 而给体的取代位置和数目存在多种可能. 不同的取代方式可以产生不同的多枝结构, 分枝之间的相互作用对非线性光学响应具有重要影响^[17,18]. 因此, 需要研究给体的位置和数目对TPA性质的影响. 虽然给体或受体强度对TPA性质的影响已经被广泛研究, 但是关于给体或受体位置和数目对TPA性质影响的研究还很少^[19]. Chattopadhyaya等^[19]研究了一系列给体/受体取代的双蔥分子的TPA性质, 发现添加三对给体/受体的双蔥分子的TPA强度比具有特定排列的一对给体/受体的双蔥分子小. 他们的结果清楚地表明, 增加给体/受体基团的数目不一定增强体系的TPA强度. 据我们所知, TPE基团上给体位置和数目对TPA性质影响的研究还未见报道.
最近, Gu等^[10]合成了一种新的光敏剂TPEDC分子. 该分子具有强TPA和荧光, 可以用于光动力学治疗. TPEDC分子含甲氧基、TPE和氰基基团, 具有D-共轭桥(π)-A型分子结构. 以TPEDC分子为模型, 我们研究了给体位置和数目对TPA性质的影响. 并且, 在研究结果的基础上, 根据具有AIE特性的分子结构特点, 综合考虑了结构与TPA性质之间的关系, 理论设计了具有更大TPA截面的分子结构, 为实验者合成具有TPA和AIE特性的功能材料提供了理论指导.

当忽略非共振吸收影响时, 双光子跃迁矩阵元${S_{\alpha \beta }}$可表示如下^[20]:

${S_{\alpha \beta }} = \sum\limits_s {\left[ {\frac{{\left\langle 0 \right|{\mu _\alpha }\left| s \right\rangle \left\langle s \right|{\mu _\beta }\left| f \right\rangle }}{{{\omega _s} - \omega }} + \frac{{\left\langle 0 \right|{\mu _\beta }\left| s \right\rangle \left\langle s \right|{\mu _\alpha }\left| f \right\rangle }}{{{\omega _s} - \omega }}} \right]} ,$

式中${\mu _{\alpha (\beta )}}$是电偶极矩算符; $\alpha $和$\beta $分别代表分子的x, y, z轴; $\left| 0 \right\rangle $和$\left| f \right\rangle $表示初态和末态. 假设共振条件是$2\omega = {\omega _{\rm f}}$, 其中$\omega $是激光的频率, $\hbar {\omega _{\rm f}}$是末态的激发能, 求和包含所有的电子态(包括初态、末态和所有中间态), $\hbar {\omega _s}$表示中间态$\left| s \right\rangle $的激发能.
采用响应函数方法^[21]来计算双光子跃迁矩阵元. 响应函数方法是一种含时微扰方法. 在该方法中, 双光子跃迁矩阵元可以通过二次响应函数的留数得到

$\mathop {\lim }\limits_{\omega \to {\omega _{\rm f}}} \left( {{\omega _{\rm f}} - \omega } \right){\left\langle {\left\langle {{\mu _\alpha };{\mu _\beta },{\mu _\gamma }} \right\rangle } \right\rangle _{(1/2){\omega _{\rm f}},\omega }} = {S_{\alpha \beta }}\left\langle f \right|{\mu _\gamma }\left| 0 \right\rangle ,$

其中${\mu _\gamma }$是电偶极矩算符; $\gamma $代表分子的x, y或z轴.
当单色偏振光激发分子材料时, 微观TPA截面$\delta $可表示为^[22]

$\delta = \sum\limits_{\alpha ,\beta } {\left( {2{S_{\alpha \alpha }}S_{\beta \beta }^ * + 4{S_{\alpha \beta }}S_{\alpha \beta }^ * } \right)} ,$

从而可以得到与实验测量结果相比较的TPA截面^[22]:

$\sigma = \frac{{4{{\text{π}}^2}a_0^5\alpha }}{{15c}}\frac{{{\omega ^2}}}{{{\varGamma _{\rm{f}}}}}\delta ,$

式中${a_0}$是玻尔半径; $\alpha $是精细结构常数; c是真空中光速; $\omega $是入射光频率; ${\varGamma _{\rm{f}}}$是与末态寿命有关的末态能级展宽, 采用一个通常的值, ${\varGamma _{\rm{f}}} = 0.1\;{\rm{eV}}$. TPA截面的单位是GM, 1 GM = 10^–50 cm⁴·s/photon.
应用Gaussian16^[23]程序包, 在杂化密度泛函B3LYP的水平上, 采用6-31g(d, p)基矢, 对所有分子结构进行了几何优化. 在CAM-B3LYP泛函的水平上, 采用6-31g(d)基矢, 在Dalton2013^[24]程序包中计算了分子的TPA截面. 并且, 通过极化连续模型考虑了水溶剂的影响. 我们曾应用B3LYP泛函计算过各种类型分子的TPA性质^{[15,16,25-29]}, 因此, 也采用B3LYP泛函计算了TPA截面. 发现两种泛函的计算结果相对趋势是一致的, 可以得到基本一致的结论. 对于电荷转移分子, CAM-B3LYP泛函由于考虑了长程修正, 原理上计算结果更准确, 近年来被广泛使用. 因此, 本文均采用CAM-B3LYP泛函计算TPA性质.

2

-->

3.1.给体位置效应

TPEDC分子简称T分子, 其化学结构式见图1. 通过观察T分子的结构式, 可以想到, 在TPE单元上的两个甲氧基可能存在几种不同的取代方式. 并且, 两个乙烯基桥存在顺式和反式异构体结构. 考虑这两方面, 得到了T分子的几种异构体结构T1—T5. 它们的化学结构式如图1所示. T, T2和T4分子的结构差异是TPE单元上的两个甲氧基取代位置不同. T1, T3和T5分子具有顺式构型, 相应的反式构型分别是T, T2和T4分子. 优化的几何结构如图2所示. 优化结构显示, 所有分子的TPE部分均成螺旋桨结构. 分子中心的两个苯环不在一个平面上, 有一定角度的扭转, 二面角约为33°. 菁基两侧的苯环也不在一个平面上, 二面角约为72°. 此外, 计算结果显示, 这些分子异构体的能量从小到大依次为T, T1, T4, T5, T3, T2, 能量差异非常小. T与T1分子的能量差只有0.002 kcal/mol, T2与T3能量差为0.003 kcal/mol, T4与T5能量差为0.001 kcal/mol, T与T2的能量差也只有0.08 kcal/mol.
图 1 T和T1?T5分子的化学结构式
Figure1. Chemical structures of T and T1?T5 molecules.

图 2 优化的T和T1?T5分子的结构
Figure2. Optimized geometries of the T and T1?T5 molecules

通过响应函数方法计算了水溶液下所有异构体的TPA性质. 六个最低激发态的TPA波长${\lambda _{{\rm{tp}}}}$和截面$\sigma $列于表1中. 结果显示, 所有体系的第一、第三和第四激发态均有较强的TPA, ${\lambda _{{\rm{tp}}}}$分别对应于740, 610和575 nm附近. 最大的TPA截面均发生在第三激发态S3, 对应的${\lambda _{{\rm{tp}}}}$是610 nm左右. 与T分子相比, T2和T4分子的三个较强吸收态的TPA截面均有所减小. 对于T2, 最大TPA截面在614 nm处, 为893 GM. 对于T4, 最大TPA截面减少到880 GM, 位于615 nm. 这些结果表明给体的位置对TPA强度有重要影响. 此外, 相对于T4分子, T和T2分子的TPA截面较大, 说明位于分子末端的甲氧基给体能有效地提高TPA强度. 可以看到, 与T, T2和T4分子反式结构相比, 对应的顺式结构T1, T3和T5分子具有较低的TPA强度. T1的最大TPA截面为858 GM, 相对于T的值944 GM减少了86 GM. 对于T3和T5, 最大TPA截面分别减少了20和53 GM. 因此, 如果考虑顺式异构体, 可以预测整个体系的TPA强度会有所减弱.

	T			T1			T2			T3			T4			T5
	${\lambda _{{\rm{tp}}}}$/nm	$\sigma $/GM		${\lambda _{{\rm{tp}}}}$/nm	$\sigma $/GM		${\lambda _{{\rm{tp}}}}$/nm	$\sigma $/GM		${\lambda _{{\rm{tp}}}}$/nm	$\sigma $/GM		${\lambda _{{\rm{tp}}}}$/nm	$\sigma $/GM		${\lambda _{{\rm{tp}}}}$/nm	$\sigma $/GM
S1	743	719		743	696		740	707		738	672		743	638		743	629
S2	650	4		649	2		651	10		651	6		652	8		653	4
S3	612	944		612	858		614	893		612	873		615	880		615	827
S4	572	305		572	334		578	212		575	259		578	136		580	175
S5	556	3		556	5		557	4		556	5		557	4		557	5
S6	540	15		540	9		542	2		540	5		542	3		541	2

表1分子六个最低激发态的TPA波长${\lambda _{{\rm{tp}}}}$(nm)和TPA截面$\sigma $(GM)
Table1.The TPA wavelength ${\lambda _{{\rm{tp}}}}$(nm) and the TPA cross section $\sigma $(GM) of the lowest six excited states.

2 -->

3.2.给体数目效应

可以看出, 这些分子体系具有多枝结构, 分枝之间的复杂耦合决定了分子的TPA性质. 已有研究表明, 对于多枝分子, 分枝间的耦合对分子的光学性质有重要影响^[17,18]. 根据耦合作用的强弱, TPA强度相对于分枝单元会表现出协同加强、简单加和、甚至削弱的不同趋势^[30-32]. 人们通常采用简单的弗兰克激子模型来研究分枝间的耦合作用^[17,18]. 在该模型中, 分枝间的相互作用主要考虑偶极-偶极相互作用. 在TPE各分枝上是否添加给体, 会影响TPE各分枝的偶极矩, 进而影响分枝间的相互作用. 因此, 在TPE上添加更多的给体取代基能否产生更强的TPA, 还需要进一步仔细研究. 为此, 我们考虑了R, S和U几种分子结构, 它们的化学结构式和相应的优化几何结构如图3所示. 对于R, S, T和U分子, TPE部分的给体数目不同. 结构R中的TPE部分没有连接甲氧基, 结构S中只有一个末端甲氧基, 结构U包括三个甲氧基, 其中两个添加在TPE基团的侧位上, 一个位于分子的末端.
图 3 R, S和U分子的化学结构式和优化的几何结构
Figure3. Chemical structures and optimized geometries of the R, S and U molecules.

R, S和U分子的TPA性质的计算结果列于表2中. 与T分子类似, 这些分子仍然具有三个较强的TPA态. 对于S和U分子, 第三激发态具有最大的TPA截面, 而R分子TPA截面最大的态是第五激发态. R分子的第四和第五激发态的能量几乎是简并的. 可以发现, 随着取代基数目的增加, 三个TPA吸收峰的位置依次发生红移. 例如, 第三激发态的${\lambda _{{\rm{tp}}}}$依次为595, 603, 612 和621 nm. 与R和S分子相比, T和U分子结构具有较强的TPA强度. 说明添加给体取代基能够有效增强TPA. 从整体上看, 分子T和U具有类似的TPA特性. 在T结构的基础上, 在TPE侧位增加一个给体取代基(U分子)并没有有效地增强TPA. 而我们发现, 在S分子的基础上, 在TPE侧位增加一个甲氧基成为T分子结构时, 最大TPA截面有较大提高, 由785 GM增加到944 GM. 这可能是因为两个侧位位置相对于体系的给体氰基位置不同引起的. 我们还注意到, 当只有末端位置有取代基的时候, S分子在729, 603和567 nm处有三个较强的TPA峰, 而且这三个TPA吸收峰强度差别不大.

	R			S			U
	${\lambda _{{\rm{tp}}}}$/nm	$\sigma $/GM		${\lambda _{{\rm{tp}}}}$/nm	$\sigma $/GM		${\lambda _{{\rm{tp}}}}$/nm	$\sigma $/GM
S1	719	500		729	646		754	769
S2	631	27		642	19		658	7
S3	595	597		603	785		621	931
S4	557	4		567	640		580	118
S5	556	853		557	4		557	4
S6	540	99		541	29		541	11

表2分子六个最低激发态的TPA波长${\lambda _{{\rm{tp}}}}$(nm)和TPA截面$\sigma $(GM)
Table2.The TPA wavelength ${\lambda _{{\rm{tp}}}}$(nm) and the TPA cross section $\sigma $(GM) of the lowest six excited states.

2 -->

3.3.电荷转移

TPA性质与分子内电荷转移密切相关. 当分子从基态跃迁到激发态时, 分子内的电荷会重新分布. 为了更好地理解给体位置和给体数目对分子内电荷转移的影响, 计算了T, T2和T4以及R, S和U在基态和第一激发态的自然键轨道电荷分布情况. 为了便于分析, 将所研究的分子分成两部分, 四苯基乙烯基团连同给体甲氧基一起作为A部分, 剩余部分为B部分. 以T分子为例, 如图4所示.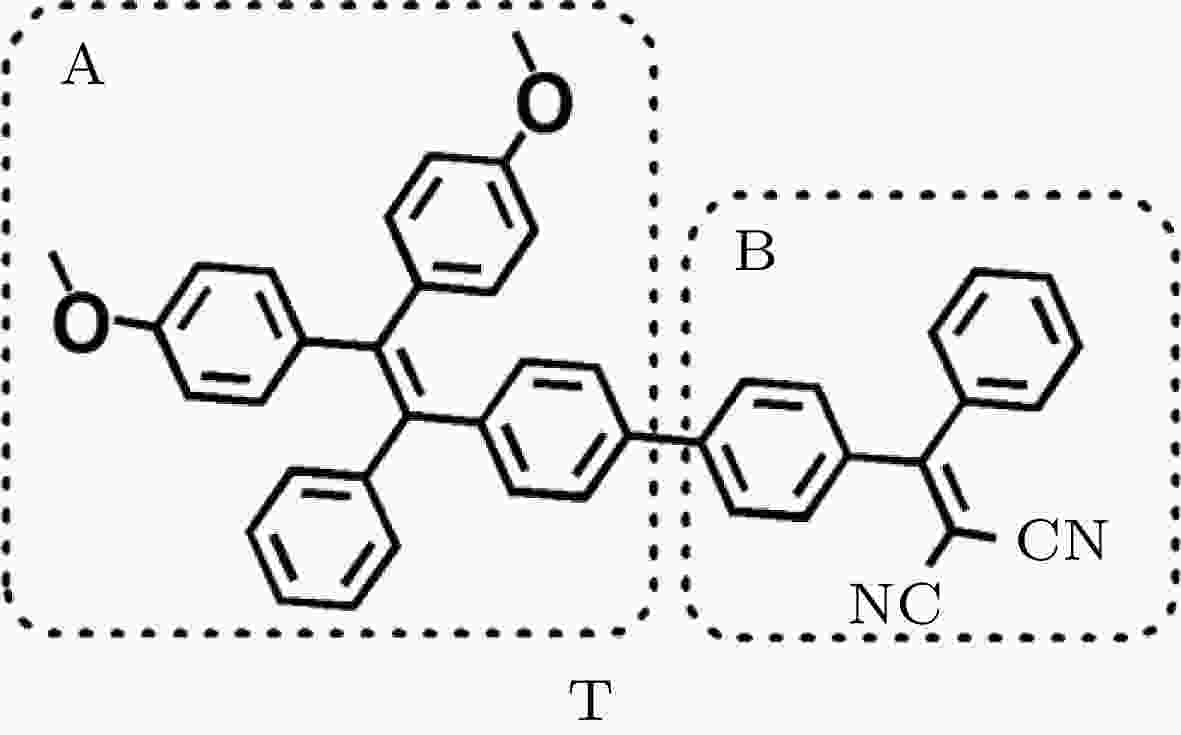
图 4 T分子的A和B两部分
Figure4. The A and B parts of the T molecule.

表3列出了分子基态和激发态A和B两部分的电荷计算结果. 其中Q_A0和Q_A1分别代表A部分基态和第一激发态的电荷, Q_A表示A部分基态和第一激发态的电荷差. 同样, Q_B0和Q_B1分别代表B部分基态和第一激发态的电荷, Q_B表示B部分基态和第一激发态的电荷差. 所有电荷单位为e, 1e = 1.602 × 10^–19 C. 分子T的A部分第一激发态电荷是0.3978e, 比基态电荷0.0298e具有更强的电正性. 相应地, B部分的第一激发态相比基态表现出更强的电负性. 这说明分子T的A部分是电子给体, 而B部分为电子受体. 对于其他分子, 情况亦如此. 可以看到, T给体电荷差Q_A为0.3680e, T2和T4的Q_A分别为0.3609e和0.3772e, 电荷差相差不大. 这说明给体位置对分子内电荷转移有影响, 但影响并不明显. 比较R, S, T和U分子的电荷差, 发现它们的电荷差依次增大. S比R的电荷差增加了0.0377e, T比S的电荷差增加了0.0438e, U比T又增加了0.0625e. 因此, 随着给体数目的增加, 从基态到第一激发态的分子内电荷转移明显增强.

	QA0/e	QA1/e	QA/e	QB0/e	QB1/e	QB/e
T	0.0298	0.3978	0.3680	– 0.0298	– 0.3978	– 0.3680
T2	0.0292	0.3901	0.3609	– 0.0292	– 0.3901	– 0.3609
T4	0.0294	0.4066	0.3772	– 0.0294	– 0.4066	– 0.3772
R	0.0271	0.3136	0.2865	– 0.0271	– 0.3136	– 0.2865
S	0.0284	0.3526	0.3242	– 0.0284	– 0.3526	– 0.3242
U	0.0305	0.4340	0.4305	– 0.0305	– 0.4340	– 0.4305

表3分子各部分的基态电荷和第一激发态电荷(单位: e)
Table3.Net charges (unit: e) for divided parts of the molecules in the ground states and in the first excited states.

2 -->

3.4.分子设计

理论设计出同时具有较强TPA和AIE特性的材料对双光子荧光显微成像技术的应用具有重要意义. 在分子设计中, 需要考虑已经确定的结构与性质关系. 已有研究表明, 许多结构因素在增强有机分子的TPA中起到了重要作用, 如给电子基团和吸电子基团的强度, π共轭中心特性和分子平面性, 以及分子的共轭长度和聚集方式等. 我们在TPEDC体系的基础上, 考虑了一些结构因素, 理论设计了同时具有TPA和AIE特性的分子, 并计算了设计分子的TPA性质.
设计分子的化学结构式和相应的优化几何结构如图5所示. 为了提高分子的平面性, 增加分子的共轭长度, 设计了T分子的同分异构体X分子. 考虑到三苯胺基团也具有螺旋桨结构, 并且常用于AIE材料设计中, 在T分子的基础上, 用三苯胺基团代替四苯基乙烯基团, 设计了Y分子. 最后将Y做进一步改进, 设计了Z分子. 优化结构显示, X分子中心的三个苯环相互之间扭转了约33°, 均位于分子的主干方向上, 相比于T分子, 增加了分子的平面性和共轭长度. 与T分子类似, Y分子中菁基两侧的苯环扭转角约为70°左右. 含有三苯胺基团的Z分子与Y分子相比, 平面性更好, 共轭长度也有所增加.
图 5 X, Y和Z分子的化学结构式和优化几何结构
Figure5. Chemical structures and optimized geometries of the X, Y and Z molecules.

X, Y和Z分子TPA性质的计算结果列于表4. 相对于实验中的T分子, 三个设计分子的TPA截面均有明显提高. X和Y分子的最大TPA态仍在第三激发态. X分子的最大TPA截面$\sigma $为1906 GM, 位于615 nm. 与T分子相比, $\sigma $有显著提高, 说明增加分子的平面性和共轭长度可以有效提高TPA截面. Y分子的最大TPA截面为1763 GM, 位于579 nm. 与T分子比较, $\sigma $也明显增大, 说明三苯胺基比四苯基乙烯基更有利于分子内的电荷转移, 具有更强的给电子能力. Z分子在802 nm处具有最大的TPA截面, 值为2259 GM. 与X分子相比, Z分子的吸收截面更强, 也说明三苯胺基比四苯基乙烯基更有利于分子内的电荷转移, 具有更强的给体强度. 在所有研究的分子中, Z分子的TPA强度最大, 这是因为Z分子具有较好的平面性和较长的共轭长度, 并且具有较强的给体三苯胺基.

	X			Y			Z
	${\lambda _{{\rm{tp}}}}$/nm	$\sigma $/GM		${\lambda _{{\rm{tp}}}}$/nm	$\sigma $/GM		${\lambda _{{\rm{tp}}}}$/nm	$\sigma $/GM
S1	747	947		824	1543		802	2259
S2	663	40		634	737		602	1362
S3	615	1906		579	1763		582	1
S4	560	1		576	91		540	57
S5	542	65		570	606		527	738
S6	525	502		560	50		546	4

表4分子六个最低激发态的TPA波长${\lambda _{{\rm{tp}}}}$(nm)和TPA截面$\sigma $(GM)
Table4.The TPA wavelength ${\lambda _{{\rm{tp}}}}$(nm) and the TPA cross section $\sigma $(GM) of the lowest six excited states.

为了便于比较, 还模拟了X, Y, Z和T分子的TPA光谱, 如图6所示. 可以看到, 这些分子在600—850 nm之间均有多个较强的TPA吸收峰. 设计分子的吸收峰强度均比实验中的T分子强. X, Y和Z在长波范围内均有较强的吸收峰, 这些吸收峰相对T分子有不同程度的红移. 当三苯胺基代替四苯基乙烯基之后, Y和Z的吸收峰都发生了较大红移. 根据(1)式, 双光子跃迁矩阵元与分子的激发能和偶极矩有直接关系. 相关的激发能越低, 越有利于增大TPA截面. 与X和T相比, Y和Z的吸收波长有较大的红移, 说明它们的激发能较低, 因此Y和Z具有更强的TPA.
图 6 X, Y, Z和T分子的TPA谱
Figure6. TPA spectra of the X, Y, Z and T molecules.

对于设计TPA和AIE材料, 不仅要求分子材料具有大的TPA截面, 还要求在高浓度下具有较高的荧光量子产率. 例如, 双光子荧光探针的性能通常采用TPA活性截面来表征, 即TPA截面与荧光量子产率的乘积. 因此, 在提高TPA截面的同时, 还应该考虑对荧光量子产率的影响. 比如, 增加分子平面性可以提高TPA截面, 但可能会降低分子的发光效率. 我们理论设计的分子采用了具有螺旋桨结构的四苯基乙烯基和三苯胺基, 可以有效避免紧密堆积和荧光猝灭, 因此可能具有AIE特性^[3-6], 从而具有较好的应用前景.

应用密度泛函响应函数方法结合极化连续模型研究了含四苯基乙烯和氰基基团的一系列D-π-A型有机分子的TPA性质. 研究了给体位置和数目对TPA性质的影响, 分析了给体位置和数目对分子内电荷转移的影响, 并且, 根据已有的结构与性质关系, 理论设计了三种分子结构, 并计算了它们的TPA性质. 结果表明, 给体的位置和数目对TPA强度有重要影响. 位于分子末端的甲氧基给体能有效地提高TPA强度. 随着取代基数目的增加, TPA吸收峰的位置发生红移. 在四苯基乙烯不同的侧位上添加电子给体基团对TPA性质的影响有明显差异. 由于分子呈现分枝结构, 分枝间复杂的耦合导致了这些性质差异. 给体位置对分子内电荷转移有影响, 但影响并不明显. 随着给体数目的增加, 分子内电荷转移明显增强. 跟实验中的分子相比, 理论设计的分子TPA截面均有明显提高. 由于这些分子均含有螺旋桨结构的四苯基乙烯或三苯胺基团, 因此可能具有AIE特性, 从而可以应用于双光子光动力学治疗, 频率上转换激射和双光子荧光探针等领域.