摘要:背景杂散光信号的干扰制约了激光片光成像技术的发展, 本文将结构光照明技术应用到激光片光成像测量中来消除杂散光的干扰. 介绍了基于结构光照明技术的工作原理和实验测量系统, 基于Matlab软件理论分析了相位移动结构光照明技术具有完全消除杂散光的作用, 并针对稳定罗丹明B溶液进行了二维激光诱导荧光成像实验, 进一步验证了相位移动结构光照明技术具有消除杂散光影响、提高二维成像精确度的作用. 最后利用基于锁相放大原理的结构光照明技术实现了非稳态扩散罗丹明B溶液的二维荧光瞬态成像实验, 并分析了罗丹明B溶液扩散的相关规律.
关键词: 结构光照明/
杂散光/
激光诱导荧光/
罗丹明B溶液

English Abstract

全文HTML

--> --> -->

20世纪80年代以来, 激光片光成像技术已被广泛应用于军事和民用领域, 因其具有非接触、可视化及其低成本等优势, 该技术已经迅速在流场显示和流场参数测量中崭露头角, 并得到快速发展^[1—4]. 目前基于激光片光成像的技术主要有激光诱导荧光(laser induced fluorescence, LIF)^[5,6]、瑞利散射成像^[7,8]、激光诱导磷光^[9,10]等. 但是受测试环境及其测试方法的影响, 这些光学成像技术在实际测量过程中会受到背景杂散光的强烈干扰, 严重影响了该类测量技术的光学成像质量^[11]. 因此, 在激光片光成像和处理领域, 消除杂散光的干扰是最基本的问题之一.
采用窄带宽滤波片对信号光进行滤波处理是当前消除杂散光干扰常用的方法, 该方法可实现对背景杂散光信号的有效抑制, 进而可提高激光片光成像的信噪比^[12—14]. 但是, 当有效信号强度较弱, 且杂散光干扰严重时, 窄带滤波片并不能完全滤除掉杂散光信号, 同时会吸收掉部分有效信号, 此时激光片光成像方法难以得到理想的光学成像结果^[15].
近年来, 国外****提出了一种新型的去杂散光技术—结构光照明技术(structured laser illumination planar imaging, SLIPI)^[16,17]. 该方法可以将原始信号谱图分为有效信号和杂散光两部分, 在后期数据处理中, 有效信号强度会保持不变, 而杂散光会因为空间频率不同而被剔除掉, 因此该技术具有消除杂散光干扰、提高光学成像质量的作用^[18]. 目前发展的SLIPI技术主要有相位移动SLIPI技术(phase-shift SLIPI, PS-SLIPI)^[19]和基于锁相放大技术的SLIPI方法(lock-in amplifier SLIPI, LA-SLIPI)^[20]. 这两类技术都在激光片光成像、图像处理及其分析等领域有着广阔的应用前景^[21]. Kristensson等指出, 多次散射造成的杂散光干扰问题将会较大地影响到喷雾场Mie图像拍摄, 并利用PS-SLIPI技术解决了多次散射干扰问题^[22], 并成功获取了喷雾场液滴尺寸分布的图像^[23]. Aldén等^[24]基于PS-SLIPI技术开展了二维LIF燃烧场诊断实验研究, 消除了壁面和颗粒物质引起的杂散光干扰. 此外, Kristensson等^[25]将LA-SLIPI方法应用到瑞利散射测温图像获取中去, 得到了燃烧火焰瞬态温度分布结果. PS-SLIPI和LA-SLIPI这两种技术各有优缺点, LA-SLIPI方法可进行瞬态图像获取, 但当杂散光强度较高时, 该方法抑制杂散光的能力不高; PS-SLIPI技术对杂散光的抑制能力较强, 但目前不能进行瞬态图像获取.
本文将两种SLIPI方法同时应用到LIF成像技术中来消除杂散光的影响, 进而提高LIF技术的成像质量. 首先利用MATLAB仿真计算的方法对SLIPI去除杂散光的能力进行了评估, 并针对罗丹明B稳态和非稳态溶液, 分别开展了二维LIF去杂散光平均和瞬态成像实验研究.

当一束激光入射到流场中时, 会伴随有瑞利散射光和荧光等, 其大小S可表示为

$S \propto C{I_0} \times \sum\limits_k {{\chi _k}} {\Re _k}(P,T,\eta ),$

式中, C为校准常数; I₀为探测点处的激光能量; χ_k为流场中第k种分子的摩尔组分; ${\Re _k}$为激光诱导发光信号函数, 该函数与流场温度T、流场压强P、流场分子密度η等参数相关.
在激光片光后放置Ronchi光栅, 再通过探测器收集显示包含有激光诱导发光信号和杂散光的正旋图样, 其中显示的二维图样(R代表行, C代表列)中每一个点处的探测光强(S_C(R), 包含激光诱导发光信号强度和杂散光强度等)可由下式表示^[20]:

$\begin{split} {S_{\rm{C}}}(R) =\,& \left[ {{I_{\rm{s}}}(R)\sin (2{\text{π}} {f_{{\rm{sig}}}}R + {\varphi _{_1}}) + {I_{\rm{C}}}(R) + {I_{\rm{B}}}(R)} \right]\\ &*\left[ {C{I_0} \times \sum\limits_k {{\chi _k}} {\Re _k}(P,T,\eta )} \right] \\ =\,& A(R)\sin (2{\text{π}} {f_{{\rm{sig}}}}R + {\varphi _{_1}}) + B(R),\\[-10pt]\end{split} $

其中, f_sig为空间调制频率(由Ronchi光栅决定), I_s(R)为光栅调制振幅, I_C(R)为光栅调制直流分量, I_B(R)为杂散光强度分布, φ₁为调制初始相位. 因此, A(R)和B(R)可以表示为

$A(R) = C{I_{\rm{S}}}(R){I_0} \times \sum\limits_k {{\chi _k}} {\Re _k}(P,T,\eta ),$

$\begin{split} B(R) = \, & {B_1} + {B_2} = C{I_{\rm{C}}}(R){I_0} \\ & \times \sum\limits_k {{\chi _k}} {\Re _k}(P,T,\eta ) + C{I_{\rm{B}}}(R){I_0}\\ & \times \sum\limits_k {{\chi _k}} {\Re _k}(P,T,\eta ),\end{split}$

其中调制振幅项A(R)与激光诱导发光信号函数${\Re _k}$相关, 因此可以通过测量调制振幅项A(R)的强度分布来获取流场的关键参数, 如流场温度T、流场压强P和流场分子密度η等.
SLIPI技术后期处理方法主要有LA-SLIPI方法和PS-SLIPI方法, 下面阐述两种方法的基本原理.
2

-->

2.1.LA-SLIPI方法^[20]

理论假定两行参考正旋函数, 其相位相差π/2, 分别为

${S_X}(R) = \sin (2{\text{π}} {f_{{\rm{sig}}}}R + {\varphi _1}),$

${S_Y}(R) = \sin (2{\text{π}} {f_{{\rm{sig}}}}R + {\varphi _1} + {\text{π}} /2).$

再将(2)式分别与(5)和(6)式相乘, 得到:

$\begin{split}{S_{X,{\rm{C}}}}(R) =\, & {S_{\rm{C}}}(R) \cdot {S_X} = \frac{1}{2}A(R)[\cos ({\varphi _{\rm{C}}} - {\varphi _1}) \\ & - \cos (4{\text{π}} {f_{{\rm{sig}}}}R + {\varphi _{\rm{C}}} + {\varphi _1})] \\ & + {B_{\rm{C}}}(R)\sin (2{\text{π}} {f_{{\rm{sig}}}}R + {\varphi _1}), \end{split}$

$\begin{split}{S_{Y,{\rm{C}}}}(R) =\, & {S_{\rm{C}}}(R) \cdot {S_Y} = \frac{1}{2}A(R)[\sin ({\varphi _{\rm{C}}} - {\varphi _1}) \\ & - \sin (4{\text{π}} {f_{{\rm{sig}}}}R + {\varphi _{\rm{C}}} + {\varphi _1})] \\ & + {B_{\rm{C}}}(R)\sin (2{\text{π}} {f_{{\rm{sig}}}}R + {\varphi _1} + {\text{π}} /2).\end{split}$

在(7)和(8)式中添加一个低通滤波器(f_c = f_sig)去掉与f_sig相关的项, 得出X_C(R) = 0.5A(R)× cos(φ_C – φ₁)和Y_C(R) = 0.5A(R)sin(φ_C – φ₁), 进而得到激光诱导发光信号振幅项A₁(R):

$A1(R) = 2\sqrt {{X_{\rm{C}}}{{(R)}^2} + {Y_{\rm{C}}}{{(R)}^2}} .$

2 -->

2.2.PS-SLIPI方法

在平行激光光束后面添加自动旋转玻璃片(具有一定的厚度), 如图1所示. 当玻璃片旋转θ后, 激光光束偏移dx距离:
图 1 旋转玻璃片改变激光光束位置示意图
Figure1. Diagram of laser beam transmission changed by rotating glass sheet.

${\rm{d}}x = \frac{{d\sin \theta }}{{\sqrt {1 - {{\left( {{{{n_0}\sin \theta }}/{{{n_1}}}} \right)}^2}} }},$

其中d是玻璃片厚度, n₀为空气折射率, n₁为厚玻璃片折射率.
连续改变光栅正弦调制图像的位置, 位移量dx₁ = T/n对应的相位改变值为dφ = 2π/n, T为激光诱导发光图像的正弦调制周期. 再对改变相位(dφ₁ = 0, dφ, 2dφ, ···, (n – 1)dφ)后的激光诱导发光信号图像I_i进行采集处理, 可得到^[19]:

$AA = \frac{{\sqrt 2 }}{n}\left[ \sum\limits_{l = 1}^{n - 1} \sum\limits_{k = l + 1}^n \left( {I_l}(i,j) - {I_k}(i,j)\right)^2\right]^{1/2} ,$

$BB = ({{{I_1} + {I_2} + \cdots + {I_n}}})/{n},$

其中n为相位变换次数, AA为计算出的振幅值, BB为计算出的杂散光和光栅调制直流分量平均值.

本文设计的结构光照明测量装置可对非稳态流场进行去杂散光瞬态图像获取, 测量装置主要由连续激光光源、片光系统、Ronchi光栅和电子倍增电荷耦合器件(EMCCD)组成, 如图2所示. 连续激光器输出激光波长为532 nm, 激光能量为100 mW. 激光经过扩束镜组后变成光斑直径为5 cm的光束, 该光束再经过Ronchi光栅后变成正旋光强分布的平行激光光束, Ronchi光栅的周期分别为2/mm (PS-SLIPI方法)和8/mm (LA-SLIPI方法). 使用片光系统将平行激光光束变成平行片光光束照射到非稳定罗丹明B溶液(见图2中的RB所示). 激光片光照射测试流场产生的荧光信号再次进入EMCCD相机进行采集拍摄. 最后通过后期SLIPI数据处理方法可得到去杂散光后的瞬态激光诱导发光信号图像. 同时本文设计的结构光照明测量装置可对稳态流场进行去杂散光平均图像获取, 主要是在正弦调制的平行激光光束后添加旋转的厚玻璃片(由自动旋转台控制), 相位可改变0, dφ, 2dφ, ···, (n – 1)dφ, 最后对相位调制后的激光诱导发光信号图像进行PS-SLIPI方法处理可得到去杂散光后的平均图像. 此外, 罗丹明B溶液可产生稳态和非稳态流场, 同时本文设计了四种不同条件下的实验环境, 分别记为Case 1, Case 2, Case 3和Case 4, 前三种用于PS-SLIPI方法, 第四种用于LA-SLIPI方法. Case 1为最优条件(杂散光干扰最小), Case 2是将金属障碍物放置在液体溶液正后方来增加杂散光干扰, Case 3是将金属屏幕放置在液体溶液侧后方来增加杂散光干扰, Case 4是将金属柱形物体放置在液体溶液正后方来增加杂散光干扰, 四种条件下的流场参数及其EMCCD采集参数列于表1.
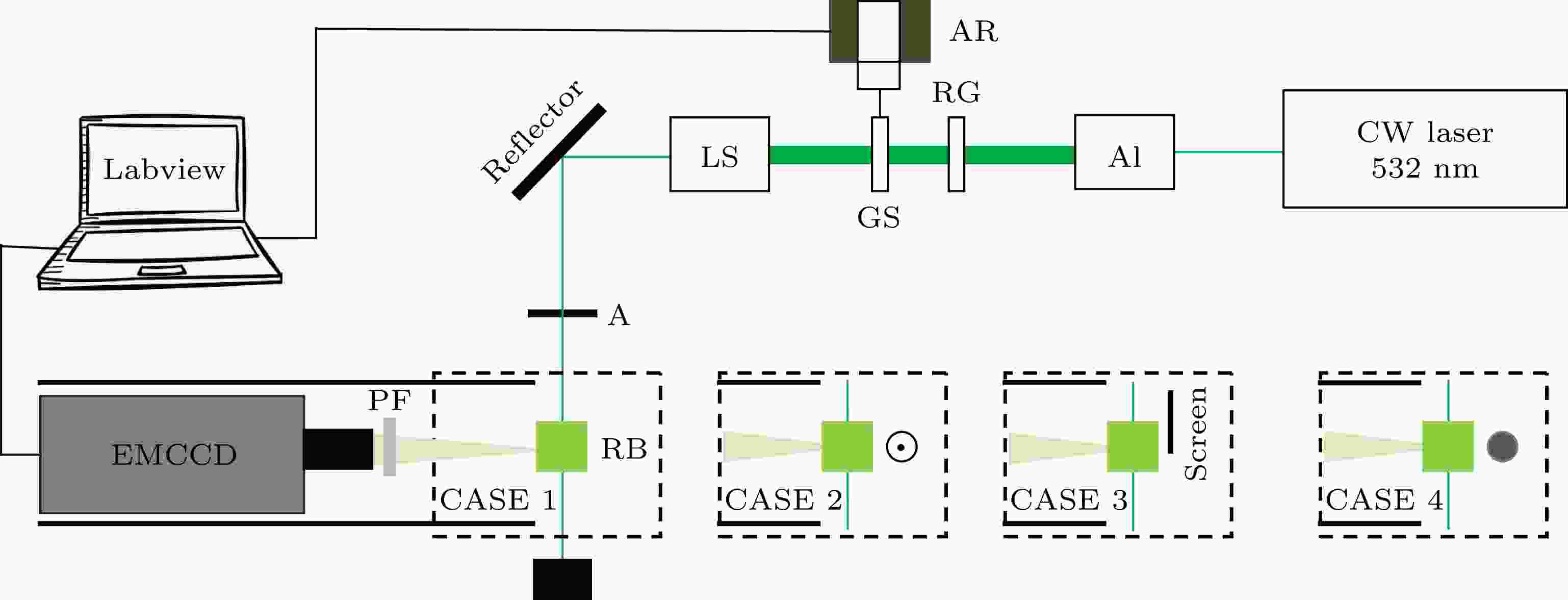图 2 基于结构光照明技术的激光诱导发光图像测量装置(A1, 5×扩束镜; RG, Ronchi光栅; AR, 自动旋转台; GS, 玻璃片(5.3 mm); LS, 片光系统; A, 光阑; RB, 罗丹明B溶液; PF, 滤光片)
Figure2. LIF imaging setup based on the SLIPI technique (A1, 5 × beam expander; RG, Ronchi grating; AR, automatic rotary table; GS, glass sheet (5.3 mm); LS, light system; A, aperture slot; RB, Rhodamine B solution; PF, fliter).

	背景分类	激光输出能量	相机曝光时间	相机增益	罗丹明B溶液浓度	图像正弦调制周期/像素
相位移动SLIPI技术	Case 1	100 mW	0.025 s	30	稳态溶液：1 × 107 mol/L	0.058593
	Case 2	100 mW	0.025 s	30	稳态溶液：1 × 107 mol/L	0.058593
	Case 3	100 mW	0.025 s	30	稳态溶液：1 × 107 mol/L	0.058593
基于锁相放大原理的SLIPI技术	Case 4	100 mW	0.025 s	30	非稳态扩散溶液: 将1 × 106 mol/L溶液注入到1 × 107 mol/L溶液.	0.144536

表1两种SLIPI技术实验参数
Table1.Experimental parameters of two SLIPI technique.

2

-->

4.1.理论模拟计算

为了具体说明SLIPI消除杂散光干扰的原理和效果, 本文基于Matlab软件对LA-SLIPI和PS-SLIPI方法进行理论模拟计算研究, 其中LA-SLIPI理论和实验研究在文献[26]中已经进行了深入研究. 在计算中, 假定行坐标x为1到512, A(x) = –0.001 × (x – 256)² + 80, 如图3杂散光分量I_a为(0, 40)的随机值, 直流分量I_b = (0, 130)的随机值, 因此求出干扰分量(B₁ + B₂)幅值是设定的信号量(A)幅值的2至11倍. f_sig = 0.1 Hz为光栅调制频率, f_c = 0.005 Hz代表LA-SLIPI技术中的截止频率, φ_C = 0为初始相位.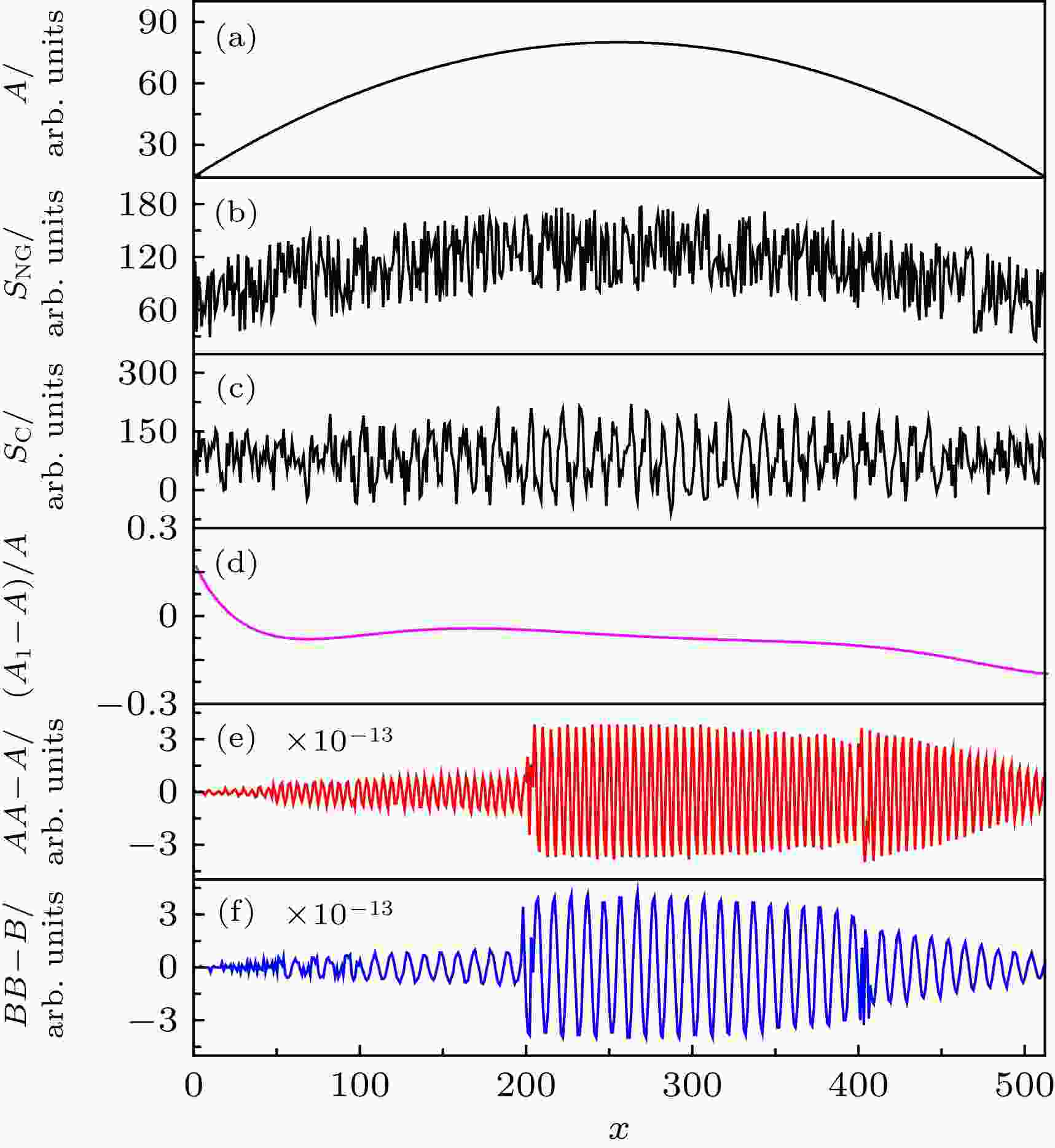
图 3 PS-SLIPI方法仿真计算全过程　(a) 调制振幅项A的值; (b) 无光栅调制时的强度值S_NG = A(R) + B₁(R) + B₂(R); (c) 光栅调制后的强度值S_C; (d) LA-SLIPI计算后的振幅相对误差值dA/A = (A₁ – A)/A, 截止频率f_c = 0.005 Hz; (e) PS-SLIPI计算后的振幅误差值dA/A = AA – A, n = 3; (f) PS-SLIPI计算后的干扰分量误差值dB = BB – B, n = 3
Figure3. Simulation process of the PS-SLIPI method: (a) The modulated amplitude value, A; (b) the intensity without grating modulation, S_NG = A(R) + B₁(R) + B₂(R); (c) the intensity with grating modulation, S_C; (d) the relative error of modulated amplitude value, A, calculated by LA-SLIPI method, dA = (A₁ – A)/A, f_c = 0.005 Hz; (e) the error of modulated amplitude value, A, calculated by PS-SLIPI method, dA = AA – A, n = 3; (f) the error of interference components calculated by PS-SLIPI method, dB = BB – B, n = 3.

图3(a)首先给出了调制振幅项A的值, 基于调制振幅项A, 本文计算得到了有无光栅调制作用下的总强度值, 分别记为S_C (如(2)式)和S_NG = A(R) + B₁(R) + B₂(R), 如图3(b)和图3(c). 对比两者的强度值可知, S_C图像中除直流分量外还有调制频率(f_sig)项. 利用LA-SLIPI技术对调制强度S_C进行处理, 可直接得到去除杂散光后的光栅调制振幅项A₁, 并求出A₁相对于理论设定值A的相对误差值dA/A = (A₁ – A)/A, 如图3(d)所示. 由图3(d)可知: LA-SLIPI方法处理后的数值与理论数值A (如图3(b))较好地吻合; 同时调制振幅强度A越小, 相对误差值dA/A越大. 例如当A为最小值15 (干扰分量约为A的11倍)时, 相对误差为15%, 但当A为最大值90 (干扰分量约为A的2倍)时, 相对误差基本为0. 此外, 再利用PS-SLIPI方法对调制强度S_C进行处理可得到振幅项AA和干扰分量BB的值, 并求出两者相对于理论设定值的误差, 如图3(e)和图3(f). 可知: PS-SLIPI方法处理后的数值与理论数值A (如图3(b))极好地吻合, 两者的误差值基本为0. 最后, 对比LA-SLIPI和PS-SLIPI技术的杂散光滤除能力, 可知: LA-SLIPI可针对瞬态光栅调制图像直接进行杂散光滤除处理, 但是当杂散光较强时, PS-SLIPI比LA-SLIPI的杂散光滤除能力要强.
2 -->

4.2.实验结果分析

为了实验验证两种SLIPI方法的去杂散光作用, 本文按照图2所示的SLIPI测量光路, 分别开展了稳态和非稳态流场的去杂散光实验研究. 首先对于稳定的罗丹明B溶液, 利用自动旋转台使得光栅条纹移动0, T/3, 2T/3, 进而改变相位0, π/3, 2π/3, 结果如图4所示. 在得到改变相位后的激光诱导发光图像后, 再利用(11)式可进一步获得去杂散光后的调制振幅AA的值.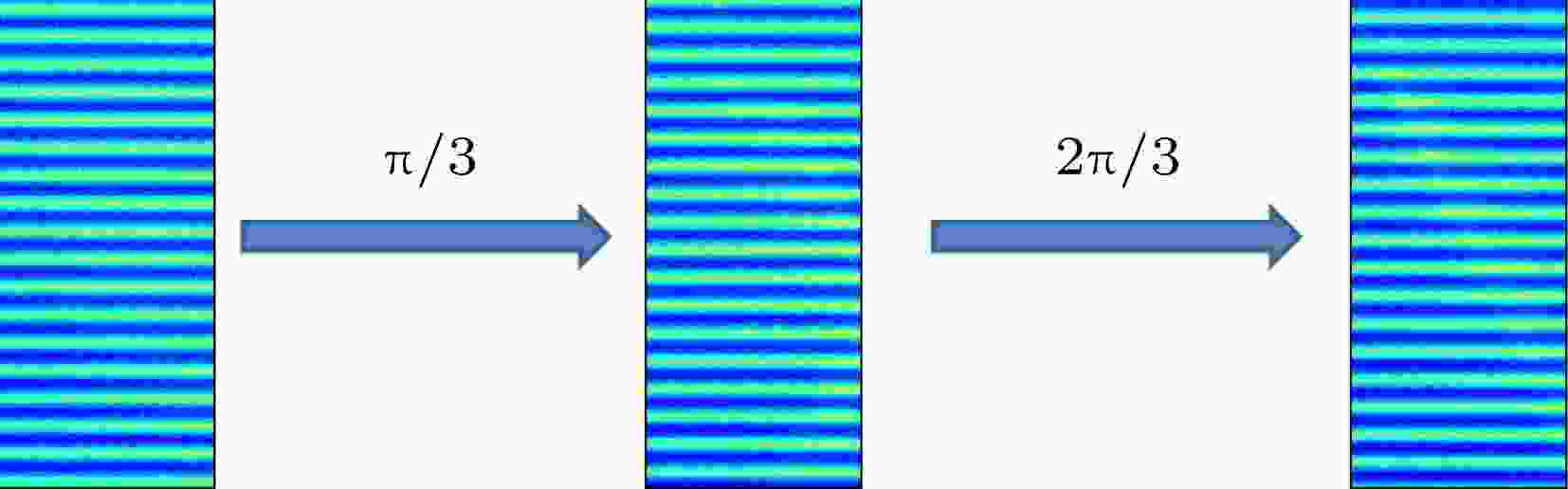
图 4 PS-SLIPI方法的光栅条纹移动图像
Figure4. Grating fringe changing images based on phase shifting SLIPI method.

在未利用SLIPI方法滤波前, 得到稳定罗丹明B溶液的激光诱导发光图像, 如图5(a)所示. 对比Case 1, Case 2和Case 3可知: LIF图像中除了可以观察到的荧光图像外, 还能够观察到大量的杂散光, 其强度很高, 很容易将罗丹明B溶液荧光信号掩盖, 极大地影响了探测到的荧光图像的信噪比. 此外为了更好地比较SLIPI方法处理后的图像, 又在罗丹明B溶液器皿池壁上粘贴两条较细的金属丝作为标记, 如图5(a)中的蓝色标记线. 将Ronchi光栅布置在片光系统前, 即可获得光栅调制作用下的LIF图像, 如图5(b)所示. 再采用PS-SLIPI的方法对三种不同拍摄环境下的图像进行去杂散光处理, 分别得到图5(c)中的3个图像, 可以看出三种不同测试环境中得到的SLIPI处理后的图像、数值大小基本一致, 说明PS-SLIPI去杂散光方法的准确性; 此外, 从图5(c)可以明显看出, 由金属障碍物、金属屏幕引入的杂散光全部被滤除掉, 也进一步说明了该种方法能够实现对杂散光干扰的有效抑制.
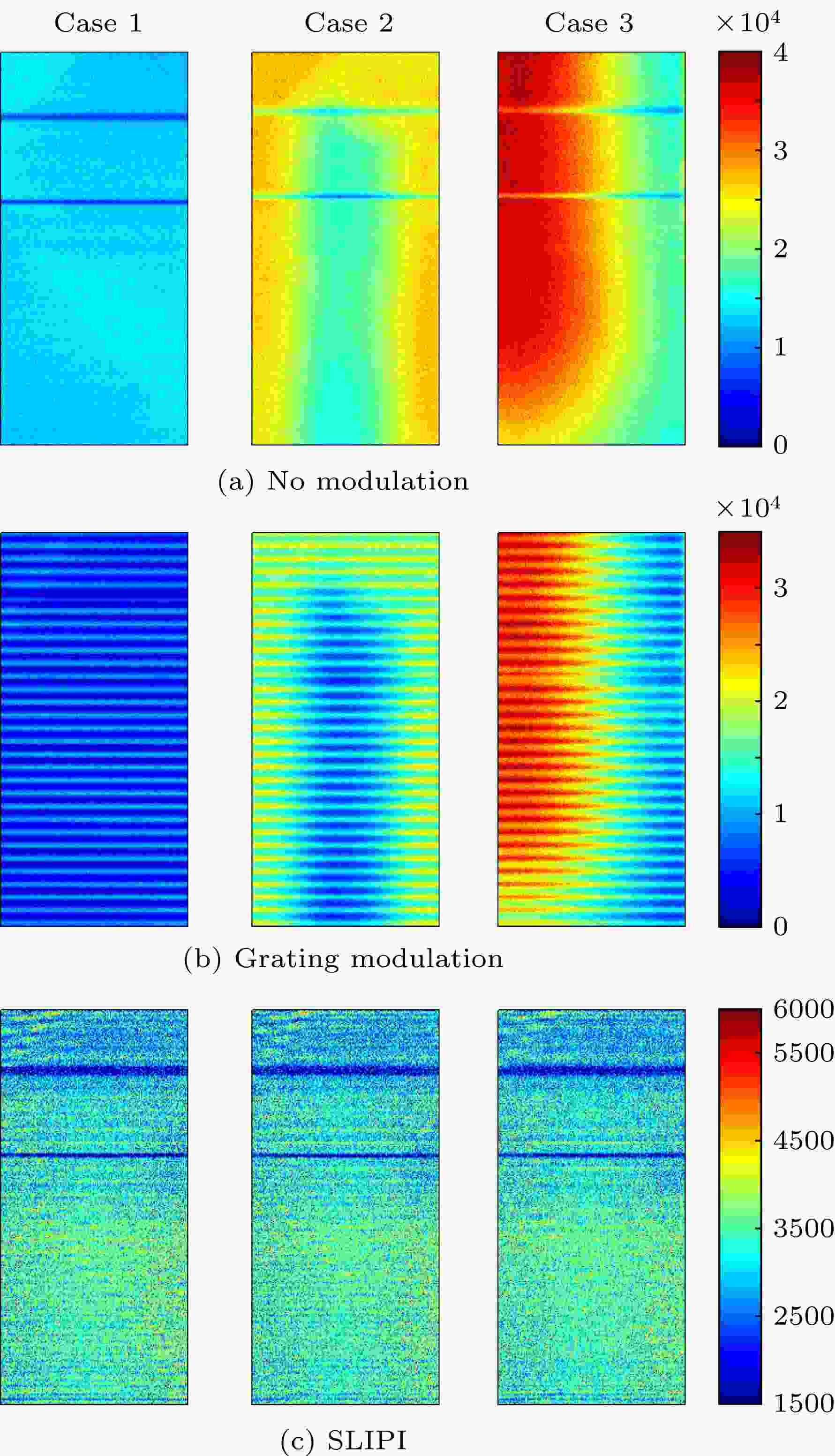图 5 (a) 三种不同测试环境下的原始LIF图像; (b) 光栅调制LIF图像; (c) PS-SLIPI方法处理后的调制振幅(A)分布图像
Figure5. (a) Conventional (raw data) LIF images without grating modulation in three different measurement cases; (b) LIF images with grating modulation; (c) images of modulated amplitude value, A, calculated by phase shifting SLIPI method.

但是PS-SLIPI的方法仅能够对于稳态流场进行去杂散光处理, 无法得到非稳态流场的瞬态图像. 为了获得非稳态流场的变化规律, 本文将LA-SLIPI技术应用到非稳定罗丹明B溶液中, 消除背景杂散光的干扰, 进一步研究罗丹明B溶液的扩散规律. 其中, 本文在低浓度稳定罗丹明B溶液底部添加较高浓度的罗丹明B溶液来形成非稳定扩散溶液(实验参数见表1). 图6(a)为光栅调制作用下的LIF图像, 图中红黄较亮区域为背景杂散光和荧光信号叠加区域, 由图可知, 由于杂散光的干扰, 溶液的扩散图像不明显, 无法对其扩散规律进行分析. 同时对6(a)图样进行傅里叶变换, 可得出光栅调制频率为f_sig = 0.144536/像素. 因此对不同时刻的光栅调制图像进行LA-SLIPI去杂散光处理, 分别得到图6(b)中的8个图像. 由图6(b)可知, 由金属障碍物引入的杂散光被滤除掉, 进一步说明了该种方法能够实现对杂散光干扰的有效抑制. 最后为了精确地描述罗丹明溶液的扩散规律, 本文利用红色虚线描绘出较高浓度罗丹明B溶液(对应较高荧光信号强度)的型面, 如图6(b)所示. 由图6(b)可知: 随着时间的推移, 较高浓度的罗丹明B溶液向低浓度的溶液方向扩散, 即扩散方向为溶液底部→溶液顶部. 同时溶液整体浓度梯度随时间递减, 即较高浓度溶液向四周扩散. 此外由于溶液器皿轻微晃动造成溶液扩散出现漩涡图案, 这和理论预测基本一致. 因此, LA-SLIPI技术有效抑制了杂散光的干扰, 提高了LIF采集图像的准确性.
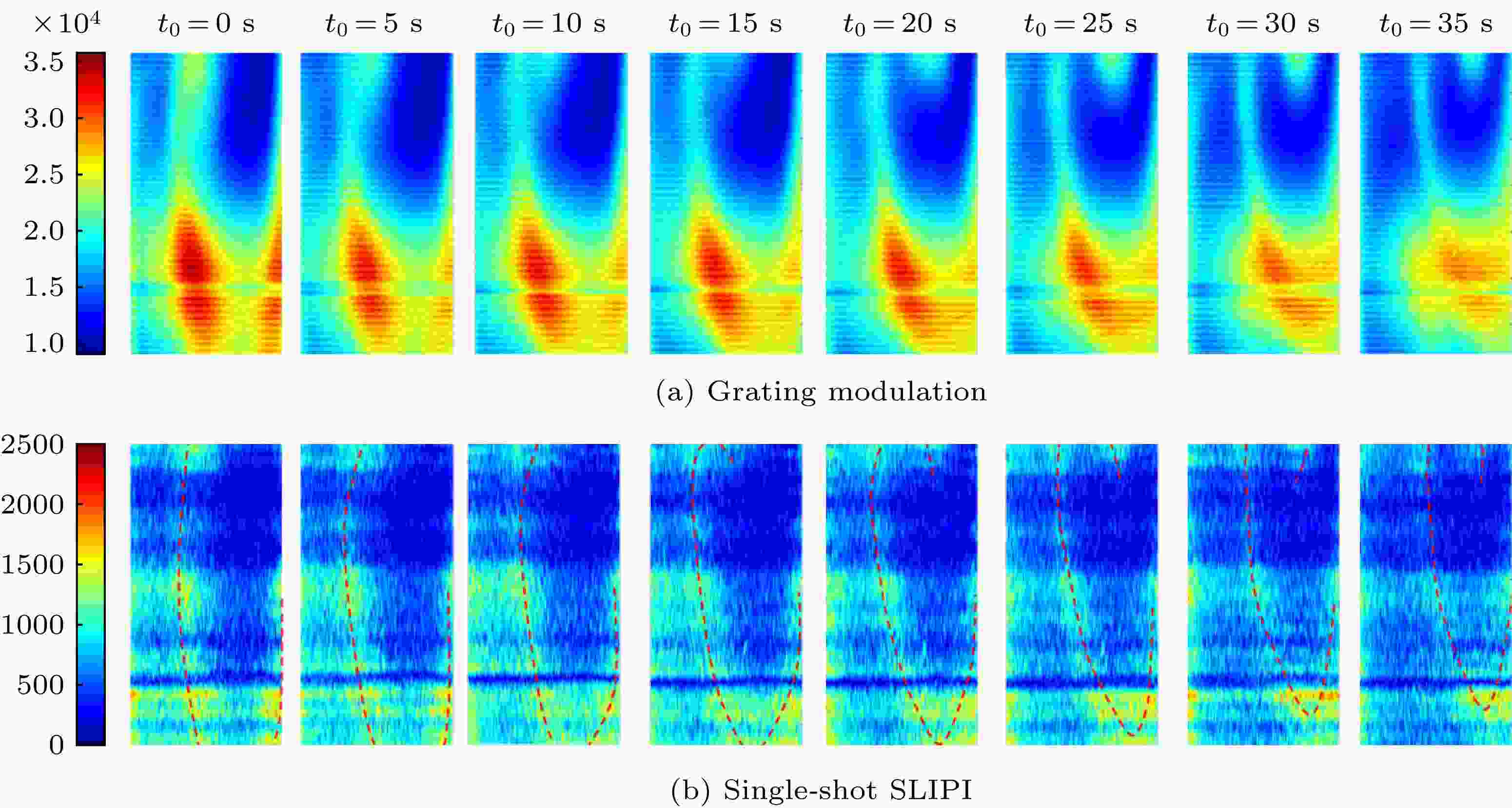图 6 (a) 不同测量时刻下的光栅调制LIF瞬态图像; (b) LA-SLIPI方法处理后的调制振幅(A)分布的瞬态图像
Figure6. (a) LIF images with grating modulation; (b) images of modulated amplitude value, A, calculated by LA-SLIPI method.

本文将结构光照明的方法应用到LIF图像测量中, 来消除图像采集中的杂散光干扰. 结果表明:
1)通过MATLAB理论仿真计算, 验证了PS-SLIPI的方法具有完全消除杂散光干扰的作用.
2)利用Ronchi光栅建立了一套可用于稳态和非稳态流场二维显示的激光诱导发光图像采集装置, 并针对稳态罗丹明B溶液开展了LIF图像去杂散光实验, 验证了PS-SLIPI方法可以克服杂散光对成像质量的影响.
3) LA-SLIPI方法能够原位复原出具有清晰纹理的非稳态流场图像, 并且具有能够很好地消除杂散光干扰的优点, 符合高质量激光片光成像问题的实际需求.
两种SLIPI处理方法在杂散光抑制方面各具优缺点, 但将两者有效结合后可实现稳态和非稳态流场的二维精确显示, 同时这两种SLIPI方法适用性较强, 因此在其他激光片光成像技术(瑞利散射图像测量、粒子成像测速及其激光诱导磷光图像测量技术等)中的应用前景十分广阔.