摘要: 基于心脏电影磁共振图像的右心室(RV)分割, 对心脏疾病的诊疗及预后有着十分重要的意义. 右心室结构复杂, 传统图像分割方法始终未能达到较高的精度. 多图谱方法通过配准和融合来实现RV分割, 是近几年RV分割中的主要方法之一. 本文提出一种新的右心室多图谱分割方法, 能够实现RV的全自动准分割. 本文首先采用自适应仿射传播算法获取一系列图谱集, 并基于豪斯多夫距离和归一化互信息选择与目标图像最相似的图谱集; 然后, 依次采用多分辨率的仿射变换和Diffeomorphic demons算法将目标图像配准到最相似图谱集, 并将配准得到的形变场应用于标记图像获得粗分割结果; 最后, 本文采用COLLATE算法融合粗分割结果得到RV轮廓. 30例心脏电影磁共振数据被用于回顾性分析. 本文算法与放射专家手工分割的RV 相比, Dice指标和豪斯多夫距离的平均值分别为0.84, 11.46 mm; 舒张末期容积, 收缩末期容积, 射血分数的相关系数和偏差均值分别是0.94, 0.90, 0.86; 2.5113, –3.4783, 0.0341. 与卷积神经网络相比, 本文算法在收缩末期的分割精度更接近手动分割结果. 实验结果表明, 该方法从有效的图谱选择和基于多分辨率的Diffeomorphic demons算法的多级配准提高了右心室分割的精度, 有望应用于临床辅助诊断.
关键词: 心脏磁共振图像 /
右心室 /
多图谱分割 /
微分同胚demons English Abstract A new method of multi- atlas segmentation of right ventricle based on cardiac film magnetic resonance images Su Xin-Yu 1 ,Wang Li-Jia 1 ,Zhu Yan-Chun 2 1.School of Medical Instrument and Food Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China Fund Project: Project supported by the Shenzhen Provincial Research Foundation for Basic Research, China (Grant No. JCYJ20160429172357751)Received Date: 21 April 2019Accepted Date: 02 July 2019Available Online: 01 October 2019Published Online: 05 October 2019Abstract: Segmentation of right ventricle (RV) in a cine cardiac magnetic resonance (CMR) image is essential for the diagnosis and therapy of cardiac diseases. Traditional image segmentation methods fail to achieve high accuracy due to the complex structure of RV. Multi-atlas frame, which transforms the segmentation into registration and fusion, has become one of the main segmentation methods of RV in recent years. In this paper, we suggest a new multi-atlas frame for the automatical and accurate segmentation of RV. Firstly, an adaptive affinity propagation algorithm is used to obtain a series of atlases, in which the atlas set most similar to the target image based on hausdorff distance and normalized mutual information is selected. Then, the target image is registered onto the selected atlas by using multi-resolution strategy-based affine transform and Diffeomorphic demons algorithm to generate a deformation field, which is applied to the label image to obtain coarse segmentation results of RV. Finally, the Consensus Level, Labeler Accuracy and Truth Estimation (COLLATE) algorithm is used to fuse the coarse segmentation result to obtain the RV. The 30 cine CMR datasets are applied to the retrospective analysis. The comparison between RV value from the present algorithm and that from the manual segmentation shows that the average dice index and hausdorff distance are 0.84 and 11.46 mm, respectively, the correlation coefficients and deviation means of endo-diastolic volume, endo-systolic volume and ejection fraction are 0.94, 0.90, 0.86, and 2.5113, –3.4783, 0.0341, respectively. Compared with convolutional neural networks, the new multi-atlas frame has an endo-systolic volume close to the manual result. The results show that the suggested method improves the accuracy and robustness of segmentation of RV from the effective atlas selection and multi-resolution Diffeomorphic demons algorithm-based registration, and it promises to be applied to clinical diagnosis.Keywords: cardiac magnetic resonance imaging /right ventricle /multi-atlas segmentation /diffeomorphic demons 全文HTML --> --> --> 1.引 言 据世界卫生组织(world health organization)报道, 2016年大约有1790万人死于心血管疾病, 占全球死亡总数的31%[1 ] ; 《中国心血管病报告2018》显示, 中国心血管疾病发病率及死亡率仍处于上升阶段[2 ] . 心血管疾病已经成为严重威胁人类健康的头号杀手. 借助影像手段评价心脏功能指标是临床心脏疾病日常诊断的主要依据. 心脏电影磁共振成像(cine cardiac magnetic resonance imaging, Cine-CMRI)软组织对比度高、时空分辨率好、可以动态观察心脏解剖结构, 可重复性和高准确度使Cine-CMRI成为评估心脏功能指标的金标准. 基于Cine-CMRI的右心室(right ventricular, RV)分割对肺动脉高压、三尖瓣闭锁、法洛四联症等心脏疾病的功能评价具有独特的重要参考意义[3 ,4 ] , 是目前心脏分割领域的研究热点. 然而, RV心肌薄且个体差异大, 心外膜毗邻脂肪, 心内膜连接小梁肌, 给传统的分割方法带来了不小的难度.[5 ] , 被首次用于RV多图谱分割中图谱集的获取[6 ] . 与固定图谱相比, AP算法避免了所有图谱图像与目标图像的配准过程, 显著减少了分割时间, 且同时提高了分割精度. 但是, 图谱图像聚类过程时间过长、心尖图像的分割效果不佳仍然是目前存在的问题. 自适应仿射传播聚类(Adaptive AP)算法在AP算法的基础上进行改进, 主要包括三个方面: 自动调整偏向参数的大小来搜索聚类集群数量寻找最优聚类结果; 自适应调整阻尼因子来消除振荡; 以及阻尼效果不佳时, 降低偏向参数逃离振荡, 以寻找出最优聚类结果[7 ] .[8 -12 ] , FFD将图像形变参数化表示, 虽然降低了计算量, 但也限制了形变的复杂程度. 通过局部形变近似求得整体形变, 容易产生物理折叠, 不能确保图像的拓扑结构. 对于形变较大的心脏图像来说, FFD并不能实现精确配准. Thirion[13 ] 根据麦克斯韦妖的原理首先提出将无参数非刚性配准视为扩散过程, 以图像梯度信息作为驱动力实现配准过程的Demons方法. Demons作为小形变配准模型, 在计算效率和配准效果方面皆表现出良好的性能, 然而传统Demons只将参考图像的梯度信息作为驱动力[14 ] , 导致形变程度不高、鲁棒性差, 最重要的是不能维持其拓扑结构. 为了克服上述局限性, Vercauteren等[15 ] 提出Diffeomorphic demons模型, 结合李群空间实现优化策略确保形变场具有拓扑保持性, 同时采用快速计算指数映射实现了对大形变配准的高效性和鲁棒性, 更适用于处理心脏图像.[16 ] .[7 ] 获取一系列初始的图谱集, 并再次根据豪斯多夫距离和归一化互信息从初始图谱集中选出最相似的图谱集; 然后, 本文利用Diffeomorphic demons算法将目标图像与最相似的图谱集进行配准, 得到一系列保持较好拓扑结构的粗分割结果; 最后, COLLATE算法将粗分割结果进行融合, 获得精确、鲁棒的RV轮廓.2.基础方法概述 22.1.AP算法 2.1.AP算法 AP算法通过识别具有代表性的样本子集对数据进行聚类. $s\left( {i,k} \right)$ 表示数据点i 与数据点k 之间的相似性, 通常使用欧式距离$s\left( {i,k} \right){\rm{ }} = - {\left| {\left| {{x_i} - {\rm{ }}{x_k}} \right|} \right|^2}$ . $s\left( {k,k} \right)$ 作为输入, 其大小影响聚类中心的选择, 因此又被称为偏向参数p (preferences). 当所有的数据点都同样适合作为聚类中心, p 通常被设置为相似值的均值以控制生成的集群数量. 吸引度$r\left( {i,k} \right)$ 和归属度$a\left( {i,k} \right)$ 是数据点之间的两种消息交换方式, 按照以下公式迭代更新:$a\left( {i,k} \right) = 0$ . 在仿射传播过程中, 每一个数据点都将通过吸引度与归属度之和来确定是否作为聚类中心. 更新消息时, 为避免出现数值振荡设置阻尼系数$\lambda $ , 更新结果由上一次迭代结果和当前迭代结果加权得到, $\lambda $ 和$1 - \lambda $ 分别为二者权重, 默认值为0.5. 与其他方法相比, AP算法更加精确、高效, 并应用于人脸图像聚类、基因检测、文本识别等领域.k 个类代表, 并检测是否振荡; 2)若发生振荡, 则逐步增大阻尼因子$\lambda $ , 否则转步骤1); 3)检测k 个类代表是否收敛, 若不收敛转步骤1); 4)继续若干次循环以验证结果是否稳定, 结果稳定逐渐减小偏向参数p , 否则转步骤1); 5)重复以上步骤直至达到停止条件. 相比较于AP算法, Adaptive AP在聚类质量和消除振荡方面具有更优或不低于原算法的结果.2.2.Diffeomorphic demons算法 -->2.2.Diffeomorphic demons算法 Diffeomorphic demons是目前医学图像中常用的一种高效、鲁棒的非刚性配准算法, 通过使全局能量函数最小化实现最终的配准过程. 该方法分为优化过程和正则化过程, 其中, 优化过程采用的全局能量函数的标准形式如下[15 ] :F 为参考图像, M 为浮动图像, ${\sigma _i}^2$ 为图像的噪声大小, ${\sigma _x}^2$ 为形变场正则化的程度, s 为上一次迭代后的形变, u 为迭代更新的形变场, ${\left\| {F - M \circ s \circ \exp \left( u \right)} \right\|^2}$ 表示作为相似性测度的均方误差, $\dfrac{{\sigma _i^2}}{{\sigma _x^2}}{\rm{dist}}{\left( {s,s \circ \exp \left( u \right)} \right)^2}$ 表示形变场的误差函数. 而正则化过程一般通过高斯卷积完成, 得到流体模型或扩散模型的正则化效果.p 的形变, 可通过最小化全局能量函数得到:4 )式计算图像的形变场, 并在李群中实现形变场的复合得到最终的配准结果图像. 由于每次迭代都需要计算形变场的指数映射$\exp \left( u \right)$ , 因此利用单参数子群的性质${\rm{exp}}\left( u \right) = {\rm{ exp}}{\left( {{K^{ - 1}}u} \right)^K}$ 和SS ( scaling and squaring method)快速计算:N , 让${2^{ - N}}$ 趋近于零, 例如${\rm{max}}\left\| {{2^{ - N}}u\left( p \right)} \right\| \leqslant 0.5$ ;p : $v\left( p \right) \leftarrow {2^{ - N}}{\rm{ }}u\left( p \right)$ , 对v 做N 次复合运算$v \leftarrow v \circ v$ ;${v_1}$ 与${v_2}$ 并不是简单相加, 而是通过${v_2}$ 驱动形变, 重新插值得到${v'_1} $ , ${v'_1}$ 和${v_2}$ 再相加得到.F 和图谱图像M , 仿射变换后的形变场s 作为初始形变场;E , 即(4 )式计算更新后的形变场u ;u 做高斯卷积, 让$u \leftarrow {K_{{\rm{fluid}}}} * u$ , 产生流体模型的正则化效果;$c \leftarrow s \circ {\rm{exp}}\left( u \right)$ ;c 做高斯卷积, 让$s \leftarrow {K_{{\rm{diff}}}} * c$ , 产生扩散模型的正则化效果;E 收敛或达到最大迭代次数, 得到最终形变场s 及配准结果.2.3.COLLATE算法 -->2.3.COLLATE算法 COLLATE作为一种统计标签融合算法, 可以准确估计和解释空间变化的性能. 假设一幅图像有N 个像素点, R 个标签信息用来评估其真实结果. D N × R 的矩阵, 描述所有N 个体素中所有R 个配准结果的标记决策. 设T 为N 个元素的向量, 表示所有体素的隐式真分割, 其中${T_i}\{ 0,1, \cdots ,L - 1\} $ . 定义一个包含N 个元素的向量C , 它表示在每个体素的一致或混淆特征, 共有F 个等级, ${C_i} \in \{ 0,1, \cdots\!,F - 1\} $ . 定义 $\theta = [{\theta _1},{\theta _2},\! \cdots\!,$ ${\theta _R}] $ , 表示R 个配准结果对应的性能水平估计; 结合上述定义, 将$f(D,T,C|\theta )$ 定义为概率质量分布函数, 并通过最大期望算法(E-M algorithm, E-M)来实现性能水平参数$\theta $ 的估计, 其中, E-Step将估计图像体素i 属于每个一致性水平的概率, 这个概率在M-Step中估计性能水平参数时对每个体素的权重至关重要. COLLATE作为一种准确、鲁棒的融合算法, 已经成功用于RV分割[17 ] . 因此提出使用COLLATE算法进行RV标记图像的融合.3.一种新的RV多图谱分割框架 本文提出了结合Diffeomorphic demons算法的多图谱分割框架, 从心脏磁共振图像中自动精确提取RV轮廓, 一系列图像处理流程如图1 所示. 算法具体步骤如下:图 1 结合多图谱和Diffeomorphic demons算法的右心室分割流程图Figure1. Flow diagram of right ventricular segmentation combined with multi-atlas and Diffeomorphic demons algorithm.3.1.图谱集选择 3.1.图谱集选择 本文结合Adaptive AP算法和图谱集特点提出适合RV分割的图谱聚类方法, 具体流程如图2 所示.图 2 图谱图像聚类流程图Figure2. Atlas image clustering flow chart${l_1} - {l_n}$ 采用豪斯多夫距离(Hausdorff distance, HD)作为相似性度量进行Adaptive AP聚类, 得到结果${C_1}\left( l \right), {C_2}\left( l \right), \cdots ,$ ${C_m}\left( l \right) $ ; 取相应的图谱图像子集${C_1}\left( g \right), {C_2}\left( g \right), \cdots , $ ${C_m}\left( g \right) $ 采用归一化互信息(normal mutual information)作为相似性度量分别进行Adaptive AP聚类, 得到进一步的聚类子集${C_1}\left( g \right), {C_2}\left( g \right), \ldots , $ ${C_k}\left( g \right) $ . 多图谱在图谱数量的选择要平衡分割精度和速度之间的关系, 研究表明图谱数量在15—20幅范围之间, 可以保证分割精度的同时提高速度[18 ] . 因此, 我们将子集数量是否大于等于15作为满足条件进行筛选, 最后将符合要求的聚类子集再一次进行聚类, 得到一组聚类中心${g_1},{g_2}, \cdots ,{g_i}$ ; ${l_1},{l_2}, \cdots ,{l_i}$ 和集群${C_1}\left( g \right), {C_2}\left( g \right), \cdots , $ ${C_i}\left( g \right) $ ; ${C_1}\left( l \right), {C_2}\left( l \right), \cdots , {C_i}\left( l \right)$ .T 与i 个聚类中心经配准、融合得到初始分割结果L ; 然后依据相似性测度的大小选择图谱集. 文献[5 ]使用了Dice系数作为选择依据, 但是其只考虑了L 与${l_1},{l_2}, \cdots ,{l_i}$ 的重叠区域的大小. 本文从配准算法出发, 考虑其驱动力主要依靠图像梯度信息提出了一个新的相似性测度:${l_1},{l_2}, \cdots ,{l_i}$ 与L 之间最大差异的对称距离度量. NMI代表归一化互信息, 测量两幅图像的灰度相似性. D 表示相似性测度, 由 HD和NMI共同决定, $\alpha $ 和$1 - \alpha $ 代表二者的权重. 计算目标图像T 与各聚类中心的相似性测度, 选择相似性最高的聚类中心所代表的图谱集用于接下来的RV分割.3.2.配准和融合 -->3.2.配准和融合 Diffeomorphic demons算法保证了配准前后的拓扑保持性, 高效、灵活的计算方式对心脏图像的大形变配准表现出良好的性能. 为了提高结果的鲁棒性, 在进行Diffeomorphic demons配准之前, 首先对两幅图像进行仿射变换, 得到粗配准结果. 图3 是RV配准的典型例子, 可以看出Diffeomorphic demons在RV图像配准中取得了较好的结果.图 3 四个右心室配准的典型例子 (a) 目标图像; (b) 图谱图像; (b) 标记图像; (d) 配准结果Figure3. Four examples of typical right ventricular registration: (a) Target image; (b) atlas image; (c) label image; (d) registration result.图4 所示.图 4 RV标记图像的融合过程Figure4. RV label image fusion process4.实验结果与对比 24.1.实验数据 4.1.实验数据 Cine-CMRI短轴图像在GE1.5 T扫描仪上通过SSFP序列获取, 采集8—16层连续的电影短轴切片以覆盖整个心室. 具体成像参数: 图像矩阵大小256 × 256, FOV是360 mm × 360 mm, 层厚6—8 mm, 层间距2—4 mm, 一个完整的心动周期包括20—28个时相. 数据来源者均签署知情同意书. 随机选取34例短轴电影图像, 由专家手动勾画出ED, ES时相的RV轮廓, 该标记图像用于图谱制作. 另外随机选取30例数据用于算法验证, 同时将专家手动勾画得到的RV轮廓作为金标准, 用于实验结果评估.4.2.评估指标 -->4.2.评估指标 分割结果的评估是图像分割的重要步骤, 本文采用互补的两个客观指标对分割结果进行评估: 几何指标和临床表现, 综合两种评估指标可以防止对分割结果的片面评估, 保证评估结果的客观性和准确性. 定量评估金标准与算法分割结果的几何指标包括: Dice指标和豪斯多夫距离. Dice指标是两个区域重叠的度量, 其范围在0—1之间:${S_a}$ , ${S_b}$ 分别代表自动分割算法和金标准中的RV区域. Dice指标越高代表算法分割与金标准之间的重合程度越高. 豪斯多夫距离提供了两个标记轮廓之间最大差异的对称距离度量, 定义为:A , B 表示自动分割算法和金标准的RV轮廓, a 和b 分别表示轮廓A 和B 中的点, $d\left( {a,b} \right)$ 代表欧几里得距离.4.3.实验结果 -->4.3.实验结果 本文对30例临床心脏磁共振数据进行处理, 并与专家手动勾画的金标准进行比较. ED及ES的典型分割如图5 和图6 所示, 图中依次是RV的基底到顶端.图 5 ED从基底到顶端的RV分割结果Figure5. RV contour at ED from base to apex.图 6 ES从基底到顶端的RV分割结果Figure6. RV contour at ES from base to apex.表1 给出了RV分割结果在ED和ES的Dice指数和HD, 其中数据以均值(方差)形式呈现. 表中数据可以得到ED及ES的Dice指标平均为0.87, 0.81; ED和ES的HD平均为10.76和12.16 mm. 从结果比较, ED的分割结果与金标准的重合度更高. 与现有分割方法存在的问题相同, ES时相的分割结果精度相对较低. 主要原因是ED时相RV结构简单, 边界清晰; 而ES时相由于部分容积效应导致边界模糊且心室腔相对较小, 分割难度更高. 30例分割结果的Dice指标箱形图如图7 所示, 其中ED, ES的中位数分别为0.875, 0.820. 从图中可以看出ED时相的分割结果优于ES时相, 且分割结果更加稳定.Dice HD/mm ED 0.87(0.10) 10.76(4.5) ES 0.81(0.16) 12.16(6.54)
表1 ED, ES的平均Dice指数和豪斯多夫距离Table1. Average Dice index and Hausdorff distance of ED and ES.图 7 Dice指标的箱形图Figure7. Box diagram of the Dice index.图8 所示, 图中Data表示30例数据结果. 图8(a)、(c)、(e) y 表示线性回归方程并在图中标出. EDV, ESV及 EF的相关系数R 分别为 0.94, 0.90, 0.86. 其中, EDV的结果与真实临床指标的相关性最高. 图8(b)、(d)、(f) 图 8 本文算法与金标准结果分析 相关性分析 (a) 舒张末期容积; (b) 收缩末期容积; (c) 射血分数; Bland-Altman分析 (d) 舒张末期容积; (e) 收缩末期容积; (f) 射血分数Figure8. Analysis of algorithm and gold standard results. Correlation analysis (a) EDV; (b) ESV; (c) EF; Bland-Altman analysis (d) EDV; (e) ESV; (f) EF.http://www.circlecvi.com/ )开发的心脏分析软件心血管成像(CVI)得到. 卷积神经网络是CVI分割心脏图像的主要方法, 其结果的准确性也已得到验证[19 ,20 ] . 图9 为深度学习结果与金标准的相关性及Bland-Altman分析(图中各符号物理意义均同图8 ). EDV, ESV, EF的相关系数R 分别为0.93, 0.86, 0.66, 与本文算法得到的相关系数 0.94, 0.90, 0.86相比, 深度学习方法的ESV和EF的一致性水平明显偏低. 图9(b)、(d)、(f) 图 9 深度学习与金标准结果分析 相关性分析 (a) 舒张末期容积; (b) 收缩末期容积; (c) 射血分数; Bland-Altman分析 (d) 舒张末期容积; (e) 收缩末期容积; (f) 射血分数Figure9. Analysis of deep learning and gold standard results. Correlation analysis (a) EDV; (b) ESV; (c) EF; Bland-Altman analysis (d) EDV; (e) ESV; (f) EF.5.结 论 RV复杂结构和Cine-CMRI的影像学特点是其分割的主要困难: RV内包括随心动周期变化的乳头肌和小梁肌; 部分容积效应和心脏运动常导致Cine-CMRI短轴图像的低信噪比. 在基底部, 可以观察到RV, LV, 心房及周围结构往往难以区分, 导致RV边界不确定. 在心室顶端, 心室腔狭窄且心肌及内部结构分布不均, 分割更加困难. 针对这些问题, 提出一种从心脏磁共振短轴图像中自动分割RV的新方法. 该方法采用多图谱框架和Diffeomorphic demons算法结合, 并且依据豪斯多夫距离和归一化互信息采用Adaptive AP获得图谱集. 实验结果表明, 该方法取得了与金标准具有较高一致性的分割结果, 无论在几何指标和临床表现中, 都成功验证了方法的可行性和准确性. 与其他现有方法比较, 我们提出的方法可以做到准确、快速地分割出RV轮廓, 具有更强的鲁棒性和准确性, 特别是心室腔狭小的图像. 提出的新方法有望辅助临床心脏疾病的诊断、治疗和预后. 同时, 为了更好地提高分割效果, 还可以结合图像特征进一步优化配准算法, 提高多图谱分割精度和速度将是下一步要做的工作. 










































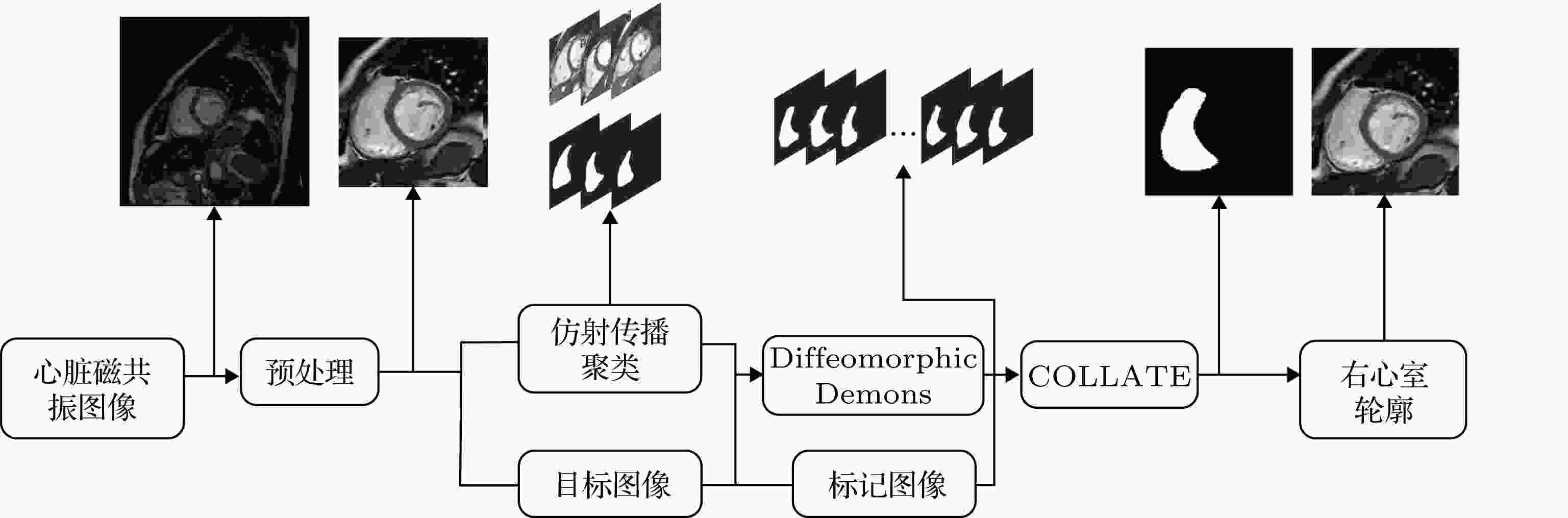 图 1 结合多图谱和Diffeomorphic demons算法的右心室分割流程图
图 1 结合多图谱和Diffeomorphic demons算法的右心室分割流程图 图 2 图谱图像聚类流程图
图 2 图谱图像聚类流程图

















 图 3 四个右心室配准的典型例子 (a) 目标图像; (b) 图谱图像; (b) 标记图像; (d) 配准结果
图 3 四个右心室配准的典型例子 (a) 目标图像; (b) 图谱图像; (b) 标记图像; (d) 配准结果 图 4 RV标记图像的融合过程
图 4 RV标记图像的融合过程


 图 5 ED从基底到顶端的RV分割结果
图 5 ED从基底到顶端的RV分割结果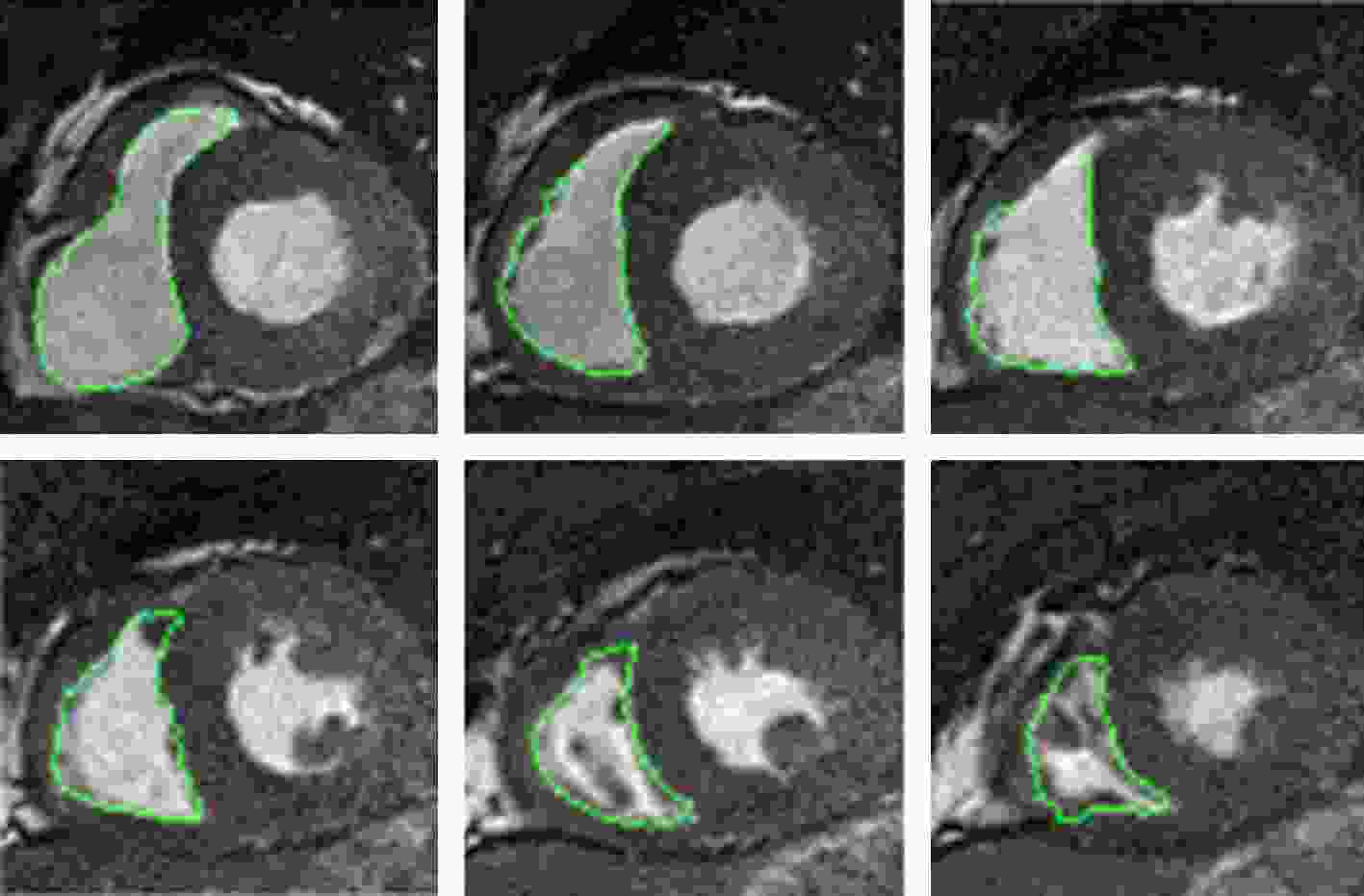 图 6 ES从基底到顶端的RV分割结果
图 6 ES从基底到顶端的RV分割结果 图 7 Dice指标的箱形图
图 7 Dice指标的箱形图 图 8 本文算法与金标准结果分析 相关性分析 (a) 舒张末期容积; (b) 收缩末期容积; (c) 射血分数; Bland-Altman分析 (d) 舒张末期容积; (e) 收缩末期容积; (f) 射血分数
图 8 本文算法与金标准结果分析 相关性分析 (a) 舒张末期容积; (b) 收缩末期容积; (c) 射血分数; Bland-Altman分析 (d) 舒张末期容积; (e) 收缩末期容积; (f) 射血分数 图 9 深度学习与金标准结果分析 相关性分析 (a) 舒张末期容积; (b) 收缩末期容积; (c) 射血分数; Bland-Altman分析 (d) 舒张末期容积; (e) 收缩末期容积; (f) 射血分数
图 9 深度学习与金标准结果分析 相关性分析 (a) 舒张末期容积; (b) 收缩末期容积; (c) 射血分数; Bland-Altman分析 (d) 舒张末期容积; (e) 收缩末期容积; (f) 射血分数