摘要:颗粒分离的物理机制目前没有统一解释. 本文采用三维离散元模型, 模拟了剪切槽内两种尺度的球形二元颗粒在高度方向上位置互相颠倒的现象. 关注大颗粒跃升过程中的运动学和动力学行为特征, 观测到大颗粒跃升过程分三个阶段: 弛豫阶段、起跳阶段和平衡阶段. 定量分析了摩擦系数对颗粒受力等具体影响. 结果显示弛豫时间随着摩擦系数的增大而减少, 颗粒最终的平衡高度随着摩擦系数的增大而增大. 定义了浮升因子, 发现浮升因子在大颗粒起跳点处陡降, 形成大颗粒跃升的“窗口时间”. 揭示大颗粒的起跳是受力脉动高频特性和浮升因子陡降两个因素共同作用的结果, 即颗粒的上升运动由受力和周围空间决定.
关键词: 离散元模拟/
剪切分离/
颗粒动力学/
摩擦系数

English Abstract

全文HTML

--> --> -->

颗粒是自然界常见的离散物质, 静止时呈现固体状态, 而整体运动时呈现类流体状态^[1]. 不同的颗粒在剪切或者振动等外力激励条件下, 会出现不同的移动分离和混合现象^[2](花瓣形, 圣诞树形, 指形, 三明治^[3]等). 颗粒的分离与混合广泛应用在制药、食品、化工和能源等领域^[4], 利用二元颗粒密度、尺寸、几何形貌以及其他性质的差异, 施加外部作用, 能够实现颗粒分离或混合^[5-7]. 除工业领域, 自然界的山体滑坡、泥石流、雪崩中亦有颗粒独特的分离运动, 如大石块聚集在顶部, 小石块沉降在底部的现象^[6]. 正因为颗粒运动的高应用价值和复杂性, 在过去的几十年中, 颗粒流一直是研究热点^[8].
针对剪切二元颗粒体系分离的现象已经开展了实验^[9-12]、数值模拟^[13]研究, 而对分离现象的理论研究以三种典型机制为主导: “渗流”机制理论^[14]; “对流”机制^[15]; “凝聚”机制^[16]; 颗粒分离的新机制^[17-19], 对于不同的分离运动倾向于用多种机制竞争或主导机制解释. 随着新分离现象的发现不断提出不同机制, 因此目前依旧没有统一的颗粒运动的物理解释. 主要原因在于以往分析集中于对颗粒群使用经典流体理论类比分析, 颗粒系统作为软凝聚物质系统不能被其套用; 其次, 缺乏物理机制的揭示^[11,20], 包括1)缺乏底层颗粒在向上跃升过程中的运动学以及动力学行为特征分析, 2)缺乏讨论底层颗粒向上起跳的控制条件, 3)缺乏研究细观颗粒群的空间分布结构对颗粒分离过程的影响规律. 本文的重要工作就是探讨以上三点. 同时, 颗粒间的摩擦耗散作用是区别于其他物质状态的主要特征^[21], 摩擦力的变化导致颗粒系统的能量耗散变化, 甚至导致颗粒分离的变化发生逆转^[22], 因此研究摩擦系数对颗粒运动的变化具有重要意义.
本文采用三维离散元(DEM)方法, 模拟大小两种尺度球形颗粒初始时刻处于底层的大颗粒向顶层跃升的运动过程, 研究颗粒间的摩擦作用强弱对颗粒上升变化的影响, 获得摩擦力对颗粒跃升行为动力学的影响规律, 揭示大颗粒跃升的物理机制, 为后续人们理解颗粒分离运动理论提供参考依据.

2

-->

2.1.物理模型

本文模拟的二元颗粒系统, 周侧固定的两个内外圆柱面和底部旋转的圆环形底盘构成, 7501颗颗粒(7500颗直径为0.002 m和1颗直径为0.003 m的球形颗粒)自由堆积在圆环槽型限域空间中, 如图1所示. 底面以一定的角速度旋转, 对槽内的颗粒群产生恒定剪切力. 圆环槽内径为0.294 m, 外径为0.317 m, 高度为颗粒群的堆积高度. 模拟系统置于重力环境, 以剪切盒的底部中心为坐标原点, 重力反方向为z轴正方向, 坐标轴设立满足右手系定则. 颗粒系统的填注方式如下: 首先将大颗粒置于剪切槽底层, 然后在容器上方随机生成小颗粒倾倒入槽, 释放完预设数目的小颗粒后再合上顶盘. 系统在重力条件下弛豫足够长时间以确保总动能稳定在较低的范围内后旋转底盘, 旋转周期为20 s. 观察大颗粒在小颗粒群中的运动特征.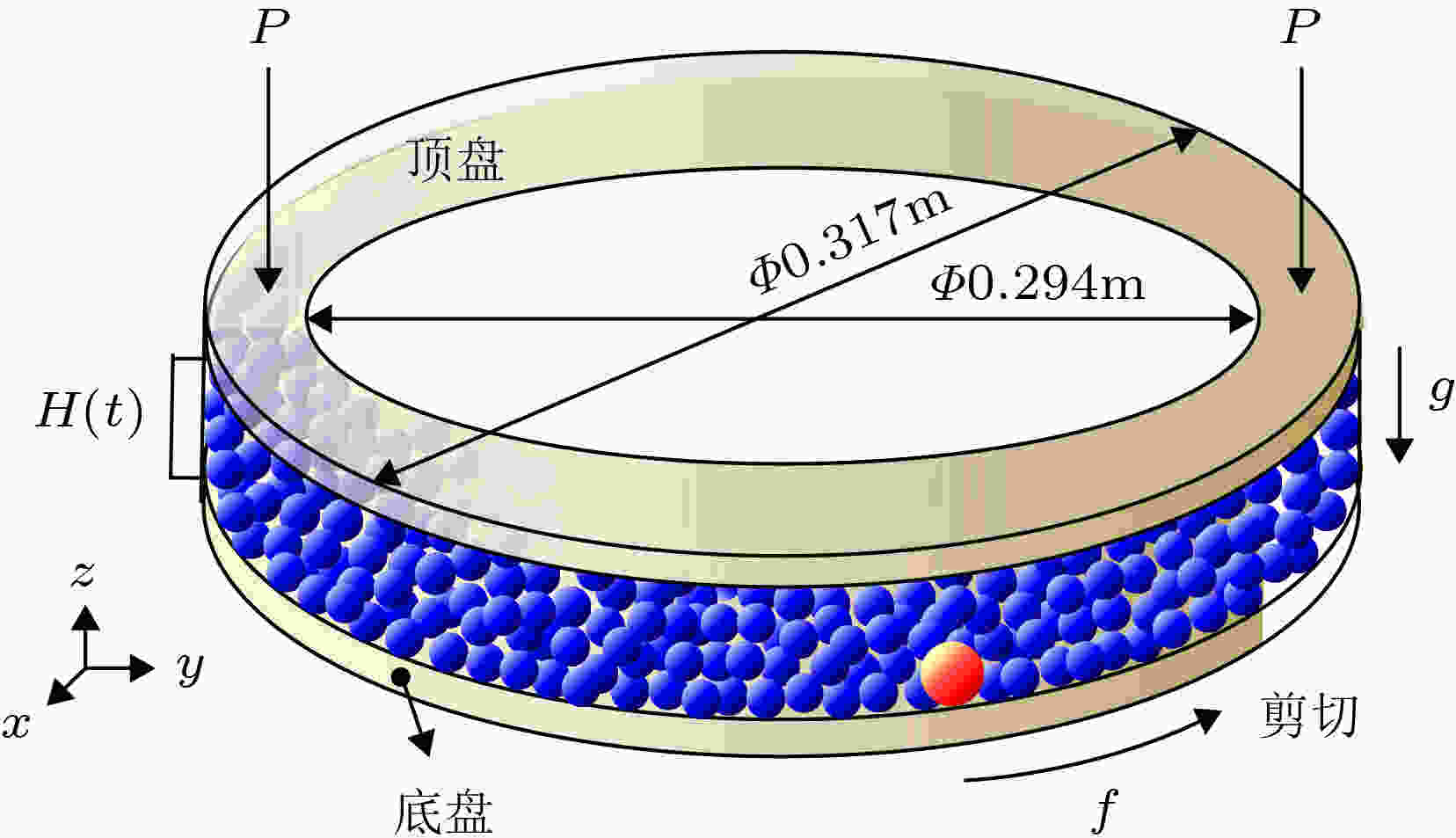
图 1 三维剪切颗粒体系示意图
Figure1. Schematic diagram of shear granular system.

2 -->

2.2.数学模型

模拟中颗粒的运动包括平动和转动, 分别采用(1)式和(2)式进行描述

$m{\ddot X} = {{F}_n} + {{F}_t} + {{F}_b},$

${I}\frac{{{\rm{d}}{{\omega }}}}{{{\rm{d}}t}} = {{{r}}_c} \times {{F}_t},$

其中F_n是颗粒间碰撞的法向接触力, F_t是颗粒间碰撞的切向接触力, F_b是除碰撞力以外的力. 重力及颗粒间的法向和切向接触力使颗粒发生平动; 切向接触力产生力矩, 导致颗粒发生旋转.
颗粒间的相互碰撞采用弹簧阻尼软球模型描述. 弹簧模型考虑颗粒因弹性碰撞受到的作用力, 颗粒在法向和切向分别发生弹性形变, 弹性形变量与颗粒受到的弹性作用力成正比. 阻尼模型模拟颗粒因非弹性形变导致的机械能损失, 也可以分解为法向和切向分量. 因此, 当球i, j发生碰撞时, 球i受到的切向和法向作用力为

$\begin{aligned}{{F}}& = {{{F}}_n} + {{{F}}_t}\\& = \left( {{k_n}{{{\delta }}_{{n_{ij}}}} - {\gamma _n}{{{\nu }}_{{n_{ij}}}}} \right) + \left( {{k_t}{{{\delta }}_{{t_{ij}}}} - {\gamma _t}{{{\nu }}_{{t_{ij}}}}} \right),\\&\underbrace {\begin{array}{*{20}{c}}{\underbrace {}_{\text{法向位移}}} & {\underbrace {}_{\text{法向相对速度}}}\end{array}}_{\text{法向力}}\underbrace {\begin{array}{*{20}{c}}{\underbrace {}_{\text{切向位移}}} & {\underbrace {}_{\text{切向相对速度}}}\end{array}}_{\text{切向力}}\end{aligned}$

其中${k_n}$表示法向弹性碰撞系数, ${{{\delta }}_{{n_{ij}}}}$是两个颗粒之间的法向重叠距离; ${\gamma _n}$是法向黏弹性阻尼系数, ${{{\nu }}_{{n_{ij}}}}$是法向相对速度; ${k_t}$是切向弹性碰撞系数, ${{{\delta }}_{{t_{ij}}}}$是两个球状颗粒的切向相对位移向量; ${\gamma _t}$是切向接触的黏弹性阻尼系数, ${{{\nu }}_{{t_{ij}}}}$是切向相对速度. 其中${{{\delta }}_{{t_{ij}}}}$必须满足摩擦屈服准则${{{F}}_t} \leqslant {X_\mu }{{{F}}_n}$, ${X_\mu }$是最大静摩擦系数. 以上参数的计算公式如下:

$\begin{split}& {k_n} = \frac{4}{3}{Y^*}\sqrt {{R^*}{{{\delta }}_{{n_{ij}}}}} ,{\gamma _n} = - 2\sqrt {\frac{6}{5}} \beta \sqrt {{S_n}{m^*}} \geqslant 0,\\& {k_t} = 8{G^*}\sqrt {{R^*}{{{\delta }}_{{n_{ij}}}}} ,{\gamma _t} = - 2\sqrt {\frac{6}{5}} \beta \sqrt {{S_t}{m^*}} \geqslant 0,\\& {S_n} = - 2{Y^*}\sqrt {{R^*}{{{\delta }}_{{n_{ij}}}}} ,{S_t} = 8{G^*}\sqrt {{R^*}{{{\delta }}_{{n_{ij}}}}} ,\\& \beta = \frac{{\ln \left( e \right)}}{{\sqrt {{{\ln }^2}\left( e \right)} + {{\text{π}}^2}}}\frac{1}{{{Y^*}}} = \frac{{\left( {1 - {\nu _i}^2} \right)}}{{{Y_i}}} + \frac{{\left( {1 - {\nu _j}^2} \right)}}{{{Y_j}}},\\& \frac{1}{{{G^*}}} = \frac{{2\left( {2 - {\nu _i}} \right)\left( {1 + {\nu _i}} \right)}}{{{Y_i}}} + \frac{{2\left( {2 - {\nu _j}} \right)\left( {1 + {\nu _j}} \right)}}{{{Y_j}}},\\& \frac{1}{{{R^*}}} = \frac{1}{{{R_i}}} + \frac{1}{{{R_j}}}\frac{1}{{{m^*}}} = \frac{1}{{{m_i}}} + \frac{1}{{{m_j}}},\end{split}$

式中${R_i},{R_j}$为颗粒半径, ${m_i},{m_j}$是颗粒质量, ${Y_i},{Y_j}$是杨氏模量, ${\nu _i},{\nu _j}$是泊松系数, e为恢复系数.
模拟采用美国圣地亚实验室开发的三维DEM程序LIGGGHTS^[23]. 微分方程采用verlet积分算法. 模拟中力学参数和其他参数的设置详见表1.

参量	数值
杨氏模量Y/Pa	107
泊松系数ν	0.25
恢复系数e	0.5
摩擦系数f	0.3, 0.35, 0.4, 0.45, 0.47, 0.49, 0.51, 0.55, 0.6
颗粒直径R/m	0.002 (小颗粒), 0.003 (大颗粒)
颗粒密度ρ/kg·m–3	1000
时间步长t/s	2 × 10–6
模拟物理时间t/s	80

表1模拟参数
Table1.Simulation parameters.

本文的数值模型初始时刻大颗粒在下部, 小颗粒在上部, 经过中间的掺混过程, 最终达到位置颠倒的平衡状态, 与May等^[10] 的实验结果一致, 如图2所示. 验证了本文数值模型以及参数设置的可行性.
图 2 实验与模拟结果对比图　(a) May等^[10]实验获得大小颗粒位置互相颠倒的现象; (b)本文的模拟结果
Figure2. Comparison between the present simulation and the previous experimental results: (a) The Brazil-nut effect phenomenon from May^[10]; (b) the present numerical simulation results.

模拟结果显示, 对于所有的摩擦系数, 大颗粒向上跃升的过程都会经历三个阶段: 1)弛豫阶段, 大颗粒随着剪切槽底面周向旋转, 但高度位置不变; 2)起跳阶段, 大颗粒经历极短的时间跨度迅速到达颗粒群顶层; 3)平衡阶段, 到达顶层的大颗粒在高度方向上下脉动, 但不会再回落到底层, 完成颗粒空间位置的颠倒. 以下的结果与讨论, 按照跃升过程经历的三个阶段为顺序展开, 首先, 以摩擦系数为0.3为例, 介绍大颗粒运动的整体特征; 其次, 讨论摩擦系数对大颗粒运动的影响规律; 最后, 探讨颗粒起跳的物理机理.
2

-->

3.1.大颗粒的整体运动特性

图3(a)为大颗粒三维空间位置随时间的演变过程. 由图可见, 大颗粒做逆时针旋转上升运动, 三维轨迹可以分为三个阶段: 1)定义t从0—29.92 s的时间跨度为起跳弛豫时间, 大颗粒在剪切槽底部做旋转运动, 在高度方向上变化很小, 间歇性地发生小幅度不规则跳动; 2) t = 29.92 s开始起跳上升, 起跳的过程很短, 经历3.88 s后, t = 33.8 s时刻跃升过程完成; 3)大颗粒上升到顶部, 在顶部平衡位置附近上下脉动.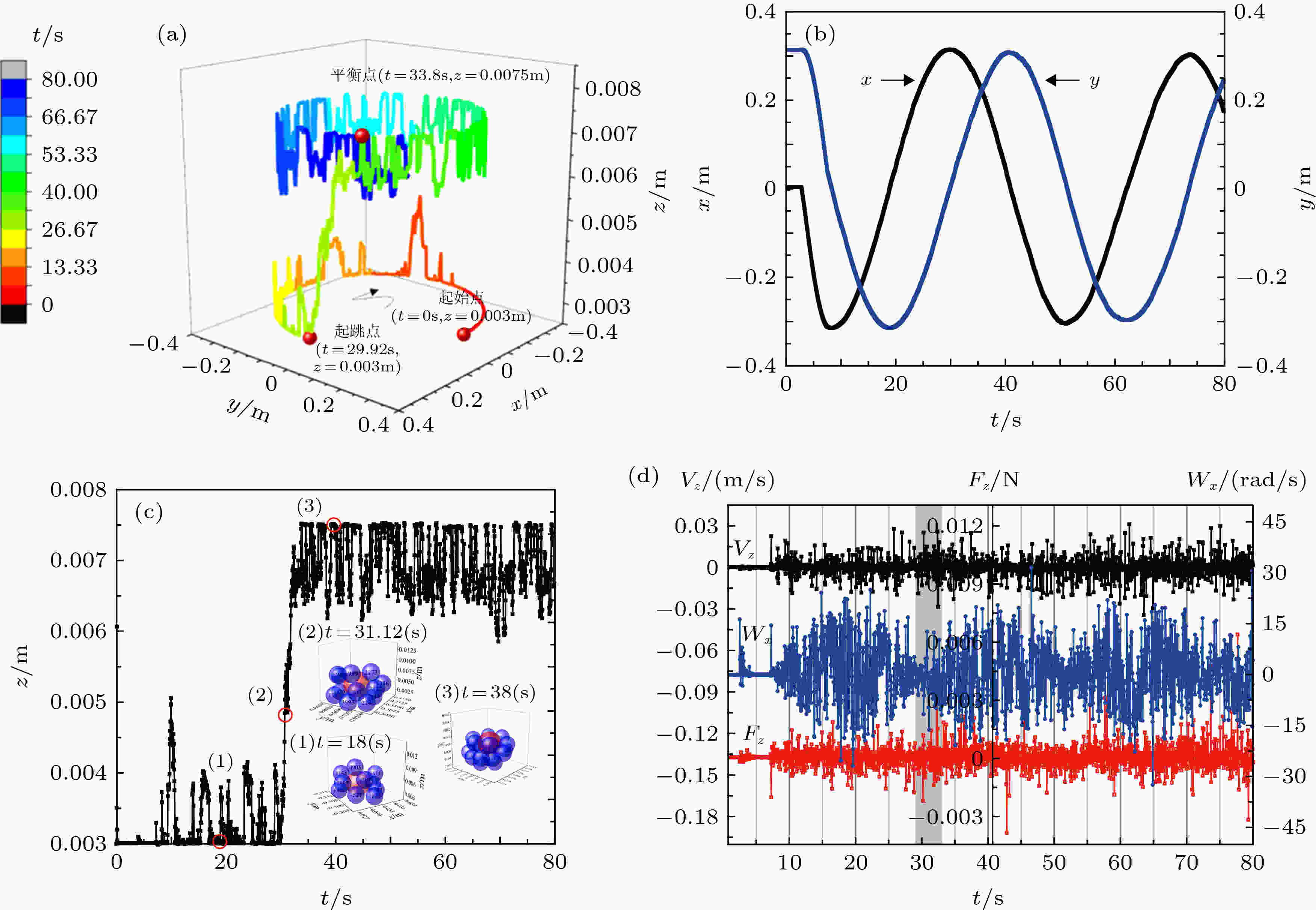
图 3 摩擦系数为0.3的大颗粒运动及力学特征图　(a)大颗粒轨迹随时间演变图; (b)大颗粒x, y方向位移随时间变化图; (c)大颗粒z方向位移随时间演变图; (d)大颗粒在z方向线速度、受力以及旋转角速度随时间变化规律, 灰色条带对应起跳过程
Figure3. Characteristics of the large particle kinetics and kinematics with friction coefficient of 0.3: (a) Large particle trajectory evolution over time; (b) changes of large particle trajectory components in x and y directions with time; (c) changes of large particle trajectory components in z direction with time; (d) changes of translational velocity, force and rotational velocity with time.

为了进一步探究颗粒轨迹特征, 将图3(a)所示的颗粒三维轨迹分解为水平方向的x和y位移曲线, 如图3(b)所示, 以及高度方向上的z位移曲线, 如图3(c)所示. 由图3(b)可见, 颗粒在水平方向的位移特征为类圆周运动, 周期为43 s, 是剪切槽底面旋转周期的一半, 说明大颗粒的运动落后于剪切槽底面的旋转运动, 这是由颗粒与底面间的相对滑动引起的. 图3(c)所示的z方向位移时间序列清楚地描述了颗粒瞬间跃升的特征. 大颗粒在整个过程中的运动并非平稳直线运动, 而是伴随着回落的运动, 起跳上升运动前大颗粒在底部发生多次假“起跳”, 但均回落到底部, 直到t = 29.92 s后不再落回, 而是逐渐上升到达顶部, 最后停留在顶部做小幅度脉动, 脉动幅度为0.00135 m.
大颗粒起跳的临界条件与颗粒受力平衡以及邻域内小颗粒空间排布结构密切相关, 首先探查小颗粒空间密度分布对大颗粒起跳的影响规律. 选取三个关键时间点, 如图3(c)中(1)、(2)和(3)点所示, 对应于上升过程的“起跳”起始点, “跃升”中间点和“平衡”点, 考察这三个时刻大颗粒邻域空间内小颗粒的空间排列结构, 如图3(c)中插图所示. 发现在“起跳”起始点, 大颗粒上方的小颗粒排列密度较其他区域稀疏, 这样给大颗粒的“起跳”提供了上升空间; 在“跃升”中间点, 大颗粒底部小颗粒排列较顶部紧密, 大颗粒似乎是被周围颗粒“挤压”上升的; 在“平衡”点, 大颗粒下部的小颗粒密集排列, 支撑大颗粒在剪切槽顶部达到动态平衡.
引起大颗粒起跳的另外一个可能因素是大颗粒在高度方向的受力特征, 特别需要关注大颗粒起跳前后在高度方向上的受力F_z是否具有明显的变化, 为此, 我们对大颗粒进行z方向的力学分析, 提取速度V_z, 受力F_z, 以及转动角速度ω_z的时间序列, 如图3(d)所示, 图中的灰色条带对应起跳过程. 从图中可以看出, 速度、受力和转动角速度在“起跳”时刻以及“跃升”过程中, 呈现均值为0的脉动分布状态, 没有呈现出直觉预期的上升力大于下沉力的规律. 因此, 在起跳前后, 颗粒在高度方向上的受力没有特殊性, 受力特征本身不是颗粒起跳的决定因素.
2 -->

3.2.摩擦系数对颗粒群动量传输以及整体堆积密度的影响

本文模拟中, 颗粒群的堆积高度代表颗粒堆积的松散程度, 通过大颗粒到达顶部后的平衡高度表征. 如图4(a)所示, 大颗粒的平衡高度随着摩擦系数的增大而增大, 这也意味着小颗粒群空间排列更为松散, 有利于大颗粒由下至上的跃升过程, 对应于大颗粒的起跳弛豫时间将会更短, 这一推论由图4(b)所示的大颗粒起跳弛豫时间随摩擦系数的变化规律.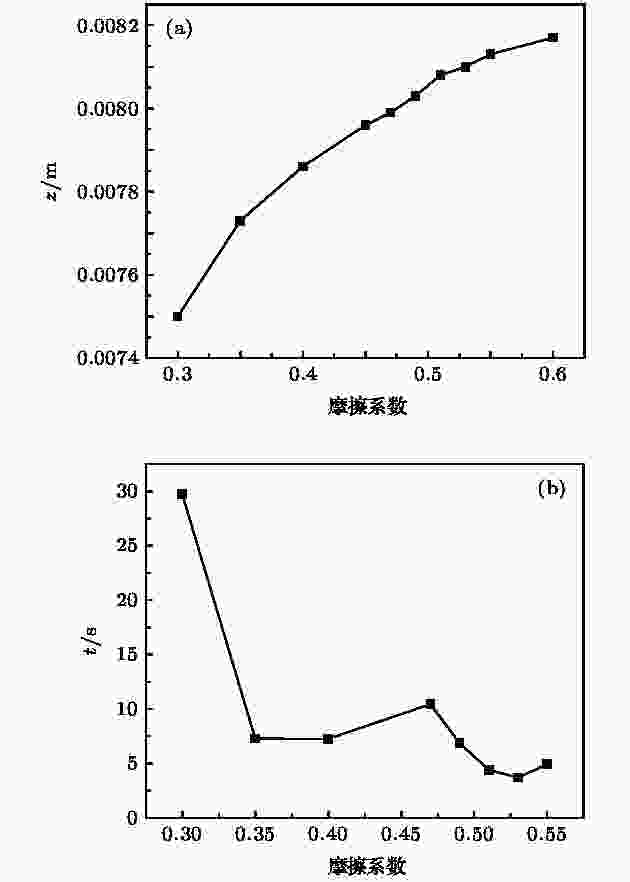
图 4 (a)平衡高度随摩擦系数变化图; (b)起跳弛豫时间随摩擦系数变化图
Figure4. (a) Equilibrium height versus friction coefficient; (b) relaxation time changes with friction.

验证表明, 总体上大颗粒的起跳弛豫时间随摩擦系数的增大而减小, 即随着摩擦系数的增大, 大颗粒能够更快地达到起跳临界点. 当摩擦系数为0.47时, 起跳时间点较为特殊, 这个特殊现象的原因会在后续研究中进一步分析.
在模拟过程中, 因小颗粒注入满剪切槽的随机性, 可能出现大颗粒被小颗粒击中弹起无法回落到底部而是其他小颗粒上方的情况, 这种情况下大颗粒的跃升不是本文探讨的内容. 本文模拟中摩擦系数为0.45和0.6两种情况下, 会出现以上情况, 因此, 在分析颗粒上升过程随摩擦系数的变化规律时, 将这几个数据点剔除.
2 -->

3.3.摩擦系数对大颗粒动力学特征的影响规律

图5(a)为不同摩擦系数下z方向分力的全程变化曲线, 可以看出, 针对不同的摩擦系数, F_z均随时间表现为0值附近上下脉动的特征, 且F_z在对应的起跳时间点附近无明显变化, 因此颗粒的突跳并非是受力的突然变化造成的. 对于不同的摩擦系数, 我们观察到, 随着摩擦系数的增加, F_z上下脉动的幅值范围变大. 为了提取这种幅值变化特征, 采用如下方法: 首先针对整体脉动数据去掉时均值, 然后分别求出正负脉动波的均值, 最后对两均值绝对值求和即为脉动域宽值. 图5(b)所示即为F_z脉动波域宽随摩擦系数的变化曲线图, 由图可看出, 随着摩擦系数的增加, F_z域宽呈现增大的趋势, 即每次脉动, 大颗粒获得了更大的弹跳的能力. 因此, 摩擦系数的增大, 有利于大颗粒在更短的时间内实现起跳.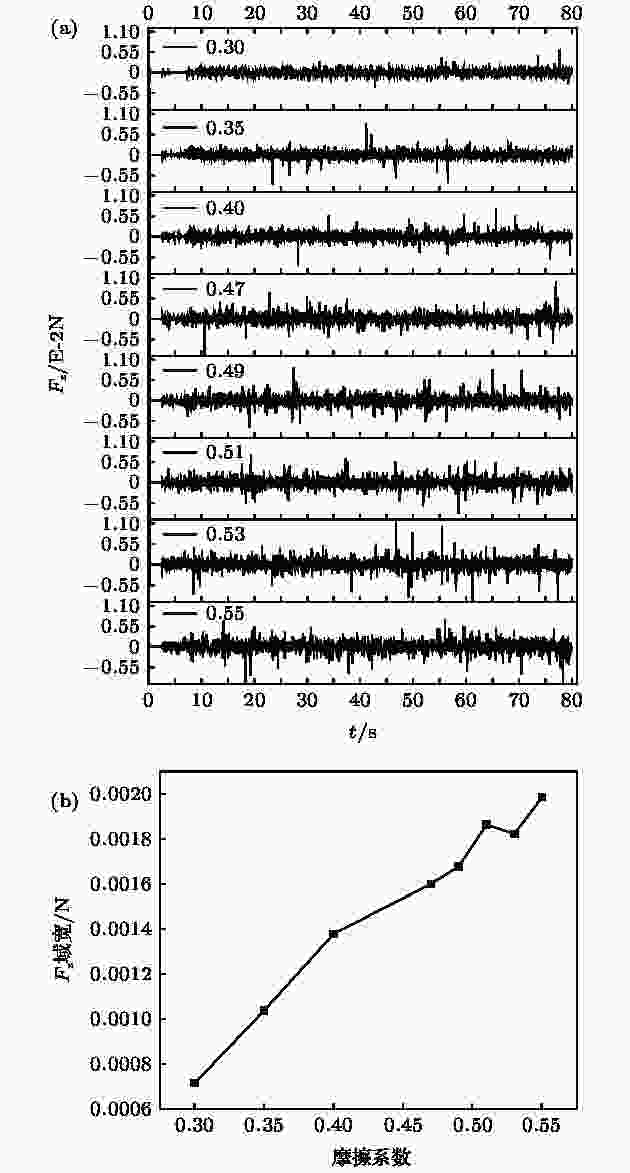
图 5 (a)不同摩擦系数下z方向受力Fz时间变化序列; (b) F_z脉动域宽随摩擦系数的变化规律
Figure5. (a) F_z changes with time for different friction coefficients; (b) F_z oscillation magnitude changes with friction coefficients.

2 -->

3.4.大颗粒邻域空间内小颗粒群空间排列结构

小颗粒群在空间的排列状态对大颗粒的行为特征具有重要的影响, 甚至影响大颗粒的起跳过程. Zhang和Campbell^[24]提出沿用至今的思路: 颗粒群体运动行为存在两种状态, 即类液态和类固态, 类固态行为下, 颗粒群整体呈现出固体特性, 颗粒的相对位置以及间距变化很小; 类液态行为下, 颗粒群呈现流体流动特征, 颗粒间相对位置呈现较大变化. 更为重要的是, 这两种状态能够同时存在于颗粒群体系中, 中间存在一个明显的界面划分类液态和类固态区域. 联系本文的模拟结果, 提出以下假设理论: 大颗粒在跃升过程中, 处于大颗粒上部的小颗粒呈现类流体运动态, 小颗粒间的间距变化较大, 给大颗粒向上跃升提供了可能的空间; 另一方面, 处于大颗粒下部的小颗粒呈现类固体运动态, 小颗粒间的间距变化较小, 使得大颗粒能够获得底部的支撑作用, 不再回落到剪切槽的底部, 从而完成跃升过程, 在顶部达到动态平衡.
为了验证以上理论, 我们引入浮升因子的概念, 表征大颗粒周围球形邻域空间内, 上半部分和下半部分小颗粒个数的差异. 浮升因子计算方法示意图如图6所示, 考虑到本文模拟薄层颗粒体系, 我们以大颗粒球心为原点、0.007 m(大颗粒半径与小颗粒直径之和)为半径划定球形邻域. 设立上下区域分界面AB, 分界面穿过大颗粒球心并且平行于xy平面, 分别统计分界面上下的小颗粒数目, 定义浮升因子为上区域颗粒数目与下区域颗粒数目的比值, 浮升因子越小, 说明下部颗粒比上部颗粒排列越密集, 越有利于大颗粒跃升.
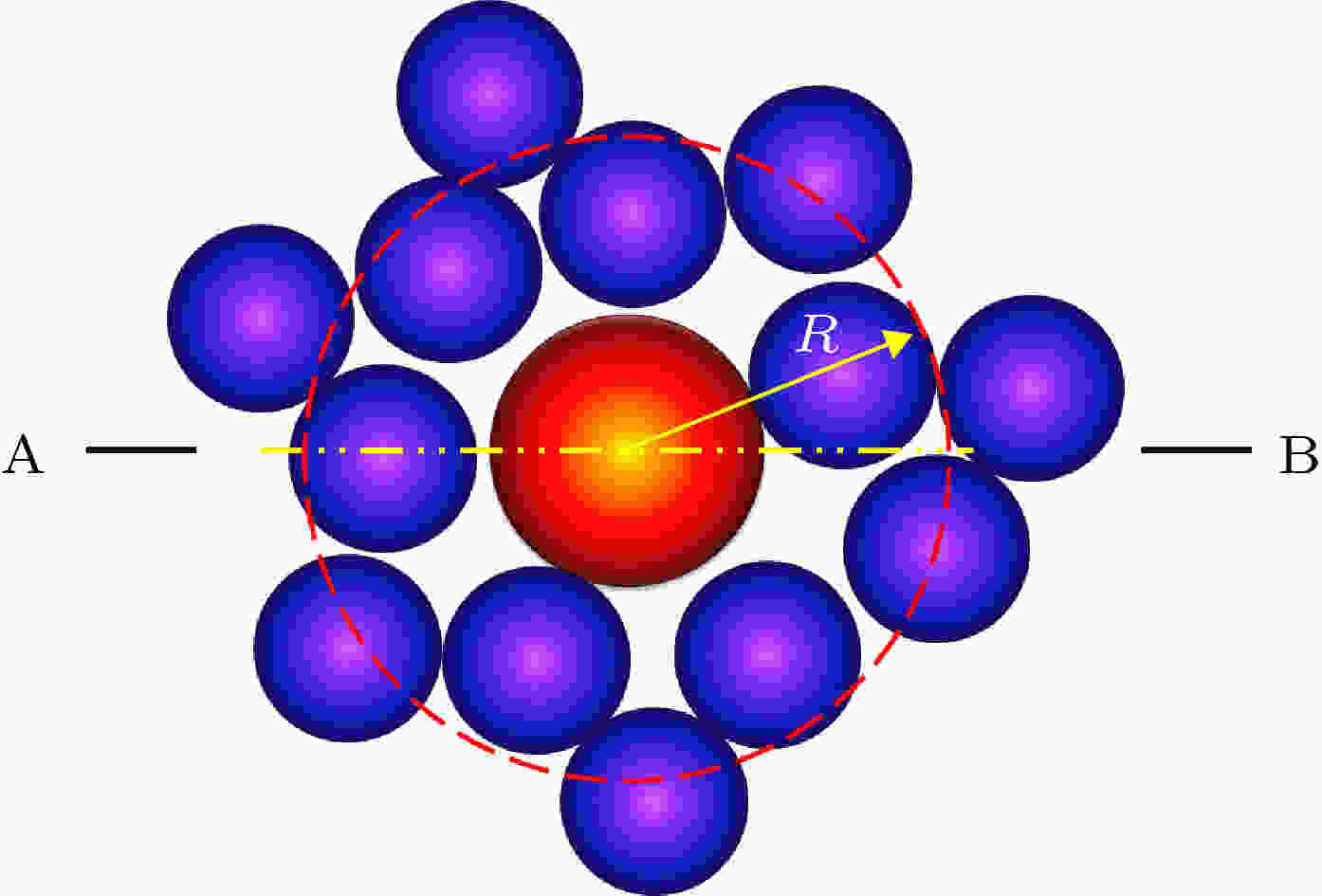图 6 浮升因子计算模型
Figure6. Floating factor calculation model.

针对低、中、高三种摩擦系数, 鉴别浮升因子随时间的变化过程, 其中低摩擦系数为0.35、中摩擦系数为0.49、高摩擦系数为0.55.
图7(a)—图7(c)分别描述了三种摩擦系数下颗粒起跳轨迹与浮升因子随时间变化的对应关系: 起跳前, 浮升因子的数值大于1, 大颗粒在底部; 起跳过程中, 浮升因子减小, 下部小颗粒的数目大于上部小颗粒的数目, 大颗粒获得了起跳必要的上升空间, 下部颗粒群提供了必要的底部支撑; 起跳结束, 浮升因子小于1, 大颗粒到达顶部. 由图7(a)—图7(c)可见, 大颗粒的起跳轨迹与浮升因子的突降转变点具有很好的对应关系, 在起跳时刻, 浮升因子的陡降, 大颗粒上层的小颗粒排列疏松, 为大颗粒的跃升提供至为关键的“窗口时间”. 图7(d)比较了浮升因子突降转变点随摩擦系数增大更快出现, 发现随摩擦系数的增大, 大颗粒起跳弛豫时间变短, 对应的浮升因子更快地下降到平衡状态.
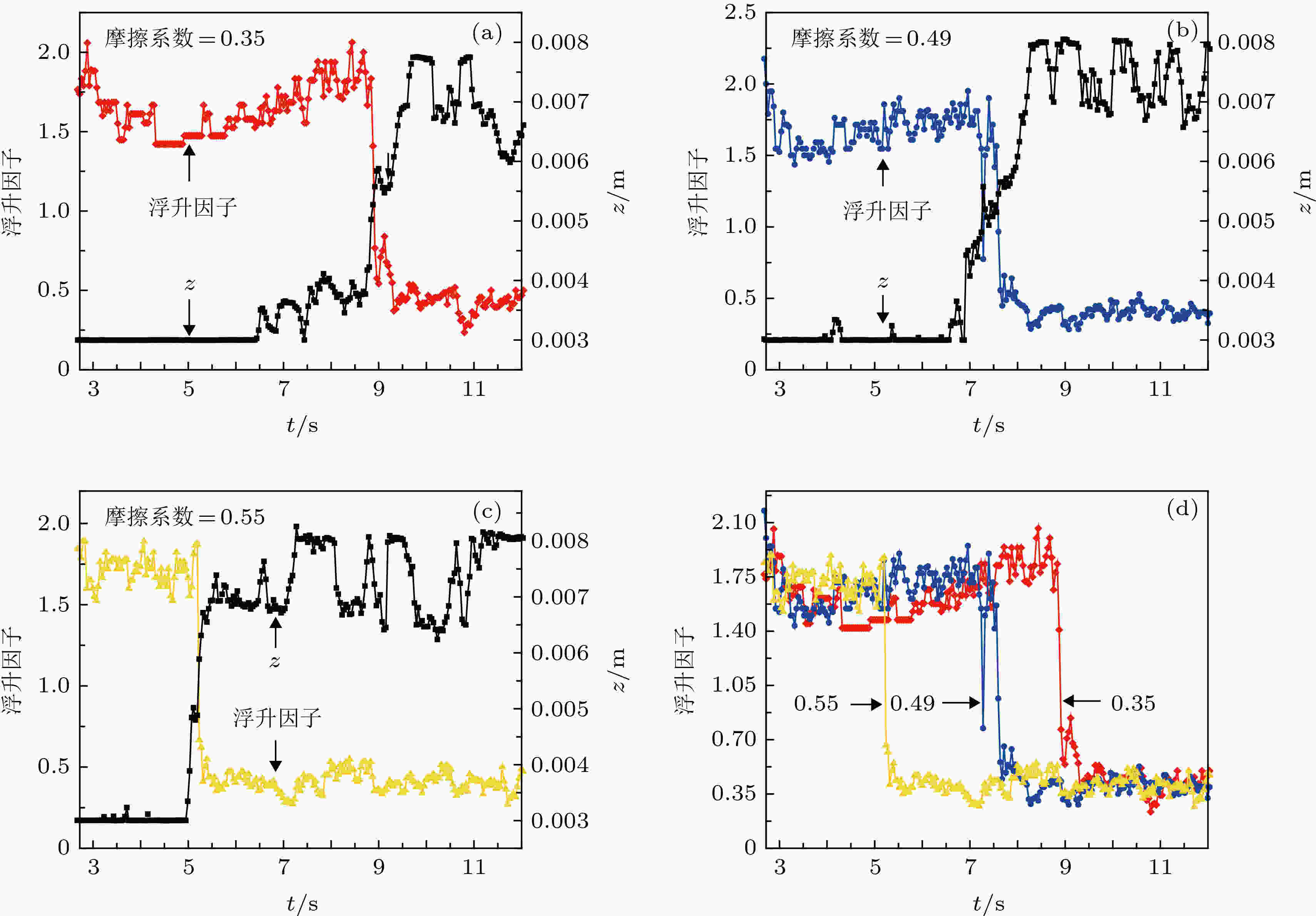图 7 起跳过程中浮升因子随时间变化图　(a)?(c)浮升因子在颗粒起跳过程中的变化规律, 摩擦系数分别为0.35 (a) 0.49 (b) 0.55 (c) 图中彩色线表示浮升因子, 黑色实线表示对应时刻颗粒高度的变化过程; (d)随摩擦系数增大浮升因子突降转变点提前
Figure7. The floating factor variation with time under the friction coefficients of 0.35 (a), 0.49 (b) and 0.55 (c). The color line indicates the floating factor, and the black line represents the z trajectory. (d) sharp decrease point of the floating factor occurs earlier with friction coefficient increment.

大颗粒的平均起跳过程为3 s左右, 在这个时间跨度内颗粒受力脉动为15—30次, 即大颗粒受力的高速脉动特性为大颗粒提供多次跃升的力学可能性, 当且仅当大颗粒上部和下部的小颗粒数目比减小到临界值(即顶部小颗粒逐渐稀疏, 为大颗粒上升提供可能空间, 底部小颗粒逐渐紧密, 为大颗粒上升提供底部支撑), 大颗粒才能够开始跃升.
综合来看, 大颗粒起跳的控制因素是高度方向受力的高频率脉动和起跳过程中浮升因子逐渐减小共同作用的结果. 摩擦系数的增加, 使颗粒群的运动加剧, 整体颗粒密度呈下降趋势, 即颗粒群高度上升, 由0.0075 m升至0.00817 m, 因而大颗粒能够到达更高的平衡高度; 摩擦系数增大, 大颗粒受到颗粒群更大的碰撞力, 由原来的低摩擦系数(0.3)受力域宽0.000714N到高摩擦系数(0.55)受力域宽 0.00199N, 致使大颗粒能够更快上升；同时，浮升因子与大颗粒运动轨迹对应说明大颗粒周围空间排布对其运动具有重要作用.

本文针对薄层剪切槽中的二元颗粒分离过程开展了离散元数值模拟, 发现初始时刻位于剪切槽底层的大颗粒最终在剪切槽顶部脉动平衡. 通过对大颗粒的运动学、动力学分析, 获得了大颗粒的运动总体特征, 发现了大颗粒起跳的临界条件. 结论如下:
1)大颗粒跃升过程分为三个典型的阶段: 起跳前的弛豫阶段, 快速的起跳阶段和动态平衡阶段;
2)颗粒在平衡位置的高度随着摩擦系数的增加而增大, 即颗粒群更为松散, 颗粒群的排布松散有利于颗粒的上升. 同时颗粒的受力幅度随着摩擦系数的增加而增大, 导致大颗粒的起跳弛豫时间随着摩擦系数的增大而减小;
3)提出浮升因子概念, 为颗粒运动提出局域分析思想. 大颗粒的起跳控制因素是颗粒受力高频脉动和浮升因子逐渐减小综合作用的结果.