摘要: 空分复用(SDM)与波分复用(WDM)的结合有效提升了光纤通信系统的容量, 其中光纤的非线性影响不可忽视. 本文将光纤四波混频作用过程由WDM频域推广到模分复用(MDM)空间域, 第一次给出抽运消耗情形下空频域四波混频的统一解析表达式. 通过数值计算非简并四波混频耦合模方程的幅度和相位演化特性, 验证了解析分析方法的正确性. 讨论了解析解在多波耦合方程简化、大规模并行相位运算器设计以及快速非线性补偿等方面的应用.
关键词: 空分复用 /
少模光纤 /
四波混频 /
解析解 English Abstract Analytical method for four wave mixing in space-frequency multiplexing optical fibers Wan Feng Wu Bao-Jian Cao Ya-Min Wang Yu-Hao Wen Feng Qiu Kun Key Laboratory of Optical Fiber Sensing and Communication, Ministry of Education, School of Information and Communication Engineering, University of Electonic Science and Technology of China, Chengdu 611731, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 61671108, 61505021).Received Date: 03 December 2018Accepted Date: 02 April 2019Available Online: 01 June 2019Published Online: 05 June 2019Abstract: In recent years, the transmission capacity of wavelength division multiplexing (WDM) communication systems has gradually approached to the nonlinear Shannon limit. To meet the increasing demand for communication capacity, space division multiplexing (SDM) has become one of the most concerned technologies. In this paper, the four-wave mixing process (FWM) in fibers is considered from the frequency domain to the mode division multiplexing (MDM) spatial domain under pump depletion and the exact analytical solution to the FWM coupled-mode equations in the space-frequency domain is in detail deduced. The analytical method is verified by numerically calculating the amplitude and phase evolution of the idler wave in non-degenerate four-wave mixing. We discuss three new applications of the analytical solution as follows. 1) Using the phase matching condition we select the terms in the multi-wave coupling equation, and only retain the coupling term that plays a major role. According to the analytical solution in this paper, the phase matching percentage parameter is introduced to determine the FWM coupling terms necessary for multi-wave coupling equations, thus simplifying the multi-wave coupling problem in the study. 2) Combining the analytical solution with the numerical calculation results, we find the initial phase relationship between the output idler and the input guided wave for phase-insensitive FWM, and we provide the analytical expression for a theoretical basis to efficiently design the FWM-based phase arithmetic devices in parallel operating at WDM and MDM systems. 3) We propose a nonlinear compensation algorithm based on analytical solution, which can be used in the few-mode transmission system. The algorithm can fast evaluate or compensate for the fiber nonlinearity by taking into account the pump depletion of the FWM effect. Compared with the traditional digital back propagation (DBP) algorithm, our algorithm has the advantage of lower complexity.Keywords: space division multiplexing /few mode fiber /four-wave mixing /analytic solution 全文HTML --> --> --> 1.引 言 近年来, 波分复用(wave division multiplexing, WDM)通信系统传输容量已逐渐逼近非线性香农极限[1 ,2 ] . 为满足通信容量不断提高的需求, 空分复用(space division multiplexing, SDM)应运而生, 已成为备受关注的技术之一[3 -7 ] . SDM主要应用形式是与当前的WDM系统相结合, 构成空频复用传输系统, 使通信容量得到大幅提升. 因此, 以少模光纤等为代表的模分复用(mode division multiplexing, MDM)技术成为光通信领域中研究的热点[8 ,9 ] . 利用光纤中各导波模式之间的正交性, 可构建MDM传输系统[10 ] .[11 ] . 近年来, MDM系统的非线性效应也开始受到关注. 2013年, Mumtaz等[12 ] 建立了少模或多芯光纤中的非线性传输模型, 并通过该模型研究了114 Gb/s信号在少模光纤中传输1000 km的通信性能. 同年, Mumtaz等[13 ] 和Essiambre等[14 ] 通过实验验证了少模光纤中模间FWM效应, 证明在大频率间隔(THz)和较大模式色散条件下也能满足相位匹配条件. 文献[15 ]提出了MDM系统中高斯噪声非线性理论模型, 将信道间非线性作用近似为高斯噪声处理, 研究非线性对空频复用光纤传输系统的影响. 2017年, Trichili等[16 ] 给出了小信号条件下空频耦合模方程的近似解, 分析了少模相敏参量放大过程, 该理论不适用于抽运消耗的情形.[17 ] . 解析解能更好地反映非线性过程的参数依赖关系, 最近我们给出了单模高非线性光纤中简并和非简并FWM闲频光幅度和相位的统一解析表达式, 证明了非相敏放大(phase insensitive amplify, PIA)模式下闲频光相位与输入光初始相位之间的关系, 揭示了FWM相位加减混合运算器的工作原理[18 ] . MDM光纤系统的非线性比单模情形复杂, 自相位调制、交叉相位调制、四波混频等非线性项的系数均与模场交叠因子相关, 目前的理论研究主要集中在数值模拟或基于特定场景的半解析模型上, 精确的解析分析方法还未有报道[12 ,19 -22 ] .2.理 论 22.1.空频域FWM耦合模方程 2.1.空频域FWM耦合模方程 利用少模光纤并采用WDM技术, 可实现光场的空频复用传输. 在单模光纤中, FWM过程发生在具有不同频率的相同模式之间; 在模式复用系统中, 具有相同或不同频率的模式之间也会发生FWM. 因此, 空频复用系统中的非线性耦合方程会更加复杂. 为了使推导过程更加清晰, 本文考虑准连续线偏振导波光的非简并FWM过程. 空频域复用系统中导波光的光场复振幅${A_l}$ (l = 1—4)满足如下FWM耦合方程组:c 为真空中光速, z 表示少模光纤的长度; ${\omega _l}$ (l = 1—4)为各导波光的角频率, 导波光之间满足能量守恒关系, 即${\omega _4} + {\omega _3} - {\omega _2} - {\omega _1} = 0$ ; 相位失配因子$\Delta \beta = {\beta _4} + {\beta _3} - {\beta _2} - {\beta _1}$ , 其中${\beta _l}$ (l = 1—4)为各导波光的传播常数. 归一化横向模场分布${F_{l, m, n, p}}(x, y)$ 的交叠积分为${n_2}(x, y)$ 为光纤的非线性折射率参量, F 为归一化模场分布函数. 当所有涉及的模场交叠积分均相同, 且光频率间隔较小时, 非线性系数可以统一表示为${\gamma _{{\rm{NL}}}} \approx {{{n_2}{k_0}} / {{A_{{\rm{eff}}}}}}$ , 此时(2 )式可化为单模光纤情形[23 ] , 其中${k_0}$ 为真空中导波光波数, ${A_{{\rm{eff}}}} = {\left[ {\displaystyle\iint {{{\left| F \right|}^4}{\rm{d}}x{\rm{d}}y}} \right]^{ - 1}}$ 为模场面积.${A_l} = \sqrt {{P_l}} {\rm{exp}}$ $({\rm{i}}{\varphi _l})$ 的形式, 其中${P_l}$ (l = 1—4)为光功率, ${\varphi _l}$ (l = 1—4)为各导波光的相位. 因此, 对复振幅方程(1 )式的求解可转换为实数场分量的求解. 将复振幅的表示代入(1 )式, 得到功率演化的方程如下:$\theta = \Delta \beta z + {\varphi _3}(z) + {\varphi _4}(z) - {\varphi _1}(z) - {\varphi _2}(z)$ , 且满足关系${O_1}$ , ${O_2}$ , ${O_3}$ , ${O_4}$ 与四个光波的功率、频率分布以及模场归一化交叠积分有关, 即5 )式中的参数包括了多模光纤中不同频率和模式的光场作用, 体现了多模光纤中导波光的空域和频域耦合特性. 与单模光纤情形相比, 多模光纤中四波混频耦合模方程的非线性系数发生了改变, 各项的非线性系数之间不再保持固定的大小关系, 而是取决于耦合光场的模场分布. (4 )式也与单模情形的表达式不同, 不能直接利用单模光纤的推导过程进行解析求解, 因此这种非线性系数的变化增加了推导解析解的难度.${P_i} = {\omega _i}{Q_i}{\rm{ }}$ (i = 1—4)和$\gamma = \dfrac{{{f_{1234}}}}{c}\sqrt {{\omega _1}{\omega _2}{\omega _3}{\omega _4}} $ , 则(3 )式—(5 )式可重新表示为${o_1}$ , ${o_2}$ , ${o_3}$ , ${o_4}$ 表示为6 )式可知, 各导波光之间存在如下关系:${Q_{i0}} = {P_{i0}}/{\omega _i} \;{\rm{ (}}i = 1, 2, 3, 4)$ , 与导波光的初始功率有关, $q(z)$ 表示FWM的转移能量. $q(z)$ 的物理意义可由(9 )式加以分析, 即$q(z) = \Delta {Q_i} = \Delta {P_i}/{\omega _i} = $ $\Delta {P_i}{T_i}/({\omega _i}{T_i}) = \Delta {E_i}/(2{\rm{π}})$ , 其中${T_i}$ 为光波相位周期, ${E_i} = {P_i}{T_i}$ 为一个周期的能量. 由(6 )式—(9 )式可知, $q(z)$ 满足如下方程:${I_0} = 4\gamma \sqrt {{Q_{10}}{Q_{20}}{Q_{30}}{Q_{40}}} \cos {\theta _0}$ 为积分常数, 由初始输入的各光波功率和相位确定, ${\theta _0} = {\varphi _{40}} + $ $ {\varphi _{30}} - {\varphi _{20}} - {\varphi _{10}}$ ; 参数$K(q)$ 是转移能量参数q 的二次多项式, 其系数R 1 —R 4 由多模光纤的各模场交叠积分和频率共同确定, 具体可表示为10 )式和(11 )式求出转移能量参数q 随光纤长度z 的变化关系, 进而给出功率和相位的解析表达式.2.2.功率的解析解表示 -->2.2.功率的解析解表示 由(11 )式可知, $f(q)$ 是关于转移能量参数q 的四次多项式, 在初始条件确定的情况下, 可以表示为$f(q) = C_0^2(q - {\eta _1})(q - {\eta _2})(q - {\eta _3})(q - {\eta _4})$ 的形式, 其中${\eta _1} < {\eta _2} < {\eta _3} < {\eta _4}$ 是满足$f(q) = 0$ 的、依次按照从小到大的顺序排列的四个根, ${C_0}^2$ 表示$f(q)$ 最高次项的系数. 于是(10 )式可以进一步表示为$\xi = {\rm{sign} }(\sin{\theta _0})$ , 依赖于输入光波的初始相位关系.$q(z)$ 随长度z 演化的表达式. 当初始条件给定时, (14 )式能够表示为第一类椭圆积分. 根据第一类椭圆积分与雅可比椭圆函数${\rm{sn}}(\mu , k)$ 之间的互逆运算关系, FWM转移能量参数$q(z)$ 的解析表达式为[17 ] 9 )式和(15 )式, 多模光纤中导波光的功率演化规律可解析地表示为15 )式—(17 )式描述了空频复用多模光纤FWM作用中导波光的光功率演化规律, 也适用于单模光纤的情形, 其中参数${\eta _1}$ —$ \eta_4$ 计及了空频耦合作用.$ {\omega _1} +$ $ {\omega _2} = {\omega _3} + {\omega _4}$ , 由(17 )式可知, 光波沿光纤传播时${P_1}(z) \!+\! {P_2}(z) \!+\! {P_3}(z) \!+\! {P_4}(z) = {P_{10}} \!+\! {P_{20}} \!+\! {P_{30}} $ $ \, +{P_{40}}$ , 即总功率始终保持不变, 符合FWM作用过程中能量守恒的条件, 一定程度上表明了我们理论推导的正确性.2.3.相位的解析解表示 -->2.3.相位的解析解表示 由(4 )式可知, 导波光的相位与$q(z)$ 相关, 即相位的解析解可以由$q(z)$ 的解析式推导得到. 为简单起见, 本文以闲频光的相位${\varphi _4}$ 为例, 将${o_4}$ 和$K(q)$ 分别表示为${o_4} = A + Bq$ 和$K(q) = Cq + D{q^2}$ 的形式, 其中A , B , C , D 由(8 )式、(12 )式和(13 )式给出. 则相位${\varphi _4}$ 的演化方程为a , b , c , d 表示如下:18 )式具有如下通解形式[17 ] :$\varphi _{40}^ * $ 与输入导波光初始相位关系可通过解析方法确定[18 ] , 本文将通过数值计算方法得到同样的结果. 其中${\varphi _{\rm I}}$ 和${\varphi _\Pi }$ 均与导波光的初始条件有关, 可用第三类椭圆积分表示为:20 )式—(24 )式给出了多模光纤中导波光场相位演化的解析解, 尽管形式上与单模光纤的解析解类似, 但其中涉及的诸多参量如A , B , C , D 以及${\eta _1}$ —$\eta_4$ 等有所不同.$q(z)$ 单调区间内得到的. 事实上, 随着光纤长度z 的增加, $q(z)$ 的演化具有周期震荡特性, 在(10 )式符号改变的位置$q(z)$ 的单调性也发生改变, 此时相位解析解出现奇异(相位跳变). 此外, 在$z=0$ 的初始位置, 由于$q(z)=0$ , 当没有闲频光输入时$f(q) = 0$ , 相位的解析解也存在奇异性. 因此, 需单独分析各单调区间的情况, 并考虑$q(z)$ 周期变化对相位的累积影响, 有关相位的完整表示在文献[17 ]中已有详细的讨论.3.解析解的验证 下面利用解析解来分析多模光纤中非简并FWM过程, 并采用数值方法直接对空频复用FWM耦合模方程(1 )式进行求解, 来验证上述解析解的正确性. 令两个抽运光的频率为${f_1}$ 和${f_2}$ , 探测光为${f_3}$ , 产生的闲频光频率为${f_4}$ , 它们的模场分布对应于两个模群的三个线偏振模${\rm{L}}{{\rm{P}}_{01}}$ , ${\rm{L}}{{\rm{P}}_{{\rm{11a}}}}$ 和${\rm{L}}{{\rm{P}}_{11{\rm{b}}}}$ , 具体的模场分布和频率分配如图1 所示. 结合文献[9 ,24 ]给出的少模光纤的参数, 选择参考频率${f_0}$ 为194.81 THz, 传输光纤长度为4.5 km; 简并模${\rm{L}}{{\rm{P}}_{{\rm{11a}}}}$ 和${\rm{L}}{{\rm{P}}_{{\rm{11b}}}}$ 具有相同的传播常数, 差模群时延(DMGD)$\beta _1^{{\rm{L}}{{\rm{P}}_{11}}} - \beta _1^{{\rm{L}}{{\rm{P}}_{01}}}$ = 100 ps/km, 对应的色散参量为$\beta _2^{{\rm{L}}{{\rm{P}}_{01}}}$ = –24.3 ps2 /km和$\beta _2^{{\rm{L}}{{\rm{P}}_{11}}}$ = –23.03 ps2 /km, 并且假定所有模式具有相同的色散斜率.图 1 非简并FWM过程中导波光的模式与频谱分布Figure1. Mode and frequency distribution in the non-degenerate FWM process.1 )式进行求解, 首先要知道导波光场的交叠积分${f_{lmnp}}$ 和相位失配$\Delta \beta $ . 文献[9 ,24 ]已给出模场归一化交叠积分的参数${f_{lmnp}}/{f_{{\rm{LP01}}}}$ , 如表1 所列, 其中${f_{{\rm{LP01}}}}$ 为${\rm{L}}{{\rm{P}}_{01}}$ 模的交叠积分. 下面通过优化导波光的频率分布, 尽可能满足相位匹配条件$\Delta \beta \approx$ $ 0$ . 选择参考频率${f_0} = {f_1}$ , 则相位失配因子$\Delta \beta $ 为模场分布 f lmnp /f LP01 /arb.units4束光都为LP01 模 1.000 4束光都为LP11a 或LP11b 模 0.747 2束光为LP01 模、2束光为LP11a 或LP11b 模 0.496 2束光为LP11a 模、2束光为LP11b 模 0.249
表1 模场的归一化交叠积分参数Table1. Normalized overlap integral parameters of mode fields.25 )式, 可画出相位失配随$\Delta {f_1}$ 和$\Delta {f_2}$ 变化的情况, 如图2 所示. 优化频率参数$\Delta {f_1}$ 和$\Delta {f_2}$ 的取值, 可使相位匹配失配$\left|\Delta \beta \right|$ 取到最小. 由图2 可知, $\left|\Delta \beta \right|$ 对$\Delta {f_2}$ 的改变更加敏感. 选择$\Delta {f_1}$ = 0.13 THz和$\Delta {f_2}$ = 0.33 THz, 使$\left|\Delta \beta \right|$ = 0. 则参与FWM过程的导波光频率为${f_1}$ = 194.81 THz, ${f_2}$ = 195.14 THz, ${f_3}$ = 194.68 THz, ${f_4}$ = 195.27 THz.图 2 相位失配因子对$\Delta {f_1}$ 和$\Delta {f_2}$ 的依赖Figure2. Dependency of phase mismatching factor on $\Delta {f_1}$ and $\Delta {f_2}$ .1 )式进行数值求解[25 ] , 相同参数也代入解析式(15 )式—(17 )式和(20 )式—(24 )式, 分别得到闲频光的功率和相位随长度z 的变化曲线, 如图3 所示, 其中抽运1的功率为0.5 W, 抽运2的功率为0.35 W, 输入探测光功率分别为0.01, 0.05和0.1 W. 由图3(a) 可知, 闲频光输出功率的解析解和数值计算结果完全相同, 探测光输入功率越大, 输出闲频光功率达到饱和所需的光纤长度越短. 再结合图3(b) 可知, 在功率单调变化的区间内, 闲频光相位的解析解与数值结果也非常符合, 探测光输入功率越大, 相位随光纤长度的变化也越大. 由图3(b) 可知, 无闲频光输入时, 相位在光纤输入端出现了跳变, 计算时闲频光功率取了一个很小的值(如10–10 W). 实际上, 由于噪声的存在, 闲频光输入会从噪声中产生, 解析解的条件自动得到满足, 因此在应用中并不会受到限制. 总之, 在解析式的适 用范围内, 本文得到的解析解与数值结果完全 一致.图 3 解析解与数值结果的比较 (a)闲频光功率; (b)闲频光相位Figure3. Comparison of analytical and numerical results: (a) Idler output power; (b) idler output phase.4.解析分析方法的应用 与数值计算方法相比, 解析分析方法更加便捷. 本文给出的空频复用FWM解析解适用范围更加广泛, 可快速分析少模光纤中的FWM效应, 也可以用于拟合模场交叠积分等. 下面讨论解析解在多波耦合方程简化、大规模并行相位运算器设计以及快速非线性补偿等方面的新型应用.4.1.多波耦合项的选择 4.1.多波耦合项的选择 在级联FWM中, 特别是在空频复用多模光纤中, 多组FWM过程可能同时发生, 需用多波耦合方程组加以描述. 每个耦合方程对应一个特定模式和频率的光波, 并涉及与其他导波光的FWM耦合项, FWM耦合项数随着导波光数目的增加指数增长, 将导致传统分步傅里叶算法的计算效率急剧下降. 此时可利用本文给出的解析解计算FWM耦合项的贡献大小并筛选出起主要作用的耦合项, 从而简化多波问题的分析和研究.图4(a) 是在不同相位失配下, 由本文解析式计算得到的转移能量参数$q(z)$ 随光纤长度变化的曲线, 可以看出, FWM转移能量的极大值${q_p}$ 与$\Delta \beta $ 密切相关. 定义一个相位匹配度参数$\mu (\Delta \beta )$ 为图 4 (a) FWM转移能量在不同相位失配$\Delta \beta $ 随光纤长度L 的变化; (b) 相位匹配度$\mu $ 随$\Delta \beta $ 的变化Figure4. (a) FWM energy transfer $q(z)$ of different $\Delta \beta $ with fiber length L ; (b) variation of phase matching parameter $\mu $ with $\Delta \beta $ .${q_p}(\Delta \beta )$ 表示$q(z)$ 的极大值是相位失配$\Delta \beta $ 的函数, 它不依赖于光纤长度; ${q_{\max }}$ 为完全相位匹配时FWM的最大转移能量[17 ] , 即${q_{\max }} = \min ({P_{{\rm{pump}}1}}/ $ ${\omega _{{\rm{pump}}1}},{P_{{\rm{pump}}2}}/{\omega _{{\rm{pump}}2}})$ . 显然, 相位匹配度参数描绘了不同相位失配因子下FWM耦合项的贡献大小. 利用FWM的解析解, 可画出相位匹配度$\mu $ 随$\Delta \beta $ 的变化曲线, 如图4(b) 所示. 若所计算的FWM耦合项的实际相位失配因子处于$\mu $ ≥${\mu _{\rm{c}}}$ 的范围, 则该FWM耦合项的贡献不能忽略, 即保留该耦合项, 其中${\mu _{\rm{c}}}$ 为临界值, 如可取${\mu _{\rm{c}}}$ = 0.05; 否则该FWM耦合项可忽略, 从而达到简化多波FWM耦合方程的目的.4.2.多通道相位运算器 -->4.2.多通道相位运算器 由多模光纤解析解的相位关系(20 )式可知, 对于没有闲频光输入的非相敏情形, 输出闲频光相位可为如下形式:$\varphi _{40}^*$ 为积分常数, $ \Delta \varphi = \left( {a + b{\eta _1} + \dfrac{c}{{d - {\eta _1}}}} \right) \times $ $z +{\phi _{\rm I}} + {\phi _\Pi }$ 依赖于光纤长度z . 本文通过对(1 )式进行数值计算的方式, 得到多模光纤中输出闲频光相位${\varphi _4}$ 与输入初相位运算(${\varphi _{10}} + {\varphi _{20}} - {\varphi _{30}}$ )的关系, 如图5 所示, 可以看出它们之间具有固定的相移$\Delta \varphi $ = 0.5236 rad, 它不依赖于输入导波光的初相位. 进一步地, 由(27 )式可知, 输出相位积分常数$\varphi _{40}^*$ 满足运算关系$\varphi _{40}^* = {\varphi _{10}} + {\varphi _{20}} - {\varphi _{30}}$ , 此式揭示了FWM相位运算器的本质.图 5 输出闲频光相位${\varphi _4}$ 与输入初相位运算${\varphi _{10}} + $ ${\varphi _{20}} - {\varphi _{30}}$ 之间的关系Figure5. Dependence of output idler phase ${\varphi _4}$ on the initial phase operation of ${\varphi _{10}} + {\varphi _{20}} - {\varphi _{30}}$ .图1 所示的模间FWM过程为例, 利用解析解计算少模光纤相位运算器的性能. 将三路四进制数字序列调制到频率为$f_1^{{\rm{L}}{{\rm{P}}_{11{\rm{a}}}}}$ , $f_2^{{\rm{L}}{{\rm{P}}_{{\rm{01}}}}}$ 和$f_3^{{\rm{L}}{{\rm{P}}_{{\rm{01}}}}}$ 的导波光场上, 生成QPSK光信号, 同时叠加一个零均值的高斯白噪声; 经过少模光纤传输后在频率$f_4^{{\rm{L}}{{\rm{P}}_{11{\rm{b}}}}}$ 处产生闲频光, 最后由光接收机进行相位解调. 输出闲频光的信噪比(SNR)随输入SNR的变化如图6 所示, 可以看出, 输出闲频光的SNR与输入导波光的SNR成正比, 该相位运算器会导致约1.6 dB的SNR劣化.图 6 输入信号SNR与输出信号SNR的关系Figure6. Input signal SNR vs. output signal SNR.[26 -31 ] . 并且, 若将数字运算序列分别调制到几个模式上, 利用MDM的FWM过程也能够实现多路全光相位运算, 换句话说, 通过设计优化少模高非线性光纤的参数, 可设计空频域复用系统的多通道相位运算器.4.3.少模非线性补偿 -->4.3.少模非线性补偿 数字后向传播算法(digital back propagation, DBP)是目前光通信系统中重要的非线性补偿算法之一[32 ] , 它基于分步傅里叶算法反向计算出原始信号, 以补偿实际传输中的非线性损伤. 将DBP算法直接用于少模光纤系统的计算复杂度会更高[33 ] , 我们提出利用FWM解析解的逆运算来对少模传输系统进行非线性补偿的方法, 一个算法处理流程如图7 所示. 首先, 通过训练序列得到通信链路的非线性响应, 并采用遗传算法或二分法对解析式中的非线性参量进行估计; 然后在实际补偿中, 根据解析解对应的逆函数方程, 利用不动点迭代法对接收信号运算, 得出发送端的幅度信息. 最后, 采用相似的方式恢复出发送信号的相位, 从而实现少模光纤非线性的补偿.图 7 基于FWM解析解的非线性补偿框图Figure7. Block diagram of nonlinear compensation based on the analytic solution for FWM effect.5.结 论 详细推导了空频复用系统中非简并FWM闲频光幅度和相位的解析表达式, 并通过数值仿真验证了解析解的正确性. 讨论了解析分析法的三个新型应用. 1)根据FWM的解析解, 通过引入相位匹配度参数来筛选级联FWM多波耦合方程的耦合项, 为简化空频域多波耦合问题提供了理论方法; 2)将解析解和数值计算结果相结合, 揭示了非相敏FWM相位运算器的物理本质, 解析式为空频复用系统的相位运算器设计提供了理论依据; 3)提出了基于解析解的非线性补偿方法, 可用于少模传输系统, 与传统DBP算法相比, 解析法具有低复杂度的优势. 

















































































































 图 1 非简并FWM过程中导波光的模式与频谱分布
图 1 非简并FWM过程中导波光的模式与频谱分布
















































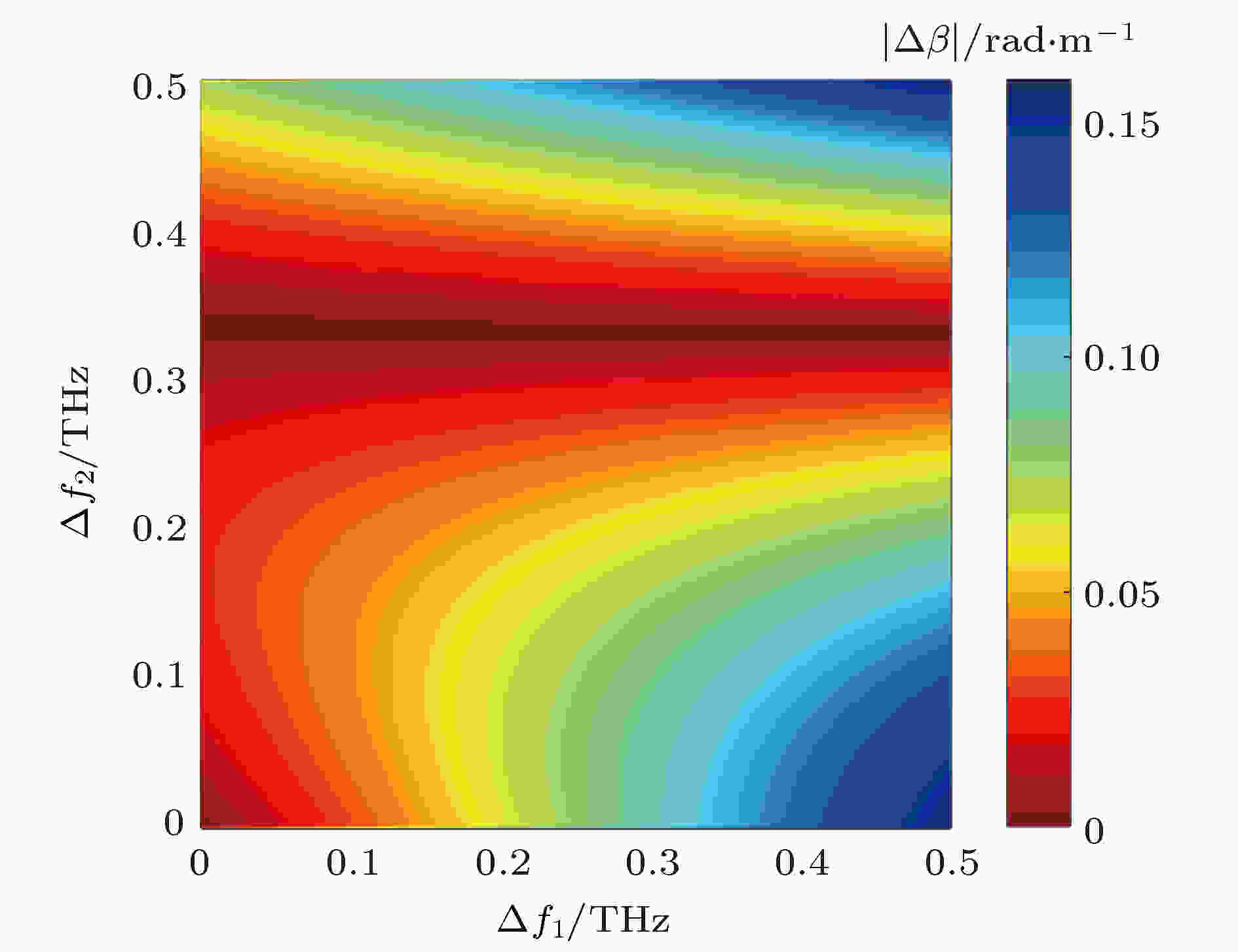 图 2 相位失配因子对
图 2 相位失配因子对



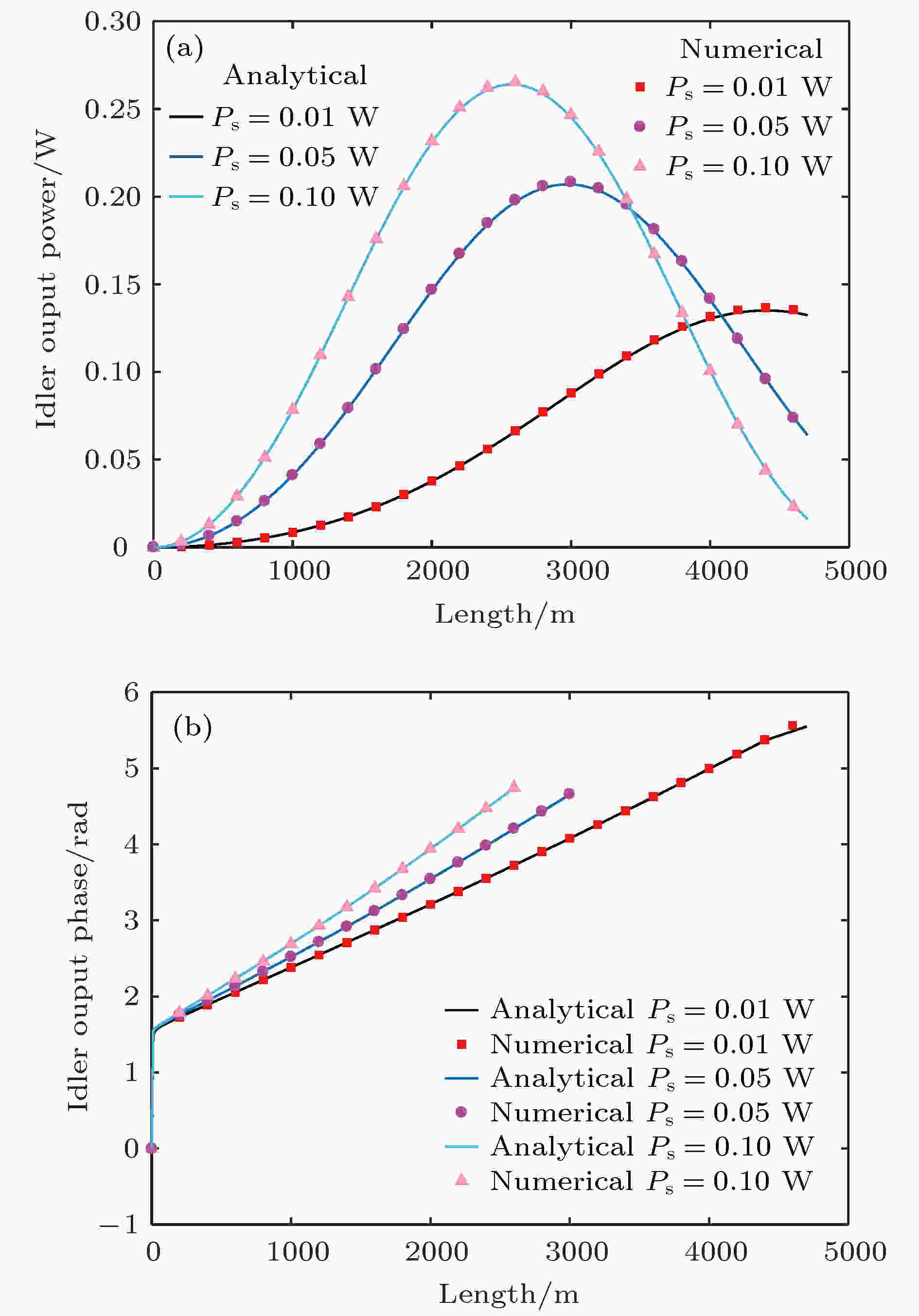 图 3 解析解与数值结果的比较 (a)闲频光功率; (b)闲频光相位
图 3 解析解与数值结果的比较 (a)闲频光功率; (b)闲频光相位



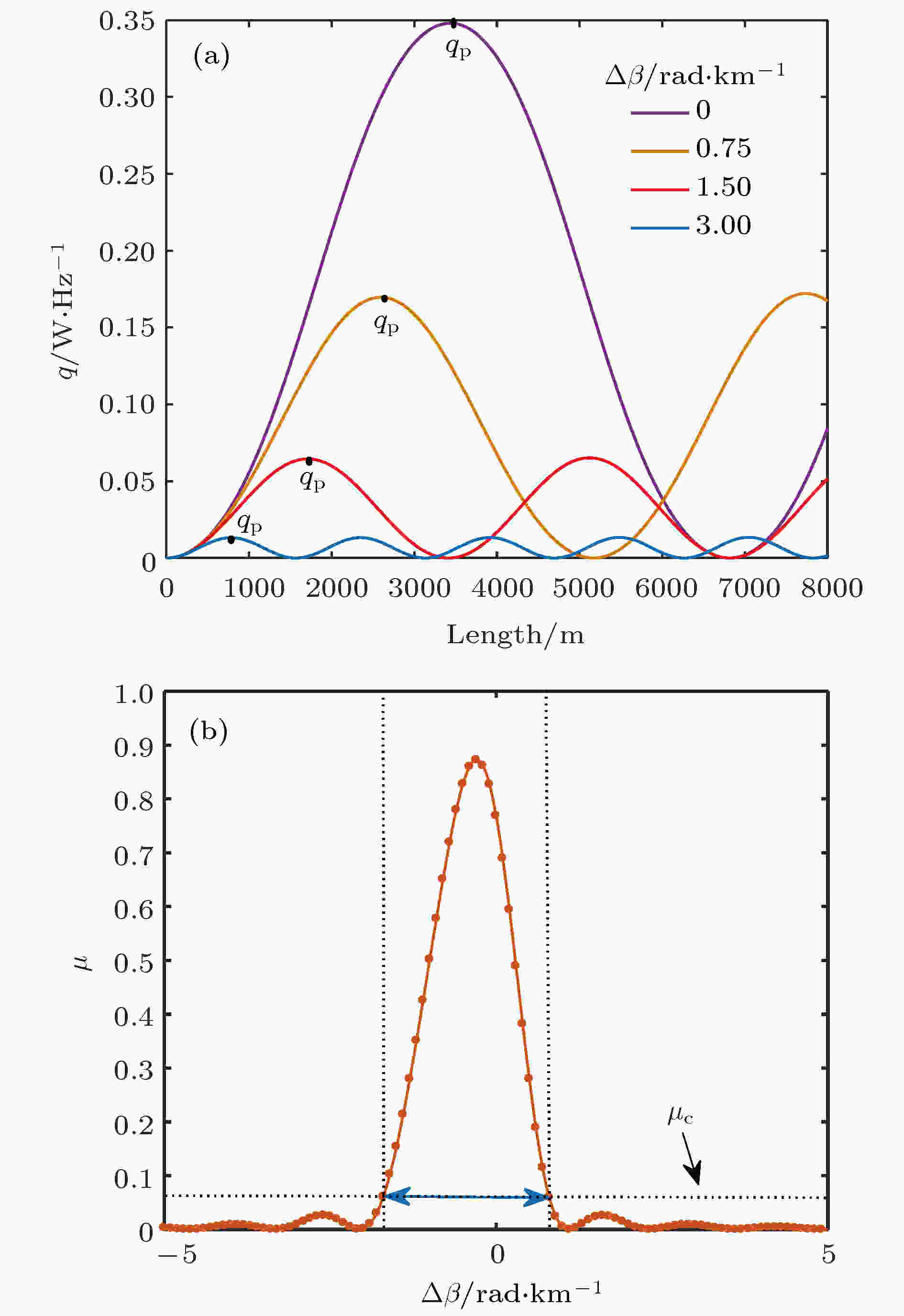 图 4 (a) FWM转移能量在不同相位失配
图 4 (a) FWM转移能量在不同相位失配










































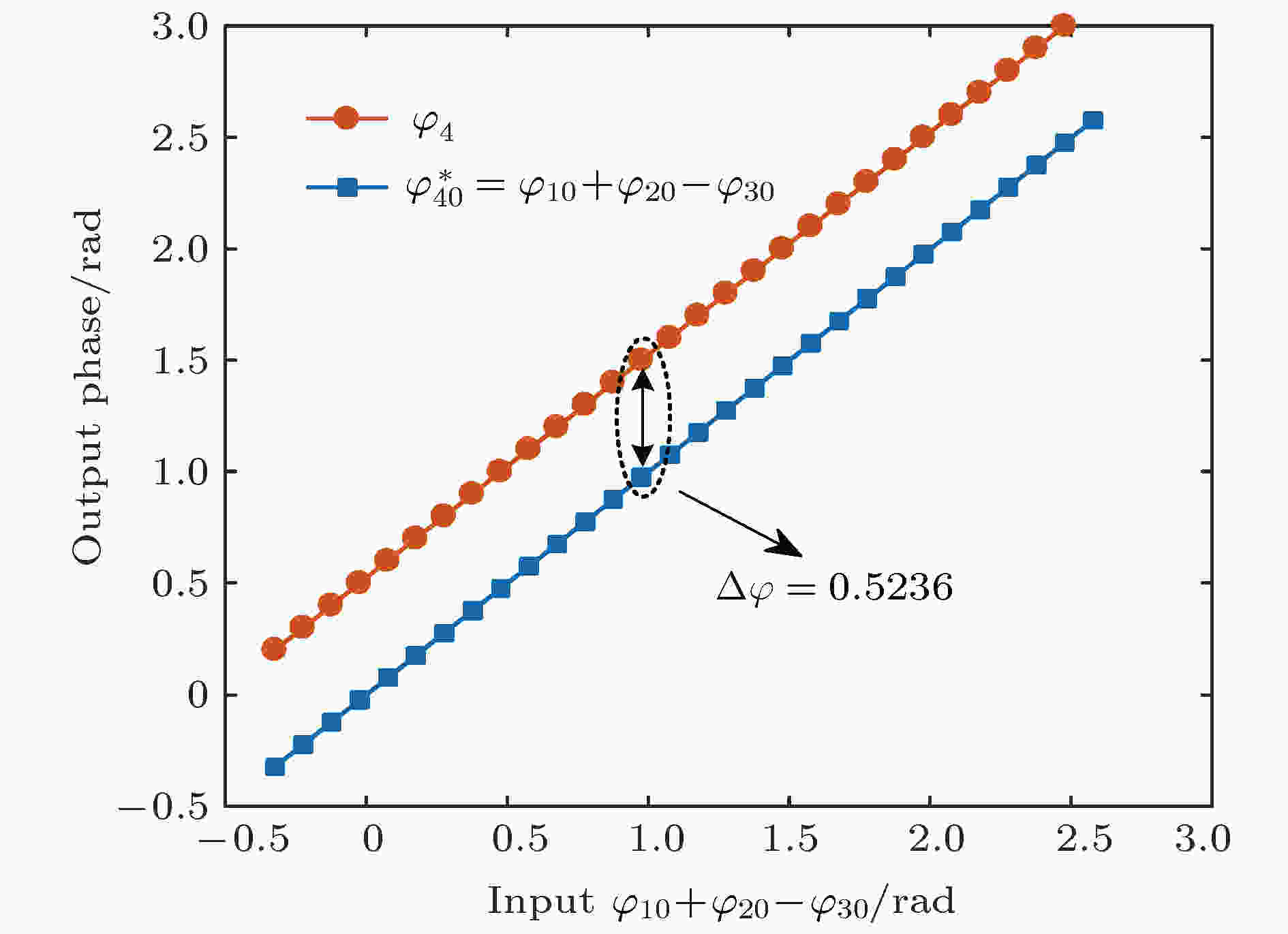 图 5 输出闲频光相位
图 5 输出闲频光相位








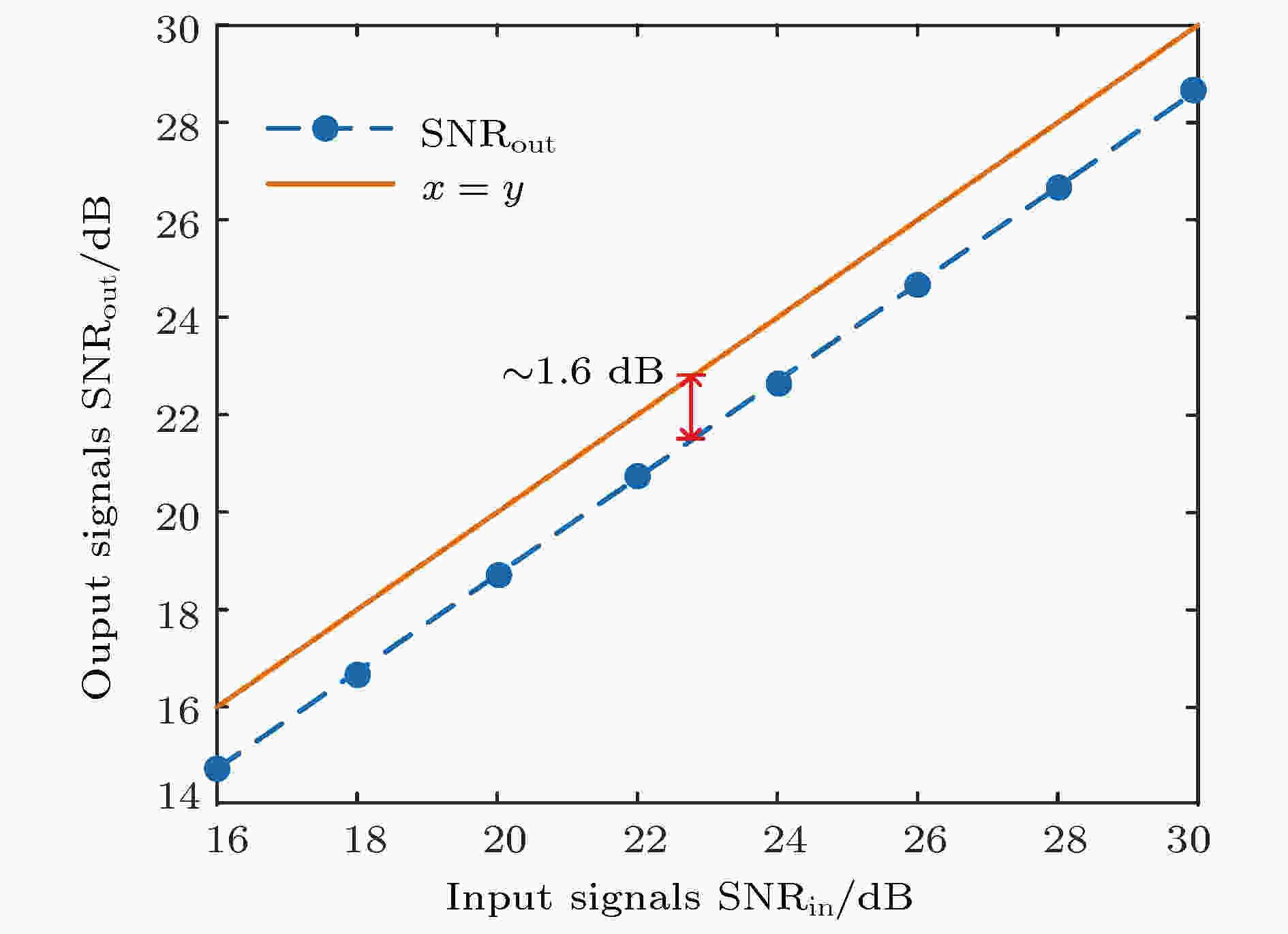 图 6 输入信号SNR与输出信号SNR的关系
图 6 输入信号SNR与输出信号SNR的关系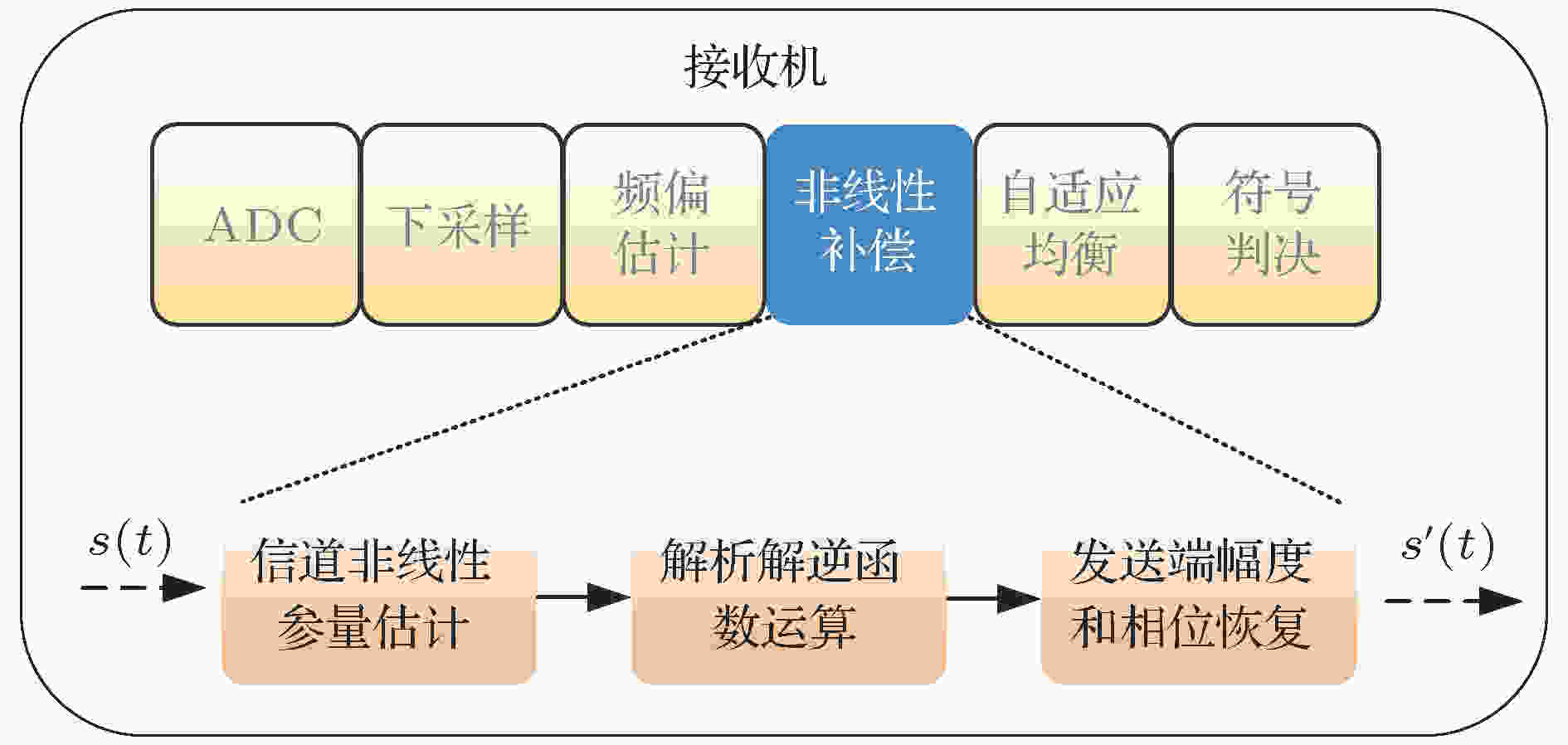 图 7 基于FWM解析解的非线性补偿框图
图 7 基于FWM解析解的非线性补偿框图