摘要: 在晶格弛豫理论框架内, 电子-体纵光学声子耦合的Fr?hlich模型基础上, 系统研究了PbSe量子点的3个最低激发态之间及其与基态之间的带内弛豫过程. 具体讨论了各个弛豫过程中的黄-里斯因子、弛豫率与量子点半径的变化关系, 进一步讨论了弛豫率的温度依赖性. 得出的理论结果很好地解释了相应的实验.
关键词: 量子点 /
黄-里斯因子 /
带内弛豫 English Abstract Intraband relaxation process in PbSe quantum dot studied by lattice relaxation method Liang Yu-Hong Li Hong-Juan Yin Ji-Wen School of Physical and Electronic Information Engineering, Chifeng University, Chifeng 024000, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11264001).Received Date: 02 February 2019Accepted Date: 04 April 2019Available Online: 01 June 2019Published Online: 20 June 2019Abstract: Within the frame of lattice relaxation model, several intraband relaxation processes between the three lowest excited states and ground state in a PbSe quantum dot are studied based on the electron-longitudinal optical phonon coupling via Fr?hlich mechanism. We find that Huang-Rhys factors decrease with the radius of quantum dot increasing in different relaxation processes. More important is the fact that the obtained values of Huang-Rhys factors satisfy the experimental measurements in the strong coupling limit. These intraband relaxation processes follow the asymmetrical Gaussian distribution with respect to the radius, in which the probabilities with which these intraband relaxation transitions occur are different. Among these relaxation processes, two intraband transitions from the third excited state to ground state and to second excited states dominate the relaxation processes on a several nanometer scale of radius. Moreover, the temperature dependence for each of these relaxation processes can be modulated by the radius of quantum dot. These theoretical results are consistent with the experimental measurements and provide an important insight into the intraband relaxation in quantum dots in experiments.Keywords: quantum dot /Huang-Rhys factor /intraband relaxation 全文HTML --> --> --> 1.引 言 近年来, 胶体量子点由于在红外发射器、太阳能电池等诸多方面潜在的应用前景迅速成为学术研究的一个热点[1 -7 ] . 胶体量子点具有较好的尺寸可调性, 从而能够获得一些可控制的量子和光学特性, 也因此成为验证纳米颗粒的多方面奇特量子光学性质的理想载体. 特别是, 这种量子点的带内弛豫过程对其这些特性有直接的影响, 引起了研究人员对这一方面的广泛关注和研究. 现在实验上可以获得尺寸非常小的胶体量子点, 量子点带内能级间距远超过一个或几个光学声子能量, 理论预计这会使得带内的弛豫过程变得很慢, 这一效应被称为“声子瓶颈”效应, 然而过去在对CdSe, ZnO等[8 ] 胶体量子点的诸多实验观察中发现: 带内弛豫时间非常短(通常在飞秒或亚飞秒量级), 未能证实“声子瓶颈”效应的存在. 对此, 俄歇型电子-空穴散射机制[9 ,10 ] : 导带电子由高能级向低能级跃迁辐射的多声子能量被价带电子吸收, 从而产生一新的电子-空穴对, 很好地解释了上述实验. 但对有一些胶体量子点, 这一机制解释却行不通, 例如PbSe量子点[11 ,12 ] . 这主要源于PbSe量子点中的电子和空穴数量近乎相等, 且均具有较小的有效质量, 一方面导致PbSe量子点形成了非常对称的导带和价带能级结构, 因此不能提供上述俄歇型散射所依赖的高密度空穴态分布; 另一方面, 带内能级间距超过十几个光学声子能量甚至更大, 因此PbSe量子点有望成为验证“声子瓶颈”效应的又一理想载体. 可近些年在PbSe量子点的诸多实验表明: 带内弛豫时间仍然在飞秒和亚飞秒量级[12 -14 ] . 由此提出了以杂质为媒介的多声子弛豫机制[15 ,16 ] : 电子由高能级向低能级跃迁过程中, 先被杂质态俘获, 再由杂质能级通过多声子辐射弛豫到低能级. 这一机制很好地解释了这些实验且进一步得到证实[17 ] . 但Schaller等[12 ] 的实验在排除以上两种弛豫机制的前提下, 仍然得到了激发态到基态的快速带内多声子弛豫过程, 因此可以看出带内弛豫过程是一个本质的过程, 需要新的理论模型来解释带内弛豫过程.[18 ,19 ] 在20世纪50年代提出的晶格弛豫理论模型, 在考虑电子-体纵光学(LO)声子耦合的Fr?hlich机制下, 具体研究了PbSe量子点的3个最低激发态之间及其与基态之间的带内弛豫过程, 系统讨论了各个过程的黄-里斯因子, 弛豫率与量子点半径的变化关系及温度依赖性. 本文的理论结果给予Schaller等[12 ] 的实验结果强有力的理论支持. 同时, 理论得出了弛豫率与温度的变化规律依赖于量子点的尺寸, 期盼这一结论得到实验的进一步证实.2.理论模型 在单个量子点模型中假设受限势为抛物型$V\left( r \right) = \dfrac{1}{2}{m^*}\omega _0^2{r^2}$ , 量子点中电子和晶格相互作用系统的哈密顿量可写为${H_{\rm{e}}} = {{{p^2}} / {2{m^*}}} + V\left( r \right)$ 和${H_{\rm{L}}}$ 分别表示电子和晶格振动的哈密顿量; ${m^*}, \;r,\; {\omega _0}$ 分别表示电子的有效质量、位置坐标、量子点受限强度; ${H_{{\rm{eL}}}}$ 表示Fr?hlich型电子-LO声子线性相互作用${V_q} = {\rm{i}}\left( {\hbar {\omega _{{\rm{LO}}}}/q} \right){\left( {\hbar /2{m^*}{\omega _{{\rm{LO}}}}} \right)^{{1 /4}}}{\left( {{{4{\text{π}}\alpha } / V}} \right)^{{1 /2}}}$ ; 无量纲电子-LO声子耦合常数$\alpha = \left( {{{{{\rm{e}}^2}} / {2\hbar {\omega _{{\rm{LO}}}}}}} \right) \times$ ${\left( {{{2{m^*}{\omega _{{\rm{LO}}}}} /\hbar }} \right)^{{1 / 2}}}\left( {{1 / {{\varepsilon _\infty }}} - {1 / {{\varepsilon _0}}}} \right)$ ; q ${\omega _{{\rm{LO}}}}$ 分别表示LO声子的波矢和频率; ${Q_q}$ 是晶格振动模的简正坐标. 按照绝热近似, 系统的波函数可以写成${\psi _i}\left( {r,\left\{ {{Q_q}} \right\}} \right) = {\varphi _i}\left( {r,\left\{ {{Q_q}} \right\}} \right){\varPhi _i}\left( {\left\{ {{Q_q}} \right\}} \right)$ , ${\varphi _i}$ 是电子波函数, 在电子波函数中${Q_q}$ 仅起一个可变参数的作用. ${\varPhi _i}$ 是晶格振动波函数, 其平衡位置依赖于不同的电子态. 基于费米黄金规则, 初、末电子态之间的跃迁可表为[20 ,21 ] $n_q^{\rm{f}},\; n_q^i$ 是初态和末态的声子数, 对初态声子态进行热统计平均, 对末态声子态进行求和; ${E_{\rm{f}}}\left( {{E_{\rm{i}}}} \right)$ 是包括晶格弛豫能的电子初态和末态能级, 例如${E_j} = E_j^0 - \sum\limits_q {{{\omega _{{\rm{LO}}}^{\rm{2}}} / {2\varDelta _{jq}^2}}} $ , $E_j^0$ 是单纯电子能级, ${\varDelta _{jq}} = {{\left\langle {{\psi _j}\left| {\left( {q \cdot r} \right)} \right|{\psi _j}} \right\rangle } /{\omega _{{\rm{LO}}}^2}}$ 表示晶格偏离平衡位置的参数; 电子跃迁矩阵元${H'_{{\rm{fi}}}} = \left\langle {{\psi _{\rm{f}}}\left| {{H_{{\rm{eL}}}}} \right|{\psi _{\rm{i}}}} \right\rangle $ 在康顿近似下不依赖于晶格坐标${Q_q}$ . 根据晶格弛豫理论, 对(3 )式初态声子态求热统计平均和末态声子态的求和运算后可得5 )式中${\varDelta _{{\rm{fi}}q}} = {\varDelta _{{\rm{f}}q}} - {\varDelta _{{\rm{i}}q}}$ 描述了电子跃迁前后晶格振动平衡位置的改变; ${K_{\rm{B}}}$ 是玻尔兹曼常数. 对LO声子模采用单一频率模型, 假设两电子态能级差远大于单LO声子能量, 采用最陡下降法求得多声子无辐射的弛豫率可表述为[20 ,21 ] $S = \sum\limits_q {\left( {{\omega _{{\rm{LO}}}}/2\hbar } \right)\varDelta _{{\rm{fi}}}^{\rm{2}}} $ 是描述晶格弛豫强弱的黄-里斯因子, ${S_{\rm{T}}}\overline {{{\left( {\hbar {\omega _{{\rm{LO}}}}} \right)}^2}} = \sum\limits_q \left( {{\omega _{{\rm{LO}}}}/2\hbar } \right)\varDelta _{{\rm{fi}}}^{\rm{2}}{{\left( {\hbar {\omega _{{\rm{LO}}}}} \right)}^2}\times$ $\coth ({\hbar {\omega _{{\rm{LO}}}}}/2{K_{\rm{B}}}T)$ .6 )式中与弛豫过程相关的物理量, 需要明确量子点中电子基态和激发态波函数. 在各向同性的抛物线性限制势近似下, 量子点基态和激发态波函数可选为:${\phi _{\rm{G}}} = {{{\lambda ^{{3 / 2}}}} /{{{\text{π}}^{{3 /4}}}\exp \left( {-{\lambda ^2}{r^2}/2} \right)}},$ ${\phi _{\rm{E}}} = {{2{\lambda ^{{5 / 2}}}} / {{{\text{π}}^{{3 / 4}}}r\exp \left( { - {\lambda ^2}{r^2}/2} \right)}},$ $\lambda $ 是变分参数, 在小尺寸量子点中$\lambda = {1 /R}$ , $R = \sqrt {{\hbar /{{m^*}{\omega _0}}}} $ , $R$ 表示量子点半径, 关于这一点的详细讨论可参见文献[22 —24 ]. 为了使理论模型与实验结果进行对比, 在计算中具体选用PbSe材料进行计算, 其具体参数如下[11 ] : $\hbar {\omega _{{\rm{LO}}}} = 16.7\;{\rm{meV}}$ , $m{}^* = 0.04{m_0}$ , ${\varepsilon _0} = 210$ , ${\varepsilon _\infty } = 24$ .3.结果与讨论 图1(a) 描述了PbSe量子点中电子的基态(G)与3个最低的激发态(I, II, III)位型坐标关系. 4条带内能级对应的6种弛豫过程分别为: 第三激发态到第二激发态(III-II), 第三激发态到第一激发态(III-I), 第二激发态到第一激发态(II-I), 第三激发态到基态(III-G), 第二激发态到基态(II-G), 第一激发态到基态(I-G). 图1(a) 中${S_{{\rm{III}} \text{-} {\rm{II}}}}, $ ${S_{{\rm{III}} \text{-} {\rm{I}}}},\; {S_{{\rm{II}} \text{-} {\rm{I}}}},\; {S_{{\rm{III}} \text{-} {\rm{G}}}},\; {S_{{\rm{II}} \text{-}{\rm{G}}}}, \;{S_{{\rm{I}} \text{-} {\rm{G}}}}$ 表示与上述的弛豫过程一一对应的黄-里斯因子.图 1 (a) PbSe量子点中电子的基态(G)与3个最低的激发态(I, II, III)位型坐标关系; (b) 6种带内弛豫过程的黄-里斯因子与量子点半径的关系Figure1. (a) Configuration coordinates for the ground state (G) and three lowest excited states (I, II, III) of electron in PbSe quantum dot; (b) Huang-Rhys factors as a function of the radius of quantum dot for six types of intraband relaxation processes.图1(b) 为6种带内弛豫过程的黄-里斯因子与量子点半径的关系, 从图1(b) 可知, 随量子点半径的增加, 黄-里斯因子逐渐减小. 在本文的计算模型中其与半径是一种反比例关系, 这与文献[25 , 26 ]的结论是一致的. 具体分析每一种弛豫过程可以看出, ${S_{{\rm{I}} \text{-} {\rm{G}}}}$ 的值很小, 量子点尺寸变化几乎不影响其值的大小, 因此第一激发态到基态的多声子弛豫过程在我们所讨论的量子点尺寸范围内发生的概率明显小于其他过程. ${S_{{\rm{II}} \text{-} {\rm{G}}}},\; {S_{{\rm{II}} \text{-} {\rm{I}}}},\; {S_{{\rm{III}} \text{-} {\rm{II}}}}$ 三个黄-里斯因子的值很接近, 在图示的尺寸范围内均小于2.5, 其中在半径为3.5 nm时, ${S_{{\rm{II}} \text{-} {\rm{I}}}}$ 的值等于0.85, 这与Bonati等[13 ] 的实验测量值${S_{{\rm{II}} \text{-} {\rm{I}}}} \leqslant $ 1.0很接近. 实验测量${S_{{\rm{II}} \text{-} {\rm{G}}}},\; {S_{{\rm{III}} \text{-} {\rm{II}}}}$ 的值目前还不明确. 对于${S_{{\rm{III}} \text{-} {\rm{G}}}},\; {S_{{\rm{III}} \text{-} {\rm{I}}}}$ 的值在目前研究的量子点尺寸范围均大于3, Schaller等[12 ] 的实验证实了PbSe量子点中激发态到基态的多声子无辐射弛豫过程, 并对相应的黄-里斯因子进行了估算, 其估算值要求满足大于6的强耦合范围, 计算的${S_{{\rm{III}} \text{-} {\rm{G}}}}$ 值虽与其有所偏差, 但也达到了强耦合的要求, 而其他两个激发态到基态弛豫的黄-里斯因子与其估算值偏差更大, 所以可以初步判定Schaller等[12 ] 实验验证的应是第三激发态到基态的弛豫, 这一结论将在下一节的讨论中得到进一步的证实.图2(a) 和图2(b) 分别为温度为5和300 K时, PbSe量子点带内弛豫率与半径的变化关系. 可以看出, 除(I-G)弛豫过程外, 其他5种过程的弛豫率与半径的变化关系都可以用非对称的高斯型曲线来形容, 而各个过程在不同的半径范围内发生的概率是不同的. 在半径变化范围为0.8 nm $ < R < $ 1.4 nm时, 主要发生的是激发态内部之间的弛豫过程, ${W_{{\rm{III}} \text{-} {\rm{II}}}}$ 的值最大, 即在这一尺寸范围内主要发生的是第三激发态到第二激发态的弛豫. (III-I)过程同时存在但其弛豫率值${W_{{\rm{III}} \text{-} {\rm{I}}}}$ 远小于${W_{{\rm{III}} \text{-} {\rm{II}}}}$ , 同时从${W_{{\rm{III}} \text{-} {\rm{II}}}}$ 和${W_{{\rm{III}} \text{-} {\rm{I}}}}$ 随半径的变化关系可知, (III-II)过程的弛豫率开始变小时, 才会有(II-I)过程的发生. 半径变化范围在1.4 nm $ < R < $ 2.2 nm时, 主要是激发态到基态的弛豫, 可以看到${W_{{\rm{III}} \text{-} {\rm{G}}}}$ 的值最大, 即在这一量子点尺寸范围第三激发态到基态的多声子弛豫过程是主体, 而Schaller等[12 ] 的实验主要是在PbSe量子点半径为1.4—1.9 nm时测量激发态到基态的多声子弛豫, 故其应属于上述主体过程. 同样也可以看到当(III-G)的过程开始变慢时, 才会有(II-G)过程的发生. 由图2(a) 和图2(b) 的对比可知, 随温度的升高, 各个过程的弛豫率最大值都变小, 但弛豫过程发生的量子点尺寸范围明显扩大. 更详细的讨论每一种弛豫过程与温度的变化关系在图3 中给出.图 2 不同温度下, PbSe量子点中带内弛豫率与半径的依赖关系 (a) 5 K; (b) 300 KFigure2. Intraband relaxation rates as a function of the radius of PbSe quantum dot at different temperature: (a) 5 K; (b) 300 K.图 3 在不同的量子点半径下, 弛豫率与温度的变化关系 (a) ${W_{{\rm{II}} \text{-} {\rm{G}}}}$ ; (b) ${W_{{\rm{II}} \text{-} {\rm{I}}}}$ ; (c) ${W_{{\rm{III}} \text{-} {\rm{I}}}}$ ; (d) ${W_{{\rm{III}} \text{-} {\rm{G}}}}$ ; (e) ${W_{{\rm{III}} \text{-} {\rm{II}}}}$ Figure3. Relaxation rates as a function of the temperature at different radii of quantum dot: (a) ${W_{{\rm{II}} \text{-} {\rm{G}}}}$ ; (b) ${W_{{\rm{II}} \text{-} {\rm{I}}}}$ ; (c) ${W_{{\rm{III}} \text{-} {\rm{I}}}}$ ; (d) ${W_{{\rm{III}} \text{-} {\rm{G}}}}$ ; (e) ${W_{{\rm{III}} \text{-} {\rm{II}}}}$ .图3(a) 给出了在不同的半径尺寸下, ${W_{{\rm{II}} \text{-} {\rm{G}}}}$ 与温度的变化关系, 可知, 在研究的量子点半径范围内随温度升高弛豫率变大. 图3(b) 和图3(c) 描述的${W_{{\rm{II}} \text{-} {\rm{I}}}}$ 和${W_{{\rm{III}} \text{-} {\rm{I}}}}$ 分别与温度的变化关系, 弛豫率都随温度的升高而变小. 且随量子点尺寸的增加其对温度的依赖性明显变弱. 图3(d) 和图3(e) 分别显示了不同半径下, 两种主要弛豫过程的弛豫率${W_{{\rm{III}} \text{-} {\rm{G}}}}$ 和${W_{{\rm{III}} \text{-} {\rm{II}}}}$ 的温度依赖性, 可以得到这两种过程随温度的变化规律是相同的, 随着半径的增加, 弛豫率则随着温度的升高先变大然后逐渐减小, 因此这两种过程的弛豫率对温度的依赖性取决于量子点尺寸的大小. 目前在一些实验中得出弛豫率随温度的升高而变大的结论得到广泛的证实[27 ,28 ] . 同时, 基于杂质态为媒介的弛豫机制, 也得出了弛豫率随温度升高既有变大又有减小的结论, 其归因于杂质位置的不同[29 ] , 这明显与我们得出的起因是不同的.4.结 论 本文应用晶格弛豫理论, 采用Fr?hlich的电子-声子耦合模型, 研究了PbSe量子点的3个最低激发态之间及其与基态之间的带内弛豫过程. 结果显示: 随量子点半径的增加, 各个弛豫过程的黄-里斯因子逐渐减小. 其与半径是一种反比关系, 重要的是得出了满足强耦合弛豫过程所要求的黄-里斯因子. 各个过程的弛豫率与半径的变化关系都可以用非对称的高斯型曲线来形容, 且在不同的半径范围内, 发生的概率是不同的. 在所讨论的量子尺寸范围内得出了第三激发态到基态, 第三激发态到第二激发态是两个主要的弛豫过程, 其与温度的变化关系又取决于量子点半径的大小. 这都充分显示了量子点尺寸的大小对其光学性质的重要影响. 







































 图 1 (a) PbSe量子点中电子的基态(G)与3个最低的激发态(I, II, III)位型坐标关系; (b) 6种带内弛豫过程的黄-里斯因子与量子点半径的关系
图 1 (a) PbSe量子点中电子的基态(G)与3个最低的激发态(I, II, III)位型坐标关系; (b) 6种带内弛豫过程的黄-里斯因子与量子点半径的关系
























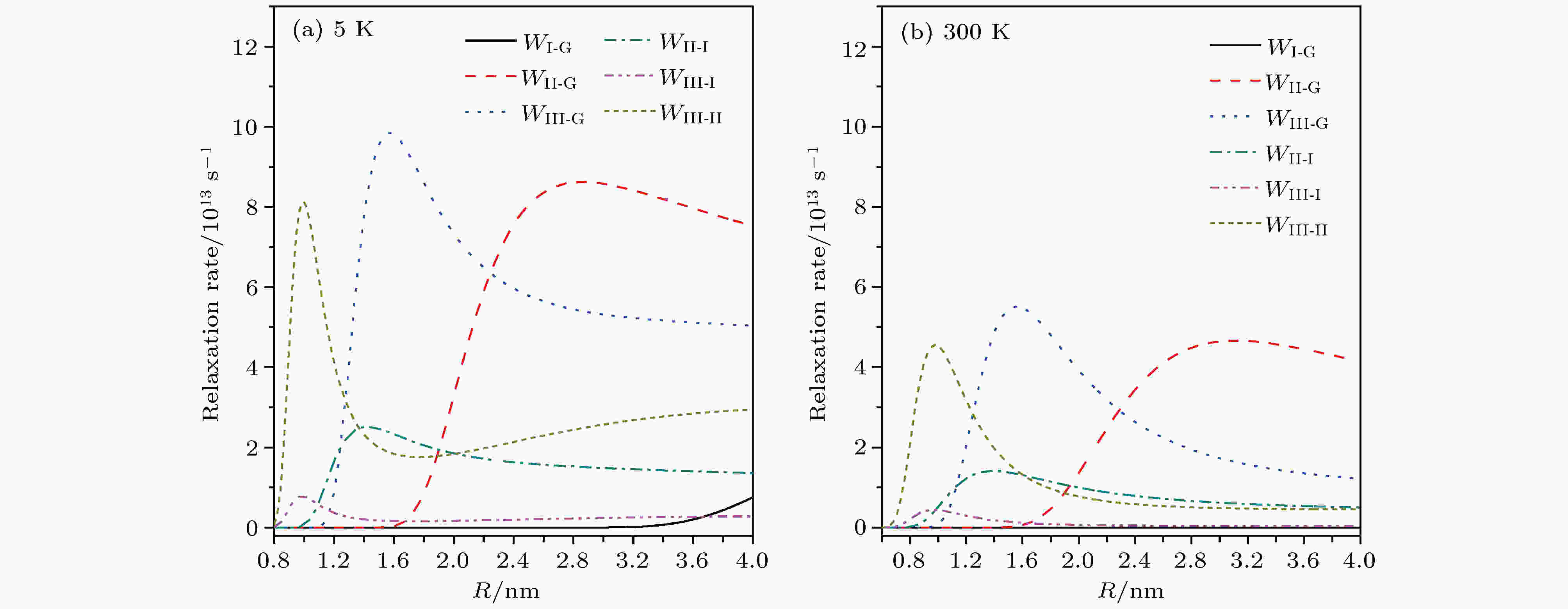 图 2 不同温度下, PbSe量子点中带内弛豫率与半径的依赖关系 (a) 5 K; (b) 300 K
图 2 不同温度下, PbSe量子点中带内弛豫率与半径的依赖关系 (a) 5 K; (b) 300 K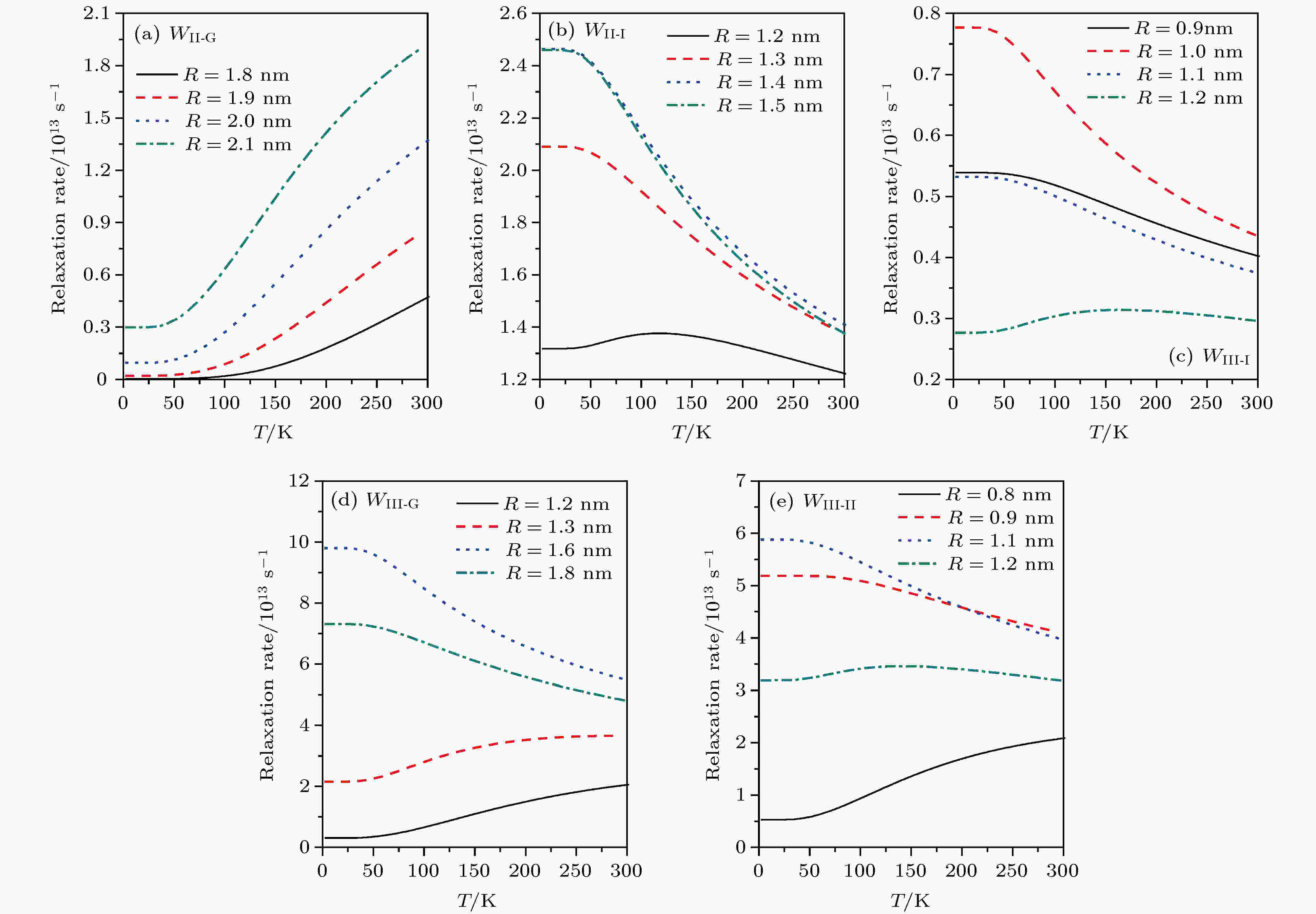 图 3 在不同的量子点半径下, 弛豫率与温度的变化关系 (a)
图 3 在不同的量子点半径下, 弛豫率与温度的变化关系 (a) 














