摘要:离轴积分腔输出光谱技术(off-axis integrated cavity output spectroscopy, OA-ICOS)是一种高灵敏度的激光光谱测量技术. 但由于使用密集的高阶模进行光谱探测, OA-ICOS输出信号强度较低, 使得探测灵敏度高度依赖于光源功率. 针对该问题, 本文引入光学再入射的方法, 使激光再次注入光腔, 以提高能量利用率和输出信号强度. 本文使用三维光追踪模拟软件, 设计再入射结构, 研究了影响信号增益的多个因素. 并搭建一套2 μm波段的再入射OA-ICOS装置, 开展了一系列研究实验. 实验数据表明: 再入射方法使OA-ICOS信号增强了8倍, 信噪比提升了4.6倍, 有效改善了探测灵敏度和光谱的吸收深度, 缓解了探测中遇到的信号功率低的问题, 为使用低功率光源和高反射率腔镜提供了有效的方法.
关键词: 再入射/
离轴积分腔/
中红外/
高灵敏度

English Abstract

全文HTML

--> --> -->

在激光光谱探测领域, 腔增强吸收光谱技术(cavity enhanced absorption spectroscopy, CEAS)凭借着高灵敏度一直受到业界广泛的关注. 当激光与Fabry-Pérot光腔模共振时, 不但能使腔内能量剧增, 还让光与物质在数公里级别的光程上相互作用, 使原本微弱的吸收信号获得3—6个数量级的提升^[1]. 但由于模式匹配的存在, 腔增强技术探测灵敏度依赖于功率稳定且线宽极窄的光源^[1,2], 并对压强、温度和机械振动等环境变化极为敏感^[3].
离轴积分腔输出光谱技术(off-axis integrated cavity output spectroscopy, OA-ICOS)^[4,5]是腔增强吸收光谱的一个分支, 近年来广泛应用于大气和环境科学^[6—9]、医疗诊断^[10—12]、工业生产过程^[13—18]等领域. OA-ICOS通过离轴入射的方法破坏模式匹配^[3], 减少自由光谱范围以激发大量腔模^[19,20], 使各波段激光都能均匀通过光腔, 有效地抑制了腔模波动引起的噪声^[2,21], 并对环境干扰产生一定的免疫能力. 因此, OA-ICOS具有实现容易、复杂度低、环境鲁棒性强和对激光入射角度不敏感等优点^[22]. 但在OA-ICOS放弃模式匹配的同时, 高能基模中的能量被分摊到密集的高阶模中, 输出信号强度大幅降低, 这无疑对激光功率和探测灵敏度都提出了很高的要求. 特别是在中远红外波段, 激光器功率和种类有限, 光电探测器灵敏度也比近红外波段要低10—10³个数量级^[3]. 在激光功率不足或腔镜反射率过高的情况下, OA-ICOS装置信噪比将降低, 甚至无法获得输出信号, 这加剧了高精细度Fabry-Pérot腔技术中存在的矛盾: 高灵敏度和高信噪比难以兼得.
然而, OA-ICOS的离轴特性为反射光的再利用提供了可能. 2014年, Leen和O'Keefe^[3]首次提出了再入射概念, 他们用Zemax光学软件对光路进行追踪模拟, 通过用带孔的反射镜在光腔外搭建类多通池结构, 使得输出信号强度提高22倍和信噪比提高10倍. 同年, Centeno等^[23,24]进行基于光学矩阵的模拟实验, 研究了增益系数与多种变量间的关系, 实现噪声等效吸收灵敏度4倍和10倍增强. 2018年, Nadeem等^[2]通过网格搜索和遗传算法等进行模拟, 发现3 cm短腔可以产生1000倍增益, 为紧凑型OA-ICOS提供了思路. 同年, Nadeem等^[22]使用再入射OA-ICOS测量CO₂, 获得噪声等效吸收灵敏度为1.6 × 10^–8 cm^–1·Hz^–1/2. 目前, 再入射技术已成为解决OA-ICOS信号强度弱的有效方法, 逐渐受到研究人员的关注.
本文利用Lighttools光学设计软件, 对再入射OA-ICOS进行优化设计, 在此基础上搭建了一套2 μm波段再入射OA-ICOS装置, 测量了大气CO₂的吸收信号, 并开展了一系列研究实验, 研究了多种变量对增益系数的影响规律, 形成了一种高效实用的再入射结构搭建方案.

在OA-ICOS装置中, 假定腔长为d, 两边腔镜反射率为r_cavity, 腔镜透过率为t_cavity, 再入射镜反射率为r_re. 初始光强为I₀, 腔内光强为I_in, 输出光强为I. 对于光强信号, 可忽略波长与电场相位信息. 描述没有吸收介质的OA-ICOS光腔内功率的速率方程为^[19]

$\frac{{{\rm{d}}{I_{{\rm{in}}}}}}{{{\rm{d}}t}} = \frac{c}{{2d}}\left[ {{I_0}C{t_{{\rm{cavity}}}} - 2{I_{{\rm{in}}}}\left( {1 - {r_{{\rm{cavity}}}}} \right)} \right],$

其中, 光速为c; 时间为t; 光腔耦合参数为C ∈ [0, 1], C主要取决于光源的空间模式质量(spatial-mode quality)和光腔耦合度. 损耗项中的2, 考虑的是光从两个腔镜出射, 但只从一段入射. 求解(1)式可得腔内光强为

${{I}_{\rm{in}}}=\frac{{{I}_{0}}C{{t}_{\rm{cavity}}}}{2\left( 1-{{r}_{\rm{cavity}}} \right)}\left[ 1-\exp \left( -t/\tau \right) \right],$

$\tau ={d}/{\left[ c\left( 1-{{r}_{\rm{cavity}}} \right) \right]},$

其中, τ是时间常数, 为光在光腔中的衰荡时间. 当激光为恒定输入时, 光在各个方向上均为稳态, 此时OA-ICOS腔内光强为

${{I}_{\rm{in}}}=\frac{{{I}_{0}}C{{t}_{\rm{cavity}}}}{2\left( 1-{{r}_{\rm{cavity}}} \right)}=\frac{I}{{{t}_{\rm{cavity}}}},$

当t_cavity + r_cavity = 1时, 意味着OA-ICOS输出光强比入射光光强衰减了Ct_cavity/2. 当充入吸收系数为α(ν)的气体分子后, 腔镜反射率替换为r′_cavity = r_cavityexp[–α(ν)d], OA-ICOS的输出信号光强I可以表示为^[23]

$I={{I}_{0}}C\frac{t_{\rm{cavity}}^{\rm{2}}}{2\left[ \left( 1-{{r}_{\rm{cavity}}} \right)+\alpha \left( v \right)d \right]},$

其中, 光腔耦合参数C可以表示为^[23]

$C = \frac{m}{F},$

光在腔内的往返次数为m, 光腔的精细度为F. 定义增益系数为再入射OA-ICOS输出光强度I_re与传统OA-ICOS输出光强度I_origin之比, 由于腔镜存在吸收无法忽略, 因此t_cavity + r_cavity + a_cavity = 1, 增益系数gain可表示为

$\begin{split}&gain=\frac{{{I}_{\rm{re}}}}{{{I}_{\rm{origin}}}}\\&=\frac{\displaystyle\frac{{{t}_{\rm{cavity}}}}{2\left[ \left( 1-{{r}_{\rm{cavity}}} \right)+\alpha \left( v \right)d \right]}\sum\nolimits_{i=0}^{n}{{{\left( {{r}_{\rm{re}}}{{r}_{\rm{cavity}}} \right)}^{i}}{{C}_{i}}{{t}_{\rm{cavity}}}{{I}_{0}}}}{{{C}_{0}}\displaystyle\frac{t_{\rm{cavity}}^{\rm{2}}}{2\left[ \left( 1-{{r}_{\rm{cavity}}} \right)+\alpha \left( v \right)d \right]}{{I}_{0}}}\\&=\frac{\displaystyle\sum\nolimits_{i=0}^{n}{{{\left( {{r}_{\rm{re}}}{{r}_{\rm{cavity}}} \right)}^{i}}{{m}_{i}}}}{{{m}_{0}}},\end{split}$

其中, n为激光再次注入光腔的次数. OA-ICOS技术吸收系数写作^[21]:

$\alpha \left( \nu \right) = \frac{1}{d}\left| {\ln \left\{ {\frac{1}{{2{r_{{\rm{cavity}}}}^2}}\left[ {\sqrt {4{r_{{\rm{cavity}}}}^2 + \frac{{I_0^2}}{{{I^2}}}{{\left( {1 - {r_{{\rm{cavity}}}}^2} \right)}^2}} - \frac{{{I_0}}}{I}\left( {1 - {r_{{\rm{cavity}}}}^2} \right)} \right]} \right\}} \right|.$

当R → 1时, exp(αd) → 0, 此时(1)式可以简化为

$\alpha \approx \frac{1}{d}\left( {\frac{{{I_0}}}{I} - 1} \right)\left( {1 - {r_{{\rm{cavity}}}}} \right).$

搭建的再入射OA-ICOS装置图如图1所示. 激光器输出的激光依次经过光纤隔离器、准直器、凸透镜、反射镜、再入射镜, 最后耦合进高精细度腔. 激光光源为Nanoplus公司生产的连续可调谐分布反馈式激光器, 中心波长为2004 nm, 可调节范围为2001—2005 nm, 线宽小于3 MHz, 典型输出功率为8.2 mW, 入射光的功率为5 mW, 激光束腰直径为1.1 mm. 光纤隔离器中心波长2000 nm, 回光损耗为50 dB, 一方面可防止光反馈损伤激光器, 另一方面可减少反射光对光源的干扰, 使得激光器输出功率和波长保持稳定. 高精细度腔由两片高反射镜(Layertec, 曲率半径1 m, 直径1英寸) M_in与M_out组成, 两镜通过模式匹配完成对准, 间距55 cm, 一面镀有反射率99.86%的高反膜, 另一面镀有实测2%吸收的增透膜. 为防止气压过低导致腔镜形变, 高精细度腔入射口和出射口使用窗口片密封, 其透射率为99.5%. 输出信号由离轴抛物面反射镜汇聚于探测器上. 探测器(PDA10DT-EC, Thorlabs)在2000 nm处的峰值响应为1.2 A/W, 放大器增益在0 dB到70 dB之间可调, 低通滤波带宽在500 Hz到1 MHz之间可调. 依照模拟结果定制的银膜再入射镜M_re反射率为95%, 直径1 in (1 in = 2.54 cm), 曲率半径为734 cm, 与M_in间距16 cm. He-Ne光源作为光路调节和调腔时的指示光.
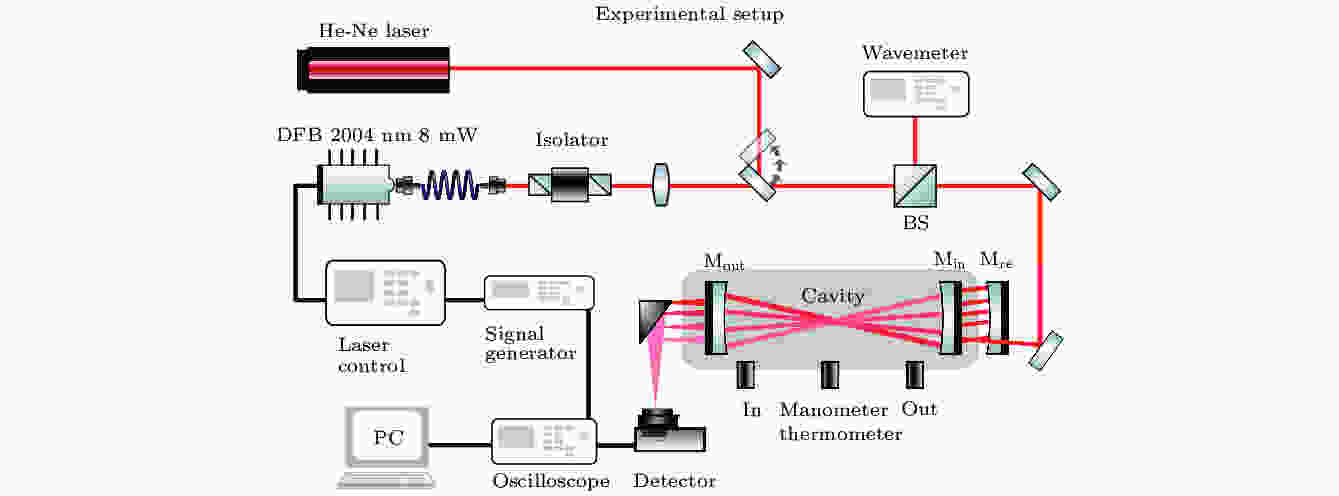图 1 再入射OA-ICOS实验装置光路图
Figure1. Reinjection OA-ICOS experimental setup.

2

-->

4.1.参数设置与约束条件

本文使用光学设计软件Lighttools设计再入射OA-ICOS模型, 基于几何光学进行三维光线追踪模拟计算. 设计的目标为: 依据现有条件, 优化再入射结构, 使OA-ICOS装置输出信号功率的增益系数最大化. 主要优化和讨论的参数包括: 再入射曲率半径R、再入射镜M_re与腔镜M_in间距L、XY方向入射光角度和系统损耗. 模拟设置与真实实验设置仅有四点不同: 其一, 假设将要定制的M_re的反射率为98%; 其二, 忽略腔镜增透膜存在的吸收; 其三, 忽略光腔密封的楔形窗口片, 以符合当前主流腔镜外露结构; 其四, 忽略OA-ICOS信号收集问题.
在OA-ICOS中, 离轴越大, 单次传输光程越长, 自由光谱范围越小, 激发高阶模越均匀, 信噪比就越高^[25], 但与此同时输出信号强度降低, 激光也更容易与腔壁接触, 产生衍射噪声. 本次实验光腔内半径只有7 mm, 为保留调节余地和防止腔壁反射损耗, 设置直径2 mm的再入射孔(约为入射光束腰直径1.1 mm的两倍), 孔中心与镜片中心线相距5 mm. 为使信号增益最大化, 并降低复杂度, 控制光斑尽可能按圆形排布, 以充分利用5 mm离轴半径. 模拟低损耗光学器件运算量大, 运算时间漫长, 为减少模拟计算时间, 设定当计算误差低于1%时停止计算.
2 -->

4.2.光斑分布分析

M_re上反射光斑的数量代表激光再入射的次数, 与增益系数有着重要关联. 为分析反射光斑分布情况, 对再入射OA-ICOS进行一系列模拟, 分别选择M_re和M_out截面进行观测, 模拟结果如图2—图4所示. 根据分析结果, 不同参数对光斑分布的影响如下.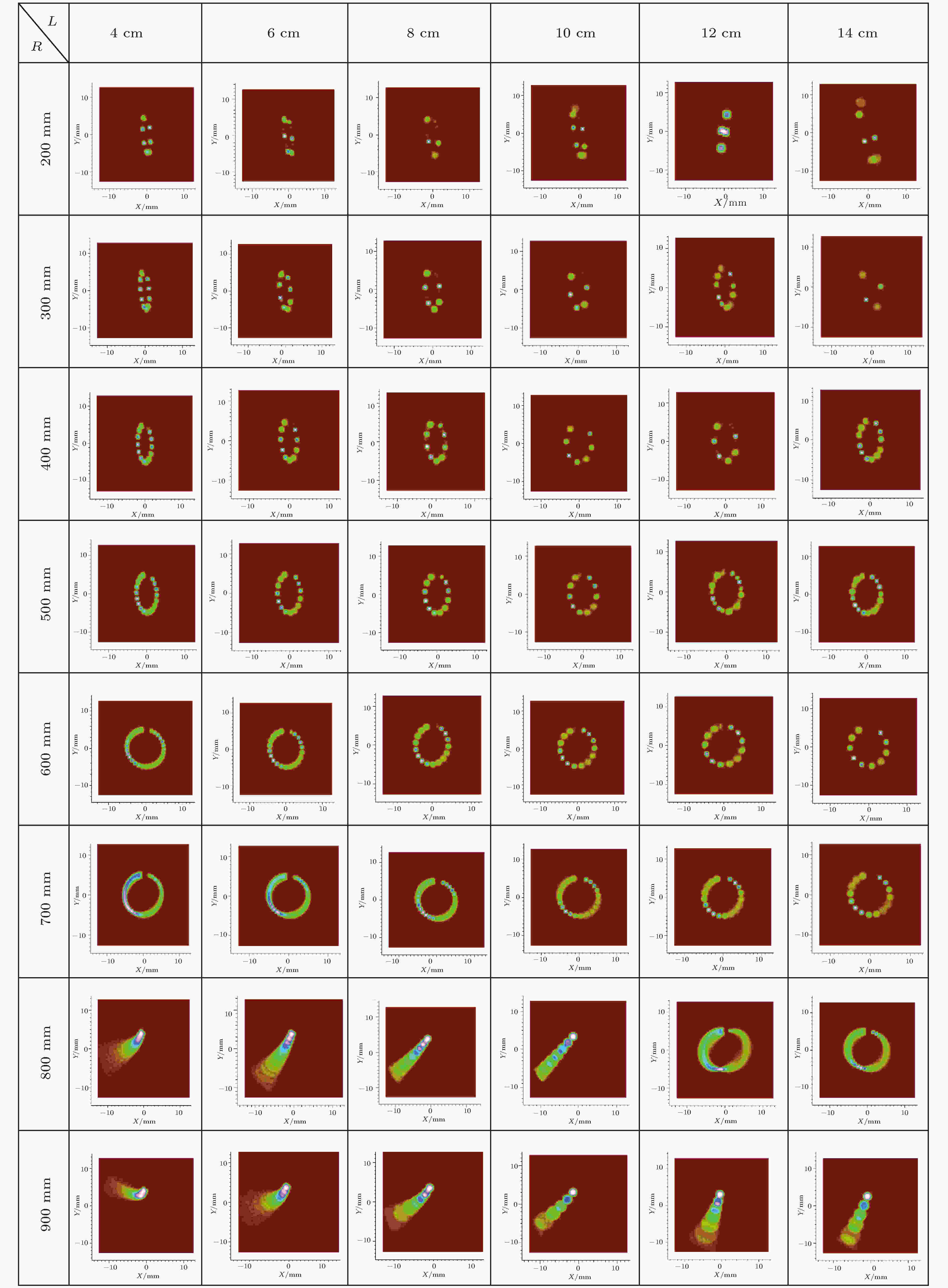
图 2 在不同L和R时再入射镜M_re上光斑排布情况
Figure2. Distribution of spot on the re-injection mirror M_re with different L and R.

图 4 在不同入射角度时再入射镜M_re上的光斑排布情况
Figure4. Distribution of spot on M_re with different incidence angles.

1)再入射镜M_re的曲率半径R: 主要控制M_re上光斑分布密度和M_out上能量分布密度. M_re上光斑分布密度与R的大小呈正相关. 随着R变小, 反射光圈在M_out上变得难以按圆形排布, 能量密度降低, 反射光将超出光腔半径7 mm范围, 造成腔壁反射损耗和噪声; 随R着变大, 在M_out上的反射光圈越发聚拢, 能量密度不断增大; 当R > 800 mm后, 在M_re上光斑已无法产生成稳定光圈, 如图2和图3所示.
图 3 在不同L和R时腔镜M_out上光斑排布
Figure3. Distribution of spot on cavity mirror M_out with different L and R.

2)M_re与M_in的间距L: M_re上光斑分布密度与L的大小成负相关. 另外, 当L变小, 激光需要更大入射光角度才能形成再入射; 当L变大, 激光随着传输距离变长, 方向性将变差, 光斑尺寸将变大, 不利于紧凑型系统搭建, 如图2所示.
3)XY方向的入射光角度: Y方向的入射光角度主要控制光斑左旋或右旋排布, 无法约束光斑在Y方向上的扩散; X方向的入射光角度主要控制光斑在X方向的扩散情况, 可调整光斑密度. 在R = 700 m, L = 10 cm时, 不同入射角度对M_re上光斑分布的影响如图4所示.
4)再入射孔的离轴距离: 决定可排布M_re上光斑的空间大小. 离轴距离越大, 在腔镜上周长越长, 可以排布不重合的光斑也越多, 增益系数上限越大, 因此大尺寸腔镜有利于再入射提升性能.
总结不同参数对光斑分布的影响, 如表1所列. 在这些参数中, 入射角度受初始设置条件约束, 离轴距离受光腔内径限制, 无过多优化空间, 因此M_re上反射光斑总数仅由R和L所决定.

影响参数	光斑分布
	Mre光斑数量上限	Mre光斑总数	Mre光斑密度	Mre光斑分布形状	Mout能量分布密度	约束入射角度
Mre曲率半径R		√	√		√
Mre与Min间距L (再入射位置)		√	√			√
XY方向入射光角度			√	√	√
再入射孔离轴距离	√

表1再入射结构中不同参数的影响
Table1.Effects of different parameters in reinjection.

2 -->

4.3.增益系数分析与参数选择

依据常理, 再入射次数越多, 入射光腔的能量也应该越多. 对图3中M_out截面光强进行计算, 可获得不同L和R条件下的模型的增益系数分布, 如图5所示. 当M_re上反射光斑稀疏时, 增益系数与光斑数量成正相关; 随着光斑排列紧凑, 有轻微重叠, 增益系数到达顶峰; 但随着光斑重叠面积继续增大, 增益系数与光斑数量开始呈现不符合常理的负相关. 针对负相关模型进行光线追踪模拟发现, 过分密集的光斑排布会使入射光的部分能量在初次反射后便沿再入射孔泄漏, 导致再入射次数即便增多, 信号增益也依然下降. 综上, 增益最优的光斑排布可总结为: 在离轴距离确定的情况下, 尽可能排布最多的反射光斑, 以保证高增益; 同时避免光斑间过度重合, 以减少入射能量泄漏和干涉噪声.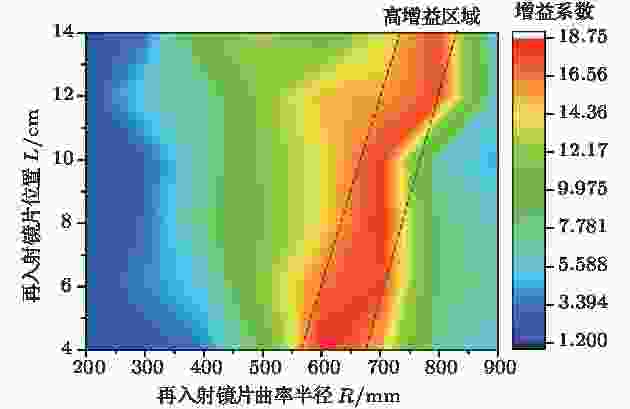
图 5 在不同L和R时M_out截面的增益系数
Figure5. Gain coefficients of M_out with different L and R.

如图5所示, 这类最优增益光斑排布不只有唯一解, 它们形成了连续的高增益区域, 可通过R和L的互补调节来维持最优增益系数. 但是在实际搭建过程中, 调节再入射距离L的代价远低于更换镜片曲率半径R的代价. 因此在高增益区域中选择参数时, 应首先依据光腔内反射光能量分布密度选择合适的R; 然后, 依据入射角可调节范围选择合适的L; 最后, 微调L以平衡增益系数与干涉噪声.
在高增益区域中, 选取多个最优增益点进行对比, 部分M_out能量分布如图6所示. 第一组(a)参数为R = 600 mm, L = 4 cm, 增益为18.74倍, 但光斑在光腔中单位面积功率密度低, 发散性强, 光线容易与腔壁接触产生噪声; 第二组(c)参数为R = 700 mm, L = 10 cm, 增益为18.04倍, 其单位面积能量密度高, 能量分布与(b)传统OA-ICOS相似, 且入射光可调节角度更大, 因此作为最优模拟结果.
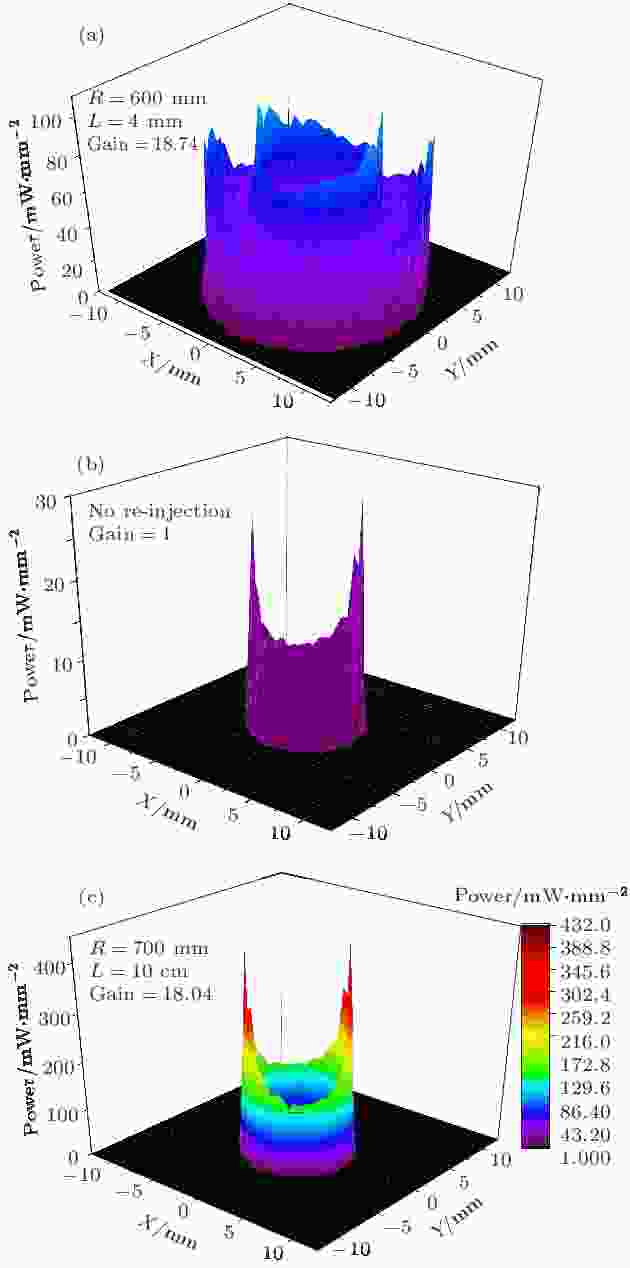图 6 M_out能量分布图
Figure6. Power distribution of M_out

2

-->

5.1.增益规律验证

为评估光学模拟的准确性, 需要对实验中对模拟增益进行验证. 依据设计定制再入射镜片M_re, 反射率实测为95%, 曲率半径R为734 mm, M_in增透膜透射率实测有2%的吸收, 实验选取位于2003.57 nm的CO₂吸收峰进行. 本节实验依据模拟设置搭建多组L不同的再入射OA-ICOS装置, 在常压下进行测量, 激光扫描频率为10 Hz, 对1000次扫描结果进行平均, 测得光谱吸收信号如图7.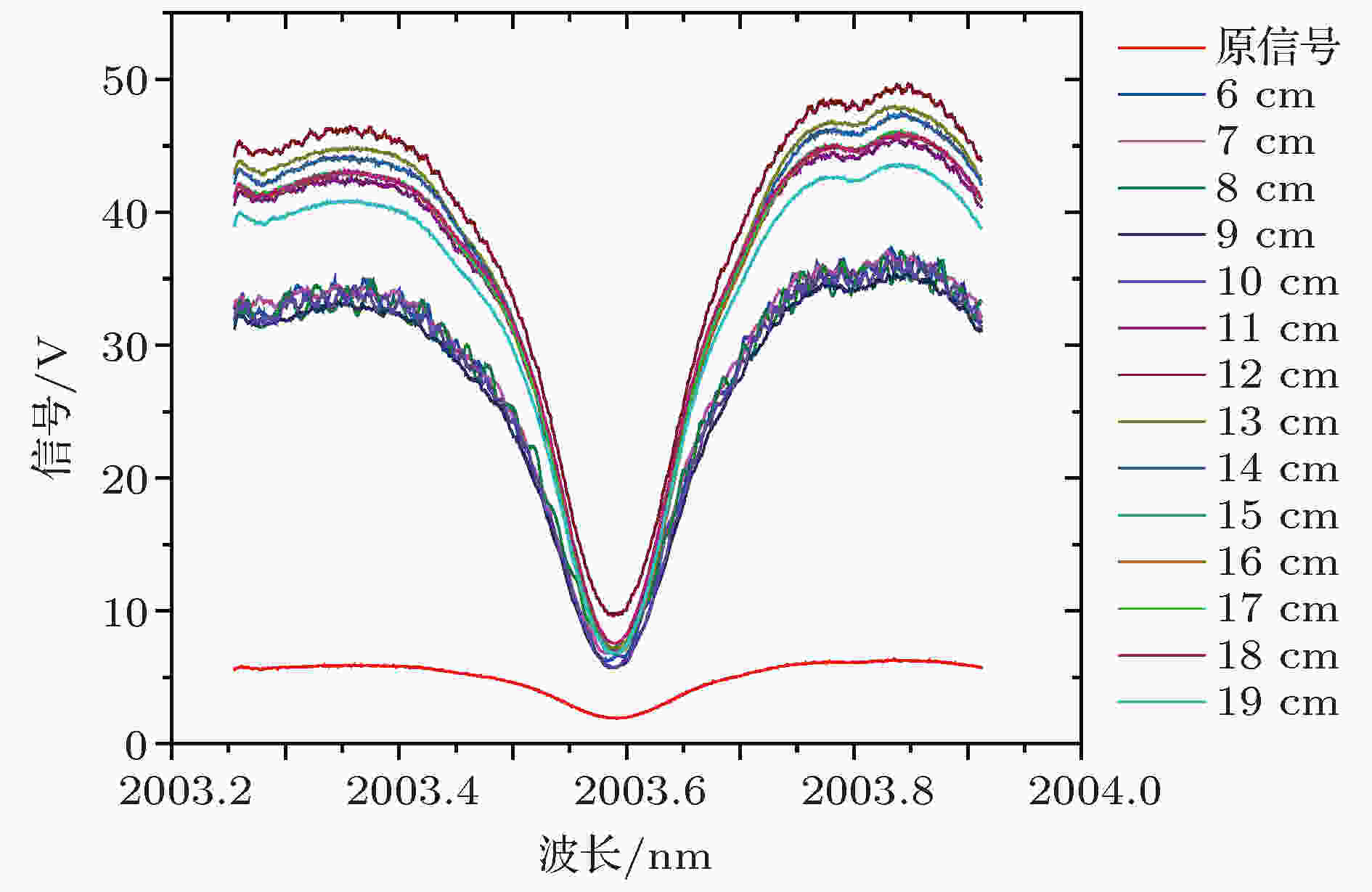
图 7 在不同再入射位置L时系统输出信号
Figure7. Output signal at different re-injection position L.

为保证模拟增益准确性, 本文依据系统实际损耗和M_re曲率半径进行重新模拟, 然后进行对比, 结果如图8所示. 其中, 定义光束由M_re出发经M_in的高反射镜面再回到M_re时的衰减为系统(单次再入射)损耗, 计算损耗时需要同时考虑到M_re反射率95%、M_in增透膜存在2%吸收和高反膜反射率99.86%, 在这种情况下计算的单次损耗约为8.7%.
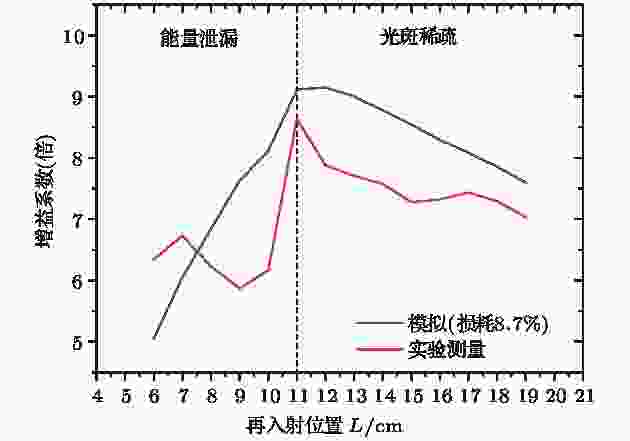图 8 模拟与实验增益对比
Figure8. Gain comparison between simulation and experiment.

通过对比可以看出, 随着L的减少, 光斑逐渐由稀疏变得紧密, 增益系数缓慢增加; 当L为11 cm时, 光斑排列紧凑, 有轻微重叠, 增益系数到达峰值(8.6倍); 随着L继续减少, 光斑重叠面积增大, 初次反射光开始沿再入射孔返回, 造成能量泄漏, 与此同时再入射结构对入射角度的要求不断提高, 增益开始下降, 并伴随强烈的干涉噪声.
由图8可见, 通过实验获得的最优增益为8.6倍, 实验与模拟趋势基本保持一致, 有效证明了模拟设计的准确性. 对于实验与模拟结果间的偏差, 总结原因如下: 1)激光入射角度需要同时满足传统OA-ICOS结构和再入射结构, 导致调腔难度加大; 2)粗糙的再入射孔边缘损耗入射光能量; 3) OA-ICOS光腔输出的光信号存在发散与倾斜^[26], 导致探测器无法收集完整输出信号.
在模拟分析时, 注意到当再入射镜的反射率M_re由98%下降到95%时, 增益系数下降严重, 为此本文增加了系统损耗对增益系数影响的模拟研究, 如图9所示. 当使用高损耗镜片时, 再入射产生增益较低, 且增益曲线平坦; 当使用低损耗镜片时, 再入射增益提升明显, 且最优增益也将向反射光斑更密集的参数偏移. 可以看出, 再入射结构对系统损耗非常敏感, 即使微弱的损耗增加, 也将在多次反射后产生叠加效应, 最终让增益系数产生显著衰减.
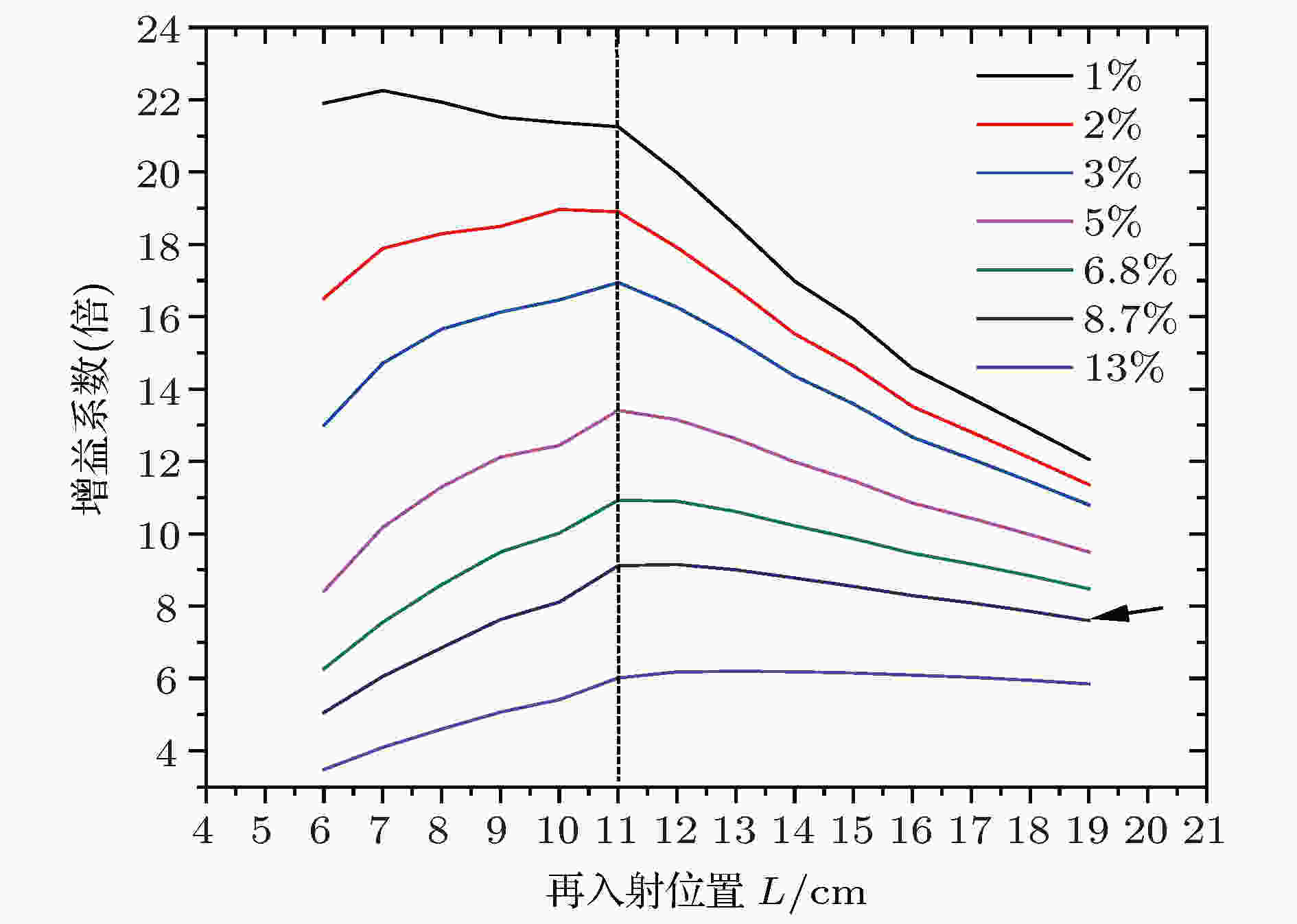图 9 在不同损耗情况下的增益系数模拟结果
Figure9. Simulation gain of system with different losses.

2 -->

5.2.信噪比提升

为进行低压测量, 在光腔两端安装楔形窗片口进行密封, 将气压抽至2500 Pa, 激光波长以30 Hz频率扫描, 调节M_re位置使信号强度最优. 最终, 在L = 16 cm时获得最优信噪比, 对1000次扫描结果平均, 获得吸收光谱如图10所示. 依据(9)式对吸收信号进行处理, 可获得结果如图11所示.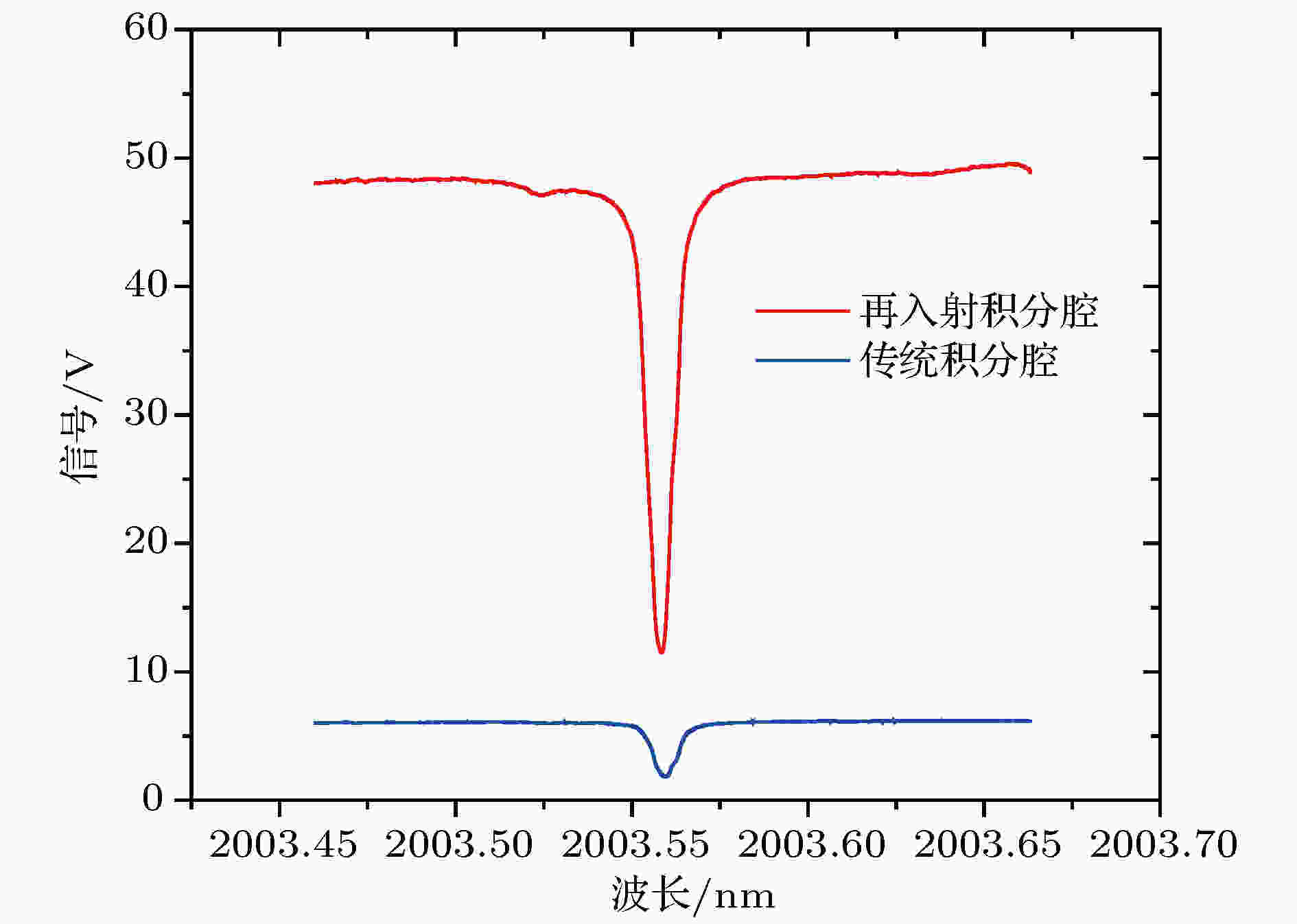
图 10 系统吸收光谱对比
Figure10. Comparison of absorption spectra of the system.

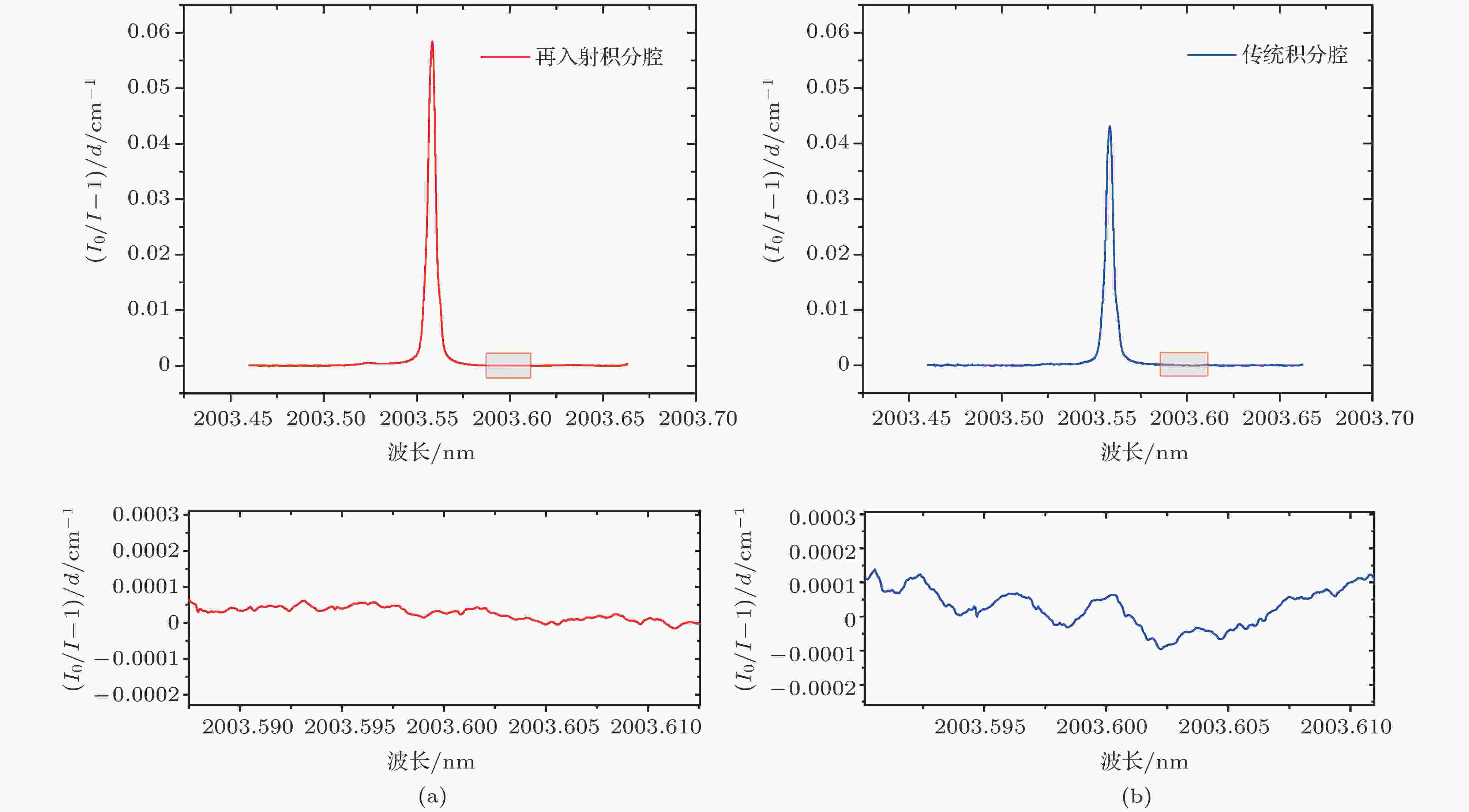图 11 系统灵敏度对比　(a)有再入射; (b)无再入射
Figure11. Comparison of system sensitivities: (a) With reinjection; (b) without reinjection.

实验数据表明: 加入再入射结构前后, OA-ICOS吸收深度获得明显提升, 光谱吸收信号由原来的6 V增强至48 V, 增强了8倍; 信噪比由原来的460提升至2120, 提高了4.6倍, 显著改善了探测灵敏度. 在原理上, 再入射技术相当于让一束入射光变成了多束, 入射光总功率的倍增让输出信号强度获得明显提高, 光谱信号的收集不再受探测器探测极限的制约, 表现为更大的吸收深度; 同时, 多束激光激发的高阶模产生叠加, 让腔模更为密集和均匀, 由此探测出的吸收光谱信号也更为平滑, 表现为信噪比得到有效提升.

本文使用Lighttools三维光追踪软件设计再入射结构, 优化系统参数, 相比Zemax^[3]和光学矩阵方法^[23,24]更加直观和便捷. 依据设计结果搭建了再入射OA-ICOS测量装置并开展实验, 实验验证了模拟设计的有效性和准确性, 实验和模拟误差在合理范围内. 实验结果表明: 在低功率激光器和一英寸小尺寸腔镜的条件下, 再入射方法有效提高了吸收深度, 光谱信号增强8倍, 信噪比提升4.6倍. 在OA-ICOS中引入再入射方法, 有效缓解了测量中遇到的入射光功率低的问题, 为使用低功率光源获取更高探测灵敏度提供了解决方法, 使得OA-ICOS的探测灵敏度接近甚至超越其他高精细度腔光谱成为可能.