摘要:基于铯原子阶梯型6S_1/2-6P_3/2-8S_1/2 (852.3 nm + 794.6 nm)能级系统, 一束波长为852.3 nm的圆偏振光作为抽运光, 将室温下气室中的铯原子由基态6S_1/2激发到中间激发态6P_3/2并极化, 另一束波长为794.6 nm的线偏振光作为探测光, 其频率在6P_3/2—8S_1/2态之间扫描, 经过原子气室后差分探测便可获得铯原子激发态6P_3/2—8S_1/2能级跃迁之间的双色偏振光谱. 实验上系统地测量、分析了抽运光频率失谐、偏振, 以及抽运光与探测光同反向实验构型对双色偏振光谱的影响, 并将其用于794.6 nm半导体激光器的稳频, 锁频之后, 225 s内的残余频率起伏约为0.5 MHz.
关键词: 双色偏振光谱/
激发态/
光抽运/
激光稳频

English Abstract

全文HTML

--> --> -->

原子激发态的光谱不仅揭示了原子激发态能级结构的信息, 为理论工作者提供了必要的参数及实验检验, 而且有广泛的应用价值, 如原子滤波器, 双色激光冷却/俘获中性原子、频率上转换、原子能级结构的精密测量、里德伯原子的激发、及激光稳频等^[1-7]. 目前, 常见的获得原子激发态光谱的技术有: 光学双共振吸收光谱(optical-optical double resonance, OODR)^[8]和双共振光抽运光谱(double resonance optical pumping, DROP)^[9,10], 但这两种光谱对工作于激发态跃迁之间的激光稳频时, 都需要对激光器进行直接或间接的频率调制, 然后通过锁相放大器解调出鉴频信号来锁定该激光器. Carr 等^[11]和Yang 等^[12]基于一个阶梯型的三能级原子系统, 实验演示了一种获得原子激发态偏振光谱的技术, 用工作于基态–中间激发态的圆偏振激光作为抽运光, 将原子极化、布居到中间激发态, 然后用另一波长、工作于中间激发态–更高激发态的线偏振光作为探测光, 进行差分探测即可获得原子激发态的偏振光谱. 区别于早在1976年, Wieman等^[13]基于二能级原子系统(基态–激发态), 使用单一波长的激光分为两束, 一束作为抽运光极化原子, 另一束作为探测光差分探测来获得偏振光谱 (polarization spectroscopy, PS), 把激发态偏振光谱称为双色偏振光谱 (two-color polarization spectroscopy, TCPS). 2012年, Kulatunga等^[14]基于铷原子5S_1/2-5P_3/2-5D_5/2三能级系统, 实验初步研究了抽运光频率失谐对TCPS的影响; 同年, Noh^[15] 基于铯原子6S_1/2-6P_3/2-7S_1/2系统, 理论上研究了TCPS线形随相关参数的演化; 2014年, 我们研究组基于铯原子6S_1/2-6P_3/2-7S_1/2系统实验上获得了TCPS, 并结合电光调制(electro-optic modulator, EOM)边带技术, 发展了一种将激光器无频率调制、且偏频锁定到原子激发态超精细跃迁线上的方法^[12]. 2014年, Cha等^[16]基于铷原子5P_1/2-5S_1/2-5P_3/2 V型三能级系统, 也获得了TCPS. TCPS光谱与OODR, DROP激发态光谱技术相比, 突出的优点表现在可将激光器无频率调制地锁定, 有望进一步提高激光器锁频之后的频率稳定度.
本文基于铯原子阶梯型6S_1/2-6P_3/2-8S_1/2能级系统, 实验上侧重研究抽运光频率失谐、抽运光与探测光同反向实验构型对TCPS的影响, 以及将其用于794.6 nm半导体激光器的频率锁定.

图1为与实验相关的铯原子6S_1/2-6P_3/2-8S_1/2超精细能级图及双色偏振光谱TCPS原理示意图. 中间激发态6P_3/2 F' = 2, 3, 4, 5超精细能级之间的频率间隔分别为151.2, 201.3和251.1 MHz, 其自然线宽为5.22 MHz. 激发态8S_1/2 F'' = 3, 4超精细能级之间的频率间隔为876.5 MHz, 其自然线宽为2.18 MHz. 工作于 6S_1/2→6P_3/2能级跃迁之间的852.3 nm圆偏振激光作为抽运光, 工作于 6P_3/2→8S_1/2能级跃迁之间的794.6 nm线偏振光作为探测光.
图 1 (a) 与实验相关的铯原子6S_1/2-6P_3/2-8S_1/2超精细能级图; (b)双色偏振光谱原理示意图
Figure1. (a) The related hyperfine energy levels of Cs atoms 6S_1/2-6P_3/2-8S_1/2; (b) schematic diagram of the two-color polarization spectroscopy (TCPS).

假设探测光的偏振方向沿x轴、传播方向沿z轴, 它可以表示为

$E = {E_{\rm{o}}}{{\rm{e}}^{{\rm{i}}\left( {\omega t - {k_0}z} \right)}},\quad {E_{\rm{o}}} = \left\{ {{E_{{\rm{o}}x}},0,0} \right\},$

其中${k_{\rm{o}}}$为探测光在真空中的波矢, $\omega $为其角频率, $E$为电磁场振幅. 当无852.3 nm圆偏振抽运光时, 室温下气室中的铯原子服从麦克斯韦-玻尔兹曼分布, 均匀地布居在基态6S_1/2 F = 3, 4的不同Zeeman态上. 当抽运光频率共振于铯原子6S_1/2→6P_3/2的某一超精细跃迁线时, 由于不同Zeeman态之间的CG (Clebsch-Gordan) 系数不同, 造成中间激发态6P_3/2的超精细能级的不同Zeeman态上原子布居数不均匀分布, 使得光路中处于中间激发态的铯原子变成各向异性介质. 线偏振的探测光可以看成左旋圆偏振光${\sigma ^ + }$和右旋圆偏振光${\sigma ^ - }$的组合, 它们在各向异性的铯原子介质中传播时, 其折射率系数${n^ + }$, ${n^ - }$及吸收系数${\alpha ^ + }$, ${\alpha ^ - }$均不相同, 如图1(b)所示. 这两个圆偏振光在铯原子气室输出窗端口处(z = L为铯气室的长度)又合成一个椭圆偏振光, 即有

$ {E^ \pm }\left( {z = L} \right) = \frac{1}{2}{E_{\rm{o}}}{{\rm{e}}^{{\rm{i}}\left( {\omega t - {k^ \pm }L + {{{\rm{i}}L{a^ \pm }} /2}} \right)}}\left( {x \pm {\rm{i}}y} \right), $

其中${k^ \pm } = \displaystyle\frac{\omega }{c}{n^ \pm }$, 令$n = \displaystyle\frac{{{n^ + } + {n^ - }}}{2}$, $\Delta n = {n^ + } - {n^ - }$, $\alpha = \displaystyle\frac{{{\alpha ^ + } + {\alpha ^ - }}}{2}$, $\Delta \alpha = {\alpha ^ + } - {\alpha ^ - }$, 则有

$\begin{split}& E\left( {z = L} \right) = {E^ + } + {E^ - } \\= &{E'_{\rm{o}}}\left( {{{\rm{e}}^{ - {\rm{i}}\varDelta }} + {{\rm{e}}^{{\rm{i}}\varDelta }}} \right)x + {\rm{i}}{E'_{\rm{o}}}\left( {{{\rm{e}}^{ - {\rm{i}}\varDelta }} - {{\rm{e}}^{{\rm{i }}\varDelta }}} \right)y.\end{split}$

(3)式中${E'_{\rm{o}}} = {E_{\rm{o}}}{{\rm{e}}^{{\rm{i}}\left( {\omega t - {{\omega Ln} / c}} \right)}}{{\rm{e}}^{{ - {L\alpha }}/{2}}}$, $\varDelta = - {\rm{i}}\displaystyle\frac{L}{4}\Delta \alpha +$$ \displaystyle\frac{{\omega L}}{{2c}}\Delta n$.
透射过铯原子气室的探测光(左右旋圆偏振光)被半波片λ/2和偏振分光棱镜PBS分为两束线偏振光后(偏振方向相互垂直), 入射到一个差分探测器上, 将光信号转换为电信号. 设其中一个线偏振光的方向与y轴之间的夹角为$\delta $, 其大小可通过旋转λ/2波片调整. 由于$\Delta n$与$\Delta \alpha $都是小量, 计算中保留到二次项, 以及${I_{\rm{o}}} = c{\varepsilon _{\rm{o}}}{\left| {{E_{\rm{o}}}} \right|^2}$($c$为光速, ${\varepsilon _0}$为真空中介电常数), 则有这个方向上透射光强${I_1}\left( \delta \right)$为

$\begin{split}{I_1}\left( \delta \right) = & {I_{\rm{o}}}{{\rm{e}}^{ - L\alpha }} \left\{ {{\sin }^2}\delta + \frac{{\omega L\Delta n}}{{2c}}\sin 2\delta \right. \\& + \left. \left[ {{{\left( {\frac{{\omega L\Delta n}}{{2c}}} \right)}^2} +{{\left( {\frac{{L\Delta \alpha }}{4}} \right)}^2}} \right]{{\cos }^2}\delta \right\}.\end{split}$

同理可得另一线偏振光方向上透射光强${I_2}\left( \delta \right)$为

$\begin{split}{I_2}\left( \delta \right) = & {I_{\rm{o}}}{{\rm{e}}^{ - L\alpha }}\left\{ {{\cos }^2}\delta - \frac{{\omega L\Delta n}}{{2c}}\sin (2\delta ) \right. \\& \left. +\left[ {{{\left( {\frac{{\omega L\Delta n}}{{2c}}} \right)}^2} + {{\left( {\frac{{L\Delta \alpha }}{4}} \right)}^2}} \right]{{\sin }^2}\delta \right\}.\end{split}$

旋转半波片λ/2改变$\delta $角度, 当$\delta = \displaystyle\frac{{\text{π}}}{4}$时, 差分探测器输出的电信号正比于光强差:

$\Delta I = {I_1}\left( {\frac{{\text{π}}}{4}} \right) - {I_2}\left( {\frac{{\text{π}}}{4}} \right) = {I_{\rm{o}}}\frac{{\omega L\Delta n}}{c}{{\rm{e}}^{ - L\alpha }}.$

根据Kramers-Kroning色散关系$\Delta n = \Delta {\alpha _{\rm{o}}}$$\displaystyle\frac{{2c}}{{{\omega _{\rm{o}}}\varGamma }}\frac{{{\varDelta _{\rm p}}}}{{1 + {{\left( {{{2{\varDelta _{\rm{p}}}} / \varGamma }} \right)}^2}}}$^[11], (6)式可表示为

$\Delta I = \frac{{2{I_{\rm{o}}}\omega L\Delta {\alpha _{\rm{o}}}}}{{{\omega _0}\varGamma }} \cdot \frac{{{\varDelta _{\rm{p}}}}}{{1 + {{\left( {{{2{\varDelta _{\rm{p}}}} /\varGamma }} \right)}^2}}}{{\rm e}^{ - L\alpha }},$

其中${\omega _0}$为铯原子6P_3/2→8S_1/2能级跃迁的中心频率, $\Delta {\alpha _{\rm{o}}} = \Delta \alpha \left( {\omega = {\omega _{\rm{o}}}} \right)$为探测光与原子能级共振时的左右旋圆偏振光的吸收系数之差, $\varGamma $为8S_1/2能级的自然线宽, ${\varDelta _{\rm{p}}} = \displaystyle\frac{{\omega - {\omega _{\rm{o}}}}}{{2{\text{π}}}} $ 为探测光相对于原子共振能级处的频率失谐. 从(7)式可以看出$\Delta I$为完全色散型函数, 是一个类色散信号, 即TCPS, 可作为鉴频信号来无频率调制地锁定794.6 nm半导体激光器的频率.
图2为实验装置示意图, 852.3 nm的半导体激光器通过饱和吸收光谱SAS可将其频率锁于6S_1/2→6P_3/2某一超精细跃迁线上. 同时, 通过λ/2波片和立方偏振棱镜PBS分出一部分852.3 nm 激光后, 然后通过λ/4波片将其转变为圆偏振光, 作为抽运光, 将原子由基态6S_1/2 布居到中间激发态6P_3/2, 并导致6P_3/2态超精细子能级上的不同Zeeman态原子布居数分布不均, 使得光路中的铯原子变成各向异性介质. 另一束线偏振的794.6 nm激光作为探测光, 其频率在6P_3/2→8S_1/2跃迁线之间扫描. 抽运光和探测光都是经过单模保偏光纤整形(图2示意图中未画出), 其光斑呈近圆形, 抽运、探测光束～1/e²直径分别约为 1.6和1.2 mm, 两激光束在铯泡 (Cs cell, 直径25 mm, 长50 mm)中通过双色镜DF (对852.3 nm 激光具有高反射率, 对794.6 nm激光具有高透射率)共线重合和分离. 分离后的794.6 nm探测光再经过λ/2波片和PBS后差分探测, 即可在光电探测器PD2和PD3处获得同向、反向光路布局构型下的原子激发态TCPS光谱. 将获得的TCPS光谱通过比例积分微分放大器PID负反馈794.6 nm半导体激光器压电陶瓷PZT端口, 实现频率锁定.
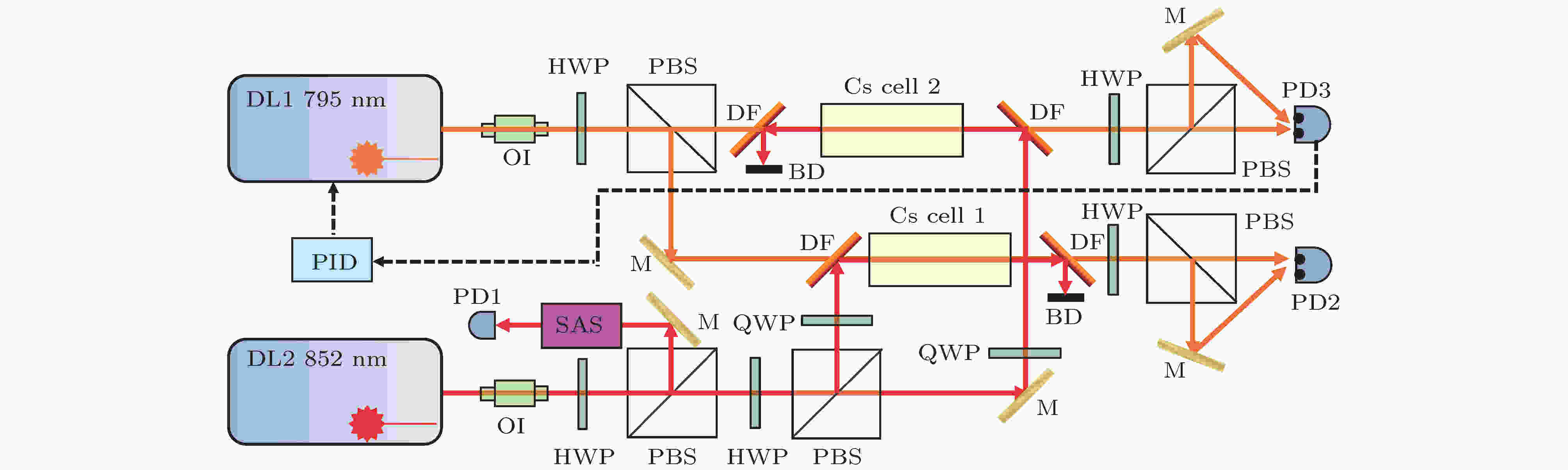图 2 实验装置示意图　DL为 852和795 nm光栅外腔反馈半导体激光器, OI 为光隔离器, SAS为饱和吸收光谱装置, PID为比例积分微分放大器, HWP为1/2波片, QWP为1/4波片, M为45°高反镜, PBS为立方偏振分光棱镜, Cs Cell为 25 mm × 50 mm 铯原子泡, DF为双色镜, BD为挡光板, PD为光电探测器
Figure2. Schematic diagram of experimental setup for the TCPS. Keys to the figure: DL, external-cavity diode laser; OI, optical isolator; SAS, saturated absorption spectroscopy; PID, proportion-integration-differentiation controller; HWP, half-wave plate; QWP, quarter-wave plate; M, mirror; PBS, polarization beam splitter cube; Cs cell, cesium vapor cell; DF, dichroic filter; BD, beam dump; PD, photodiode.

2

-->

3.1.抽运光频率失谐对双色偏振光谱的影响

为了将794.6 nm半导体激光器无频率调制地锁于6P_3/2→8S_1/2跃迁的某一超精细跃迁线上, 研究852.3 nm抽运光频率失谐对TCPS光谱的影响. 实验中, 在铯泡入射端面处, 852.3 nm抽运光的功率约为1.0 mW (功率密度约0.50 mW/mm²), 794.6 nm探测光的功率约为0.3 mW (功率密度约0.26 mW/mm²). 当抽运光频率分别锁于6S_1/2 (F = 3)→6P_3/2 (F' = 2, 3, 4) 超精细跃迁线时, 在探测器PD2和PD3处差分探测794.6 nm光信号, 获得典型的同向、反向实验构型下的TCPS, 如图3和图4所示.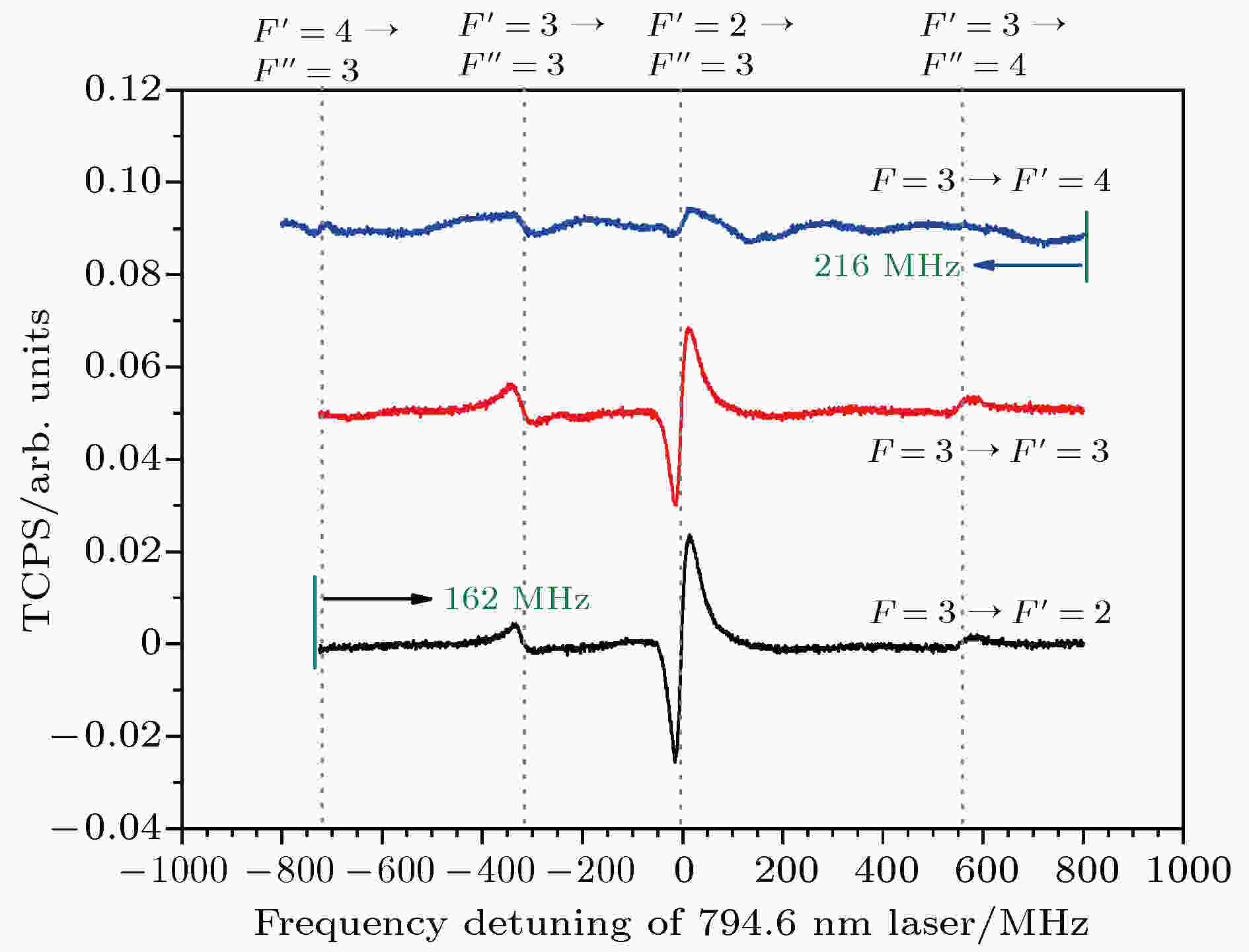
图 3 同向传输实验构型, 852.3 nm抽运光频率锁于6S_1/2 (F = 3)→6P_3/2 (F′ = 2, 3, 4)时, 794.6 nm激光作为探测光的TCPS
Figure3. The TCPS for the co-propagation configuration when the 794.6 nm probe laser is scanned over the whole 6P_3/2→8S_1/2 transition, and the frequency of 852.3 nm pump laser is locked on the 6S_1/2 (F = 3)→6P_3/2 (F' = 2, 3, 4) transition, respectively.

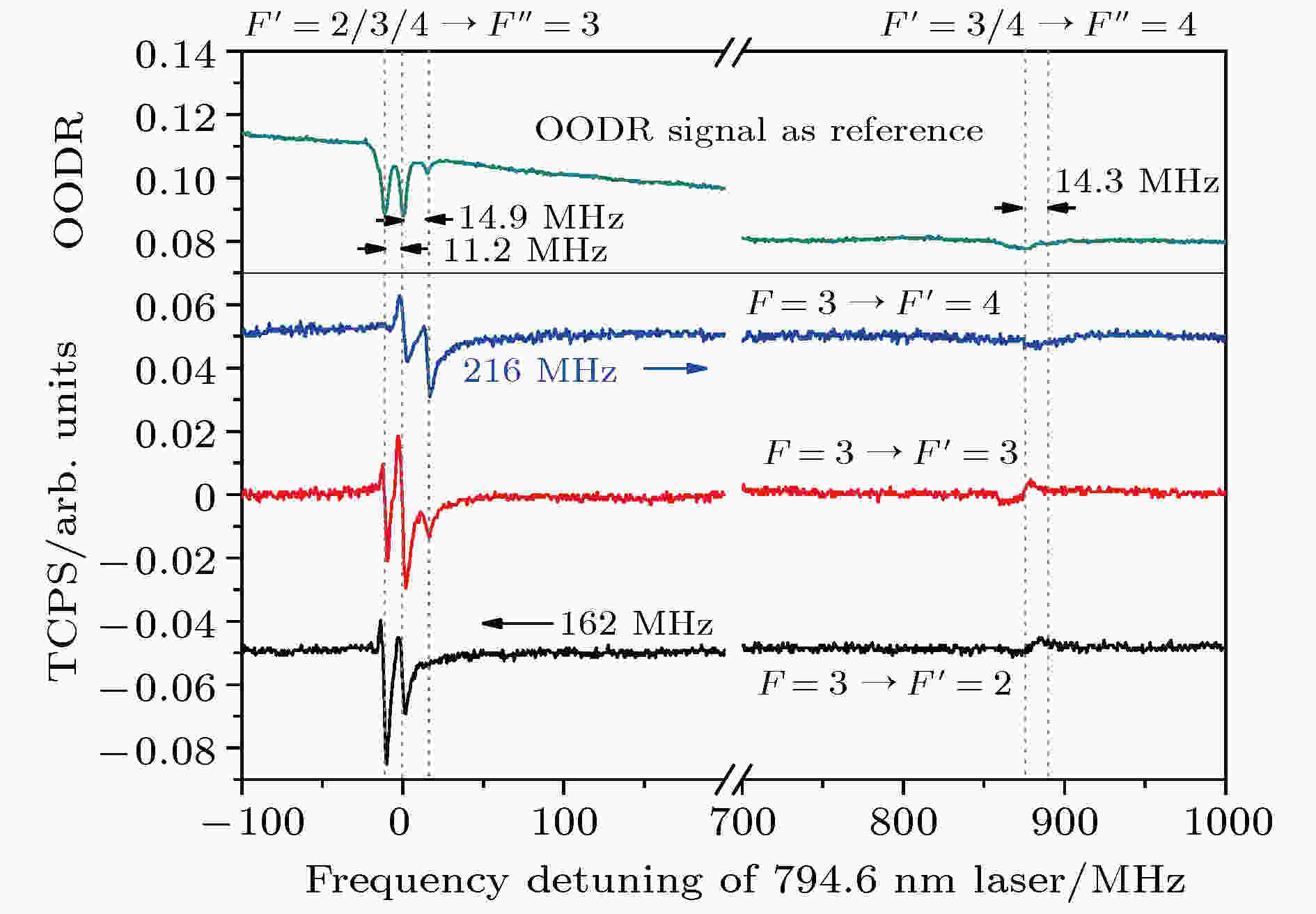图 4 反向传输实验构型, 852.3 nm抽运光频率锁于6S_1/2 (F = 3)→6P_3/2 (F' = 2, 3, 4)时, 794.6 nm激光作为探测光的TCPS
Figure4. The TCPS for the counter-propagation configuration when the 794.6 nm probe laser is scanned over the whole 6P_3/2→8S_1/2 transition, and the frequency of 852.3 nm pump laser is locked on the 6S_1/2 (F = 3)→6P_3/2 (F' = 2, 3, 4) transition, respectively.

图3为852.3 nm抽运光和794.6 nm探测光同向作用于室温下气室中铯原子时的TCPS, 从左到右这些谱线对应于激发态6P_3/2→8S_1/2的超精细跃迁线分别为: F' = 4→F'' = 3, F' = 3→F'' = 3, F' = 2→F'' = 3, F' = 4→F'' = 4, F' = 3→F'' = 4, 如图3中垂直虚线所示. 这些谱线的识别及其之间的频率间隔, 以抽运光频率锁于6S_1/2 (F = 3)→6P_3/2 (F' = 3) 超精细跃迁线时的TCPS为例简要说明: 当抽运光频率共振于F = 3→F' = 3跃迁线时, 中间激发态6P_3/2 (F' = 3)上会布居抽运光方向上速度分量为零的原子. 由于室温下气室中的铯原子服从玻尔兹曼-麦克斯韦速度分布, 以及多普勒效应的存在, 同时在F' = 2, F' = 4态上也布居速度分量不为零的原子: 852.3 nm抽运光频率对于F = 3→F' = 2,4超精细跃迁线的失谐量分别为+151.2和–201.3 MHz. 因此, 当失谐量Δ = 151.2 MHz时, 根据多谱勒频移公式Δ = ν_852.3/c × v (v为原子在抽运光方向上的速度分量, c为光速, ν_852.3为抽运光频率), 即可计算出布居在F' = 2态的原子速度分量大小为128.9 m/s (方向与抽运光同向); 当Δ = 201.3 MHz时, F' = 4态上也布居了速度分量大小为171.6 m/s的原子(方向与抽运光反向). 然而, 这两群特定速度分量的原子, 对于794.6 nm的探测光而言, 其感受到的多普勒频移分别为–162.2 MHz和+215.9 MHz. 进而, 按照探测光的频率由低到高扫描过激发态6P_3/2→8S_1/2跃迁的超精细能级时, 便可计算、排列出这些谱线的相对位置为: F' = 4→F'' = 3, F' = 3→F'' = 3, F' = 2→F'' = 3, F' = 4→F'' = 4, F' = 3→F'' = 4超精细跃迁谱线之间的频率间隔依次为417.2, 313.3, 146.0和417.2 MHz, 与图3中展示的实验结果一致(由于F' = 4→F'' = 3, 4的TCPS谱线强度太弱, 实验上不易观察到). 当抽运光频率锁于6S_1/2 (F = 3)→6P_3/2 (F' = 2)时, 相对于抽运光频率锁于6S_1/2 (F = 3)→6P_3/2 (F' = 3), 超精细子能级6P_3/2 (F' = 2)将会布居更多的原子, 因此F' = 2→F'' = 3的TCPS信号必然增强, 而此时F' = 3→F'' = 3, F' = 3→F'' = 4的TCPS信号将会减弱; 对于抽运光频率锁于6S_1/2 (F = 3)→6P_3/2 (F' = 4)时TCPS的变化规律也是如此. 进一步注意到, 当抽运光频率锁于不同的6S_1/2 (F = 3)→6P_3/2 (F' = 2, 3, 4)超精细跃迁线时, 仅会导致TCPS光谱整体的平移和信号相对强弱的变化, 而保持不变的频率间隔. 为此, 将实验上获得的抽运光频率锁于F = 3→F' = 2, F = 3→F' = 4 的这两组TCPS分别向右、向左整体平移162.2 MHz和215.9 MHz后, 与F = 3→F' = 3时的这一组TCPS的各超精细跃迁谱线频率位置完全对应. 这是因为抽运光频率锁于不同超精细跃迁线时, 仅会导致原子布居到6P_3/2态超精细子能级上的数目和速度分量大小的不同, 从而导致TCPS信号强度的相对变化, 而其频率间隔的大小完全取决于6P_3/2, 8S_1/2态的超精细分裂的频率间隔, 这一特点对于精密测量原子激发态的能级结构以及相关的磁偶极、电四级超精细相互作用常数有一定的意义.
图4为抽运光频率锁于6S_1/2 (F = 3)→6P_3/2 超精细跃迁线, 且与探测光束反向作用于室温下气室中的铯原子时的TCPS, 其各超精细跃迁谱线的位置分析方法与图3相同. 反向构型的TCPS光谱与同向构型的相比, 一个显著的区别在于同向构型的TCPS的谱线比较离散, 而反向构型的TCPS的谱线集中于“两簇”: 一簇为F' = 2, 3, 4→F'' = 3的超精细能级跃迁, 实验测量它们之间的频率间隔依次为11.2和14.9 MHz (计算值应为10.9和14.6 MHz); 另一簇为F' = 3, 4→F'' = 4的跃迁, 频率间隔为14.3 MHz (计算值应为14.6 MHz), 如图4所示. 当探测光与抽运光束同向重叠作用于原子介质时, 布居到6P_3/2态上的原子感受到的探测光和抽运光频率的多谱勒频移方向相同, 致使谱线变得离散一些; 而当探测光与抽运光束反向重叠作用于原子介质时, 原子感受到的两激光束多谱勒频移方向相反, 且由于探测光与抽运光波长(频率)的差异, 导致其多谱勒频移的大小不同, 故导致F' = 2, 3, 4→F'' = 3 (F' = 3, 4→F'' = 4)谱线的位置有一定的差异, 即“簇”. 如若探测光与抽运光的频率再接近一些, 这种“簇”特点的谱线必将演化成一个谱线, 这就是在铷原子5S_1/2→5P_3/2→5D_5/2(780 nm + 776 nm)阶梯形实验系统中研究原子激发态光谱时, 与两激光场非直接作用的超精细能级上布居的非零速度的原子对激发态光谱谱线的贡献常被遗漏的原因所在^[14,17]. 由于反向构型的TCPS谱线比较集中, 且相互叠加致使谱线的线型较为复杂, 为了清楚地识别各超精细跃迁谱线, 实验上也同时记录了激发态的双共振吸收谱线(optical optical double resonance, OODR), 如图4所示. 此外, 同、反向构型的TCPS光谱的另一个显著的区别是谱线线宽的差异: 对于原子阶梯型能级系统, 由于反向构型存在电磁感应透明这一量子相干效应, 致使反向时的TCPS线宽明显窄于同向^[18-20], 如在相同实验条件下, 抽运光频率共振于6S_1/2 (F = 3)→6P_3/2 (F' = 2)时, 对于图3和图4中F' = 2→F'' = 3的TCPS线宽, 反向线宽的典型值为7.3 MHz, 而同向线宽为16.2 MHz. 窄线宽的谱线将有助于进一步提高激光锁频之后的频率稳定度.
图5 为852.3 nm抽运光频率锁于6S_1/2 (F = 4)→6P_3/2 (F' = 3, 4, 5) 超精细跃迁线, 与794.6 nm探测光同向作用于室温下气室中铯原子时的TCPS, 从左到右这些谱线对应于激发态6P_3/2→8S_1/2的超精细跃迁线分别为: F' = 4→F'' = 3, F' = 5→F'' = 4, F' = 3→F'' = 3, F' = 4→F'' = 4, F' = 3→F'' = 4, 如图5中垂直虚线所示. 实验测量这些谱线与F' = 5→F'' = 4谱线之间的频率间隔依次为356, 0, 61, 521和937 MHz, 考虑到探测光频率扫描时压电陶瓷PZT非线性效应的影响, 在一定的误差范围内, 其与理论计算值基本一致, 见图5中垂直虚线顶端数值. 在图5中, 852.3 nm抽运光频率锁于6S_1/2 (F = 4)→6P_3/2 (F' = 3)时的TCPS信号幅度相对较小, 为此将其放大5倍显示. 图6为在抽运光与探测光反向传输的实验构型时的TCPS信号, 依据与图3谱线识别相同的方法, 可以确定从左到右的这些谱线对应的超精细跃迁分别为: F' = 3→F'' = 3, F' = 4→F'' = 3, F' = 3→F'' = 4, F' = 4→F'' = 4, F' = 5→F'' = 4, 频率间隔计算值依次为14.6, 861.9, 14.6和18.1 MHz, 与实验结果一致. 当抽运光频率锁于不同的超精细跃迁线时, 谱线的演化规律及分析讨论与图3一致.
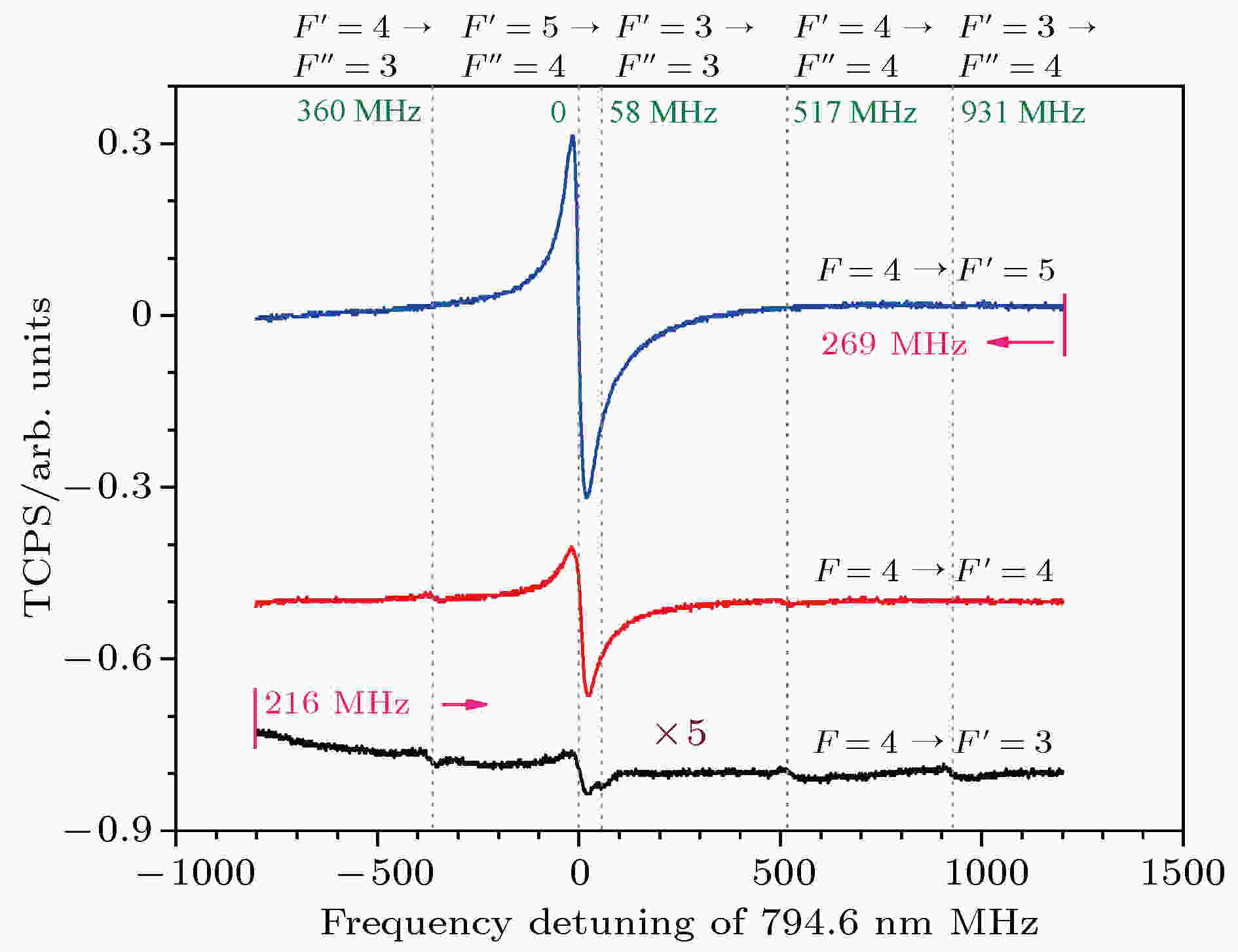图 5 同向传输实验构型, 852.3 nm抽运光频率锁于6S_1/2 (F = 4)→6P_3/2 (F' = 3, 4, 5)时, 794.6 nm激光作为探测光的双色偏振光谱
Figure5. The TCPS for the co-propagation configuration when the 794.6 nm probe laser is scanned, and the frequency of 852.3 nm pump laser is locked on the 6S_1/2 (F = 4)→6P_3/2 (F' = 3, 4, 5) transition, respectively.

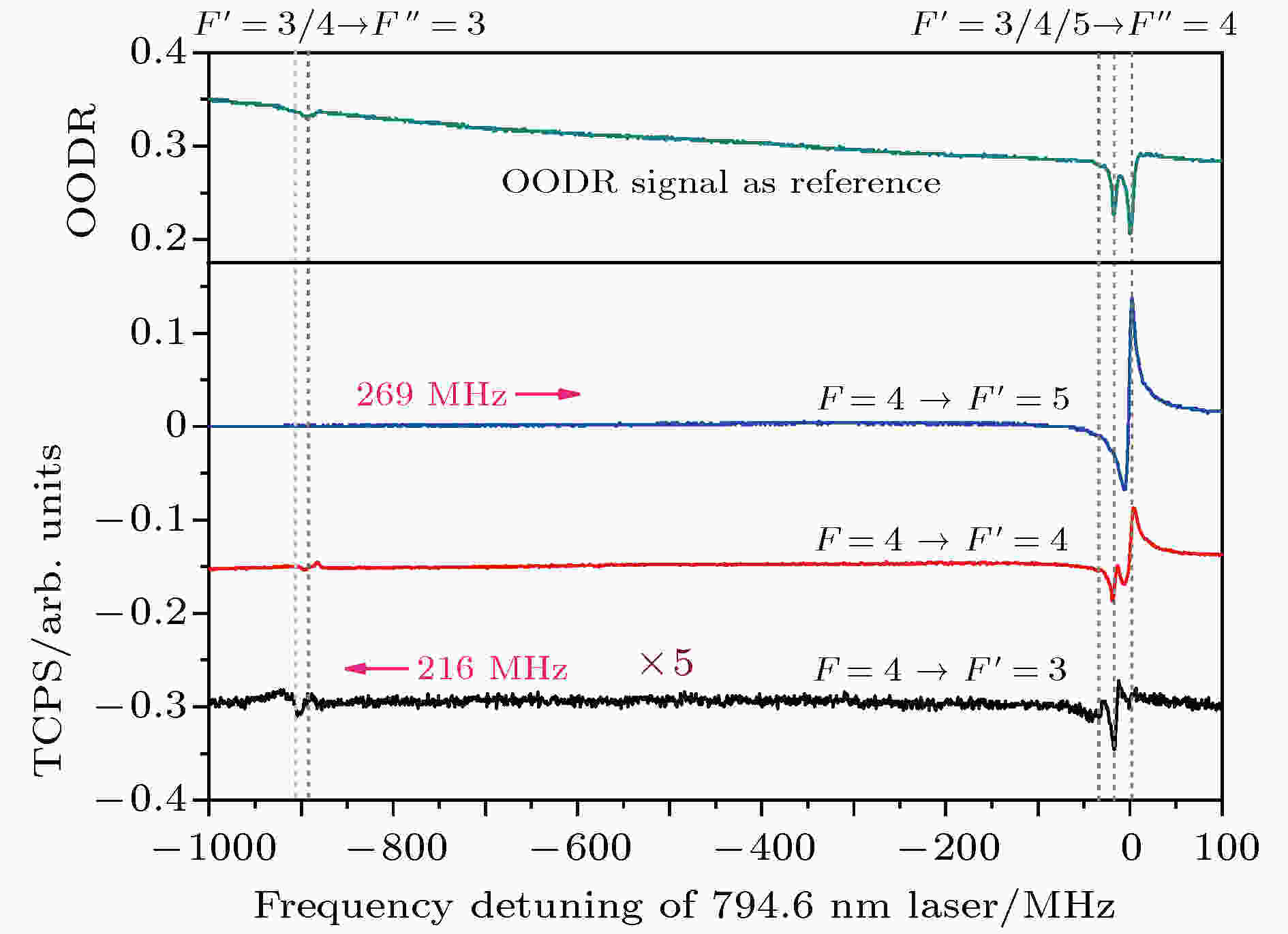图 6 反向传输实验构型, 852.3 nm抽运光频率锁于6S_1/2 (F = 4)—6P_3/2 (F' = 3, 4, 5)时, 794.6nm激光作为探测光的双色偏振光谱
Figure6. The TCPS for the counter-propagation configuration when the 794.6 nm probe laser is scanned, and the frequency of 852.3 nm pump laser is locked on the 6S_1/2(F = 4)→6P_3/2(F' = 3, 4, 5) transition, respectively.

2 -->

3.2.双色偏振光谱在794.6 nm半导体激光器稳频方面的应用

将激光器频率锁定在某一个稳定的参考频率上, 可有效地抑制激光器频率的起伏. 由于偏振光谱本身就是一个类色散信号, 可直接作为鉴频信号对激光器锁频, 无需对激光器进行额外的频率调制, 常受科学工作者的青睐. 为了将类色散的TCPS光谱信号负反馈于794.6 nm半导体激光器的电流或(和)PZT端口, 实验上常常通过旋转 λ/4波片改变抽运光的偏振在${\sigma ^ + }$和${\sigma ^ - }$之间转换(λ/4波片需要旋转90°), 实现TCPS相位反转. 实验中由于铯泡端面的双折射效应导致了抽运光、探测光偏振的改变, 当λ/4波片旋转49°时实现TCPS相位反相, 如图7所示.
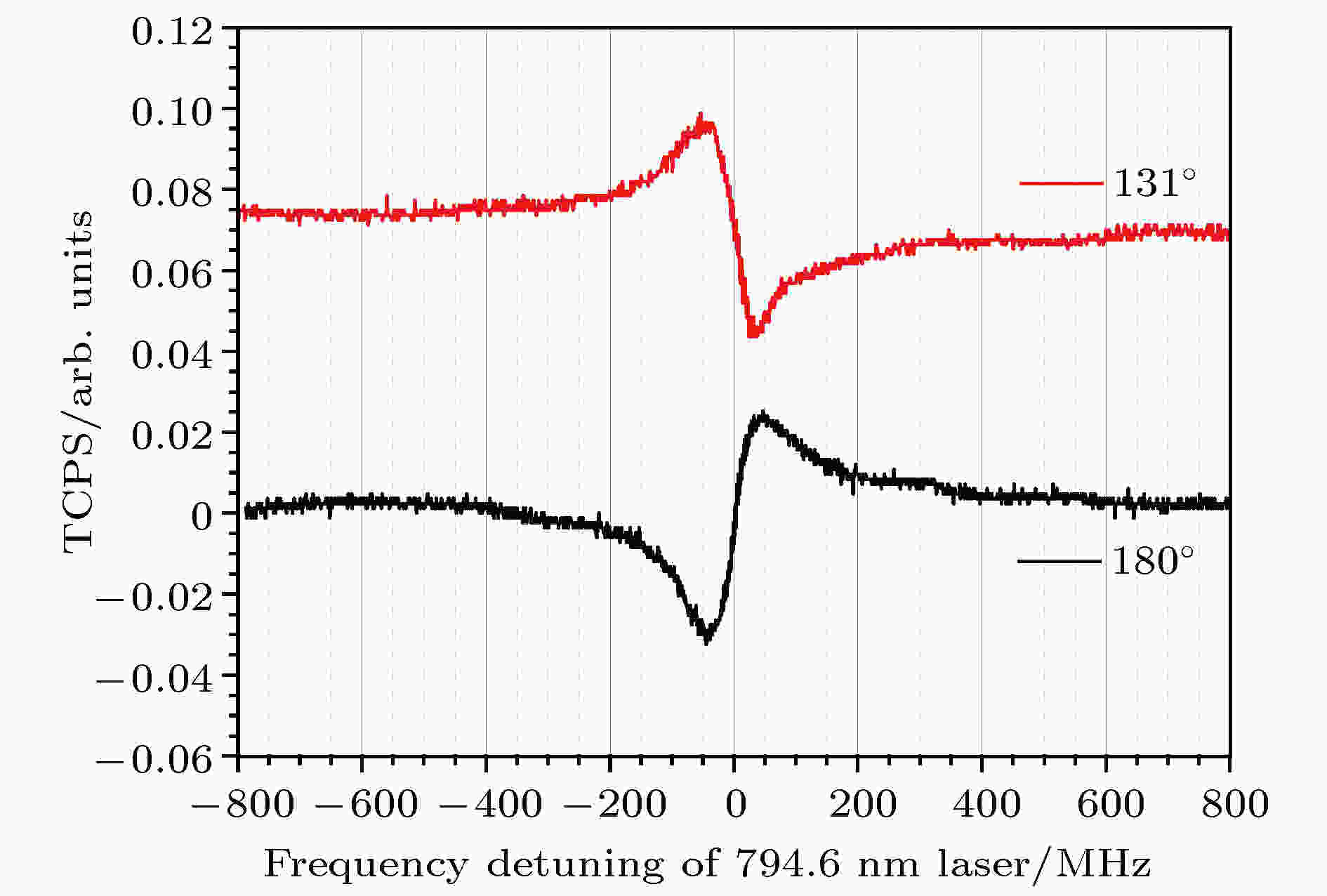图 7 相位相反的双色偏振光谱TCPS, 红色(上) TCPS对应的λ/4波片位置读数为131°, 黑色(下) TCPS对应的λ/4波片位置读数为180°
Figure7. The TCPS with opposite phase, (upper TCPS) angle of λ/4 wave plate is set to 131°; (lower TCPS) angle of λ/4 wave plate is set to 180°.

首先, 将852.3 nm激光频率通过饱和吸收光谱技术锁于6S_1/2 (F = 4)→6P_3/2 (F' = 5)超精细跃迁线上; 然后794.6 nm激光频率在6P_3/2→8S_1/2跃迁之间扫描, 在探测器PD3处进行差分探测获得 F' = 5→F'' = 4的TCPS谱线. 最后, 将此TCPS信号作为误差信号, 经过PID锁频模块及高压放大器后, 负反馈于794.6 nm激光器的压电陶瓷PZT端口. 逐渐减小794.6 nm激光器频率扫描的范围直至到0, 配合调整其激光电流及PZT的偏置电压, 保持其频率始终共振于F' = 5→F'' = 4的跃迁线, 闭合电子伺服反馈环路PID, 从而实现794.6 nm激光频率的锁定, 典型结果如图8所示. 在周围实验环境没有明显振动和噪声干扰的条件下, 794.6 nm激光器可达小时量级保持在频率锁定的状态. 方便起见, 使用数字存储示波器仅记录了在225 s内, 激光器自由运转时的频率起伏约9.2 MHz,和锁频之后的频率起伏约0.5 MHz, 794.6 nm激光器的频率稳定性有了明显的改善.
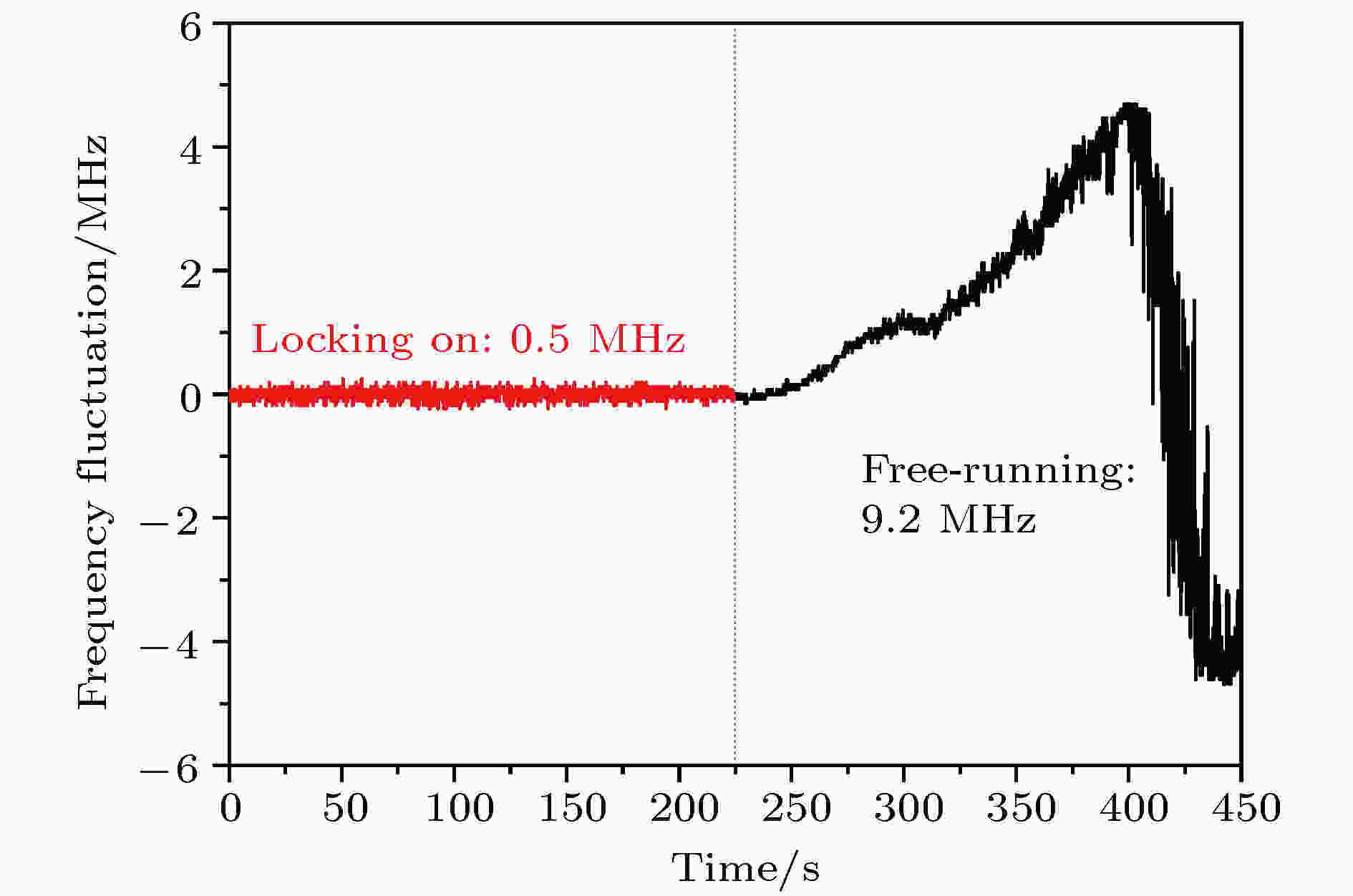图 8 794.6 nm激光器自由运转和锁频后的频率起伏
Figure8. The frequency fluctuation of 794.6 nm laser for free-running and locking on in 225 seconds, respectively.

基于铯原子6S_1/2-6P_3/2-8S_1/2 (852.3 nm + 794.6 nm)三能级阶梯型系统, 详细地研究了抽运光频率失谐、同反向实验构型以及抽运光偏振对原子激发态双色偏振光谱TCPS的影响. 发现抽运光频率失谐仅会导致TCPS光谱整体的频移(保持不变的频率间隔)和各超精细跃迁信号相对强度的变化; 实验证实了抽运光与探测光反向作用于原子介质时, 由于存在量子相干效应, 致使其TCPS信号的线宽较同向实验构型的明显要窄, 这对精密测量原子的能级结构和激光稳频具有重要的意义; 改变抽运光的偏振可实现TCPS信号线型相位的反转, 以便负反馈于激光器实现其频率锁定. 最后, 利用TCPS光谱实现了794.6 nm半导体激光器无频率调制的锁频, 可应用于原子的双色激光冷却、俘获、四波混频^[21-23]实验中, 也可将这种锁频的方法拓展到光纤通讯波段的激光稳频^[24]等, 具有一定的应用价值.