摘要:量子比特在同一时刻可处于所有可能状态上的叠加特性使得量子计算机具有天然的并行计算能力, 在处理某些特定问题时具有超越经典计算机的明显优势. 飞秒激光直写技术因其具有单步骤高效加工真三维光波导回路的能力, 在制备通用型集成光量子计算机的基本单元—量子逻辑门中发挥着越来越重要的作用. 本文综述了飞秒激光直写由定向耦合器构成的光量子比特逻辑门的进展. 主要包括定向耦合器的功能、构成、直写和性能表征, 集成波片、哈达玛门和泡利交换门等单量子比特逻辑门、受控非门和受控相位门等两量子比特逻辑门的直写加工, 并对飞秒激光加工三量子比特逻辑门进行了展望.
关键词: 量子逻辑门/
飞秒激光直写/
光波导/
定向耦合器

English Abstract

全文HTML

--> --> -->

量子计算(quantum computation)是基于量子力学基本原理具有超强并行计算能力的全新计算方式^[1-3]. 如果用二进制的“0”和“1”来表示信息, 经典计算机中处理信息的经典比特(bit)在某个特定时刻只能处于“0”或者“1”, 单次操作N个bit只能对2^N个数中的1个数进行运算, 而量子计算机中的量子比特(qubit)则可以处在|0$\left. \right\rangle$和|1$\left. \right\rangle $的任意叠加态(α|0$\left. \right\rangle$ + β|1$\left. \right\rangle$)上, 单次操作N个qubit能够同时实现对2^N个数的并行运算, 这种叠加特性使得量子计算机在处理某些特定问题如密码破译^[4]和数据搜索^[5]时具有超越经典计算机的明显优势. 与解决量子玻色采样^[6,7]和量子随机行走^[8]等专用问题的专用型量子计算机不同, 通用型量子计算机的处理器由量子逻辑门(quantum logic gate)组成. 量子逻辑门通过量子力学的幺正变换完成对量子比特的受控演化, 是实现量子计算的基础. Lloyd^[9]在1995年证明了几乎所有的两量子比特门再加上一些单量子比特门都可以进行普适的量子计算.
怎样设计一个物理系统并控制它来实现量子逻辑门, 一直是人们关注的问题. 1995年, Monroe等^[10]首次利用离子阱装置实现了两量子比特受控非门(controlled-NOT, CNOT)的演示实验, 证实了量子计算的可行性. 常见的实验系统还有超导回路^[11]、核磁共振^[12,13]、量子点^[14]、冷原子^[15]以及线性光学系统^[16]等. 其中, 线性光学系统具有一些独特的优点: 光子传播速度非常快, 适于作为传输量子信息的载体; 利用线性光学元件很容易实现光子量子比特的高精度制备和操纵; 最重要的是, 光子量子比特相干时间很长^[17], 它很难和其他光子发生相互作用, 但这也导致了光量子比特之间的控制门操作极难, 进而实现光量子计算似乎是不可能的. 2000年, Knill, Laflamme和Milburn 证明了仅使用线性光学元件、单光子源和单光子探测器就可以构建通用型量子计算机—这就是著名的KLM方案^[18], 于是线性光学系统成为备受青睐的量子信息实验平台^[19,20]. 目前的主要研究方向有两类: 一是在自由空间中操纵光子的线性光学量子计算, 它操作简单, 技术成熟, 目前绝大多数量子计算方案都是在自由空间光学系统中首先被验证的, 但其可扩展性差、稳定性差, 非常容易受到环境因素扰动; 二是基于集成芯片的光量子计算, 芯片中通常使用光波导来构建复杂的光子回路. 尽管波导芯片系统目前还是处于起步阶段, 但是具有良好的可扩展性、稳定性和高集成度, 因此前景广阔.
编码光子量子比特qubit的方式灵活而多样^[21,22], 比如路径编码(path-encoding), 即光子传播时可能通过的两条路径分别代表|0$\left. \right\rangle$态和|1$\left. \right\rangle$态, 某一时刻光子概率性地选择路径的状态构成叠加态α|0$\left. \right\rangle$ + β|1$\left. \right\rangle$—qubit, 此外, |0$\left. \right\rangle$态和|1$\left. \right\rangle$态还可以分别用光子的两种正交偏振态编码—偏振编码(polarization-encoding)、光子所处的基模和一阶模式—模式编码(spatial mode-encoding)和光子所在的不同时间组—时间编码(time bin-encoding)等来表示. 光子丰富的可编码自由度非常有利于发展高维光子量子比特, 即用同一个光子的不同自由度编码表示多个量子比特, 对节省量子光源资源具有重要意义.
2008年, Politi等^[23]利用光刻方法在硅片上制备了二氧化硅波导量子回路, 成功实现了稳定的量子干涉, 首次演示了集成的线性光学CNOT门的功能, 该实验中的量子比特采用路径编码. 2009年, 英国布里斯托尔大学的O’Brien研究组和澳大利亚麦考瑞大学的Withford研究组联合首次采用飞秒激光直写技术制备出了二维波导光量子回路, 展示了基于集成光学器件实现的多光子量子干涉^[24]. 飞秒激光直写波导的原理是Davis等^[25]提出的, 通过高阶非线性吸收, 飞秒脉冲激光可以准确地将能量沉积在透明介质内部, 引起介质折射率的永久性改变, 这种无需掩模版的单步骤加工方式能够以极低的成本在介质体内部直接加工出完整的器件. 尤为重要的是, 飞秒激光直写技术可以突破光学微加工方法中由于衍射极限给加工精度带来的限制, 并能直接在透明材料内部加工出真正的三维微结构, 这是传统光刻技术所无法企及的. 此外, 它可以提供近圆形的波导截面形貌, 波导双折射低, 非常适于操控偏振编码的量子比特^[26-29]. 许多飞秒激光加工的经典器件, 从简单的Y型分束器^[30]到更复杂的多波导集成器件^[31-33], 已经被广泛应用于通讯、集成生物传感等诸多领域^[34-37]. 量子逻辑门^[24]、量子随机行走^[38-40]、量子玻色采样^[6,7,41,42]和量子模拟^[43,44]等大量重要的光量子信息操作器件也都是利用飞秒激光直写技术制备的.
本文介绍飞秒激光直写技术在加工光量子逻辑门方面的进展. 结构安排如下: 第2节综述飞秒激光直写波导定向耦合器方面的进展, 包括定向耦合器的功能、构成和性能表征, 并以我们加工的定向耦合器为例进行说明; 第3节综述飞秒激光直写单量子比特逻辑门的进展, 主要包括哈达玛(Hadamard, H)门、泡利交换(Pauli-X)门以及集成波片的加工; 第4节综述飞秒激光直写两量子比特逻辑门的进展, 主要包括受控相位(controlled-Z, CZ或controlled-PHASE)门和CNOT门以及我们加工的CNOT门的量子性能; 第5节是飞秒激光加工三量子比特逻辑门的展望; 第6节是本文的总结与展望.

线性光学量子计算利用了光子相互影响的唯一途径即玻色对易关系, Hong-Ou-Mandel(HOM)量子干涉效应就是例证^[45,46], 它是由光子间的不可区分性引起的最基本的光学效应, 在线性光学量子计算中具有极其重要的地位. 双光子HOM干涉示意图见图1.
图 1 双光子HOM量子干涉示意图　(a)两个光子通过分束器后都透射和都反射的情况相干相消, 仅会出现一个光子透射而另一个光子反射的情况, 即光子成对的从分束器的任意一个输出端口离开; (b)在分束器两个输出端口对两个输出光子的符合计数值随两个光子进入分束器时的相对延时的变化曲线
Figure1. Two-photon HOM quantum interference in a balanced beam splitter. (a) Destructive interference of two situations: both photons are transmitted and reflected. Only one photon is transmitted and the other photon is reflected. Photons leave in pairs from any of the beam splitter's output ports. (b) The coincidence counts of detecting a photon at each output of the splitter as a function of the relative delay of the photons.

对于一个50 : 50的分束器, 当两个不可分辨的全同光子(频率、偏振、空间模式等都相同)同时从两个输入端口入射, 假定输入光子的模式是a和b, 输出光子的模式是c和d, 光子在分束器上发生反射后获得${\text{π}}/2$相移, 则初态${\hat a^\dagger }{\hat b^\dagger }\left| \varPsi \right\rangle $被转换为:

$\frac{1}{{\sqrt 2 }}\left( {{{\hat c}^\dagger } \!+\! {\rm{i}}{{\hat d}^\dagger }} \right)\frac{1}{{\sqrt 2 }}\left( {{{\hat d}^\dagger } \!+\! i{{\hat c}^\dagger }} \right)\left| \varPsi \right\rangle \to \frac{{\rm{i}}}{2}\left( {{{\hat c}^\dagger 2} \!+\! \hat d{^{\dagger 2}}} \right)\left| \varPsi \right\rangle , $

其中有两项相消, 最终得到(1)式的结果. 这说明不会出现两个光子分别从不同的端口输出的情况, 即不会发生光子都透射和都反射通过分束器的情况, 而是成对的从分束器的任意一个输出端口离开, 这是由光子的玻色子特性引起的聚束效应, 如图1(a)所示. 实验中, 两个光子的不可分辨性由两条输入路径之间的延迟差给出, 符合计数作为光子的两条路径之间延迟差的函数, 在延迟为0的地方会出现一个HOM谷(HOM Dip), 如图1(b)所示^[45]. HOM干涉的质量由干涉可见度V来衡量:

$V = \left( {{C_{\max }} - {C_{\min }}} \right)/{C_{\max }}, $

式中C_max和C_min分别表示符合计数的最大值和最小值. HOM谷越深, 干涉可见度越高, 理想情况下V = 1.
那么, 如何用集成波导实现类似于分束器的功能呢？O’Brien研究组的实验采用的是定向耦合器(directional coupler, DC)^[24], 当两个波导的空间间隔足够近时两个波导的倏逝场重叠就可以实现干涉, 如图2所示. 通过精确调节定向耦合器耦合区两个波导之间的间距d和相互作用长度L, 可以对耦合效率1–R (R相当于分束器的反射率)也即对分束比进行调节.
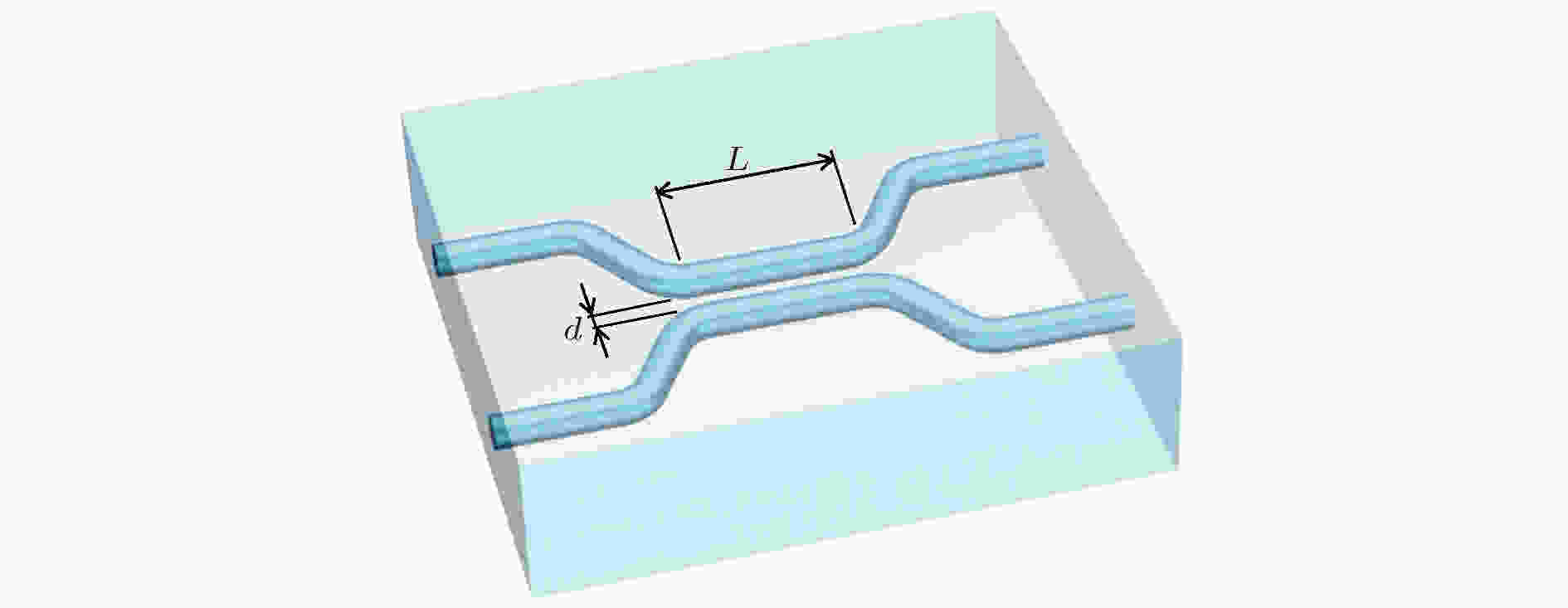图 2 基于波导的2 × 2集成定向耦合器示意图, 其中, d和L分别表示耦合区两个波导之间的间距和相互作用长度
Figure2. Schematic of anintegrated DC consisting of two waveguides. Interaction distance and length in the coupling region are denoted by d and L, respectively.

2009年, 高干涉可见度的单光子、双光子及多光子量子干涉现象首次在激光直写的集成光波导芯片中得到展示^[24], 如图3所示. 采用飞秒激光直接在熔融石英玻璃中写入的定向耦合器(R = 0.5128 ± 0.0007)的HOM干涉可见度为0.958 ± 0.005.
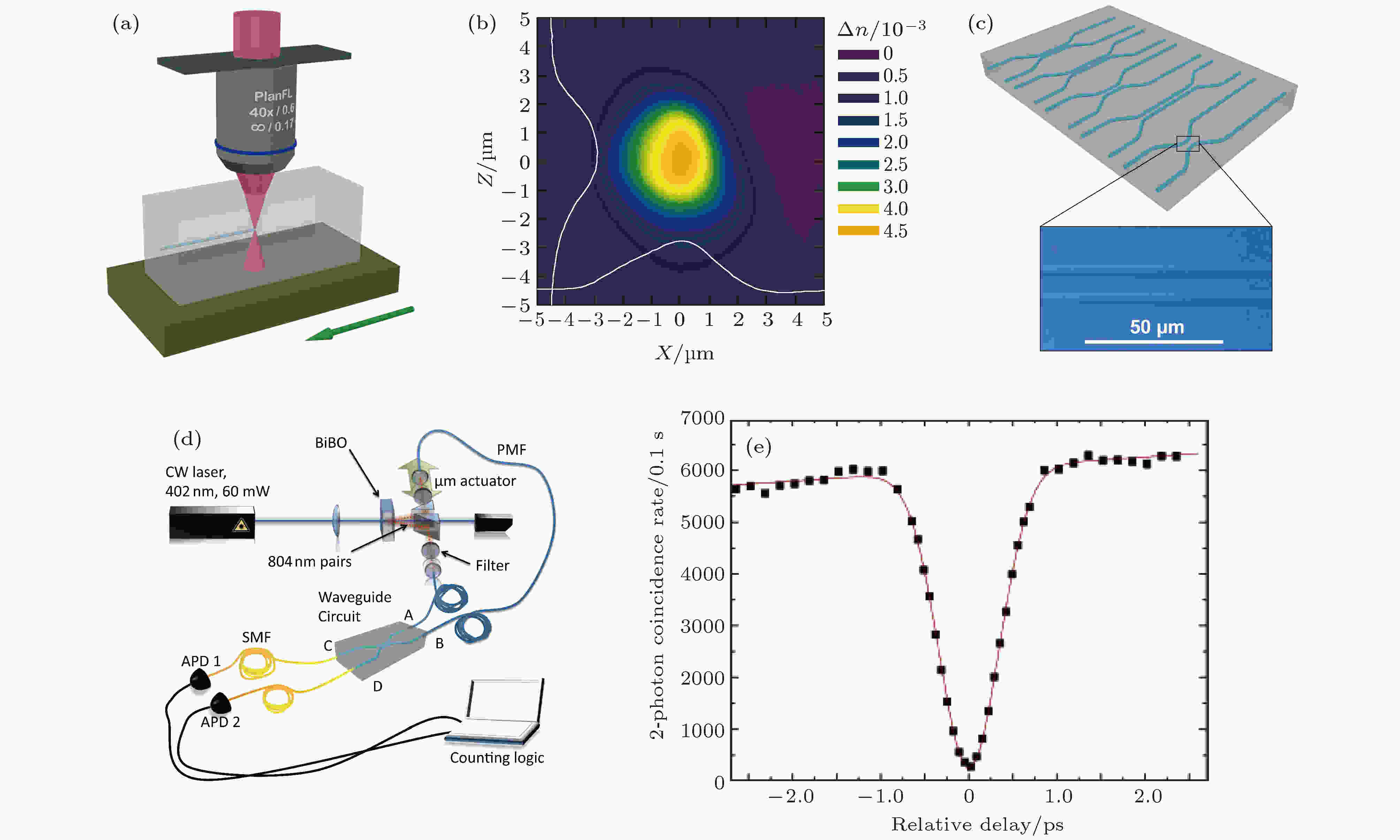图 3 飞秒激光直写定向耦合器示意图和测得的HOM干涉曲线^[24]　(a)飞秒激光横向直写波导示意图; (b)飞秒激光在波导截面引起的折射率变化; (c)飞秒激光直写的定向耦合器阵列; (d)量子光源表征定向耦合器的实验装置; (e)双光子符合计数随光子间相对延迟差的变化曲线
Figure3. Schematic of femtosecond laser direct writing of DCs based on waveguides and the coincident counts of detecting a photon at each output of the coupler as a function of the relative delay in arrival time of the photons^[24]; (a) Femtosecond laser transverse writing of waveguides; (b) femtosecond laser induced refractive index change at the cross section of the waveguide; (c) femtosecond laser written DC array; (d) experimental setup for quantum characterization of DCs; (e) the coincident counts of detecting a photon at each output of the coupler as a function of the relative delay in arrival time of the photons.

2015年, Chaboyer等^[47]利用飞秒激光独特的三维加工优势在玻璃内部制备了由两个可调谐三端口分束器串联组成的多路径类马赫-曾德尔干涉仪(Mach-Zehnder interferometer, MZI)芯片, 如图4(a)所示, 分束器的中间一臂相较其他两臂特地抬升了127 μm以接近芯片表面的热光相移器. 通过改变加载在相移器上的电压来调节该臂上产生的相移量θ, 从而调谐双光子干涉的可见度, 如图4(b)所示. 三维加工时较大的深度变化可能会对波导形貌和折射率分布产生一定影响, 可以通过在空间光调制器上加载针对球差等对深度变化敏感的像差的矫正相位板来进行实时的矫正调节.
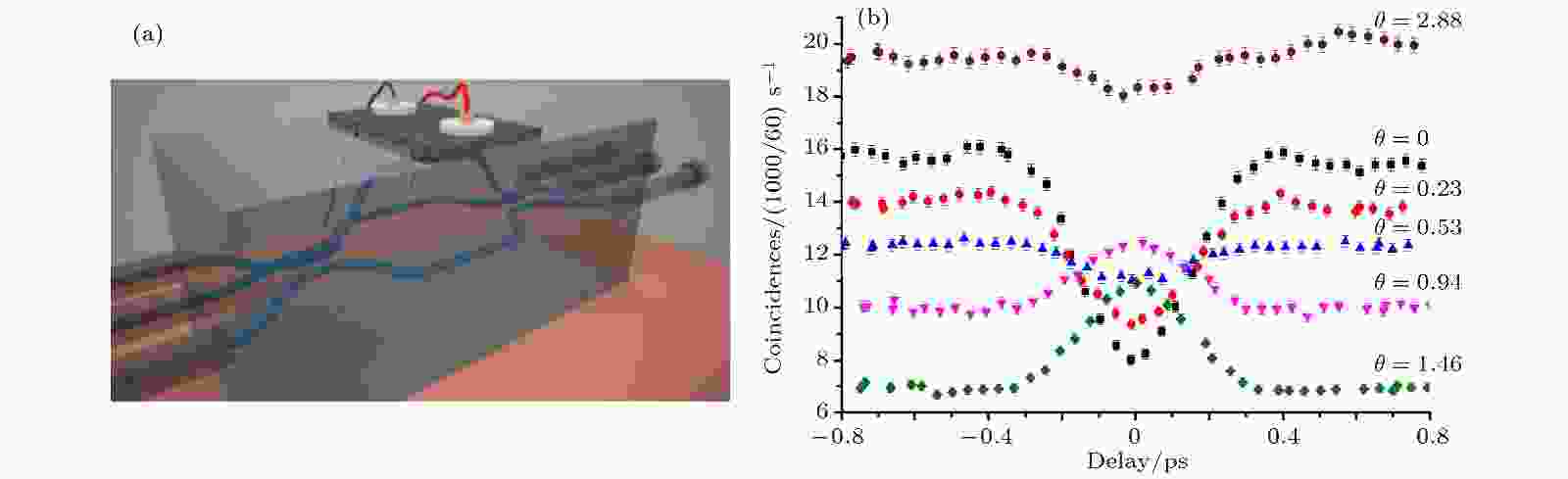图 4 可调谐三端口干涉仪(a)和不同相移量θ值下, 干涉仪输出端口两光子符合计数值随两光子进入干涉仪时的相对延迟差的变化曲线(b)^[47]
Figure4. Schematic ofa tunable 3D multi-path interferometer (a) and the coincident countsof detecting photons at outputs of the interferometer under different phase shift θ as a function of the relative delay in arrival time of the photons (b)^[47]. Copyright: http://creativecommons.org/licenses/by/4.0/ for CC BY.

波导双折射的大小会直接影响定向耦合器的偏振特性, 比如光子经过不同的输入-输出路径时将会获得不同的偏振变换, 而且输入偏振态不同也会导致不同的分束比. 那么, 如何制备出偏振不敏感的定向耦合器(polarization insensitive coupler, PIC)呢? 主要有两种方法^[48]: 一是双折射补偿法, 如图5所示, 第二根波导的写入会影响第一根波导的双折射以及两种偏振的耦合系数k_H和k_V^[49,50], 而两根波导的双折射不相同就会导致前述的路径依赖的偏振变换, 解决方法是在耦合区域内第二根波导旁边加写一根额外的损伤轨迹, 使其对第二根波导双折射的影响等同于第二根波导对第一根的影响; 二是退火法, Arriola等^[51]证明了对硼硅玻璃中写入的多模波导进行退火处理可以减小导光区域、增强芯和包层的折射率对比, 从而得到低损耗的单模波导, 此外, 这种方法还可以有效降低双折射, 减小分束比的偏振依赖程度, 有利于制备偏振无关的光量子集成回路.
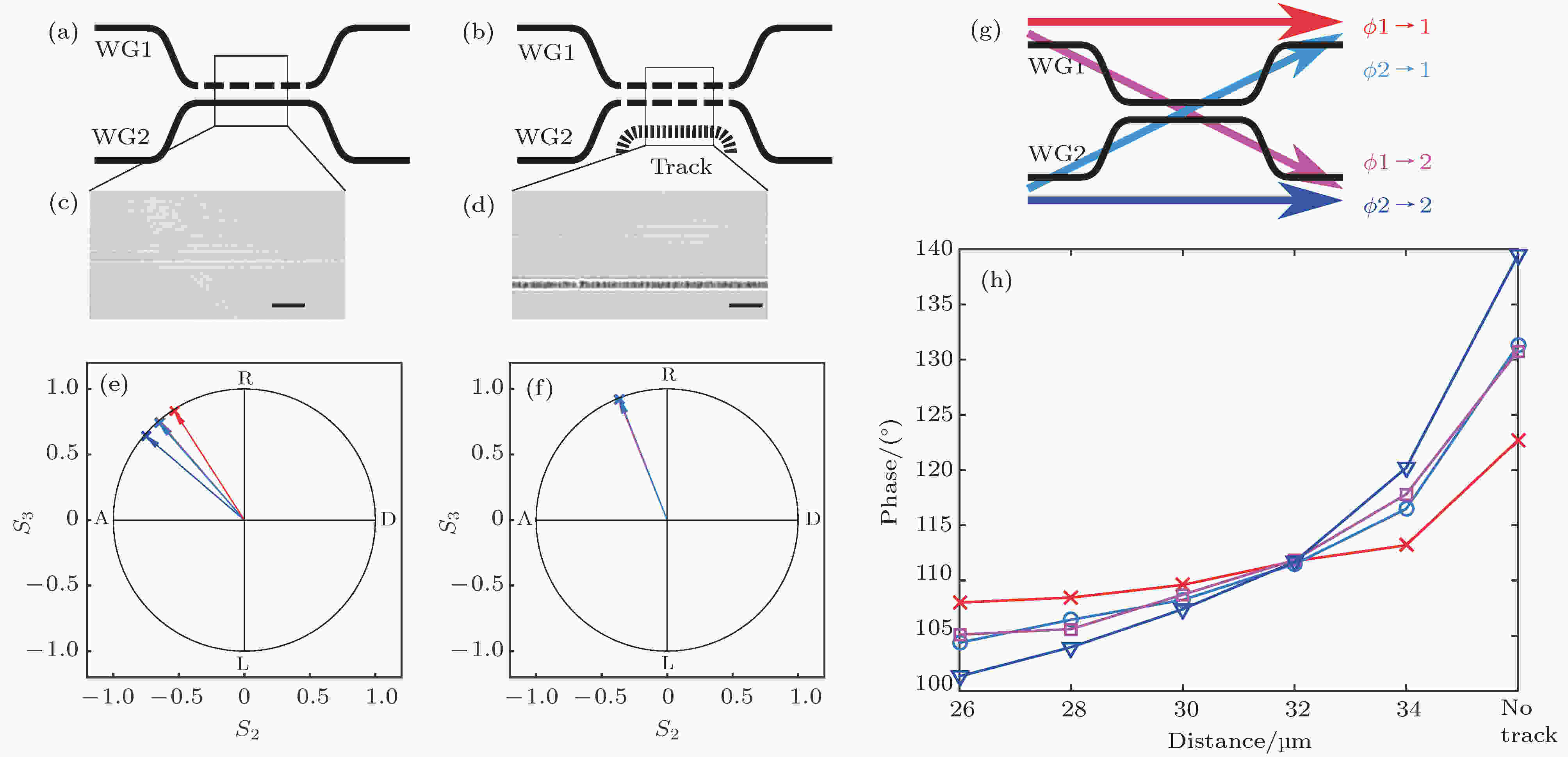图 5 双折射补偿法制备偏振不敏感的定向耦合器^[48]　(a)飞秒激光直写定向耦合器示意图, 第二根写入的波导的双折射会受到第一根写入的波导的影响; (b)利用不同的加工参数在第二根波导旁边写入一根损伤线, 可以平衡两根波导的双折射; (c), (d)定向耦合器耦合区域分别在加写损伤线之前和之后的显微镜图, 损伤线距离第二根波导32 μm, 图中标尺为20 μm; (e), (f)对角线偏振光入射时, 定向耦合器输出态分别在加写损伤线之前和之后的斯托克斯分量; (g)光从m波导入射, 从n波导出射时, 在水平偏振和垂直偏振分量之间获得了相移φ_m→n; (h)相移φ_m→n随损伤线距离的变化曲线, 当距离为32 μm时, 四种情况下的φ_m→n一致
Figure5. Polarization-independent DC based on local birefringence engineering^[48]: (a) Schematic of a femtosecond written DC, the birefringence of the second waveguide is modified by the previously inscribed first one; (b) an additional damage track, with tuned irradiation parameters, is inscribed next to the second waveguide, leading to birefringence equalization; (c), (d) microscope images of the interaction region of the DCs without and with the inscription of the additional track at a distance of 32 μm, scale bar is 20 μm; (e), (f) Stokes parameters of the output states for couplers without and with the additional track, for diagonally polarized input light and various input-output combinations. A planar projection of the Poincaré sphere is represented; (g) light that enters in waveguide m and exits from waveguide n acquires a phase shift φ_m→n between the horizontally and the vertically polarized components; (h) the different values of φ_m→n are plotted as a function of distance of the track from the second waveguide. For a distance of 32 μm, the four possible φ_m→n coincide.

我们课题组利用飞秒激光加工的基于波导的50 : 50分束的2 × 2定向耦合器的HOM干涉可见度达到约0.98. 实验装置如图6所示, 激光器(PHAROS, Light Conversation)的中心波长约1030 nm, 重复频率约1 MHz, 脉宽约为240 fs. 光束经过凹透镜L₁(焦距f₁ = －50 mm)和凸透镜L₂(焦距f₂ = 75 mm)扩束后进入物镜(20 × NA 0.5, Olympus)聚焦于一块20 mm × 25 mm × 1 mm的EAGLE2000玻璃(Corning)内部, 聚焦深度约为170 μm. 样品固定在三维气浮移动台上(ABL1000, Aerotech).
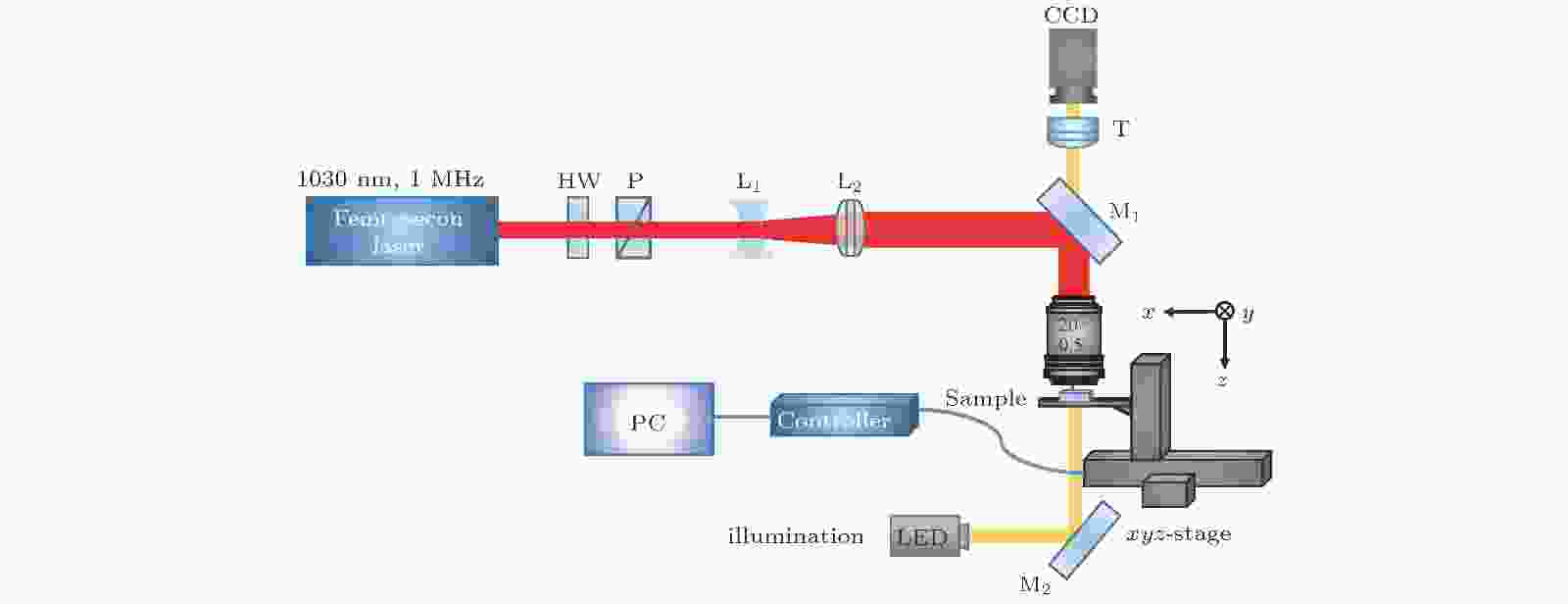图 6 飞秒激光加工光量子逻辑门实验装置图
Figure6. Experimental setup for femtosecond laser fabrication of photonic quantum logic gates.

我们首先优化单脉冲能量、扫描速度等参数以加工出在约808 nm波长处导模为单模且损耗最低的直波导. 测试波导性能时, 我们通过单模光纤将波长808 nm的连续激光导入长度约为2.5 cm的直波导中, 用物镜收集波导输出的光场, 而后用电荷耦合器(charge coupled device, CCD)拍摄导光模式. 波导的总插入损耗主要包括传播损耗、耦合损耗和菲涅尔损耗^[52]. 测量波导输入和输出的功率P₁和P₂, 根据–10log₁₀(P₂/P₁)计算插入损耗, 利用模式重叠积分法^[53]可以得到激光由光纤进入波导时的耦合损耗, 传播损耗通过截断法^[54]得到. 通过比较导光模式和损耗, 确定的最佳加工参数为: 单脉冲能量296 nJ, 扫描速度40 mm/s, 在该参数下加工出的的波导截面形貌如图7(a)所示, 最中心较亮的导光区域形状较圆, 但是周围还分布着其他不导光区域, 这些可以通过狭缝法^[55]或退火法^[56]来改善. 如图7(b)所示, 导模是单模, 1/e²强度处模场大小为14.0 μm × 16.4 μm, 数值与808 nm单模光纤的模场直径(~5.5 μm)相差较大, 导致了较大的耦合损耗, 约为 1.9 dB/facet, 测得的插入损耗和传播损耗分别约为4 dB和0.7 dB/cm, 菲涅耳损耗约为0.2 dB/facet. 以后可以通过激光焦场整形和加入损伤线等方法^[57]压缩导光模式使其与单模光纤模式尺寸匹配, 以减小耦合损耗从而减小插入损耗.
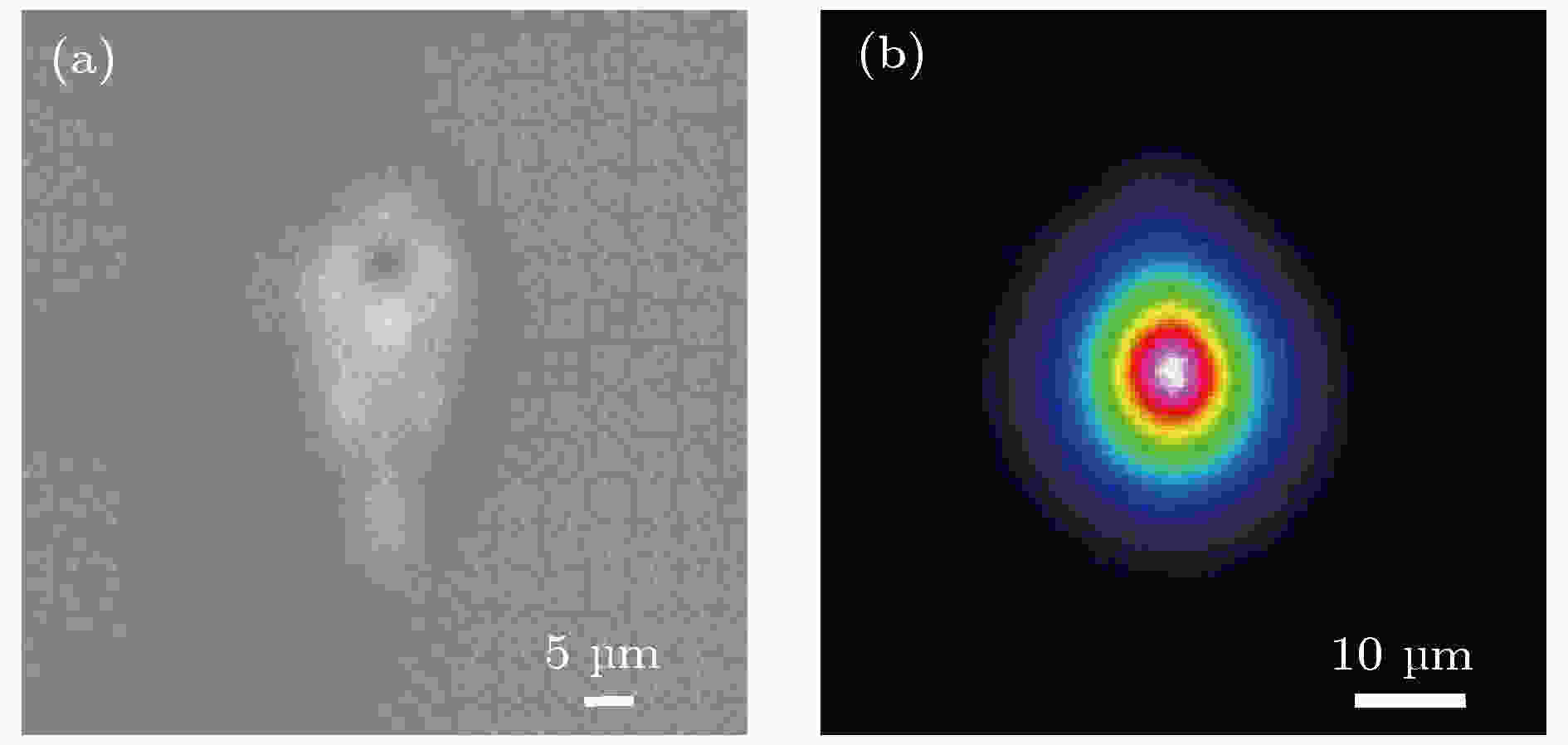图 7 波导截面形貌显微图(a)和在808 nm波长处的导光模式(b)
Figure7. Microscope image of the cross section of the waveguide (a) and the near field image of the waveguide guided mode at 808 nm (b).

我们在此基础上加工了2 × 2定向耦合器. 对于定向耦合器中的弯曲部分, 我们发现当转弯半径> 30 mm时, 弯曲波导额外引入的弯曲损耗基本可以忽略^[29], 最终我们将转弯半径设置为60 mm. 通过调控耦合区双波导的间距d和相互作用长度L, 可以得到不同的分束比. 实验中采用参数L = 130 μm, d = 8 μm加工出了R = 0.4930 ± 0.0007的耦合器, 当光从另一臂端口入射时R = 0.5010 ± 0.0007, 具有高度的对称性, 满足HOM量子干涉实验的测量要求.
定向耦合器在808 nm波长的导模如图8(a)所示, 两个导模强度均匀、对称. 我们通过中心波长约为404 nm的连续激光器(ECL801, UniQuanta)泵浦两块光轴相互垂直粘合而成的I型相位匹配BBO晶体, 自发参量下转换(spontaneous parametric down conversion, SPDC)产生808 nm波段偏振纠缠的全同单光子对, 它们的偏振要么都是垂直的, 要么都是水平的, 各有50%概率. 用两根长度一致的单模光纤分别收集两路单光子, 其中一路光纤上装有由步进电机控制的延迟线, 以便调节两路光子到达样品的相对时间, 再把两根光纤连接到一组间距为127 μm的单模光纤阵列上以将单光子输入到芯片中, 芯片输出的单光子由光纤阵列收集后通过单光子探测器(Excelitas, SPCM-850-14-FC)探测，而后送入多通道时间数字转换器(ID800, IDQ)进行符合计数测量, 实验装置类似于图3(d). 实验中通过半波片附加四分之一波片精细调控每路光子的偏振态以获得较高的量子干涉可见度. 由图8(b)所示的两路单光子符合计数随着两条路径相对延迟差的变化曲线计算得到的干涉可见度达到约 0.98.
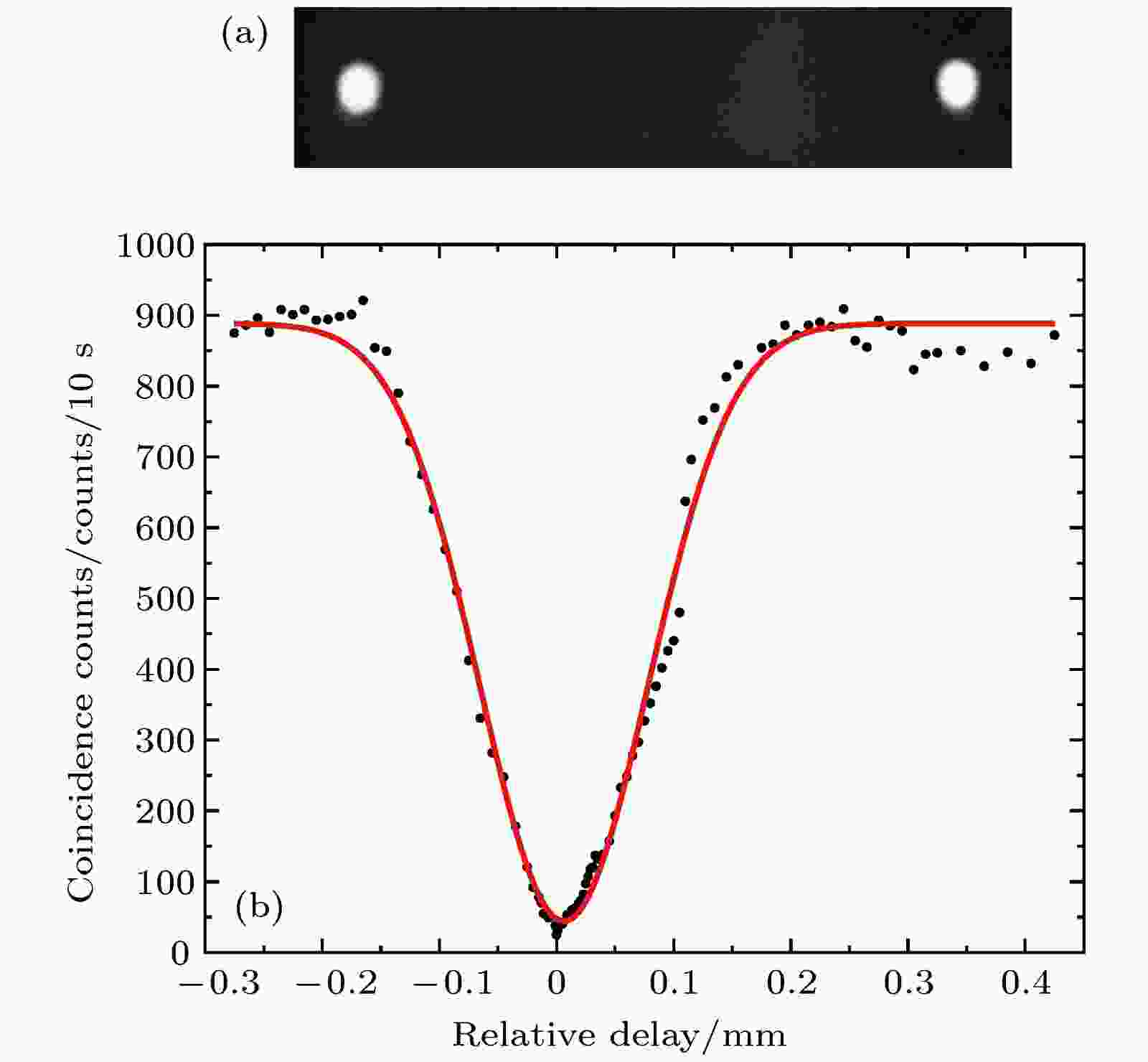图 8 50 : 50分束比定向耦合器在808 nm波长处的导光模式(a)和测得的HOM干涉曲线(b), 干涉可见度约为 0.98
Figure8. The near field image of the DC guided mode at 808 nm (a) and the coincidence counts of detecting photons at outputs of the DC as a function of the relative delay the photons(b), the visibility is ~ 0.98.

H门是最常见的一种单量子比特逻辑门, 它的变换矩阵U_H以及对量子态的作用描述如(3a)和(3b)式所示:

${{U}_{\rm{H}}} = \frac{1}{{\sqrt 2 }}\left(\!\!{\begin{array}{*{20}{c}} 1&1 \\ 1&{ - 1} \end{array}}\!\!\right),\tag{3a}$

${{U}_{\rm{H}}}\left| 0 \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| 0 \right\rangle + \left| 1 \right\rangle } \right),{{U}_{\rm{H}}}\left| 1 \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| 0 \right\rangle - \left| 1 \right\rangle } \right),\tag{3b}$

U_H|0〉相当于将|0〉顺时钟方向旋转45°, U_H$\left| 1 \right\rangle $相当于将$\left| 1 \right\rangle $逆时钟方向旋转135°. 另外, 泡利交换门也是常见的单量子比特逻辑门, 作用效果是互换$\left| 0 \right\rangle $和$\left| 1 \right\rangle $, 它的变换矩阵如(4)式所示:

${{U}_{{\rm{PX}}}} = \left(\!\!{\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}}\!\!\right).$

2014年, Heilmann等^[58]通过精确调控飞秒激光直写芯片上波导光轴的取向α来引入适当的双折射, 实现了任意的光子偏振变换, 演示了偏振编码量子比特的H门和泡利交换门. 实验中, 在待调制光轴的波导旁边用稍高于破坏阈值的能量写入一根附加的缺陷波导, 改变两根波导之间的相对位置(距离r和角度θ)可以改变波导周围的压力场分布^[59], 进而改变相邻波导双折射的强弱, 如图9所示. 当α = 22.5°和45°时, 分别实现H门和泡利交换门功能, 对应(3)式中的$\left| 0 \right\rangle $态和$\left| 1 \right\rangle $态分别由水平偏振态|H〉(Horizontal)和竖直偏振态|V〉(Vertical)来表示.
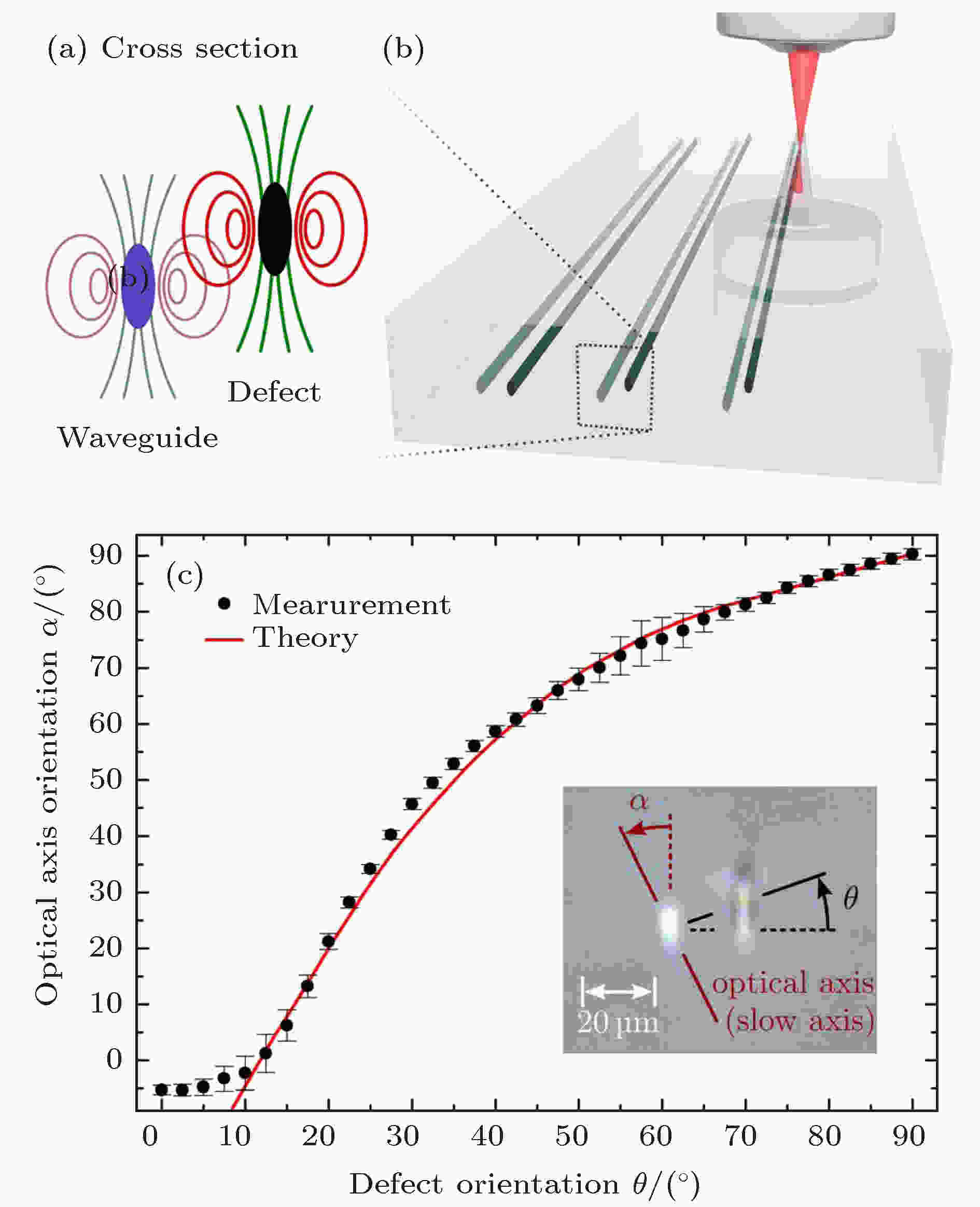图 9 压力场调控波导双折射来获得特定的波片操作^[58] (a)波导旁边附加写入的破坏线通过压力场改变波导光轴的取向; (b)飞秒激光直写三组不同相对位置破坏线示意图; (c)为波导光轴取向角α随破坏线相对位置取向角θ的变化曲线
Figure9. Settings of reorientation of the optical axis through stress fields and measured wave plate operations^[58]: (a) Schematic of the cross section of the waveguide arrangement where additional stress fields induce a reorientation of the waveguide’s optical axis; (b) sketch of the writing setting, with which the quantum gates are fabricated (here for 3 different orientations of the defect relatively to the waveguide); (c) experimental data and best fit model of the reorientation of the optical axis α as a function of the azimuthal position of the defect θ. Copyright: http://creativecommons.org/licenses/by/4.0/ for CC BY.

另外一种任意调控波导光轴取向的巧妙方法是控制激光传播方向, 使其不再像绝大多数实验中垂直于样品表面, 而是倾斜一个角度θ, 波导光轴也相应旋转了同样的角度^[60], 如图10所示. 具体来说, 采用高数值孔径油浸物镜(NA = 1.4), 让激光偏离物镜中心入射, θ的大小就取决于偏离量, 当θ = 22.5°时即实现偏振编码量子比特的H门操作.
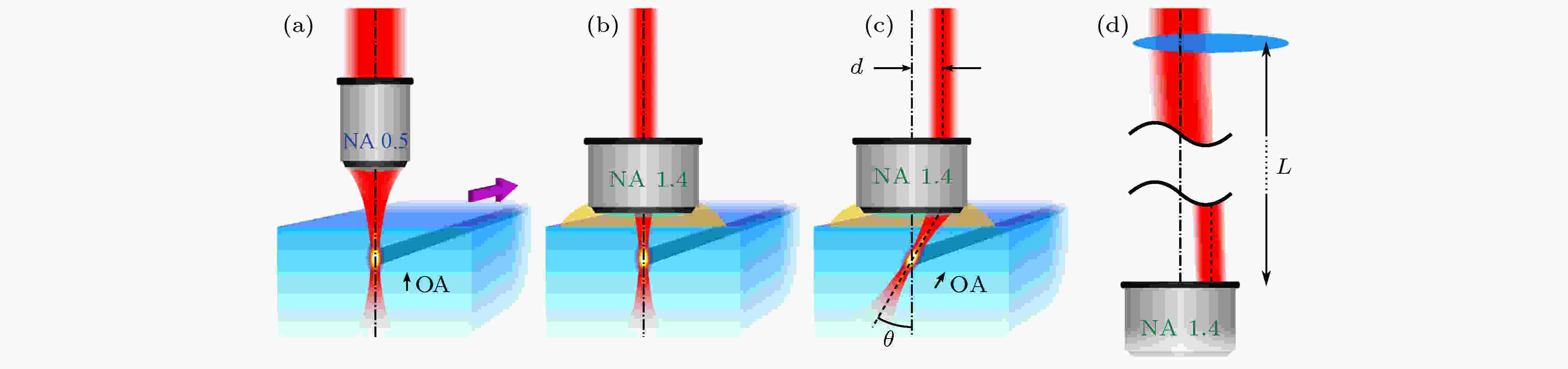图 10 直写光倾斜入射调控波导光轴方向示意图^[60]　(a)直写激光正入射充满低数值孔径物镜, 产生的双折射波导光轴OA沿激光传播方向分布; (b)直写激光正入射未充满高数值孔径物镜可以带来和图(a)相同的效果; (c)直写激光偏移距离d后入射高数值孔径物镜使得激光在样品体内旋转θ角度, 波导光轴也随之旋转相同角度, θ取决于d; (d)通过在物镜前L距离处放置长焦透镜可实现直写激光的偏移和缩束
Figure10. Conceptual scheme of the method enabling the direct writing of optical waveguides acting as integrated wave plates with tilted axis^[60]: (a) Traditional writing scheme adopting a focusing objective with moderate NA; the symmetry of the writing layout creates birefringent waveguides with the optical axis (OA) aligned as the writing beam direction; actual waveguide writing is performed by a transverse translation of the glass sample (indicated by the purple arrow); (b) equivalent waveguides can be created by underfilling a high-NA oil-immersion objective; (c) offsetting the writing beam before the objective results in waveguide writing with an inclined laser beam; the resulting waveguide has an optical axis tilted by an angle θ that depends on the amount of offset d of the writing beam with respect to the objective axis; (d) reduced beam size and offset at the objective aperture is achieved by a small transverse shift of a long focal lens placed at a distance L from the focusing objective.

可以看出, 以上实现偏振编码H门的关键是对双折射光轴的灵活操作, 而路径编码H门的实现则相对简单. Politi等^[61]在光子芯片上演示Shor算法时用到了路径编码的H门, 它实际上就是一个50 : 50分束比的定向耦合器, 如图11所示, 单量子态 $ \left| 0 \right\rangle $或 $ \left| 1 \right\rangle $通过它的作用后就按(3b)式处于 $\left| 0 \right\rangle $和 $\left| 1 \right\rangle $两条路径的叠加态上.
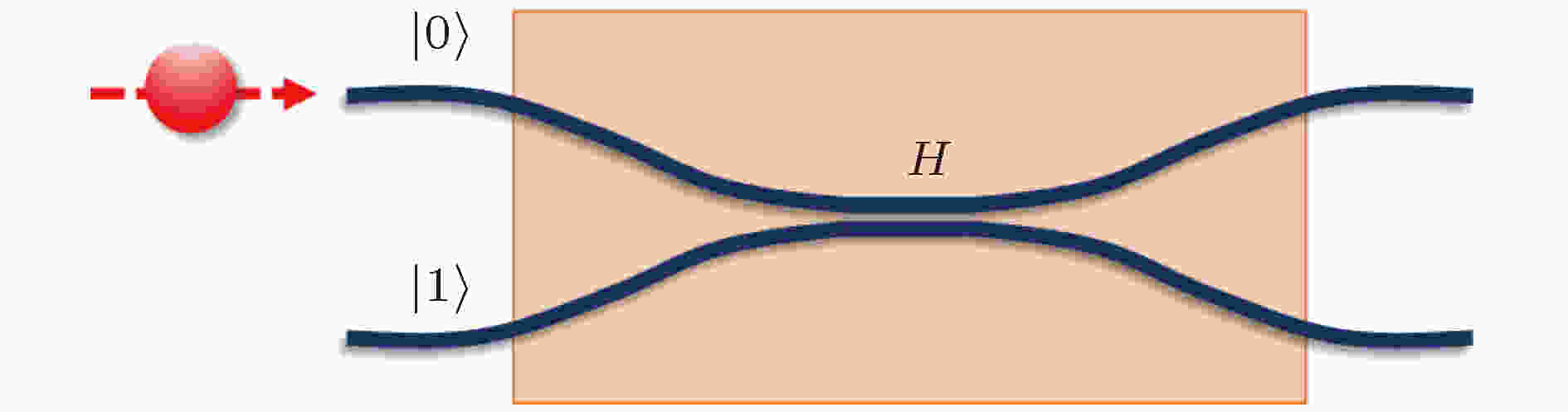图 11 路径编码量子比特的H门
Figure11. Schematic of a path-encoded qubit H gate.

线性光学的量子计算中, 最常用到的两比特量子逻辑门是CZ门和CNOT门, 它们都包含一个控制量子比特和一个目标量子比特, 其变换矩阵如(5)式所示. CZ门操作效果为: U_CZ|11$ \left. \right\rangle$→－|11$ \left. \right\rangle$, 即当且仅当控制比特和目标比特都处于|1$ \left. \right\rangle$态时, 输出态附加相位${\text{π}}$. CNOT门操作效果为: U_CNOT|10$ \left. \right\rangle$→|11$ \left. \right\rangle$, U_CNOT|11$ \left. \right\rangle$→|10$ \left. \right\rangle$, 即当且仅当控制比特处于|1〉态时, 目标比特状态翻转.

${{U}_{{\rm{CZ}}}} = \left(\!\!\!{\begin{array}{*{20}{c}}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&{ - 1}\end{array}}\!\!\!\right)\!,{{U}_{{\rm{CNOT}}}} = \left(\!\!\!{\begin{array}{*{20}{c}}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{array}}\!\!\!\right),$

二者之间互有联系, 一次CNOT门操作相当于一次CZ门操作前后各附加一次H门操作^[61].
如何利用集成波导实现CNOT门呢？首先是路径编码的CNOT门, 如图12所示, 控制比特C和目标比特T分别由两条波导路径来编码, 如果控制比特和目标比特的输出端口同时探测到了信号(概率为1/9), 则表示CNOT门操作成功. 该波导是完全根据Ralph等^[62]以及Hofmann 和Takeuchi^[63]在2002年提出的线性光学CNOT门方案来进行设计的, 整个波导芯片包含两个反射率R = 1/2和三个反射率R = 1/3的定向耦合器. 2003年, O’Brien等^[64]首先利用体光学元件在自由空间中实现了这种路径编码的CNOT门, 但其可扩展性和稳定性差, 集成度低. 2008年, 他们在硅基二氧化硅片上利用传统光刻法制备了由定向耦合器集成的CNOT门芯片^[23]. 目前还没有利用飞秒激光直写路径编码量子比特CNOT门的报道.
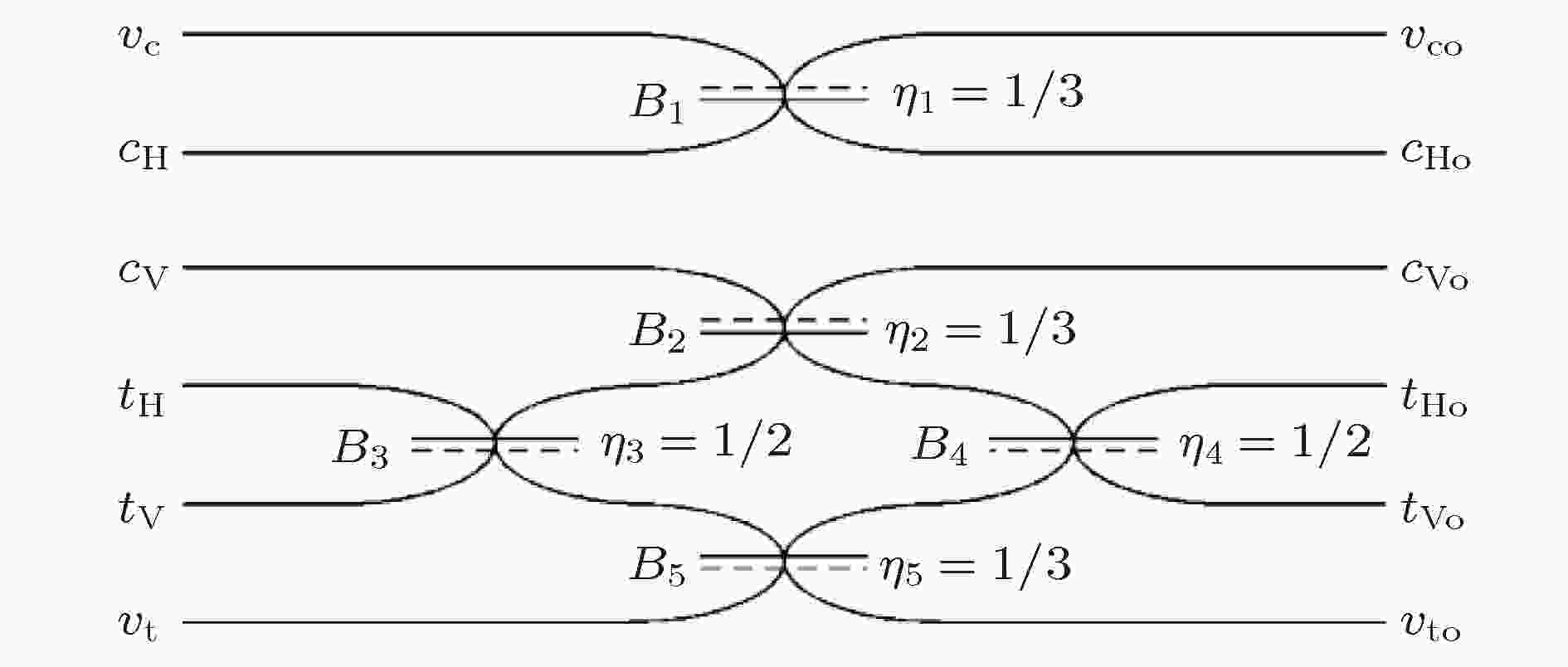图 12 路径编码量子比特的CNOT门结构图^[62] 虚线表示定向耦合器中附加相位${\text{π}}$的反射面; 路径c_H和c_V代表控制比特, 路径t_H和t_V代表目标比特, 路径v_c和v_t代表不会被占据的辅助比特; 图中数字表示对应定向耦合器的反射率
Figure12. Schematic of a path-encoded qubit CNOT gate based on waveguides^[62]. Dashed line indicates the surface from which a sign change occurs upon reflection in a DC. The control modes are c_H and c_V. The target modes are t_H and t_V. The modes v_c and v_t are unoccupied ancillary modes. The numbers indicate the reflectivity of the corresponding directional coupler.

2011年, Crespi等^[29]首次利用飞秒激光加工出了偏振编码的CNOT门, 并进行了完整的量子表征. 当光能量从一根波导传播到另一根波导时, 耦合器透射率随相互作用长度的变化遵循正弦规律, 振荡周期取决于两根波导中导模的耦合系数^[65], 如果波导有双折射, 则H偏振态和V偏振态的耦合系数不一样, 所以它们的振荡周期也不同, 如图13(a)所示, 这种对不同偏振光具有不同分束比的定向耦合器又叫做部分偏振定向耦合器(partially polarizing directional coupler, PPDC). 整个CNOT门包含三个PPDC, 如图13(b)所示, 最关键的作用是PPDC1上目标比特和控制比特的HOM干涉, 它对于H偏振光和V偏振光的透射率分别是T_H = 0,T_V = 2/3, PPDC2和PPDC3起补偿作用, 它们的透射率相同, 为T_H = 1/3, T_V = 1, CNOT门操作成功的概率是1/9.
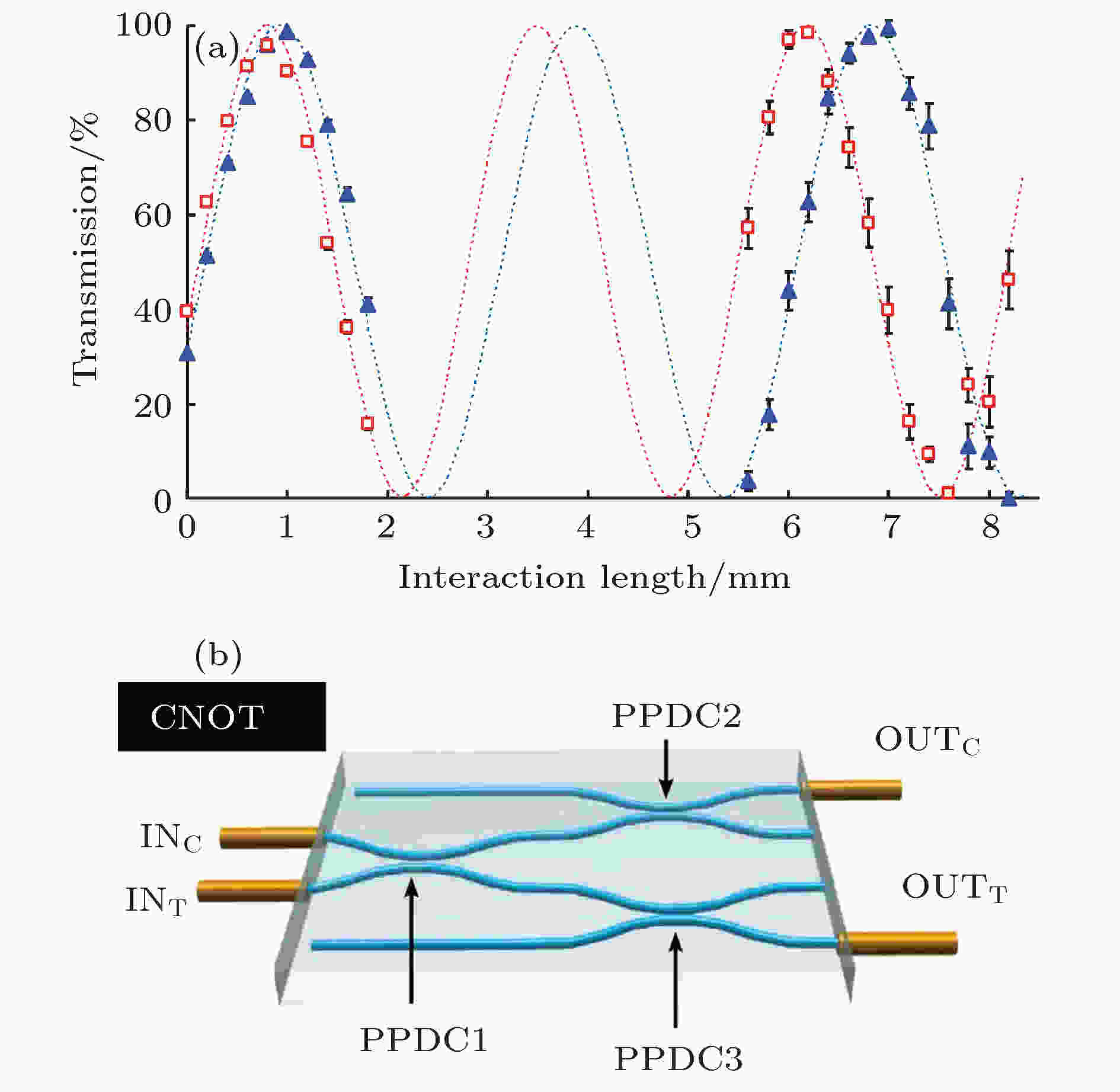图 13 部分偏振定向耦合器中两种偏振态的耦合区能量交换振荡曲线(方块代表H态, 三角代表V态)(a)和偏振编码量子比特的CNOT门波导结构图(b)^[29]
Figure13. H (squares) and V (triangles) polarization transmissions of DCs with different interaction lengths, based on slightly birefringent waveguides (a) and schematic of a polarization-encoded qubit CNOT gate based on PPDCs (b)^[29].

前面所述的CNOT门都是直接测量输出的控制比特和目标比特来检验门操作的成功与否, 称为非预报式CNOT门, 被测量的量子比特态受到破坏, 将不能继续作为后续量子回路的输入量子比特, 不利于发展大规模集成量子计算网络. 为了解决这个问题, 可预报式CNOT门应运而生, 即通过引入两个辅助光子来间接测量表征CNOT门操作, 当同时探测到两个输出的辅助光子时表明门操作成功, 避免了直接测量控制比特和目标比特, 使得它们可以接着被应用于后续的量子网络中, 有利于实现复杂量子计算的模块化. 2001年, Pittman等^[66]提出了一种由两个偏振分束器(polarization beam splitter, PBS)构成的偏振编码可预报式CNOT门简化方案, 最大的亮点是入射的两个辅助光子不再是独立的, 而是被制备在最大贝尔偏振纠缠态$\left| {{\varPhi ^ + }} \right\rangle {\rm{ = }}\left( {\left| {{\rm{H,H}}} \right\rangle {\rm{ + }}\left| {{\rm{V,V}}} \right\rangle } \right){\rm{/}}\sqrt 2 $上, 如图14(a)所示, 这样能够将门操作的成功概率从传统的1/9提高到1/4. 2018年, Zeuner等^[67]根据该方案利用飞秒激光加工出了这样的可预报式CNOT门, 量子性能表征实验装置如图14(b)所示, 通过两套量子光源产生两对处于最大偏振纠缠态的光子: 一对作为辅助光子, 另一对作为目标和控制光子, 这样方便制备出任意的目标和控制光子输入态. 该CNOT门不仅能够对处于经典计算基的入射光子对进行CNOT门操作, 还能够对处于经典计算基的量子叠加态的入射光子对进行CNOT门操作, 并且始终保持输入光子对的量子相干性, 可以制备处于最大偏振纠缠态的双光子源, 也可以明确地区分出所输入的是四种贝尔态中的哪一个态.
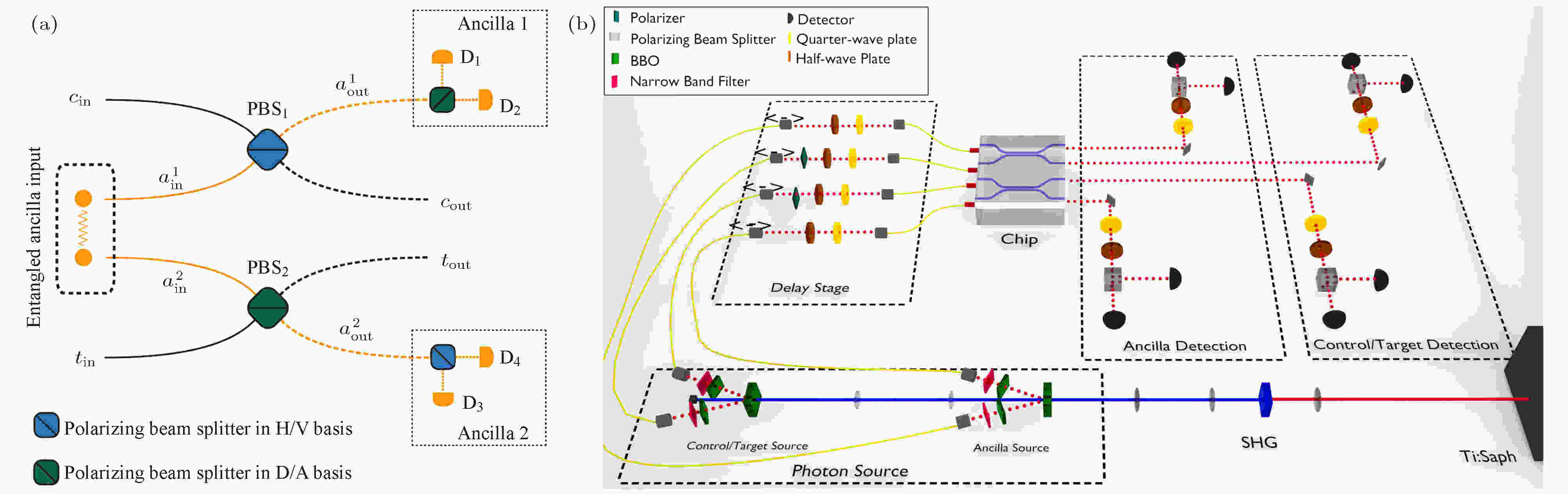图 14 纠缠态辅助光子的偏振编码可预报式CNOT门结构图(a)和量子性能表征实验装置示意图(b)^[67]
Figure14. (a) Scheme of a heralded photonic CNOT gate using a maximally entangled ancilla state with improved success probability 1/4. Detection of one photon in each of the modes $a_{out}^1$ and $a_{out}^2$ heralds successful gate operation. (b) Experimental setup for quantum characterization of the polarization-encoded qubit heralded CNOT gate^[67]. Copyright: http://creativecommons.org/licenses/by/4.0/ for CC BY.

2002年, Knill^[68]提出了一种最简单的路径编码量子比特的可预报式CZ门(hCZ门), 具有目前已知最高的成功概率, 为2/27. 如图15(a)所示, 这种hCZ门由四个定向耦合器组成, 四个不可区分的光子在其上成对地发生量子干涉, 并且第一对和第二对分束器之间有大小为${\text{π}}$的相移, 传统光刻制备不出这样的hCZ门, 因为它需要相邻波导的三维立体交叉以实现相邻模式的物理交换, 制备难度非常大, 如图15(b)所示. 直到2016年, Meany等^[69]才利用飞秒激光加工出了这样的三维立体hCZ门结构. 具体来说, 路径C和T代表控制比特和目标比特的|1$ \left. \right\rangle$态, A和B代表辅助光子态, C₀和T₀代表控制比特和目标比特的|0$ \left. \right\rangle $态, 它们不与|1$ \left. \right\rangle$态和辅助光子态相互作用, 加工时可省略. 输入两量子比特态α₀₀|00$ \left. \right\rangle$ + α₁₀|10$ \left. \right\rangle$ + α₀₁|01$ \left. \right\rangle$ + α₁₁|11$ \left. \right\rangle $, 当在两个辅助光子态输出端口各检测到一个光子时, |11$ \left. \right\rangle$项反转符号, 即hCZ门操作成功.
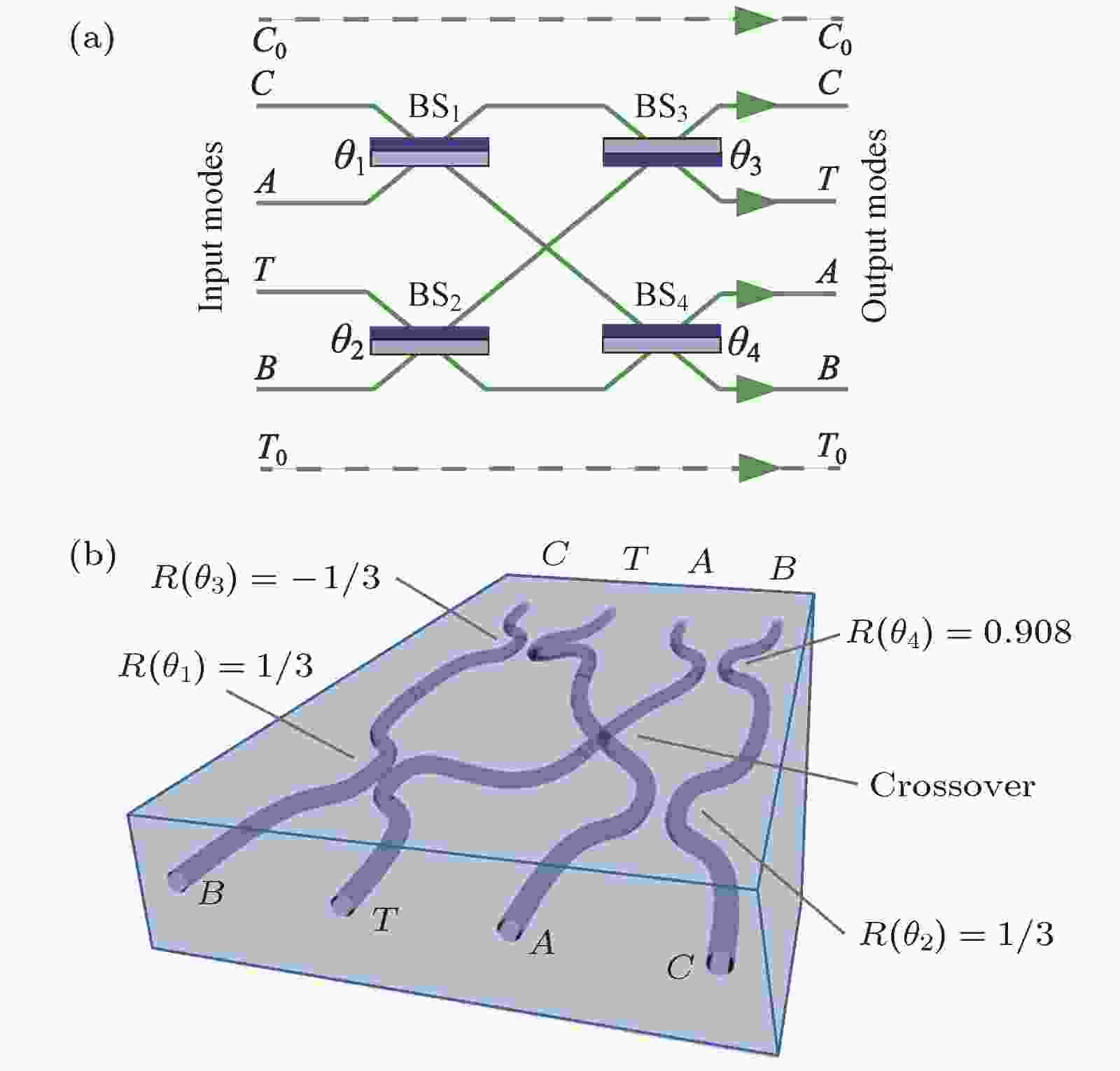图 15 路径编码的hCZ门结构图^[69]　(a)路径C₀ (T₀)代表|0〉态, 不与其他态相互作用, C (T)代表|1〉态, A和B代表辅助光子态, 它们通过四个定向耦合器相互作用, 耦合器反射率R(θ_n) =??cos²(θ_n), 图中浅色面代表附加${\text{π}}$相位的反射面; (b)由四条立体交叉波导路经构成的hCZ门结构
Figure15. Schematic of a path-encoded qubit hCZ gate^[69]. (a) The circuit for a hCZ gate showing paths for ancillary photons A and B as well as the computational qubits; the control (target) photon is encoded across spatial paths C₀ (T₀) representing |0〉 and C (T) representing |1〉. The |0〉 modes do not interact in the gate; the four remaining modes undergo four DCs operations with reflectivities R(θ_n) =??cos²(θ_n). The light-coloured side indicates the surface yielding a relative ${\text{π}}$ phase change upon reflection. (b) The four interacting circuit modes modelled as a waveguide array, showing the crossover and optimal reflectivities for the DCs implemented using evanescent coupling. Copyright: http://creativecommons.org/licenses/by/4.0/ for CC BY.

我们课题组利用飞秒激光首次在EAGLE2000玻璃中加工出了路径编码量子比特的CNOT门^[70], 结构分布同图12所示, 不同之处在于光子无论经历耦合器上表面反射还是下表面反射都会获得一个${\text{π}}/2$的相移. 其中c_H, c_V两条路径分别代表控制比特的|1$ \left. \right\rangle$态和|0$ \left. \right\rangle$态; t_H, t_V分别代表目标比特的|1$ \left. \right\rangle$态和|0$ \left. \right\rangle $态. 当且仅当控制比特处于|1$ \left. \right\rangle$态时, 目标比特状态发生|1$ \left. \right\rangle$和|0$ \left. \right\rangle$之间的态翻转. v_c, v_t为辅助光子态, 实验中不做测量. 图16是根据实验实测值构建的真值表柱状图, CNOT门保真度约为0.98.
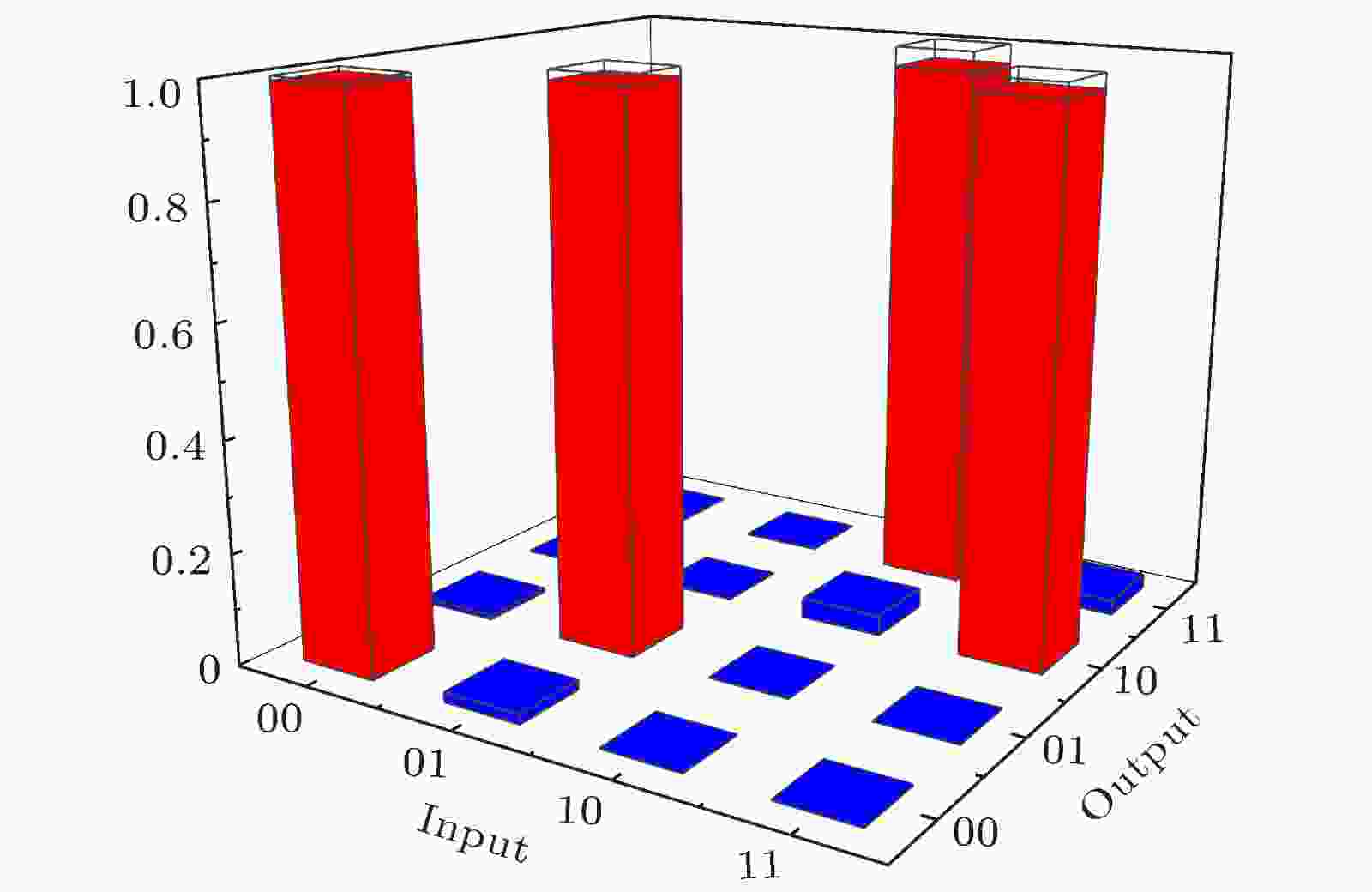图 16 根据实验实测值构建的真值表柱状图, 保真度约为0.98
Figure16. Experimentally constructed CNOT logical truth table. The labels on the Input and Output axes identify the state |C, T〉. Ideally, a flip of the logical state of the target qubit (T) occurs only when the control qubit (C) is in the logical |1〉 state. The fidelity of the gate is ~ 0.98.

受控受控非门(CCNOT门), 也即Toffoli门, 是非常重要的三量子比特逻辑门^[71], 在量子纠错^[72]和Shor算法^[73]等诸多量子算法中占有重要地位. 它包含两个控制比特和一个目标比特, 当且仅当两个控制比特都处于$\left| 1 \right\rangle $态时, 目标比特发生态翻转或相位变换, 目前已经在离子阱系统^[74]和超导回路^[75]中实现. 如果每个量子比特都是两种态的叠加态即qubit, 那么对Toffoli门最简单的分解是需要五个两量子比特逻辑门^[76,77], 如果进一步限制这里的两量子比特逻辑门为CNOT门或CZ门, 则需要六个CNOT门附加多种单量子比特门^[78]. 2007年, Ralph等^[79]提出了一种简化Toffoli门的理论方案, 他们将目标比特从两态qubit拓展为三态量子比特即qutrit, 则仅需三个CNOT门即可构成Toffoli门. 这种方案可以推广到包含n个控制比特的Toffoli门, 将目标比特变换为(n+1)维量子比特, 则需要2n－1个两量子比特逻辑门即可, 节省了大量的量子光源资源. 图17展示了目标比特为高维三态qutrit的Toffoli门方案和基于波导路径的线性光学实现方案. 2009年, Lanyon等^[80]利用体光学元件在自由空间中实现了这种理论方案, 整个实验系统如图18所示, 采用|H$ \left. \right\rangle$偏振和|V$ \left. \right\rangle$偏振编码量子比特的|0$ \left. \right\rangle$态和|1$ \left. \right\rangle$态两个状态, 通过偏振分束器PBS1扩展出一条额外的路径b, 从而将目标比特从两态系统扩展到四态系统, 即|H, t$ \left. \right\rangle $, |H, b$ \left. \right\rangle $,|V, t$ \left. \right\rangle$和|V, b$ \left. \right\rangle $四种状态, 这里只用到其中三种. 下路径b绕过了后面两个两比特逻辑门, 当在探测器D1上探测到一个光子时, Toffoli门操作成功.
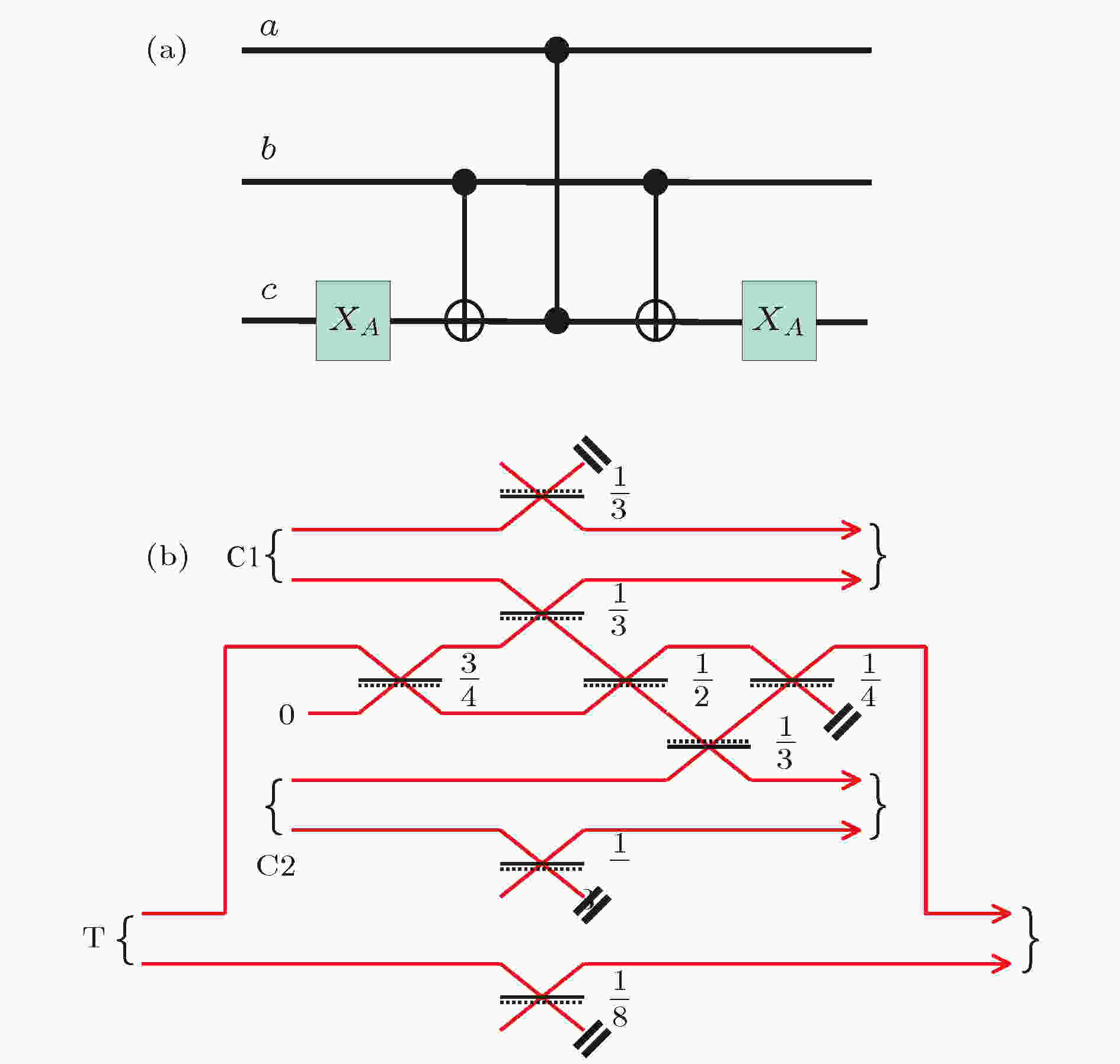图 17 控制比特(a, b)为qubit、目标比特(c)为qutrit($\left| 0 \right\rangle $,$\left| 1 \right\rangle $和$\left| 2 \right\rangle $态)的Toffoli门方案(a)和基于波导路径的线性光学实现方案(b)^[79] (a)中, 当目标比特处于第三态|2〉态时, 前后两个CNOT门中间的CZ门操作逻辑和正常两态量子比特系统相同, X_A单比特逻辑门的作用是实现|0〉和|2〉态之间的翻转; (b)中, 每个控制比特由两条波导路径表示, 目标比特则由三条波导路径表示, 图中标记为0的路径代表第三态; 当且仅当三个量子比特的上面那条路径被占据时, 输出态发生相位翻转, 即使实现Toffoli相位门操作
Figure17. (a) Realization of aToffoli gate using two qubits (a and b) and a qutrit (c). CNOT gates (first andlast two-qubit gates) operate as normal on the qubit levels andimplement the identity if the target is in the qutrit level (|2〉). Similarly for the CZ gate (middle two-qubit gate). The X_A gate flips thequtrit between the states |0〉 and |2〉. The sign change occurs on the|1,0,1〉 component. (b) A nondeterministic, post-selected, opticalrealization of a Toffoli gate^[79]. Each input qubit is represented bytwo modes (waveguide paths). An additional target mode is introduced in the central part of the diagram. DCs are represented as black lines with their reflectivity indicated to the right. A phase flip occurs by reflection off the surface indicated by a dotted line. If we take occupation of the top mode of each qubit to represent logical |0〉 and occupation of the bottom mode to represent logical |1〉, then the circuit implements a Toffoli gate in which a phase flip is only applied to the element |000〉.

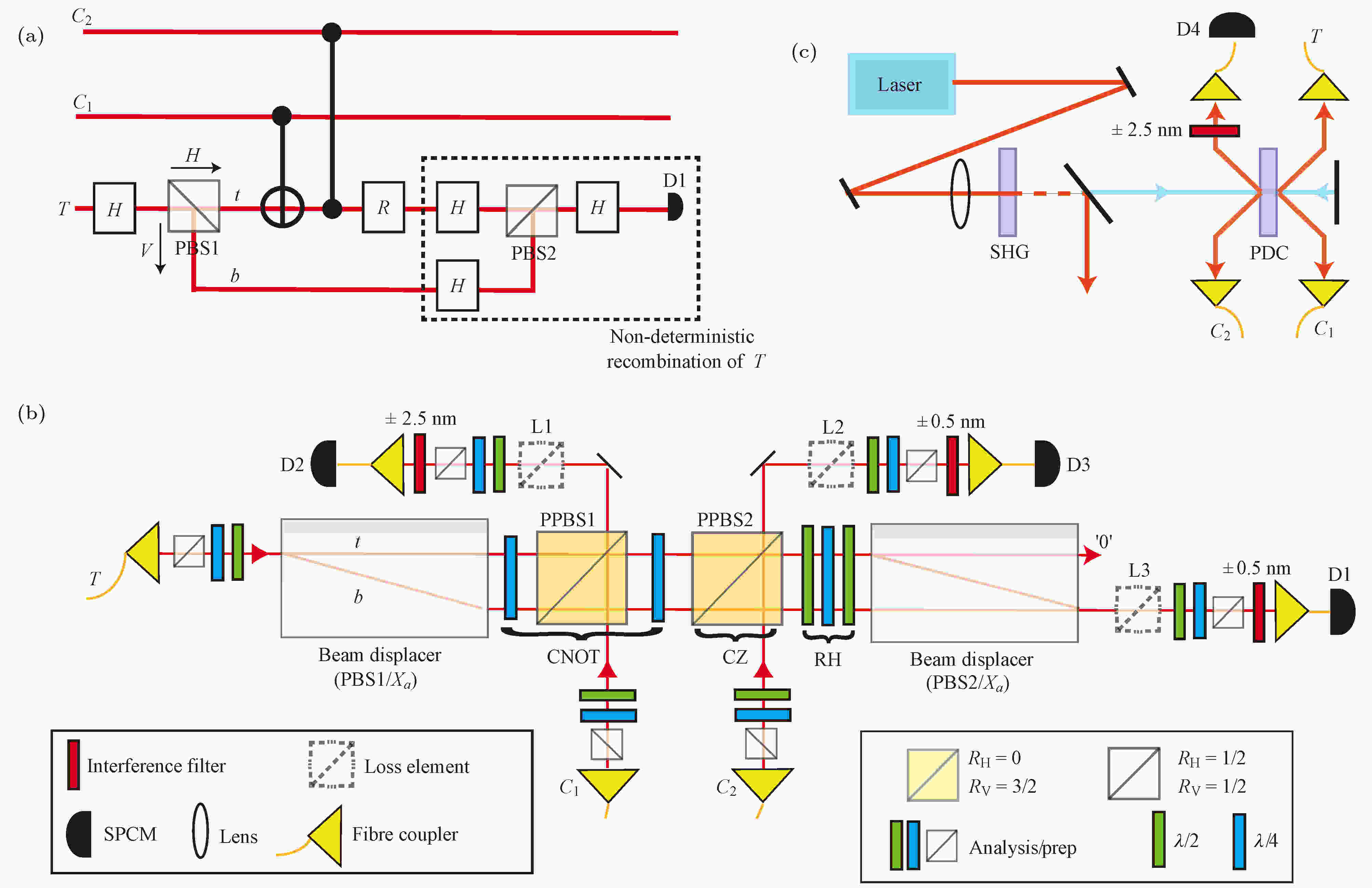图 18 利用体光学元件在自由空间中实现Toffoli门的实验装置^[80]　(a)逻辑线路图, 采用|H〉偏振和|V〉偏振编码量子比特的|0〉态和|1〉态两个状态, 通过偏振分束器PBS1扩展出一条额外的路径b, 从而将目标比特从两态系统扩展到四态系统, 即|H, t〉, |H, b〉, |V, t〉和|V, b〉四种状态, 下路径b绕过了后面两个两比特逻辑门; 当在探测器D1上探测到一个光子时, Toffoli门操作成功; (b), (c)实验装置; PPBS, 部分偏振分束器; SPCM, 单光子计数模块; PDC, 参量下转换; SHG, 二次谐波产生
Figure18. Toffoli and controlled-unitary experimental layout^[80]. (a) Conceptual logic circuit. A polarizing beam splitter temporarily expands the Hilbert space of the target information carrier, from a polarization-encoded photonic qubit to a multi-level system distributed across polarization and longitudinal spatial mode. Information in the bottom rail (b) bypasses the two-qubit gates. Detection of a photon at D1 heralds a successful implementation; (b), (c) Experimental circuit and optical source. An inherently stable polarization interferometer using two calcite beam displacers is used. PPBS, partially polarizing beam splitter; SPCM, single-photon counting module; PDC, parametric down conversion; SHG, second-harmonic generation.

另外一种通用的三量子比特逻辑门是Fredkin门, 也即受控SWAP门, 与Toffoli门明显的不同之处在于它只包含一个控制比特, 但有两个目标比特, 当且仅当控制比特处于|1〉态时, 两个目标比特相互交换所处的态^[81-84], 其门操作的本征态是纠缠的对称或非对称目标比特态, 而Toffoli门操作的本征态是分立态, 因此Fredkin门可直接应用于许多量子信息协议, 比如纠错^[72]、指纹识别^[85]、最优克隆^[86]和受控纠缠筛选等. 2008年, Fiurá?ek等在他们之前提出的偏振编码的部分SWAP门^[87,88]基础上改进, 利用两个CNOT门构成的相位门替代经典的相移器, 由控制比特态决定相位门的相位变化, 实现了自由空间的Fredkin门, 如图19(a)所示, 通过入射到两个CNOT门的两个光子态来编码控制比特输入态, 使其从非纠缠的$\left( {\alpha {{\left| H \right\rangle }_{{C_{in}}}} + \beta {{\left| V \right\rangle }_{{C_{in}}}}} \right)/\sqrt 2 $态以1/2的概率转化为$\left(\alpha {{\left| H \right\rangle }_{{C_{1in}}}}{{\left| V \right\rangle }_{{C_{2in}}}} +\beta {{\left| V \right\rangle }_{{C_{in}}}}\right.$$\left. {{\left| H \right\rangle }_{{C_{2in}}}} \right)/\sqrt 2 $纠缠态^[88]. 2017年, Ono等^[89]进一步简化了该实验, 将控制比特态直接制备于该纠缠态上, 实验装置如图19(b)所示, 当在输出端口(T_1out, T_2out, C_1out, C_2out)同时探测到光子时代表门操作成功, 成功概率为1/162, 是目前光量子Fredkin门方案中最高的. 目前, 尚未有利用飞秒激光直写技术制备三量子比特逻辑门的报道.
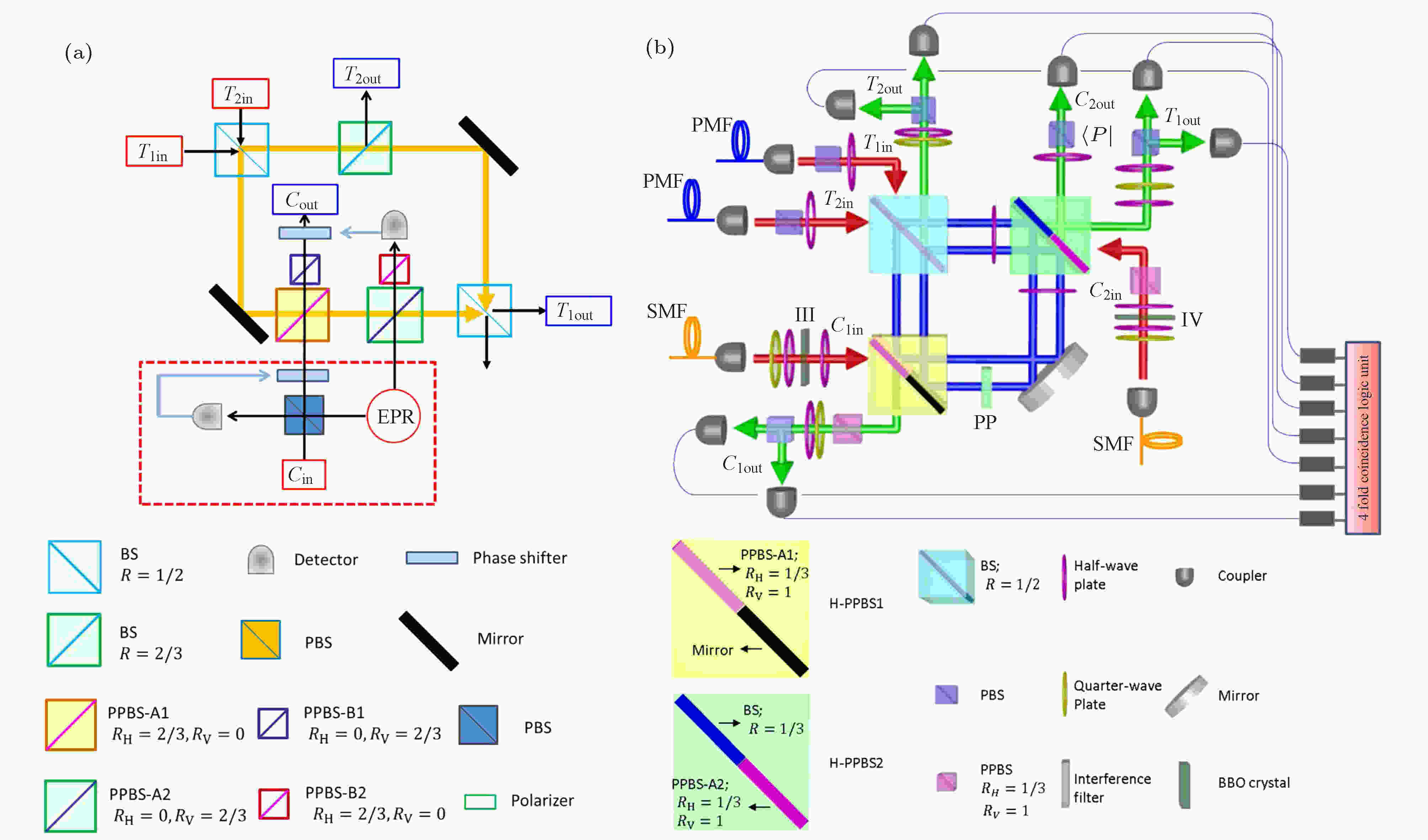图 19 利用体光学元件在自由空间中实现Fredkin门的两种实验方案　(a)早期实验方案, 控制比特态决定相位门的相位变化, 该相位门两个CNOT门构成, CNOT操作基于部分偏振分束器上的双光子干涉实现, 入射到两个CNOT门的两光子态编码控制比特输入态, 使其从非纠缠的$\left( {\alpha {{\left| H \right\rangle }_{{C_{in}}}} + \beta {{\left| V \right\rangle }_{{C_{in}}}}} \right)/\sqrt 2 $态以1/2的概率转化为$\left( {\alpha {{\left| H \right\rangle }_{{C_{1in}}}}{{\left| V \right\rangle }_{{C_{2in}}}} + \beta {{\left| V \right\rangle }_{{C_{in}}}}{{\left| H \right\rangle }_{{C_{2in}}}}} \right)/\sqrt 2 $纠缠态; (b)简化的实验方案, 控制比特态直接制备于$\left( {\alpha {{\left| H \right\rangle }_{{C_{1in}}}}{{\left| V \right\rangle }_{{C_{2in}}}} + \beta {{\left| V \right\rangle }_{{C_{in}}}}{{\left| H \right\rangle }_{{C_{2in}}}}} \right)/\sqrt 2 $纠缠态上, 当在输出端口(T_1out, T_2out, C_1out, C_2out)同时探测到光子时代表门操作成功, 概率为1/162; BS, 分束器; PBS, 偏振分束器; PPBS, 部分偏振分束器; Detector, 探测器; Phaseshifter, 相移器; Mirror, 反射镜; Polarizer, 偏振片; Half-wave plate, 半波片; Quarter-wave plate, 四分之一波片; Interferencefilter, 干涉滤波片; BBO crystal, BBO晶体^{[88, 89]}
Figure19. Two kinds of free-space experimental layouts for Fredkin gate. (a) Original proposal by Fiurá?ek. The phase of the quantum phase gate (QPG) is changed by a control qubit: φ = 0 (${\text{π}}$) when the control qubit is |0〉(|1〉). The QPG is realized by combining two CNOT gates, which are based on the two-photon interferences at the partially polarizingbeam splitters. The state of the control qubit is encoded into the state of the two photons incident to the CNOT gates by using an Einstein-Podolsky-Rosen (EPR) source and a quantum parity check: the encoder transforms the input state of the control photon $\left( {\alpha {{\left| H \right\rangle }_{{C_{in}}}} + \beta {{\left| V \right\rangle }_{{C_{in}}}}} \right)/\sqrt 2 $ into a state $\left( {\alpha {{\left| H \right\rangle }_{{C_{1in}}}}{{\left| V \right\rangle }_{{C_{2in}}}} + \beta {{\left| V \right\rangle }_{{C_{in}}}}{{\left| H \right\rangle }_{{C_{2in}}}}} \right)/\sqrt 2 $ with a probability of 1/2. (b) Simplifed scheme. The control qubit is directly encoded into the entangled photon pair $\left( {\alpha {{\left| H \right\rangle }_{{C_{1in}}}}{{\left| V \right\rangle }_{{C_{2in}}}} + \beta {{\left| V \right\rangle }_{{C_{in}}}}{{\left| H \right\rangle }_{{C_{2in}}}}} \right)/\sqrt 2 $ generated via spontaneous parametric down-conversion and local polarization operations. The Fredkin operation is successful when the photons are simultaneously detected at the output ports (T_1out, T_2out, C_1out, C_2out) with a success probability of 1/162^{[88, 89]}.

如果仅用一种编码方式(比如路径编码或偏振编码)实现飞秒激光直写Toffoli门, 所需要的两量子比特门和单量子比特门数量众多, 涉及到大量不同分束比的定向耦合器和不同相位关系的MZ干涉仪, 同时精确控制各分束比和波导相位异常困难, 且多光子输入对损耗要求非常高, 需要将现有波导损耗降低至少一个数量级. 如果利用多重自由度对光子进行高维编码, 那将会涉及到立体交叉的真三维波导构架, 同时调控路径、偏振、模式等也对加工工艺提出了前所未有的挑战. 我们正在尝试利用飞秒激光直写技术制备三比特量子逻辑门.

通用型光量子计算机都是由大量的单量子比特门和两量子比特门构成的, 而光量子逻辑门可以完成对量子比特的受控演化, 是实现通用型量子计算的基础. 构建量子逻辑门最为核心的基本单元是定向耦合器, 在其上发生的HOM量子干涉效应决定了量子门操作逻辑的正确性, 干涉可见度越高, 量子门的保真度越高. 飞秒激光直写技术以低成本、单步骤、真三维等特点成为制备集成光量子计算器件的重要利器. 本文综述了飞秒激光直写定向耦合器、单量子比特逻辑门和两量子比特逻辑门的典型研究进展, 对激光直写三量子比特逻辑门作了展望. 我们加工的定向耦合器HOM量子干涉可见度达到~0.98, CNOT门保真度达到~0.98. 飞秒激光直写技术将对未来光量子集成芯片在量子通讯、量子计算、量子模拟和量子成像等领域的发展发挥越来越重要的作用.
感谢意大利米兰理工大学R. Osellame教授及其组内F. Pellegatta等研究生对我们飞秒激光直写CNOT门实验的指导与帮助, 感谢中国科学技术大学任希锋副教授及其组内陈阳等研究生对我们量子光源的搭建及量子测试实验的指导与帮助.