摘要:模式不稳定效应已经成为高功率光纤激光器中限制输出功率和光束质量进一步提升的最大障碍. 用不同数值孔径的20/400阶跃折射率分布掺镱光纤搭建了光纤振荡器, 并测量了它们的光光效率和模式不稳定阈值. 实验结果表明, 在同等注入抽运功率和抽运波长为976 nm的前提下, 具有较低数值孔径的光纤尽管光光效率低于高数值孔径光纤的, 但却表现出更高的模式不稳定阈值. 这一结果表明数值孔径对光纤振荡器中的模式不稳定阈值有着显著的影响. 因此, 对于光纤振荡器的模式不稳定抑制而言, 适当地优化降低数值孔径是一个抑制模式不稳定效应, 进一步提升光纤振荡器模式不稳定阈值的方法, 对于进一步提升光纤振荡器的输出功率和光束质量, 有着明显的现实意义.
关键词: 模式不稳定/
光纤激光器/
掺镱光纤

English Abstract

全文HTML

--> --> -->

在过去的几十年中, 光纤激光器作为一种新型的固体激光器, 获得了长足且迅速的发展. 相较于传统的固体激光器而言, 光纤激光器有着诸多的优点: 优秀的热管理性能、高的转换效率、结构紧凑并且几乎免维护. 而且随着诸如大模场双包层光纤拉制工艺的逐渐发展与成熟和高功率高亮度半导体激光器的出现, 高功率光纤激光器的输出功率水平在近年来得到了迅速发展^[1]. 对于连续激光器, 单纤输出功率水平已经达到10 kW^[1,2]; 对于脉冲激光器而言, 超短脉冲激光器的输出也已经达到近kW的水平^[3]. 然而, 输出功率水平的继续增长受到了最近发现的新现象—模式不稳定效应(mode instability, MI)的限制. MI是指输出激光功率超过某个特定的水平后, 光纤激光器的输出模式会出现随时间明显有关的随机变化, 主要表现在光纤的激光器的输出模式成分的变化, 而且输出光的光束质量会大大恶化^[4]. MI已成为高功率光纤激光器输出功率进一步提升及其应用的最大障碍, 近年来引起全世界各国****的极大兴趣.
2010年, 德国耶拿大学的研究人员Eidam等^[3]首次在光纤激光器中观察到了模式不稳定现象, 随后科学界对于模式不稳定现象进行了大量深入的理论和实验研究, 并对这一现象的认识取得了相当大的进展. 尽管模式不稳定现象准确的物理本质尚未完全解释清楚^[4], 但是光纤中热致折射率光栅的形成是高功率光纤激光器中模式不稳定的主要原因已基本成为科学界的共识^[5-7]. 对于模式不稳定的研究, 德国耶拿大学、美国空军实验室、丹麦科技大学和美国克莱姆森大学处于国际领先^[4-6,8-19], 我国的国防科技大学对模式不稳定现象进行了大量的研究, 处于国内领先地位^[20-29]. 文献[6]指出, 若要模式之间存在能量转移, 则干涉模式与热致折射率光栅之间必须存在一定的相位差, 并认为这一相位差的根源主要是因为干涉模式之间存在一定的频率差. 目前而言, 大部分的理论模型的建模均采用这一频率差假设. 2013年, 美国克莱姆森大学的研究人员Dong^[19]指出, 光纤中MI的物理本质是光纤中的受激热瑞利散射(stimulated thermal Rayleigh scattering, STRS), 光纤材料的非线性响应与模间干涉之间存在一个相移, 而这一相移是STRS获得增益的原因所在. 2015年, 德国耶拿大学的研究人员Otto等^[30]在实验中发现光子暗化对模式不稳定有着密切而重大的影响, 并提出尽管光子暗化尽管只导致少量的功率损耗, 但仍然会大幅降低模式不稳定阈值. 2016年, 美国空军实验室的研究人员Ward^[31]和丹麦科技大学的研究人员L?gsgaard^[32]分别从理论上预言了准静态模式不稳定(quasi-static mode instability, QSMI)的存在, 并指出光子暗化和多程放大是引起QSMI的原因. 国防科技大学对模式不稳定的影响因素进行了大量的实验和理论模拟研究, 表明优化抽运波长, 降低光纤芯包比, 优化光纤弯曲直径有利于抑制模式不稳定^[23,25,27]. 但是, 以上的理论和实验研究主要针对主振荡功率放大(master oscillator power amplifier, MOPA)结构的光纤激光器, 针对光纤振荡器中的模式不稳定研究较少有公开的文献发表, 研究光纤振荡器中的模式不稳定对于理解不同机理和条件下的模式不稳定有着重要的意义.
本文从实验上利用不同数值孔径(numerical aperture, NA)的国产有源光纤搭建了输出功率为kW量级的光纤振荡器并进行了MI的研究. 通过一定程度上降低有源光纤的NA, 光纤振荡器的模式不稳定阈值得到了提升, 实验结果表明一定程度上优化降低有源光纤的NA有利于提升光纤振荡器的模式不稳定阈值, 对于进一步提升光纤振荡器的输出功率和拓展光纤振荡器的应用范围, 有着重要的现实意义.

本实验采用的有源掺镱光纤为本课题组自行设计拉制, 采用传统的改进的化学气相沉积法(modified chemical vapor deposition, MCVD)工艺制成, 纤芯直径为20 μm, 包层形状为八边形, 尺寸为400 μm. 搭建好的光纤振荡器如图1所示, 采用6个输出波长为976 nm的高功率半导体激光器作为抽运源, 经过(6 + 1) × 1的合束器再注入高反布拉格光栅(high reflective fiber bragg grating, HR FBG)后注入有源掺镱光纤中经过输出耦合光栅(output coupler fiber bragg grating, OC FBG)后输出. 合束器信号臂光纤结构为双包层光纤, 其纤芯/包层直径和NA分别为20/400 μm和0.065, HR FBG和OC FBG采用的光纤均为双包层光纤, 光纤纤芯/包层直径均为20/400 μm. HR FBG在中心波长1080 nm处的反射率为99%左右, 其3 dB带宽约为3 nm, 相对应的OC FBG在1080 nm处的反射率约为10%, 其3 dB带宽也约为3 nm. 所用光纤具体的参数见表1.

参数	光纤1	光纤2
光纤长度/m	20	20
NA(纤芯/包层)	0.064/0.460	0.059/0.460
主要掺杂元素	Yb/Al	Yb/Al
弯曲直径/cm	15	15
吸收系数@976 nm/(dB·m–1)	1.2	1.2
掺镱浓度/wt.%	0.65	0.65

表1实验中使用掺镱光纤的参数
Table1.Yb-doped fiber parameter applied in the experiment.

图 1 光纤振荡器结构图(抽运源为976 nm波长的激光器)
Figure1. Experimental setup of fiber oscillator pumped by 976 nm LDs.

OC FBG后端接入包层光滤除器和端帽用于滤除包层中的激光和抑制端面反射, 包层光滤除器的尾纤和OC FBG完全匹配, 最终通过端帽输出的激光射入功率计中测量输出功率, 光电探测器测量功率计靶面反射出的散射光信号并将其转换为电信号输入示波器. 上述所有器件均置于水冷热沉上保证足够的散热, 以维持激光器持续稳定的输出.

当使用光纤1搭建的光纤振荡器测试时, 其输出功率-抽运功率曲线如图2所示. 在注入的抽运功率在1400 W时, 经过包层光滤除器后的输出功率为1140 W, 对应的光光效率为81.4%; 当继续增加注入抽运功率到1500 W时, 输出功率从1140 W下降到1120 W, 此时对应的光光效率仅为74.7%, 光光效率出现了大幅度的降低, 并伴随有一定程度的功率起伏, 在光光效率下降的同时, 光电探测器测得的散射光信号的标准差也出现了明显的增加, 说明模式不稳定现象已经出现. 为进一步分析光纤1中的MI, 对光电探测器采集到的时域信号进行了处理, 如图3所示.
图 2 光纤1的输出功率-抽运功率曲线　(a) 输出功率/光光效率-抽运抽运功率关系; (b) 输出功率/归一化标准差-抽运功率关系
Figure2. Output power and pump power curve of fiber 1: (a) Correlation between output power/optical-optical efficiency and pump power; (b) output power/normalized standard deviation and pump power.

图 3 光纤1的输出功率时域信号　(a) 1400 W抽运源; (b) 1500 W抽运源
Figure3. Output time domain of different power of fiber 1: (a) 1400 W pump power; (b) 1500 W pump power.

由图3可知, 当注入的抽运功率为1400 W时(此时输出功率为1140 W), 对应的光光效率为81.4%, 时域输出信号基本保持稳定; 而当注入功率增至1500 W时(此时输出功率为1120 W), 对应的光光效率仅为74.7%, 时域输出信号较之前发生明显的波动, 对应在图2中表示为明显的标准差值的增加, 证明此时模式不稳定已发生. 同时, 输出功率在注入抽运功率从1400 W增加到1500 W时不升反降, 主要是由于发生模式不稳定时, 基模向高阶模耦合时因为弯曲泄露到包层之中被包层光滤除器滤掉, 在实验中观察到包层光滤除器在模式不稳定发生时温度显著升高也说明了这一点. 进一步对光纤1输出的时域信号做Fourier变换后, 得到的频域图如图4所示. 由图4可以清晰地看出, 在注入抽运功率为1400 W时, 频率信号除直流分量之外没有其他明显的频率成分; 而在增加注入抽运功率到1500 W时, 出现了一些直流分量之外的其他频率成分, 与1400 W注入功率时的频域信号大不相同. 根据以上分析, 我们认为光纤1在注入功率为1500 W时确实发生了模式不稳定.
图 4 光纤1的输出功率频域信号　(a) 1400 W抽运源; (b) 1500 W抽运源
Figure4. Output frequency domain of different power of fiber 1: (a) 1400 W pump power; (b) 1500 W pump power.

为进一步研究光纤NA对激光振荡器中的模式不稳定的影响, 换用光纤2重新测量了其激光性能, 其输出功率-抽运功率如图5所示. 在注入功率为1500 W时, 输出功率为1140 W, 其对应的光光效率为76.0%; 继续增加注入功率到1600 W时, 输出功率为1210 W, 此时对应的光光效率为75.6%, 光光效率较光纤1不发生模式不稳定时较低. 由光电探测器测量得到的标准差归一化值均在一个较小的范围之内波动, 如图5所示, 表征输出信号功率的波动较小, 无明显的剧烈波动, 而且在包层光滤除器上也未观察到明显的温度增加, 说明对于光纤2而言, 保持1600 W的注入功率未观察到明显的模式不稳定现象. 此时功率的进一步提升仅仅受限于抽运功率.
图 5 光纤2的输出功率-抽运功率曲线　(a) 输出功率/光光效率-抽运功率关系; (b) 输出功率/归一化标准差-抽运功率关系
Figure5. Output power and pump power curve of fiber 2: (a) Correlation between output power/optical-optical efficiency and pump power; (b) output power/normalized standard deviation and pump power.

为进一步确认光纤2在1600 W注入功率的条件下未发生模式不稳定, 对光纤2的输出时域信号进行了处理, 结果如图6所示. 当注入抽运功率为1500 W时, 输出的时域信号基本保持稳定, 未见明显的波动, 仅有因噪声导致的小幅度变化, 当注入抽运功率达到1600 W时, 输出的时域信号与注入抽运功率为1500 W时相比无明显变化, 也基本保持稳定且无明显波动, 而且频域信号在注入抽运功率为1500 W和1600 W时几乎保持一致(见图7), 无明显高频分量出现, 因此结合以上判据, 确认光纤2在整个输出阶段均未发生模式不稳定.
图 6 光纤2的输出功率时域信号　(a) 1500 W抽运源; (b) 1600 W抽运源
Figure6. Output time domain of different power of fiber 2: (a) 1500 W pump power; (b) 1600 W pump power.

图 7 光纤2的输出功率频域信号　(a) 1500 W抽运源; (b) 1600 W抽运源
Figure7. Output frequency domain of different power of fiber 2: (a) 1500 W pump power; (b) 1600 W pump power.

以上实验结果表明, 尽管光纤1在未发生模式不稳定之前, 其光光效率(81.4%)较光纤2的光光效率(75.6%)高, 从转换效率而言光纤1的热负载较光纤2更低, 但光纤2却表现出更高的模式不稳定阈值, 主要是因为光纤1的NA较光纤2的NA更大. 一方面, NA较大的光纤支持传输的模式越多; 另一方面, 较大的纤芯NA通常意味着较重的掺杂, 因此一般会有较大的吸收. 如图8所示, NA的减小对基模在光纤中的分布相对影响较小, 而对LP₁₁模的影响较大(图8中的$\tau$表达了对应的模式在纤芯中功率的比例), 主要会使LP₁₁模更多地延伸进入光纤包层中, 从而减小了LP₁₁模的纤芯部分与光纤掺杂(增益)区的重叠, 因此LP₁₁模的增益会随着NA的减小而降低, 模式不稳定阈值相应地上升.
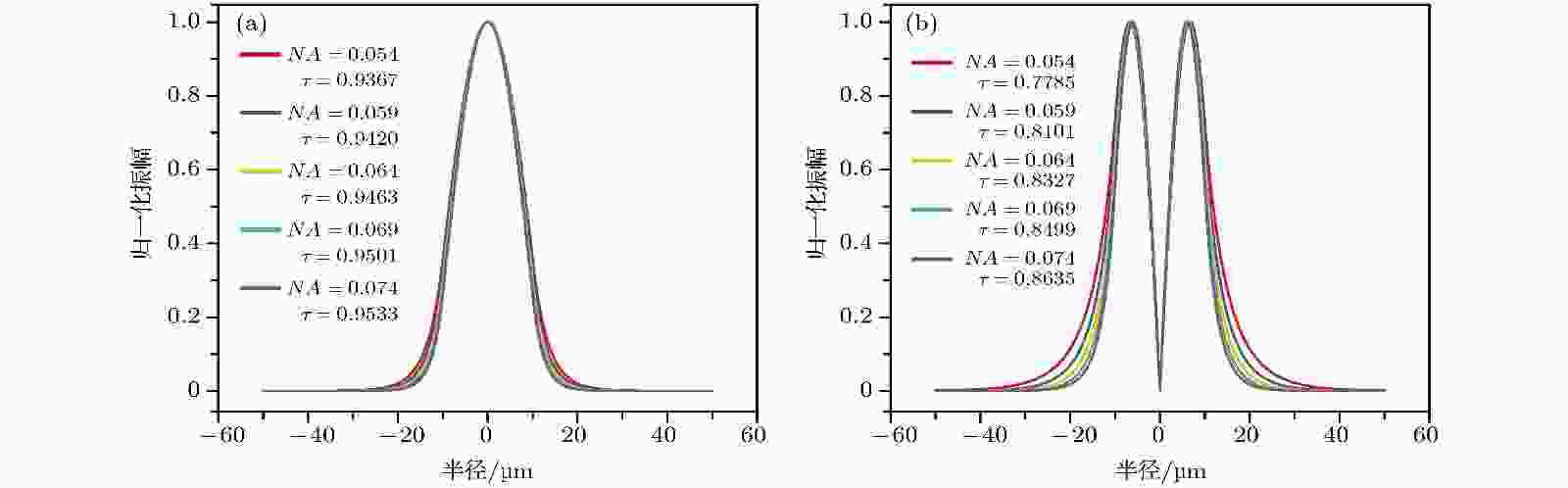图 8 具有不同NA光纤中的LP₀₁和LP₁₁模式分布　(a) LP₀₁; (b) LP₁₁
Figure8. LP₀₁ and LP₁₁ mode profile in fiber at different NA: (a) LP₀₁; (b) LP₁₁.

此外, LP₁₁模的弯曲损耗对于光纤NA的变化极其敏感, 图9给出了在不同的光纤NA下光纤的弯曲损耗随着光纤的弯曲直径变化的关系. 由图9可知, 当NA减小时, 高阶模式的弯曲损耗会极大地增加, 这会导致更多的高阶模式由于光纤的弯曲泄露进入包层之中, 减少了高阶模式和光纤掺杂(增益)区的重叠, 从而导致LP₁₁模的增益会随着NA的减小而降低, 模式不稳定阈值相应地增加.
图 9 具有不同NA光纤的LP₁₁弯曲损耗随弯曲直径变化曲线
Figure9. Bending loss of LP₁₁ versus bending radius at different fiber core NA.

本实验对不同NA的光纤搭建了激光振荡器并测试了它们的激光效率和模式不稳定阈值. 实验结果表明, 使用NA为0.064的光纤, 其模式不稳定阈值为1140 W, 功率的进一步提升受到了MI的限制; 将光纤改为NA为0.059的光纤, 最大输出功率为1210 W, 斜率效率正常, 无MI发生, 功率的进一步提升受到最大注入抽运功率的限制. 实验结果和数值模拟表明, 光纤的NA对光纤振荡器的模式不稳定阈值有显著影响, 一定程度上降低光纤的NA有利于提升光纤振荡器的模式不稳定阈值.