摘要:对光学扫描全息术中的双光瞳做出改进, 提出对多图像并行加密和任意层图像再现的新方法. 将其中一个光瞳设置成环形光瞳, 另一个光瞳处插入随机相位板, 干涉形成环形随机相位板, 实现对多层图像的快速扫描和并行加密, 扫描信号通过计算机合成为加密全息图, 在数字全息再现的过程中进行解密, 实现对任意层图像的精准重建. 该方法快捷高效、安全可靠, 抗噪声能力强. 利用相关系数评估了该方法的加密效果, 并通过仿真实验验证了该方法的有效性和安全性.
关键词: 光学扫描全息/
光学并行加密/
环形光瞳/
随机相位板

English Abstract

全文HTML

--> --> -->

光学信息加密技术是从20世纪80年代新兴起的一种加密技术, 与传统的加密技术相比, 该技术具有加密速度快、信息容量大和可多路并行等优势^[1-3]. 在加密过程中, 可以用到诸如干涉、衍射和滤波等一些光学处理手段来增强加密信息的安全性^[4-7]. 1995年, Refregier和Javidi^[8]提出了一种在传统4-F系统的输入平面和傅里叶平面各加入一块随机相位板的方法, 分别对原始图像的空间信息和频域信息进行干扰, 从而得到统计特性不随时间变化的均匀白噪声图像实现对信息的光学编码加密. 该方法在光学信息加密领域得到了广泛的关注与应用. 2002年, Takai和Mifune^[9]提出了在离轴数字全息的信息记录过程中利用双随机相位编码的方式进行图像加密, 实现了数字计算与数字全息术相结合的光学加密方式. 基于双随机相位法的光学加密技术在安全性、灵活性和可实施性等方面得到了极大的改进和拓展, 更多样化的光学加密方案相继被提出. Matoba和Favidi^[10]提出了数字相移干涉技术与同轴全息相结合的光学加密系统, 该系统可通过光学或电子方法进行解密, 便于操作. Wu等^[11]提出了偏振编码技术与数字全息术相结合的加密技术, 并将该技术应用到了信息安全领域. 在单图像加密技术逐渐成熟的基础上, 随着数据传输能力的不断增强, 多图像加密技术也受到了越来越多的关注, 出现了很多改进方案. 例如He等^[12]利用频谱移位结合双随机相位编码实现了多图像加密, Situ和Zhang^[13]利用随机相位匹配在相移数字全息系统中实现了多图像隐藏, Qin和Gong^[14]利用波长复用技术在双随机相位编码系统中实现了多图像加密, Tajahuerce等^[15]基于干涉原理在加密的方法中对迭代相位恢复算法提出了改进. 但是, 这些方法大多采用了相位迭代进行图像的加密和解密, 非常耗时, 在多图像并行加密的实现上有很大的局限性, 而且双随机相位法是在傅里叶变换系统中同时记录振幅和相位信息, 所以对光学加密系统的空间排列精度要求较高, 容偏能力低^[16,17].
光学扫描全息术(optical scanning holography, OSH)是一种特殊的非相干实时数字全息技术^[18,19]. 在OSH系统中, 采用双光瞳外差非相干图像处理技术实现全息图的记录^[20]. OSH中两个光瞳功能的选择对系统功能的实现很重要, 通过调整光学系统中的两个光瞳函数, 可以对形成的干涉条纹进行修改, 以实现不同的成像效果. 所形成的干涉条纹将用于对物体进行二维扫描来获得物体的全息信息, 并通过光电探测器和电路解调生成相应的全息图^[21,22]. 在2003年, Poon等^[23]提出了一种基于随机相位编码原理的OSH系统来实现对图像的加密, 在这种方法中, 将全息成像过程中的记录与重建分别看作密码学中的编码与解码的过程, 把光学传递函数中相应的光瞳函数作为密钥进行信息的加密^[24], 该方法可进行单张图像信息的加密和解密, 系统的执行效率不高, 解密后的图像会带有较高的随机噪声信息, 信噪比较低.
本文提出了一种在OSH系统中通过改变两个光瞳函数的方法实现多图像并行加密和任意层图像的再现. 在该方法中, 一个光瞳采用随机相位板, 另一个光瞳采用环形光瞳. 研究显示, 采用随机相位板的OSH系统在数字重建时对系统的纵向位置有很强的依赖性, 可以将离焦噪声转换为随机噪声, 有效地抑制离焦层对成像的影响^[24]. 但是在实际操作中, 需要对多次成像的结果取平均才能得到较好的解密图像, 且对随机相位板的精度要求较高. 我们曾提出一种基于环形光瞳的OSH系统, 可以实现高频信息的提取, 并获得原始图像的边缘特征^[25]. 本文辅助以环形光瞳, 可以对多数的随机噪声进行滤除, 并通过一次扫描便可实现对多层图像全部信息的记录, 同时在重建的过程中可以有效消除离焦图像的影响, 实现对任意层图像的解密. 该方法利用光电探测器快速对加密图像进行采集, 相比于传统数字全息中的CCD相机, 光电探测器的采集速度更快, 且与传统的干涉加密^[26]、波长复用^[14]和相位检索^[27]等多图像加密技术相比, 不需要复杂的算法重建和相位迭代就可以实现光学加密和解密, 大大减少了加密过程需要的时间. 解密的过程中增加了系统的密钥空间, 系统的敏感性更高, 微小的偏差也无法解密出正确的图像, 因此获得的加密图像具有更高的安全性. 本文通过计算机仿真实验验证了该方法对多图像并行加密和解密的有效性, 并通过相关系数评估了该方法的安全性和抗剪裁、抗噪声的能力.

2

-->

2.1.OSH系统的基本原理

图1所示是采用OSH系统对多图像并行加密的原理图. 在光学系统中, 激光器发出中心频率为ω_o的光束, 由分束镜(beam splitter, BS₁)分成两束. 其中一束通过调制频率为Ω的声光移频器(acousto-optic frequency shifter, AOFS), 将该路信号的频率调频至ω_o + Ω, 与未加调制的另外一束叠加可以形成外差频率为Ω的扫描信号. 透镜L₁前焦面处两个光瞳p₁(x, y)和p₂(x, y)对两路信号进行波前调制. 两路信号在分束镜BS₂处干涉合为一束光, 通过透镜L₁会聚到位于透镜L₁后焦面上的扫描反射镜M₄处实现对物体的扫描, 物体与透镜L₁后焦面的成像距离为z. 通过物体后的光信号被透镜L₂会聚到光电探测器(photodetector, PD₁)的接收面, 通过PD₁转换成电流信号i(x, y), 此时的电流信号由基带电流信号和外差电流信号共用组成. 电流信号i(x, y)通过被调谐到外差频率Ω的带通滤波器(bandpass filter, BPF₁)提取以获得外差电流, 然后通过锁相放大器(lock-in amplifier)进行信号解调. 锁相放大器包括乘法器和低通滤波器(low-pass filter, LPB)两部分, 锁相放大器的参考信号与外差频率相同, 由另一个固定的光电探测器PD₂采集并通过带通滤波器BPF₂后提供, BPF₂的调谐频率也是Ω. 通过锁相放大器的信号被分为两路, 分别与相互正交的两路单频信号cos(Ωt)和sin(Ωt)混频, 通过LPB提取出同相分量i_c(x, y)和正交分量i_s(x, y), 并经过模数转换器(analog-digital converter, ADC)后存储在数字计算机中. 其中i_c(x, y)和i_s(x, y)又可以称为正弦加密全息图和余弦加密全息图. 最后, 通过计算机合成带有图像信息的复数形式加密全息图, 可以表示为H(x, y)= i_c(x, y) + ji_s(x, y), 可以看到, 与传统的数字全息相比, OSH所成的全息加密图没有零级像与共轭像.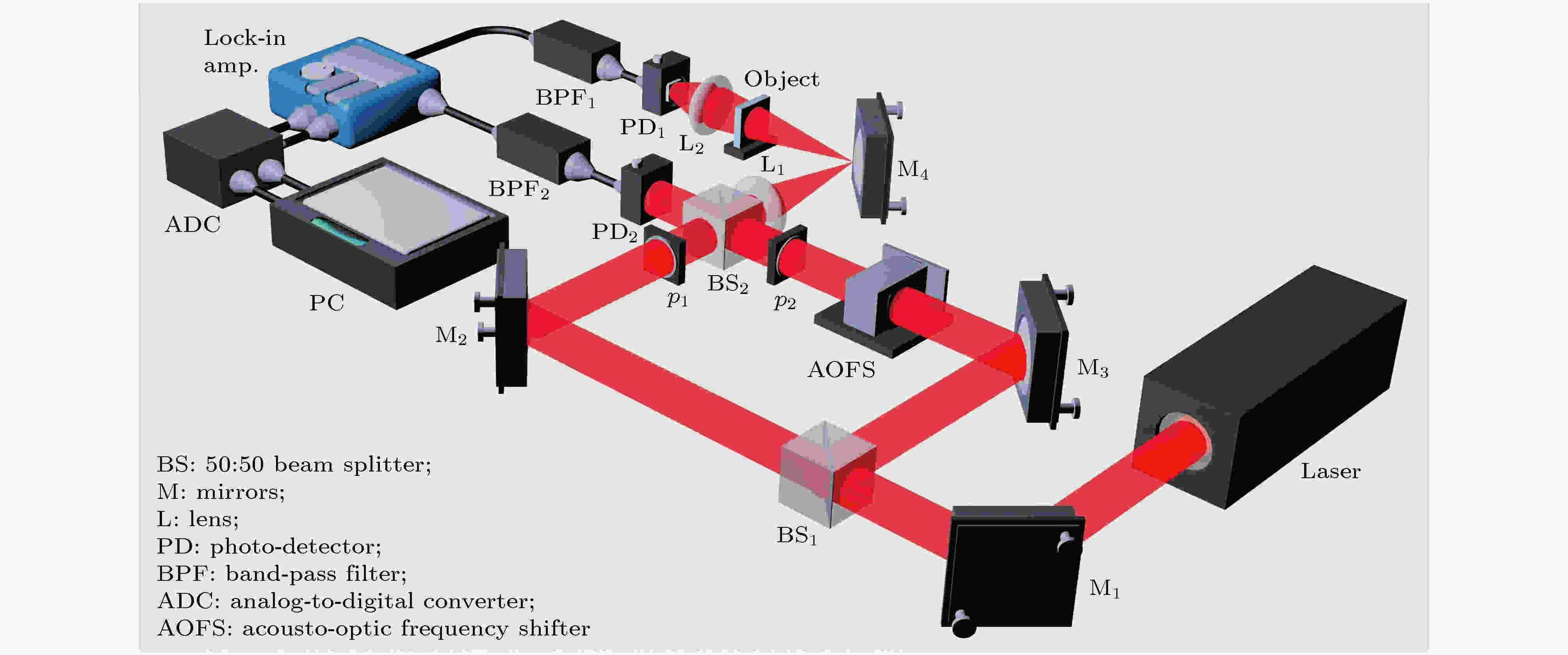
图 1 OSH系统原理图
Figure1. Schematic of the OSH system.

2 -->

2.2.加密过程的基本原理

OSH光学加密系统由两部分组成, 即加密过程和解密过程. 如图1所示, 对于多图像并行加密的过程可以看作是对多个离散全息图的记录过程. 此时的复数形式加密全息图可以表示为多个截面图像衍射的全息图总和, 表示为^[20]

$\begin{split}\;&H\left( {x,y} \right) = \sum\limits_{i = 1}^n {{H_i}\left( {x,y} \right)} \\ =\;& \sum\limits_{i = 1}^n {{F^{ - 1}}\big\{ {F\big\{ {{{| {O\big( {x,y;{z_i}} \big)} \big|}^2}} \big\}} } { {O_{{\rm{TF}}}}( {{k_x},{k_y};{z_i}} )} \big\},\end{split}$

其中H_i(x, y)为第i个截面的加密全息图, F{·}和F^–1{·}表示傅里叶变换和傅里叶逆变换,O(x, y; z_i) 表示物体振幅透过率函数. x和y分别表示空域坐标, k_x和k_y分别表示频域坐标, z_i表示多层加密图像中第i个截面图像到透镜L₁后焦面的距离. O_TF为OSH系统的光学传递函数(optical transfer function, OTF), 可表示为^[24]

$\begin{split}\;& {O_{{\rm{TF}}}}\left( {{k_x},{k_y};{z_i}} \right) \\= \;& \exp \left[ {{\rm{j}}\frac{{{z_i}}}{{2{k_0}}}\left( {k_x^2 + k_y^2} \right)} \right] \iint {p_1^ * \left( {x',y'} \right){p_2}}\\&{\times \left( {x' + \frac{f}{{{k_0}}}{k_x},y' + \frac{f}{{{k_0}}}{k_y}} \right)}{\rm{ }} \\& \times \exp \left[ {{\rm{j}}\frac{{{z_i}}}{f}\left( {x'{k_x} + y'{k_y}} \right)} \right]{\rm{d}}x'{\rm{d}}y', \end{split} $

其中$ {k_0} = 2{\text{π}} /\lambda $表示波数, λ表示光波的波长, f表示透镜L₁的焦距, 上标*表示复共轭, x′和y′分别表示横向和纵向的积分变量. p₁, p₂分别表示两个光瞳结构函数的表达式, 可以看出该系统的光学传递函数取决于两个光瞳函数的选择.
在OSH加密系统中两个光瞳函数可以看作是系统的加密光瞳结构函数, 在传统的OSH系统中选取的两个光瞳函数分别为p₁(x, y) = 1和p₂(x, y) = δ(x, y)^[18]. 在本文所提出的方法中, 采用的两个加密光瞳函数分别是环形光瞳和随机相位板, 分别表示为:

$\begin{split}{p_1}\left( {x,y} \right) =\;& t\left( {r;{w_{\rm o}},{w_{\rm i}}} \right)\\=\;& {\rm{circ}}\left( {\frac{r}{{{w_{\rm o}}}}} \right) - {\rm{circ}}\left( {\frac{r}{{{w_{\rm i}}}}} \right),\end{split}$

${p_2}\left( {x,y} \right) = \exp \left[ {{\rm{j}}2{\text{π}}\varphi \left( {x,y} \right)} \right],$

其中circ(·)表示圆孔的透过率函数; w_o和w_i分别是环形光瞳的外径和内径; r是极坐标, 可以定义为$r = \sqrt {{x^2} + {y^2}} $; 相应的频域中${k_r} = \sqrt {{k_x}^2 + {k_y}^2} $. (4)式中φ(x, y)是均匀分布在[0, 1]之间的随机噪声, 通过空间光调制器(spatial light modulator, SLM)产生. 应用(3)式和(4)式, 加密后全息图可以表示为

$ \begin{split}{H_{{\rm{encrypt}}}}\left( {x,y} \right) =\;& \sum\limits_{i = 1}^n {{F^{ - 1}}\bigg\{ {F\left\{ {{{\left| {O\left( {x,y;{z_i}} \right)} \right|}^2}} \right\}}} \\& \times \exp \left[ { - {\rm{j}}\frac{{{z_i}}}{{2{k_0}}}\left( {k_x^2 + k_y^2} \right)} \right]\\& \times \exp\! \Big[ { - {\rm{j}}2{{\text{π}}}\varphi \Big( {\frac{{ - f{k_x}}}{{{k_0}}},\frac{{ - f{k_y}}}{{{k_0}}}} \Big)} \Big]\\& { \times t\left( {\frac{{ - f{k_r}}}{{{k_0}}};{w_0},{w_i}} \right)} \bigg\}.\end{split}\$

2 -->

2.3.解密过程的基本原理

OSH光学加密系统的多层图像中任意一层的解密过程, 可以看作是对相应切片的数字重建过程. 对于某一切片的解密过程, 需要通过将加密全息图与相应的解密函数做卷积运算. 在OSH加密系统中, 解密函数就是光学传递函数的逆傅里叶变换, 也被称为空间脉冲响应, 即ψ(x, y; z_i) = F^–1{O_TF(k_x, k_y; z_i)}, 其中ψ(x, y; z_i) 表示空间脉冲响应. 在传统的OSH系统中, 两个光瞳函数分别采用p₁(x, y) = 1和p₂(x, y)= δ(x, y), 而相应的重建过程中的光瞳函数分别采用p_1d(x, y) = δ(x, y)和p_2d(x, y) = 1, 则传统OSH系统中相应的光学传递函数和空间脉冲响应分别可以表示为:

${O_{{\rm{TF}}}}\left( {{k_x},{k_y};{z_i}} \right) = \exp \left[ {{\rm{j}}\frac{{{z_i}}}{{2{k_0}}}\left( {k_x^2 + k_y^2} \right)} \right],~~~~~~~~~~~~$

$ \begin{array}{l} \psi \left( {x,y;{z_{\rm c}}} \right) = {F^{ - 1}}\left\{ {{O_{{\rm{TF}}}}\left( {{k_x},{k_y};{z_{\rm{c}}}} \right)} \right\} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \dfrac{{ - {\rm{j}}{k_0}}}{{2{\text{π}}{z_{\rm{c}}}}}\exp \left[ {\dfrac{{{\rm{j}}{k_0}}}{{2{z_{\rm{c}}}}}\left( {{x^2} + {y^2}} \right)} \right], \end{array} $

其中z_c为进行数字重建时的重建距离, 此时的重建图像可以表示为

$\left.\begin{split} \;& H\!\left( {x,y} \right) * \!\psi \!\left( {x,y;{z_{\rm{c}}}} \right) \\ =\;& \displaystyle\sum\limits_{{z_i}} {{F^{ - 1}}\!\bigg\{ {F\left\{ {{{\left| {O\left( {x,y;{z_i}} \right)} \right|}^2}} \right\}} } \\& \times\exp \left[ { - {\rm{j}}\frac{{{z_i}}}{{2{k_0}}}\left( {k_x^2 + k_y^2} \right)} \right] \\& \times \exp \left[ {{\rm{j}}\frac{{{z_{\rm{c}}}}}{{2{k_0}}}\left( {k_x^2 + k_y^2} \right)} \right] \bigg\} ,\end{split} \right. $

其中*表示二维卷积运算. 从(8)式可以看出, 当z_c = z_i, 即重建距离与全息图的记录距离相同时, 聚焦层的图像能够很好地被重建. 而非聚焦层的图像, 即z_c ≠ z_i, 则以离焦噪声的形式呈现在重建图像上.
本文提出的OSH光学加密系统中, 加密过程中的两个加密光瞳函数分别选择环形光瞳和随机相位板, 根据相位迭代算法, 解密过程选择的两个解密光瞳函数需要满足^[22]

$p_{1}^{*}\left( -x,-y \right)\cdot {{p}_{2{\rm d}}}\left( x,y \right)=1,$

$p_{2}^{*}\left( -x,-y \right)\cdot {{p}_{1{\rm d}}}\left( x,y \right)=1,$

且有

$P_{1}^{*}\left( -\frac{{{z}_{i}}}{f}{{k}_{x}},-\frac{{{z}_{i}}}{f}{{k}_{y}} \right)\cdot {{P}_{2{\rm d}}}\left( \frac{{{z}_{\rm{c}}}}{f}{{k}_{x}},\frac{{{z}_{\rm{c}}}}{f}{{k}_{y}} \right)=1,$

$P_{2}^{*}\left( -\frac{{{z}_{i}}}{f}{{k}_{x}},-\frac{{{z}_{i}}}{f}{{k}_{y}} \right)\cdot {{P}_{1{\rm d}}}\left( \frac{{{z}_{\rm{c}}}}{f}{{k}_{x}},\frac{{{z}_{\rm{c}}}}{f}{{k}_{y}} \right)=1,$

其中p_1d和p_2d分别是重建时的两个光瞳函数, P₁, P₂, P_1d和P_2d分别是p₁, p₂, p_1d和p_2d的傅里叶变换. 对于多层图像的加密全息图重建后的解密结果可以表示为

$ \left. \begin{split} \;& {{H}_{\text{decrypt}}}\left( x,y \right) \\ =\;&{{H}_{\text{encrypt}}}\left( x,y \right)*{{\psi }_{\text{decrypt}}}\left( x,y;{{z}_{\rm c}} \right) \\ =\;&\sum\limits_{{{z}_{i}}}{{{F}^{-1}}\bigg\{ F\left\{ {{\left| O\left( x,y;{{z}_{i}} \right) \right|}^{2}} \right\} } P_{1}^{*}\left( -\frac{{{z}_{i}}}{f}{{k}_{x}},-\frac{{{z}_{i}}}{f}{{k}_{y}} \right)\\ &\times {{P}_{2\text{d}}}\left( \frac{{{z}_{\text{c}}}}{f}{{k}_{x}},\frac{{{z}_{\text{c}}}}{f}{{k}_{y}} \right) P_{2}^{*}\left( -\frac{{{z}_{i}}}{f}{{k}_{x}},-\frac{{{z}_{i}}}{f}{{k}_{y}} \right)\\ &\times {{P}_{1\text{d}}}\left( \frac{{{z}_{\text{c}}}}{f}{{k}_{x}},\frac{{{z}_{\text{c}}}}{f}{{k}_{y}} \right) \exp \left[ -\text{j}\frac{{{z}_{i}}}{2{{k}_{0}}}\left( k_{x}^{2}+k_{y}^{2} \right) \right] \\ & \times \exp \left[ \text{j}\frac{{{z}_{\text{c}}}}{2{{k}_{0}}}\left( k_{x}^{2}+k_{y}^{2} \right) \right] \bigg\}. \end{split} \right. $

当z_c ≠ z_i时, 离焦图像以随机噪声的形式叠加在重建焦面, 并且通过环形光瞳的滤波功能可以滤除, 减少对聚焦面成像的影响, 提高信噪比.

2

-->

3.1.加密结果与分析

本文通过仿真实验来验证所提出方法的有效性和可行性. 如图1所示的OSH系统中, Object位置处的原始图像具有三个切片, 如图2所示. 其中图2(d)是三个切片的排列方式. 图像的分辨率均为512 pixel× 512 pixel, 激光器的输出波长为632.8 nm. 为了增加系统加密的密钥空间, 三个切片与透镜L₁后焦面之间的距离z_i分别为z₁ = 10 mm, z₂ = 12 mm和z₃ = 15 mm, 使原始加密图像的相邻两个切片之间的距离具有一定的差异性, 可以增加加密结果的安全性.
图 2 加密图像　(a) 切片1, z₁ = 10 mm; (b) 切片2, z₂ = 12 mm; (c) 切片3, z₁ = 15 mm; (d)多切片的排列方式
Figure2. Encrypted image: (a) Section image 1, z₁ = 10 mm; (b) section image 2, z₂ = 12 mm; (c) section image 3, z₃ = 15 mm; (d) the arrangement of multi-section images.

加密过程中, 选用的两个光瞳函数如(3)式和(4)式所示, 分别为环形光瞳和随机相位板. 对于环形光瞳, 归一化半径ε是一个重要的性能指标, 通过改变归一化半径, 可以调节环形光瞳的分辨率和透光比. 归一化半径又称为孔径比, 是指环形光瞳的内半径(w_i)和外半径(w_o)的比值, 可以表示为$\varepsilon = {{{w_{\rm{i}}}} / {{w_{\rm{o}}}}}$. 图3(b)和图3(c)分别显示了不同归一化半径ε的归一化强度响应曲线和强度响应曲线, 其中ε的取值分别为0.2, 0.4, 0.6和0.8. 从图3(b)中可以看出, 随着ε的增大, 主瓣的宽度在逐渐减少, 这意味着系统的分辨率在逐渐提高. 但是从图3(b)可以发现ε过大时光强的透过率在逐渐减低, 衍射强度也在降低, 能量损耗严重. 可以看出当ε的值在0.4—0.6之间时达到的成像效果较好, 同时实现一定的分辨率. 结合文献[25]中的相关研究结果, 文中采用归一化半径ε = 0.5的环形光瞳, 相应的透过率分布如图3(a)所示, 其中白色部分是透光部分, 即幅度透过率为1, 中间的黑色部分是不透光部分, 即幅度透过率为0.
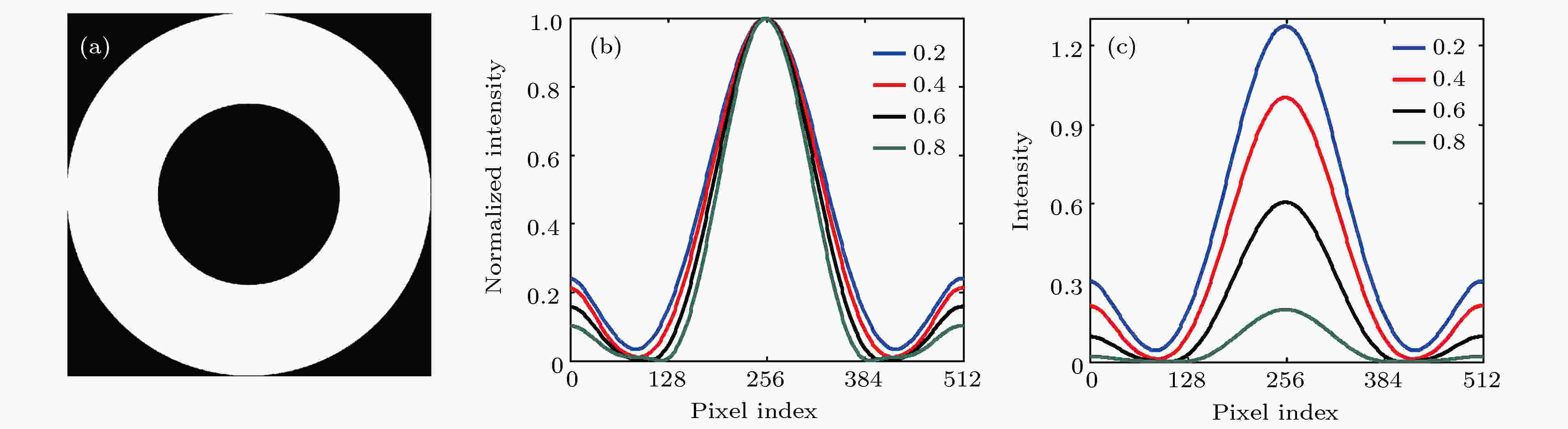图 3 环形光瞳和不同ε的归一化强度响应和强度相应曲线　(a) 环形光瞳(ε = 0.5)的透过率分布图; (b) 归一化强度响应曲线;(c) 强度响应曲线
Figure3. Annular pupil and the intensity response curves of different ε: (a) The transmission distribution diagram of annular pupil with ε = 0.5; (b) normalized intensity response curve; (c) intensity response curve.

在采用了ε = 0.5的环形光瞳和取值范围在[0, 1]之间的随机相位板后, OSH加密系统获得的加密全息图有两张, 分别是余弦加密全息图和正弦加密全息图如图4所示. 加密图像都可以看作是均匀的随机噪声, 从加密图像中无法获取任何关于原始图像的信息.
图 4 加密结果　(a) 余弦加密全息图; (b) 正弦加密全息图
Figure4. Encryption results: (a) Encrypted cosine-hologram; (b) encrypted sine-hologram.

通过对比加密图像和原始图像的统计特性, 可以分析加密图像的安全性. 为检验加密全息图的统计特性, 通过仿真得到加密全息图的灰度直方图如图5所示. 因为原始图像是二值图像, 灰度主要分布在0和255两个灰度级上, 所以与加密图像的灰度直方图相比, 各个灰度级出现的概率有着明显的差距, 因此通过统计分析的方法无法解密出原始图像的信息.
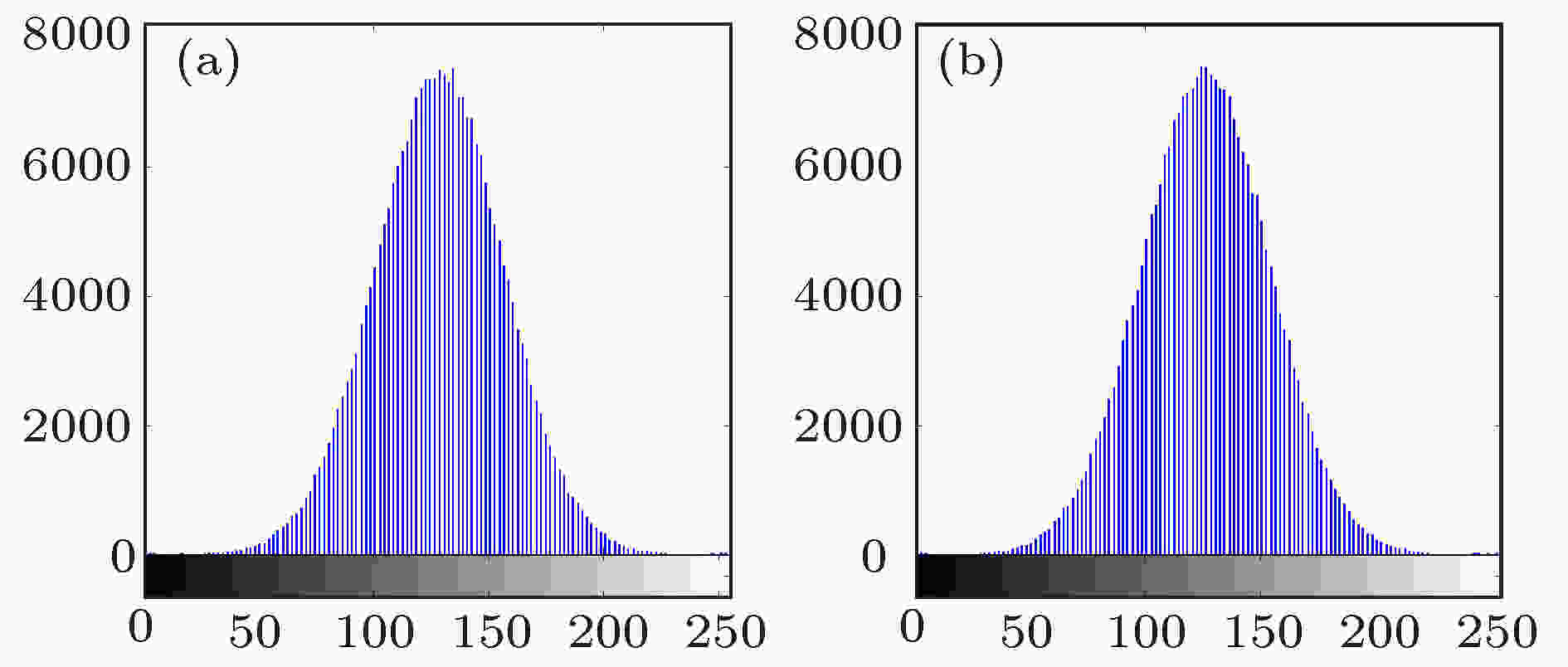图 5 灰度直方图　(a) 余弦加密全息图的灰度直方图; (b) 正弦加密全息图的灰度直方图
Figure5. Gray histogram: (a) Gray histogram of encrypted cosine-hologram; (b) gray histogram of encrypted sine-hologram.

2 -->

3.2.解密结果与分析

解密的过程可以看作是在数字全息中对全息图进行数字重建的过程. 在OSH多层图像的并行光学加密系统中, 对某一层的数字重建可以使用相应的重建函数与加密的全息图做卷积得到. 重建过程中, 每个切片的重建距离z_c与加密时的记录距离z_i相同, 分别为10, 12 和15 mm. 重建后得到的解密结果如图6所示.
图 6 不同切片的解密结果　(a) 切片1; (b) 切片2; (c) 切片3
Figure6. Decryption results of different sections: (a) Section 1; (b) section 2; (c) section 3.

在傅里叶光学中, 环形光瞳具有高通滤波的作用, 可以有效去除低频信息得到图像中的高频信息, 而这些高频信息多集中在图像的边缘细节信息较多的地方, 可以有效地通过边缘信息实现对图像信息的识别. 所以从重建后的解密结果可以看出每一切片的图像都被单独地解密出边缘信息, 通过边缘信息已经可以有效识别出原始图像的有用信息, 尤其是对于类似于偏文字类的二值图像的加密和解密. 在重建的图像中还是会有一点随机散斑噪声, 但是并不影响对结果的识别, 可以通过阈值滤波或多次采集取平均的方法消除. 为了客观地评价解密后的成像效果, 采用相关系数(C_c)作为评价标准来评估解密后图像的质量, 相关系数越大则相应的解密效果越好. 原始图像与解密图像之间的相关系数的计算方法为^[7]:

${C_{\rm{c}}} = \frac{{E\left\{ {\left[ {{g_{\rm{o}}} - E\left( {{g_{\rm{e}}}} \right)} \right]\left[ {{g_{\rm{e}}} - E\left( {{g_{\rm{e}}}} \right)} \right]} \right\}}}{{\sqrt {E\left\{ {{{\left[ {{g_{\rm{o}}} - E\left( {{g_{\rm{e}}}} \right)} \right]}^2}} \right\}E\left\{ {{{\left[ {{g_{\rm{e}}} - E\left( {{g_{\rm{e}}}} \right)} \right]}^2}} \right\}} }},$

其中$E(\cdot) $代表求数学期望, g_o(m, n)和g_e(m, n)分别代表原始图像和解密图像中某像素点的灰度值, m和n分别是水平和垂直方向的像素位置. 经过计算, 使用正确的重建函数解密后的三幅图像与原始图像直接的相关系数分别为0.7740, 0.7575和0.7267, 相关系数较高.
2 -->

3.3.系统敏感性分析

光学加密系统的敏感性分析是评估系统抗攻击能力的重要环节. 本节的实验中, 只对切片1 (z₁ = 10 mm)进行数字重建的对比实验. 在光学加密系统的解密过程中, 重建距离、波长等受到干扰时, 会在一定范围内浮动. 对于重建距离, 假设重建时的距离在一个很小的范围内浮动, 结果如图7(a)—图7(c)所示. 图7(a)是相关系数值随距离变化的曲线, δd是重建距离浮动的大小, 即δd = |z_c–z₁|, 其中图7(a)和图7(d)中的相关系数是与图6(a)的正确解密结果相对比得到的. 图7(b)和图7(c)分别是δd = 0.01 mm和δd = 0.1 mm时的重建解密图像, 相应的相关系数分别为0.1985和0.0596. 可以发现, 当距离浮动0.01 mm时相关系数很低, 图像的信息已经几乎无法识别, 而错误距离为0.1 mm时, 图像信息已经完全无法识别. 对于重建波长, 如图7(d)—图7(f)所示, 图7(d) 是相关系数值随波长变化的曲线, δλ是重建波长浮动的大小. 图7(b)和图7(c)分别是δλ = 0.1 nm和δλ = 1 nm时的重建解密图像, 和重建距离错误类似, 但是波长的敏感性比成像距离更高, 重建波长浮动的距离为1 nm时, 相应的相关系数为0.0049, 此时图像信息就已经完全无法识别, 系统的敏感性很高. 所以当解密过程中的任何一个参数错误时, 都无法从加密图像中解密出原图像的任何信息, 而且即使攻击者破解了其中一层的密钥信息, 但是由于相邻两层加密图像的位置信息都不同, 且没有规律性(每两个切片之间的距离不同), 所以也无法通过任何一个切片的密钥解密出其他切片的图像信息, 可以有效地抵抗暴力攻击.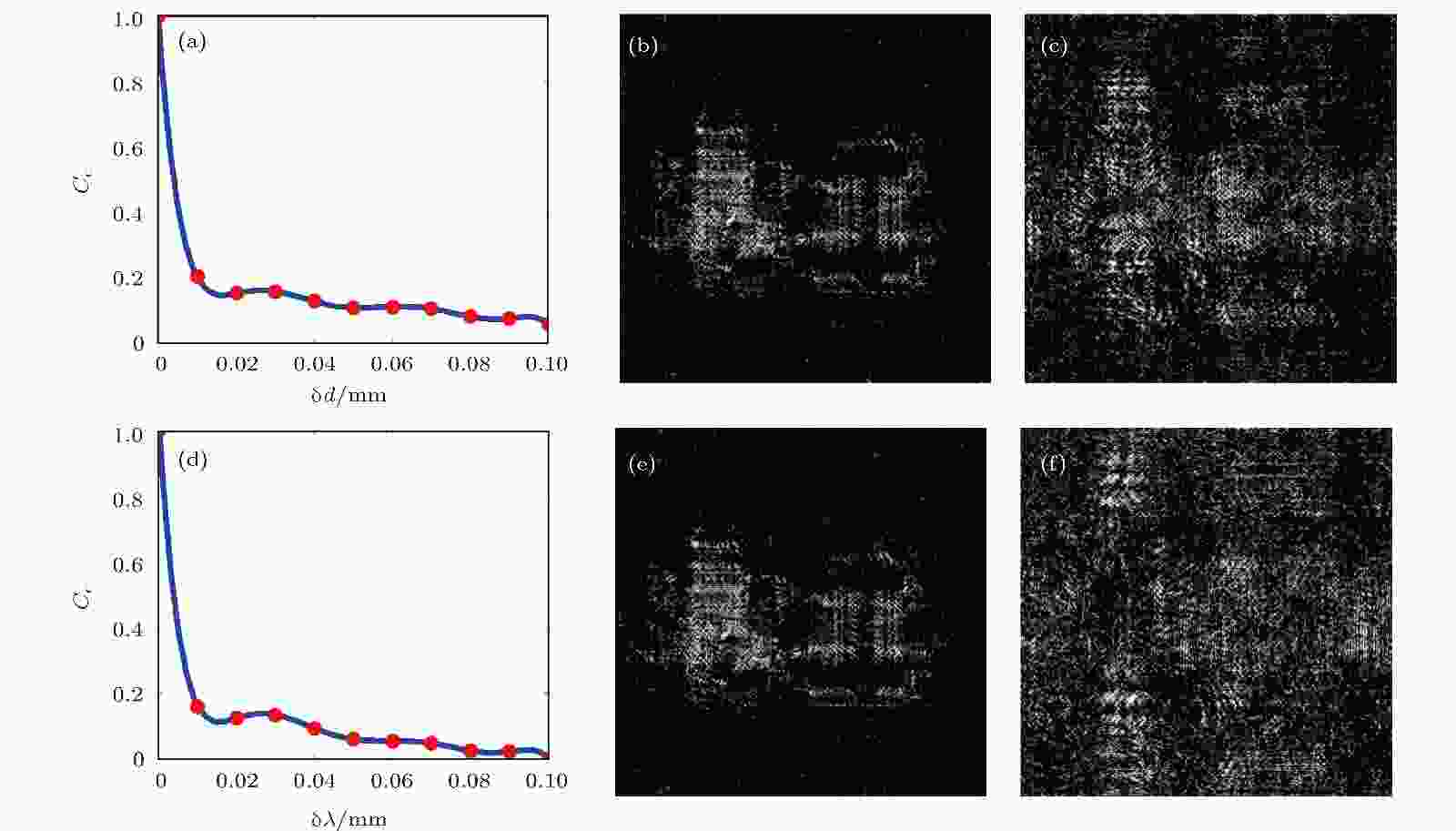
图 7 错误解密结果　(a) 相关系数C_c随δd变化的曲线图; (b) 和 (c) δd = 0.01和0.1 mm时的解密结果; (d) 相关系数C_c随δλ变化的曲线图; (e) 和 (f) δλ = 0.1和1 nm时的解密结果
Figure7. Incorrect decryption results: (a) The C_c curve of varies with δd; (b) and (c) decryption result of δd = 0.1 and 0.1 mm, respectively; (d) the C_c curve of varies with δλ; (e) and (f) decryption result of δλ = 0.1 and 1 nm, respectively.

2 -->

3.4.系统抗剪裁性能分析

在解密原理中, 加密图像的像素和解密图像的像素之间存在着一一对应的关系, 也就是说, 加密图像的部分丢失会导致解密图像也丢失相应的像素. 和传统的数字全息系统不同, OSH系统可以同时得到两张加密全息图, 如图4所示. 因此, 当一张加密图像的信息丢失严重甚至完全丢失时, 可以对另一张完整的全息图进行数字重建也可以获得解密图像, 如图8所示. 本节实验中, 只对切片1(z₁ = 10 mm)进行仿真实验. 图8(a)是余弦加密全息图丢失, 对正弦加密全息图进行解密的结果, 图8(b)是正弦加密全息图丢失, 对余弦加密全息图进行解密的结果, 两个解密结果的相关系数分别为0.6610和0.6506. 虽然单幅机密全息图解密后的噪声较大, 影响视觉效果, 但是仍然可以看到图像的主要特征, 实现对图像信息的识别, 且相关系数较高.
图 8 单幅加密全息图的解密结果　(a) 正弦加密全息图的解密结果; (b) 余弦加密全息图的解密结果
Figure8. Decryption result of single-encrypted hologram: (a) Decryption result of encrypted sine-hologram; (b) decryption result of encrypted cosine-hologram.

对于两幅加密全息图都存在部分信息丢失的情况, 仿真中将图4中的部分像素设置为0, 然后利用两幅加密全息图进行数字重建得到加密结果, 如图9所示. 其中图9(a)和图9(b)是信息丢失25%的正余弦加密图像, 图9(c)是相应的解密结果, 相关系数为0.7418. 图9(d)和图9(e)是信息丢失50%的正余弦加密图像, 图9(f)是相应的解密结果, 相关系数为0.6508. 图9(g)和图9(h)是信息丢失75%的正余弦加密图像, 图9(i)是相应的解密结果, 相关系数为0.5192. 可以看出, 解密后的图像可以识别到图像的主要特征, 可以辨认出图像的轮廓, 具有较好的相关系数, 都在0.5以上, 因此OSH光学加密系统有较强的抗剪裁能力.
图 9 抗剪裁性能模拟结果　(a) 和 (b) 信息丢失25%的正余弦加密图像; (c) 信息丢失25%后的解密结果; (d) 和 (e) 信息丢失50%的正余弦加密图像; (f) 信息丢失50%后的解密结果; (g) 和 (h) 信息丢失75%的正余弦加密图像; (i) 信息丢失75%后的解密结果.
Figure9. Simulation results of anti-shear performance: (a) and (b) The sine- and cosine-holograms with 25% occlusion; (c) decryption result with 25% occlusion; (d) and (e) the sine- and cosine-holograms with 50% occlusion; (f) decryption result with 50% occlusion; (g) and (h) the sine- and cosine-holograms with 75% occlusion; (i) decryption result with 75% occlusion.

2 -->

3.5.系统抗噪声性能分析

加密后的图像在传输过程中难免会受到噪声的干扰, 因此解密后的图像也会受到一定的影响. 利用不同方差(variance)的高斯噪声和椒盐噪声作为噪声干扰源, 对加密全息图进行叠加干扰, 并通过相关系数来定量评估解密图像的成像效果, 其中所选噪声的均值均为0. 图10(a)—图10(c)分别是受到方差为0.02, 0.05和0.08的高斯噪声(均值为0)干扰后对切片1 (z₁ = 10 mm)图像的解密结果, 相对应的相关系数分别为0.6953, 0.6649和0.5787. 图10(d)—图10(f)分别是受到方差为0.02,0.05和0.08的椒盐噪声(均值为0)干扰后对切片1 (z₁ = 10 mm)图像的解密结果, 相对应的相关系数分别为0.6825, 0.6034和0.5038. 可以看出, 由于受到噪声的影响, 解密后的图像质量有所下降, 但是解密后图像的相似度均在0.5以上, 解密图像依然可以辨别到明显的边缘特征, 可以识别到原图像的信息. 所以, 本加密系统的抗噪声干扰方面的性能较好, 具有较强的抗噪声能力.
图 10 抗噪声性能模拟结果　(a), (b) 和 (c) 方差为0.02, 0.05和0.08的高斯噪声; (d), (e) 和 (f) 方差为0.02, 0.05和0.08的椒盐噪声
Figure10. Simulation results of anti-noise performance: (a), (b) and (c) Gaussian noise with variance of 0.02, 0.05 and 0.08; (d), (e) and (f) salt and pepper noise with variance of 0.02, 0.05 and 0.08.

本文提出了一种基于光学扫描全息密码术对多图像并行加密的方法, 该方法可以通过一次光学扫描将多层图像同时加密在一组正余弦加密全息图中, 然后利用数字重建可以解密出每一层图像的边缘信息. 其中采用环形光瞳和随机相位板作为两个光瞳合成环形随机相位板对多层图像进行扫描, 由于随机相位板的特性, 可以在数字重建时将离焦层的图像以随机噪声的形式呈现在成像面上, 而通过环形光瞳可以实现对噪声的消除并提取图像的边缘特征信息. 该方法可以有效地实现对二值图像尤其是文字类信息的加密, 并能通过数字重建实现对每一层图像的解密. 通过相关系数的计算可以看出, 重建后的解密图像成像质量较好, 该系统省时, 且安全性高. 通过仿真实验验证了该方法的安全性, 同时也验证了加密后的全息图具有较高的抗剪裁和抗噪声能力, 可以有效应用于对多图像的高速加密和解密等领域.
本论文研究工作承蒙美国弗吉尼亚理工暨州立大学(Virginia Tech) Ting-Chung Poon教授指导和修改完成，谨致谢意！