摘要: 采用基于自旋密度泛函理论的平面波超软赝势方法, 研究了Cu掺杂ZnO (简称Cu
Zn )与内在缺陷共存对ZnO电磁光性质的影响. 结果表明, Cu是以替位受主的形式掺入的; 制备条件对Cu
Zn 及内在缺陷的形成起至关重要的作用, 富氧条件下Cu掺杂有利于内在缺陷的形成, 且Cu
Zn -O
i 最易形成; 相反在缺氧条件下, Cu掺杂不利于内在缺陷的形成. 替位Cu的3d电子在价带顶形成未占据受主能级, 产生p导电类型. 与Cu
Zn 体系相比, Cu
Zn -V
O 体系中载流子浓度降低, 导电性变差; Cu
Zn -V
Zn 体系中载流子浓度几乎不变, 对导电性没影响; Cu
Zn -O
i 体系中载流子浓度升高, 导电性增强. 纯ZnO体系无磁性; 而Cu掺杂ZnO体系, 与Cu原子相连的O原子, 电负性越小, 键长越短, 对磁矩贡献越大; Cu
Zn 与Cu
Zn -O
i 体系中的磁矩主要是Cu的3d电子与
Z 轴上O的2p电子耦合产生的; Cu
Zn 中存在空位缺陷(V
O , V
Zn )时, 磁矩主要是Cu 3d电子与
XY 平面内O的2p电子强烈耦合所致; Cu
Zn 中存在V
Zn 时, 磁性还包含V
Zn 周围O(5, 6)号原子2p轨道自旋极化的贡献; 所有体系中Zn原子自旋对称, 不产生磁性. Cu
Zn -V
Zn 和Cu
Zn -O
i 缺陷能态中, 深能级中产生的诱导态是O-O 2s电子相互作用产生的. Cu
Zn 模型的光学带隙减小, 导致吸收边红移; Cu
Zn -V
Zn 模型中吸收和反射都增强, 使得透射率降低.
关键词: 第一性原理 /
内在缺陷 /
Cu掺杂ZnO /
形成能 English Abstract Effect of intrinsic defects and copper impurities co-existing on electromagnetic optical properties of ZnO: First principles study Zhang Mei-Ling 1,2 ,Chen Yu-Hong 1 ,Zhang Cai-Rong 1 ,Li Gong-Ping 2 1.School of Science, Lanzhou University of Technology, Lanzhou 730050, China Fund Project: Project supported by National Natural Science Foundation of China (Grant Nos. 51562022, 11575074) and the HongLiu First-class Disciplines Development Program of Lanzhou University and Technology, China.Received Date: 20 December 2018Accepted Date: 20 February 2019Available Online: 01 April 2019Published Online: 20 April 2019Abstract: For ZnO which is not magnetic itself, it is of great significance to study the source of ferromagnetism and its photoelectric properties when Cu doped ZnO coexists with internal defects. The effects of intrinsic defects on the electronic structures, magnetic and optical properties of Cu-doped ZnO (CuZn ) are studied by using first principle calculations based on the density functional theory combined with the Hubbard U (DFT + U d + U p ). The results indicate that the doped Cu is a substitute acceptor, and the manufacturing environment plays an important role in forming the CuZn with internal defects. Under the oxygen-rich condition, the doped Cu is favorable for forming internal defects, and the CuZn —Oi bonds are easily formed. On the contrary, the Cu-doped ZnO is not conducive to forming internal defects under the O-poor condition. The 3d electrons of the substitute Cu form the unoccupied accepter energy level at the top of valence band, generating p-type conduction. Comparing with CuZn system, the carrier concentration of positive hole decreases in CuZn -VO system and the conductivity is poor. In the CuZn -VZn system, the number of carrier holes is almost constant, and the conductivity has no effect. In the CuZn -Oi model, the carrier concentration of positive holes increases and the conductivity gets better. The pure ZnO system exhibits non-magnetic behavior. The study also reveals that the smaller the electro-negativity, the greater the contribution to magnetic moment is when O atom is connected with Cu atom. The magnetic moments in CuZn and CuZn -Oi system are mainly generated by the coupling between the Cu 3d and the O 2p orbital on the c axis. When VO and VZn exist in CuZn , the magnetic moment is mainly caused by the strong coupling of Cu 3d with O 2p in ab plane. In the presence of VZn in CuZn , the magnetism also contains the contribution of the spin polarization of O(5, 6) atoms around VZn . In the defect states of CuZn -VZn and CuZn -Oi , the induced states in the deep energy levels are generated by the interaction between the O-O 2s orbital electrons. The reduced optical band gap of the CuZn model results in the red shift of absorption spectrum. The enhanced absorption and reflection of the CuZn -VZn model reduce the transmission.Keywords: first principles /intrinsic defect /Cu-doped ZnO /formation energy 全文HTML --> --> --> 1.引 言 Ⅱ-Ⅵ族化合物半导体材料ZnO的带隙宽(3.370 eV)、激子结合能高(60 meV)[1 ] , 而且储量丰富、无毒无害. 一方面, 提高ZnO的光电性质能够改善ZnO基光电器件性能; 另一方面, ZnO基半导体材料的磁性来源也是****们关注的焦点. 为了提高ZnO的电磁光性能, 避免对ZnO磁性来源引起争议, 首选Cu作为掺杂元素. Cu+ 半径(0.060 nm)、Cu2+ 半径(0.057 nm)与Zn2+ 半径(0.060 nm)相同或相近, 形成能小[2 ] , 容易掺杂, 且Cu以及Cu的氧化物(CuO, Cu2 O)本身都是非磁性的[3 ] , 它们的沉淀析出对磁性没影响, 有利于磁性来源的研究.Zn )电磁光性质的实验和理论研究方面进行了广泛研究. 在光电性质方面, Drmosh等[4 ] 用脉冲激光沉积方法在室温下研究了CuZn 的光学性质, 发现随Cu在ZnO中掺杂浓度的升高, 带隙变窄, 发射峰有红移. Suja研究组[5 ] 制备出CuZn 为p型导电材料, 光致发光谱表明, 在价带顶产生能级深度0.15 eV为受主能级, 由于缺陷的补偿作用, 经过一定的时间都能转化为n型. Chakraborty等[6 ] 用溶胶凝胶法和水热法合成了ZnO纳米棒, 实验和理论模拟研究表明, 与ZnO相比, CuZn 吸收边红移, 带隙变窄; 光致发光谱表明在紫外光电器件方面有很大的应用价值. Horzum等[7 ] 通过紫外测量技术, 发现光学带隙和透光率随Cu掺杂浓度的增加线性减小, 实验结果与其第一性原理计算结果吻合. Vachhani和Bhatnagar[8 ] 用射频磁控溅射沉积法研究了含氧率对c -轴取向ZnO和Zn0.95 Cu0.05 O薄膜带隙的影响, 研究表明, 氧流量越大, Zn0.95 Cu0.05 O材料的带隙越宽. Xia等[9 ] 用第一性原理平面波超软赝势方法研究CuZn , 结果表明: Cu的掺入使带隙变窄, 吸收边红移; 光致发光谱表明, 紫外发射峰向低能转移, 强度降低, 且发现以蓝色和绿色为中心的两个发射峰, 计算说明这主要是杂质能级接近价带顶导致的. 尽管对CuZn 在实验和理论上做了诸多研究, 但ZnO体系中内在缺陷(VO , VZn , Oi )的存在对CuZn 光电性质的影响未见系统报道.[10 ] 用第一性原理方法研究了Cu掺杂对ZnO电磁性能影响, 研究表明体系为半金属化稀磁半导体, 铜掺杂使空穴浓度增加, 导电性增强; Cu双掺杂量增加, 掺杂体系总磁距先增加后减小. Iqbal等[11 ] 研究了Cu掺杂ZnO粉末晶带与发光性能的改善, 带隙变窄, 发生红移; 掺杂浓度为3%时, Cu处于2+ 氧化态; 室温下显示顺磁性. Li等[12 ] 通过离子注入技术研究Cu掺杂ZnO的磁性, 研究结果表明, 光致发光在510 nm处有广泛的绿光发射与缺陷有关, Cu以Cu+1 和Cu+2 混合离子替带Zn+2 离子掺入, 铁磁性与Cu离子缺陷有关. Nia等[13 ] 采用密度泛函理论第一性原理研究了Cu掺杂对ZnO磁特性的影响, 结果表明, Cu单掺杂ZnO中, 掺杂体系铁磁性稳定; Cu双掺杂ZnO中, 两铜原子距离近时, 体系呈现反铁磁性(AFM)稳定, 反之, 两个铜原子距离远时, 体系呈铁磁性(FM). 而另一些研究结果表明, Cu掺入ZnO对ZnO的磁性没有影响, 磁性主要由内在缺陷引起. 如: Keavney等[14 ] 研究了脉冲激光沉积铜掺杂ZnO薄膜中的铁磁性, 研究表明: Cu 3d, O 2p, Zn 4s或3d不发生自旋极化, 不产生磁性. Xu等[15 ] 在掺铜的ZnO薄膜中没有观察到明显的铁磁性, 铁磁性是由内在缺陷引起的. Zhu等[16 ] 采用脉冲磁场辅助水热法合成了铜掺杂ZnO微棒, 研究表明, 铁磁性的起源和ZnO基体中的氧空位密切相关. 尽管国内外对Cu掺杂ZnO磁性来源有一定的研究, 但是对该体系的磁性来源还存在分歧.Zn ), 以及CuZn 与内在缺陷氧空位(VO )、锌空位(VZn )、氧间隙(Oi )共存时体系的稳定性及电磁光性质进行系统研究.2.理论模型与计算方法 22.1.理论模型 2.1.理论模型 为了研究Cu掺杂氧化锌与内在缺陷 (VO , VZn 和Oi )共存时CuZn 的电磁光性质, 综合考虑计算机的计算能力以及计算效率, 通过查阅文献[17— 21 ], 选择了2 × 2 × 2的超胞进行所有的计算. 2 × 2 × 2的超胞包含16个氧原子和16锌原子, 如图1 所示. 图1 中位置(1)为Cu替代Zn位置(CuZn ), 位置(2)为氧空位(VO ), 位置(3)为锌空位(VZn ), 位置(4)为间隙氧或间隙铜(Oi 或Cui ). CuZn 中Cu替换Zn的原子百分比浓度为6.25 at.%, CuZn 和VO , VZn , Oi 共存的情况, VO , VZn 以及Oi 的浓度分别为6.25 at.%, 6.25 at.%和5.88 at.%.图 1 2 × 2 × 2的ZnO的超胞 (红色代替O原子, 蓝紫色代替的是Zn原子)Figure1. 2 × 2 × 2 ZnO supercell (where the red components represent the O atoms, gray represents the Zn atoms)2.2.计算方法 -->2.2.计算方法 所有计算都由CASTEP[22 ] (Material studio 6.1)软件包完成. 计算采用广义梯度近似下的(generalized gradient approximation, GGA + U )平面波赝势方法, 结合PBE ( Perdew-Burke-Ernzerhof )[23 ] 交换关联泛函对体系进行结构优化及能量计算. 由于传统的密度泛函理论不能精确描述包含d电子和f电子的体系, 特别是过渡金属氧化物和氮化物, 而GGA + U 能够精确描述含有掺杂过渡族金属氧化物的电子结构, 对于强局域化的电子, 在模型中引入能够描述原子间强相关作用项——Hubbard参数U (排斥能). 对于一些非局域化的s电子和p电子, 仍然按照标准的GGA方法来处理. 通过测试计算和参阅文献, Zn-3d电子的U d 值为10 eV[21 ] , O-2p电子的U p 值为7 eV[24 ] , Cu-3d的U d 值为2.5 eV [25 ] ; 平面波截断能取380 eV; K 点设置为4 × 4 × 2 [26 ] ; 自洽场收敛为10–6 eV; 赝势采用超软赝势[27 ] 计算离子核, Zn, O, Cu的价电子分别为4s2 3d10 , 2s2 2p4 和3d10 4s1 ; 能量收敛、最大力、最大压力、以及最大位移阈值分别为10–5 eV/atom, 3 × 10–3 eV/A, 5 × 10–2 GP, 10–3 A. 计算得到的ZnO晶体的禁带宽度为3.370 eV, 与实验值(分别为3.37 eV [1 ] 和3.13 eV [28 ] )和计算[21 ] 值(3.37 eV) 符合得很好. 表明参数设置合理, U 值选择恰当, 所有结构优化及性质计算都是在上述参数基础上进行的.3.结果与讨论 23.1.形成能 3.1.形成能 为了分析掺杂及缺陷体系的相对稳定性, 一般是计算它们的形成能. 不同模型中体系的形成能表示为[28, 29 ] E tot (ZnO)为纯ZnO晶体能量; E tot (D )为缺陷体系的能量; ni 是添加或者是移除i 原子的个数, 移除时, ni 为正值, 否则ni 为负值; ${\mu}_i$ 为i 原子的化学势. 形成能与实验条件有很大的关系, 分为富氧条件(O-rich)和富锌条件(Zn-rich), 富锌条件(Zn-rich)也称为(O-poor). 在ZnO中考虑其热稳定性, 氧原子和锌原子的化学势必须满足如下关系: ${{\mu} _{{\rm{Zn}}}} + {{\mu} _{\rm{O}}} = {{\mu} _{{\rm{ZnO}}}}$ . 在O-rich条件下, 氧原子的化学势由氧分子能量的一半表示, 即${{\mu} _{\rm{O}}} = $ ${{\mu} _{{{\rm{O}}_2}}}/2$ ; 锌原子的化学势则由${{\mu} _{{\rm{Zn}}}} = {{\mu} _{{\rm{ZnO}}}} - {{\mu} _{\rm{O}}}$ 得到; 铜原子的化学势也相应地由${{\mu} _{{\rm{Cu}}}} = {{\mu} _{{\rm{Cu}}{{\rm{O}}_2}}} - 2{{\mu} _{\rm{O}}}$ . 而在O-poor条件下, ${{\mu} _{{\rm{Zn}}}}$ 和${{\mu} _{{\rm{Cu}}}}$ 分别由锌和铜块体材料计算得到, 即${{\mu} _{{\rm{Zn}}}} = {\mu} _{{\rm{Zn}}}^{{\rm{Metal}}},\;{{\mu} _{{\rm{Cu}}}} = {\mu} _{{\rm{Cu}}}^{{\rm{Metal}}}$ ; 氧的化学势则由${{\mu} _{\rm{O}}} = {{\mu} _{{\rm{ZnO}}}} - {{\mu} _{{\rm{Zn}}}}$ . 计算所得的形成能都列在表1 中. 形成能越小, 掺杂和缺陷越容易形成[30 ] , 稳定性相对较高. 缺陷类型 VO VZn Oi Cui CuZn CuZn -VO CuZn -VZn CuZn -Oi O-rich 6.603 0.915 –0.548 5.795 –0.495 6.337 0.422 –0.965 O-poor 1.308 6.210 4.747 4.026 3.031 4.569 9.244 7.856
表1 ZnO和CuZn 缺陷的形成能(单位: eV)Table1. Formation energy of ZnO and CuZn with intrinsic defects (in eV)表1 中的形成能表明: 纯ZnO以及Cu掺杂ZnO的本征缺陷产生受到实验条件氧流的影响. 对ZnO来说, 在O-rich条件下, 体系形成能的顺序为: ${E_{\rm{f}}}\left( {{{\rm{O}}_{\rm{i}}}} \right) < {E_{\rm{f}}}\left( {{\rm{C}}{{\rm{u}}_{{\rm{Zn}}}}} \right) < {E_{\rm{f}}}\left( {{{\rm{V}}_{{\rm{Zn}}}}} \right) < {E_{\rm{f}}}\left( {{\rm{C}}{{\rm{u}}_{\rm{i}}}} \right) < $ ${E_{\rm{f}}}\left({{{\rm{V}}_{\rm{O}}}} \right)$ , Oi 和CuZn 的形成能都为负值, 很容易形成, 且缺陷的相对稳定性高; VZn 形成能较小, 为正值, 缺陷较稳定; Cui 和VO 形成能较大, 实现相对较难; 在O-poor条件下, 形成能的顺序为${E_{\rm{f}}}\left( {{{\rm{V}}_{\rm{O}}}} \right) < $ ${E_{\rm{f}}}\left( {{\rm{C}}{{\rm{u}}_{{\rm{Zn}}}}} \right)<{E_{\rm{f}}}\left( {{\rm{C}}{{\rm{u}}_{\rm{i}}}} \right) < {E_{\rm{f}}}\left( {{{\rm{O}}_{\rm{i}}}} \right) < {E_{\rm{f}}}\left( {{{\rm{V}}_{{\rm{Zn}}}}} \right)$ , VO 较易实现, 稳定性相对较高; 其他缺陷形成能较大, 实现较困难, 稳定性也相对较差; 这与Lee等[20 ] 对ZnO本征缺陷的研究结果符合较好. 综上所述, 在两种实验条件下, 铜间隙缺陷都很难实现. 这是因为铜原子为29号元素, 与30号元素Zn, 原子半径相当, 由半导体物理理论可知, 一般以替位式杂质存在. O-rich条件下CuZn 本征缺陷的形成能顺序为: ${E_{\rm{f}}}\left( {{\rm{C}}{{\rm{u}}_{{\rm{Zn}}}}{{\rm{O}}_{\rm{i}}}} \right) < {E_{\rm{f}}}\left( {{\rm{C}}{{\rm{u}}_{{\rm{Zn}}}}{{\rm{V}}_{{\rm{Zn}}}}} \right) < {E_{\rm{f}}}\left( {{\rm{C}}{{\rm{u}}_{{\rm{Zn}}}}{{\rm{V}}_{\rm{O}}}} \right)$ , 与纯氧化锌在相同条件下形成能的顺序相同, 相应形成能的值都减小, 说明在O-rich下, Cu替位Zn的存在促进了ZnO本征缺陷的形成, CuZn -Oi 和CuZn -VZn 缺陷出现的概率较高; 而在O-poor条件下, ${{{E}}_{\rm{f}}}\left( {{\rm{C}}{{\rm{u}}_{{\rm{Zn}}}}{{\rm{V}}_{\rm{O}}}} \right){\rm{ < }}{{{E}}_{\rm{f}}}\left( {{\rm{C}}{{\rm{u}}_{{\rm{Zn}}}}{{\rm{O}}_{\rm{i}}}} \right){\rm{ < }}{{{E}}_{\rm{f}}}\left( {{\rm{C}}{{\rm{u}}_{{\rm{Zn}}}}{{\rm{V}}_{{\rm{Zn}}}}} \right)$ , 形成能的大小顺序也与在此条件下的ZnO的相同, 但相应的形成能都增大, 表明在O-poor下, ZnO中Cu原子的存在抑制了本征缺陷的形成. 比较来看CuZn -VO 出现的概率在三种缺陷中最低. 在计算过程中发现, CuZn -VO 模型的收敛也很难实现, 通过逐步调整参数, 才达到稳定状态, 从一定程度上说明CuZn -VO 的稳定性不高. 此外在O-poor条件下形成能相对较大, 表明缺陷不稳定, 且不易形成.3.2.电磁性质 -->3.2.电磁性质 图2(a) 和图2(b) 分别为纯ZnO的能带结构及分波态密度图(以费米能级作为能量0点). 可以看出, 导带底和价带顶均位于布里渊区G 点, 属于直接带隙半导体材料, 带隙值为3.370 eV, 与实验值[1 ,28 ] 和理论[21 ] 计算结果吻合. ZnO的价带顶主要由O的2p组成, 导带底主要由Zn的4s4p杂化组成, 也包含一定O的2p电子; 分波态密度图中自旋明显对称, 没有自旋极化, 理想材料ZnO是非铁磁性的.图 2 (a) ZnO能带结构图; (b) ZnO分波态密度图Figure2. (a) Band Structures of ZnO; (b) PDOS of ZnOO , VZn , Oi )共存时体系的结构. 图3 —图5 分别给出了优化后各体系的晶体结构图(图中标号原子是对晶体性质有主要影响的原子)、相应的能级图以及分波态密度图. 同时, 表2 给出了各个体系的带隙值和空穴的相对浓度. 由于掺杂Cu浓度相同, 故只考虑载流子浓度对导电性的影响, 没有考虑迁移率的影响. ZnO CuZn CuZn -VO CuZn -VZn CuZn -Oi 禁带宽度/eV 3.370 2.577 2.413 2.597 1.885 光学带隙/eV 3.370 0.980 0.228 1.108 0.195 P 0.068 1.344 1.107 1.321 1.574
表2 ZnO模型的带隙和空穴浓度P Table2. Band gap and hole concertration P of ZnO model图 3 优化后的晶体结构图 (a) CuZn ; (b) CuZn -VO ; (c) CuZn -VZn ; (d) CuZn -Oi Figure3. Structure of crystal cell after optimized: (a) CuZn ; (b) CuZn -VO ; (c) CuZn -VZn ; (d) CuZn -Oi 图 5 分波态密度(图中虚线为费米能级) (a) CuZn ; (b) CuZn -VO ; (c) CuZn -VZn ; (d) CuZn -Oi Figure5. PDOS (the dotted line in the graph is the Fermi energy level ): (a) CuZn ; (b) CuZn -VO ; (c) CuZn -VZn ; (d) CuZn -Oi 图1 中)的(1)号位置Zn原子被Cu原子替代, 优化后超胞的结构图、能带图和分波态密度图分别如图3(a) 、图4(a) 和图5(a) 所示, 相对于ZnO, CuZn 能带整体下移, 但导带下移比价带多, 禁带宽度减小为2.577 eV, Cu掺杂带隙减小与实验[6 , 31, 32 ] 和理论[33 ] 一致; 掺入的Cu原子主要影响价带, 对导带几乎没有影响. 这是因为Cu为29号元素, 比Zn最外层少一个电子, 则替代Zn的Cu为受主[13 , 34 ] , 产生p型导电类型[33 ] , 空穴相对浓度增加为1.344, 与文献[10 ]结果一致; 与纯ZnO相比, 增强了导电性; 对体系磁性有主要贡献的氧原子在铜原子周围. 图5(a) 表明, 主要是O原子的2p电子与Cu的3d电子在价带顶相互作用, 价带顶伸向禁带中, 这可以解释实验[31 ] 中Cu掺入ZnO薄膜使得带尾宽度增加的原因; 受主能级主要是Cu的3d电子与Z 轴上的O(5)的2p电子相互作用所致, 产生距离价带顶0.980 eV深能级, 这也是体系产生磁性的主要原因; Cu元素的掺入, 使Cu与O(2, 3, 4) 、O(5) 的键长分别减小0.020, 0.076 ?. 由电荷布居数可知, O(5)的布居数由0.94减小为0.89, 电负性降低, 磁矩为0.14${\mu}_{\rm B}$ , 而O(2, 3, 4)的布居数由0.94减小为0.93, 电负性稍有下降, 磁矩都为0.02${\mu}_{\rm B}$ , 表明Cu—O键的键长减小越多, 氧的布居数下降越多, 电负性越弱, 对磁性贡献越大. Cu原子的布居数为0.63, 可以认为Cu掺杂是以Cu+1 与Cu+2 离子混合形式存在, 与文献[12 ]实验结果一致, Cu的磁矩为0.78${\mu}_{\rm B}$ , 体系总磁矩为0.98${\mu}_{\rm B}$ , Cu单掺杂ZnO体系的磁矩接近整数1, 与实验Cu掺杂ZnO体系总磁矩为1或2整数结果一致[35 ] , 而侯清玉等[10 ] 在相同Cu浓度下体系总磁矩大小为1.9349${\mu}_{\rm B}$ , 比本文的计算结果大了1倍.图 4 能带结构图(图中虚线为费米能级) (a) CuZn ; (b) CuZn -VO ; (c) CuZn -VZn ; (d) CuZn -Oi Figure4. Band structures (the dotted line in the graph is the Fermi energy level): (a) CuZn ; (b) CuZn -VO ; (c) CuZn -VZn ; (d) CuZn -Oi 图3(b) , 图4(b) 和图5(b) 分别给出了CuZn -VO 优化后的晶体结构、能带及分波态密度图. 与CuZn 相比, VO 的出现, Z 轴上的O与Cu的相互作用减弱, 键长由1.912 ?增加为2.028 ?. 由电荷布居数可知, Z 轴的O不存在磁矩, 得到电荷由0.89增加为0.93, 与纯ZnO中类似; Cu原子失去的电荷量减小为0.59, 磁矩减少为0.74${\mu}_{\rm B}$ , O(2, 3)得到的电荷量由0.93减小为0.90, 磁矩增加为0.08${\mu}_{\rm B}$ , Cu与O(2, 3)键长稍有减小. 图4(b) 与图4(a) 相比, 能带整体下移, 但费米能级较CuZn 相对有所上移, 表明VO 缺陷能级为施主能级; 由于施主与受主之间存在互补偿作用, 使得空穴相对浓度降为1.107, 降低了导电性; 禁带宽度为2.413 eV. 由图5(b) 分波态密度可以看出, 导带主要由Zn的4s4p电子形成, 价带主要由Zn的2s2p新产生的缺陷态、O原子的2p以及Cu的3d电子组成. 如图4(b) 和图5(b) 所示, 禁带中未占据的受主能级, 距离价带顶0.228 eV, 主要是Cu的3d电子与XY 平面内O(2, 3)号原子的2p电子自旋耦合所得, 分波态密度明显不对称, 产生磁矩, 总磁矩为0.92$\mu_{\rm B}$ .Zn -VZn 优化后的晶体结构如图3(c) 所示, 能带和分波态密度分别由图4(c) 和图5(c) 给出. 与CuZn 相比, 能带图整体几乎没有移动, 禁带宽度为2.597 eV; 如表2 所示, 存在VZn 空位时, 空穴浓度几乎没有变化, 是因为VZn 影响的是深能级, 对载流子浓度不产生影响. 能带图4(c) 中在禁带中产生自旋向上的能级, 由图5(c) 分波态密度可知, 其为Cu的3d电子与O的2p电子杂化生成的, 距离价带顶1.108 eV的深能级; 自旋向上能级的变化, 主要是Cu的3d与O(2, 3, 4) 号原子的2p电子相互作用的结果, 主要影响价带顶; 价带顶主要为O的2p以及Cu的3d电子的贡献. 如图5(c) 所示, CuZn -VZn 在费米能级以下的深能级中观察到四个新生的缺陷态, 三个自旋向上, 一个自旋向下, 主要由Zn空位周围O原子的2s电子在深能级处发生自旋极化产生的; 在费米能级以上, 在导带底分别观察到两个新生态, 都为自旋向下, 主要是O(5, 6)号原子的2p电子自旋极化引起的, 导带底还包含了少量的Zn 4s电子的贡献. 由电荷布居数可知, Cu的布居数为0.67, 磁矩为–0.78${\mu}_{\rm B}$ , O(2, 3, 4)的布居数分别为–0.93, –0.93, –0.88, 磁矩分别为–0.04${\mu}_{\rm B}$ , –0.04${\mu}_{\rm B}$ , –0.16${\mu}_{\rm B}$ , Cu—O(4)的键长最短为1.908 ?, 电负性小, 磁矩贡献大; Z 轴上与Cu相连的O原子键长为2.033 ?, 无自旋极化现象; VZn 周围的O(5, 6)的布居数都为–0.52, 电负性降低, 磁矩增大, 都为1.04${\mu}_{\rm B}$ . 由上述可知, 包含VZn 的CuZn 体系磁性主要由Cu的3d电子与XY 平面内的O(2, 3, 4)原子的2p电子相互作用以及O(5, 6)原子贡献的, 总磁矩为1.00${\mu}_{\rm B}$ . 分析发现, CuZn -VO 和CuZn -VZn 的磁矩都和Z 轴上与Cu相连的O无关, 这是因为空位出现使Cu与Z 轴上O的相互作用减小, 键长拉大, 自旋极化消失, 对磁性无贡献.Zn 中存在Oi 时, 分别给出了晶体结构、能带以及分波态密度如图3(d) , 图4(d) 和图5(d) 所示. 图4(d) 与图4(a) 比较, 能带图整体下移, 导带比价带下移更多, 禁带宽度变为1.885 eV; 距离价带顶0.195 eV有一未占据的受主缺陷态, 与文献[5 ]在价带顶测到的受主能级0.15 eV相近. 此缺陷态主要是Cu的3d轨道和与Cu相连的Z 轴上O(5)的2p轨道相互耦合产生的, 且产生磁矩分别为0.78${\mu}_{\rm B}$ 和0.12${\mu}_{\rm B}$ , 布居数分别为0.63和–0.90, Cu—O(5)键的键长为1.906 ?, 与Cu相连的O(2, 3, 4)号原子布居数几乎没有变化, 由图5(d) 看出, 对磁矩贡献较小. 图5(d) 表明, Oi 主要影响价带顶, Oi 的2p电子也主要定域在价带顶, 间隙O原子产生的能态位于费米能级以下, 说明其为受主态. 如表2 所示, 空穴浓度增为1.574, 增强了导电性. 与Oi 相连的7号O, 2p电子也被定域在价带顶, 表明6, 7号O之间存在强相互作用, 两者周围的Zn原子正电性稍有下降, 值约为0.03左右. O(6)与O(7)之间键长为1.442 ?, 与O2 的键长1.209 ?相近, 表明负电性的Oi 原子有逃逸的可能, 文献[36 ,37 ]在研究TiO2 时也存在负电性的Oi 缺陷有逃逸现象; CuZn 中存在Oi 时, 价带主要由O的2p电子以及Cu的3d电子的贡献, 而导带主要由Zn的4s电子贡献, 还掺杂了一定的Zn的4p成分; 且在费米能级以下的深能级处产生四个新生的杂质态, 两个自旋向上, 两个自旋向下, 是由O(6, 7)号原子2s电子产生的. 由布居数可知, O(7)的电负性下降, 布居数由–0.94变为–0.62, O(6)的布居数为–0.48, O(6)与O(7) 原子 分波态密度(PDOS)图对称, 无自旋极化现象, 对磁性没有贡献. 体系总磁矩为0.99${\mu}_{\rm B}$ . CuZn -VZn 与CuZn -Oi 都在深能级处产生新的能态, 这是因为局部氧浓度过高, O-O之间存在强相互作用.10—13 ]报道的结果一致, 而文献[14—16 ]报道“Cu本身无自旋极化, 不产生磁性”的结论不同; 文献[15 ]报道磁性与缺陷有关; 文献[16 ]报道其磁性与VO 缺陷密切相关. 本文研究结果表明, 对于CuZn 和CuZn -Oi 体系, 磁性来源主要是Cu的3d和与Cu相连的Z 轴上的O的2p电子的自旋极化所致; CuZn -VO 和CuZn -VZn 体系, 自旋不对称主要是Cu的3d和与Cu相连的XY 平面内的O的2p电子耦合所致, 对于CuZn -VZn 体系, 磁性还包含Zn空位周围O 2p电子的自旋极化.3.3.光学性质 -->3.3.光学性质 为了研究CuZn 体系的光学性质, 可以通过介电函数的虚部来描述. 介电函数的虚部可以描述为e 为电子的电量, Ω 为为晶胞的体积, u ω 是光的频率, φk c 和φk v 分别为导带和价带的电子波函数. 介电函数的虚部可以用来推断电子跃迁. 第一吸收峰的出现, 是由于费米能级附近的占据态与非占据态之间电子跃迁的结果. 图6 给出了研究体系的介电函数虚部与电子跃迁能量的关系, 可以看出纯ZnO的第一吸收峰出现在3.60 eV附近, 由图2 可知这主要是价带顶O的2p电子跃迁到导带底Zn的4s轨道而形成的; 而CuZn , CuZn -VZn 模型, 由图4(a) 和图4(c) , 图5(a) 和图5(c) 所示, 掺入的Cu受主杂质在禁带中引入杂质能级, 由Cu的3d电子组成, 图6 看出吸收峰分别出现在1.15 eV和1.55 eV, 主要是电子由Cu原子周围O的2p向Cu的3d受主杂质态跃迁的结果; 同样CuZn -VO 中, 图6 的吸收峰出现在0.33 eV的位置, 结合图4(b) 和图5(b) 可以看出, 主要是由Cu的3d与Cu原子周围XY 平面内O(2, 3)原子2p杂化产生受主杂质态, 价带顶产生了Zn的4s4p电子组成的缺陷态, 吸收峰主要是电子从价带顶跃迁到受主杂质态的结果; 如图6 所示, CuZn -Oi 的吸收峰出现在0.38 eV处, 由图4(d) 和图5(d) 可以看出, CuZn -Oi 模型在价带顶也产生新生的缺陷态, 主要由O(6, 7)的2p电子组成, 吸收峰主要由新生的缺陷态O的2p到Cu的3d受主态跃迁产生的. 这与能带图中给出的带隙值基本吻合. 在CuZn 及含缺陷的模型中, 与ZnO相比, 吸收边发生红移现象[4 ,6 ,7 ,9 ,11 ,38 ] , 这是光学带隙变窄结果导致的, 这与图4 和图5 所给结果一致.图 6 ZnO, CuZn 及含不同内在缺陷时(CuZn -VO , CuZn -VZn , CuZn- Oi )介电函数的虚部Figure6. The imaginary part of the dielectric function of ZnO, CuZn , CuZn -VO , CuZn -VZn , CuZn- Oi 图7 给出了存在内在缺陷CuZn 时的光吸收谱. 可以看到, 与ZnO相比, 固有吸收边发生红移现象, 光学带隙减小, 这与实验和理论计算[4 ,6 ,7 ,9 ,11 ,38 ] 得到的Cu掺杂使得ZnO纳米棒吸收边向长波方向移动的结果是一致的. 与图4(a) —(d) 能带结构图、图6 及表2 给出的结果一致. 在可见光区, CuZn 以及存在内在缺陷CuZn 的吸收强度比ZnO的都高, 表明铜掺杂能够提高ZnO在可见光区的吸收. CuZn -VO 模型的吸收强度最高, 是因为氧空位的出现在价带顶产生了新生的Zn的4s4p态, 导致吸收增强, 这与图6 给出的结果也是一致的.图 7 有内在缺陷CuZn 的吸收光谱Figure7. Absorption of CuZn with varying intrinsic defects图8 给出了反射随波长的变化关系. 可以看到300—800 nm的范围内, 除了CuZn -Vzn 模型的反射增加之外, 其他掺铜的模型反射都比ZnO的低; 在适当外界条件下, CuZn 模型的透光率比ZnO的低, 可能存在VZn . 实验透射率降低[39 ] 也可能是存在锌空位导致的.图 8 有内在缺陷CuZn 的反射光谱Figure8. Reflectivity of CuZn with varying intrinsic defects4.结 论 本文研究了CuZn 以及CuZn 与内在缺陷共存对形成能、电子结构以及光学性质的影响. 研究表明: 1)对纯ZnO而言, O-rich条件下Oi 的形成能最低, 最容易形成, 且稳定性较高; O-poor条件下VO 的形成能最低, 最易形成; CuZn 在O-rich条件下形成能为负值, 说明容易形成且稳定; O-rich条件下CuZn -Oi 最易形成, 而在O-poor条件下, CuZn -VO , CuZn -VZn , CuZn -Oi 内在缺陷都不易形成; Cu替位杂质的出现, 提高了在O-rich条件下内在缺陷的形成, 但在O-poor条件下反而降低了内在缺陷的形成; 2) Cu掺杂ZnO及其缺陷模型中, Cu掺杂都为替位受主, 都产生p型导电类型; CuZn 中存在VO 时, 导电性降低; CuZn 中存在VZn 影响深能级对导电性没有影响, Oi 的存在提高了材料的导电性; 3)纯ZnO无自旋极化, 无铁磁性; Cu掺杂的ZnO, 与Cu原子相连的O原子的电负性与磁矩相关, 电负性越小, 键长越短, 贡献的磁矩越大; CuZn 中存在空位缺陷(VO , VZn )时, 磁矩主要是Cu 3d轨道与XY 面内的O的2p轨道强烈耦合所致, VZn 导致CuZn 中的磁性还包含O(5, 6)号原子2p电子自旋极化的贡献; CuZn 与CuZn -Oi 中的磁矩主要是Cu的3d与Z 轴上与铜相连的O 2p轨道耦合产生的; 所有体系中Zn原子没有自旋极化, 不产生磁性; CuZn -VZn 和CuZn -Oi 缺陷能态中, 深能级中产生的诱导态是O-O 2s轨道相互作用产生的; 4)掺Cu的ZnO吸收边发生红移; CuZn -VO 模型中可见光区吸收增强; CuZn -VZn 模型中吸收、反射都增强, 导致透光率降低.  图 1 2 × 2 × 2的ZnO的超胞 (红色代替O原子, 蓝紫色代替的是Zn原子)
图 1 2 × 2 × 2的ZnO的超胞 (红色代替O原子, 蓝紫色代替的是Zn原子)















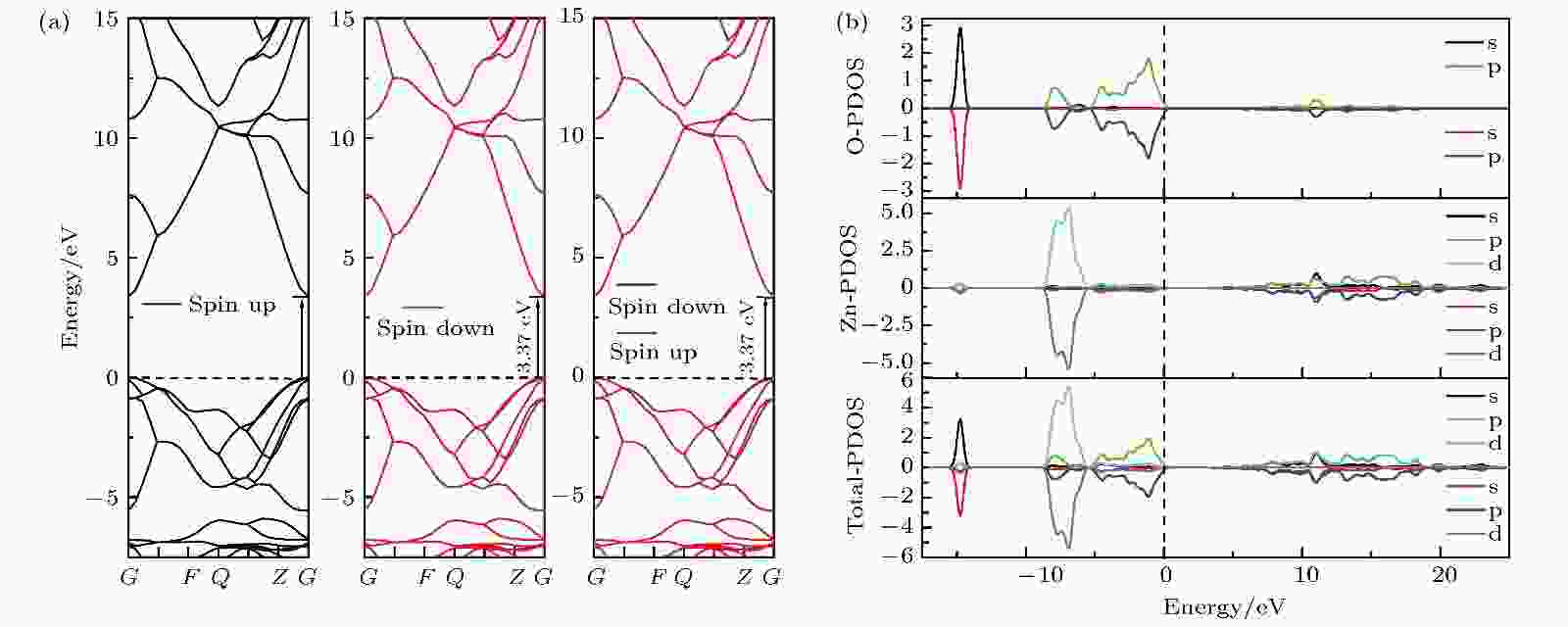 图 2 (a) ZnO能带结构图; (b) ZnO分波态密度图
图 2 (a) ZnO能带结构图; (b) ZnO分波态密度图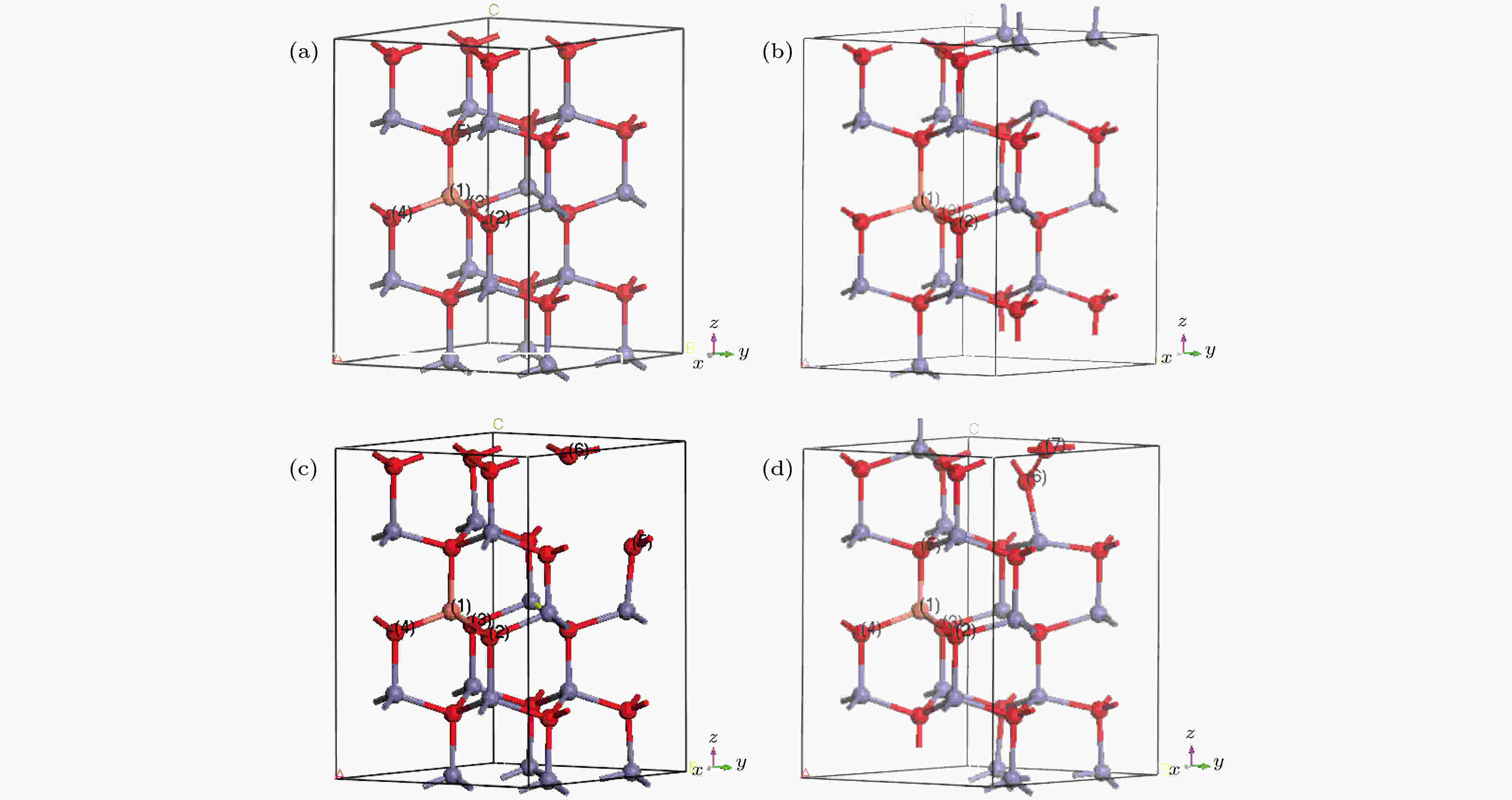 图 3 优化后的晶体结构图 (a) CuZn; (b) CuZn-VO; (c) CuZn-VZn; (d) CuZn-Oi
图 3 优化后的晶体结构图 (a) CuZn; (b) CuZn-VO; (c) CuZn-VZn; (d) CuZn-Oi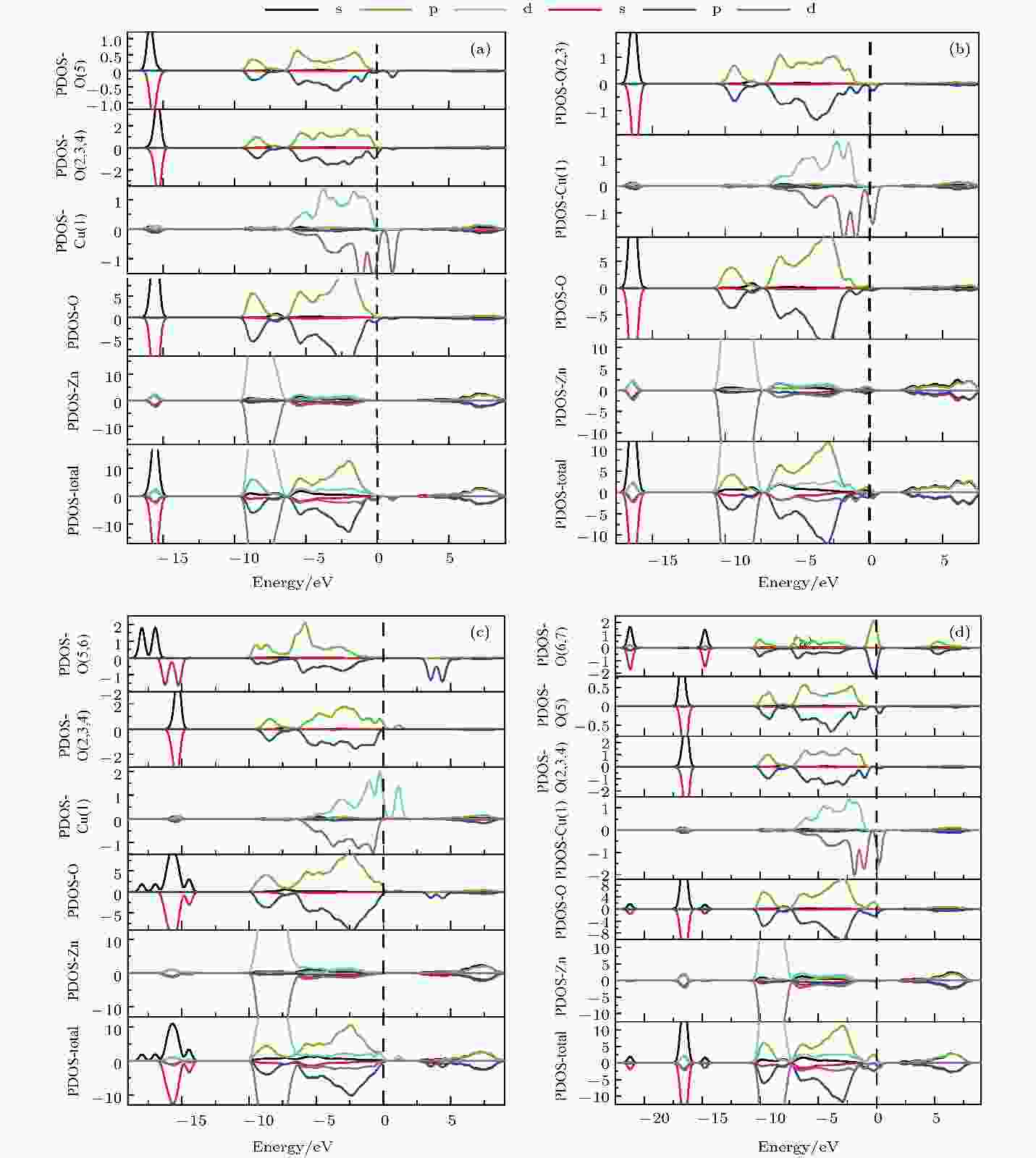 图 5 分波态密度(图中虚线为费米能级) (a) CuZn; (b) CuZn-VO; (c) CuZn-VZn; (d) CuZn-Oi
图 5 分波态密度(图中虚线为费米能级) (a) CuZn; (b) CuZn-VO; (c) CuZn-VZn; (d) CuZn-Oi
























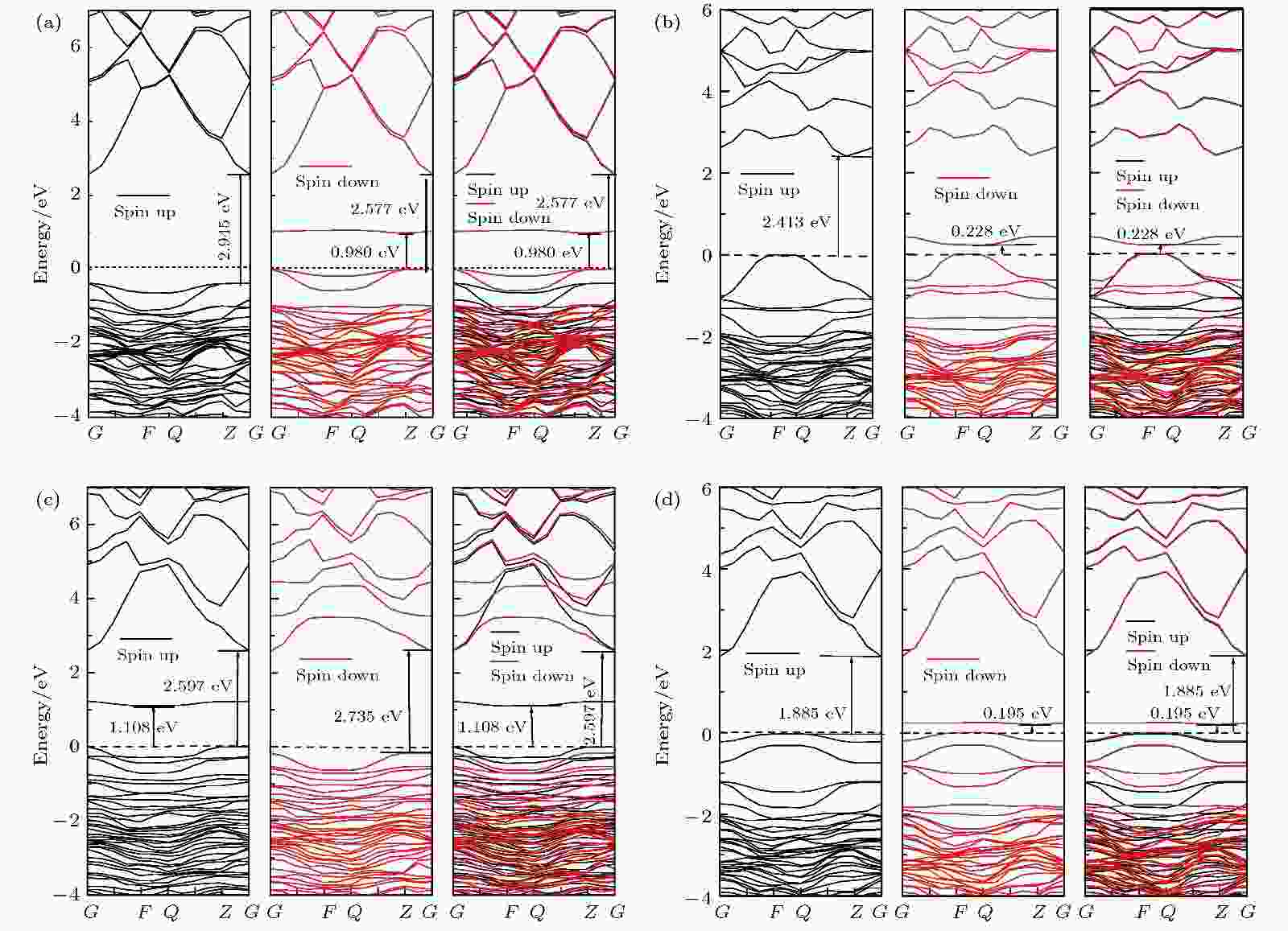 图 4 能带结构图(图中虚线为费米能级) (a) CuZn; (b) CuZn-VO; (c) CuZn-VZn; (d) CuZn-Oi
图 4 能带结构图(图中虚线为费米能级) (a) CuZn; (b) CuZn-VO; (c) CuZn-VZn; (d) CuZn-Oi

















































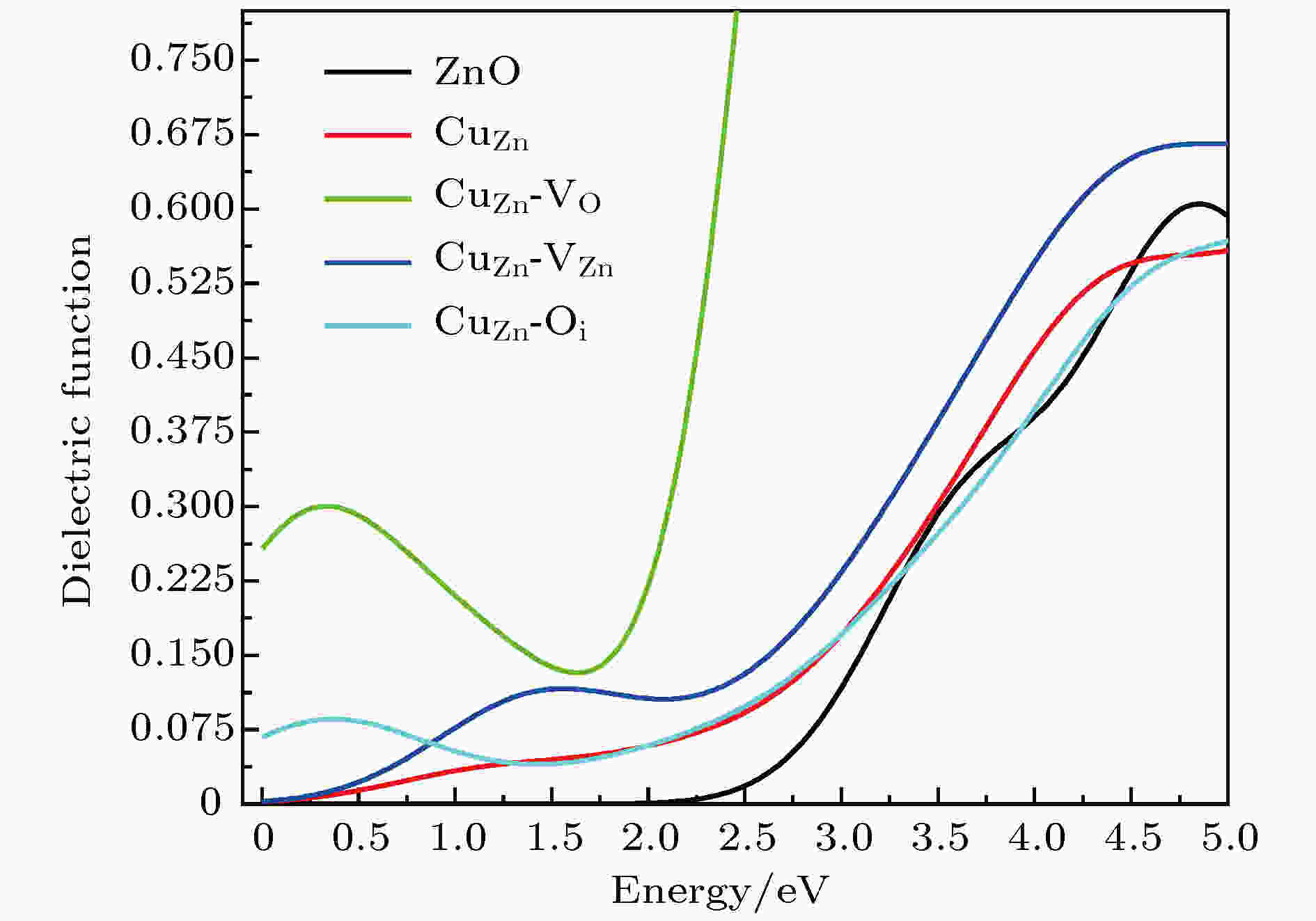 图 6 ZnO, CuZn及含不同内在缺陷时(CuZn-VO, CuZn-VZn, CuZn-Oi)介电函数的虚部
图 6 ZnO, CuZn及含不同内在缺陷时(CuZn-VO, CuZn-VZn, CuZn-Oi)介电函数的虚部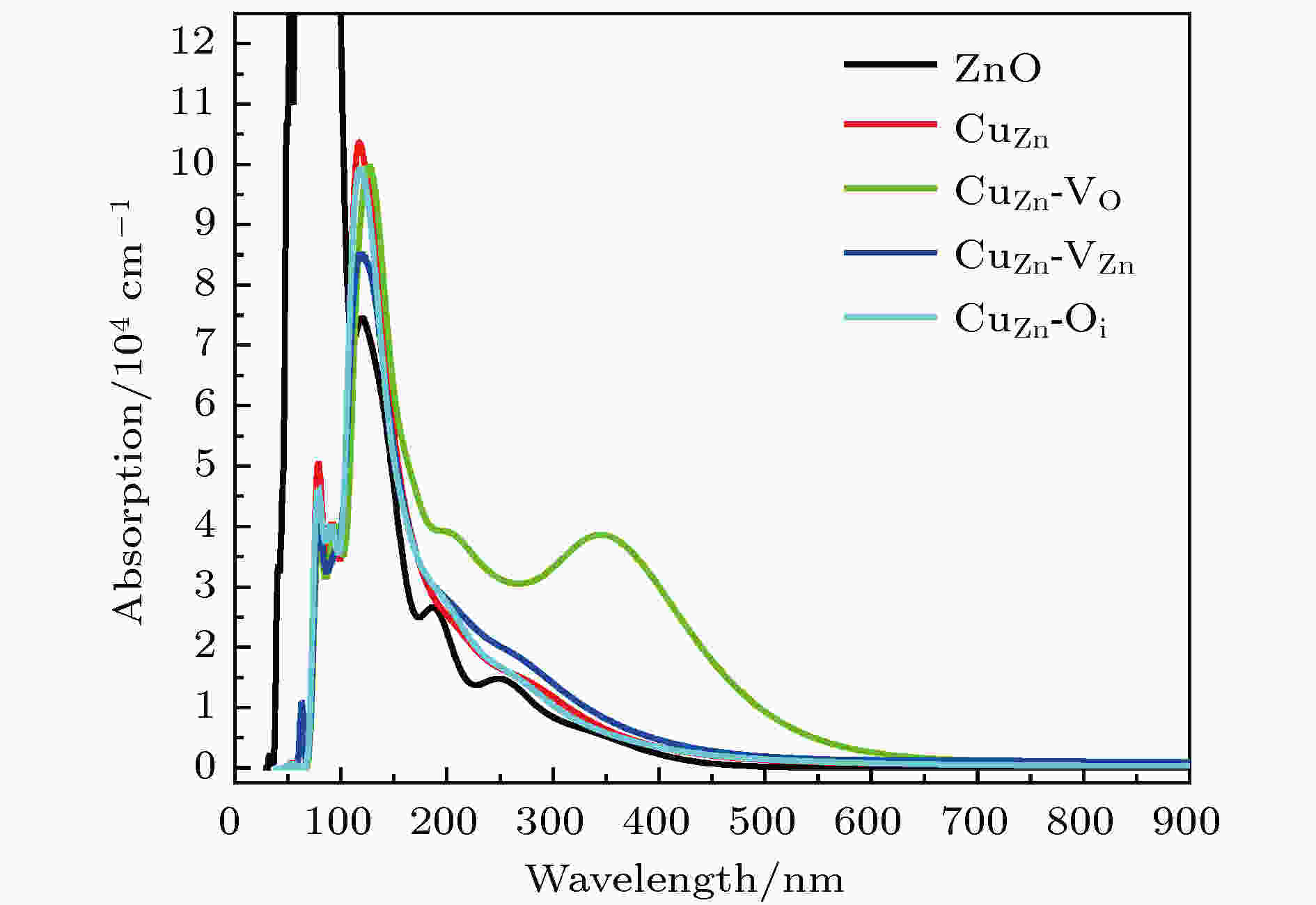 图 7 有内在缺陷CuZn的吸收光谱
图 7 有内在缺陷CuZn的吸收光谱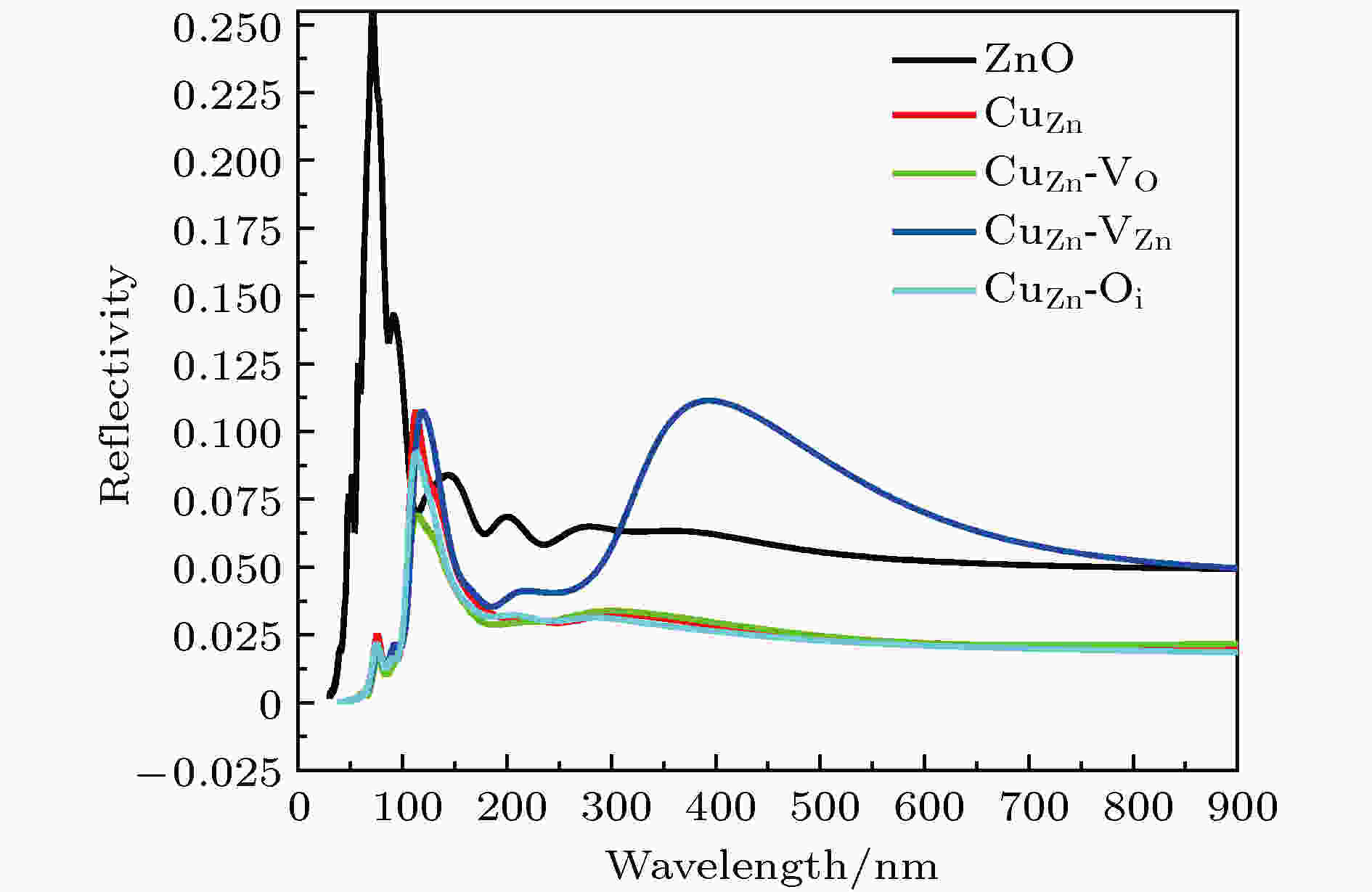 图 8 有内在缺陷CuZn的反射光谱
图 8 有内在缺陷CuZn的反射光谱