摘要:地球磁层空间的相对论电子通过内部充放电效应, 能够导致在轨航天器彻底失效. 由于对这种空间粒子的特性和物理机制仍不清楚, 磁层空间相对论电子一直是空间环境探测和空间科学研究的重要对象. 开展相关磁层空间环境特性的研究和粒子辐射环境建模等, 需要同时使用来自不同卫星、不同探测器的观测数据. 消除不同探测器之间的系统偏差, 实现不同来源数据的融合, 是开展相关研究的必要前提. 本文对我国最新的地球同步轨道卫星—风云四号A星(FY-4A)和同类轨道的美国GOES-13卫星相对论电子(> 2 MeV)观测数据, 开展在轨交叉定标及数据融合研究. 本文严格筛选出地磁宁静期(Kp < 2)的观测数据, 以保证研究对象是被地磁场稳定捕获的辐射带粒子. 根据辐射带粒子的物理特性, 即3个绝热不变量的基础之上, 以Liouville定理为依据, 在漂移壳L_m坐标下比较两颗卫星观测到的电子通量, 得到两颗卫星相对论电子观测之间的系统偏差. 依据该结果, 进行数据融合处理, 结果表明系统偏差得以很好地消除. 通过本项研究工作, 得到了国际上重要的两个地球同步轨道相对论电子观测系统之间的偏差, 并根据该研究成果, 成功实现两个探测系统观测数据之间的融合, 为后续的理论和应用研究工作打下了坚实的基础, 也为地球同步轨道其他能道高能电子观测数据的在轨交叉定标和数据融合提供了参考方法.
关键词: 相对论电子/
地球同步轨道/
在轨交叉定标/
数据融合/
风云四号A星

English Abstract

全文HTML

--> --> -->

磁层高能粒子辐射环境是地球空间最重要的空间环境之一. 通过深层充放电、辐射损伤、单粒子事件等效应, 空间高能粒子能够导致航天器故障甚至失效. 特别是其中能量大于1 MeV的相对论电子(也称杀手电子), 可以穿透2 mm的等效铝屏蔽层, 入射到航天器的各种材料中, 产生充放电反应, 导致严重的后果^[1—3]. 例如, 1994年1月, 相对论电子增强引起的内部充放电事件导致加拿大通信卫星姿态失控; 1997年1月和1998年4月的两次相对电子增强引起的内部充放电事件先后导致美国通信卫星TELSTAR-401、德国科学卫星EQUATOR-S报废. 随着高度集成化器件在航天工业中的广泛使用, 空间相对论电子环境对航天器的影响日渐突出. 目前, 对磁层相对论电子动态变化的物理特性仍然不甚清楚. 因此, 对磁层相对论电子物理机制、动态特性和建模等研究是具有理论意义和工程价值的重要课题.
开展磁层电子的理论和建模等研究需要来自多个不同卫星的观测数据^[4—7], 这要求来自不同探测器的数据之间具有良好的一致性. 各卫星的高能粒子探测器在研制阶段都经过了严格的地面定标. 但一方面, 地面的环境模拟和仿真工作是很难完全复制真实空间中的粒子环境, 另一方面, 地面定标技术和设备也难统一, 使得源于各个探测仪器之间和设计差异造成的系统偏差不可避免. 因此, 为了满足磁层粒子领域的研究对观测数据融合的需求, 必须开展各卫星观测数据之间的交叉定标, 以消除不同探测器之间的系统偏差, 实现数据融合.
Friedel等^[8]以科学卫星CRRES, Polar的高能电子观测数据为“标准”, 对3个太阳活动周内的GEO卫星(地球同步轨道卫星) GPS卫星(中地球轨道卫星)的高能电子观测结果开展了交叉定标研究. Chen等^[5]用GOES系列中不同卫星的高能电子观测数据, 论述了用相空间密度实现不同卫星/不同探测器间粒子观测数据交叉标校的可行性.
GOES系列卫星是美国的地球同步轨道气象卫星. 自70年代开始, 该系列卫星一直持续搭载空间环境探测仪器, 观测空间高能粒子及太阳X射线, 其观测数据时间跨度长, 连续性和一致性良好, 被广泛应用于磁层空间环境的特性研究及粒子辐射环境建模^[9,10]. 因此, GOES空间环境数据被认为是较理想的地球同步轨道交叉定标参照数据. 王馨悦等^[11]曾用FY2D卫星与GOES卫星进行过空间粒子观测结果的对比分析, 于超等^[12]将风云二号C/D卫星与GOES卫星的太阳X射线探测数据进行过交叉比对.
风云四号A星(FY-4A)是我国新一代地球同步轨道气象卫星, 该卫星上安装有高能粒子探测器对卫星轨道的高能粒子环境进行观测. 本文是以GOES-13卫星观测通量为参照数据, 在L_m坐标下, 开展FY-4A和GOES-13相对论电子(> 2 MeV)观测数据交叉定标工作, 得到FY-4A卫星相对论电子观测数据的系统偏差, 并根据该研究成果, 进行两个探测系统观测数据之间的融合处理. 本研究成果将为FY-4A卫星相对论电子观测数据应用于后续的理论、预报、建模等研究打下坚实基础, 也可为地球同步轨道其他能道电子观测数据的在轨交叉定标提供参考方法.

2

-->

2.1.卫星和高能粒子探测器简介

FY-4A于2016年12月11日发射, 定点于高度为36000 km、经度为东经105°的地球同步轨道, 设计寿命7年. FY-4A上安装有中国科学院国家空间科学中心研制的最新一代地球同步轨道空间高能粒子探测系统. 该系统由性能指标完全相同的三台高能粒子探测器A机、B机和C机组成. A机安装在卫星朝天面, B机和C机分别安装在卫星正东面和正西面. 三台探测器对空间带电粒子环境实施24小时的动态监测, 是我国最重要的地球同步轨道带电粒子观测数据来源之一. 每台探测器包含4个望远镜系统, 分别是HET1, HET2, HET3和HPT1望远镜系统. 其中HET2可观测能量大于1.5 MeV的相对论电子积分通量, 其能量范围见表1.

卫星	探测器	电子能量
FY-4A	HET2	≥ 1.5 MeV
		≥ 2 MeV
		≥ 3 Mev
GOES-13	EPEAED	> 0.6 MeV
		> 2 MeV

表1FY-4A和GOES-13高能电子观测能谱
Table1.Energy spectrum of FY-4A and GOES-13 energetic electron detector.

GOES-13卫星是美国第四代地球同步轨道气象卫星(西经75°, 轨道高度36000 km), 发射于2006年5月24日. 该卫星上安装有两台EPEAED (energetic proton, electron, alpha detector)探测器, 分别指向正东和正西方向, 用于观测高能电子积分通量, 其能量范围见表1.
2 -->

2.2.数据

如表1所列, 能量大于2 MeV的电子通量是FY-4A和GOES-13共同的观测对象, 本研究工作对该能量范围的观测数据进行交叉定标和融合研究. 由于FY-4A卫星A机探测器指向是朝天方向, GOES-13卫星没有与之接近的探测方向, 所以A机数据不做比较. FY-4A卫星B机和C机探测方向分别与GOES-13卫星正东和正西方向的EPEAED探测器指向相同, 因此, 本项工作对两颗卫星东、西方向的观测数据进行研究.
所用FY-4A卫星高能电子积分通量观测数据来自国家空间天气监测预警中心. GOES-13卫星高能电子积分通量的数据源自NOAA的国家地球物理数据中心(NGDC) (下载网址: https://satdat.ngdc.noaa.gov/sem/). NGDC公布的GOES-13高能电子通量数据为5 min平均数据, 时间截止于2017年底. 故本研究选用了2017年1月1日至2017年12月16日内所有的观测数据, 并将FY-4A原始观测数据进行5 min平均, 得到与GOES-13时间分辨率相同的可比较数据. 地磁指数(Dst, Kp)、太阳风参数(速度v、压力P_dyn)、行星际磁场参数(行星际磁场y分量、z分量)等数据来自NASA的OMNI数据库(下载网址: https://cdaweb.sci.gsfc.nasa.gov/index.html/).
本文的一个必要条件是观测的粒子是被地磁场稳定捕获的辐射带粒子. 在磁层环境较为宁静时, 地球同步轨道上观测到的相对论电子是被地磁场捕获的外辐射带粒子^[13]. 为保证研究的必要条件成立, 根据采样时的地磁场活动状态, 对观测数据进行严格筛选, 要求Kp < 2, 即地磁场活动处于非常宁静的状态.
图1列举了2017年3月3日至8日, 两颗卫星相对论电子积分通量5 min平均值随时间的变化, 图中的角标east和west分别代表指向为正东和正西方向的探测器探测到的电子积分通量. 由图1可见:
图 1 2017年3月3日至9日FY-4A和GOES-13卫星高能(> 2 MeV)电子积分通量
Figure1. Fluxes of relativistic electron (> 2 MeV) from FY-4A and GOES-13 during March 3–9, 2017.

1)两颗卫星观测到的相对论电子通量均呈现明显的日变化, 即以24 h为周期, 规律地达到峰值和谷值;
2)两颗卫星观测到的电子通量相位变化完全相反, 这是由于FY-4A定点于东经105°, GOES-13定点于西经75°, 二者所处地方时正好相差12 h, 表明两颗卫星观测到的相对论电子通量的地方时变化趋势完全一致;
3) GOES-13观测到的电子通量值整体高于FY-4A, 表明两个探测系统之间存在系统偏差, 为实现两个系统之间的数据融合, 需要通过在轨数据交叉定标, 得到两个探测系统间的偏差.

2

-->

3.1.基础理论阐述

地球辐射带粒子有三种基本运动: 环绕磁力线的回旋运动、沿着磁力线的弹跳运动和垂直磁力线的漂移运动. 与这三种运动相对应, 有3个绝热不变量: 磁矩不变量μ, 其定义见(1)式; 纵向积分不变量J, 其定义见(2)式; 磁通不变量Φ, 其定义见(3)式.

$\mu = \dfrac{E_{k\bot}}{B},$

$J = \int_{{s_{\rm{M}}}}^{s_{\rm{M}}^1} m {v_{//}}{\rm{d}}s,$

$\varPhi = \int_s{{{B}} \cdot {\rm{d}}{{S}}},$

其中: (1)式中E_k⊥代表的是粒子在垂直磁场运动的动能, B为磁场强度; (2)式中s_M¹和s_M代表两个磁镜点, m为运动粒子的质量, v_//是粒子平行于磁场方向的运动速度, ds为线元; (3)式中B为地磁场强度, dS为面积元. 这3个不变量组成了可以唯一描述粒子的相空间坐标. 根据Liouville定理, 被稳定捕获的辐射带粒子在相同的相空间坐标下, 其相空间密度不变^[14].
如前文所述, 本项研究对相对论电子观测数据的严格筛选, 保证了被观测粒子是被地磁场稳定捕获的外辐射带粒子, 在相同的相空间坐标下, 观测到的相对论电子相空间密度不变. 由定义可知, 在相同的磁场条件下, 粒子能量相同则μ相同, 粒子方向相同(投掷角相同)则J相同. 对于方向相同的捕获粒子, 磁通不变量Φ相同, 可近似为漂移壳L_m相同^[15]. 对本文研究的FY-4A和GOES-13相对论电子(> 2 MeV)而言, 其能量、方向和轨道都相同, 故而所处磁场条件相同. 因此, Liouville定理可简化为漂移壳L_m相同则通量相同, 在相同漂移壳坐标L_m下比较两颗卫星观测到的电子通量, 即可得到两颗卫星探测器之间的系统偏差.
2 -->

3.2.L_m值计算

McCollough等^[16]的研究表明, 在地球磁场宁静期, 地磁场模型Tsyganenko2001(T02)的计算结果最为准确. 本文用IRBEM-4.4.0软件(该软件是由SOURCEFORGE网站提供,下载网址https://sourceforge.net/projects/irbem/)所包含的T02磁场模型进行磁场及L_m计算. T02模型的输入参数为: 地磁活动指数Dst、太阳风动压P_dyn, 行星际磁场y分量的绝对值|B_y|, 行星际磁场z分量的绝对值|B_z|, 以及根据行星际相关数据合成的输入参数G₁和G₂^[16], 两个合成参数定义如下:

${G_1} = \left\langle {\nu \frac{{{{\left( {{B_ \bot }/40} \right)}^2}}}{{\left( {1 + {{{B_ \bot }}}/{{40}}} \right)}}{\rm{si}}{{\rm{n}}^3}\left( {\frac{\theta }{2}} \right)} \right\rangle ,$

${G_2} = 0.005\left\langle {\nu {B_s}} \right\rangle ,$

其中符号〈·〉代表的是一个小时内的平均值;

${B_ \bot } = \sqrt {B_y^2 + B_Z^2} ,{\rm{}}$

${B_s} = \left\{\begin{aligned}&{0,\;\;{B_z} \geqslant 0,}\\&{ - {B_z},\;\;\;\;{B_z} \leqslant 0,}\end{aligned}\right.$

$\theta = \left\{ {\begin{aligned}& {{\rm{arctan}}\frac{{\left| {{B_y}} \right|}}{{{B_z}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{B_z} \geqslant 0,}\\& {180.0^\circ - {\rm{arctan}}\frac{{\left| {{B_y}} \right|}}{{{B_z}}},\;\;\;\;\;\;\;\;{B_z} \leqslant 0,}\end{aligned}} \right.$

式中ν是太阳风速度, B_y和B_z分别是行星际磁场的y分量和z分量.
根据观测数据的时间和对应的模型输入参数, 用T02模型分别计算得到FY-4A和GOES-13相对论电子观测数据对应的漂移壳参数L_m. 图2列举了两个时间段内(世界时), 分别与FY-4A卫星和GOES-13卫星相对论电子观测数据对应的L_m值计算结果. 图2显示两颗卫星的L_m值随世界时变化相位相反, 这是因为两颗卫星地方时正好相差12 h; 两颗卫星的L_m值范围大致相当, 表明两颗卫星的粒子观测数据可以在L_m坐标下开展, 是具有统计意义的交叉比较.
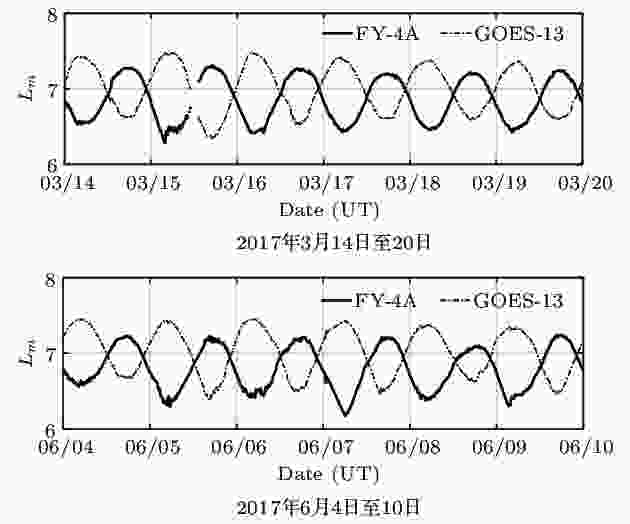图 2 FY-4A和GOES-13相对论电子观测数据对应的L_m值计算结果
Figure2. L_m values calculated by T02 for FY-4A and GOES-13 relativistic electron observations.

2 -->

3.3.在L_m坐标下相对论电子积分通量交叉定标

在地球同步轨道高度, 辐射带稳定捕获的粒子存活时间为2—3 d^[17]. 为保证参与比校的相对论电子是在同一寿命周期内被稳定捕获的粒子, 本文以2 d为时间步长, 将筛选出的通量数据划分成基本比较单元. 接下来以0.01的步长值对L_m进行网格划分, 在某个基本比较单元内, 两颗卫星相对论电子通量数据各自的L_m值落在同一网格内, 则这些通量数据即为该比较单元内、该L_m网格上的比较样本. 分别将两颗卫星在每个L_m网格中的比较样本各自做平均处理, 就可以得到每个比较单元内、每个L_m网格上, 两颗卫星“一一对应”的相对论电子通量数据(flux_-FY-4A, flux_-GOES-13). 具体算法如下:

$n = ({{{L_{m\left( {{\rm{max}}} \right)}} - {L_{m\left( {{\rm{min}}} \right)}}}})/{{0.01}},$

${L_{m\left( 0 \right)}} = {L_{m\left( {{\rm{min}}} \right)}}, ~~ {L_{m\left( n \right)}} = {L_{m\left( {{\rm{max}}} \right)}},$

${L_{m\left( i \right)}} \in \left( {{L_{m\left( {{\rm{min}}} \right)}},{L_{m\left( {{\rm{max}}} \right)}}} \right)\;i = 1,2,3, \cdots ,n$

若落在区间(L_m(i–1), L_m(i))的某卫星的L_m值有${L_{m\left( i \right)}}\_1,{L_{m\left( i \right)}}\_2,{L_{m\left( i \right)}}\_3, \cdots {L_{m\left( i \right)}}\_n\left( {n = {{num}}} \right),$ 则该区间对应的电子积分通量均值为

$\begin{split}Flux =& \frac1{{num}} \big(flu{x_{{L_{m\left( i \right)}}\_1}} + flu{x_{{L_{m\left( i \right)}}\_2}} \\ & + flu{x_{{L_{m\left( i \right)}}\_3}} \!+\! \cdots \!+\! flu{x_{{L_{m\left( i \right)}}\_num}}\big).\end{split}$

进行这样的计算, 就可以得出2017年1月1日至2017年12月16日内所有的FY-4A和GOES-13卫星电子积分通量数据集合.
以处理得到的FY-4A电子积分通量数值为横坐标轴, GOES-13电子积分通量数值为纵坐标轴, 绘制log坐标下的散点图. 图3和图4分别是探测器指向正东和正西的结果. 图中散点表征了在相同的存活周期内, FY-4A和GOES-13卫星观测到的相对论电子(> 2 MeV)积分通量的对应关系. 用最小二乘法对这些散点做线性拟合, 得到如图3和图4红线所示的线性关系. 图中C为拟合直线的斜率, 正东方向和正西方向C值分别为2.63和2.68; P为拟合直线的截距, 正东方向和正西方向P值分别为26.18和–50.31; C和P定量地描述了FY-4A和GOES-13之间对能量大于2 MeV电子观测的系统偏差.
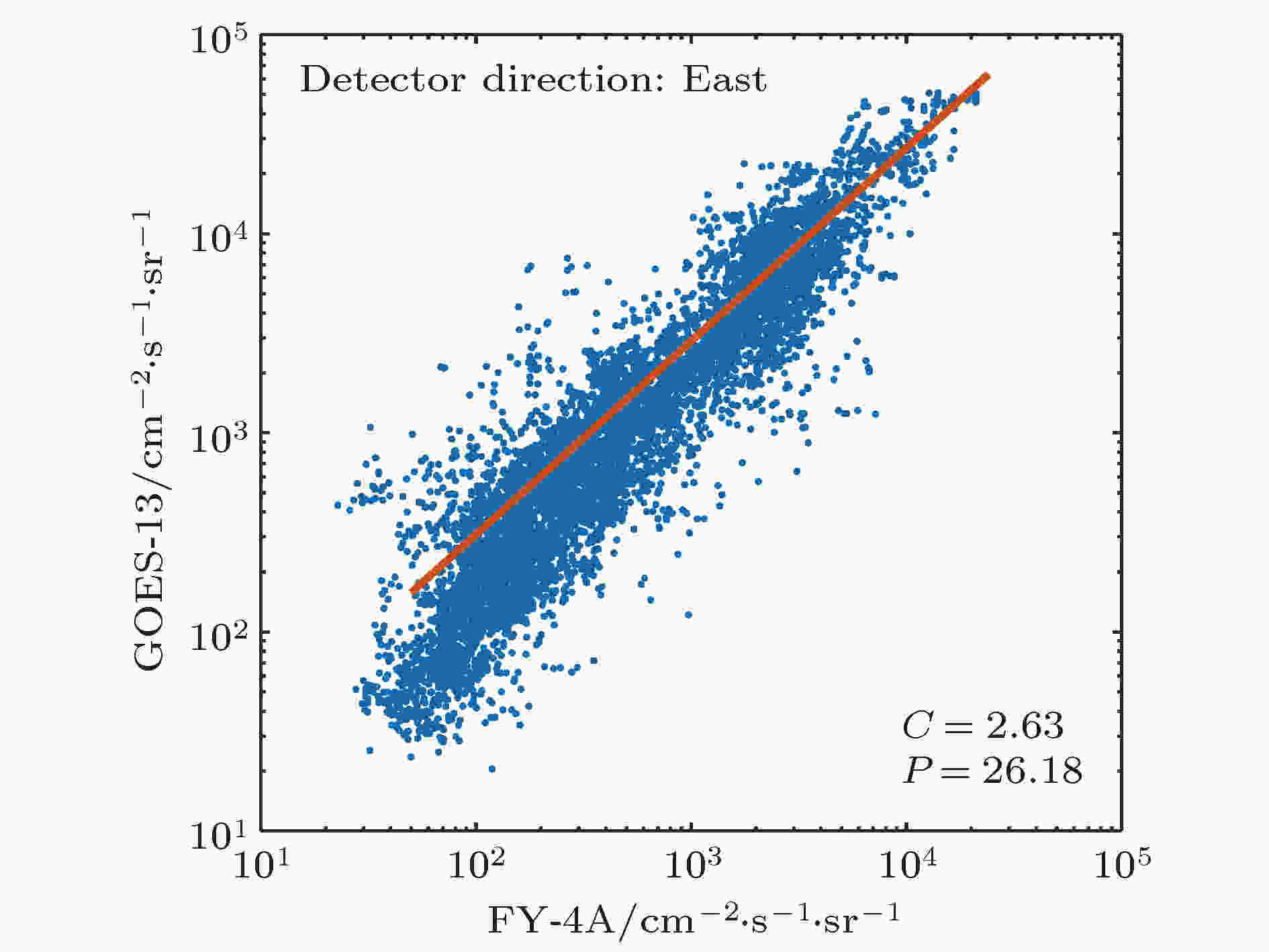图 3 正东方向FY-4A和GOES-13“一一对应”的相对论电子通量及拟合得到的系统偏差
Figure3. Corresponding relationship between relativistic electron fluxes from FY-4A and GOES-13 detectors facing east and the system deviation between them.

图 4 正西方向FY-4A和GOES-13“一一对应”的相对论电子通量及拟合得到的系统偏差
Figure4. Corresponding relationship between relativistic electron fluxes from FY-4A and GOES-13 detectors facing west and the system deviation between them.

2 -->

3.4.数据融合处理

根据交叉定标得到的结果, 即可进行消除FY-4A和GOES-13相对论电子观测系统偏差的数据融合处理, 处理方法见(11)式: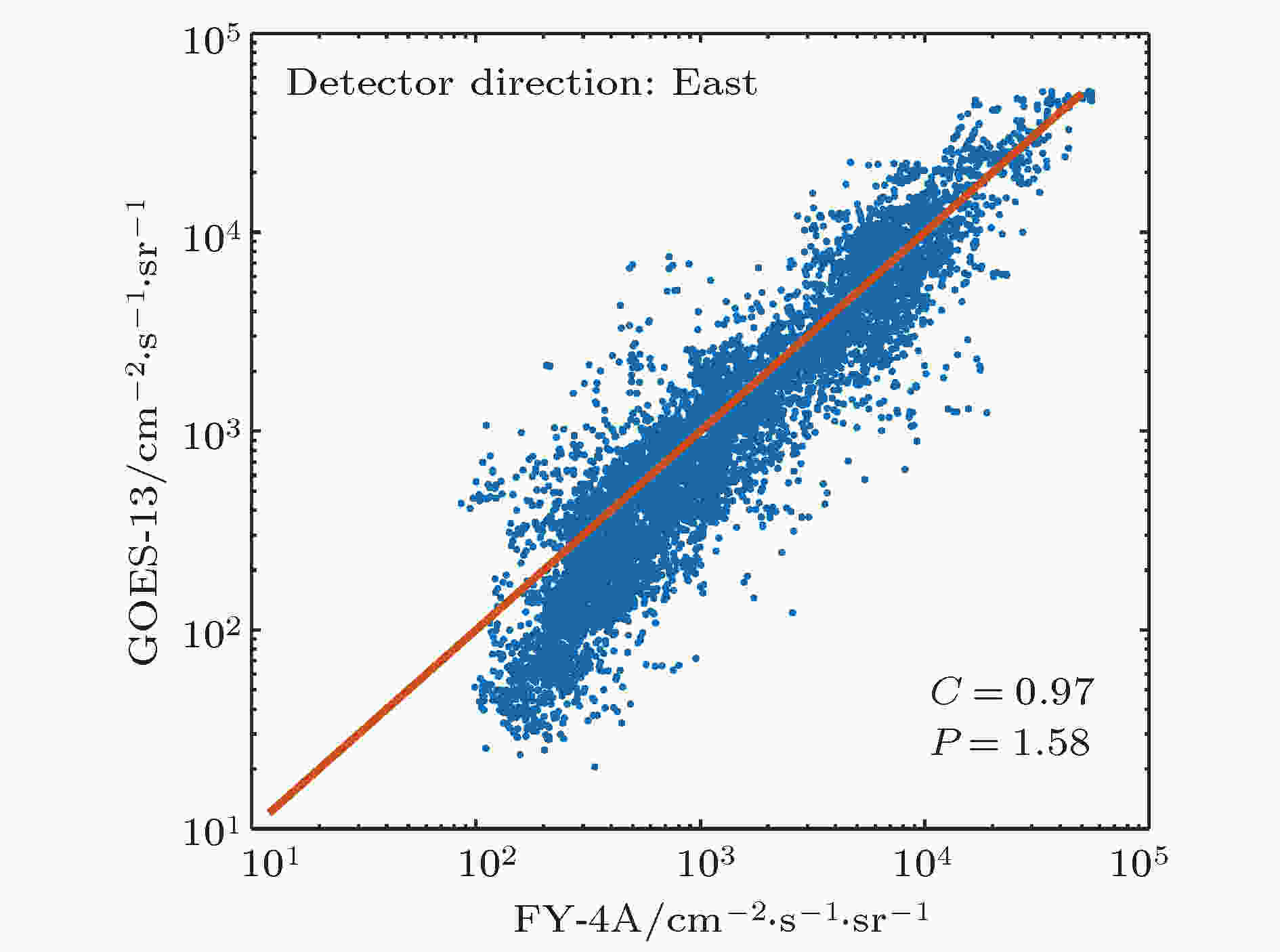

${flux'_{\_{\rm{FY}} - 4{\rm{A}}}} = flu{x_{\_{\rm{FY}} - 4{\rm{A}}}} \times C + P.$

将FY-4A观测的2017年1月1日至2017年12月16日内所有的电子通量flux_{_FY-4A}利用得到的系统偏差参数C和P处理得到flux'_{_FY-4A}之后, 和GOES13 观测数据匹配绘制散点图. 图5和图6所示分别为对图3和图4中数据做融合处理后的结果. 正东方向拟合直线斜率为0.97, 截距为1.58. 正西方向拟合直线斜率为0.98, 截距为–0.21. 表明两种探测之间的系统偏差得到很好的消除, 实现了数据融合.
图 5 正东方向FY-4A和GOES-13相对论电子通量数据拟合
Figure5. Relativistic electron flux fitting of FY-4A and GOES-13 detectors facing east.

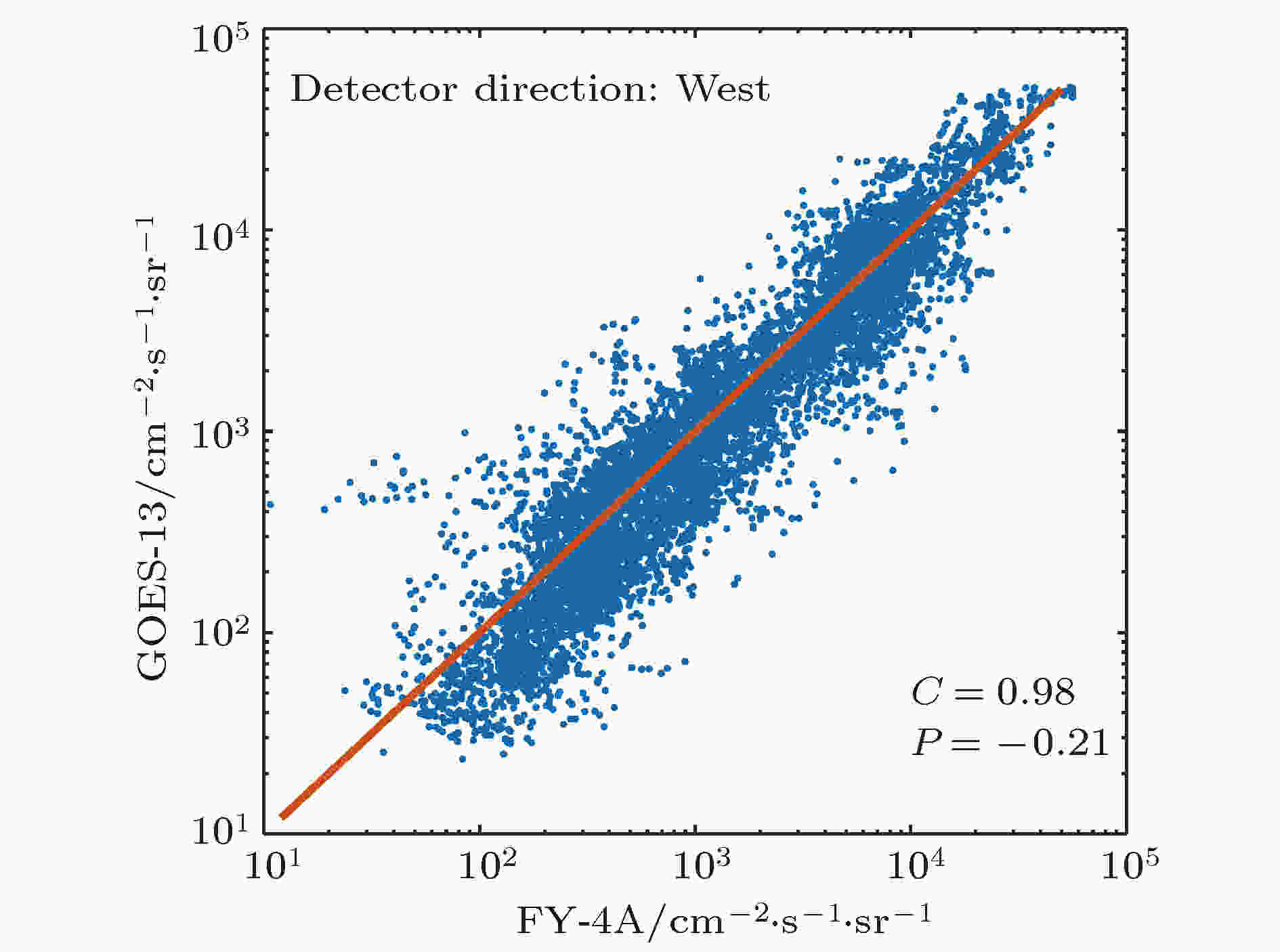图 6 正东方向FY-4A和GOES-13相对论电子通量拟合
Figure6. Relativistic electron flux fitting of FY-4A and GOES-13 detectors facing west.

交叉定标得到的系统偏差是两个探测系统之间存在的固有偏差, 该误差是源于两套探测系统器件和设计差异所造成的, 与观测对象的通量高低、是否辐射带稳定捕获粒子等特性无关, 该结果是可以应用于任何地磁场活动之下的两个系统之间观测结果的数据融合处理. 当两个探测系统在轨持续工作若干年后, 会出现由于传感器效率衰减而产生误差, 针对这种由仪器的衰减造成误差的影响, 需要重新进行仪器性能衰减评估和误差结果修正分析.

FY-4A是我国最新一代地球同步轨道气象卫星, 设计寿命7年. 该卫星上安装有我国最新的高能粒子探测器, 可持续开展高能粒子通量的就位观测, 是我国地球同步轨道最重要的高能粒子观测数据来源之一. GOES-13卫星是美国第四代地球同步轨道气象卫星, 同样开展高能粒子通量观测. 由于GOES系列卫星观测数据时间跨度长, 连续性和一致性良好, 被认为是较理想的地球同步轨道交叉定标参照数据.
为满足相关物理机制和建模研究对观测数据一致性的需求, 本文对FY-4A和GOES-13相对论电子(> 2 MeV)观测数据开展在轨交叉定标及数据融合研究. 本工作严格筛选出地磁宁静期(Kp < 2)的观测数据, 以保证研究对象是被地磁场稳定捕获的辐射带粒子. 根据辐射带粒子的物理特性, 以Liouville定理为依据, 在漂移壳L_m坐标下统计比较两颗卫星观测到的电子通量, 得到两颗卫星相对论电子观测之间的系统偏差. 依据该结果, 进行数据融合处理, 结果表明系统偏差得以很好地消除.
通过本项研究工作, 得到了国际上重要的两个地球同步轨道相对论电子观测系统之间的偏差, 并根据该研究成果, 成功实现了两个探测系统观测数据之间的融合, 为后续的理论和应用研究工作打下了坚实的基础, 也为地球同步轨道其他能道高能电子观测数据的在轨交叉定标和数据融合提供了参考方法.
感谢美国NOAA国家地球物理数据中心(National Geophysical Data Center)提供GOES-13相对论电子观测数据; 感谢NASA CDAWeb提供OMNI数据; 感谢兰州重离子加速器国家实验室(HIRFL)提供探测器地面定标条件; 感谢国家空间科学中心空间电子模拟测试定标设施(NSSC-SEF)提供探测器地面定标条件.