全文HTML
--> --> -->为了克服上述AMR存在的技术问题和难点, 引入特殊固态传热机制、创新系统模型设计和参数与结构优化成为近年来研究的热点. 2010年, Kitanovski和Egolf[19]首次提出了基于热二极管的全固态MR模型的概念, MCM和热源及散热器之间的传热由位于MCM两侧的热二极管控制, 该方案可得到较高传热速率和工作频率. 随后, 人们对该概念做了进一步拓展, 建立了一系列新的模型, 即: 基于热二极管(thermal diode, 包括电控热二极管和磁控热二极管)的全固态MR模型[21—23,25—35]和基于高热导率材料(high thermal conductivity material, HTCM)元件的全固态MR模型[24,31,36,37]. 本文第2部分综述了全固态MR系统的两类物理模型及其研究现状; 第3部分总结和比较了全固态MR模型与传统AMR模型的性能, 并简要概述和分析了几类MCM及几种固态换热介质; 第4部分对未来全固态MR技术的研究进行了分析和展望.
图 1 (a) Peltier元件作为热二极管的工作机制; (b) kH元件作为热二极管的工作机制; (c) HTCM元件工作机制Figure1. (a) Operation mechanism of Peltier element as thermal diode; (b) the operation mechanism of kH element as thermal diode; (c) the operation mechanism of HTCM element.
2
2.1.基于热二极管的全固态MR模型
基于热二极管的全固态MR模型以热二极管/MCM层/热二极管组成的三明治结构为基本架构. 热二极管两端与换热器或热源及散热器热接触, 磁卡效应产生的热量变化可以通过热二极管在MCM与换热器或散热器间进行快速传输. 这种热传递与热流切换由热二极管控制的全固态MR模型也可称为热二极管/磁卡器件复合制冷模型. 与AMR类似, 可以通过多层MCM的级联设计增大系统温跨. 此类全固态MR 模型的设计有两种, 即: Peltier元件(电控热二极管)作为固态传热介质和基于kH元件(磁控热二极管)作为固态传热介质.3
2.1.1.基于Peltier元件的全固态MR模型
Kitanovski和Egolf[19]于2010年描述了一种热电模块作为热二极管的简单热电/磁卡器件复合制冷装置, 该装置通过施加电流控制热电模块的开关和热传输. 2013年, Tomc等[21]建立了基于Peltier元件的一级全固态MR的首个详细模型, 如图2(a)所示. 当施加磁场时, MCM由于磁卡效应而升温. 此时Peltier 1开启, 快速地将热量从MCM传输到热端换热器(hot heat exchanger, HHEX); 同时Peltier 2关闭, 作为理想绝热体, 隔绝MCM与冷端换热器(cold heat exchanger, CHEX)之间的热传递. 移除磁场时, MCM温度降低, 此时Peltier 2开启, 将热量快速从CHEX传输到MCM; 同时Peltier 1关闭, 作为理想绝热体, 隔绝MCM与HHEX之间的热传递. Tomc等[21,26]建立了准二维数值模型进行仿真评估, 并与传统平行板AMR进行了比较分析. 结果表明, 基于Peltier元件的全固态MR系统可以在超过200 Hz的高频下工作(如图2(b)所示). 这是因为, 相较于对流传热, Peltier元件可以更快地从MCM中提取热量. 从图2也可以看出, 新系统在高频工作条件下最大SCP大幅提升, ?效率也有较高的提升. 当Peltier元件热流速率较大时(热流速率从小至大依次为Peltier A, Peltier B, Peltier C, Peltier D, 见图2(b)右图), 可以在很短时间内传递更多热量, 器件可以在更高频率下工作, 此时传热损失小, SCP提升, 但由于电流输入大, 电功耗高, 会导致?效率降低. 当Peltier元件热流速率较小时, Peltier元件传热能力低, 器件只能在较低的频率下工作, 会导致SCP降低, 不过由于输入电流小, 电功耗低, ?效率较高. 同时, 由于热传导过程还受到Peltier元件和MCM自身热扩散特征时间(τ, 与密度ρ、热导率k和比热容c有关, τ = ρc/k[32])的影响, SCP并不会随工作频率的提升而一直增加.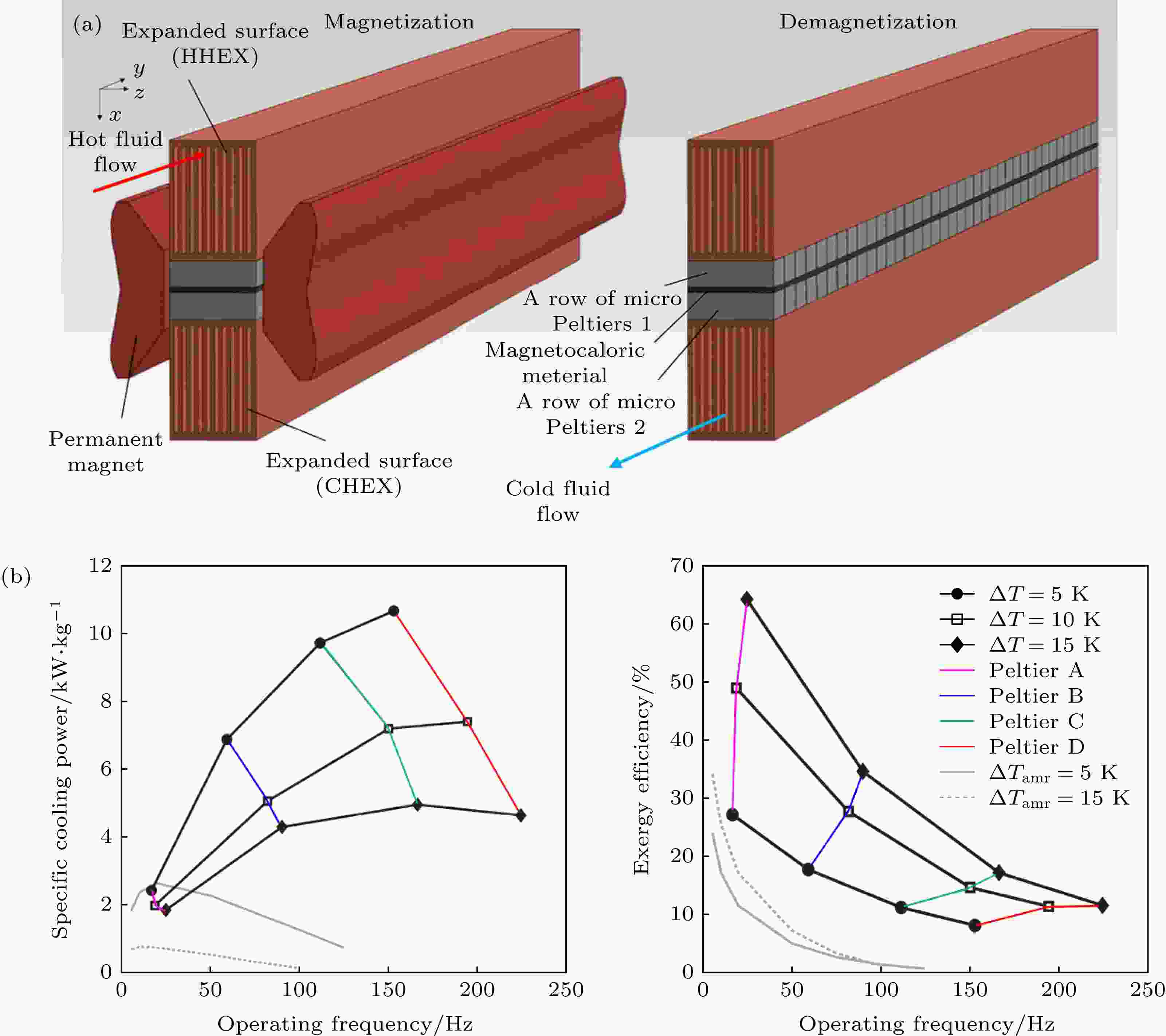
图 2 (a) 基于热二极管的全固态MR模型结构示意图[21]; (b) 带有热二极管的MR系统与平行板AMR在不同温跨和不同频率下最大SCP和?效率的比较[26]Figure2. (a) Schematic diagram of the full solid state MR model based on a thermal diode[21]; (b) comparison of maximum SCP and exergy efficiency between MR system with thermal diode and parallel-plate AMR at different temperature spans and different frequencies[26].
2014年, Egolf等[27]讨论了Ni纳米线薄膜Peltier元件对一级全固态MR系统性能的影响. 他们基于Peltier元件的实验测定值(塞贝克系数、电阻), 从理论上估算了系统性能, 并与传统AMR进行了比较. 结果表明, 在10 Hz和5 K温跨下, 全固态系统的制冷系数(coefficient of performance, COP)值为2.8, SCP值为15 kW/kg, 同样条件下, AMR系统的SCP只有2.5 kW/kg, 这表明了全固态MR系统具有较大的性能提升. 同时, 作者认为未来应考虑优化Peltier元件热阻和电阻以提升系统整体性能, 并开展热电效应和热负载等因素对系统性能影响的研究. 2015年, Kitanovski等[22]综述了固态物理领域压卡、电卡、弹卡和磁卡制冷的研究进展, 并分析了上述制冷技术的实际可行性, 指出在众多固态热制冷中基于热二极管的全固态MR具有良好应用前景. 2017年, de Vries 和van der Meer[28]考虑热电效应的影响和Peltier元件实际热阻, 通过添加热电效应模型对热电/磁卡器件全固态模型进行了二维数值模拟分析. 物理模型结构如图3(a)所示, 与Tomc等[21]所设计模型类似, 基本架构仍为热二极管/MCM层/热二极管的三明治结构, 并使用同一型号的热二极管. 不同的是, 作者对Peltier元件内部结构和实际工况进行了描述, 无电流施加时Peltier元件的热输运主要是传统的晶格热传导, 施加电流时, 热输运以电热输运为主. 同时, 构建了更为全面的热-电-磁耦合数学模型, 并考虑MCM层的纵向热传导和温度分布(如图3(b)所示), 对磁热-热电能量转换进行了更为详细的分析. 结果表明, 全固态系统可以在超过20 Hz的频率下工作, SCP获得了预期改善. 然而, 作者指出Tomc等[21]高估了Peltier元件的实际热阻, 无电流施加时的Peltier元件的晶格热传导会使得MCM与换热器间进行热流切换时产生热泄漏, 导致温跨和COP降低.
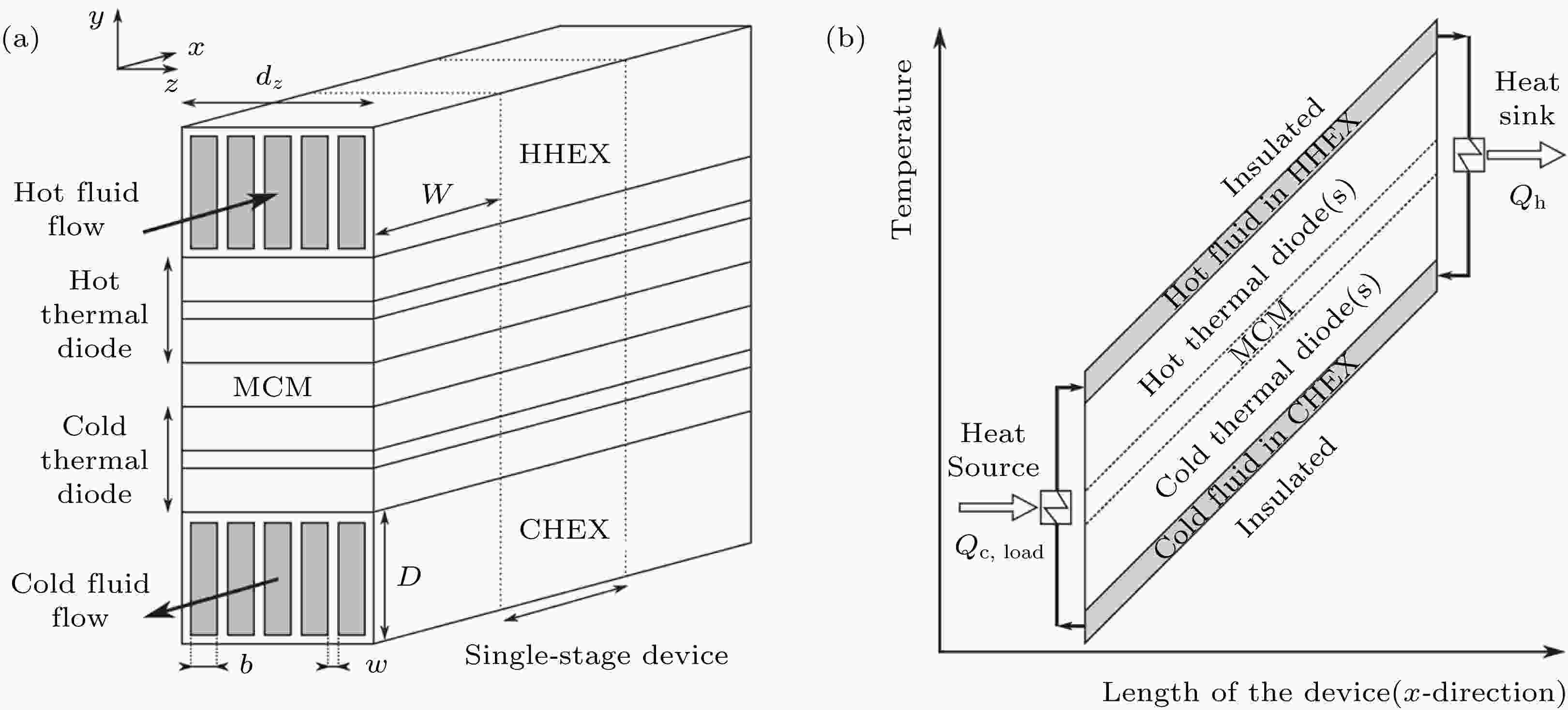图 3 (a)全固态MR系统模型结构示意图[28]; (b)器件长度方上的温度分布[28]Figure3. (a) Schematic diagram of the full solid state MR system model[28]; (b) temperature distribution over the length of the device[28].
除一级全固态MR模型外, 基于Peltier元件的级联全固态MR模型也取得了一定的进展. 2012年, Tasaki等[29]首次提出了基于热二极管的级联全固态MR的设计概念, 并由Olsen等[30]做了进一步拓展. 在该级联系统中, MCM元件与热二极管交叠设计(如图4(a)所示). Olsen等[30]没有考虑实现热二极管的具体机制, 而是假设热二极管热导率在“开”下无穷大, “关”下为无穷小, MCM热容为常数, 在此基础上探索了物理参数对系统性能的影响规律. 研究表明, 在60 K高温跨下, 系统SCP与热导率、循环频率和元件长度等有关. 随着MCM热导率增加, SCP随频率也线性增加. 同时, 较薄MCM可以更快地传输热量. 2017年, Monfared[23]对该模型进行了更为深入的研究, 同样使用Peltier元件作为热二极管, 改变外加电流大小控制Peltier元件的传热速率. 模型工作原理如图4(b)所示: 通过磁化不同MCM层和控制不同层Peltier元件的打开、关闭实现热量定向输运和循环制冷. 单个制冷循环主要分为四个步骤: 1)奇数MCM层被磁化而升温, Peltier元件关闭; 2) 偶数Peltier元件打开, 并将奇数MCM层的热量泵送到偶数的MCM层; 3) Peltier元件关闭, 偶数MCM层被磁化而升温, 奇数MCM层由于退磁变冷; 4)奇数Peltier元件打开, 热量从热MCM层泵送到较冷MCM层. 研究表明, 增加MCM元件数, 温跨随之增加. 另外, 电流大小对系统效率有着决定性的影响. 电流过大, Peltier元件传热速率加快, 但也伴随着焦耳热的增大, 从而导致COP减小(如图4(c)所示). 降低电流可以提高系统COP, 但Peltier元件热输运速率会减小, 导致SCP降低. 同时, 在高频条件下, 若电流值过小, Peltier元件则不能够将MCM产生的热量提取出来, 会进一步导致系统SCP和COP减小. 此外, Peltier元件长度的增加会使系统SCP增加, 但也会导致焦耳热增大, 使COP减小; 若长度过小, 则会使Peltier元件轴向传导热阻减小, 导致SCP和COP均减小(如图4(d)所示). 因此, 同热泄漏一样, 应用Peltier元件时必须考虑焦耳热问题. 未来应进一步优化电流、几何形状等其他参数并研制高性能热电元件以最小化焦耳热的影响.
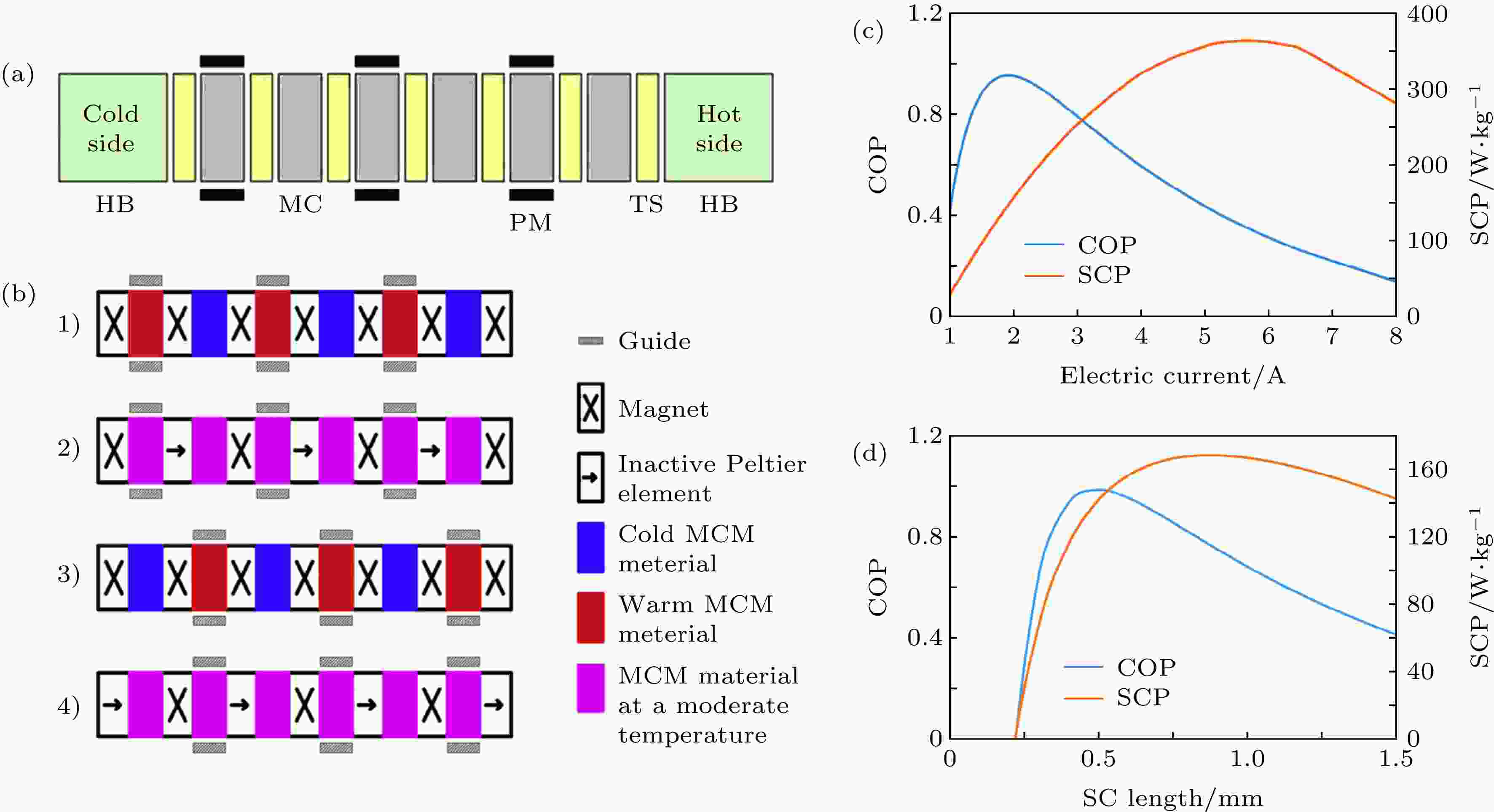图 4 (a)基于热二极管的全固态MR模型示意图[30]; (b)工作原理[23]; (c)不同电流下COP和SCP的变化[23]; (d) Peltier元件不同长度下COP和SCP的变化[23]Figure4. (a) Schematic diagram of a full solid state MR model based on thermal switch[30]; (b) operating principle[23]; (c) variation of COP and SCP with different current[23]; (d) variation of COP and SCP with the length of Peltier element [23].
最近, Wu等[24]和Lu等[31]通过采用Cu/Gd复合磁工质以增强MCM有效热导率, 建立了以新型微元回热(micro-unit regeneration, MUR)循环为制冷循环的级联全固态MR系统模型. 物理模型由两个多级Cu/Gd复合层组成的MUR板、两个永磁体和一个中间传热板构成(如图5(a)所示). MUR板被分成若干网格以扩展温跨, 相邻网格由隔热材料隔开以避免热泄漏, 热端位置和冷端位置与外部换热器连接. 中间传热板由支撑框架和Peltier元件组成. MUR板A和B的成对网格通过Peltier元件彼此交换热量. 模型工作原理如图5(b)所示: MCM在位置1磁化并向HHEX释放热量; 然后, 从位置2旋转到位置n时, 通过回热冷却; 在位置n+1退磁并从CHEX吸收热量; 最后, 从位置n+2旋转到位置2n时, 通过回热加热, 完成一个循环过程. 整个系统通过旋转方式实现连续制冷输出. Lu等[31]研究了仅Gd(仅Gd作为MCM, 如图5(c)所示)、平行板(Cu/Gd平行板式复合, 如图5(d)所示)和拓扑优化结构(Cu层为拓扑结构, 如图5(e)所示)三种配置下的全固态模型的行为和性能, 同时, 为了验证模型的有效性, 通过实验研究了两成对网格回热期间的温变过程. 实验设置如图5(f)所示, 使用热电偶监测Peltier元件温度变化并通过电加热获得冷热块初始温差. 研究表明, 模拟结果和实验验证结果是一致的, 在平行板和拓扑结构配置下, 系统可以在更短的时间内达到温度平衡. 并且, 拓扑优化结构下和Peltier元件电压为3 V时系统获得最佳制冷性能. 在5 K温跨下最大SCP为160.9 W/kg, 10 K温跨下最大SCP为79.8 W/kg (如图5(g)所示). 同样, 过低电压下Peltier元件传热能力不足和过高电压下焦耳热增大均会使制冷功率降低. 此外, 优化后的传热结构表现出更佳传热能力, 较大转速下Peltier元件冷热端仍可以快速的吸收和排出热量, 获得更大Peltier COP值和更小温差(如图5(h)所示).
图 5 (a) 全固态MR系统示意图[24]; (b) MUR循环原理[31]; (c) 仅Gd[31]; (d) 平行板[31]; (e) 拓扑优化结构[31]; (f) 实验设置[31]; (g)最大SCP随Peltier电源电压的变化[31]; (h) Peltier COP和温差随转速的变化[31]Figure5. (a) Schematic diagram of the full solid state magnetic refrigeration system[24]; (b) MUR cycle principle[31]; (c) Gd-only[31]; (d) parallel sheets[31]; (e) topology optimization structure[31]; (f) experiment setup[31]; (g) variation of maximum SCP with different Peltier supply voltages[31]; (h) variation of Peltier COP and temperature difference with different rotating speeds[31].
对于基于Peltier元件的全固态MR系统, 具有工作频率提升和SCP增大的优势, 但存在热泄漏和焦耳热等负面问题. 针对技术中存在的问题, 人们可以通过采用创新的设计和深入的优化等方式来改善或解决.
3
2.1.2.基于kH元件的全固态MR模型
除基于Peltier元件的全固态制冷模型外, 基于kH元件的全固态MR模型的研究也取得了一定突破. kH材料是指热导率随磁场变化的材料. 带电粒子可以在磁场中传输热量, 施加外磁场能够影响磁电阻进而影响热导率[38]. 2012—2019年, Silva等[32—35]对基于kH元件的全固态MR模型进行了一系列的研究, 建立了一级MCM全固态MR模型和多层MCM级联全固态MR模型.一级全固态MR系统模型及机制如图6(a)所示[32]. 模型仍然基于热二极管/MCM层/热二极管的三明治结构, 当无磁场时, k1(0) < k2(0), 施加磁场时, k'1(0) = k1(0)+?k1 > k'2(0) = k2(0) – ?k2. 制冷循环基于磁Brayton循环, 主要分为如下4个过程: 在绝热加磁过程1中, MCM温度升高, 上端kH元件热导率增大, 下端kH元件热导率减小; 随后, 进入等场过程2, MCM中热量更容易流向高温热源; 在绝热退磁过程3中, MCM温度降低, 两kH元件热导率恢复初始状态; 随后, 进入等场过程4, 热量更容易从低温热源流向MCM. 作者在进行数值模拟时进一步假设: 无磁场时, k1(0) = 0, k2(0) = 10.5 W/(m·K); 当施加1 T磁场时, k1(0) = 10.5 W/(m·K), k2(0) = 0. 研究表明, 系统在约95 Hz的工作频率、296 K的工作温度和1 mm MCM厚度下, 获得2.75 W/cm2的最大SCP和1.5的COP值(如图6(b)和图6(c)所示). 制冷功率密度随着工作频率先增加后减小, 存在着最佳工作频率和截止频率, 截止频率取决于施加磁场后与MCM居里温度有关的热扩散特征时间. 当工作温度接近296 K时, 对应着最小COP值和最大制冷功率密度, 两个参数不能同时获得最优值. 同时, 一级全固态系统获得了2.5 K温跨, 这不能满足实际需求.
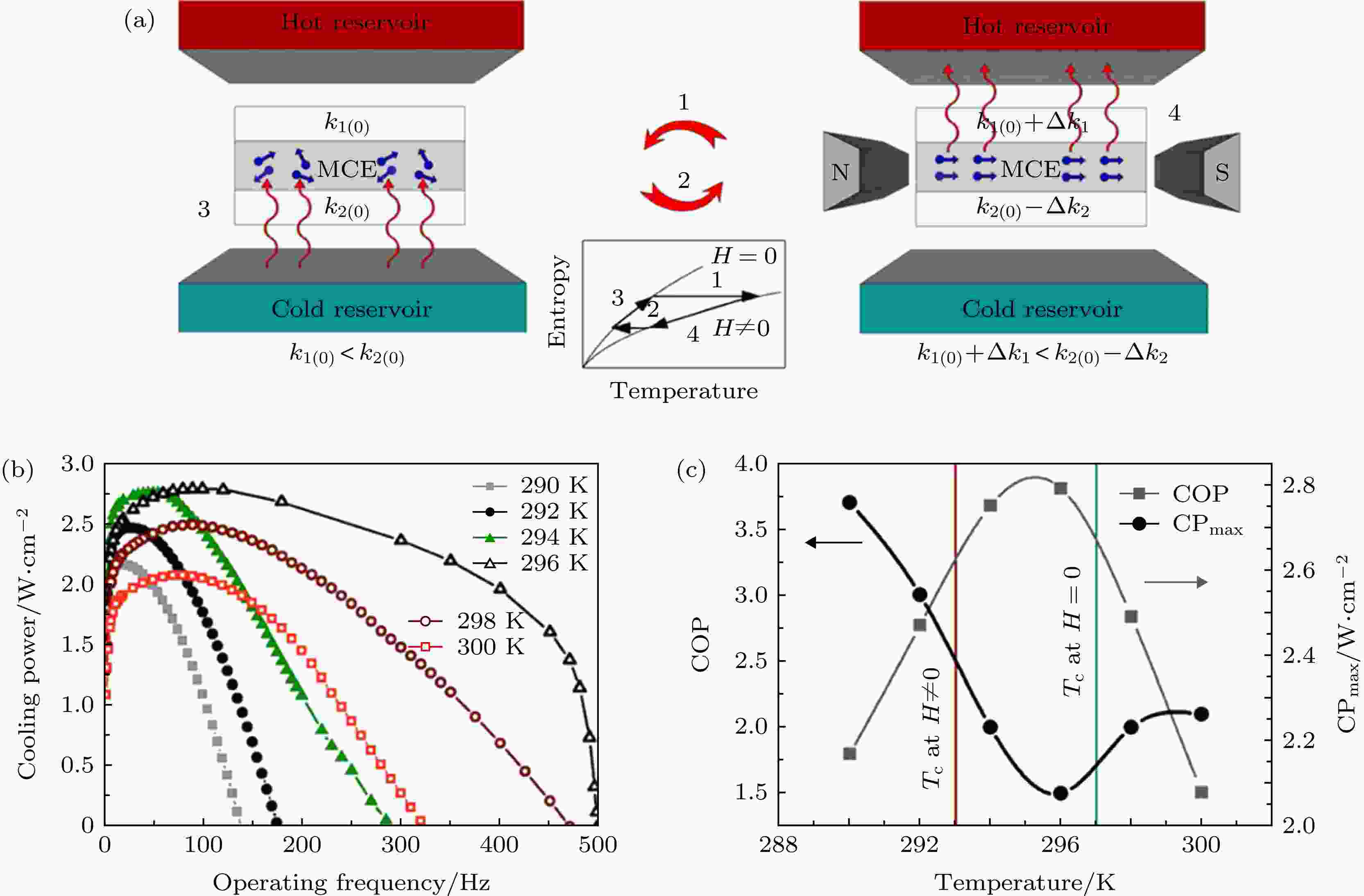图 6 (a) 基于kH元件和磁Brayton循环的全固态MR模型[32]; (b) 不同工作温度下SCP随工作频率的变化[32]; (c)最大SCP和COP随温度的变化[32]Figure6. (a) A full solid state magnetic refrigeration model based on kH element and magnetic Brayton cycle[32]; (b) variation of SCP with operating frequency at different operating temperatures[32]; (c) maximum SCP and COP as a function of temperature[32].
为了实现上述一级系统的温跨最大化, 2014年, Silva等[33]进一步设计了级联系统模型, 中间为n个MCM元件级联堆叠. 系统温跨扩大机制如图7(a)所示: 首先, 在所有MCM元件中施加磁场, 此时热端kH元件k值与MCM相同, 冷端kH元件k为零, 热量从第一元件流向高温热源, 该元件温度降低, 与第二元件形成温度梯度使得热量从第二元件传递到第一元件; 然后, 从高温热源到最接近低温热源的元件逐渐去除磁场, 当第一元件去除磁场时, 冷热两端kH元件k值为零, MCM与热源热隔离. 在磁场去除过程中, 元件间形成温差, 建立从低温热源区域到高温热源区域的热流. 整个磁场移除时, 系统实现了最大的温跨. 级联系统的温跨在MCM元件为24时达到11.5 K (如图7(b)所示), 与一级全固态系统相比, 性能提升超过450%. 2016年, Silva等[34]对级联模型进行了MCM物理性能(热导率、密度、比热容等)的优化. 结果表明, 热导率增加, 最佳工作频率增大, 同时, 温跨的提升将导致工作频率降低(如图7(c)所示). 最佳工作频率会随MCM密度的增加而减小, 而最大温跨则会增大. 比热容的影响与密度相似. 此外, 他们指出MCM热扩散特征时间将是未来研究趋势中的主要参数之一. 2019年, Silva等[35]研究了磁场扫描方式及磁场在匀速、加速和减速条件下对温跨的影响, 以进一步寻求提高全固态MR机性能的最佳工作模式. 研究表明, 当磁场以单步方式施加, 或者从低温热源到高温热源以匀速或减速模式施加, 并由高温热源到低温热源加速模式移除时, 温跨相较之前可以提升达20%.
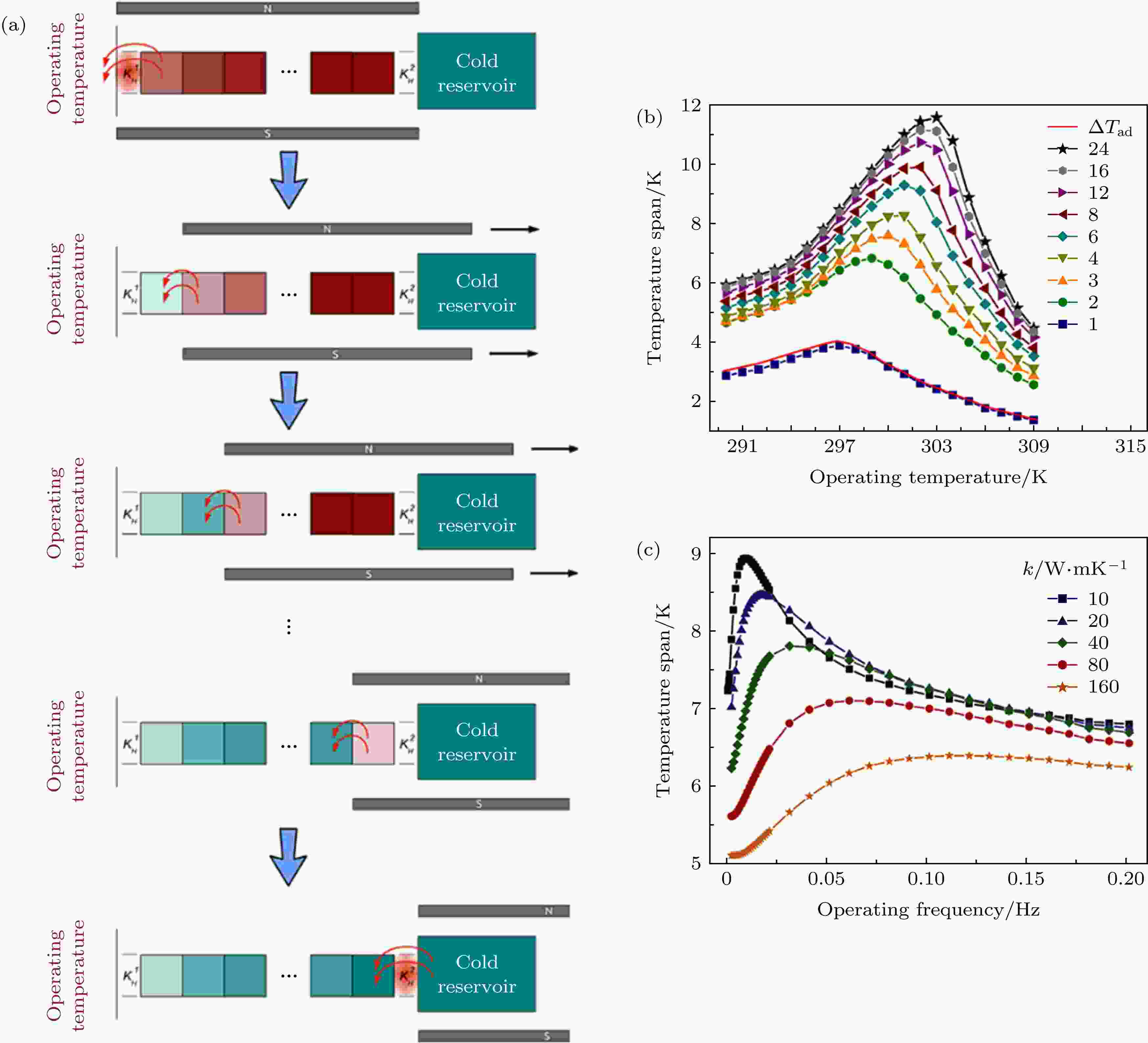图 7 (a) 级联全固态MR系统的工作机制[33]; (b) 不同MCM元件数量下温跨随工作温度的变化[33]; (c) 不同热导率的MCM下温跨与工作频率的关系[34]Figure7. (a) Working mechanism of the cascaded full solid state magnetic refrigeration system[33]; (b) variation of temperature span with operating temperature for different MCM components[33]; (c) dependence of the temperature span on the operating frequency for different thermal conductivities of the MCM[34].
在应用kH元件的全固态MR系统的仿真结果中, SCP, COP和温跨都有一定的提升, 显示出巨大的应用潜力. 然而, 关于kH材料的研究较少, 如锰酸盐化合物[39]、巨磁热导率的Co/Cu磁性薄膜[40,41]等, 满足模型工作机制的实际kH材料可能会难以获得. 未来应深入研究和开发高性能kH材料并设计适用性更广的实际可行的kH元件, 进一步评估此类全固态MR系统的性能和可行性.
2
2.2.基于HTCM元件的全固态MR模型
HTCM元件是基于高热导率材料所设计的一类固态换热介质, 通过与MCM接触和非接触实现热量传递的开关动作, 在全固态MR模型中多使用Cu作为HTCM. 除替代传热流体外, HTCM也可与MCM进行宏观复合设计成有效MCM以增强MCM传热能力, 这在前文所介绍的Lu等[31]的工作中已有体现. 目前, 基于HTCM元件的全固态模型的相关研究较少. 2016年, Zhang等[36]提出了使用HTCM移动杆/片代替传热流体以增强制冷能力的全固态MR概念模型. 数值敏感分析研究了该全固态MR模型效率的影响因素. 结果表明, HTCM移动杆/片的引入提高了传热速率, 模型在高频下具有较好的性能表现. 2018年, Wu等[24]对该概念进行了拓展, 设计了更为详细的基于HTCM元件的全固态MR模型(如图5(a)所示). 其中Cu块作为中间传热板, 工作原理与基于Peltier元件的模型相似(如图5(b)所示), 回热主要基于Cu块的热传导. 研究表明, 系统在36或72网格数和Gd/Cu体积分数比为0.7时表现出较佳性能. 当系统网格数为72时获得了50.9 K的最大空载温跨(如图8(a)所示)和105.8 W/kg的最大SCP (如图8(b)所示). 同时, 在36网格下获得3.2的最大COP (如图8(c)所示), 而当网格数增加到72时, 最大COP可达4.2. 级联网格数的增加可以增强有效回热效率, 从而提升系统性能. Gd/Cu体积分数比则需要达到最适的比例参数, 过大Gd体积分数可以增加Gd质量, 但会降低热传导效应. 另外, 温跨、SCP和COP也对应着不同的最佳转速, 大转速下热传导时间不足而导致温跨减小. 这同基于热二极管的全固态MR模型的[33]研究工作一致, 各性能参数很难达到一致, 人们需要进一步寻找参数的优化组合.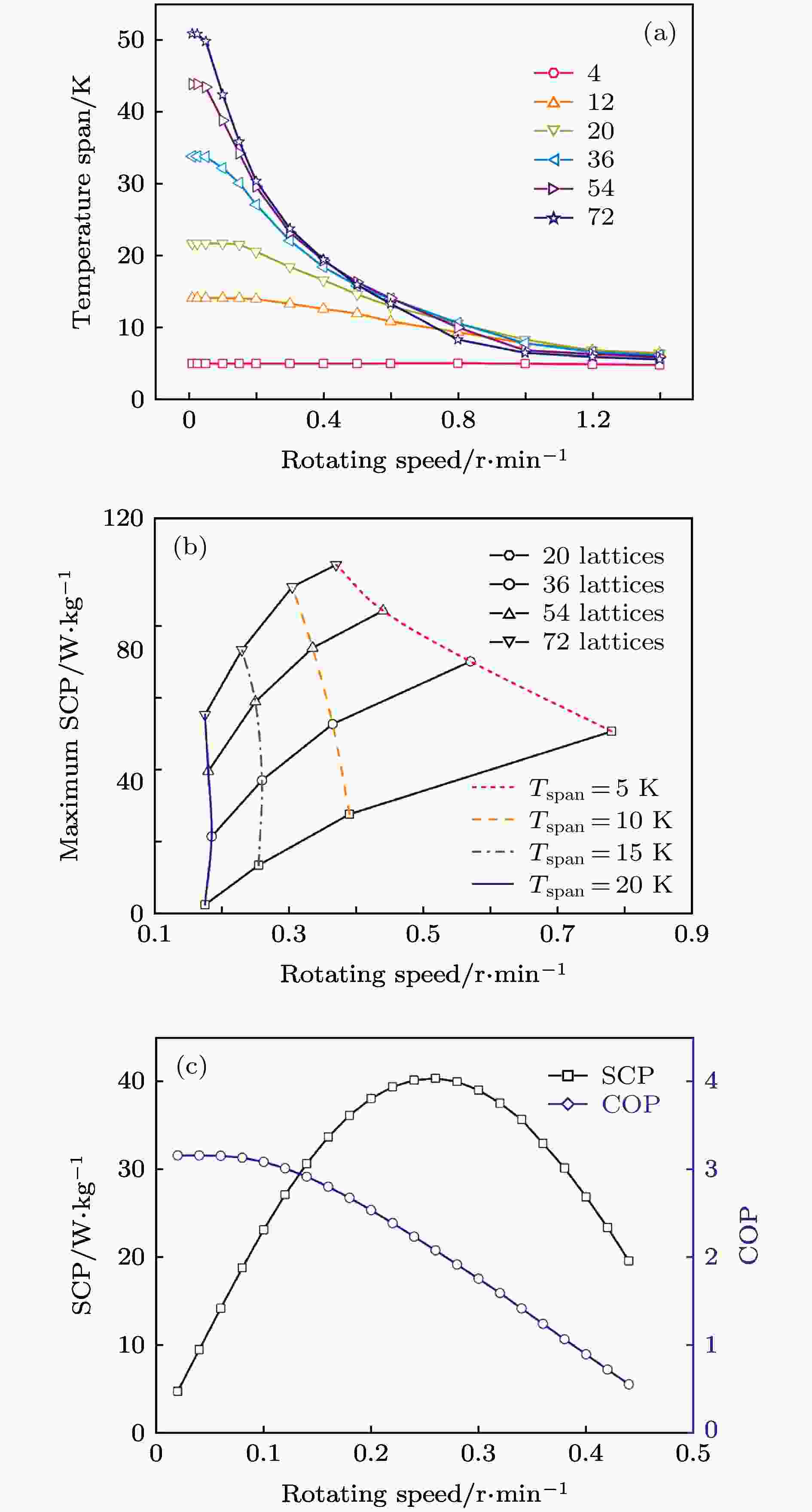
图 8 (a)不同网格数下温跨与转速的关系[24]; (b)不同温跨网格数下最大SCP与转速的关系[24]; (c) 32网格下最大SCP和COP与转速的关系[24]Figure8. (a) Variation of temperature span with rotating speed at different lattice numbers[24]; (b) variation of maximum SCP with rotating speed at different temperature spans and lattice numbers[24]; (c) variation of maximum SCP and COP with different rotating speeds at 32 lattices[24].
Lu等[31]研究了不同传热结构优化方式对基于Cu块的全固态MR系统行为和性能的影响, 并比较了Cu块回热模式下和Peltier元件回热模式下的制冷性能(如表1所列). 在仅使用铜块回热时, 拓扑优化结构下获得的最大SCP相较平行板和仅Gd配置下分别平均增加32%和391%. 与仅使用铜块回热相比, 添加Peltier元件快速回热时, 最大SCP增加82%—149%. 最近, Utaka等[37]设计了一种使用高导热涂层作为固态换热介质的级联全固态MR. 他们发现, 磁卡单元的尺寸对系统最适工作频率有重要影响, 并且, 适当增加单元的数量可以有效地提高系统整体性能. 可以看出, HTCM元件和Peltier热电元件在全固态MR中均具有良好的应用潜力, 其中, Peltier元件显示更大优势. 同时, 传热结构的优化在全固态MR系统的未来研究中也将扮演着重要角色.
| 配置 | 温跨/K | 最大SCP/W·kg–1 | 增加 百分比/% | |
| 铜块 | Peltier元件 | |||
| 平行板 | 5 | 67.6 | 133.8 | 98 |
| 10 | 26.1 | 64.9 | 149 | |
| 拓扑优 化结构 | 5 | 88.5 | 160.9 | 82 |
| 10 | 35.7 | 79.8 | 124 | |
表13 V电压下, 带有铜块的MR和带有Peltier元件的MR的最大SCP比较[31]
Table1.Maximum SCP comparison between MR with copper blocks and MR with Peltier elements under a 3 V supply voltage[31].
| 类型 | 磁工质 | 传热介质 | 工作频率/Hz | 温跨/K | SCP/W·kg–1 | COP | 参考文献 | |
| 全固态MR | 准2D全固态MR | Gd | Peltier元件 | 0—225 | 5—15 | 1 × 104 | — | [21] |
| 全固态MR | Gd | Peltier元件 | 10 | 50 | 1.5 × 104 | 2.8 | [27] | |
| 2D全固态MR | Gd | Peltier元件 | 20 | — | — | 5.3—6.5 | [28] | |
| 全固态MR | Gd | Peltier元件 | 20—200 | 60 | — | 4.0 | [30] | |
| 1D全固态MR | Gd | Peltier元件 | — | 5 | — | 0.96—9.21 | [23] | |
| 准2D全固态MR | Gd | Peltier元件 | — | 10 | 79.8 | — | [31] | |
| 1D全固态MR | Gd | kH元件 | 0—500 | 2.5 | — | 1.5 | [32] | |
| 1D全固态MR | Gd | kH元件 | — | 11.5 | — | 4.0 | [33] | |
| 准2D全固态MR | Gd | Cu块 | — | 5—50.9 | 2.6—105.8 | 1.5—4.2 | [24] | |
| 传统AMR | 1D AMR | Gd | 水 | — | 15 | — | 1.49—5.27 | [42] |
| 2D AMR | Gd | 水 | — | 3 | — | 5.4 | [43] | |
| 1D AMR | Gd | 水 | 0.125 | 6 | — | 12.16 | [44] | |
| AMR/旋转床 | Gd | 水+乙二醇 | 0~10 | < 18.9 | — | — | [45] | |
| 2D AMR | Gd | 水+乙二醇 | 0.75 | 10.2 | 60.59 | 3.1 | [46] | |
| 2D AMR | Gd | 水 | 1.5 | 14.5 | — | ~2 | [47] | |
| AMR/旋转床 | Gd | 水+乙二醇 | 0.8 | 7.1 | — | 0.54 | [48] | |
| 1D AMR | Gd | 水+乙二醇 | 0.3—10 | 20 | 100 | 7.6—11.2 | [49] | |
| 2D AMR | ${\rm Gd_5(Si}_x{\rm Ge}_{1-x})_4 $ | 水 | 1.25 | ~10—16 | — | ~5 | [50] | |
| AMR/平行板床 | ${\rm MnFeP}_{1-x}{\rm As}_x $ | 水+乙二醇 | 0.8 | 32 | — | — | [51] | |
| 1D AMR | LaFeSiMnHy | 水+乙二醇 | 0.15 | 19.8 | 12.4 | — | [52] |
表2全固态MR模型与传统AMR模型的主要性能比较
Table2.Comparison of main performances between full solid state MR model and traditional AMR model.
由表2可以发现, 全固态MR系统工作频率可达100 Hz以上[21,30,32], 而传统AMR工作频率最高在10 Hz左右[45,49]. 我们知道, 由于传统AMR的对流传热限制, 提高工作频率将会降低系统效率. 采用热二极管或HTCM元件代替流体时, 频率将主要取决于热二极管或HTCM元件的固态传热机制. 相较于流体对流传热, 固态热传输速率更快. 理论上, 随着工作频率增加, 全固态MR系统的SCP可以提升到10000 W/kg以上[21,27], 而传统AMR的SCP最高则在100 W/kg左右[49], 这揭示了MR器件中运用固态传热机制可以将功率密度提升一个或多个数量级. 同时, SCP对应着一个最佳工作频率, 工作频率不是越大越好, 而是受热传导控制, 取决于热二极管或HTCM元件从MCM提取热量的能力及MCM本身传热能力. 此外, 温跨和COP是评价制冷机性能的两大重要指标. 全固态MR模型的温跨可以超过50 K[24,30], COP最高可达9以上[23], 传统AMR温跨可以超过30 K[51], COP则可以达到12以上[44]. 温跨主要取决于MCM绝热温变, AMR和全固态MR系统的温跨均可以通过提高磁场强度和优化设计等方面来提升. 单一考虑COP值时, 全固态MR系统并没有表现出理想的结果. 由于固态传热机制的局限性, 在过高频率下仍然会遇到与流体传热相似的问题, 全固态MR机仍然无法同时达到高工作频率、高SCP、高温跨和高COP. 综合考虑各性能参数时, 需要折中方案. 然而, 基于固态传热机制的全固态MR技术的研究还处于初步阶段, 报道的模型数量有限, 系统性能仍具有较大提升潜力, 因此应大力发展全固态MR技术以实现高效磁热能转换的新突破.
如表2所列, MR机采用的磁工质主要是Gd, 其具有良好的绝热温变和可制备性. 进一步研究发现, 具有巨磁卡效应的材料如Gd5(SixGe1–x)4基化合物[53,54]、La(Fe1–xSix)13基化合物[55—57]、MnFeP1–xAsx基化合物[51,58]等也十分重要, 有望大幅度提升制冷机性能. 我们知道, MR材料在直接进入实际应用之前必须在较宽温度范围内具有足够大的磁卡效应, 巨磁卡材料的出现为MR机的设计拓宽了方向. 同时, La(Fe1–xSix)13基化合物表现出较小的滞后效应、较佳的综合性能和合理的成本[57,59], 具有较大的应用前景.
表2也列出了两类固态传热器件: 热二极管和HTCM元件. 其中, Peltier热电元件研究较为广泛, 具有更大的应用潜力. 然而, 若使Peltier元件高效运用在系统中, 需要优化的电阻、热阻、电流和几何设计等. 因此, 在热电/磁卡器件复合全固态MR模型开发过程中, 先进热电材料的开发、高效Peltier元件的设计和Peltier元件在制冷系统内的参数匹配至关重要. 最近, 武汉理工大学热电磁研究团队[60]通过单畴软磁金属纳米粒子(Fe, Co, Ni)与热电材料(Ba0.3In0.3Co4Sb12)纳米复合, 发现了电子多重散射效应与热电磁多功能新材料. 利用单畴软磁金属纳米粒子超顺磁性产生的热-电-磁新效应, 可以协同调控电子/声子输运, 大幅度提高塞贝克系数等热电性能. 这为Peltier元件的设计和热电磁全固态制冷模型架构设计提供了新思路. 可以利用高性能热电磁材料设计新型高效Peltier元件, 以进一步提升系统综合性能. 同时, 基于热-电-磁新效应的发现, 可以考虑将MCM以复合的方式引入的热电材料中, 从材料复合方面出发设计新的模型, 以期实现热电-磁卡协同制冷, 而不仅仅限于器件复合. 相对于Peltier元件, kH
1)高效Peltier元件的优化设计. 研究Peltier元件绝缘导热、通电导热、热界面和热疲劳等问题, 建立电-热多效应(Peltier效应、塞贝克效应、傅里叶效应、焦耳热效应等)耦合数值模型, 对Peltier元件多个结构和工艺参数同时进行分析和优化, 寻求最优设计参数以匹配全固态系统的高效运行. 同时, 研究磁性材料对热电材料性能的影响, 基于新材料设计新型Peltier元件, 并测定其服役性能.
2)高性能kH材料研究及其元件设计. 深入研究和理解kH材料的结构和热导率-磁场依变性的物理机制, 建立基于kH材料的热磁输运机制数学模型. 开发性能稳定、适用性广的kH材料并设计高效kH元件, 测定元件实际性能参数并运用到全固态MR系统中, 建立仿真模型和实验以进一步评估其可行性.
3)高性能HTCM的选择及其元件设计. 运用不同的HTCM进行数值比较分析, 寻求不同工况下的最适HTCM. 同时, 设计HTCM与热二极管及MCM的高效组合结构, 进一步优化传热效率, 提升系统综合性能.
4)全新的模型架构设计. 不同于器件复合, 从材料复合方面出发, 研制性能稳定的新型多功能热电/磁卡复合材料, 基于新材料和新功能设计全新的热电磁全固态复合制冷模型架构, 热电材料同时充当换热材料和制冷材料, 实现热电-磁卡协同制冷.
5)高效全固态MR系统及样机的设计和优化. 开发创新的全固态MR系统模型, 辅以经典制冷循环或设计潜在制冷循环, 实现全固态制冷系统的高效运行和热能转换. 建立不同维度的数值仿真模型对全固态MR系统进行更为全面的评估和更为深入的参数优化, 并设计器件进行实验验证. 同时, 研制全固态MR样机, 进行更为全面的实验验证, 测试其可靠性和稳定性, 推动全固态MR技术的进一步发展.
