全文HTML
--> --> -->螺旋波等离子体的电离机制十分复杂, 其核心是波-粒能量耦合机制, 自1960年Aigrain[7]首次提出螺旋波概念, 1970年Boswell[8]首次实现螺旋波等离子体放电以来, 人们对螺旋波产生高密度的等离子体的物理机理、螺旋波能量耦合到等离子体中的物理方式始终没有给出最终的解释. 1991年, Chen[9]利用朗道阻尼机制导出了均匀有界等离子体中螺旋波的色散关系, 认为电子通过朗道阻尼进行加热具有很高的吸收效率. 1999年, Chen和Blackwell[10]又提出了螺旋波放电中朗道阻尼的限制. 朗道阻尼可以解释在一般的放电实验中的螺旋波等离子体的能量沉积, 但在较大尺度实验装置中或者在天线长度大于半个波长的情况下, 朗道阻尼沉积将不再成立. 通过深入研究发现, 在螺旋波放电能量沉积过程中, 存在着螺旋波之外的一种静电性质的表面波Trivelpiece-Gould (TG)波[11]. Shamrai和Taranov[12]认为放电过程中RF功率通过两种通道转移给等离子体, 即体吸收的螺旋波(H波)和表面吸收的TG波实现的, 这两种波在等离子体柱径向位置上进行耦合, 而大部分的RF功率通过强阻尼的TG波转移给等离子体. 到目前为止, 有关螺旋波高功率耦合到等离子体中的机理和能量沉积的机制仍在不断探索中. 因此, 磁场对两种波的影响需进一步讨论, 但TG波能量沉积机理的假设已逐渐成为主流共识[13].
近年来, 螺旋波等离子体的放电模拟取得了较大发展, 促进了人们对螺旋波放电机理的认识. 如: 由Chen和Arnush[14-16]开发的HELIC代码, 通过电磁场理论分析计算了螺旋波和TG波的能量沉积及其电场、磁场和电流的分布情况; 由Mouzouris和Scharer[17]开发的ANTENA2代码利用碰撞机制和朗道阻尼加热机制, 计算了等离子体中的电磁场和功率沉积; 2012年, Melazzi等[18]开发了SPIREs代码, 采用FDTD算法对圆柱等离子体中的电磁场问题和功率沉积问题进行了快速求解; 2015年, Melazzi和Lancellotti[19]开发了ADAMANT代码, 该代码利用MOM算法研究了天线几何结构及其在功率沉积方面的影响. 国内方面, 成玉国等[20]考察了径向电子数密度非均匀分布条件下, 不同强度磁场对能量沉积的影响; 杨雄等[21]建立三维条件下螺旋波放电模型,充分考虑了电离过程中的粒子碰撞和电化学反应,利用漂移-扩散输运方程计算等离子体中各粒子密度及电子温度;苌磊等[22,23]针对径向密度梯度对于螺旋波等离子体中电磁波和能量吸收进行了数值模拟.
HELIC代码常用于射频等离子体源设计和实验中, 该程序利用特定的边界条件求解6个径向耦合微分方程, 得到两个独立的波-螺旋波和TG波. 这比将非均匀等离子体划分成层并在每个界面匹配边界条件(如ANTENA2代码)要快得多, 而且改变天线的几何形状也特别容易. 本文首次采用HELIC代码对高密度螺旋波等离子体原型实验装置(helicon physics prototype experiment, HPPX)中等离子体放电现象进行数值模拟, 分析了HPPX装置中螺旋波天线种类、天线长度及运行频率等参量对功率沉积的影响, 从而得到了发射天线的最佳结构和尺寸. 众所周知, 忽略电子质量me的简单螺旋波理论, 只有当轴向电场Ez消失时才成立, 而实际实验中并未满足这一条件. 通过对冷等离子体方程中有限的me和Ez进行精确求解, 预测出了TG波的存在, 这极大改变了人们对等离子体放电的认识. 因此, 在分析静磁场大小和轴心等离子体密度对波-粒耦合能量的影响时, 本文对等离子体中的螺旋波和TG波的功率沉积机理做了进一步探讨, 进而, 研究了等离子体放电时的感生电磁场与电流密度等参数. 本文所研究的成果对HPPX装置上螺旋波天线设计和今后相关物理实验开展具有一定的指导意义.
2.1.理论分析
为了研究RF天线产生的螺旋波耦合到等离子体中的功率沉积, 从麦克斯韦方程出发, 得到电场E和磁场B满足的法拉第定律和安培定律:




假设天线是一个半径r = Rb







对于等离子体的吸收功率, 定义特定的等离子体功率谱函数







2
2.2.计算模型
HPPX是2016年中国科学院合肥等离子体研究所自主研发的螺旋波放电装置. 该装置采用高功率射频源和模块化的设计, 束流密度高达1023 m–2·s–1量级, 可产生高密度高能量等离子体, 是用于研究核聚变的新型材料装置(图1). 该装置总长度为4 m, 分为4个腔室, 其径向中心处是等离子体, 等离子体外有个法拉第屏蔽罩, 缠绕在屏蔽罩外是螺旋波天线, 放置在等离子体轴向中心处(z = 0 m), 用以产生螺旋波来激发等离子体, 最外面是一个真空腔. 等离子体参数和边界条件如表1所列. 图 1 HPPX装置结构图
图 1 HPPX装置结构图Figure1. The structure of HPPX.
| 参数 | 数值 |
| 等离子体半径Ra/m | 0.075 |
| 天线半径Rb/m | 0.2 |
| 真空腔半径Rc/m | 0.25 |
| 工质粒子种类 | Ar+ |
| 射频天线运行频率f/MHz | 13.56 |
| 射频天线长度LA/m | 0.4 |
| 中心轴处等离子体密度ne0/cm–3 | 4 × 1012 |
| 轴向静磁场强度B0/T | 0.04 |
| 电子温度Te0/eV | 5 |
| 中性轴压强Pg0/mTorr | 10 |
| 步长N | 49 |
| 碰撞因子 | 1 |
表1HPPX装置参数及等离子体参数
Table1.HPPX device parameters and plasma parameters.
磁场密度沿轴向为均匀的, 粒子的密度分布沿轴向也是均匀的, 径向密度可以由下面函数确定:
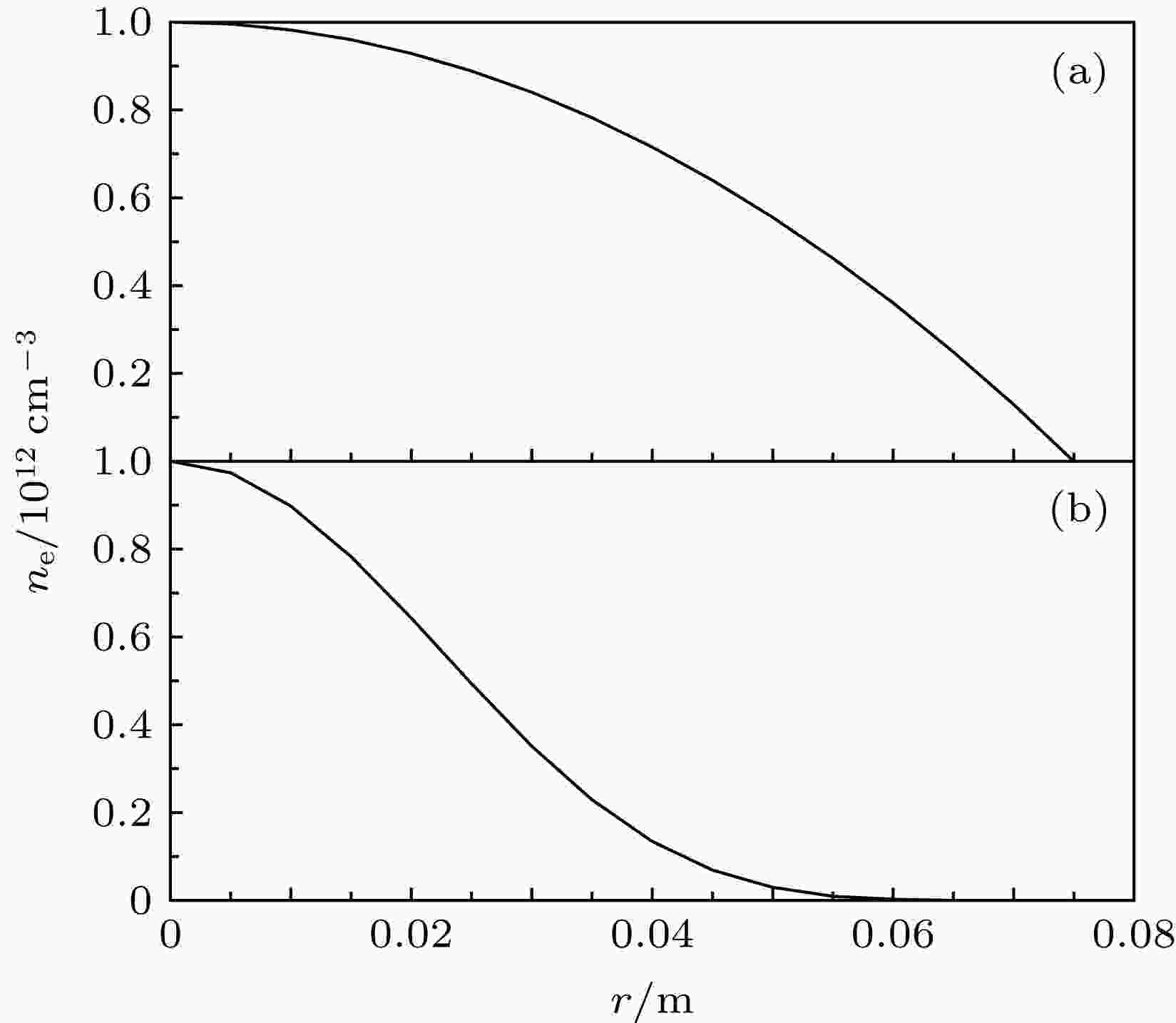 图 2 等离子体径向密度分布 (a) 抛物面分布; (b)高斯分布
图 2 等离子体径向密度分布 (a) 抛物面分布; (b)高斯分布Figure2. Radial profiles of plasma density: (a) Parabolic density profile; (b) Gaussian density profile.
螺旋波属于哨声波, 对于绝缘介质为边界、半径为Ra的等离子体中产生的m = 1螺旋波, 有如下关系成立[25]:



2
3.1.螺旋波天线种类
螺旋波通过TG-H耦合模式将能量传输给电子, 要求天线能很好地将射频源供给的能量耦合传递给螺旋波, 因此天线的选择至关重要. 目前, 用于直线磁约束产生等离子体的螺旋波天线主要有3种, 即Nagoya III型[26]、Boswell型[27]和Half helix型[28]. 这3种天线可有效激发m = +1的波动, 其能量沉积主要是角向模式[29]. 因其结构简单, 可激发高效螺旋波, 因此逐渐应用于各类螺旋波等离子体实验装置中. 从图3(a)中可以看出, 在抛物面密度分布下, Half helix型天线在等离子体中心及边缘处较Nagoya III型、Boswell型天线有较高的径向相对吸收功率, 且Nagoya III型天线和Boswell型天线在等离子体中耦合的效果差不多. 沿轴向的相对吸收功率(图3(c))更能明显地看出各种天线的吸收功率大小, Half helix型天线产生的电磁波在等离子体中的相对吸收功率最高, 其次是Nagoya III型天线, 最差的是Boswell型天线.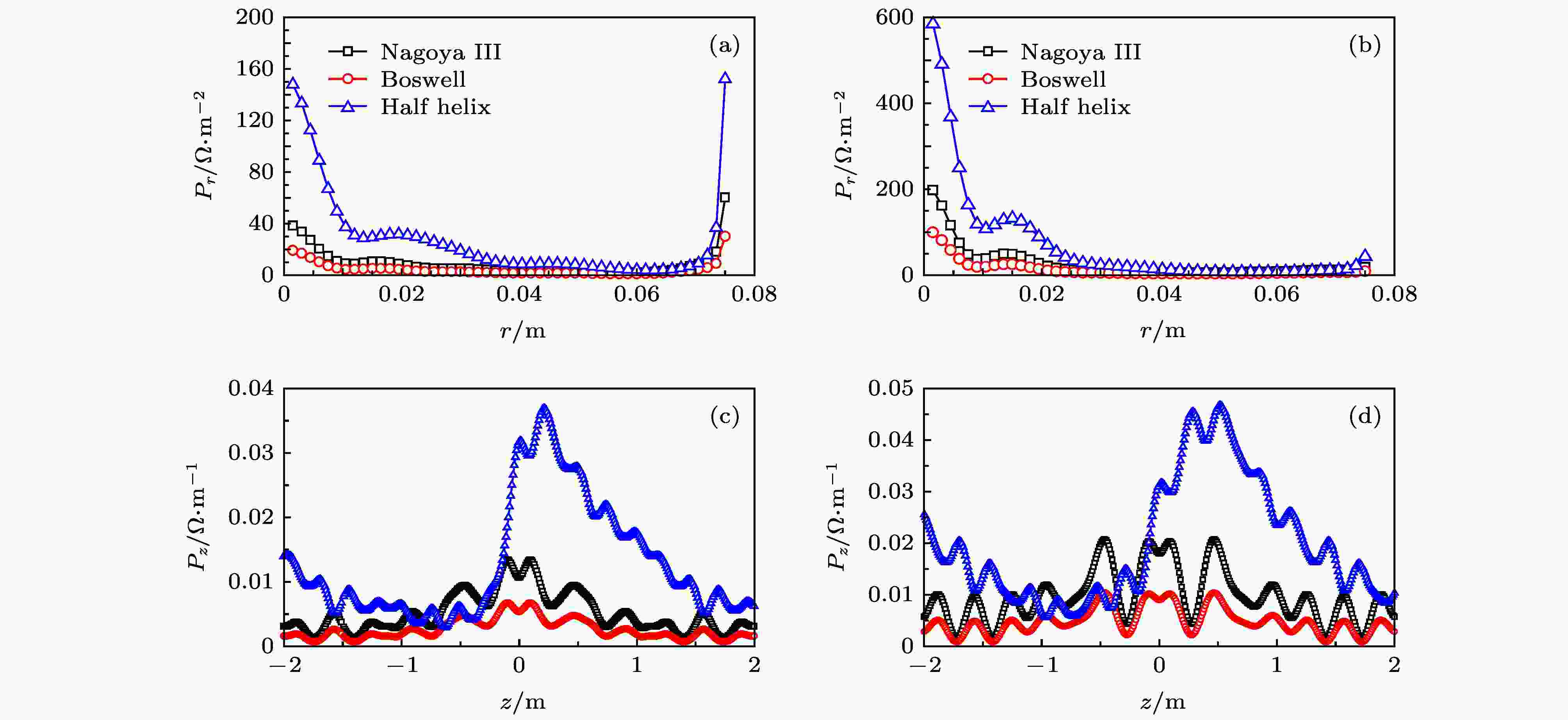 图 3 3种典型的螺旋波天线的径向(z = 0.2 m)和轴向(r = 0.02 m)相对吸收功率 (a)抛物面密度分布下3种天线的径向相对吸收功率; (b)高斯密度分布下3种天线的径向相对吸收功率; (c)抛物面密度分布下3种天线的轴向相对吸收功率; (d)高斯密度分布下3种天线的轴向相对吸收功率
图 3 3种典型的螺旋波天线的径向(z = 0.2 m)和轴向(r = 0.02 m)相对吸收功率 (a)抛物面密度分布下3种天线的径向相对吸收功率; (b)高斯密度分布下3种天线的径向相对吸收功率; (c)抛物面密度分布下3种天线的轴向相对吸收功率; (d)高斯密度分布下3种天线的轴向相对吸收功率Figure3. Relative power absorption in radial (z = 0.2 m) and axial (r = 0.02 m) directions for three typical helicon wave antennas: (a) Radial relative absorption power of three antennas under parabolic density distribution; (b) radial relative absorption power of three antennas under Gaussian density distribution; (c) axial relative absorption of power of three antennas under parabolic density distribution; (d) axial relative absorption of power of three antennas under Gaussian density distribution.
图3(b)和图3(d)是高斯密度分布下的相对吸收功率, 从径向及轴向上都可以看出, 吸收效果最好的是Half helix型天线, 最差的仍是Boswell型天线. 而且在这两种密度分布下, 除了Half helix型天线外, 其余两种天线都关于天线的中心处对称. 这种非轴对称的能量耦合主要与Half helix天线自身结构和静磁场的方向有关, 在很多螺旋波设备中[23]都被观察到过, 且高斯密度分布下的径向相对功率沉积高于抛物面下的.
通过以上分析, 可以得出, Half helix天线产生的是非轴对称的射频能量耦合, 较其他两种天线能激发产生出更高的电子密度. 因此, 在HPPX装置中选用Half helix型天线作为激励天线.
2
3.2.天线长度
天线的长度也是HPPX装置中天线设计的一项重要指标. 在密度均匀的等离子体中, 轴向螺旋波的波长由(23)式得到: λz ≈ 0.1862 m, 由文献[30]可知, 天线和螺旋模式耦合较好时, kz ≈ π/LA, 3π/LA等, 对应的波长为λz ≈ 2LA, 2LA/3, 2LA/5等. 根据HPPX装置尺寸, 取λz ≈ 2LA/5, 则天线长度为LA ≈ 5λz/2 ≈ 0.4655 m, 考察不同天线长度下的吸收功率, 如图4所示.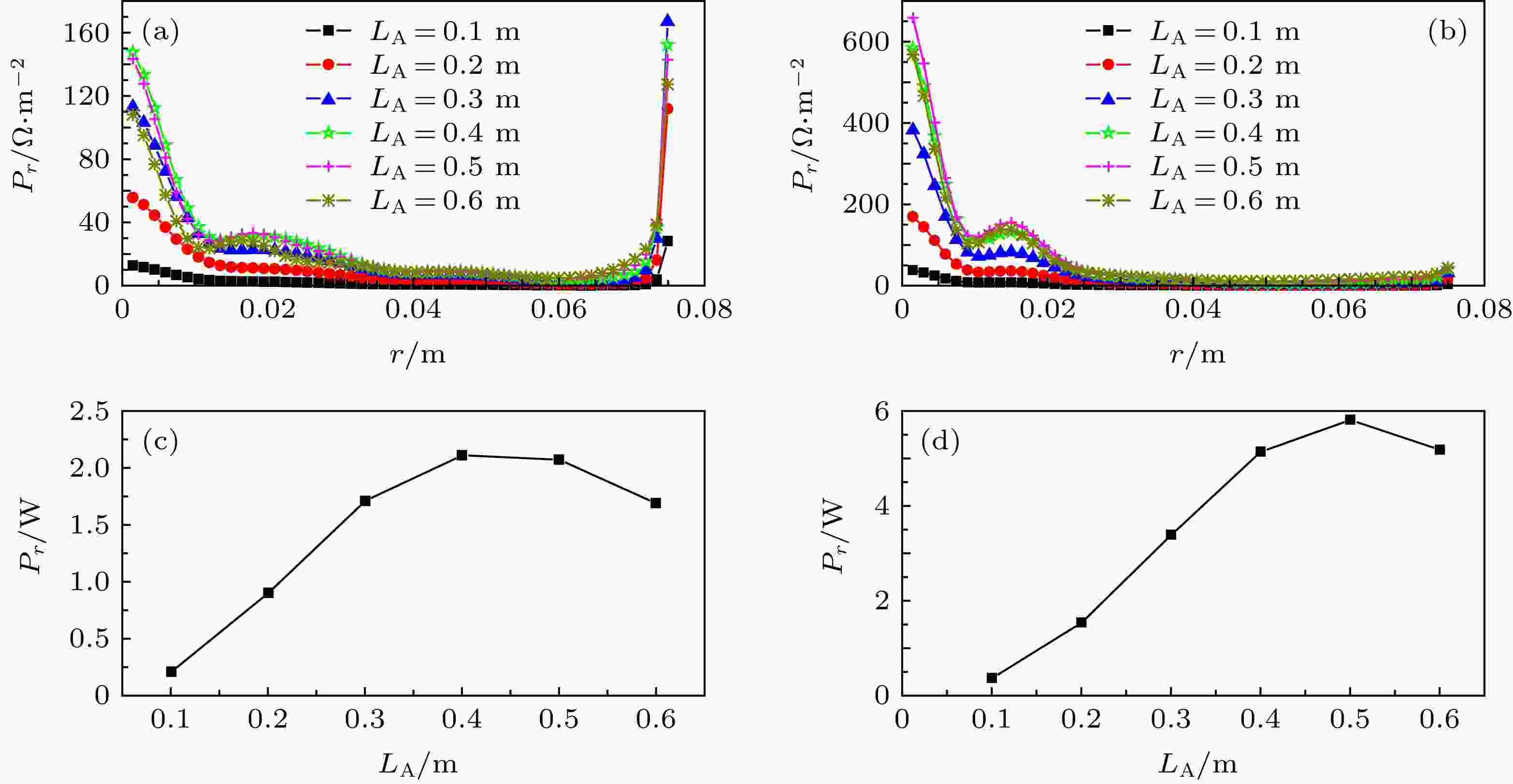 图 4 不同天线长度下的径向(z = 0.2 m)吸收功率 (a)抛物面密度分布下天线长度对径向相对吸收功率的影响; (b)高斯密度分布下天线长度对径向相对吸收功率的影响; (c)抛物面密度分布下径向吸收功率随天线长度的变化曲线; (d)高斯密度分布下径向吸收功率随天线长度的变化曲线
图 4 不同天线长度下的径向(z = 0.2 m)吸收功率 (a)抛物面密度分布下天线长度对径向相对吸收功率的影响; (b)高斯密度分布下天线长度对径向相对吸收功率的影响; (c)抛物面密度分布下径向吸收功率随天线长度的变化曲线; (d)高斯密度分布下径向吸收功率随天线长度的变化曲线Figure4. Relative power absorption in radial (z = 0.2 m) directions for different antenna lengths: (a) Effect of antenna length on radial relative absorption power under parabolic density distribution; (b) effect of antenna length on radial relative absorption power under Gaussian density distribution; (c) radial relative absorption power of different antennas lengths under parabolic density distribution; (d) radial relative absorption power of different antennas lengths under Gaussian density distribution.
从图4(a)可以看出, 在抛物面密度分布下等离子体在中心及边缘的相对吸收功率比中间的要高很多, 并且随着天线长度的增大, 径向相对吸收功率也慢慢变大, 当天线长度等于0.4 m时, 相对吸收功率达到最大, 但之后天线长度再增大, 相对吸收功率却随之减小. 为了更清楚地看清天线长度对吸收功率的影响, 利用公式

在高斯密度分布下, 等离子体的径向相对吸收功率在等离子体中心处且LA = 0.5 m时较强些(图4(b)). 同样利用公式

2
3.3.运行频率
天线的运行频率是一个非常重要的参数, 它影响着天线发射出的螺旋波在等离子体中的耦合效果. 选择6种典型的射频频率仿真对比它们的相对吸收功率(图5). 从图5(a)可以看出, 随着频率的增大, 相对吸收功率在等离子体边缘和中心处都逐渐减小, 而中心处的相对吸收功率降低更为明显, 说明TG波比H波在高频处能吸收更多的功率, 这可能是由于运行频率增加导致快速的电子运动和强烈的静电加热造成的. 减少径向压力, 使碰撞阻尼增大从而增加电子自由路径, 可能有助于将能量吸收从等离子体边缘重新分配到中心处. 图5(b)显示, 随着频率增加, 总体上等离子体中心处的径向吸收明显降低, 而边缘处变化不大, 这是由于高斯型密度分布下边缘处密度梯度变化较抛物面型分布平缓许多. 从这2幅图中可以看出, 并不是运行频率越高, 相对吸收功率就越高. 在径向吸收功率上, f = 13.56 MHz时的吸收最好, 之后随着运行频率的增加, 相对吸收功率下降得很快, 这从图5(c)和(d)中也可以明显地看出来. 因此, 在HPPX实验中13.56 MHz是螺旋波等离子体常用的频率[31]. 再次, 从图5中可以看出高斯分布下的等离子体的相对吸收功率要比抛物面时的大, 这和前面提到的基本一致.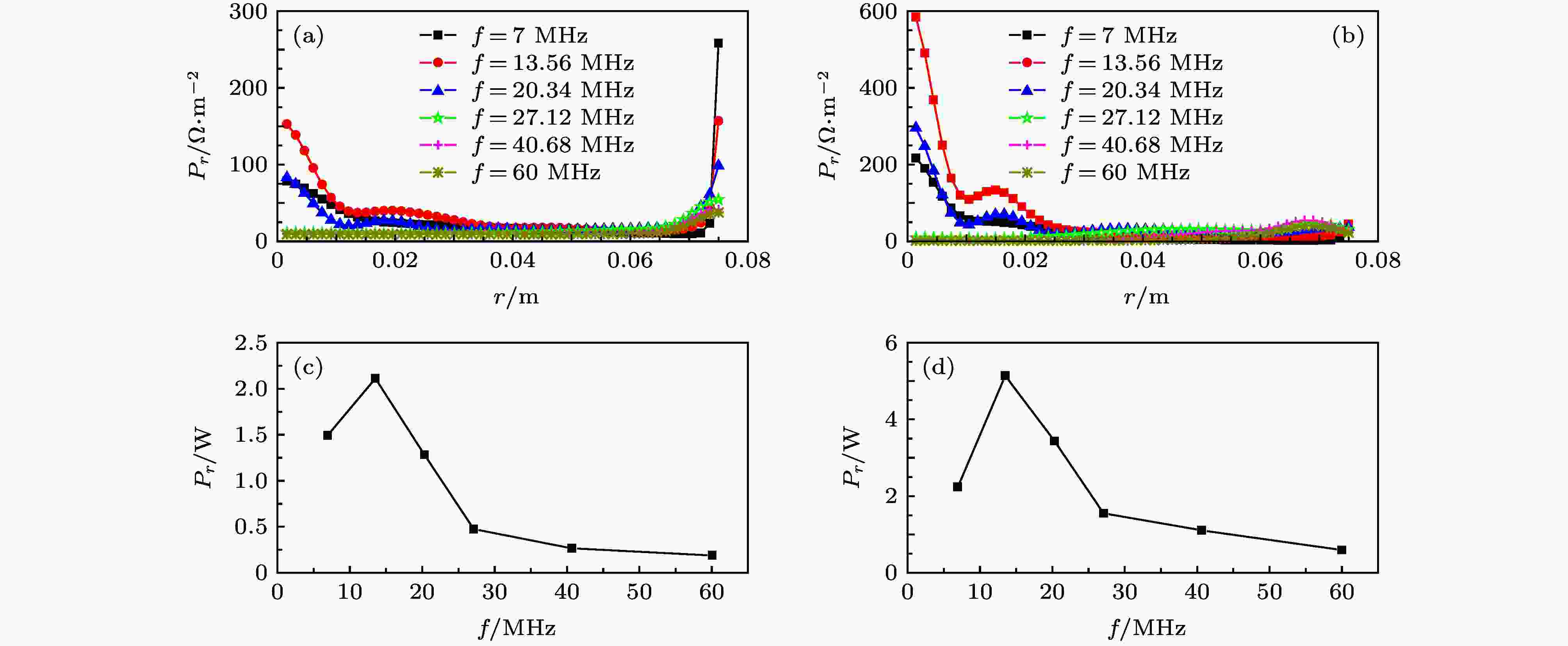 图 5 不同运行频率下的径向(z = 0.2 m)吸收功率 (a)抛物面密度分布下天线运行频率对径向相对吸收功率的影响; (b)高斯密度分布下天线运行频率对径向相对吸收功率的影响; (c) 抛物面密度分布下径向吸收功率随运行频率的变化曲线; (d)高斯密度分布下径向吸收功率随运行频率的变化曲线
图 5 不同运行频率下的径向(z = 0.2 m)吸收功率 (a)抛物面密度分布下天线运行频率对径向相对吸收功率的影响; (b)高斯密度分布下天线运行频率对径向相对吸收功率的影响; (c) 抛物面密度分布下径向吸收功率随运行频率的变化曲线; (d)高斯密度分布下径向吸收功率随运行频率的变化曲线Figure5. Relative power absorption in radial (z = 0.2 m) directions for various operating frequencies: (a) Effect of various operating frequencies on radial relative absorption power under parabolic density distribution; (b) effect of various operating frequencies on radial relative absorption power under Gaussian density distribution; (c) radial relative absorption power of various operating frequencies under parabolic density distribution; (d) radial relative absorption power of various operating frequencies under Gaussian density distribution.
2
3.4.静磁场强度
等离子体中引入外部约束静磁场, 使得螺旋波深入等离子体柱中传播, 获得了高的功率耦合效率. 静磁场大小的改变对带电粒子的运动轨迹产生影响, 改变了各种粒子间的碰撞频率, 从而致使等离子体介电张量随之变化. 同时静磁场对电子与离子绕磁力线的回旋尺度的影响导致带电粒子的能量吸收区域发生改变, 从而产生波在等离子体中能量沉积的不均匀性问题, 可见磁场对等离子体的影响比较大. 设定磁场值从100 Gs (1 Gs = 10–4 T)到1000 Gs之间变化, 采样间隔为50 Gs, 计算得到等离子体的相对径向吸收功率(图6).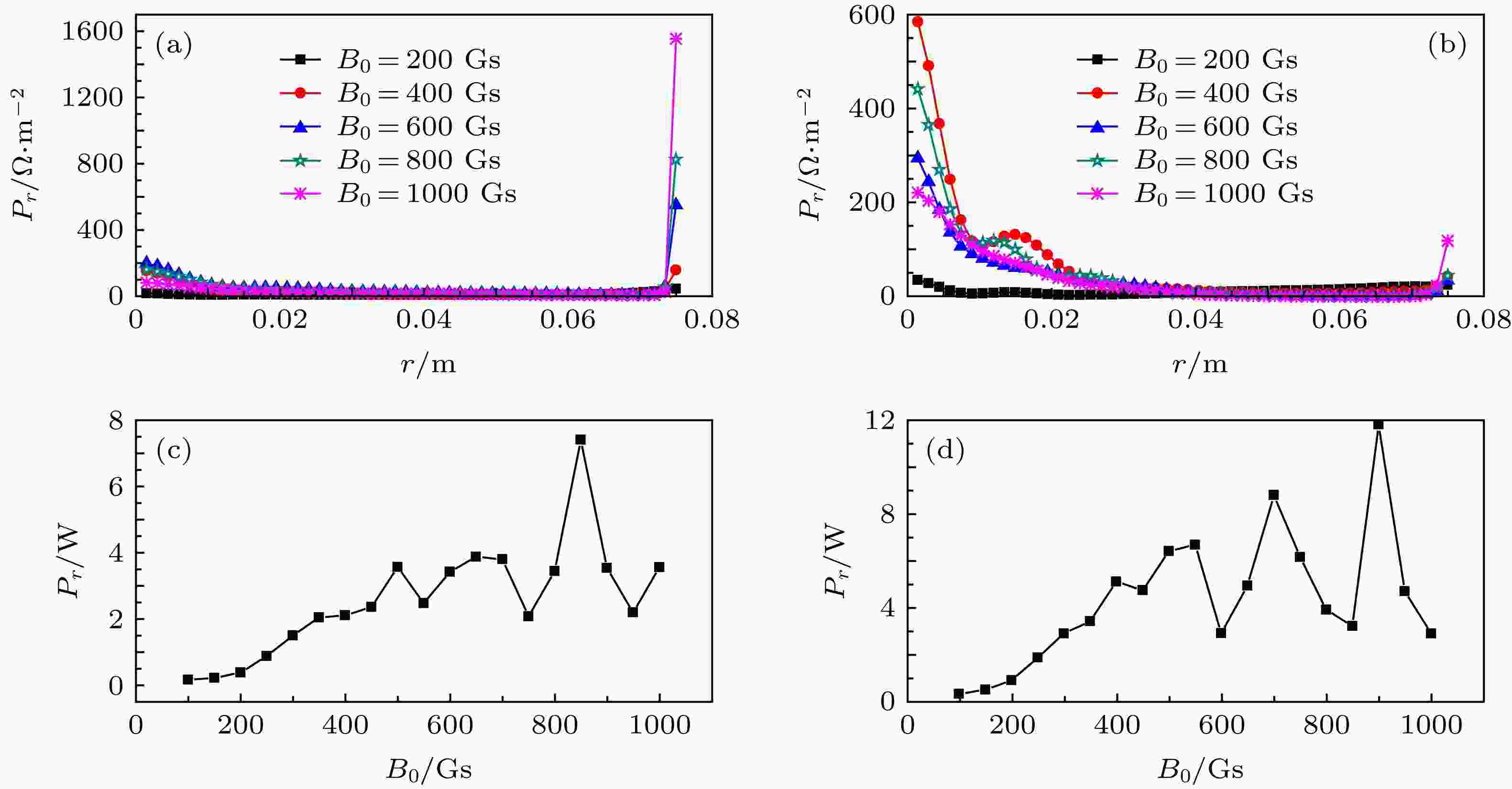 图 6 不同静磁场下的径向(z = 0.2 m)吸收功率 (a)抛物面密度分布下磁场对径向相对吸收功率的影响; (b)高斯密度分布下磁场对径向相对吸收功率的影响; (c)抛物面密度分布下径向吸收功率随磁场强度的变化曲线; (d)高斯密度分布下径向吸收功率随磁场强度的变化曲线
图 6 不同静磁场下的径向(z = 0.2 m)吸收功率 (a)抛物面密度分布下磁场对径向相对吸收功率的影响; (b)高斯密度分布下磁场对径向相对吸收功率的影响; (c)抛物面密度分布下径向吸收功率随磁场强度的变化曲线; (d)高斯密度分布下径向吸收功率随磁场强度的变化曲线Figure6. Relative power absorption in radial (z = 0.2 m) directions for various static magnetic intensity: (a) Effect of various magnetic intensity on radial relative absorption power under parabolic density distribution; (b) effect of various magnetic intensity on radial relative absorption power under Gaussian density distribution; (c) radial relative absorption power of various magnetic intensity under parabolic density distribution; (d) radial relative absorption power of various magnetic intensity under Gaussian density distribution.
不同的磁场条件下, 螺旋波和TG波的径向波长不同且所受阻尼不同, 其在等离子体中沿径向的传播距离或者功率耦合范围就会有较大的差异. 在磁场很低时, 由于磁场太小, 从色散关系上分析TG波被禁止传播, 此时不存在TG波(图6(a)). 随着磁场强度增大, 在等离子体边缘处的相对吸收功率迅速增大, 这是由于在强磁场下TG波所受的阻尼较大, 径向波长较短, 很难在等离子体柱中传播, 所以TG波影响范围由径向全场缩减至边界的极小范围[20], 同时能量的吸收逐渐集中于等离子体-真空边界处, 说明外加稳恒磁场较大不利于TG波的深入传播, 较高的磁场限制TG波的传播, 从而造成径向能量分布的严重不均. 与抛物面分布不同的是, 在高斯分布中(图6(b)), H波所受阻尼小, 在等离子体内的穿透能力强, 可沿径向传播距离远, 等离子体中的功率沉积主要发生在等离子体中心位置. 随着磁场的增大, TG波和H波耦合模式发生转变, TG波会被抑制, H波可以在磁化等离子体柱内部进行传播, 将能量耦合给等离子体.
从图6(c)和图6(d)中可以看出, 在某些磁场强度处有一些功率峰值点, 说明该处天线和等离子体有较强的耦合, 而总体的耦合程度在上升. 在HPPX装置的实验设计中, 可以参考仿真结果, 选择合适的磁场值, 获得更高的等离子体吸收功率.
2
3.5.轴心等离子体密度
同样, 径向等离子体密度的非均匀性导致径向扰动电场的产生, 造成带电粒子的径向漂移, 从而改变了各种粒子间的碰撞频率, 进而使等离子体色散方程中介电张量也随之改变, 最终对等离子体的径向功率沉积产生影响. 设定密度值从1 × 1012到1 × 1013 cm–3之间变化, 每隔0.3 × 1012 cm–3进行一次采样, 计算得到等离子体吸收功率(图7). 在抛物面密度分布下(图7(a)), 当密度较低时, 等离子体中心处的吸收功率较低, 大部分功率集中在等离子体边缘部分. 这是由于TG波强烈的边缘加热, TG波是短波长准静电波, 当波在等离子体中向中心运动时, TG迅速衰减, 而H波只有微弱的阻尼, 能够深入等离子体中心处, 因此边缘处H波功率转换到TG波中. 但是随着密度逐渐变大, 等离子体中心的吸收有所下降. 在高斯密度分布下(图7(b)), 密度低时等离子体中心处的相对吸收功率较高, 但随着密度的逐渐增大, 中心处的吸收功率也慢慢变小, 边缘处变化不大明显.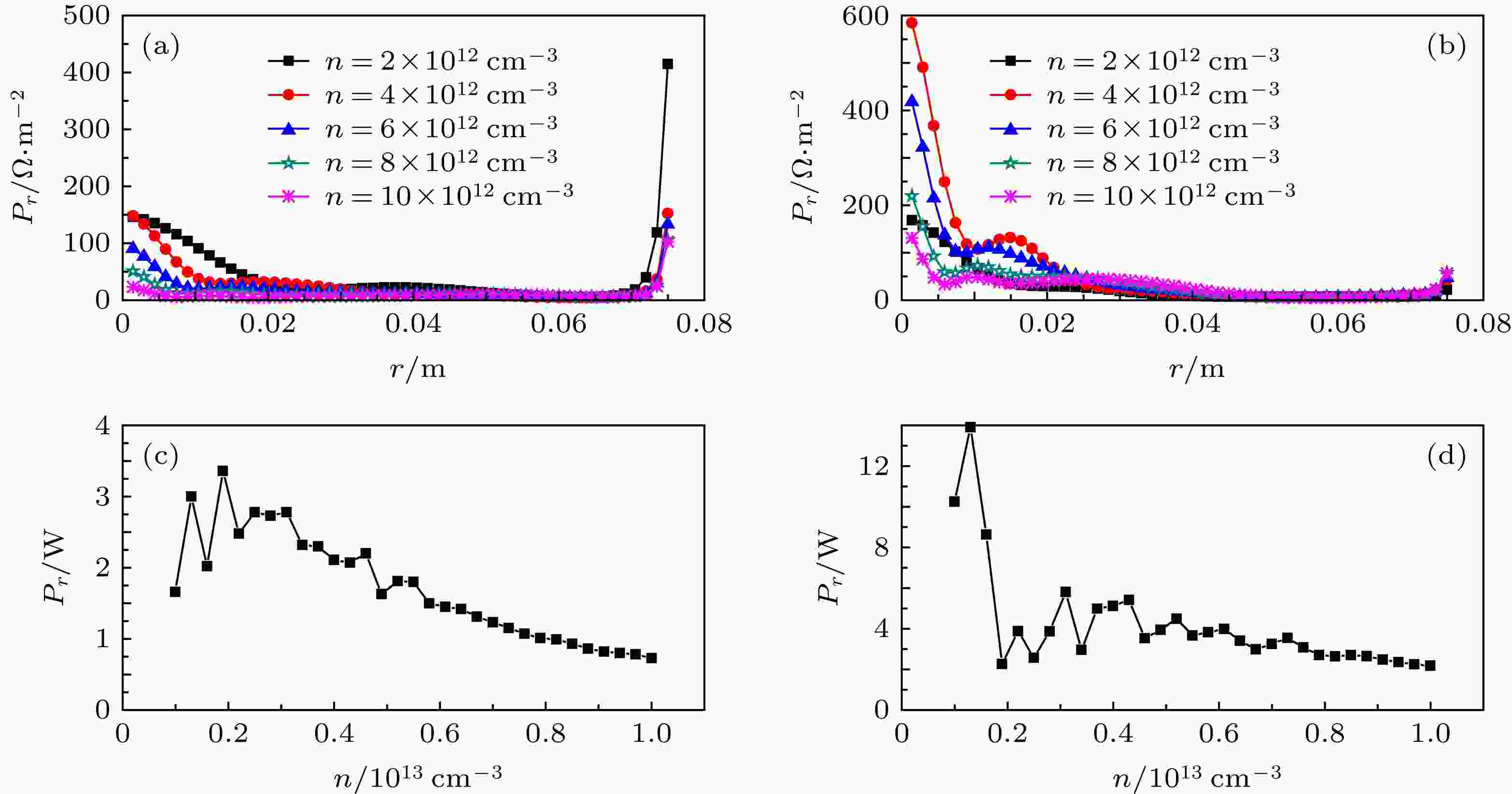 图 7 不同密度下的径向(z = 0.2 m)吸收功率 (a)抛物面密度分布下密度对径向相对吸收功率的影响; (b)高斯密度分布下密度对径向相对吸收功率的影响; (c)抛物面密度分布下径向吸收功率随密度大小的变化曲线; (d)高斯密度分布下径向吸收功率随密度大小的变化曲线
图 7 不同密度下的径向(z = 0.2 m)吸收功率 (a)抛物面密度分布下密度对径向相对吸收功率的影响; (b)高斯密度分布下密度对径向相对吸收功率的影响; (c)抛物面密度分布下径向吸收功率随密度大小的变化曲线; (d)高斯密度分布下径向吸收功率随密度大小的变化曲线Figure7. Relative power absorption in radial (z = 0.2 m) directions for various density: (a) Effect of various density on radial relative absorption power under parabolic density distribution; (b) effect of various density on radial relative absorption power under Gaussian density distribution; (c) radial relative absorption power of various density under parabolic density distribution; (d) radialrelative absorption power of various density under Gaussian density distribution.
从图7(c)和(d)可以看出, 在径向上某些密度处有一些功率峰值点, 而总体的耦合程度在下降, 这意味着并不是密度越大, 等离子体吸收波的情况越好, 而是在某一特定的密度下吸收效果最好. 同样地, 等离子体在高斯分布下比抛物面分布下有着更高的相对吸收功率. 因此通过对等离子体中不同密度下的吸收功率模拟, 能为HPPX实验指导提供良好的理论依据.
2
3.6.感生电磁场与电流密度
为了进一步研究HPPX装置中螺旋波与等离子体的耦合, 图8给出了螺旋波等离子体的电场强度、感应磁场及电流密度的分布. 从图8(a)中可以看出, 在r < 0.07 m时抛物面下的电场强度和高斯分布下的电场强度相差不大, 越靠近边缘处高斯分布下的电场值越大, 这是因为两种密度分布下等离子体边缘处电子密度较小, 边缘处趋肤效应较小, 使得电子与离子碰撞几率增加, 相对于边缘处的电阻增大, 必然造成边缘处负载电压增大, 进而感生电场显著增大. 总体来说高斯分布下的电场强度径向分布较抛物面密度分布下的要大. 从图8(b)和图8(c)中可以看出在, 等离子体中心处高斯分布下的感生磁场和电流密度比抛物面下的分布大很多, 而靠近边缘处的磁场和电流逐渐变小, 这是因为从密度分布位型上看, 高斯分布时中心处电子密度最高, H波能够深入中心处传播引起电子运动速度加大进而导致电流密度增大, 从中心至r = 0.05 m处高斯分布下密度梯度变化较大, 由电流密度公式J = eneve (其中e为电子电荷量, ne 为电子密度, ve为电子速度)可以看出, 随着密度的降低, 磁感应强度及电流大小逐渐变小的趋势较为明显, 抛物面分布情况下, 磁感应强度及电流变化趋势相对平缓些, 说明场能量较均匀地分布在等离子体中.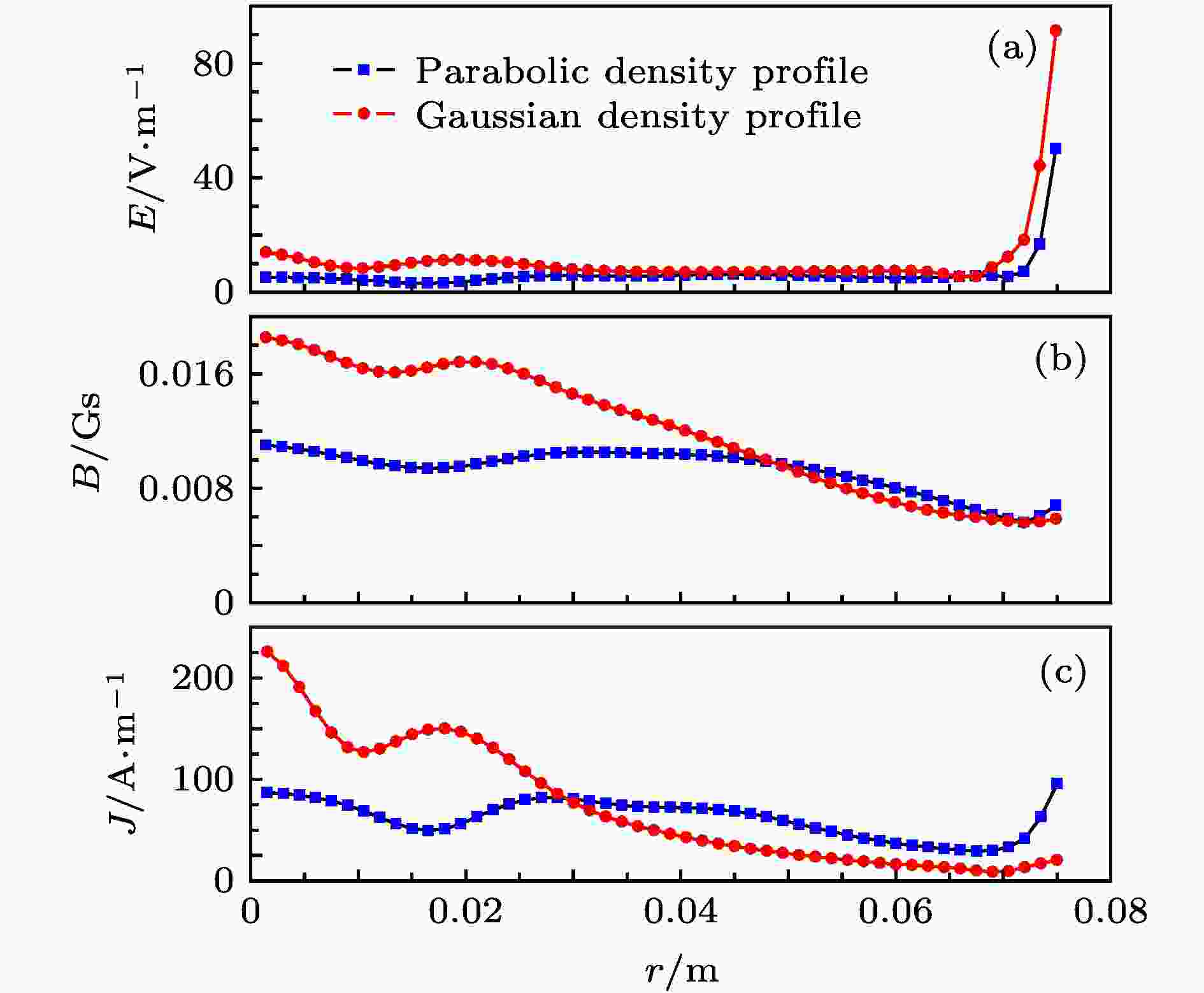 图 8 不同密度分布下的等离子体径向(z = 0.2 m)感应电场、感应磁场及电流密度分布
图 8 不同密度分布下的等离子体径向(z = 0.2 m)感应电场、感应磁场及电流密度分布Figure8. Radial profiles (z = 0.2 m) of wave electric field, magnetic field and current density in parabolic density profile and Gaussian density profile.
1) Half helix螺旋波天线能够产生非轴对称的射频能量耦合, 较Nagoya III型天线和Boswell型天线可激发出更高的电子密度; 通过理论分析及仿真计算, 得出天线长度为0.4 m, 运行频率为13.56 MHz时等离子体与天线有着较好的能量耦合, 从而得到了HPPX装置中螺旋波系统发射天线的最优设计;
2)外加稳恒的静磁场时, 螺旋波天线在等离子体中激发出两种不同的性质的波, 即H波和TG波, 在抛物面密度分布下, 随着磁场的增大, TG波所受的阻尼大, 很难在等离子体柱中传播, 能量的吸收逐渐集中于等离子体-真空边界处, 说明较高的磁场限制了TG波向中心处的传播; 而在高斯分布中, 随着磁场增加, TG波会被抑制, H波所受的阻尼小, 可以在磁化等离子体柱内部进行传播, 将能量耦合给等离子体; 通过对径向积分计算可以看出, 吸收功率在多个磁场处有不同的峰值功率点, 且整体的耦合趋势是在上升的;
3)当轴心等离子体密度增加时, 在抛物面密度和高斯密度分布下, H波所受的阻尼增大, 限制了H波的传播, H波的功率转换到TG波中; 同样, 通过积分可发现吸收功率在多个密度处有不同的峰值功率点, 但整体的耦合趋势却是在下降的;
4)总体上高斯密度分布下感应电场、感应磁场及电流大小较抛物面密度时要大, 但由于抛物面密度梯度变化较小, 等离子体中各场值和电流值较为平缓, 所以能量较均匀地分布在等离子体中, 此特点在之前计算功率沉积时已有体现.
以上这些分析可为HPPX装置的螺旋波天线设计及相关物理实验提供参考, 同时也能为螺旋波等离子体的放电机理研究提供一定的技术支持.
