摘要: 本文模拟研究了背景电离层在一维和二维扰动下产生等离子体泡的过程, 在模拟过程中引入行进式电离层扰动(traveling ionosphere disturbances, TIDs)模型激发生成电子密度的二维扰动, 同时通过改变化学复合率来研究不同复合率对等离子体泡结构形态的影响. 模拟结果表明, 复合率对等离子体泡的生成速度有较大影响, 复合率越大, 激发等离子体泡所需时间越长. 另外, 在二维扰动情况下电离层生成等离子体泡的速度要比一维扰动情况下的速度慢. 在一维扰动情况下, 不同复合率对等离子体泡结构形态影响不大, 而在TIDs激发的等离子体泡中, 不同复合率对等离子体泡的结构形态有较大影响. 在较小复合率的情况下, TIDs激发的等离子体泡可以产生分叉结构, 并伴有大量小尺度的等离子体泡结构, 同时模拟结果存在等离子体泡底部收缩现象. 模拟结果还表明, 当存在大量小尺度等离子体泡时, 单个等离子体泡周围的极化电场方向在非线性的演化过程中可能会发生变化, 因此并不是所有底部等离子体泡都能够抬升到电离层顶部, 只有其周围极化电场方向一直是东向的等离子体泡, 才能够进一步抬升到电离层顶部.
关键词: 化学复合率 /
赤道等离子体泡 /
行进式电离层扰动 /
数值模拟 English Abstract Numerical simulation of recombination rate effect on development of equatorial plasma bubbles Jiang Chun-Hua Zhao Zheng-Yu School of Electronic Information, Wuhan University, Wuhan 430072, China Fund Project: Project supported by the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 41604133)Received Date: 30 January 2019Accepted Date: 02 July 2019Available Online: 01 October 2019Published Online: 05 October 2019Abstract: Plasma bubbles in the ionosphere have a significant effect on radio wave communication and navigation. Under the worst condition, it will fail to function the systems relying on the ionosphere. On the other hand, the physical mechanisms of evolution and diurnal variations of the plasma bubbles in the ionosphere are still unclear. Therefore, it is still worthy to simulate the plasma bubbles in the ionosphere for radio wave propagation and science. In this study, the equatorial plasma bubbles induced by one- and two- dimensional disturbance in the ionosphere are simulated, where traveling ionospheric disturbance (TID) is used to produce the two-dimensional disturbance in the ionosphere. The dispersion relationship of gravity wave is used to represent the corresponding wavelength of TID in this study. More importantly, we investigate the effect of recombination rate on the development of plasma bubbles by numerical simulation. The simulation results show that the recombination rate of the plasma in the ionosphere has a significant effect on the development of plasma bubbles. The greater the recombination rate, the more time it takes to produce the plasma bubbles. For one-dimensional disturbance in the ionosphere, there is no significant effect in the structure of plasma bubbles for the recombination rate of the plasma. However, the recombination rate plays a significant effect on the structure of plasma bubbles induced by TID. When the recombination rate is less in numerical simulation, the complex structure including bifurcation, plume-like structures, and pinching of plasma bubbles can occur in the development of bubbles. In contrast, the structure of plasma bubbles is simpler when the recombination rate is greater in simulation. As a result, the recombination rate of the plasma is a significant factor for simulating the plasma bubbles in the ionosphere. The greater recombination rate can result in the slowing down of equatorial plasma bubbles and the simplifying the structure of the bubbles as well. In addition, it is found that not all of plasma bubbles at the bottom of the ionosphere can grow to the top of the ionosphere when many bubbles occur on the bottom side. The direction of the polarization electric field near the bubbles can be changed in the non-linear development of the bubbles. Therefore, only the bubbles where the polarization electric field is always eastward can develop to the topside.Keywords: chemical recombination rate /equatorial plasma bubble /travelling ionospheric disturbances /numerical simulation 全文HTML --> --> --> 1.引 言 电离层F层区域经常存在一种不均匀体结构, 该结构的存在会导致无线电波在传播过程中信号的幅频特性发生明显的变化, 从而导致无线电信号的闪烁. 这种F层不均匀体结构一般称之为等离子体泡或赤道扩展F. 该不均匀体结构主要分布在磁赤道和高纬地区, 但是在中低纬度地区也经常可以观测到, 并且大部分出现在夜晚. 当短波通信、星载遥感以及卫星导航等无线电通信导航系统的电波信号发生电离层反射或穿透电离层, 存在这种等离子体泡结构时, 会严重影响通信和导航的质量, 极端情况下有可能导致这些无线电系统无法正常工作. 另外, 电离层中等离子体泡结构产生的物理过程及其时空演化, 一直是空间物理学领域的一个难点和热点问题, 是人们能够有效预测预报电离层等离子体泡结构出现的理论基础. 因此, 对于电离层等离子体泡结构的研究, 具有重要的工程应用价值及科学意义.[1 -3 ] , 而其触发机制主要是由于电场[4 -5 ] 、中性风[4 ] 或者重力波[6 -7 ] 等因素在电离层F层底部产生初始扰动. Rayleigh-Taylor不稳定性可以用来解释电离层F层底部的等离子泡的产生, 但是F层顶部的等离子泡结构却无法用Rayleigh-Taylor的线性理论来解释, 因为在电离层F层顶部其线性理论是稳定状态, 不会产生等离子体泡结构. 因此非线性的数值模拟研究成为研究等离子体泡结构演化的重要手段. Scannapieco和Ossakow[8 ] 首次利用非线性数值模拟方法研究了等离子体泡从电离层F层底部发展到其顶部的演化过程. 此后, 国内外大量****开展了电离层F层中等离子体泡的非线性数值模拟研究. Zalesak和Ossakow进一步研究了不同扰动尺度[9 ] , 中性风和背景佩德森电导率[10 ] 对扩展F发展的影响. Sekar等[4 ] 模拟了垂直中性风和电场对赤道扩展F发展的影响. 谢红和肖佐[11 ] 模拟了中低纬地区扩展F的发展过程, 认为Rayleigh-Tyalor不稳定性和东向电场一起作用可以成为中低纬扩展F发展的一种机制. Huang和Kelley[7 ] 模拟了重力波对赤道扩展F的影响, 并引入了二维电子密度的扰动. 高泽等[12 ] 模拟了一维电子密度扰动的不同波长对扩展F的影响. 近年来, 用来研究扩展F的三维数值模型也发展了起来, 比较著名的有SAMI3/ESF[13 ] 和high-resolution bubble(HIRB)模型[14 ] . 有关赤道等离子体泡模拟研究的详细进展可以参考相关文献综述[15 ] .[13 ] , 二维电场行进式扰动模型[16 ] 和二维中性风扰动模型[17 ] . HIRB模型使用的是一维正弦电子密度扰动[14 ] . Huang和Kelley[7 ] 利用重力波作为激发源, 提供了二维电子密度扰动, 即重力波引起的电离层行进式扰动(traveling ionosphere disturbances, TIDs), 其水平扰动参数和垂直扰动参数是存在一定的关联的[18 -21 ] . 本文结合实际扰动情况, 利用TIDs模型给出的电子密度的二维初始扰动, 研究其对赤道等离子体泡结构形态发展的影响. 此外, 除了背景中性风和电场, 电子离子的复合率也会对等离子体泡的发展过程产生重要影响[22 ] . 由于电离层F层夜晚所处高度较高, 其化学复合率很小[23 ] , 所以一般认为F层等离子体主要以输运过程为主. 根据前人的研究结果, 发现部分****完全忽略了夜晚F层的化学复合[10 ] , 即在模拟过程中化学复合率设置为0[10 ] , 来模拟等离子体泡激发的过程, 而有部分****的研究工作则考虑了夜晚F层化学复合过程, 引入了等离子体的复合系数[9 ] . 鉴于此, 本文通过引入不同量级的复合系数来研究不同复合率对等离子体泡形态发展的影响.2.基本理论 22.1.TIDs扰动模型 2.1.TIDs扰动模型 在本文中, (1 )式用来表示由TIDs扰动引起的二维电子密度初始扰动.${N_0}$ 表示背景电子密度, A 表示TIDs的扰动幅度, ${k_x}$ 表示水平波数, ${k_z}$ 表示垂直波数, ${\phi _0}$ 是扰动的初始相位.[24 ] 和Miyoshi等[25 ] 的相关工作表明, 通过大气重力波色散关系来计算TIDs的相关参数是可行的. 因此, 在TIDs扰动过程中, 当垂直波长小于等于500 km时[20 ] , 本文TIDs扰动的垂直波长和水平波长可以近似用(2 )式[18 ] 表示.$\omega $ 表示扰动角频率, ${\omega _g}$ 表示Brunt-Vaisala频率(在本文中, ${\omega _g}$ 约等于 $2{\rm{\pi }}/(14\ \min )$ [26 ] , ${\lambda _x}$ 表示水平波长, ${\lambda _z}$ 表示垂直波长.2.2.等离子体泡理论模型 -->2.2.等离子体泡理论模型 等离子体泡的非线性发展过程主要由电子和离子的连续性方程、运动方程以及电流连续性方程控制. 在电离层F层区域, 假设只存在O+ 离子, 忽略压力项, 则整个方程表示如下所示[15 ] :N 表示电子或者离子密度, 在准中性条件下, $N = {N_e} = {N_i}$ ; $ V$ 表示电子或者离子的速度; ${\nu _R}$ 表示电子或离子复合系数; ${N_0}$ 表示背景电子密度; ${M_e}$ 和${M_i}$ 分别表示电子和离子的质量; ${ V_e}$ 和${ V_i}$ 分别表示电子和离子的速度; $ E$ 表示电场, $ E = { E_0} - \nabla \varphi $ , ${ E_0}$ 是背景电场, $\varphi $ 是扰动电势; $\vec B$ 表示背景磁场强度; $ U$ 表示中性风速; ${\upsilon _{en}}$ 和${\upsilon _{in}}$ 分别表示电子和离子与中性气体分子的碰撞频率; $ g$ 表示重力加速度; q 表示单位电荷; $ J$ 表示总的电流密度.4 -5 )的惯性项(方程等式左边项为0)[15 ] , 则可计算得到电子和离子速度.3 )和(6 ), 并且令$ E = { E_0} - \nabla \varphi $ , ${ E_0}$ 是背景电场, $\varphi $ 是扰动电势, 则方程可以转化成如下形式:x 轴表示东西方向, 向东为正, z 轴表示垂直方向, 向上为正, y 轴表示磁场方向, 向北为正, 只考虑x-z 二维平面, 即$\nabla = \dfrac{\partial }{{\partial x}}\hat x + \dfrac{\partial }{{\partial z}}\hat z$ , 则方程(8 )和(9 )可以进一步转化成如下形式:$\nabla \cdot = \dfrac{\partial }{{\partial x}} + \dfrac{\partial }{{\partial z}}$ , 则方程可进一步转化为$\alpha $ 是本文中引入的一个复合率因子系数$\alpha $ , 分别选取不同值(如: 0, 0.01, 0.1或1等), 用来研究在不同复合率情况下, 电子离子复合率对等离子体泡形态发展的影响. 在模拟计算时, 碰撞频率${\upsilon _{in}}$ 和复合率${\nu _R}$ 采用Zalesak和Ossakow[9 ] 提供的数值.3.模拟与讨论 本文利用方程(14 -15 )对等离子泡进行非线性数值模拟. 在数值模拟等离子体泡的发展过程时, Yokoyama[15 ] 认为constrained interpolation profile (CIP)方法比常用的FCT方法效果更好, 因此本文通过CIP方法[27 ] 求解方程(14 ). 采用Krylov子空间方法biconjugate gradient stabilized (BiCGSTAB)来求解方程(15 ), 该方法比常用的SOR方法收敛更快.图1 所示是本次模拟所采用的背景水平电场的剖面, 类似于HIRB模型[14 ] , 在大约450 km时, 东向电场值开始指数衰减. 图2 所示是本次模拟采用的背景电子密度剖面, 图3 所示是存在TIDs扰动时的二维电子密度, 其中TIDs的水平波长为300 km, 周期为40 min, 这是一个典型的中尺度TIDs. 本文利用图3 所示的二维电子密度作为非线性模拟的初始电子密度结构. 为了和一维电子密度扰动进行比较, 本文将同时模拟波长为300 km, 周期为40 min的正弦扰动下等离子体泡的发展过程.图 1 水平东向电场值随高度的变化Figure1. Altitudinal variation of eastward electrical field in the simulation.图 2 背景电离层电子密度剖面Figure2. Electron density profile in the background ionos phere.图 3 存在TIDs(波长为300 km, 周期为40 min)扰动的背景电离层Figure3. Background ionosphere with TIDs (horizontal wavelength is 300 km and period is 40 min).x 轴和z 轴网格点同为201个, 网格间距均为2 km, 垂直方向的起始高度为250 km, 时间步长为0.5 s, 水平方向采用周期边界条件, 垂直方向边界条件采用$\partial N/\partial z = 0$ 和$\partial \varphi /\partial z = 0$ .3.1.正弦扰动激发等离子体泡 3.1.正弦扰动激发等离子体泡 图4 —6 所示是波长为300 km, 周期为40 min的正弦扰动激发的等离子体泡的发展过程, 该扰动属于一维(x 轴方向)电子密度扰动, 分别对应复合率因子$\alpha $ 为1, 0.1和0.01的模拟结果. 根据线性Rayleigh-Taylor不稳定性的增长率, 光化学复合率越大, 增长率越小[22 ] . 从图4 —6 可知, 当$\alpha = 1$ 时, 等离子体泡发展到450 km, 大约需要1900 s; 当$\alpha = 0.1$ , 则需要1750 s; 当$\alpha = 0.01$ 时, 等离子体泡所需时间最短, 大约需要1700 s即可. 非线性的模拟结果进一步验证了复合率对等离子体泡增长率的贡献. 另外, 从图4 —6 可知, 电子密度的一维正弦扰动所激发的等离子体泡是东西对称的[8 -9 ] , 而复合率并不会明显影响该扰动下的等离子体泡的形态特征. 但是实际观测结果显示等离子泡是东西非对称性的, 为了研究等离子体泡的东西非对称性, Zalesak等[10 ] 引入了背景中性风, 模拟结果显示水平东向中性风会导致等离子体泡向西偏转. 但是, 电子密度的一维扰动是不符合实际扰动情况的, 这对认识等离子体泡的激发过程很有帮助, 而对于等离子泡的结构形态研究, 则显得过于简单. 本文下一节将重点讨论TIDs所激发的等离子体泡的发展过程.图 4 $\alpha = 1$ 时一维正弦扰动产生等离子体泡的发展过程Figure4. Evolution of plasma bubbles caused by one dimensional disturbance with $\alpha = 1$ .图 6 $\alpha = 0.01$ 时一维正弦扰动产生等离子体泡的发展过程Figure6. Evolution of plasma bubbles caused by one dimensional disturbance with $\alpha = 0.01$ .图 5 $\alpha = 0.1$ 时一维正弦扰动产生等离子体泡的发展过程Figure5. Evolution of plasma bubbles caused by one dimensional disturbance with $\alpha = 0.1$ .3.2.TIDs激发等离子体泡 -->3.2.TIDs激发等离子体泡 为了研究二维电子密度扰动对激发等离子体泡的影响, 本文引入了简单的TIDs模型. 本文中的TIDs模型与Huang和Kelley[7 ] 工作中最大的区别是根据实际情况, 利用大气重力波的色散关系给出了TIDs的垂直波长和水平波长之间的关系. 图7 —图8 所示是由TIDs激发产生的等离子体泡的发展过程, 其对应的复合率因子$\alpha $ 分别为1和0.1. 由图7 —图8 可知, 相比较一维扰动激发等离子体泡的生成速度, 二维扰动激发等离子体泡的速度较慢. 根据Rayleigh-Taylor不稳定性的线性增长率, Huang和Kelley[7 ] 计算得到一维扰动和二维扰动增长率的比值关系$\dfrac{{\gamma \left( {1D} \right)}}{{\gamma \left( {2D} \right)}} = \dfrac{{k_x^2 + k_z^2}}{{k_x^2}}$ , 其中${k_x}$ 和${k_z}$ 分别表示x 轴和z 轴方向上的扰动波数. 从二者的比值可知, 等离子体泡一维扰动的线性增长率大于二维扰动的情况, 并且当x 方向的波长比z 方向的波长越大, 二维扰动下的等离子泡的增长速度越慢. 当$\alpha = 1$ 时, 从图7 可知, 除了背景电子密度东西不对称外(由于TIDs扰动所致), 等离子体泡结构基本上是东西对称的. 但是当$\alpha = 0.1$ 时, 等离子体泡在上升到峰值高度附近时(大约为450 km), 其结构开始出现分叉现象(图8 中t = 2400 s). 当t = 2500 s时, 等离子体泡的分叉结构更加明显, 其结构也存在东西不对称性. 针对等离子体泡结构的分叉现象, Huang和Kelley[7 ] 通过重力波引入中性风的扰动, 在没有初始电子密度扰动的情况下模拟出了等离子体泡的分叉结构, Zalesak等[10 ] 在考虑了背景E层电导率的情况下, 也模拟出等离子泡的分叉结构, 但是其分叉结构是东西对称的. 图7 和图8 的对比结果表明, 等离子体的复合率对等离子体泡的结构存在重要的影响. 在二维等离子体泡的非线性模拟过程中, 电子离子化学复合率的选取可能是个比较重要的过程, 尽管对等离子体泡的生成影响不大, 但是对其结构特征具有明显的影响.图 7 $\alpha = 1$ 时TIDs产生等离子体泡的发展过程Figure7. Evolution of plasma bubbles caused by TIDs with $\alpha = 1$ .图 8 $\alpha = 0.1$ 时TIDs产生等离子体泡的发展过程Figure8. Evolution of plasma bubbles caused by TIDs with $\alpha = 0.1$ .图9 —图10 所示分别是$\alpha = 0.01$ 和$\alpha = 0$ 时, TIDs激发产生等离子体泡的过程. 从图9 的模拟结果发现, 从t = 2000 s的模拟结果开始, 在较大尺度的等离子体泡内部, 存在很多较小的等离子体泡结构. Huang和Kelley[7 ] 与Yokoyama等[28 ] 的模拟结果中也存在大尺度结构内部的多个小尺度等离子体泡结构, 但是上述结果是通过人为加入小尺度扰动产生的, 而本文出现的小尺度等离子体泡结构并没有人为引入小尺度扰动. 图9 中t = 2350 s模拟结果显示, 小尺度等离子体泡在发展过程中, 其底部出现收缩现象, 这种等离子体泡底部收缩的现象在以前的二维等离子体泡的模拟研究中没有出现过, 而在三维的等离子体泡的模拟过程中出现过[14 ] . 从图10 的模拟结果发现等离子体泡的底部收缩现象更加明显. 另外, 图10 的模拟结果显示其产生的小尺度等离子体泡结构也比图9 更加丰富, 并且等离子体泡内部的电子密度梯度比图9 更大. 图9 —图10 的模拟结果表明, 虽然在电离层底部会产生大量的小尺度等离子体泡, 但是并不是所有的小尺度结构都能够发展演化到电离层顶部, 只有部分等离子体泡结构才能够最终抬升到电离层顶部. 这主要是在等离子体泡的非线性演化过程中, 等离子体泡周围极化电场方向的不一致性导致的, 如果等离子体泡周围的极化电场方向一直是东向的, 则促进其发展, 如果在非线性演化过程中, 其周围极化电场转化成西向的, 则会抑制其进一步发展. 从图9 —图10 的模拟结果看, 在二维等离子体泡的模拟过程中, 选取比以前工作[9 ] 更低的电子离子化学复合率, 似乎更符合实际情况.图 9 $\alpha = 0.01$ 时TIDs产生等离子体泡的发展过程Figure9. Evolution of plasma bubbles caused by TIDs with $\alpha = 0.01$ .图 10 $\alpha = 0$ 时TIDs产生等离子体泡的发展过程Figure10. Evolution of plasma bubbles caused by TIDs with $\alpha = 0$ .4.结 论 本文模拟了TIDs激发产生的赤道等离子体泡的非线性发展过程, 在TIDs的模型中引入扰动的水平和垂直方向的参数相关性, 以使扰动更接近真实状态. 从模拟结果得出主要结论如下: 








































 图 1 水平东向电场值随高度的变化
图 1 水平东向电场值随高度的变化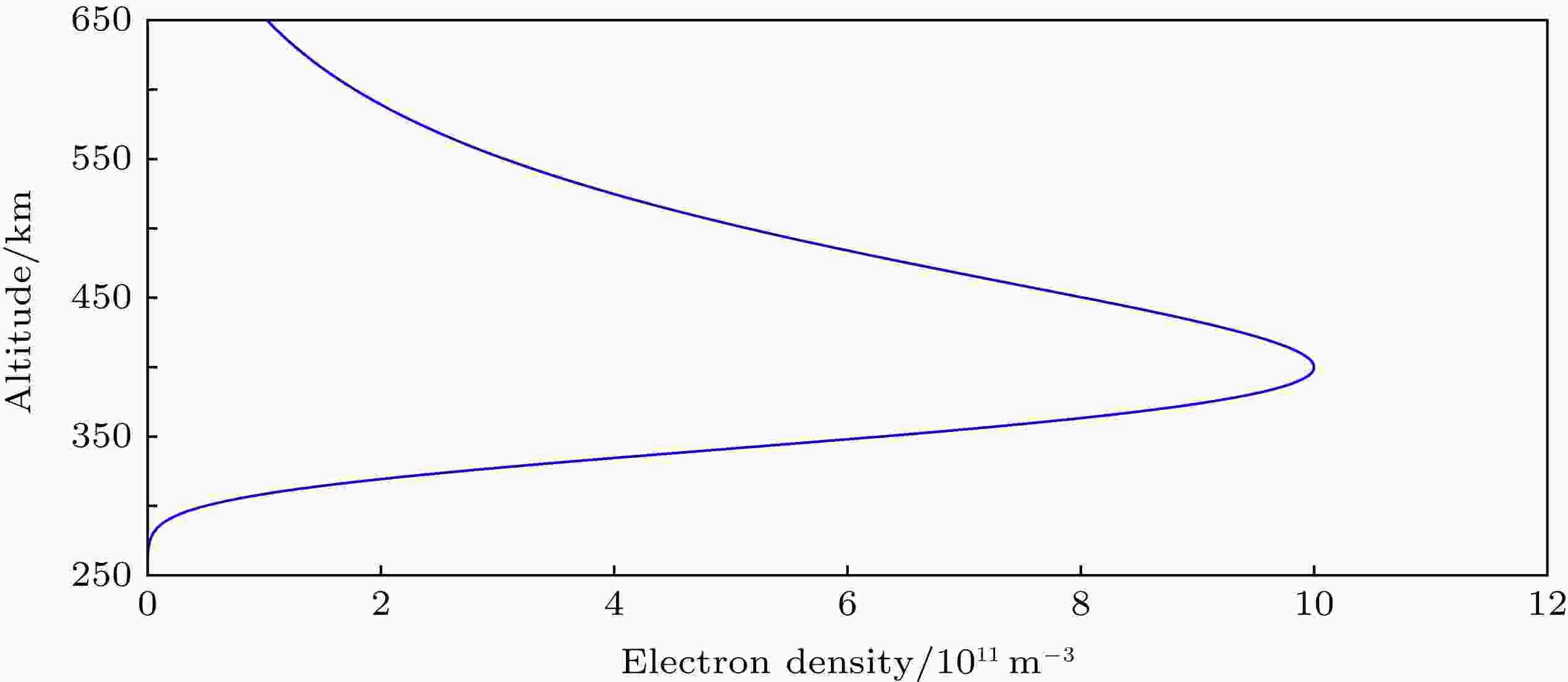 图 2 背景电离层电子密度剖面
图 2 背景电离层电子密度剖面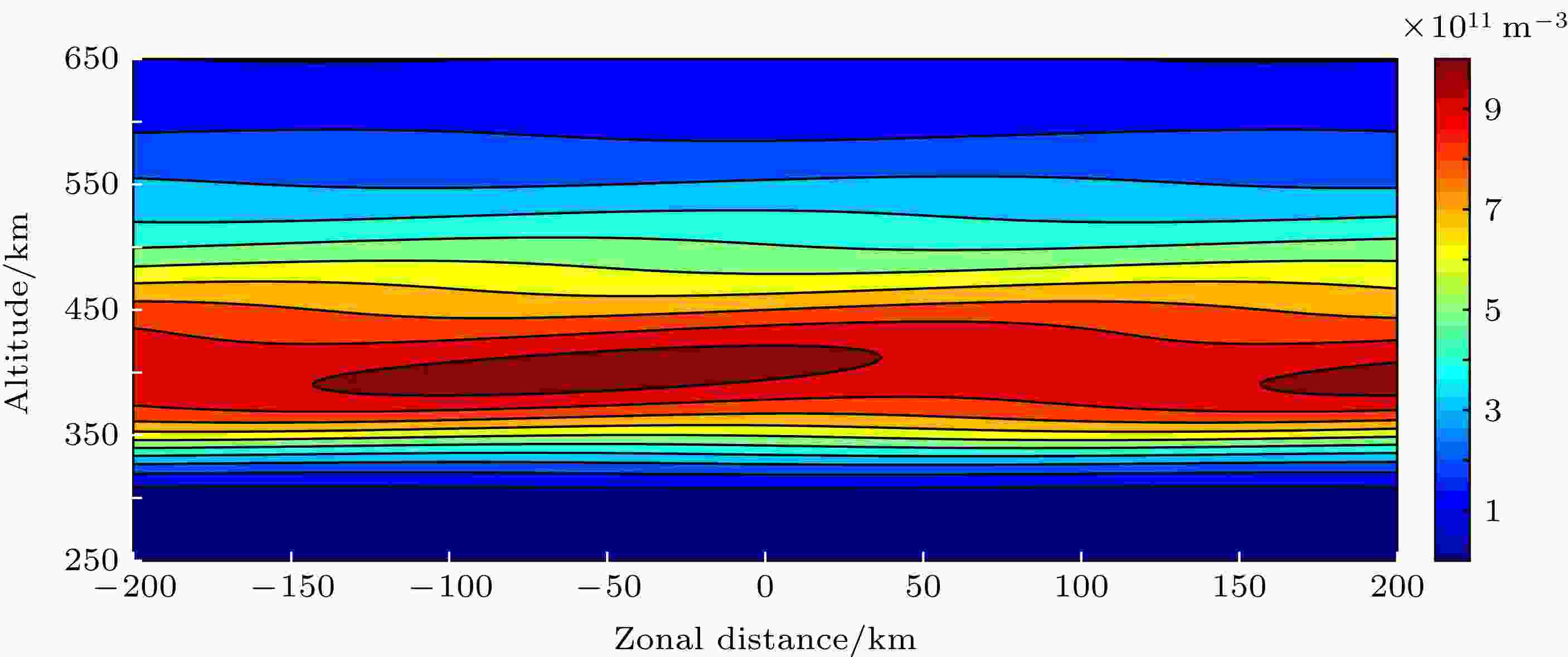 图 3 存在TIDs(波长为300 km, 周期为40 min)扰动的背景电离层
图 3 存在TIDs(波长为300 km, 周期为40 min)扰动的背景电离层





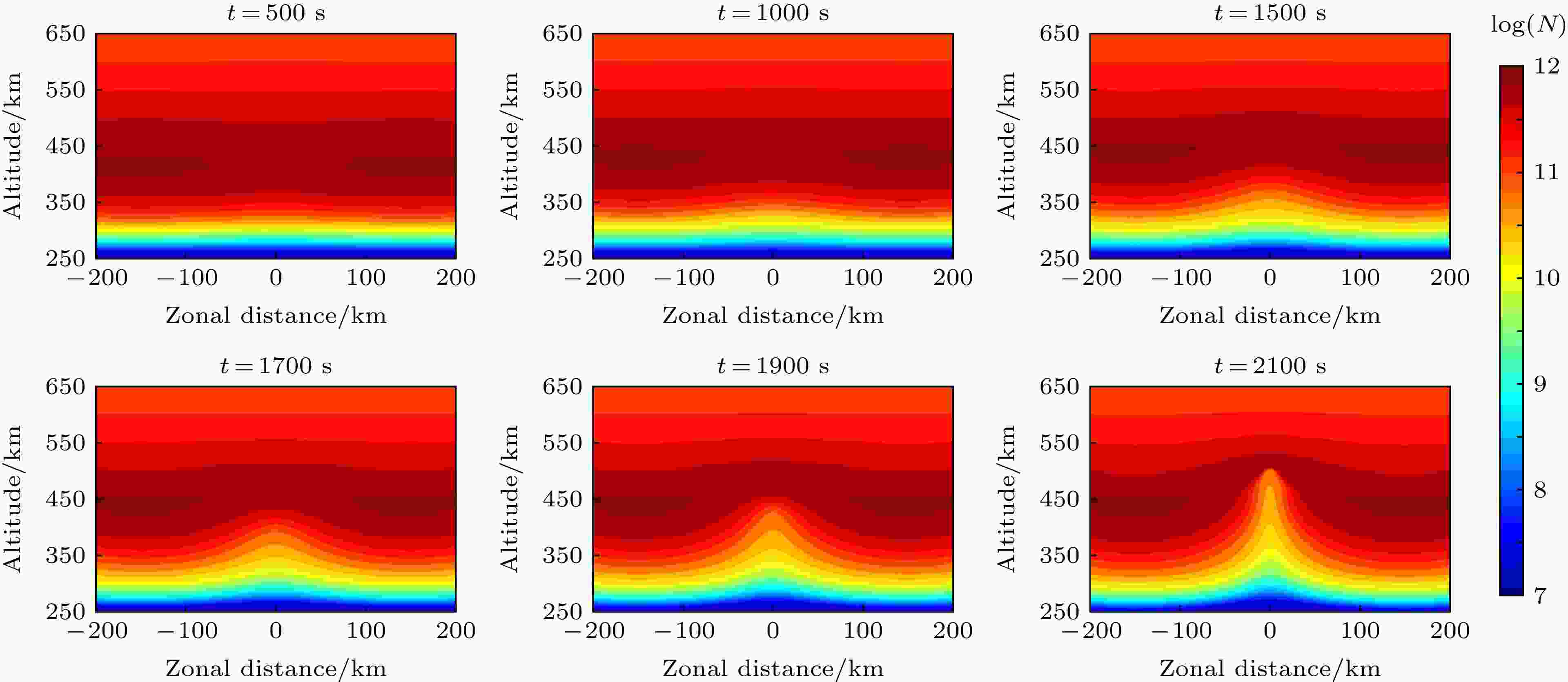 图 4
图 4 

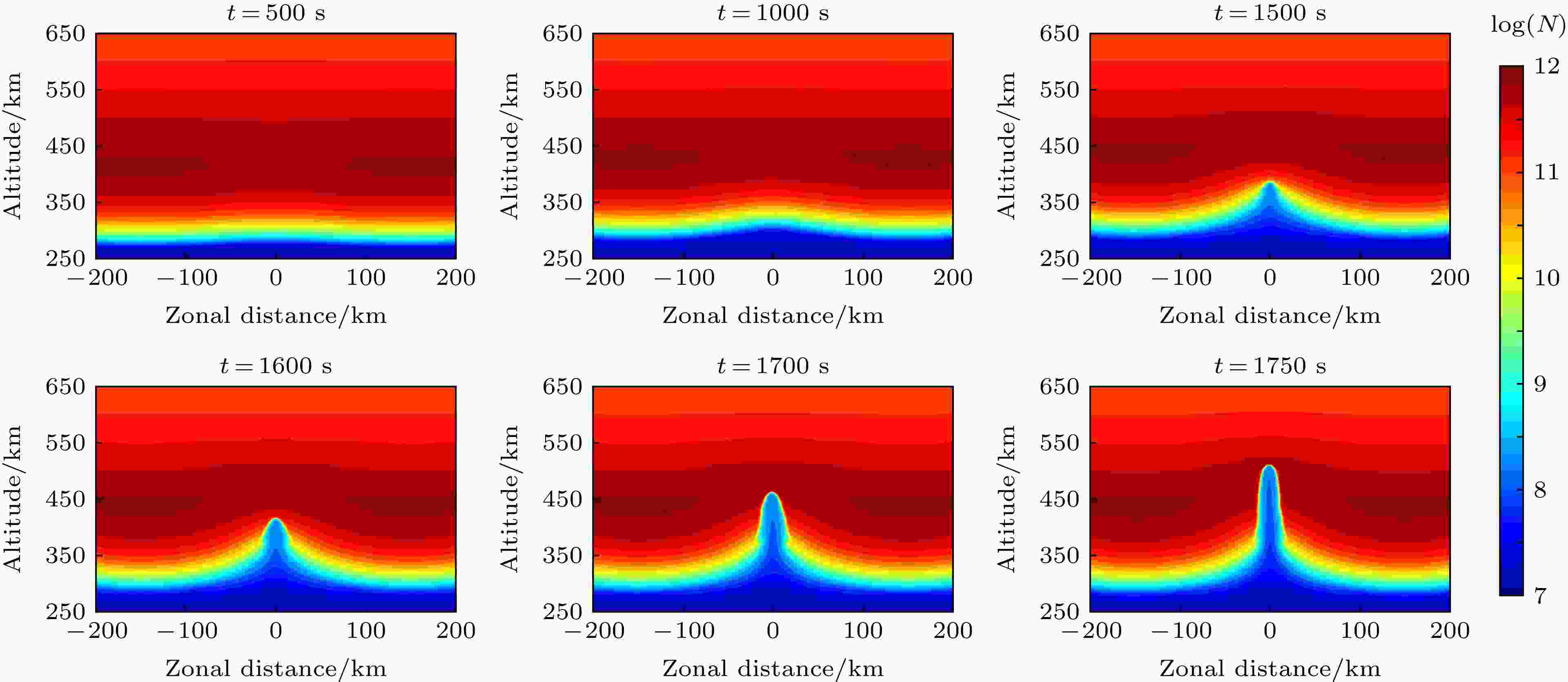 图 6
图 6 

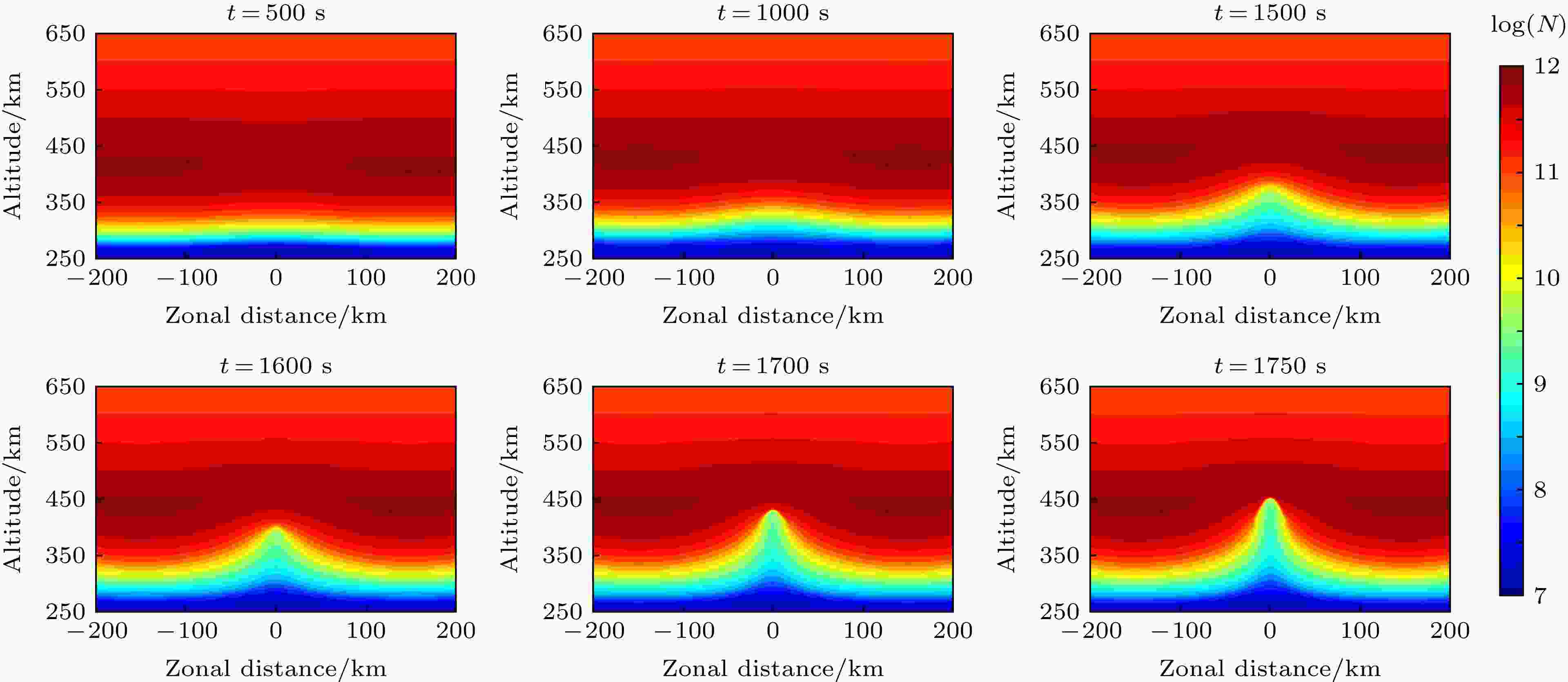 图 5
图 5 







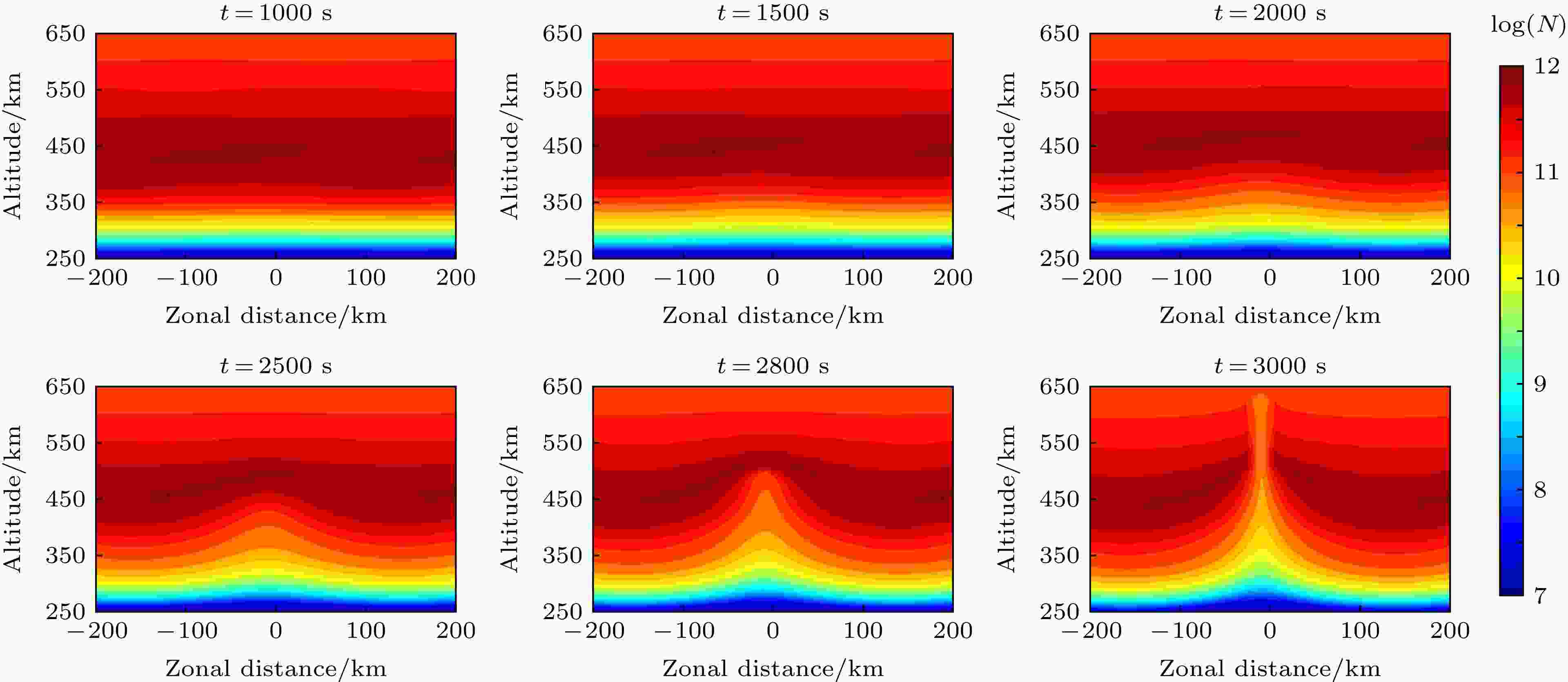 图 7
图 7 

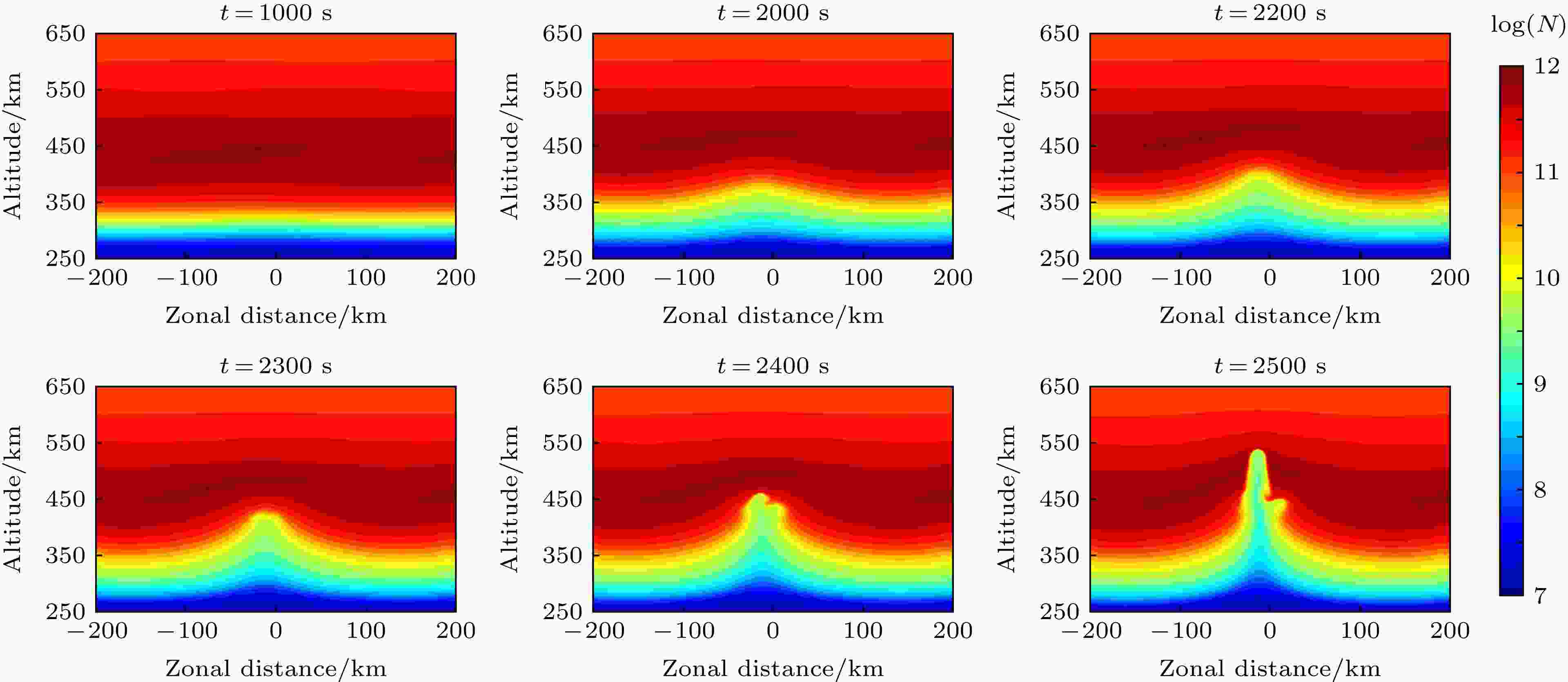 图 8
图 8 



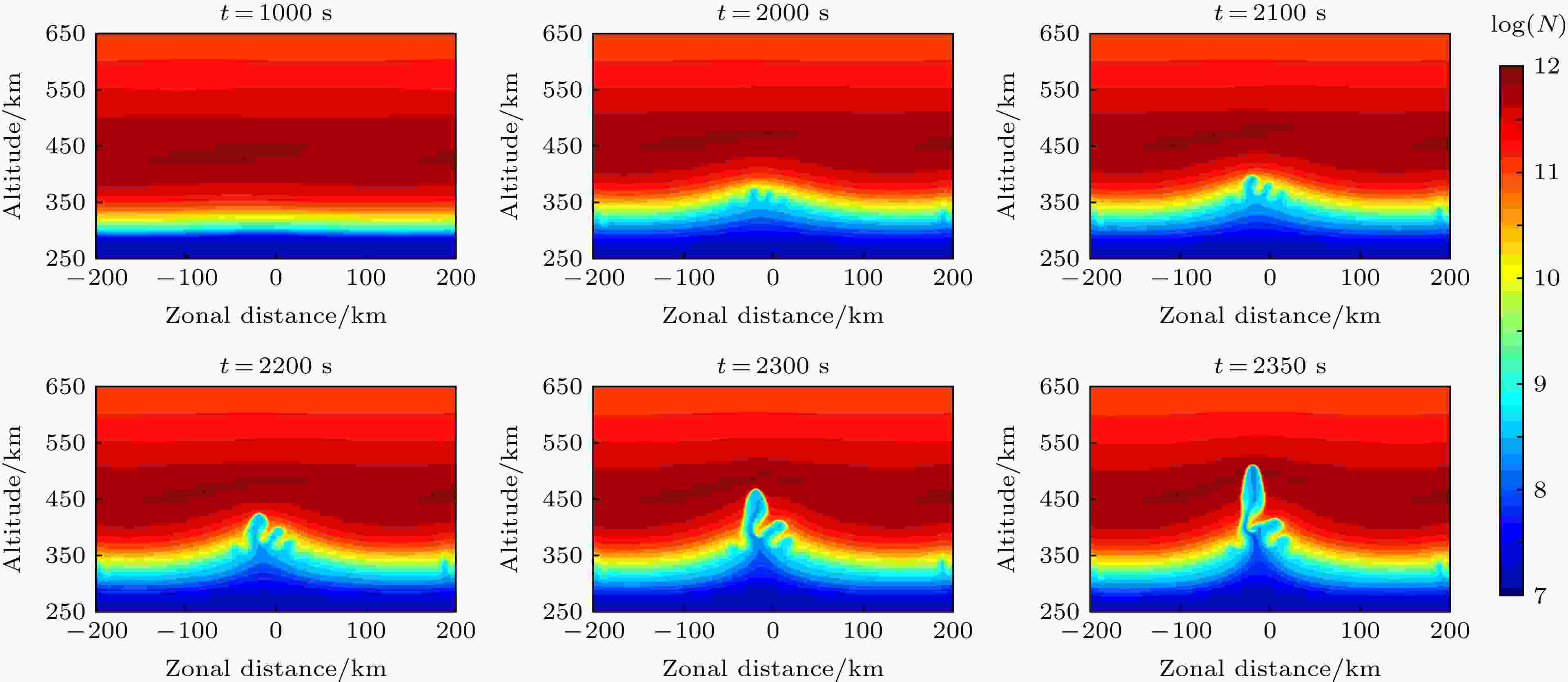 图 9
图 9 

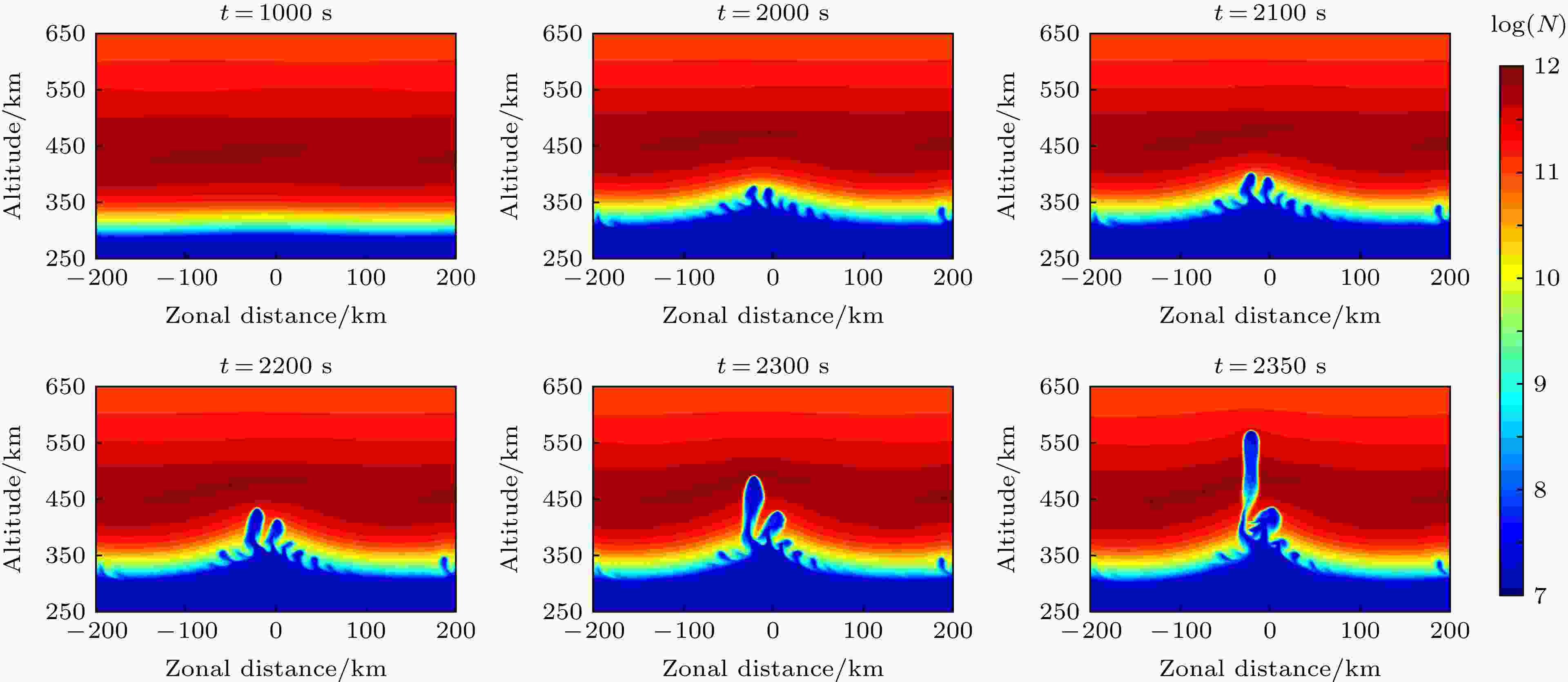 图 10
图 10 

