摘要:采用基于密度泛函理论的第一性原理方法计算了λ和β相Ti₃O₅的电子结构、弹性性质和光学性质. 这两相间的相变可以被光、热、压力、电流等多种方式驱动, 在光学存储以及热能存储领域都有广泛的应用前景. 本文报道了这两相一系列的弹性常数. 计算发现, 两相间的光吸收及光反射性质具有很大差异. 同时提出了两相间的光致相变机制是由受激辐射效应决定的构想.
关键词: Ti₃O₅/
第一性原理/
弹性性质/
电子结构

English Abstract

全文HTML

--> --> -->

信息技术是21世纪的重要技术, 而信息的存储与处理则是信息技术的核心. 随着当今信息的多媒体化和网络通讯的发展, 人们对数据存储的要求越来越高, 信息技术的发展将在信息存储领域兴起. 因此, 对信息存储材料的研究成为了新世纪的研究重点. 光存储是自磁存储和半导体存储后兴起的一种重要的信息存储技术, 其原理是将具有高度相干性和单色性的激光束照射在光衍射极限的斑点上, 使这个斑点区域内的记录介质发生物理或化学变化, 导致该斑点区域的某种光学性质与周围介质出现较大的反衬度, 从而实现信息的存储和读出. 如果按照工作原理划分的话, 光存储无机材料可以分为三类: 热分解存储材料, 如AgO_x, NiO_x, CrO_x^[1]等; 化学反应存储材料, 如WO_x, ZnO, Ga₂O₃, In₂O₃^[2]等; 相变存储型材料, 主要以BiFeO^[3], Ge-Sb-Te^[4]系和Ag-In-Sb-Te^[5]系相变材料为主. 其中, 热分解与化学反应存储材料存在可控性差以及使用寿命较短等缺点, 而相变存储材料具有非易失性、低功耗、低成本、循环寿命长、高速读取、多级存储和元器件可纳米化等诸多优点, 是极有潜力的一类光存储材料. Ge-Sb-Te系合金是目前研究得最多和应用最成熟的光相变存储材料, 如我们常用的DVD和蓝光光盘, 通常便是以Ge-Sb-Te合金为原料生产的, 但是其具有成本高和存储容量较小的缺点, 因此人们便将目光投向了新的光存储相变材料的研发.
自λ-Ti₃O₅和β-Ti₃O₅之间存在光致可逆相变被发现以来^[6], 其在光学存储领域的应用前景就引起了广泛的关注^[7—17]. 这种材料存在超快速的光致相变现象, Ould-Hamouda等^[11]发现λ向β的转变只需900 ns, 而在20 ns内就观察到了β向λ的转变, Asahara等^[12]在几百飞秒内就观察到了β向λ的转变. λ为金属相, 而β为半导体相, 两相间存在较大的光学和电学差异性, 有望成为新一代光相变存储器记录材料. 当制备得到的λ纳米结晶颗粒粒径达到20 nm时, 如果将其应用于光盘存储, 其存储密度就可达到1 Tbit/inch², 是DVD光盘的200倍^[6]; 而当前的研究报道中已成功制备了粒径尺寸小于8 nm的λ-Ti₃O₅, 预计其存储密度将达到10 Tbit/inch^2[10], 其存储量将远大于目前光存储中应用的蓝光光盘, 而作为廉价的钛氧化物其成本将远低于目前常用的Ge-Sb-Te材料.
除此之外, Tokoro等^[18]发现λ-Ti₃O₅在一定的温度范围内可以长期存储潜热, 而在室温下施加一定的压力时迅速释放热能并转变为β相. 因此, λ-Ti₃O₅作为热存储材料具有随取随用所存储热能的优点. 考虑到这两相之间存在如此多种驱动方式的相变, 对这两相的研究能够使我们对相变现象产生更深的理解.
一些研究^[6,18,19]已经报道了这两种结构的晶体构成以及制备方式. 然而, 对这两相的电子、弹性以及光学性质的研究还不充分, 本文采用密度泛函理论^[20,21]对λ和β相进行了系统的研究. 首先采用多种方法计算了这两相的晶体结构. 用最精确的方法进一步进行了计算, 比较了两相的晶体结构、电子和光学特性.

我们采用vasp软件对两相进行计算. 交换关联势采用LDA, GGA, PW91, RP, PS等多种泛函. 为描述Ti的3d电子间的强相互作用, 在LDA和GGA泛函计算中加入了Hubbard参数U. 布里渊区的K点网格划分采用Monkhorst-Pack^[22]方法. K点选取为3 × 7 × 3, 截断能为800 eV. 计算采用的超胞如图1所示, λ和β分别包含12个Ti原子和20个O原子. 灰色圆球表示Ti原子, 红色圆球表示O原子. λ和β相是单斜晶体, 其空间群为C2/m.
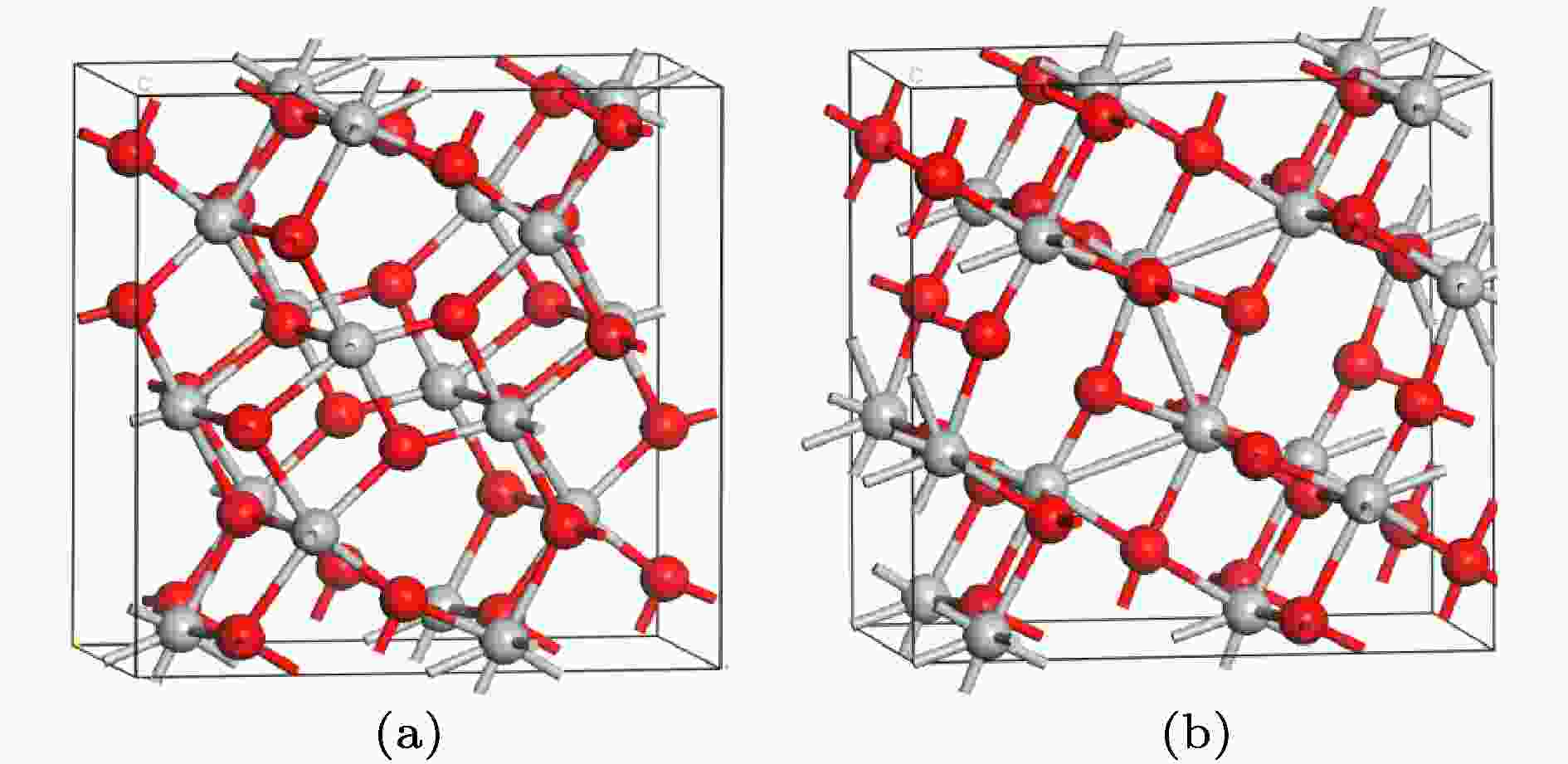图 1 (a) λ-Ti₃O₅和(b) β-Ti₃O₅的晶体结构
Figure1. Crystal structures of (a) λ-Ti₃O₅ and (b) β-Ti₃O₅.

2

-->

3.1.U值和晶格参数测试

采用禁带宽度来表现β的半导体性质, U = 5 eV时, GGA + U方法所得到的禁带宽度为0.14 eV, 与实验报道一致^[6]. 然而当采用LSDA + U方法时, 本文使用Liu等^[23]建议的U = 5 eV和Olguin等^[24]建议的U = 7 eV时均未能得到符合实验值的禁带宽度. 因此, 我们采用了一系列的U值来计算β相的禁带宽度, 如图2所示. 当U = 6.5 eV时, 采用LSDA + U方法计算得到的禁带宽度与实验值相符. 计算得到的两相晶格参数列于表1. 由于U值的影响所得到的晶格参数有所增加. LSDA + U计算得到的晶格参数与实验值符合最好. 因此, 采用LSDA + U方法进行后续计算.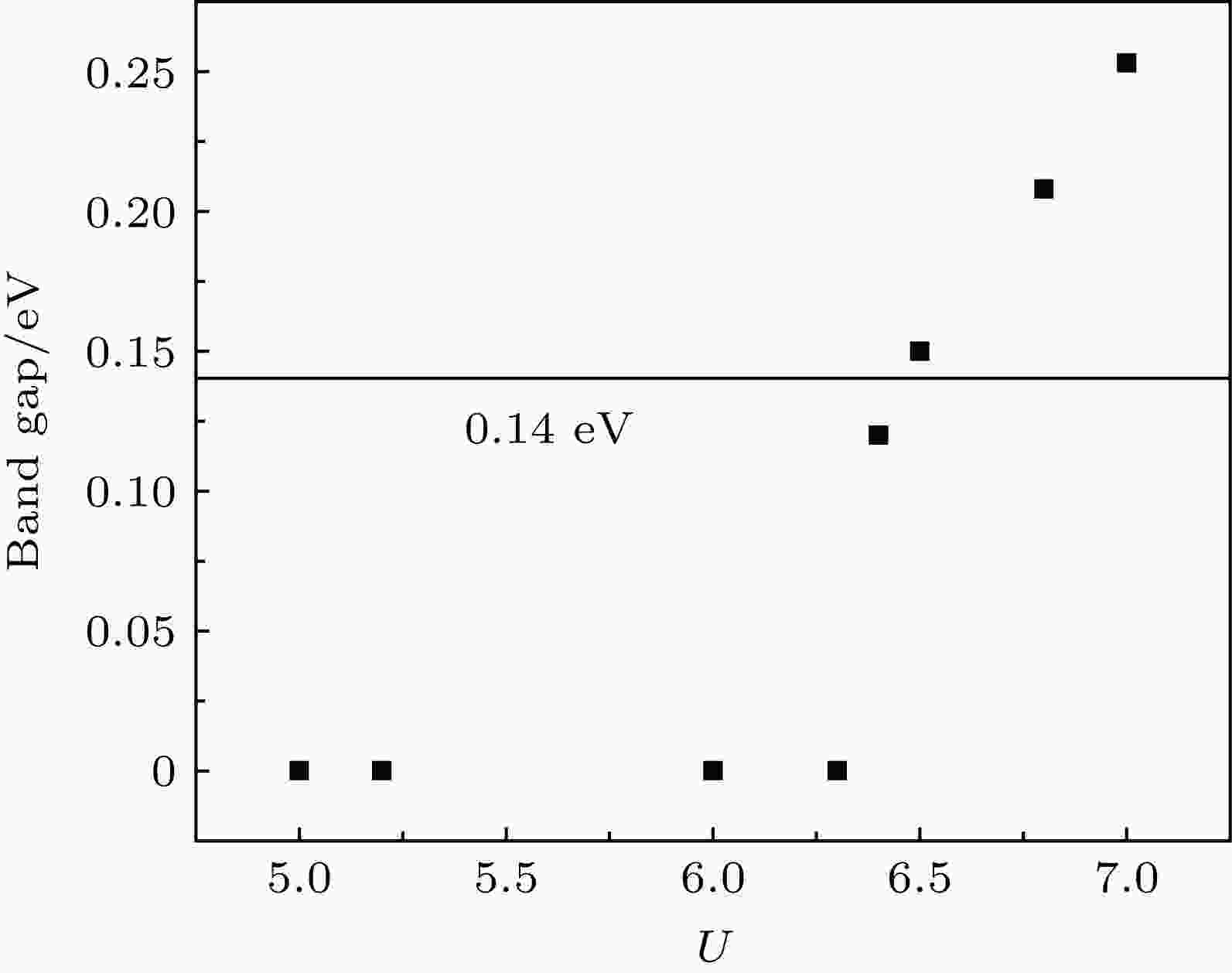
图 2 LSDA泛函计算得到的β-Ti₃O₅的禁带宽度随U值的变化
Figure2. The band gap of β-Ti₃O₅ calculated by LSDA as a function of U values.

		a/?	b/?	c/?	Ref.
λ-Ti3O5	exp.	9.84	3.79	9.99	[6]
		9.84	3.79	9.97	[6]
		9.83	3.79	9.97	[18]
	LSDA + U	10.02	3.90	10.15
	GGA-PBE + U	10.23	3.96	10.39
	GGA-91 + U	10.22	3.95	10.38
	GGA-PS + U	10.22	3.96	10.38
	GGA-RP + U	10.32	3.98	10.49
β-Ti3O5	exp.	9.75	3.80	9.44	[19]
		9.75	3.80	9.44	[18]
	LSDA + U	9.92	3.94	9.67
	GGA-PBE + U	10.37	4.03	9.79
	GGA-91 + U	10.35	4.03	9.79
	GGA-PS + U	10.25	4.00	9.66
	GGA-RP + U	10.45	4.06	9.90

表1计算得到的晶格常数
Table1.Calculated lattice parameters.

2 -->

3.2.弹性性质

Wu等^[25]采用公式d = d₀ + k_d × P描述β的轴压缩性, d₀为0 GPa下的晶格常数, k_d为轴压缩系数, P为压力. 其得到的轴压缩系数为: k_a = –0.022 ?/GPa, k_b = –0.0006 ?/GPa, k_c = –0.0171 ?/GPa, 说明b轴最难压缩而a轴最易压缩. 本文计算得到的弹性常数C₁₁ = 207.4 GPa, C₂₂ = 428.1 GPa, C₃₃ = 334.5 GPa, 如表2所列. C₂₂即晶体b轴方向的弹性常数要大于C₁₁和C₃₃, 与Wu等的结论一致.

	C11	C22	C33	C44	C55	C66	C12	C13	C15	C25	C35	C46	C23
λ-Ti3O5	262.7	342.5	283.2	56.3	87.7	25.5	142.8	109.2	–20.4	–9.4	0.3	–2.0	113.9
β-Ti3O5	207.4	428.1	334.5	50.0	93.0	10.6	114.8	101.6	–4.5	4.6	30.8	–8.7	94.6

表2计算得到的弹性常数(单位为GPa)
Table2.Calculated elastic constants (C_ij in GPa).

弹性常数可以提供关于两相结构各向异性的信息. C₁₁, C₂₂和C₃₃比其他弹性常数大得多, 说明两相是弹性各向异性的. 对于β相, C₃₃比C₁₁大得多, 而λ相中C₁₁和C₃₃很接近, 说明在(010)晶面上, λ相的弹性各向异性要比β相弱. λ相和β相晶体结构的稳定性需要它们的弹性常数满足Born稳定性判据^[26,27]:

$\begin{split} & {C_{ii}} > 0\left( {i = 1\text{---}6} \right),\;\left( {{C_{22}} + {C_{33}} - 2{C_{23}}} \right) > 0,~~\left( {{C_{33}}{C_{55}} - C_{35}^2} \right) > 0, ~~ \left( {{C_{44}}{C_{66}} - C_{46}^2} \right) > 0, \\ & \left( {{C_{11}} + {C_{22}} + {C_{33}} + 2{C_{12}} + 2{C_{13}} + 2{C_{23}}} \right) > 0, ~~\left[ {{C_{22}}\left( {{C_{33}}{C_{55}} - C_{35}^2} \right) + 2{C_{23}}{C_{25}}{C_{35}}} \right. \left. { - C_{23}^2{C_{55}} - C_{25}^2{C_{33}}} \right] > 0,\\ & 2 \left[ {{C_{15}}{C_{25}}\left( {{C_{33}}{C_{12}} - {C_{13}}{C_{23}}} \right)} \right. + {C_{15}}{C_{35}}\left( {{C_{22}}{C_{13}} - {C_{12}}{C_{23}}} \right) \left. { + {C_{25}}{C_{35}}\left( {{C_{11}}{C_{23}} - {C_{12}}{C_{13}}} \right)} \right] - \left[ {C_{15}^2\left( {{C_{22}}{C_{33}} - C_{23}^2} \right)} \right.\\ & \left. { + C_{25}^2\left( {{C_{11}}{C_{33}} \!-\! C_{13}^2} \right) \!+\! C_{35}^2\left( {{C_{11}}{C_{22}} \!-\! C_{12}^2} \right)} \right] \!+\! {C_{55}}\left( {{C_{11}}{C_{22}}{C_{33}} \!-\! {C_{11}}C_{23}^2 \!-\! {C_{22}}C_{13}^2} \right. \left. { \!- {C_{33}}C_{12}^2 \!+\! 2{C_{12}}{C_{13}}{C_{23}}} \right) > 0.\end{split}$

计算得到的弹性常数满足(1)式, 说明λ相和β相是结构稳定的. 本文中, 我们使用Voigt-Reuss-Hill方法^[28]计算了体积模量B_H, 剪切模量G_H, 杨氏模量Y_H以及泊松比ν, 如表3所列. Asbrink等^[29]采用Murnaghan公式拟合得到了β相的体积模量B_M = (173 ± 10) GPa. Wu等^[25]采用三阶Birch-Murnaghan公式得到了β相随压力变化的体积模量B_BM = (216 ± 9) GPa. 本文中, 第一性原理计算得到的体积模量为B_H = 187.4 GPa, 这个数值基本上为Asbrink等和Wu等结果的平均值. 计算得到的体积模量B_H比杨氏模量Y_H和剪切模量G_H大得多, 说明这两相相对于形状改变更倾向于抵抗体积变化. B_H/G_H值可以说明固体的脆韧性特征^[30], 计算得到的两相B_H/G_H值都大于标准判据值(1.75), 表现为韧性材料. λ相的杨氏模量Y_H大于β相, 而泊松比ν小于β相, 说明λ相的硬度比β相高.

	BH	GH	YH	ν	BH/GH
λ-Ti3O5	210.8	63.4	173.0	0.36	3.32
β-Ti3O5	187.4	52.8	144.8	0.37	3.54

表3计算得到的体积模量(B_H, GPa), 剪切模量(G_H, GPa), 杨氏模量(Y_H, GPa)和泊松比(ν)
Table3.Calculated bulk modulus (B_H, in GPa), shear modulus (G_H, in GPa), Young's modulus (Y_H, in GPa) and Poisson's ratio (ν).

2 -->

3.3.电子结构

图3所示为λ和β相的能带结构和态密度. 在–2 eV到费米能级之间λ相有一个自旋向上的峰, 而β相有两个自旋向上峰. 该区域内β相的能带表现较为分散而λ相的能带较为聚集. 因此, 该区域内λ相的电子比β相要更容易发生带间转移. 除此外, β相在–1.5 eV处有一个又大又窄的局域峰, 说明β相是一个电荷局域系统, 这与其表现半导体性质相符. 相比之下, λ相对比β相表现为电荷非局域系统, 因此表现为金属相特征.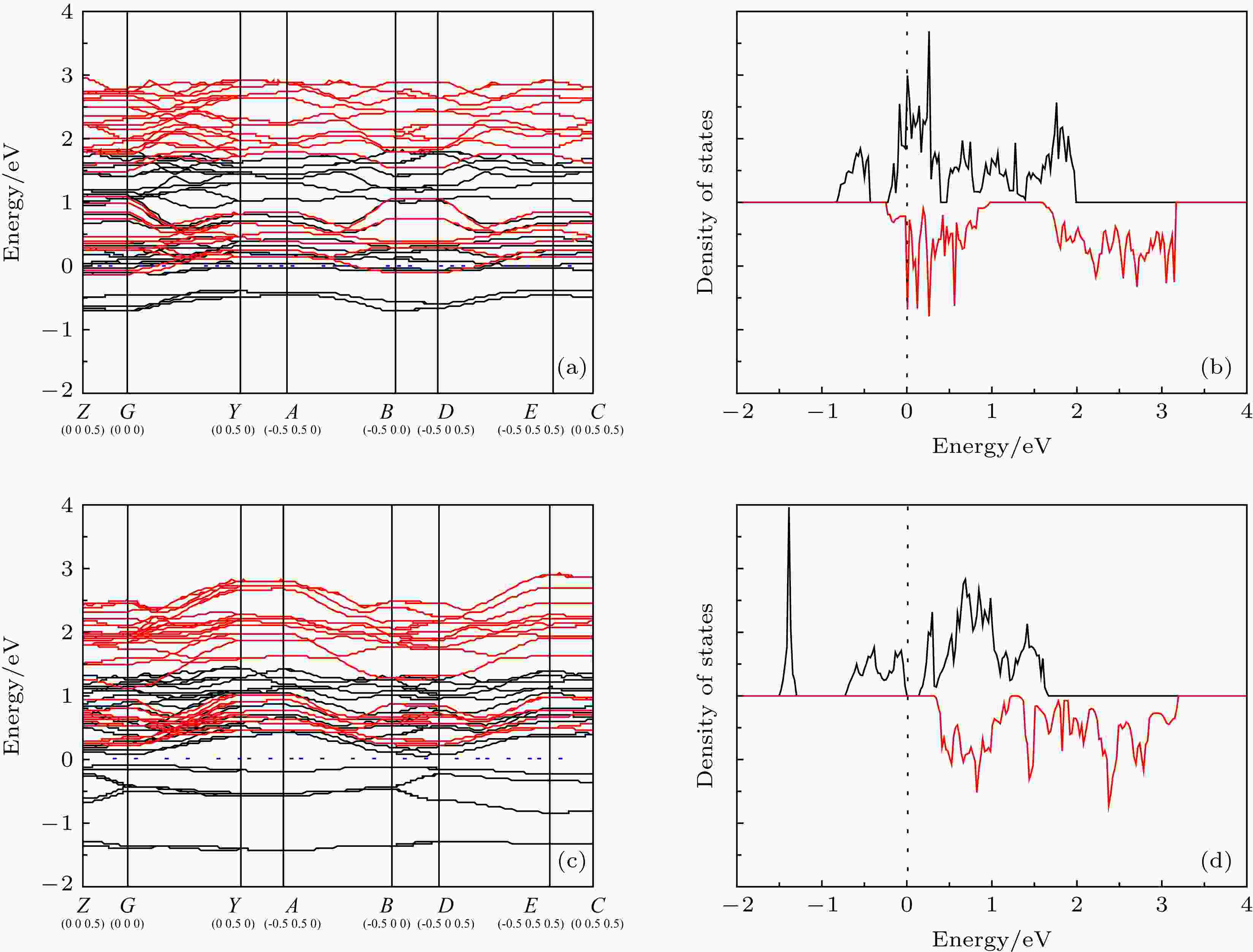
图 3 λ-Ti₃O₅的(a)能带结构和(b)态密度以及β-Ti₃O₅的(c)能带结构和(d)态密度
Figure3. The calculated (a) band structure and (b) total density of states of λ-Ti₃O₅; the calculated (c) band structure and (d) total density of states of β-Ti₃O₅.

图4为两相的分态密度图. 对于β相, 在–1.5 eV处同时出现了一个Ti-3d态窄峰和一个O-2p态窄峰. 它们共同构成了β相中又大又窄的局域峰(见图3(d)). 这个杂化峰说明β相具有比λ相更强的共价键特征. 因此, λ相的金属相特征更明显而β相的半导体特征更明显. 如图4(b)所示, 费米能级附近的Ti-3d态可以分为两部分: 在1 eV处对称的自旋向上和自旋向下态, 以及2.5 eV处单独的自旋向下态. 而在图4(a)中, 对称的自旋态下降到了费米能级处, 而单独的自旋向下态上移到了能量更高的区域. 这个现象可以用Jahn-Teller效应^[31]来解释. 随着β相转变为λ相, 系统中的晶体场结构扭曲, Ti-3d态发生退简并, 因此其3d轨道劈裂为了一个高能量部分和一个低能量部分.
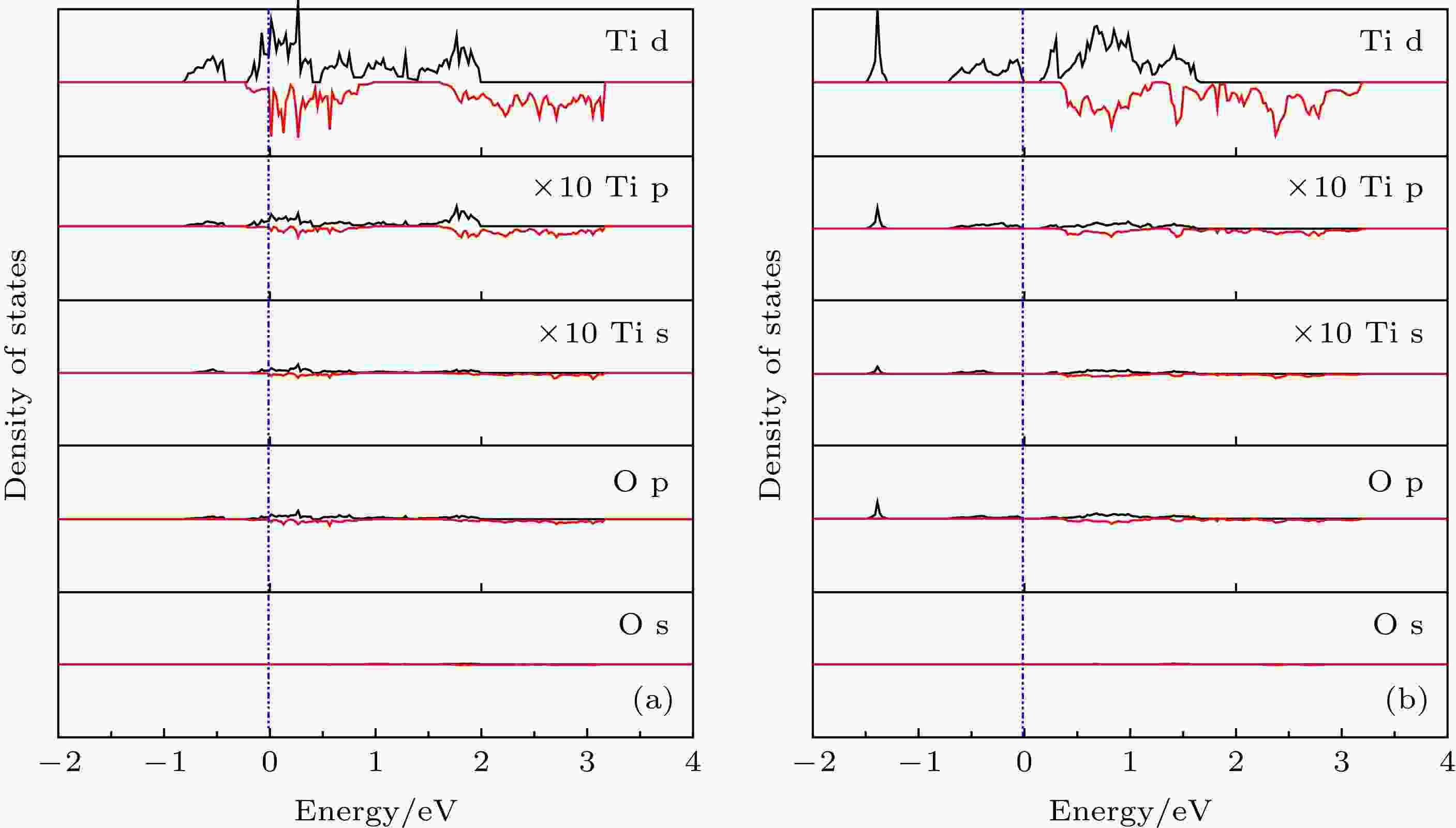图 4 (a) λ-Ti₃O₅和(b) β-Ti₃O₅ 的分态密度
Figure4. The partial density of states for (a) λ-Ti₃O₅ and (b) β-Ti₃O₅.

为进一步描述两相的电子结构, 计算了(010)晶面的差分电荷密度, 如图5所示,红色代表得到电子, 蓝色表示失去电子. 如图5(a)所示, λ相中Ti₃失去了最多电子. 如图5(b)所示, β相中Ti₂失去了最多电子. 这与Ohkoshi等^[6]给出的Ti离子价态数相符合(λ相中Ti₁, Ti₂和Ti₃的价态分别为+3.37, +3.20和 +3.53; β相中Ti₁, Ti₂和Ti₃的价态分别为+3.00, +3.79和 +3.32). 实际上, 两相电子结构的差异主要是由Ti₁, Ti₂和Ti₃的状态变化决定. 对图5中电荷状态的分析, 我们得到了和Tokoro等^[18]一样的结论: Ti₃上的局域电荷转移到了Ti₂上, 导致了半导体β相向金属λ相的转变.
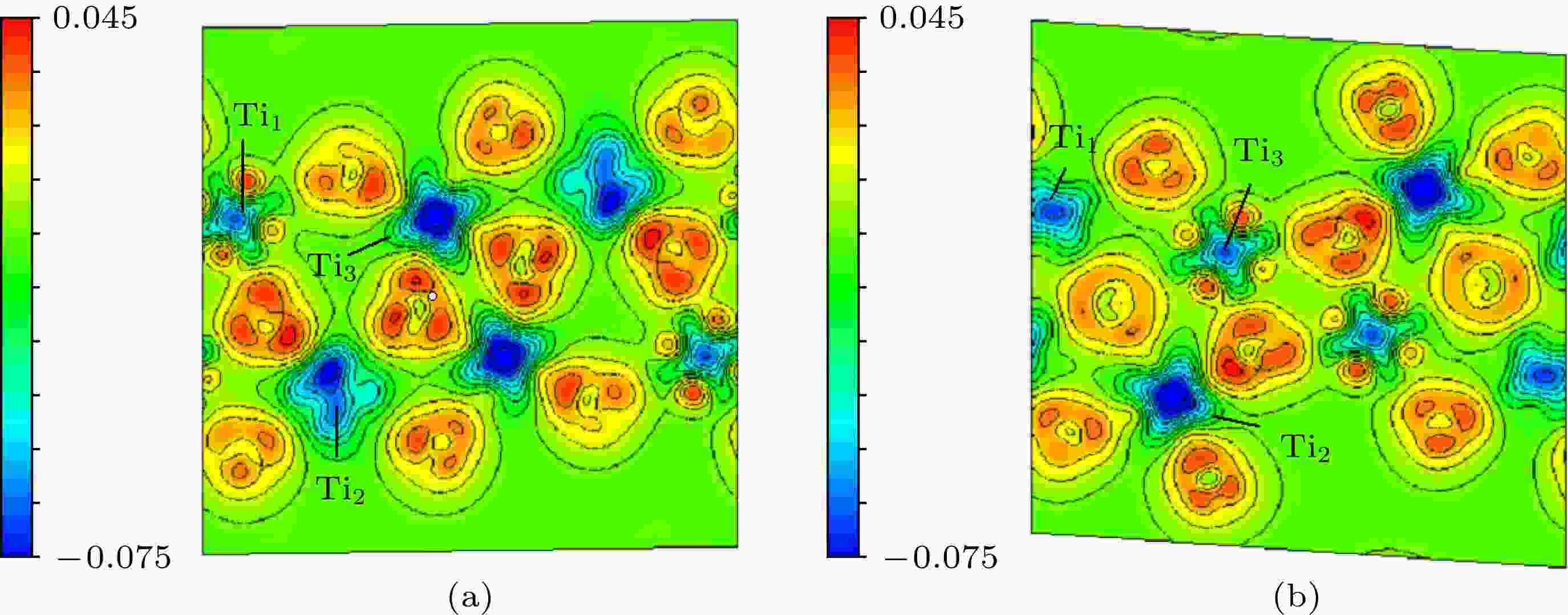图 5 (a) λ-Ti₃O₅和(b) β-Ti₃O₅的(010)晶面上的差分电荷密度
Figure5. The calculated charge density differences of (010) plane for (a) λ-Ti₃O₅ and (b) β-Ti₃O₅.

2 -->

3.4.光学性质

图6为两相的光吸收以及反射率谱图. 从整体上来看, 两相的光吸收能力相差不大. 在425—570 nm波长内, β相的光吸收能力要高于λ相, 而在更高的波长范围内却出现了相反的趋势. 在低于250 nm和450—570 nm范围内, β相的反射系数高于λ相. 而在250—450 nm和高于570 nm范围内, λ相的反射系数高于β相. 这两相间的反射系数差异使得它们可以应用于光学存储材料领域.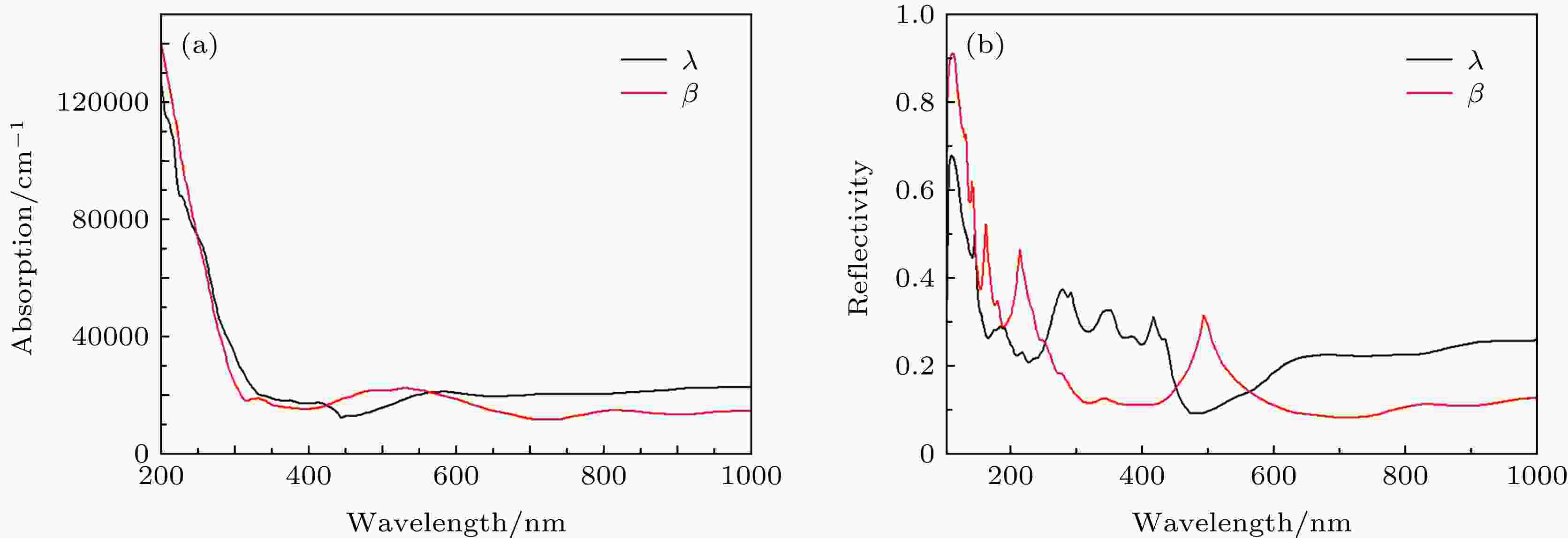
图 6 λ-Ti₃O₅和β-Ti₃O₅的光吸收以及反射率谱图
Figure6. The calculated absorption spectra and reflection coefficients of λ-Ti₃O₅ and β-Ti₃O₅.

为分析两相间的光致相变, 我们描绘了两相费米能级附近的能带结构, 如图7所示. 相变过程发生前后体系的变化可以分为原子排列方式的变化和电子结构的变化两部分, 该体系中的相变属于一级相变, 因此原子排列方式和电子结构都有所变化.考虑到电子结构的状态变化要先于晶体结构的变化发生, 因而, 电子结构受到外界作用后将会把这种扰动作用体现在晶体结构的变化上, 而晶体结构的变化又会反过来影响电子结构的状态, 而相变正是在这样不断互相影响的过程中进行. 基于此观点, 激光诱发相变的过程中β相E₁价带上的电子受到光激发后将会发生跃迁, 由于β相E₂导带上没有电子占据, 而E₁上的电子不可能无限制的过量跃迁, 因此在光激发过程中, E₁上的电子数无法大于E₂上的电子数, 无法满足受激辐射效应的基本条件, 故而, β→λ相的转变过程属于常见的电子结构变化引起晶体结构变化, 在电子结构和晶体结构交互影响变化的过程中, 由于E₁上的电子持续受到激发跃迁至E₂, 因此这个过程中E₁和E₂上都有电子存在, 此时如果单独定义某个瞬时态, 费米能级要向高能量的方向移动, 这个过程中若某个瞬时态达到了能量极小值, 体系的结构将会稳定下来形成λ相, 故而就形成了λ相的这种能带结构状态. 而λ相的E₂能级上原本就有一定量的电子占据, 此时受到光激发后, E₁电子向E₂的跃迁会很容易造成E₂能级上的电子数多于E₁能级, 这样将会导致电子数分布反转, 满足受激辐射效应的基本条件, 若发生了受激辐射效应, E₂上的电子将会迅速向E₁上跃迁, 此时的费米能级将会向低能量方向移动, 当结构稳定下来后就会形成β相的这种能带结构状态. 除此之外, β相作为低温相具有较低的体系能量, 而λ相作为高温相具有较高的体系能量, 当一个光子入射到β相体系, 发生相变转化为λ相是满足能量守恒的, 而对于λ相体系, 若发生了受激辐射效应, 则一个光子入射后将会射出两个光子, 这样的解释也是满足能量守恒的. 故而我们提出了这样一种光相变机制: 如图7(b)所示, 价带E₁被电子满占据, 而导带E₂部分未被电子占据. 当β相受到激光照射, E₁上的电子吸收光子后跃迁至E₂后发生相变. 而λ相中部分E₂能带低于费米能级, 如图7(a)所示. 因此当λ相受到激光照射, E₁上的电子向E₂跃迁后, 可能会出现E₁和E₂能带上的电子数分布反转. 此时, 将会发生受激辐射效应, E₂上的电子受到激发跃迁至E₁, 同时释放出光子能量, 发生λ相向β相的转变.
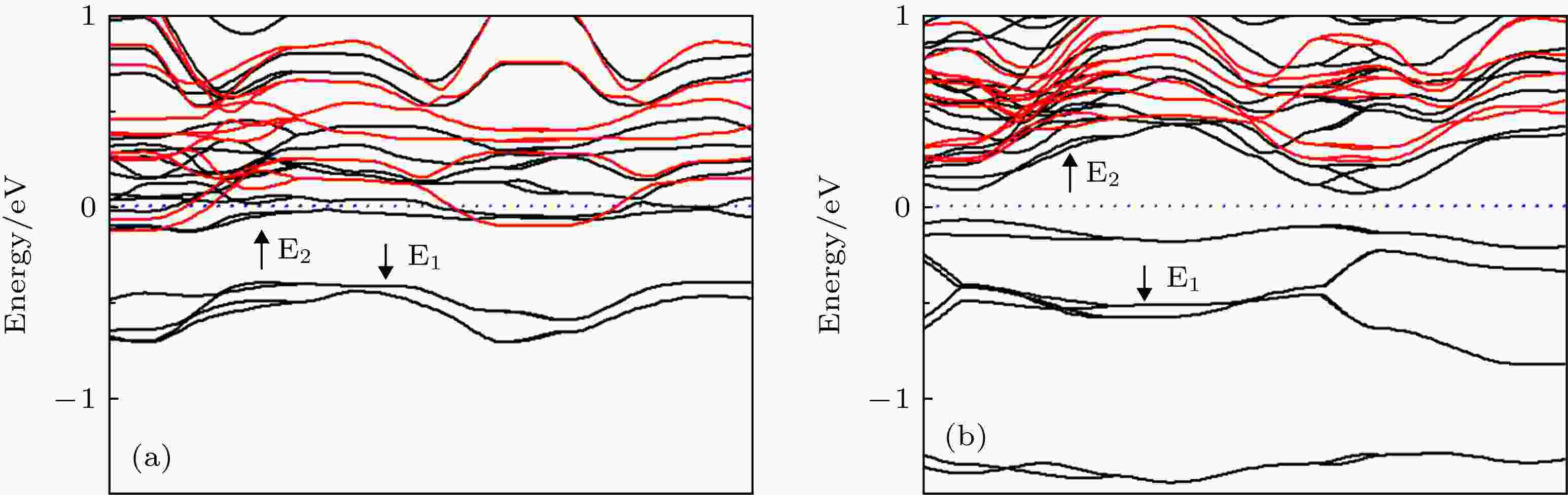图 7 (a) λ-Ti₃O₅和(b) β-Ti₃O₅费米能级附近的能带结构
Figure7. The band structures near the Fermi level of (a) λ-Ti₃O₅ and (b) β-Ti₃O₅.

对λ相和β相超胞结构进行了第一性原理计算. 选用了U = 6.5 eV的LSDA + U方法进行模拟. 计算了λ和β两相的弹性性质, 报道了一系列的弹性常数并给出了结构稳定性判据. 结果表明, 两相结构都满足Born稳定性判据且倾向于表现为韧性材料. 对电子结构的计算表明随着β相向λ相的转变, Ti₃上的局域电荷转移到了Ti₂上. 两相的光吸收和反射系数表现出差异, 表明它们在光学材料领域有潜在应用价值. 本文还提出了λ相到β相的光致转变与受激辐射效应相关的构想, 为理解λ相和β相间的光致相变现象提供了一条新的思路.